Integrative Analysis of Cancer Diagnosis Studies with Composite Penalization

Summary

In cancer diagnosis studies, high-throughput gene profiling has been extensively conducted, searching for genes whose expressions may serve as markers. Data generated from such studies have the “large d, small n” feature, with the number of genes profiled much larger than the sample size. Penalization has been extensively adopted for simultaneous estimation and marker selection. Because of small sample sizes, markers identified from the analysis of single datasets can be unsatisfactory. A cost-effective remedy is to conduct integrative analysis of multiple heterogeneous datasets. In this article, we investigate composite penalization methods for estimation and marker selection in integrative analysis. The proposed methods use the minimax concave penalty (MCP) as the outer penalty. Under the homogeneity model, the ridge penalty is adopted as the inner penalty. Under the heterogeneity model, the Lasso penalty and MCP are adopted as the inner penalty. Effective computational algorithms based on coordinate descent are developed. Numerical studies, including simulation and analysis of practical cancer datasets, show satisfactory performance of the proposed methods.

1. Introduction

In cancer research, high-throughput gene expression profiling studies have been extensively conducted, searching for markers that may assist diagnosis, prognosis prediction and treatment selection. In this article, we focus on diagnosis studies, where the response variables are categorical, for example, presence or absence of cancer or different stages of cancer. Data generated in high-throughput studies have the “large d, small n” characteristic, with the number of genes profiled d much larger than the sample size n. In addition, it is expected that in whole-genome studies, only a subset of the profiled genes are associated with the response variables. Thus, analysis of cancer high-throughput data demands regularized estimation as well as variable selection.

Among the available approaches, penalization has attracted extensive attention. The most popular penalization approach is Lasso, which, unfortunately, is not selection consistent in general (Zhang & Huang, 2008). Penalization approaches that may have better selection properties include adaptive Lasso, elastic net, bridge, smoothly clipped absolute deviation (SCAD), minimax concave penalty (MCP) and others. See Bühlmann & van de Geer (2011), Zhang (2010), Huang et al. (2011a) and references therein for more discussions. In recent studies, the “group” counterparts of these penalties have been developed. Here, a group is usually composed of multiple genes with coordinated biological functions or correlated expressions.

In practical data analysis, markers identified from the analysis of single datasets may be unsatisfactory. For example, they may suffer a lack of reproducibility and have unsatisfactory prediction performance. Multiple factors may contribute to the unsatisfactory performance, among which the most important one is the small sample sizes of individual studies. Recent studies suggest that pooling and analyzing data from multiple studies may increase sample size and so improve properties of the identified markers (Guerra & Goldsterin, 2009). Multi-dataset methods include meta-analysis and integrative analysis methods. Integrative analysis methods pool and analyze raw data from multiple studies and can be more informative than meta-analysis methods, which analyze multiple studies separately and then pool summary statistics (lists of identified genes, p-values, effect sizes, etc).

Among the available integrative analysis studies, the following are the most relevant to the present study. Ma et al. (2011a) investigate the integrative analysis of multiple cancer diagnosis studies. A composite penalty, where the outer penalty is bridge and the inner penalty is ridge, is adopted for marker selection. Huang et al. (2011c) also analyze cancer diagnosis studies but adopt a sparse boosting approach for marker selection. This approach needs to iteratively maximize a non-differentiable objective function and thus may incur high computational cost. Ma et al. (2011b) analyze cancer prognosis studies with censored survival outcomes. The proposed penalty is a composite of MCP (outer) and ridge (inner). In the aforementioned studies, it is reinforced that the same set of markers are identified in all studies, that is, the homogeneity model described in Section 2.1. Ma et al. (2009) analyze diagnosis studies on multiple types of cancers. A gradient thresholding approach is proposed for marker selection. This approach allows different sets of markers in different studies, that is, the heterogeneity model described in Section 2.2.

In this article, we investigate the integrative analysis of multiple cancer diagnosis studies with binary response variables. We propose using composite penalization for marker selection. With multiple models, multiple composite penalties are proposed. This study may advance from the existing ones along the following aspects. First, it provides a more systematic study of both the homogeneity and heterogeneity models, whereas published studies focus on a single model. Second, under the homogeneity model, the MCP outer penalty may have better computational properties (for example lower computational cost) over the bridge. In addition, the composite penalization approach may have lower computational cost than the sparse boosting. Third, for the heterogeneity model, this study is the first to investigate penalized marker selection. Penalization can be preferred over gradient thresholding, which may be inconsistent even under simple settings (Zhang, 2007).

The rest of the article is organized as follows. The data and model settings are described in Section 2. Marker selection using composite penalization is described in Section 3. Multiple approaches are proposed to tailor multiple models. Numerical studies, including simulation in Section 4 and data analysis in Section 5, are conducted to investigate practical performance of the proposed approaches. The article concludes with discussion in Section 6. Multi-dataset analysis is inevitably more complicated than single-dataset analysis. In this article, we focus on methodological development and refer to published studies for discussions on the basic strategy of integrative analysis, datasets selection, model interpretation and practical applications.

2. Integrative Analysis of Multiple Cancer Diagnosis Studies

Assume that there are M independent studies, and there are n^m iid observations in study m(= 1,…, M). The total sample size is $n={\sum }_{m=1}^M{n}^m$. In study m, denote y^m as the response variable. Consider diagnosis studies where the response variables are the binary indicators of the presence of cancer. Denote x^m as the length-d covariates (gene expressions in this study) for a single observation. For simplicity of notation, assume that the same covariates are measured in all M studies. For better comparability, assume that each component of x^m has been standardized to have zero mean and unit variance. No further constraint is imposed on the correlation structure of covariates. Assume the model y^m ~ φ (x^m′β^m), where φ is the known link function, and β^m is the length-d vector of regression coefficients. Denote ${\beta }_j^m$ as the jth component of β^m. Then ${\beta }_j={({\beta }_j^1,\dots ,{\beta }_j^M)}^{\prime }$ is the length-M vector of regression coefficients, representing the effects of gene j in M studies. Published studies suggest that it is reasonable to assume the same link function in different studies. However, because of the heterogeneity across studies, for a covariate, its strengths of association with response variables, which are measured with regression coefficients, may be different in different studies.

In study m(= 1,…, M) with n^m subjects, denote Y^m as the length-n^m vector of response variables and X^m as the n^m×d covariate design matrix. Then the M models can be combined into a single model Y ~ φ (Xβ), where Y = (Y ^1′,…, Y^M′)′, X = diag(X¹, …, X^M) and β = (β^1′,…,β^M′) ′. With binary responses, assume logistic regression models. Denote R(β) as the unnormalized log-likelihood function for the unified model. It is easy to see that R(β) is simply the sum of M individual log-likelihood functions constructed from the M studies separately. Consider the following two models.

2.1 Homogeneity model

Under this model for any j(= 1,…, d), $\mathrm{I}({\beta }_j^1=0)=\dots \mathrm{I}({\beta }_j^M=0)$. That is, the M datasets have the same set of cancer-associated covariates, i.e., the same sparsity structure. The homogeneity model has been studied in Huang et al. (2011c), Ma et al. (2011a, 2011b) and others. It is a sensible model when multiple datasets have been generated under comparable protocols (the same outcome variable, similar patient selection criteria, similar profiling protocols, etc). In gene expression profiling studies, data characteristics can be summarized with the MIAME criterion (Minimum Information About a Microarray Experiment; www.mged.org/Workgroups/MIAME/miame.html; Oliver, 2003), and it is feasible to select datasets with similar MIAME descriptions. With those selected datasets, it is reasonable to expect them to have the same set of cancer markers.

2.2 Heterogeneity model

Under the heterogeneity model, a covariate can be associated with the response variables in some studies but not others. It is easy to see that the heterogeneity model includes the homogeneity model as a special case. There are multiple scenarios under which the heterogeneity model is meaningful. The first is where different studies are on different types of cancers (Ma et al., 2009). Despite significant differences, different types of cancers share the same characteristics of uncontrolled growth and metastasis. In addition, a large number of studies have shown that some cancers, for example breast cancer and ovarian cancer, are “tightly connected”. Thus it is reasonable to expect multiple cancers to have overlapping but different genomic basis. The second scenario is the analysis of different subtypes of the same cancer. Different subtypes may have different risks of occurrence and progression patterns, and it is not sensible to reinforce the same genomic basis. The third scenario is where subjects in different studies have different clinical risk factors, environmental exposures or treatment regimens. For genes not intervened with those additional covariates, their importance is consistent across multiple studies. However, for other genes, after accounting for the additional covariates, they may be important in some studies but not others.

3. Penalized Estimation and Marker Selection

In integrative analysis, the model and regression coefficients have two dimensions. The first is the gene dimension as in many other studies. The second is the study dimension which is unique to integrative analysis. To accommodate the two dimensions, composite penalties are needed for marker selection. We adopt the MCP for outer penalty and different inner penalties under the homogeneity and heterogeneity models.

3.1 MCP

The MCP is proposed in Zhang (2010). It belongs to the family of quadratic spline penalties. In single-dataset analysis, it has been shown to have satisfactory variable selection properties. The penalty is defined as

$$\rho (t;\lambda ,\gamma )=\lambda {\int }_0^{\mid t\mid }{(1-x/(\gamma \lambda ))}_{+}dx,$$ (1)

where λ is a penalty parameter, γ is a regularization parameter that controls the concavity of ρ, and x₊ = xI(x ≥ 0). The MCP can be easily understood by considering its derivative, which is

$$\stackrel{.}{\rho }(t;\lambda ,\gamma )=\lambda {(1-\mid t\mid /(\gamma ))}_{+}sgn(t),$$

where sgn(t) = −1,0, or 1 if t< 0, = 0, or >0, respectively. As |t| increases from zero, MCP begins by applying the same rate of penalization as Lasso, but continuously relaxes penalization until |t| >γλ, a condition under which the rate of penalization drops to zero. It provides a continuum of penalties where the Lasso penalty corresponds to γ = ∞ and the hard-thresholding penalty corresponds to γ → 1+. Compared with other penalties that also enjoy selection consistency, MCP may be preferred because of its computational simplicity (Mazumder et al., 2011). The MCP approach has been developed for single-dataset analysis. With multiple datasets, we consider the following MCP-based composite penalties.

3.2 Homogeneity model

Under the homogeneity model, consider the estimate

$$\widehat{\beta }={\mathit{argmin}}_{\beta }\left\{-\frac{1}{n}R(\beta )+\sum _{j=1}^d\rho (\Vert {\beta }_j\Vert ;\sqrt{M_j}\lambda ,\gamma )\right\}.$$ (2)

Here ρ(· λ,γ) is defined in expression (1). M_j is the size of group j. When the M studies have matched gene sets, $M_j\equiv M.\Vert {\beta }_j\Vert =\sqrt{{\sum }_{m=1}^M{({\beta }_j^m)}^2}$ is the l₂ norm of β_j, which is the square root of a ridge penalty, with the convention that ${\beta }_j^m=0$ if gene j is not measured in study m. Because of its specific form, the penalty defined above is also referred to as 2-norm group MCP, or 2-norm gMCP hereafter (Huang et al., 2011a, 2011b; Ma et al., 2011b).

Formulation (2) has been motivated by the following considerations. In our study, genes are the basic functional units. Thus the overall penalty is the sum of d individual penalties, with one for each gene. For gene selection, we propose using MCP. For a specific gene, its effects in the M studies are represented by a “group” of M regression coefficients. Under the homogeneity model, all the M studies should identify the same set of genes. Thus, within a group, the ridge penalty is adopted, which encourages shrinkage but does not conduct selection. M_j is introduced to more easily accommodate partially matched gene sets.

3.3 Heterogeneity model

Under the heterogeneity model, we first consider the estimate

$$\widehat{\beta }={\mathit{argmin}}_{\beta }\left\{-\frac{1}{n}R(\beta )+\sum _{j=1}^d\rho \left(\mid {\beta }_j\mid ;\sqrt{M_j}\lambda ,b\right)\right\}.$$ (3)

Here $\mid {\beta }_j\mid ={\sum }_{m=1}^M\mid {\beta }_j^m\mid$ is the Lasso penalty (l₁ norm of β_j). Because of its specific form, the penalty defined in (3) is referred to as 1-norm gMCP (Huang et al., 2011a).

Under the heterogeneity model, gene selection is still needed, which is achieved using the MCP outer penalty. In addition, for a selected gene, it is necessary to identify the studies in which it is associated with responses. Thus, the second level of selection is needed, which is accomplished with the Lasso penalty in (3). This strategy shares a similar spirit with the group bridge approach in Huang et al. (2009). The difference is that in Huang et al. (2009), there is only one dataset, and a group is composed of multiple genes. In contrast in this study, there are multiple datasets, and a group corresponds to only one gene.

The Lasso penalty is adopted in formulation (3) because of its computational simplicity. In single-dataset analysis, it has been shown that MCP has better selection properties than Lasso (Zhang, 2010; Zhang & Huang, 2008). Motivated by such a result, we consider

$$\widehat{\beta }={\mathit{argmin}}_{\beta }\left\{-\frac{1}{n}R(\beta )+\sum _{j=1}^d\rho \left(\sum _{m=1}^M\rho (\mid {\beta }_j^m\mid ;\lambda ,a);\sqrt{M_j}\lambda ,b\right)\right\}.$$ (4)

We refer to the penalty defined in the above formulation as the composite MCP. Breheney & Huang (2009) suggest that although a and b can be chosen separately, it is sensible to set them connected in a manner to ensure that the group level penalty attains its maximum if and only if all of its components are at the maximum.

3.4 Computation

Existing algorithms are not directly applicable to solve the minimizations in (2), (3) and (4). Below we describe computational algorithms for (2) and (4). Formulation (3) can be solved in a similar manner. We first consider a linear regression problem with E(Y|X) = Xβ, which has a least squares objective function. Here Y, X and β have similar definitions as in Section 2. The logistic model can then be transformed into a sequence of least squares problems.

3.4.1 Least squares with 2-norm gMCP

Consider the homogeneity model, where the estimate is defined as

$$\widehat{\beta }={\mathit{argmin}}_{\beta }\left\{\frac{1}{2n}{\Vert Y-X\beta \Vert }^2+\sum _{j=1}^d\rho (\Vert {\beta }_j\Vert ;\sqrt{M_j}\lambda ,\gamma )\right\}.$$ (5)

We adopt a coordinate descent approach (Friedman et al., 2010), which minimizes the objective function with respect to one group of coefficients at a time and cycles through all groups. It transforms a complicated minimization problem to a series of simple ones. With fixed tuning parameters, the coordinate descent algorithm proceeds as follows:

1. Initialize s = 0 and the vector of residuals $r=Y-{\sum }_{j=1}^d{X}_j{\stackrel{\sim }{\beta }}_j^{(0)}·{\stackrel{\sim }{\beta }}_j^{(0)}$ is an initial estimate of β_j. A convenient choice for the initial estimate is zero (component wise). X_j is the component of X that corresponds to β_j.

2. For j = 1,…, d:

   Given the group parameter vectors β_k (k ≠ j) fixed at their current estimates ${\stackrel{\sim }{\beta }}_k^{(s)}$, minimize the objective function (5) with respect to β_j. Here only terms involving β_j matter. Some algebra shows that this problem is equivalent to minimizing

   $$C(\stackrel{\sim }{\beta })+\frac{1}{2}{\beta }_j^{\prime }{\beta }_j-b_j^{\prime }{\beta }_j+c_j\Vert {\beta }_j\Vert ,$$ (6)
   where C(β̃) is a constant free of $b_j=n^{-1}{X}_j^{\prime }r+{\stackrel{\sim }{\beta }}_j^{(s)}$ and $c_j=\lambda \sqrt{M_j}$. It can be shown that the minimizer of expression (6) is

   $${\stackrel{\sim }{\beta }}_j^{(s+1)}={\left(1-\frac{c_j}{\Vert b_j\Vert }\right)}_{+}{b}_j.$$ (7)

   Update $r\leftarrow r-X_j({\stackrel{\sim }{\beta }}_j^{(s+1)}-{\stackrel{\sim }{\beta }}_j^{(s)})$

3. Update s ← s + 1;

4. Repeat Steps 2 and 3 until convergence.

This algorithm starts with a null model. In each iteration, it cycles through all d genes. For each gene, as equation (7) only involves simple computations, the update can be accomplished easily. There are multiple choices for the convergence criterion. In our numerical study, we use the l₂ norm of the difference between two consecutive estimates smaller than 0.01 as the convergence criterion, which has reasonable performance. In practice, other convergence criteria can be adopted, depending on data characteristics. In objective function (5), the first term is continuously differentiable and regular in the sense of Tseng (2001). The second term, the penalty, is separable. Thus, the coordinate descent algorithm converges to a coordinatewise minimum of the first term, which is also a stationary point (Tseng, 2001).

3.4.2 Least squares with composite MCP

Even with the simple least squares objective function, composite MCP does not have a convenient form for updating individual groups. We adopt a local coordinate descent approach (LCD; Breheny & Huang, 2011) to compute

$$\widehat{\beta }={\mathit{argmin}}_{\beta }\left\{\frac{1}{2n}{\Vert Y-X\beta \Vert }^2+\sum _{j=1}^d\rho \left(\sum _{m=1}^M\rho (\mid {\beta }_j^m\mid ;\lambda ,a);\sqrt{M_j}\lambda ,b\right)\right\}.$$ (8)

Consider update with the jth group. By taking the first order Taylor expansion approximation about β̃_j (the current estimate), the penalty as a function of ${\beta }_j^k$ is approximately proportional to ${\stackrel{\sim }{\lambda }}_{jk}\mid {\beta }_j^k\mid$ where

$${\stackrel{\sim }{\lambda }}_{jk}={\rho }^{\prime }\left(\sum _{m=1}^M\rho (\mid {\stackrel{\sim }{\beta }}_j^m\mid ;\sqrt{M_j}\lambda ,a);\lambda ,b\right){\rho }^{\prime }(\mid {\stackrel{\sim }{\beta }}_j^k\mid ;\lambda ,a).$$

Thus for update with each ${\beta }_j^k$, we have an explicit solution:

$${\beta }_j^k\leftarrow \mathrm{S}\left(\frac{1}{n}{X}_{jk}^{\prime }r+{\stackrel{\sim }{\beta }}_j^k,{\stackrel{\sim }{\lambda }}_{jk}\right),$$ (9)

where $X_{jk}^{\prime }$ is the kth row of $X_j^{\prime }$, r is the current residual, ${\stackrel{\sim }{\beta }}_j^k$ is the current estimate, and S(z,λ) = sgn(z)(|z| − λ)₊ is the soft-thresholding operator. Then the LCD can be carried out in a similar manner as the regular coordinate descent.

3.4.3 Computation with logistic regression

In study m(= 1 … M), consider { $(y_i^m,x_i^m),i=1,\dots ,n^m$}, the n^m iid copies of $(y^m,x^m).x_i^m={(x_{i1}^m,\dots ,x_{id}^m)}^{\prime }$. Under the logistic regression model, $p(x_i^m)=Pr(y_i^m=1\mid x_i^m)=1/(1+exp(-({\beta }_0^m+{\sum }_{j=1}^d{x}_{ij}^m{\beta }_j^m)))$. Note that unlike with linear regression, the intercept term ${\beta }_0^m$ is necessary. The log-likelihood function is

$$R^m({\beta }_0^m,{\beta }^m)=\sum _{i=1}^{n^m}\left[y_i^m·({\beta }_0^m+\sum _{j=1}^d{x}_{ij}^m{\beta }_j^m)-log(1+e^{({\beta }_0^m+{\sum }_{j=1}^{\mathrm{d}}{x}_{ij}^m{\beta }_j^m)})\right].$$ (10)

Under the logistic regression models, there is no simple, closed-form solution for update with a single group. To tackle this problem, we resort to a majorization minimization (MM) approach (Ortega & Rheinboldt, 2000). Note that the negative log-likelihood function is convex. With the MM approach, when the current estimate is ( ${\stackrel{\sim }{\beta }}_0^m$, β̃ ^m), we majorize the negative log-likelihood function by a quadratic loss given by

$$R_Q^m({\beta }_0^m,{\beta }^m\mid {\stackrel{\sim }{\beta }}_0^m,{\stackrel{\sim }{\beta }}^m)=\frac{1}{8}\sum _{i=1}^{n^m}{(z_i^m-{\beta }_0^m-\sum _{j=1}^d{x}_{ij}^m{\beta }_j^m)}^2+C({\stackrel{\sim }{\beta }}_0^m,{\stackrel{\sim }{\beta }}^m),$$

where $z_i^m={\stackrel{\sim }{\beta }}_0^m+{\sum }_{j=1}^d{x}_{ij}^m{\stackrel{\sim }{\beta }}_j^m+\frac{y_i^m-\stackrel{\sim }{p}(x_i^m)}{\stackrel{\sim }{p}(x_i^m)(1-\stackrel{\sim }{p}(x_i^m))}$ and $\stackrel{\sim }{p}(x_i^m)=\frac{1}{1+e^{-({\stackrel{\sim }{\beta }}_0^m+{\sum }_{j=1}^d{x}_{ij}^m{\stackrel{\sim }{\beta }}_j^m)}}$ are evaluated at the current estimate ( ${\stackrel{\sim }{\beta }}_0^m$, β̃^m), and C ( ${\stackrel{\sim }{\beta }}_0^m$, β̃^m)is free of ( ${\beta }_0^m$, β^m). Note that the above approximation can be conducted for all M studies separately. The approximated objective function has a least squares form.

With fixed tuning parameters, our computational algorithm consists of a sequence of nested loops:

• Outer loop: Update the majorized quadratic function $R_Q^m(m=1,\dots ,M)$ using the current estimate ( ${\stackrel{\sim }{\beta }}_0^m$, β̃^m).

• Inner loop: Run the algorithm developed for the penalized least squares problem with the objective function $\frac{1}{n}{\sum }_{m=1}^M{R}_Q^m$.

When the true models are identifiable, under mild regularity conditions, the overall decreasing trend of the objective function and hence convergence of this algorithm can be derived from the convergence of the coordinate descent algorithm following Vaida (2005).

3.5 Tuning parameter selection

The MCP (1) involves two tuning parameters λ and γ. The effect of λ is similar to that with other penalization approaches, with larger values leading to sparser estimates. Generally speaking, smaller values of γ are better at retaining the unbiasedness of MCP for large coefficients. However, they also have the risk of generating objective functions that have a nonconvex region, which may introduce difficulty to optimization and yield solutions that are discontinuous with respect to λ. Loosely speaking, it is advisable to choose a γ value that is “big enough” to avoid this problem but “not too big”. Following published studies, we have experimented with a few values for γ, particularly including 1.8, 3, 6 and 10. In our simulation and data analysis, γ = 6 leads to the best performance. We search for optimal λ values using V-fold cross validation (V=5 in numerical study; Hastie et al. 2009). As shown in Breheney & Huang (2011, Figure 2), when λ is too small, the cross validation criterion may not be locally convex. In such a region, the criterion may not be reliable, and the estimates are discontinuous and noisy. To avoid such a problem, we select λ where the criterion first goes up.

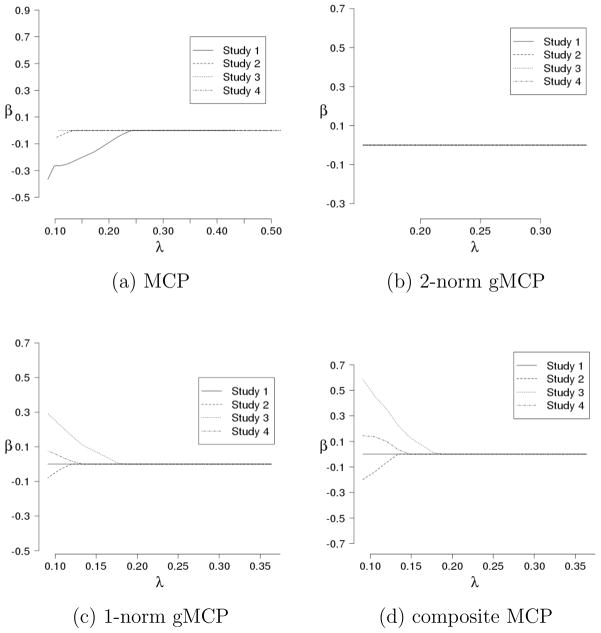
Figure 2.

Solution paths under the homogeneity model for a simulated dataset for a gene not associated with responses.

4. Simulation Study

Simulation is conducted to better gauge performance of the proposed approaches. Here we investigate solution paths and compare selection performance of the proposed approaches with alternatives.

4.1 Simulation settings

We simulate four datasets, each with 50, 100 or 200 subjects. For each subject, we simulate the expressions of 1,000 genes. The gene expressions are jointly normally distributed, with marginal means equal to zero and variances equal to one. We consider two correlation structures. The first is the autoregressive correlation, where expressions of genes j and k have correlation coefficient ρ^|j–k|. We consider two scenarios with ρ = 0.2 and 0.7, corresponding to weak and strong correlations, respectively. The second is the banded correlation. Here two scenarios are considered. Under the first scenario, genes j and k have correlation coefficient 0.33 if |j – k| = 1 and 0 otherwise. Under the second scenario, genes j and k have correlation coefficient 0.6 if |j – k| = 1, 0.33 if |j – k| = 2, and 0 otherwise. Under the homogeneity model, all four studies share the same ten cancer-associated genes. Under the heterogeneity model, studies 1 and 2 share the same ten cancer-associated genes, and studies 3 and 4 share the same ten cancer-associated genes. The two sets have five overlapping genes. Thus, under both models, across the four datasets, there are a total of forty true positives. The nonzero regression coefficients are scattered between 0.3 and 1.9. We generate binary response variables from the logistic regression models and Bernoulli distributions.

4.2 Solution paths

We investigate solution paths, which are estimates as a function of λ with γ or a=6. We simulate four datasets under the homogeneity and heterogeneity models and compute estimates using the algorithms described in Sections 3.4.1–3.4.3. The sample size per study is 50. The correlation structure is autoregressive with ρ= 0.7. Under the homogeneity model, Figures 1 and 2 (Appendix) provide the solution paths for an important and a noisy gene, respectively. Under the heterogeneity model, Figures 3–5 (Appendix) provide the solution paths for a gene associated with responses in all studies, a gene associated with responses in some but not all studies, and a gene not associated with responses, respectively. As the homogeneity model is a special case of the heterogeneity model, all three proposed penalties are applicable. For the heterogeneity model, conceptually, the 2-norm gMCP approach may not be appropriate as it does not conduct within-group selection. However, to more clearly see the difference, we also analyze the heterogeneity model with 2-norm gMCP. In addition, as a benchmark, we analyze each dataset separately using MCP. The solution paths clearly show the “all in or all out” nature of 2-norm gMCP. The sparsity structures are always consistent across studies. With the three alternative approaches, however, when λ is large enough, the sparsity structures are not consistent. The 1-norm gMCP and composite MCP approaches conduct within-group selection and may be more appropriate for the heterogeneity model. Their solution paths are similar for the two simulated datasets.

Figure 1.

Solution paths under the homogeneity model for a simulated dataset for a gene associated with responses.

Figure 3.

Solution paths under the heterogeneity model for a simulated dataset for a gene associated with responses in all four studies.

Figure 5.

Solution paths under the heterogeneity model for a simulated dataset for a gene not associated with responses in all four studies.

4.3 Results

Simulation suggests that the proposed approaches are computationally feasible. When the sample size per study is 200, analysis of one replicate on a regular desktop PC takes about ten minutes for all three proposed penalties.

When employing the proposed approaches and MCP, tuning parameters are selected using five-fold cross validation. Summary statistics based on 100 replicates, including the number of genes identified and number of true positives, are shown in Table 1 (homogeneity model) and 2 (heterogeneity model) respectively. Under the homogeneity model, 2-norm gMCP significantly outperforms MCP and composite MCP by having more true positives and fewer false positives. Under some simulation scenarios, 1-norm gMCP may identify a few more true positives, however, at the price of a large number of false positives. When taking both the number of true positives and model size into consideration, 2-norm gMCP may be preferred over alternatives under the homogeneity model. Under the heterogeneity model, the pattern is not as clear. The relative performance of different approaches may depend on data settings. For example, when the sample size per study is 200 and under the autoregressive correlation structure with ρ= 0.2, 2-norm gMCP has the best performance. Under a few simulation scenarios, 1-norm gMCP has significantly more true positives than alternatives, again at the price of many more false positives. The composite MCP approach may have a lower false positive rate, however, it may also identify fewer true positives. The satisfactory performance of 2-norm gMCP may be “counterintuitive”. It may be related to the surprisingly satisfactory performance of ridge regression with high-dimensional data (Park & Hastie, 2008; Zhu & Hastie, 2004). It is also interesting to note that the performance of composite MCP may not be as good as expected. Similar phenomena have been observed with MCP in published studies. We suspect that it may be because the cross validation selected tuning parameters are too large, leading to overly parsimonious models. Without solid theoretical development, we are unable to provide full justification for the observations. The simulation results further confirm the complexity of integrative analysis with high-dimensional data and the need to explore multiple approaches in practical data analysis.

Table 1.

Simulation under the homogeneity model. In each cell, the first row is the number of true positives (standard deviation), and the second row is the model size (standard deviation).

Correlation	nm	MCP	2-norm gMCP	1-norm gMCP	composite MCP
Autoregressive ρ = 0.2	50	1.5 (1.1)	16.2 (5.9)	2.9 (3.3)	1.7 (2.0)
		3.7 (2.3)	19.9 (9.4)	9.2 (11.4)	3.6 (4.1)
	100	8.9 (2.5)	33.6 (4.0)	19.7 (4.7)	14.6 (4.0)
		13.1 (4.5)	35.4 (4.9)	62.1 (25.4)	25.1 (8.0)
	200	24.0 (2.5)	39.8 (0.8)	35.0 (1.4)	31.2 (2.6)
		27.1 (3.6)	40.8 (2.0)	154.1 (24.6)	49.4 (8.4)
Autoregressive ρ = 0.7	50	5.3 (2.2)	11.4 (2.8)	15.3 (2.3)	7.3 (1.7)
		6.5 (2.7)	11.6 (2.8)	37.0 (8.8)	9.1 (2.2)
	100	10.5 (1.9)	13.0 (3.2)	26.7 (2.5)	9.7 (1.5)
		11.1 (2.2)	13.0 (3.2)	75.6 (17.5)	10.8 (2.1)
	200	13.0 (1.6)	18.2 (4.1)	33.7 (1.7)	13.0 (2.2)
		13.4 (1.7)	18.3 (4.3)	122.5 (21.6)	14.3 (2.8)
Banded scenario 1	50	2.3 (1.3)	17.7 (5.6)	4.6 (3.4)	3.1 (2.3)
		5.2 (2.3)	21.3 (7.2)	13.9 (13.9)	5.9 (4.8)
	100	10.0 (3.3)	29.6 (4.2)	21.9 (3.5)	15.0 (3.1)
		13.0 (4.1)	29.9 (4.4)	70.0 (20.4)	24.3 (6.5)
	200	23.1 (2.2)	37.4 (3.2)	35.2 (1.8)	27.3 (2.5)
		25.6 (3.2)	37.5 (3.3)	147.2 (30.8)	39.3 (6.7)
Banded scenario 2	50	4.6 (1.8)	13.0 (4.1)	11.9 (4.0)	6.0 (2.5)
		6.4 (2.7)	13.3 (4.2)	30.1 (14.9)	8.4 (3.7)
	100	11.0 (2.0)	15.4 (3.9)	24.4 (2.6)	10.7 (1.6)
		12.4 (2.5)	15.5 (4.1)	71.0 (16.9)	13.7 (3.0)
	200	15.1 (1.8)	21.0 (4.8)	33.1 (2.0)	14.8 (1.9)
		15.8 (2.3)	21.9 (5.1)	126.2 (25.5)	19.4 (4.2)

5. Analysis of Cancer Diagnosis Studies

5.1 Analysis of liver cancer studies

Gene profiling studies have been conducted on hepatocellular carcinoma, which is among the leading causes of cancer death in the world. Four microarray studies are described in Choi et al. (2003). Brief descriptions are provided in Table 3. Studies that generated the four datasets (referred to Data D1–D4) were conducted in three different hospitals in South Korea. Although the same protocol was used in all four studies, the researchers were not able to directly merge the data even after normalization (Choi et al., 2003). 9,984 genes were profiled in all four studies, among which we selected 3,122 with less than 30% missingness. We analyze the 1,000 genes with the highest variations. We also remove eight subjects that have more than 30% gene expression measurements missing. The effective sample size is 125.

Table 3.

Liver cancer studies. Tumor: the number of tumor samples. Normal: the number of normal samples. Numbers in the “()” are the number of subjects used in analysis. Version 2 chips have different spot locations from Version 1 chips.

Data set	D1	D2	D3	D4
Experimenter	Hospital A	Hospital B	Hospital C	Hospital C
Tumor	16 (14)	23	29	12 (10)
Normal	16 (14)	23	5	9 (7)
Chip type	cDNA(Version 1)	cDNA(Version 1)	cDNA(Version 1)	cDNA(Version 2)
(Cy5:Cy3)	Sample:normal liver	Sample:placenta	Sample:placenta	Sample:sample

We analyze data using the four approaches. Genes identified and their estimated regression coefficients are provided in Table 5 (Appendix). With MCP, a total of six genes are identified in the four datasets, with no gene identified in more than one datasets. 2-norm gMCP identifies two genes. 1-norm gMCP identifies a total of eighteen genes, among which one gene is identified in three datasets, and all other genes are identified in one dataset only. Composite MCP identifies five genes, with no overlap between different gene sets.

Table 5.

Liver cancer studies: parameter estimates.

Method	Gene #	D1	D2	D3	D4
MCP	287	−0.25
	442	−0.02
	921	−0.04
	122		−0.48
	942		−0.04
	942				−1.37
2norm gMCP	439	−0.19	−0.13	−0.36	0.10
	942	−0.31	−0.74	−0.91	−0.71
1-norm gMCP	122		−0.35
	255	−0.02
	287	−0.14
	332		0.02
	379				0.02
	442	−0.11
	497			−0.05
	498		0.11
	523			−0.20
	679	−0.06
	713	−0.07
	735	−0.10
	774		−0.10
	849		0.03
	914				0.04
	921	−0.13
	942		−0.27	−0.05	−0.32
	992			−0.01
composite MCP	122		−0.48
	287	−0.18
	442	−0.02
	921	−0.02
	942				−0.17

Without having access to independent validation studies, we are not able to objectively evaluate gene identification accuracy. Here we investigate prediction performance. In the analysis of genomic data, marker selection and prediction are related but, in general, they represent different aspects. Prediction evaluation can only provide a partial evaluation of identification results. It is expected that if the identified genes are more meaningful, prediction using these genes may be more accurate. We adopt a cross-validation based prediction evaluation (Huang & Ma, 2010). The numbers of false prediction are 52 (MCP), 34 (2-norm gMCP), 30 (1-norm gMCP) and 43 (composite MCP), respectively. The 2-norm gMCP approach identifies a small number of genes showing consistent effects across multiple datasets. Its prediction performance is much better than that of MCP and composite MCP and comparable to that of 1-norm gMCP.

5.2 Analysis of multiple cancer studies

Different types of cancers may share common susceptibility genes (Ma et al., 2009). For some cancers, for example breast cancer and ovarian cancer, there exist a large number of epidemiologic evidences that may assist the identification of common susceptibility genes. For other cancers, there is a lack of such evidence, and finding the common genes will have to rely on genomic data analysis. As shown in Table 4, we collect data from four studies conducted by different research groups who investigated cancers of different tissues and used different profiling platforms. The four datasets have a combined sample size of 475. The expressions of 3,239 genes were measured on all subjects.

Table 4.

Multiple cancer studies. Normal: the number of normal samples. Tumor: the number of tumor samples.

Tissue	Reference	Platform	Normal	Tumor
Kidney	Boer et al. (2001)	membrane	81	81
Liver	Chen et al. (2002)	cDNA	76	76
Prostate	Singh et al. (2002)	U95A	50	52
Stomach	Chen et al. (2003)	cDNA	29	29

We analyze using the four different approaches. Genes identified and their regression coefficients are shown in Table 6 (Appendix). MCP identifies one gene in each study with no overlap across studies. 2-norm gMCP identifies three genes. 1-norm gMCP identifies six genes in total, with two genes identified in two studies and the rest identified in only one study. Composite MCP identifies five genes with no overlap across studies. When applying the cross validation based prediction evaluation, the numbers of false predictions are 14 (MCP), 4 (2-norm gMCP), 2 (1-norm gMCP), and 6 (composite MCP), respectively. The patterns demonstrated in Table 6 are similar to those observed with the liver cancer data. The 1-norm gMCP approach has the best prediction performance. It is of interest to note the satisfactory prediction performance of 2-norm gMCP and composite MCP, with different sets of identified genes. In the literature, it has been noted that with practical gene expression data, different sets of genes may have similar prediction performance. In this set of analysis, the three proposed penalties have comparable performance, with no one significantly dominating the other two.

Table 6.

Multiple cancer studies: parameter estimates.

Method	Gene #	Kidney	Liver	Prostate	Stomach
MCP	525				−9.03
	824			−7.72
	1145		12.41
	2573	3.91
2-norm gMCP	317	−2.11	−1.42	−5.11	−2.92
	1145	−2.30	10.33	0.96	3.81
	2211	11.51	0.62	−5.00	1.21
1-norm gMCP	530				−0.94
	672	−0.99
	1145		2.65		0.22
	2211	1.64		−0.52
	2991			1.18
	3031	0.01
composite MCP	40	−8.62
	110				−4.01
	220			9.93
	703	6.31
	1145		12.15

6. Discussion

In cancer genomic data analysis, multiple studies have established the advantages of integrative analysis over meta-analysis and analysis of single datasets. In this article, for cancer diagnosis studies, we consider both the homogeneity and heterogeneity models, propose MCP-based composite penalties for marker selection, and develop effective computational algorithms. Simulation studies and data analysis show satisfactory performance of the proposed approaches.

In the analysis of single datasets, multiple penalization approaches have been shown to have satisfactory performance, including bridge, SCAD, adaptive Lasso and others. MCP is adopted in this study because of its computational simplicity and satisfactory empirical performance. It is possible to follow a similar strategy and develop composite penalties based on, for example, SCAD. A more systematic development is beyond the scope of this article. In this study, we have focused on methodological development. As shown in Huang et al. (2011a, 2011b), theoretical studies of MCP-based composite penalties can be extremely challenging, even for simple linear regression with a single dataset. The present data and model settings are more complicated than that in Huang et al. (2011a, 2011b) because of the heterogeneity across multiple datasets and adoption of generalized linear models. As a limitation of this study, we are not able to establish the theoretical properties and postpone such effort to future studies. The four datasets analyzed in Section 5.2 have also been analyzed in Ma et al. (2009), which includes three additional datasets. In general, adding more datasets increases sample size and power of analysis. However, all datasets analyzed in Ma et al. (2009) come from early experiments where the gene annotations were less satisfactory. For this specific example, adding more datasets reduces the number of genes measured in all datasets. Thus, to keep a reasonable number of genes measured in all datasets, we choose to focus on analyzing the four datasets.

Figure 4.

Solution paths under the heterogeneity model for a simulated dataset for a gene associated with responses in studies 1 and 2.

Table 2.

Simulation under the heterogeneity model. In each cell, the first row is the number of true positives (standard deviation), and the second row is the model size (standard deviation).

Correlation	nm	MCP	2-norm gMCP	1-norm gMCP	Composite MCP
Autoregressive ρ = 0.2	50	1.1 (1.3)	11.9 (4.3)	2.9 (3.4)	1.5 (2.0)
		4.4 (2.1)	20.8 (10.1)	8.1 (12.1)	3.4 (4.3)
	100	9.4 (2.7)	26.9 (3.8)	20.7 (3.9)	15.0 (4.0)
		13.0 (4.4)	41.0 (8.4)	66.6 (23.1)	26.2 (8.2)
	200	24.1 (2.4)	36.5 (2.4)	34.7 (1.7)	30.6 (2.1)
		28.1 (3.8)	54.7 (5.3)	152.7 (29.0)	51.4 (7.3)
Autoregressive ρ = 0.7	50	5.3 (2.0)	11.7 (2.9)	15.4 (3.7)	6.8 (1.7)
		6.8 (2.7)	16.6 (3.5)	36.2 (11.8)	8.5 (2.7)
	100	10.8 (1.6)	12.7 (1.9)	26.1 (2.2)	9.4 (1.2)
		11.6 (2.0)	18.3 (2.6)	72.9 (12.5)	10.2 (1.7)
	200	13.3 (1.6)	16.8 (3.2)	33.94(1.83)	13.0 (2.2)
		14.0 (2.2)	24.5 (5.0)	132.1 (22.9)	14.2 (3.0)
Banded scenario 1	50	2.3 (1.6)	11.0 (4.4)	4.3 (3.4)	2.0 (2.0)
		4.7 (2.4)	19.0 (10.5)	12.4 (13.1)	3.9 (3.8)
	100	10.7 (2.8)	24.1 (4.5)	23.0 (3.1)	15.7 (2.5)
		13.6 (3.8)	37.3 (9.6)	72.8 (17.2)	27.3 (5.8)
	200	23.3 (2.3)	33.7 (2.9)	35.0 (1.7)	27.9 (2.4)
		25.7 (2.9)	49.3 (4.8)	148.7 (28.5)	41.8 (6.4)
Banded scenario 2	50	4.8 (1.8)	11.3 (3.4)	11.08(3.47)	5.9 (2.6)
		7.1 (2.5)	16.6 (5.5)	27.7 (13.7)	9.0 (4.1)
	100	10.8 (2.2)	14.7 (3.4)	24.6 (2.7)	10.5 (1.6)
		12.0 (2.5)	21.0 (4.8)	74.9 (18.6)	13.1 (3.3)
	200	15.2 (1.9)	19.3 (3.7)	33.8 (1.9)	14.1 (2.0)
		15.8 (2.0)	28.0 (5.3)	138.7 (29.0)	17.9 (4.0)