Child Gender and Parental Investments In India: Are Boys And Girls Treated Differently?

Abstract

Previous research has not always found that boys and girls are treated differently in rural India. However estimates of the effect of gender on parental investments could be biased if girls end up in larger families due to son-biased stopping rules. Using a novel identification strategy that exploits that gender at conception is random, we document that boys receive more childcare time than girls, they are breastfed longer and they get more vitamin supplementation. Compared to other developing countries, boys have an advantage in height and weight relative to girls. Neither greater needs nor anticipated family size explain the results.

Women in developing countries fare worse than men in many dimensions: They obtain less schooling, have lower labor force participation, earn lower salaries, are more likely to be poor, and often lack fundamental rights, such as voting rights or the right to own property (Duflo 2005). One often-cited extreme manifestation of this phenomenon is that mortality rates are substantially higher for girls than for boys in many developing countries (Chen, Huq and D'Souza 1981; Arnold, Choe and Roy 1998; Sen 1990), although this is not true in developed countries (United Nations Secretariat 1988). These patterns are particularly marked in countries with “son preferences,” such as India, where families have explicit preferences for having sons over daughters (Pande and Astone 2007).

Surprisingly, though, the previous literature does not always support the hypothesis that these differences in outcomes are the result of differential treatment of boys and girls. Although many papers find that boys receive more health care (Basu 1989, Ganatra and Hirve, 1994), are breastfed longer (Kuziemko and Jayachandran 2011), and are more likely to be vaccinated (Borooah 2004) than girls, others find no evidence of differential investments. For example, Harriss (1995) finds that girls in India receive just as much nutrition as boys, and Deaton (2003) reports that vaccination rates are identical for boys and girls in India. Most notably, Deaton (1997) reviews studies that use the “adult goods method” and finds that there is no evidence of parents spending more on boys than girls.¹ Duflo (2005) concludes that“[e]ven in the countries where the preference for boys is strongest, it is hard to find evidence that girls receive less care than boys under normal circumstances.”²

However, previous work has assumed that boys and girls live in families with similar characteristics, in terms of both observables and unobservables. Yet this assumption is incorrect if families have a preference for sons and follow male-biased stopping rules of childbearing (Yamaguchi 1989, Jensen 2005), which appears to be the case in India.³ As a consequence, these empirical estimates of differential treatment are biased. In particular, if couples’ fertility is driven by their desire to have a certain number of boys, then girls will end up in larger families on average. If, in turn, children in larger families have fewer per-capita resources, as hypothesized by Jensen (2005), then estimates of differential treatment will be biased upwards: In other words, it will appear as if girls on average get less, but this is because girls are in larger families (and, thus, have lower per-capita resources) rather than because of differential parental treatment. On the other hand, if there are returns to scale, then estimates of differential treatment will be biased downwards.

We propose a novel empirical strategy that addresses this issue. It relies on the observation that—in the absence of sex-selective abortion—a child’s sex at birth is randomly determined. If that is the case, then families who just had a boy are identical to families who just had a girl. Thus, any differences we observe in terms of parental inputs can be attributed to the sex of the newborn. However, a correlation will develop over time between the youngest child’s gender and the family characteristics, because families with a newborn daughter are less likely to stop having children. To overcome this problem, we restrict our sample to families with children who are still “young enough” whose mothers have not had the opportunity to respond to the gender of their youngest child by having other children. Our data suggest that families with boys and girls between 0 and 15 months of age look identical in terms of observables—we use them to study whether boys receive more inputs than girls.

Our analysis allows us to rule out that observed differences in investments are driven by family size; this is important because it affects how one would design policies to improve the lot of girls. If girls get less because they live in poorer larger families, then transfers to those families would help girls. However, if parents would like to devote more resources to boys no matter what, then transfers to the same families might not help girls. In that case, female-focused interventions might be needed.

Another contribution of this paper is to use our identification strategy to investigate whether boys and girls are treated differently in terms of an important but not frequently studied type of investment in children: childcare time. Beginning with Becker (1965), economists have recognized that, in addition to money, time is a key input into the “child production function.” Time is particularly important to the extent that it is complementary to many other inputs. For example, feeding children requires both food and the time to cook it and feed the children. However, no estimates of gender differences in parental time allocation based on dedicated time-use surveys exist for developing countries.⁴ Using data from the Indian Time Use Survey, we are able to investigate whether families spend more time on childcare after the birth of a son than after the birth of a daughter. Also, using data from the Indian Demographic and Health Survey (hereafter, DHS), we study gender differences in other frequently used measures of parental investments, such as breastfeeding and vaccinations. We focus on rural households because the literature suggests that gender differences in India are present mostly in rural areas, but we also present results for urban areas.

Our results indicate that families treat boys and girls differently. Rural households with an infant boy under the age of one spend roughly 30 minutes more per day—or 14% more time—on childcare than households with an infant girl. The quality of the childcare also appears to be higher for baby boys. The effect is larger for households with only one child under the age of six: they spend more than 60 minutes more per day (about 30% more) on childcare when their youngest child is a boy. Our results also show that boys are more likely to be breastfed longer, and to be given vitamin supplements. In general, we find these inputs to be at least 10% higher for boys than for girls in rural areas. We also confirm that boys in India fare better in terms of their anthropometrics when compared to boys in other developing countries. However we do not find evidence of higher vaccination rates for boys in objectively collected data coming from vaccination cards or interviewer observations, despite maternal reports of higher rates for boys.

Our approach has limitations. As in previous work, we cannot fully address the issues of sex-selective abortion and differential mortality. These behaviors most likely will bias our estimates of boy–girl differences towards zero, so our effects can be taken to be lower bounds. To limit the potential bias from sex-selective abortion, we restrict our study to the 1992 DHS, the most recent DHS survey conducted before ultrasound technology became widely available (Bhalotra and Cochrane 2010). We show that for the 1992 survey, child gender is uncorrelated with prenatal characteristics (e.g., prenatal care). This provides further evidence that families did not know the sex of the child and were not able to discriminate before birth, neither in terms of prenatal investments nor through sex-selective abortion.⁵ Our results also suggest that the bias associated with sex-selective abortion in our sample is small. This is consistent with Anderson and Ray (2010), who report that prenatal factors account for only 10% of missing women in India. To assess the bias caused by postnatal mortality, we compute bounds for our estimates and find that mortality potentially generates large biases: Differences between boys and girls could be as much as 50% larger than our baseline estimates.

Another limitation of our results is that we can only study children who are under the age of 15 months. This is an important subset of the population, because at this age investments have large returns in the short and long run: Lower investments in childhood are associated with worse health and economic outcomes in adulthood and for future generations (Almond and Currie, 2011). But we cannot study older children.

We investigate some possibilities for why parents give girls fewer resources. One possibility is that anticipated family size is responsible for the effects we observe: Children in families who just had a girl may receive fewer parental investments if parents anticipate they will have another child. We address this issue by estimating an upper bound of how much of the effect of child gender on investments may work through anticipated family size. Our estimates indicate that the anticipated family size mechanism accounts for at most 38% the effect of child gender (and, for most inputs, much less than that). Another possibility is that boys might be seen as needing more resources, although it is not clear why parents would think that is the case, given that girls have higher mortality than boys from age 6 months onwards. We provide suggestive evidence that boys do not in fact “need” more than girls: If we look at South Africa, a developing country with data on investments and no evidence of a son preference, we find that there are no systematic gender differences in most inputs. Although the evidence is not conclusive, it does suggest that other possibilities—such as higher returns for investments in boys (because of the gender gap in wages, for example) or a preference for boys—drive the differential investments.

I. Identification Issues in the Presence of Son-biased Stopping Rules

In this section, we present evidence that families in India follow son-biased stopping rules and discuss the implications of this behavior for estimates of boy– girl differences in parental investments. We then propose a method for overcoming the problems that arise in this context.

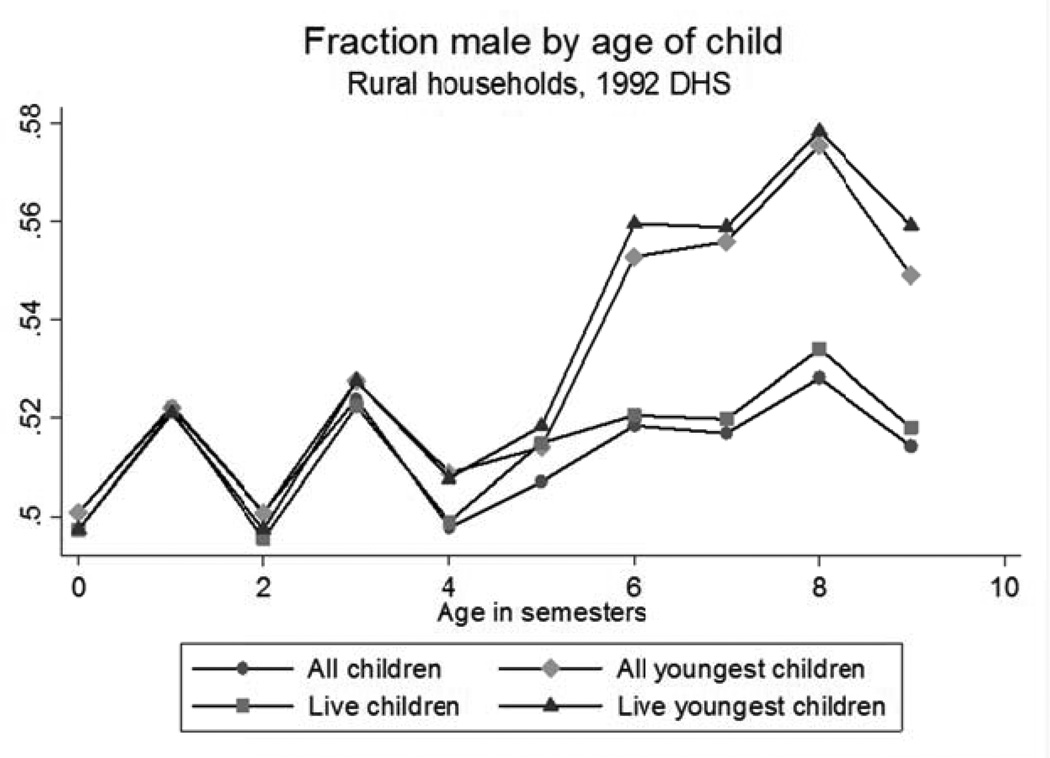
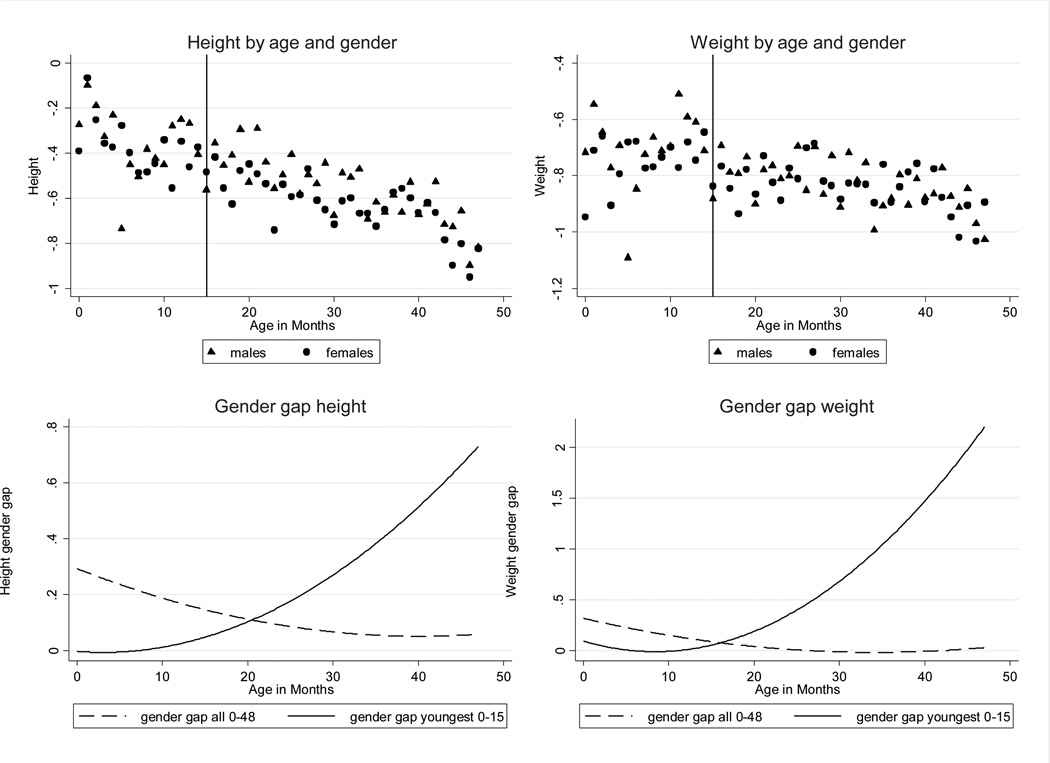
We begin by presenting suggestive evidence that families in rural India do follow son-biased stopping rules. At birth, the sex ratio is determined by biological odds. But if families are more likely to stop having children after a boy, then the sex ratio among the youngest will be skewed towards boys, and this effect should be larger for those that remain the youngest in their families at older ages. This prediction is in fact consistent with the data. In Figure 1, we plot the fraction of boys by age using data from the 1992 DHS (described in greater detail below). The figure shows that the fraction of boys among all living children is somewhat constant across ages. But among the youngest child in the family, the fraction of boys increases from 51% for children 0–5 months old to 58% for the children 54–59 months old. In other words, if a child is still the youngest at age 4, then the probability that the child is a boy is 58%. This is a large deviation from the natural sex ratio at birth and suggests that in rural India families indeed follow son-biased stopping rules.⁶

Figure 1. Son-biased stopping rules and gender ratios by age.

Sources: Authors’ calculations using the 1992 Indian Demographic and Health Survey

If families follow a stopping rule based on the gender composition of their children, then, as shown by Yamaguchi (1989) and by Jensen (2005), girls will have more siblings than boys on average. A simple example provides the intuition for this result. Consider a family that wants one boy. If the firstborn is a boy, then the family stops having children; but if the firstborn is a girl, the family continues having children. If all families behave this way, then all girls have siblings, but not all boys do. The simulations in Jensen (2005) suggest that the resulting differences in number of siblings can be quite large. These stopping rules imply that the previous estimates of gender differences are biased. Suppose we estimate boy-girl differences by regressing some measure of child investment on a constant and a boy dummy (as in Sen and Sengupta 1983; Das Gupta 1987; Sommerfelt and Piani 1997):

$$Z_{ih}={\alpha }_0+{{\alpha }_1}^{*}{B}_{ih}+u_{ih},$$

where Z_ih is the investment in child i in household h, B_ih is a dummy that is equal to one if child i in household h is a boy, and u_ih is an error term. Son-biased stopping rules imply that B_ih is correlated with family size. Therefore, B_ih will also be correlated with the error term, and α₁ will be biased if child investment depends on the number of children in the family. The sign of the bias may be different for different measures of child investment. On the one hand, children in large families may have to share resources with more siblings (e.g., food)—this is the issue that Jensen (2005) investigates. On the other hand, children in large families may ceteris paribus receive more investments if there are large returns to scale for the child’s investment (e.g., vaccination in public campaigns or supervision and teaching).

Given that girls tend to be part of larger families than boys, it may seem reasonable to control for family size (and/or sex-composition of siblings), as in Oster (2009) or Deaton (1989). This strategy essentially compares outcomes of boys and girls in families of the same size. However, son-biased stopping rules also imply that if we compare children in families of the same size, girls are on average in families that desire fewer sons (than the family of the average child). In other words, conditional on family size, the child's sex is not exogenous; it is correlated with parental preferences for the gender composition of children. The intuition is as follows: Suppose that we observe two families who stopped having children after their second child. Family A has a girl and a boy; family B has two boys. Family A stopped having children despite the fact that they have only one boy; family B stopped because they had two boys, but otherwise would have continued. This example illustrates that for families with two children, girls live in families that desire fewer sons than does the average family.

In general, the sign of the bias that results from controlling for family size is unknown and depends on the relationship between preferences for the gender composition of children and the treatment of boys and girls.⁷ Controlling for family size poses other challenges as well, because it is related to many unobserved determinants of parental inputs (such as income) and, thus, is potentially correlated with the error term. Our empirical strategy is designed to overcome these limitations.

This discussion raises the question of why we are interested in knowing how girls would be treated if they were randomly assigned to families: The fact is that they are not. They are more likely to be in larger families. And controlling for family size, they are disproportionately in families that want them relative to the average family. But knowing the extent to which families want to treat girls differently is important because it informs policy. Suppose, for instance, that as suggested by Jensen, all the differences we observe are driven by family size. Then, policies that transfer income to large and/or poor families will benefit girls. However, if this is not the case and parents want to devote more resources to boys, then transfers to these families will not necessarily benefit girls.

II. Empirical Strategy

Our empirical strategy relies on the observation that in the absence of sex-selective abortion the child’s sex is randomly determined at birth. If that is true, then families who just had a boy are identical to families who just had a girl. Therefore, any differences we observe in terms of parental inputs can be attributed to the sex of the newborn. However, over time this is no longer true: Families that follow a son-biased stopping rule are more likely to stop having children after a boy. In time, a correlation will develop between the youngest child’s sex and preferences. To overcome this problem, we restrict our sample to families in which the youngest child is “young enough” as determined by our data: We select our sample such that baby-boy and baby-girl families look identical in terms of their observable characteristics. Formally, we estimate whether boys and girls are treated differently using the following equation:

$$Z_{ih}={\alpha }_0+{{\alpha }_1}^{*}{B}_{ih}+X_{ih}\rho +u_{ih}.$$

The OLS estimate of α₁ is an unbiased estimator of the parameter of interest if the child’s sex is exogenous (conditional on X) —i.e., Cov(B_ih,u_ih|X)=0. Our identifying assumption is that the child’s sex is exogenous at birth for the youngest child in the family while they are young enough. In the next section, we provide evidence that predetermined characteristics (in particular, number and gender of siblings) are not correlated with gender for very young children. We also show that, as the model above predicts, this no longer holds true as the family’s youngest child gets older. Notice that, if gender is indeed random, then we do not need to condition on any additional variables.⁸ Conditioning on predetermined variables should have no impact on our point estimates and should reduce the standard errors (if these variables predict parental investments).

Our assumption may fail if there is sex-selective abortion of girls or excess girl mortality. We test this directly in the data by comparing the characteristics of families with a baby girl and a baby boy. Still, it is possible that families differ in terms of unobservables. Sex-selective abortion and excess female mortality most likely bias our estimator against finding boy–girl differences: Because the surviving girls are expected to be in families that like girls more than the average family, they should receive more care than they otherwise would have.⁹ Thus, our estimates can be taken as lower bounds of the effect of gender in child investments.¹⁰

III. Testing Random Assignment and Selecting the Estimation Sample

To test whether the gender of the youngest child is uncorrelated with predetermined family characteristics, we restrict the sample to children who are the youngest in their families and estimate the following linear equation:

$$I({\mathit{\text{boy}}}_{ia}=1)=X_i{\beta }_a+{\epsilon }_{ia},$$

where the dependent variable is an indicator of whether child i in age category a is a boy, and X is a set of predetermined characteristics. Independence implies that β_a = 0, namely that the Xs do not jointly predict the gender of the child. The prediction is that we will not reject the null for very young children, but that we will always reject it for children who are “old enough.”

We use India’s 1992 DHS (also known as the National Family Health Survey), a large representative survey that contains several variables determined before birth. The DHS surveyed ever-married women of reproductive ages, each of whom was interviewed separately and asked questions about her characteristics and reproductive history. The DHS files contain full birth histories: There is a record for every child born, including date of birth and gender, whether the child has died, and whether s/he continues to live at home. For every child born, we know the characteristics of the mother, and we can compute the number of siblings by gender and age (including the number of those who have died). To minimize the bias attributable to sex-selective abortion, we use only the 1992 survey: The previous literature suggests that ultrasound technology became widespread in India only in the mid-1990s, particularly after 1995 (Bhalotra and Cochrane 2010). We also focus on rural households, as the previous literature has done.¹¹ The final data set contains one observation per family and includes children (excluding twins¹²) born to women ages 15–49 living in rural areas in 25 states.

Next, we pool children into 12-month age groups and run a joint test for each age group.¹³ We use these results to determine at which age the test starts to systematically reject the null. Table 1 shows all the predetermined characteristics of the child and the mother that we can include, 20 in all. We selected variables that were most likely to be predetermined before birth for all children, regardless of their age. Therefore, we do not include location, household composition, marital status, spouse characteristics, or number of living siblings, because some of these characteristics may be affected by the gender of one’s children (Morgan, Lye and Condran 1988, Mott 1994, Dahl and Moretti 2009). (In fact, we document that household composition is affected by the gender of the youngest in Web Appendix Table 1.) However, we do look at family size and composition at birth, maternal characteristics, and the use of prenatal care. Prenatal care use allows us to investigate whether ultrasound technology was important in 1992: Access to, and use of, prenatal care should predict the gender of the baby only if parents knew the child’s gender before birth and treated boys and girls differentially in terms of prenatal variables. If this is not the case, then sex-selective abortion—a more radical type of differential treatment—should be less of a concern. However, a limitation of the prenatal care variables is that they are not available for older children (only for those under age four).

TABLE 1.

TESTING RANDOM ASSIGMENT (DHS 1992). MEAN DIFFERENCES BY GENDER AMONG THE YOUNGEST CHILD ALIVE.

Sample:	Age 0–15 months		Age 16–47 months		Age 48–59 months
	Mean for females	Coefficient on Male=1	Mean for females	Coefficient on Male=1	Mean for females	Coefficient on Male=1
Child characteristics
# of siblings ever born	2.088	0.009 [0.046]	2.185	0.062 [0.041]	2.69	−0.02 [0.101]
# of brothers ever born	1.011	−0.037 [0.027]	1.079	0.003 [0.024]	1.432	−0.103 [0.062]*
# of sisters ever born	1.076	0.046 [0.029]	1.106	0.058 [0.028]**	1.259	0.083 [0.062]
Birth month	6.866	−0.109 [0.077]	6.723	0.024 [0.069]	6.762	−0.17 [0.164]
Mother’s characteristics
Mother’s age	24.716	0.028 [0.125]	26.669	0.147 [0.124]	30.1	−0.208 [0.276]
Mother’s ethnicity (scheduled caste omitted)
Scheduled tribe	0.114	−0.005 [0.007]	0.114	−0.001 [0.007]	0.086	0.01 [0.013]
Other	0.744	0.005 [0.009]	0.753	−0.003 [0.009]	0.773	0.003
Mother’s religion (other omitted)
Hindu	0.818	−0.002 [0.008]	0.832	0 [0.007]	0.817	0.031 [0.018]*
Muslim	0.132	0.003 [0.008]	0.126	−0.003 [0.006]	0.126	−0.037 [0.015]**
Christian	0.021	0 [0.002]	0.018	−0.002 [0.002]	0.025	−0.006 [0.006]
Mother’s years of education	1.954	−0.042 [0.074]	1.929	−0.023 [0.065]	2.154	−0.088 [0.176]
Mother born in urban area	0.063	−0.005 [0.005]	0.063	−0.002 [0.005]	0.072	0.001 [0.012]
Mother’s age first married	16.36	0.041	16.223	−0.02 [0.056]	16.092	0.005 [0.137]
Mother’s age at first birth	18.551	0 [0.066]	18.459	−0.032 [0.061]	18.534	−0.288 [0.150]*
Mother speaks Hindi	0.483	−0.016 [0.011]	0.422	0.018 [0.011]*	0.361	0.038 [0.025]
Pvalue: mother and child charateristics predict gender?		0.2803		0.6013		0.005
Prenatal characteristicsa
Any prenatal care?	0.607	−0.004 [0.011]	0.582	0.007 [0.010]
# prenatal visits	2.245	−0.033	2.304	0.007 [0.055]
Any tetanus shots?	0.587	0.009 [0.011]	0.564	0.006 [0.011]
# tetanus shots	1.28	0.026 [0.027]	1.3	−0.002 [0.026]
non-home delivery	0.157	0.01 [0.008]	0.174	−0.005 [0.008]
Pvalue of test that prenatal predict gender		0.1937		0.6283
Test results from regressions that include all charateristics
Pvalue prenatal only (Joint Test)		0.135		0.5104
Pvalue excl. prenatal (Joint Test)		0.2268		0.5405
Pvalue all (Joint Test)		0.1435		0.661		0.005

Standard errors (in brackets) are computed taking survey design into account. Coefficients reported from separate linear regressions, where each characteristic is regressed on a dummy for male and a constant. The p-value for the joint test comes from regressing the youngest child’s gender on all the charateristics (except number of all siblings, since that is collinear to the number of borthers and number of sisters) and testing whether they are jointly significant.

^aPrenatal characteristics only available for children 0–47 months old.

^***p<0.01,

^**p<0.05,

^*p<0.1

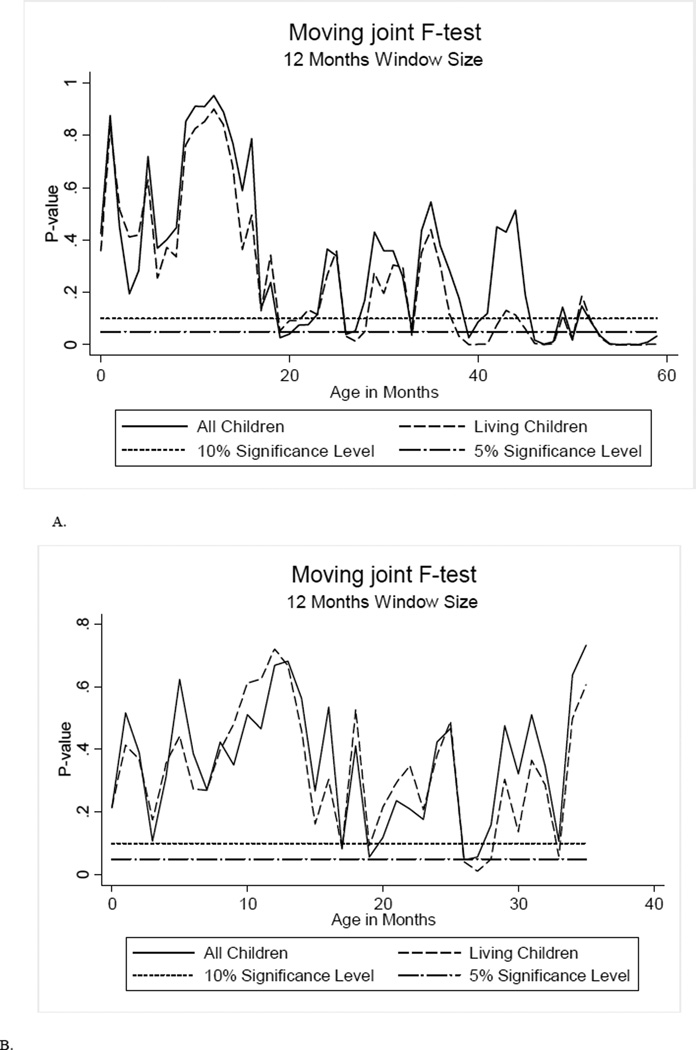
Figures 2a and 2b display the results of our test graphically. They plot the p-value of the joint test that the Xs do not predict the gender of the youngest child. Figure 2a includes all children up to age five. For this full sample, we include all predetermined characteristics, except prenatal care, which is not available for the older children. Figure 2b repeats the exercise including prenatal care use, and considers children up to age four. The first point in either figure corresponds to children 0–11 months old. Starting with Figure 2a, we observe that for the youngest group (the first p-value reported), we cannot reject the null that families whose youngest child is a girl look the same in terms of observable characteristics as families whose youngest child is a boy. For living children, we can reject the null at the 10% level for the first time for the age group 19–30 months. Thereafter, we reject the null often. When we include prenatal care (Figure 2b), we reject the null at the 5% level for the first time for children ages 19–30 months. Based on these results, and to be conservative, we keep children all ages 0–15 months for our analysis.

Figure 2.

The Predicting child gender using maternal and child characteristics

Predicting gender using mother and family characteristics, and prenatal care use

Notes: Authors’ calculations using the 1992 Indian Demographic and Health Survey.

Table 1 shows the results of our tests in more detail, for both our final estimation sample and for older children. For each predetermined characteristic, we test whether the means are the same for families whose youngest child is a boy versus those whose youngest child is a girl. The bottom of the table reports the p-value from the joint test that all characteristics predict gender. For the sample of the youngest children, no coefficient is significant at the 5% or 10% level, and the joint test cannot reject the null that all characteristics do not predict gender. We also reject the null that prenatal care variables (only) are jointly significant. For comparison, the last two columns show the result of the tests for the youngest children who are ages 16–47 months and 48–59 months. For the children 16–47 months, two of the variables we examine are statistically different at the 10% level, even though the joint p-test does not reject the null. Interestingly, we now observe that if the youngest child is male, he is more likely to have more sisters. This is consistent with son-biased stopping rules. He is also more likely to have a mother who speaks Hindi, a characteristic that predicts son preferences (Pande and Astone 2007). Finally, for the oldest children ages 48–59 months (for whom we do not observe prenatal care), we see that four out of 14 of the predetermined family and mother characteristics are statistically significant predictors of gender. The joint test rejects the null, despite the fact that this sample is substantially smaller.

Note that if the bias from sex-selective abortion were large enough, even our youngest sample would not appear to be balanced between boys and girls.¹⁴ Also, given that prenatal care use does not predict gender, we conclude that there is not enough use of ultrasound technology and sex-selective abortion in this period to matter. This is consistent with Bharadwaj and Lakdawala (2013).

To assess the effect of excess female mortality on our results, we also plot the p-value of the test for the sample of ever-born children (including children whose mothers reported them to have died by the time of the survey). Our results are basically the same, implying that the observed differences are mainly the result of stopping rules.

Two caveats remain. First, as in other tests of random assignment, our test is imperfect because we can only observe that the samples are identical based on observables—it is possible that they are different based on unobservables. Second, although our samples are large, they are not large enough to precisely identify the precise age at which the covariates become unbalanced. In summary, the data support the assumption that gender is as good as “randomly assigned” among the youngest children, 15 months and younger. We use this sample to estimate whether girls receive fewer resources than boys.

IV. Gender Differences in Inputs: Results from the DHS

We start by investigating whether there are boy–girl differences in child investments using the DHS data. The results are reported in Table 2. All estimations use survey weights and correct the standard errors for survey design.

TABLE 2.

EFFECT OF CHILD GENDER ON PARENTAL INPUTS, YOUNGEST CHILDREN 0–15 MONTHS OLD. DHS (1992)

	Coefficient on Male = 1		Mean of Y	Model:
	no controls	with controls
Dependent variable:
Was child ever breastfed?	0.005 [0.004]	0.006 [0.004]	0.95	OLS
	0.121 [0.100]	0.138 [0.100]		Logit (beta reported)
Breastfeeding
# months breastfed	1.811 [0.579]***	1.937 [0.564]***	7.67	Censored regression
Log(# months breastfed)	0.291 [0.093]***	0.313 [0.092]***	1.80	Censored regression
# months breastfed	0.413 [0.130]***	0.438 [0.130]***		Accelerated Failure Time
	−0.411 [0.130]***	−0.434 [0.131]***		Proportional Hazard
Was child given vitamin A supplements?	0.014 [0.007]**	0.013 [0.006]*	0.12	OLS
	0.132 [0.063]**	0.139 [0.069]**	0.12	Logit (beta reported)
Did mother have vaccination card at interview?	0.043 [0.009]***	0.041 [0.009]***	0.27	OLS
	0.215 [0.046]***	0.232 [0.051]***		Logit (beta reported)

Notes: Standard errors [in brackets] are computed taking survey design into account. Child ever breastfed is equal to zero if mother reports that child was not breastfed or if breastfeeding duration was less than a month. Each coefficient corresponds to a separate estimation, and survey weights are used. The number of observations for each age group varies from outcome to outcome because there are a few missing values. Controls include all variables in Table 1: # of brothers, # of sisters, birth month, mother’s age, mother’s caste (2 dummies), mother’s religion (3 dummies), mother’s years of education, whether mother was born in rural area, mother’s age at first marriage, mother’s age at first birth, whether mother speaks Hindi, prenatal care use, number of prenatal care visits, tetanus shot, number of tetanus shots, and home delivery.

^***p<0.01,

^**p<0.05,

^*p<0.1

First, we look at breastfeeding, which is deemed to be the ideal source of nutrition for infants, particularly in developing countries where food is in limited supply and water and sanitation are poor.¹⁵ We do not find that boys are more likely to have ever been breastfed (defined as ever breastfed, or breastfed for less than one month). The effect sizes are precisely estimated zeroes, which may not be surprising, because 95% of children are breastfed.

In the next set of columns, we look at the duration of breastfeeding. We estimate censored linear (or log-linear) regressions, because many children are still being breastfed at the time of the interview. We find a positive and statistically significant effect of gender on the duration of breastfeeding. In a proportional hazard model, the odds of stopping breastfeeding are lower for males. The magnitudes suggest that breastfeeding duration increases as much as 24% when the child is a boy, which is consistent with Jayachandran and Kuziemko (2011).

Next, we look at whether children are given Vitamin A, which protects against night blindness, measles, and diarrhea.¹⁶ Using either a linear or nonlinear model, we find that boys are about 13% more likely to receive Vitamin A. Finally, we look at whether mothers have a vaccination card on hand at the time of the interview. Only about 27% of mothers have a vaccination card, but they are 4 percentage points (or 16%) more likely to have the vaccination cards of boys. For all outcomes, the results are not sensitive to the inclusion of predetermined covariates—the point estimates are almost identical, as expected, if these characteristics are orthogonal to gender.

In Table 3, we investigate whether boys are more likely to be vaccinated. Panel A reports the results using vaccination information from either the mother or the vaccination card—we construct three measures: having at least one vaccination, number of vaccinations, and complete vaccination record.¹⁷ Boys do better for all three measures. However these regressions include a large fraction of maternal reports. If we instead only analyze the results using the information vaccination cards only, we do not find any gender differences. However this sample is substantially smaller and contains a larger fraction of boys (since mothers are more likely to have cards for them).

TABLE 3.

EFFECT OF CHILD GENDER ON VACCINATIONS. YOUNGEST CHILDREN 0–15 MONTHS OLD.

	controls?	Number of immunizations	At least one immunization	Completely immunized	BCG scar
Panel A: Youngest kids 0–15 months old. DHS. All India.
Male = 1	no	0.170 [0.040]***	0.051 [0.011]***	0.019 [0.007]***	-
Male = 1	yes	0.16 [0.037]***	0.048 [0.010]***	0.018 [0.007]***	-
Obs		11445	11445	11445	-
Mean of Y		1.67	0.509	0.12
Panel B: Youngest kids 0–15 months old. DHS. All India. Children with vaccination cards.
Male = 1	no	0.025 [0.058]	0.004 [0.002]*	0.008 [0.018]	-
Male = 1	yes	0.046 [0.056]	0.004 [0.002]*	0.012 [0.018]	-
Obs		3327	3327	3327	-
Mean of Y		3.411	0.997	0.249
Panel C: Children 0–15 months old. Rajasthan Immunization Survey (Banerjee et al. 2010)
Male = 1	no	−0.095 [0.067]	−0.001 [0.030]	0.000 [0.004]	−0.001 [0.026]
Obs		986	986	989	899
Mean of Y		0.656	0.329	0.004	0.184
Panel D: Youngest kids 0–15 months old. DHS. Rajasthan.
Male = 1	no	0.307 [0.119]**	0.113 [0.032]***	0.035 [0.020]*	-
Male = 1	yes	0.323 [0.101]***	0.112 [0.029]***	0.036 [0.020]*	-
Obs		790	790	790	-
Mean of Y		1.190	0.370	0.084

Notes: Standard errors [in brackets]. Each coefficient corresponds to a separate estimation. Panel A reports results using immunization data (from baseline) collected by Banerjee et al. (2010) in rural Rajasthan. Interviewers collected mother-reported immunization data and examined children to check for the presence of the distinctive lesion left by the BCG vaccine. Panels B, C and D report results estimated using DHS data. In the Rajasthan Immunization Survey “Completely immunized” is defined as having received 5 vaccinations. In the DHS it is defined as having received measles, BCG and 3 doses of DPT. The number of observations for each age group varies from outcome to outcome because there are a few missing values. Controls include all variables in Table 1: # of brothers, # of sisters, birth month, mother’s age, mother’s caste (2 dummies), mother’s religion (3 dummies), mother’s years of education, whether mother was born in rural area, mother’s age at first marriage, mother’s age at first birth, whether mother speaks Hindi, prenatal care use, number of prenatal care visits, tetanus shot, number of tetanus shots, and home delivery. For DHS data survey weights are used and the standard errors are computed taking survey design into account.

^***p<0.01,

^**p<0.05,

^*p<0.1

To further investigate this question we used data from two surveys conducted by Banerjee et al. (2010) in rural Rajasthan. Interviewers collected mother-reported immunization data and examined each child under seven to check for the presence of the distinctive lesion left by the BCG vaccine. In this sample there is no evidence of gender differences, neither differences in the objective measure of vaccination based on scars nor differences based on maternal reports. However Panel D shows there are gender differences in the DHS data for Rajasthan, which is also based on maternal reports (and on vaccination cards when available). It is not clear why maternal reports differ between these two Rajasthan samples. On the one hand the evidence on whether mothers misreport immunization is mixed (Lim, Stein and Murray 2008; Banerjee et al. 2010). On the other hand the objective data from vaccination cards and scars show no bias, but they come from small possibly unrepresentative samples. We conclude that the evidence is insufficient to assert gender differences in vaccinations exist.

Last, we report the results for urban areas (Web Appendix Table 4). These coefficients are substantially smaller and always insignificant, although the standard errors are large. This findings support the hypothesis that differential gender treatment is greater in rural areas. In summary, for most of the measures we looked at, we find that boys receive more investments than girls. In general, girls receive at least 10% less than boys, with the notable exception of vaccinations.

V. Gender Differences in Anthropometrics: Results from the DHS

We now look at the effect of gender on anthropometric measures. Height and weight were measured at the interview for all children in our sample (rather than reported), and they are known to be important correlates of long-term outcomes (e.g., Almond and Currie 2010, 2011; Currie 2011).

For our purposes, these measures have two limitations. First, anthropometric measures are outcomes, not inputs, and parental control over them is limited. But the main difficulty in using these measures is that they require some normalization (Thomas 1990, Moestue 2009): For biological reasons, boys are (on average) taller and heavier than girls at all ages. Therefore, we expect boys to look “better” than girls in the absence of parental differences in investments, and we would like to estimate the extent to which this advantage is greater in India. Thus, to properly measure the differential effect of gender in India, we need to establish what gender gaps would look like in the absence of differential treatment.

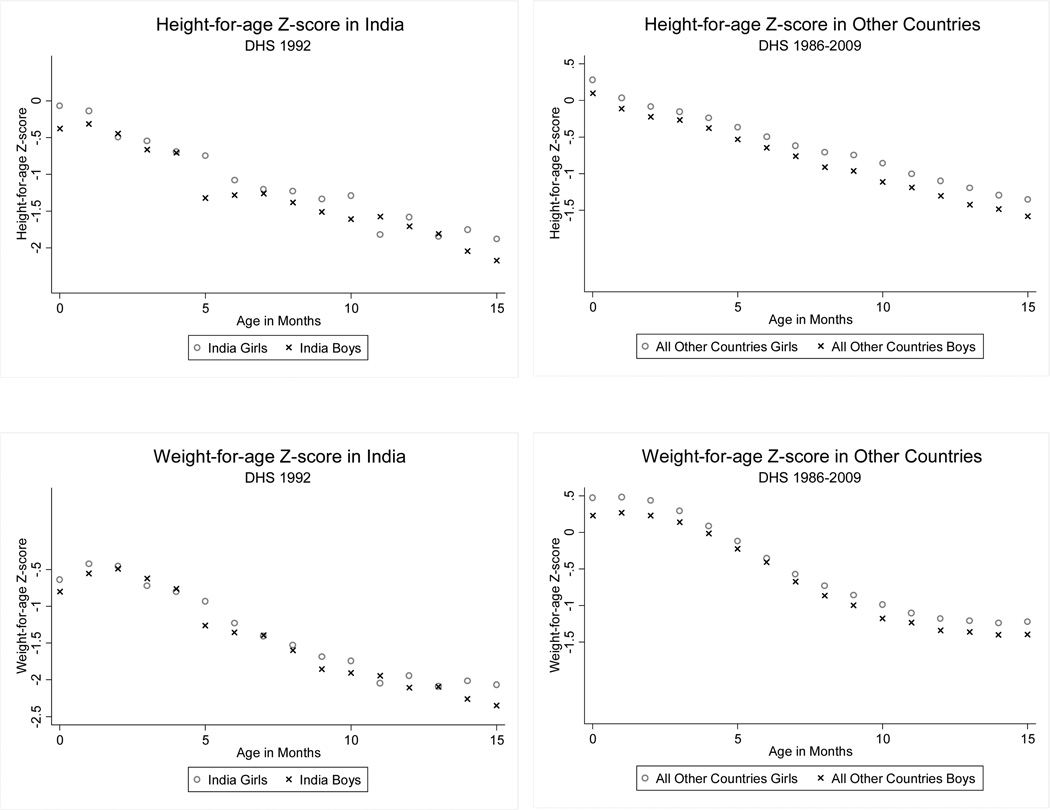
We use data from all the DHS surveys conducted between 1986 and 2009 that collected data on anthropometrics (141 surveys from 58 countries) to create a comparison group for the 1992 Indian survey (we do not include the later Indian surveys in our data). Figure 3 shows the gender-specific age-profile of average height-for-age (upper panel) and average weight-for-age (lower panel) in India in 1992 (left column) and in all other DHS surveys other than India (right column). The Z-score (estimated by WHO and provided by DHS) is a normalized value, computed by taking a child’s height (weight), subtracting the median height (weight) in the reference population, and dividing by the standard deviation of the reference population, for that age and gender. The reference populations used by the DHS are children growing up in the United States in the 1970s (DHS I, II, III) or in well-fed populations in a few countries around the world (DHS IV and V). The figures show that girls fare better than boys in other developing countries, but that boys and girls in India seem to have comparable anthropometrics.

Figure 3. Anthropometric measures by gender In India and around the world.

Notes: The figure shows the average height-for-age and weight-for-age separately by gender in India (DHS 1992) and in other countries in which anthropometric data were collected (all countries and all years).

We then estimate a “difference-in-difference” model by regressing height on a dummy for gender, a dummy for India, and an interaction between the two (and dummy variables for age in months and survey year). Table 4 shows the results. The gender gap in height is statistically significantly greater in India than it is in other countries, measured in absolute or proportional terms (columns 1 and 2). The other coefficients show that on average boys are indeed taller than girls but that all children are shorter in India. The magnitudes imply that the gender gap in height is about 10% greater in India than in the average DHS country (0.117/1.2). The results are similar for weight (columns 5 and 6), although they are significant only in the log specification.

TABLE 4.

BOY-GIRL DIFFERENCE IN ANTHROPOMETRICS IN INDIA IN 1992 AND IN OTHER DEVELOPING COUNTRIES. YOUNGEST CHILDREN 0–15 MONTHS OLD, DHS 1986–2009

	Height				Weight
	Height	Log(height)	Height-for- age Z-score (DHS/WHO)	Height-for- age Z-score (Sample)	Weight	Log(weight)	Weight-for- age Z-score (DHS/WHO)	Weight-for- age Z-score (sample)
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Panel A: DHS 1986–2009
Male * India	0.117 [0.030]***	0.002 [0.000]***	0.034 [0.011]***	0.030 [0.008]***	0.003 [0.009]	0.007 [0.002]***	0.050 [0.011]***	0.027 [0.008]***
Male	1.259 [0.030]***	0.019 [0.000]***	−0.181 [0.011]***	−0.001 [0.008]	0.459 [0.009]***	0.063 [0.002]***	−0.147 [0.011]***	−0.001 [0.008]
India	−1.928 [0.313]***	−0.030 [0.005]***	−0.717 [0.117]***	−0.496 [0.081]***	−0.836 [0.135]***	−0.127 [0.018]***	−0.923 [0.139]***	−0.688 [0.105]***
Observations	204,014				202,731
Panel B: DHS 1986–1995
Male * India	0.040 [0.052]	0.001 [0.001]	0.009 [0.018]	0.012 [0.013]	−0.003 [0.014]	0.006 [0.002]***	0.046 [0.012]***	0.025 [0.010]**
Male	1.333 [0.051]***	0.020 [0.001]***	−0.156 [0.018]***	0.017 [0.013]	0.464 [0.014]***	0.063 [0.002]***	−0.144 [0.012]***	0.000 [0.010]
India	−1.891 [0.309]***	−0.029 [0.005]***	−0.705 [0.115]***	−0.487 [0.079]***	−0.832 [0.136]***	−0.127 [0.018]***	−0.921 [0.140]***	−0.686 [0.106]***
Observations	54,554				54,554

Notes: Standard errors [in brackets] clustered at the country level. The table compares boy-girl differences in anthropometrics in India and in all other developing countries in which DHS collected children’s anthropometric data. Panel A includes data from 58 countries for a total of 141 surveys (excluding the 2 other Indian surveys). Panel B includes data from 30 countries and 38 surveys. The sample is restricted to children that were the youngest in their families and were 15 months old and younger. All regressions include age dummies in months and year fixed effects (results without controls are identical and available upon request.)

^***p<0.01,

^**p<0.05,

^*p<0.1

We also show the findings if we use the Z-scores provided by the DHS as the dependent variable. These results also show that the interaction between India and male is positive for both weight and height scores (columns 3 and 7). However, the main coefficients on male are now negative, suggesting that the normalized Z-scores exhibit a male disadvantage (or a female advantage): The mean gender gap in height across developing countries is smaller than in well-fed populations. Indeed, if we just compute gender differences in height and weight Z-scores in our data, we find a negative effect of male (see Web Appendix Table 5). What these regressions suggest is that this is true in all the DHS countries (on average). If we recompute the Z-scores using the DHS countries as the reference population, then we find no effect of gender as expected, but we still find an advantage for boys in India relative to other countries (Table 4, columns 4 and 8).¹⁸ We obtain similar results for weight—that is, the gender gap benefits boys in India. Because sex-selective abortion became available in the early 1990s in India and perhaps in other countries as well—we re-estimate the results using only surveys prior to 1995. Panel B shows that in this sample the coefficients for male are still significant in the weight regression, but not for height. However we prefer the results in Panel A which contain four times as many observations and many more countries and surveys.

Overall, these results suggest that, relative to girls, boys are taller and heavier in India than in other developing countries, although they also highlight the difficulty in establishing baseline gender gaps in anthropometrics.

VI. Results from the Time Use Survey

We now investigate whether families spend more time in childcare if their youngest child is a boy. We use data from the Indian Time Use Survey (hereafter, TUS) conducted from July 1998 to June 1999 by the Social Statistics Division of the Central Statistical Organization of India. The TUS asked about the time use of all household members over five years of age during the previous 24 hours. The diary section was open-ended in terms of both describing the activities and giving beginning and ending times, with each activity identified as multiple (simultaneous) or not.¹⁹ The survey collected data in six states chosen to be representative of the different regions of the country: Gujarat, Haryana, Madhya Pradesh, Meghalaya, Orissa and Tamil Nadu. There were 12,750 rural and 5,841 urban households interviewed, totaling roughly 75,000 respondents. Following the existing literature, we focus on rural households. We also analyze time-use data corresponding to “normal” days only (excluding holidays, etc).²⁰ The main variable of interest is the amount of time spent on childcare by household members over age five. We follow Guryan, Hurst and M.Kearney (2008) as closely as possible and classify the following activities as childcare: physical care of children (washing, dressing, feeding); teaching, training and instruction of own children; accompanying children to places; travel related to care of children; and supervising children.

These data have some limitations for our analyses. Aside from containing information on only six states, there is very little information about the participants; thus, we cannot meaningfully reproduce our test that the predetermined covariates do not predict gender.²¹ Since families cannot be identified, we can only identify the youngest child in the household (not in the family): For this reason, we restrict the sample to those who are the children or grandchildren of the household head.²² We also do not know the identity of the child who was being cared for; we only know that individuals reported being occupied with childcare. However, this feature has one advantage: Because the questions on childcare do not refer to a particular child, respondents are less likely to systematically bias their responses based on the gender of their youngest child.

Age in months is not available in the TUS. We look at children under age one; this group is closest to the experimental sample in the DHS. Because the TUS is small, and because there is substantial age-heaping at age one that differs by gender (Coale and Demeny 1967, and Bhat 1990), we also report results for children under age two.

Table 5 presents summary statistics. Households with children under two on average spent more than three hours on childcare per day, while households with older children spent a little less than two hours.²³ Women provided more than 80% of the total time spent on childcare by the household. About 70% of childcare consisted of the physical care of children. During roughly half the time devoted to childcare, the caregiver reported no simultaneous activity: We use this as a measure of the quality of childcare.

TABLE 5.

DESCRIPTIVE STATISTICS, TIME USE SURVEY (1998–1999). RURAL AREAS.

	HHs with youngest below age 1		HHs with youngest ages 0–1		HHs with youngest ages 2–5
	Mean	S.D.	Mean	S.D.	Mean	S.D.
Percentage of all households	0.04		0.15		0.30
Time Use:
Time spent on child care (minutes per day)	236.62	159.28	196.90	152.19	107.19	129.05
Time spent on child care by female members	192.15	134.80	166.23	132.76	88.87	108.79
Time spent on child care by male members	44.47	82.20	30.67	64.70	18.31	51.21
Time spent on physical care	165.22	125.96	137.89	121.83	73.06	94.29
Time spent supervising children	55.50	114.87	48.96	105.50	24.26	76.10
Time spent instructing children	5.25	27.37	4.10	23.10	5.24	26.62
Time spent taking children to places	10.65	67.78	5.94	42.81	4.62	39.92
Time spent on exclusive child care	132.44	153.63	95.55	137.45	57.43	105.52
Household characteristics:
Household size	4.68	1.87	4.54	1.83	3.95	1.54
Male youngest	0.46	0.50	0.51	0.50	0.55	0.50
Scheduled tribe	0.24	0.43	0.23	0.42	0.21	0.41
Scheduled caste	0.14	0.35	0.18	0.38	0.20	0.40
Hindu	0.91	0.28	0.91	0.29	0.92	0.28
Per capita expenditure	393.31	175.58	393.83	188.92	408.61	196.36
Land owned and possessed	4.85	7.97	4.51	8.25	3.89	9.13
Observations	562		1,947		3,815

Notes: Weighted statistics for households in each sample. The statistics in the first two columns are for households where the youngest child is under 1, columns (3) and (4) for households where the youngest child is under 2, and the last two columns for households where the youngest is between 2 and 5 years of age. Time use is expressed in minutes per day.

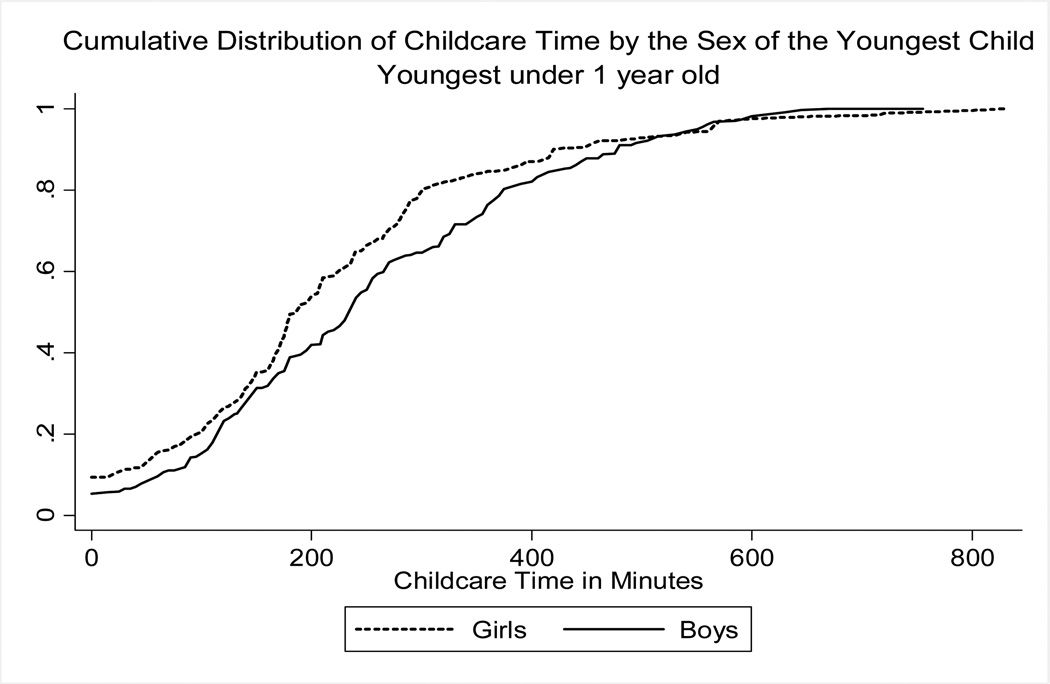
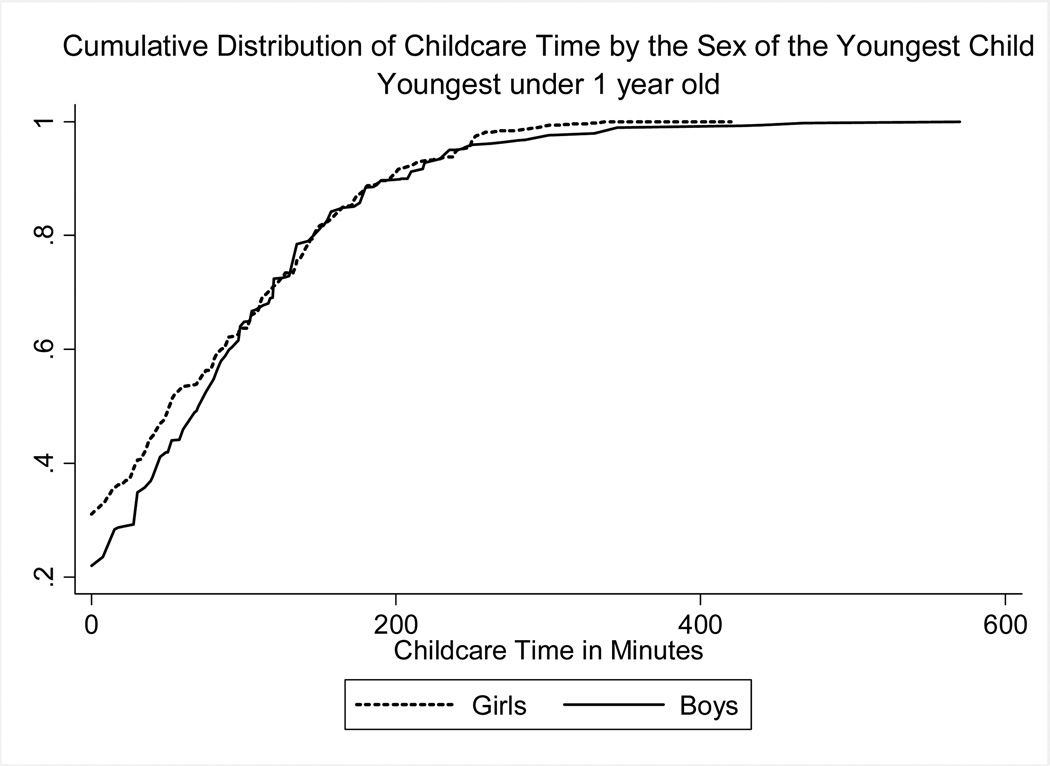
Preliminary evidence of differential treatment by gender is presented in Figure 4, which shows the cumulative distribution of childcare by gender of the youngest child under age one.²⁴ The baby-boy distribution appears to first-order stochastically dominate that of baby girls, suggesting that boys receive more childcare than girls. To obtain estimates of the effect of gender on childcare time, we estimate:

$$Z_h={\alpha }_0+{{\alpha }_1}^{*}{B}_h+X_h\rho +u_h,$$

where Z_h is the total amount of time that all members in the household spent on childcare, and B_h is a dummy for whether the household’s youngest child is a boy. We present the results with and without controlling for predetermined household-level covariates, X_h. The standard errors are estimated using White’s correction for heteroskedascity, and we use the survey weights.²⁵

Figure 4. Childcare time by gender.

Notes: Authors’ computations using the Indian Time Use Survey 1998–1999

The main results are in Table 6. The first column estimates a simple OLS model where the dependent variable is the total number of minutes spent on childcare, including zeroes. It shows that households where the youngest child is a boy spend roughly 33 minutes more per day taking care of children than households whose youngest child is a girl, or about 14% more relative to the mean. Column 2 shows that this estimate is robust to controlling for religion, ethnicity, and the area of land that the household owns. In Column 3, we estimate a logit of whether the household spends any time on childcare. Although the estimates are positive, they are not statistically significant, and they are somewhat small (about 4%). If we estimate an OLS model instead for those who report some care (column 4), we find that households whose youngest child is a boy spend roughly 24 minutes more (about 10% more) per day on childcare than households whose youngest child is a girl. If we estimate a Tobit model to account for censoring at zero (Column 5), we also find a statistically significant increase in childcare of 15%. Results are similar if we look at households whose youngest child is under 2 (panel B). In Column 6, we repeat the estimation for urban households. The effect of gender is actually negative, but the sample is small, and the standard errors are large.

TABLE 6.

EFFECT OF CHILD GENDER ON HOUSEHOLD CHILD CARE TIME, TIME USE SURVEY (1998–1999)

Model:	OLS	OLS	Logit	OLS	Tobit	OLS
Dependent variable:	Number of minutes per day, including 0s	Number of minutes per day, including 0s	Any care? (Beta reported)	Number of minutes per day>0	Number of minutes per day	Urban Households
	(1)	(2)	(3)	(4)	(5)	(6)
Panel A: Youngest kids under 1 year old
Male=1	32.772 [17.669]*	30.018 [17.511]*	0.613 [0.397]	24.226 [17.344]	36.309 [18.855]*	−5.709 [34.546]
Controls?	no	yes	no	no	no	no
Obs	562	562	562	516	562	204
Mean Y	236.62	236.62	0.93	255.51	236.62	265.737
Panel B: Youngest kids under 2 years old
Male=1	18.689 [8.643]**	16.602 [8.593]*	−0.052 [0.182]	21.951 [8.629]**	18.647 [9.509]**	−15.867 [16.173]
Controls?	no	yes	no	no	no	no
Obs	1947	1947	1947	1747	1947	677
Mean Y	196.90	196.90	0.90	219.17	196.90	235.373

Notes: Robust standard errors in brackets. The dependent variable in all columns except (3) is the number of minutes per day spent with child care by all household members. The dependent variable in column (3) is an indicator variable for positive childcare time. Panel A reports results for households whose youngest child is under 1 year old and panel B for those whose youngest is under 2. The controls include dummies for household caste (2 dummies), a dummy for whether the household was Hindu and the area of the land owned and possessed by the household. Survey weights are used in estimation.

^***p<0.01,

^**p<0.05,

^*p<0.1

Table 7 tests if the effects of gender differ based on observable household characteristics and on the type of care. Column 2 restricts attention to families with no other children under age six: For these families, all childcare is directed toward the youngest child. (For our main results, we do not know who in the household is receiving the childcare.) We find that infant boys receive 60 more minutes of care than infant girls (about 30% more). The TUS was conducted in 1998–1999, a period where ultrasound technology was already available in India (Bhalotra and Cochrane 2010); therefore, sex-selective abortion could bias our results. In Column 4, we repeat the estimation for households with only one child under 15 years of age—this child is likely to be the firstborn, a group among which selective abortion is believed to be less prevalent (Jha et al. 2006, Retherford and Roy 2003). We find similarly large effects for this group.

TABLE 7.

HETEROGENEITY IN CHILDCARE TIME, TIME USE SURVEY (1998–1999).

	Households w/ ONLY 1 child under 6	Households w/ ONLY 1 child under 15	Physical Care		Supervising		Exclusive Care
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Panel A: Youngest kids under 1 year old
Male = 1	59.855 [30.143]**	55.177 [34.848]	30.139 [13.444]**	5.4 [23.359]	20.217 [12.220]*	55.231 [16.674]***	28.517 [15.577]*	59.261 [24.936]**
Male* (# other children under 6)				20.59 [14.671]		−28.721 [11.020]***		−27.47 [15.135]*
# Other children under 6				−10.209 [8.372]		18.098 [7.163]**		−3.689 [9.636]
Constant	204.183 [21.463]***	194.695 [25.245]***	151.245 [8.622]***	164.184 [15.016]***	46.131 [8.397]***	23.193 [7.541]***	119.165 [11.078]***	123.841 [16.318]***
Observations	151	113	562	562	562	562	562	562
Panel B: Youngest kids under 2 years old
Male = 1	50.777 [15.969]***	40.999 [17.269]**	14.673 [6.597]**	20.442 [11.150]*	10.643 [6.077]*	35.414 [9.874]***	8.635 [7.575]	37.278 [12.577]***
Male* (# other children under 6)				−4.725 [7.181]		−20.231 [6.003]***		−23.943 [7.496]***
# Other children under 6				1.606 [4.471]		8.315 [4.061]**		−3.696 [5.001]
Constant	168.946 [10.742]***	168.042 [11.828]***	130.381 [4.346]***	128.368 [7.393]***	43.516 [3.723]***	33.092 [5.369]***	91.12 [5.297]***	95.753 [8.097]***
Observations	481	389	1947	1947	1947	1947	1947	1947

Notes: Robust standard errors in brackets. Panel A reports results for households whose youngest child is under 1 year old, panel B for those whose youngest is under 2.The dependent variable in columns (3) and (4) is the amount of time spent taking physical care of children (e.g., washing, dressing and feeding). The dependent variable in columns (5) and (6) is the amount of time spent supervising children. The dependent variable in columns (9) and (10) is the amount of time spent exclusively on childcare -- i.e., the caretaker was not multi-tasking. The variable “# other children under 6” excludes the youngest child. Its mean is equal to 1.23 children. All columns are estimated using OLS. Survey weights are used for estimation.

^***p<0.01,

^**p<0.05,

^*p<0.1

In Columns 3 and 5, we show that households spend more time in all types of childcare if the baby is a boy. The amount of supervision per child increases with the number of children, but not the amount spent on physical care (Columns 4 and 6). Most interestingly, gender differences in physical care do not decrease with the number of other siblings, whereas the effect of gender disappears for supervising if there are two additional children under age six. These patterns can be explained by the “private-good versus public-good” nature of childcare activities. Because supervising is a “public good” type of care, as the number of young children in the household increases, members will spend disproportionally more time in this type of care, and this time will not be closely related to the sex of the youngest child. In contrast, physical care is a “private good,” so there is room for differential treatment even when other young children are present.

Columns 7 and 8 show estimates of the effect of gender on “exclusive childcare time”—our proxy for quality care—defined as the number of minutes that adults spent caring for children and not doing anything else. Households whose youngest child is a boy provide more exclusive childcare than households whose youngest child is a girl. The coefficient in Column 7 corresponds to 24% more exclusive time spent on boys. Just like for supervision, the effects are smaller if there are more children present in the household.

We also investigate who in the household provides the care. All members report spending substantially more time on childcare if the youngest child is a male, even though in general the estimates are significant only for adult women (Web Appendix Table 3). Overall, we find that more time is spent on childcare in households whose youngest child is a boy, and the quality of this time is higher.

VII. Robustness Checks

Differential misreporting

One concern with our results is that boy–girl differences in inputs may be overestimated because mothers are systematically misreporting on the basis of gender. For instance, mothers of boys might be more likely to report that a boy was vaccinated when in fact he was not because they feel they are expected to vaccinate boys (social desirability). Or they might overstate the length of time the boy was breastfed.

Several pieces of evidence suggest that not all the differences by gender can be explained by misreporting. First, we find gender differences in two objectively measured outcomes that are not based on mother reports: anthropometrics and the rate at which mothers have vaccination cards at the interview. We also find gender differences in childcare time, which is unlikely to have been misreported based on the gender of the youngest—respondents did not identify the child who was being cared for, only the overall time spent taking care of children. Moreover, we do not find any evidence of gender biases in prenatal care measures (Table 1), which could have been inflated when mothers of boys reported them retrospectively.

Sex-selective abortion

In Web Appendix Table 6, we report estimates limiting the sample to firstborn children—previous literature suggests that sex-selective abortion is less important among firstborn (Retherford and Roy 2003). However, previous literature also suggests that discrimination against girls increases with birth order (Das Gupta 1987), so it is not entirely clear a priori what to expect in this sample. Nevertheless, we find that even among firstborn, boys appear to receive more inputs, although the magnitudes are smaller and not always significant. (However, this sample is substantially smaller.) We also documented in Table 4 that gender differences in childcare are large among firstborns (although in the TUS we cannot identify them well).

Sex-selective mortality

One advantage of the 1992 DHS data (unlike later waves) is that mothers were asked to report on investments even for children who had died before the interview. Assuming that these maternal reports are not gender-biased, we can gauge the effect of mortality on our estimates by simply including these deceased children in our estimation sample. The results do not differ from our main results (Web Appendix Table 6). Alternatively, we can compute bounds by imputing the missing information under best- and worst-case scenarios for children who died before the investment was possible²⁶ or for whom the maternal report was missing.²⁷ Our bounds are not very tight as many include zero. However, if one assumes that only the upper bounds are likely (deceased girls were treated worse than deceased boys), then our upper bounds imply that our estimates could be underestimated by as much as 50%.

VIII. Investigating Reasons for Differential Investments

Greater needs

We begin by investigating whether boys appear to need more inputs from their parents, which could be the case if boys are more active or if they get sick more frequently. The mortality data from India is inconsistent with the view that boys in India need more investments, because girls have larger mortality rates than boys from about 6 months of age to well into adulthood. Nevertheless, we looked at the medical literature to assess whether any of the inputs we studied are known to provide greater benefits to boys than girls. The meta-analysis of RCTs performed by Beaton et al. (1994) shows that Vitamin A supplementation has the identical proportional effect on mortality for boys and girls. Not much is known about other inputs from randomized trials. But the benefits of breastfeeding appear to be the same for boys and girls—if anything females appear to benefit more.²⁸ BCG vaccines appear to benefit girls more (Roth et al. 2006), and so do measles vaccines (Koenig et al. 1990). This evidence, though scant, does not support the idea of greater benefits for boys.

Nevertheless, parents could still perceive greater benefits to providing particular inputs to boys. To assess how much of the observed differences in inputs could be driven by boys’ greater needs, we look at whether in South Africa parents also give boys more inputs and interpret this as an upper bound on the greater needs of boys. South Africa is the only developing country we are aware of with a dedicated time-use survey,²⁹ a DHS survey, and for which fertility patterns suggest no son preference (Gangadharan and Maitra 2003).

Figure 5 plots the cumulative distribution of household childcare time by gender of the youngest child among children under the age of one. There is a small difference between the genders: Households in which the youngest child is a girl are more likely to report no childcare.³⁰ In Table 8, we report the point estimates for the gender differences: We find that boys are more likely to get any childcare (the implied marginal effect is about 13%), but that conditional on getting childcare, girls appear to get more childcare than boys. This evidence does not strongly support the idea that boys need more childcare time. Table 8 also reports whether boys are given more of all other inputs in the DHS. Most of the coefficients on the male dummy are statistically insignificant; furthermore, most coefficients are negative and small for most inputs, which suggests that there is no greater need among boys. Of course, this evidence is only suggestive, since it is not clear that South Africa provides a good counterfactual for India.

Figure 5. Childcare Time by gender.

Sources: Authors’ computations using the South Africa Time Use Survey 2000.

TABLE 8.

DO BOYS NEED MORE? MEAN GENDER DIFFERENCES IN PARENTAL INPUTS

Dependent variable:	Model:	Coefficient on I(male=1)	s.e.	N	Mean Y	Percent effect
Panel A: 2000 SOUTH AFRICA TIME USE SURVEY (TUS) CHILDREN UNDER 1
Childcare, mins. per day >= 0	OLS	1.184	[12.055]	521	99.6	1%
Childcare, mins. per day >= 0	Tobit	9.874	[16.353]	521	99.6	10%
Childcare, mins. per day > 0	OLS	−15.233	[13.303]	386	136	−11%
Any care?	Logit (Beta)	0.471	[0.265]*	521	0.733	13%
Panel B: 1998 South Africa DHS CHILDREN AGES 0–15 MONTHS
Ever breastfed?	OLS	0.024	[0.033]	723	0.875	3%
# months breastfed	censored regression	−0.409	[1.218]	632	6.941	−6%
log(# months breastfed)	censored regression	−0.085	[0.234]	632	1.663	−5%
Vaccination card?	OLS	−0.05	[0.035]	732	0.835	−6%
Number of immunizations	OLS	0.027	[0.111]	705	3.487	1%
At least one immunization	OLS	−0.004	[0.010]	705	0.98	0%
Completely immunized	OLS	0.037	[0.036]	705	0.3	12%
Vitamin A	OLS	na	na	na	na	na

Notes: Standard errors [in brackets] are computed taking survey design into account. Vitamin A supplementation information is not available for South African DHS. Results reported do not include demographic controls.

^***p<0.01,

^**p<0.05,

^*p<0.1

Changes in anticipated family size

Another possible explanation for our results is that families change their expectations once the gender of the baby is revealed at birth. Parents who desire boys but have a girl anticipate having more births in the future: They might start saving, or go back to work earlier (Rose 2000), which could explain why girls receive fewer investments. In Table 9, we investigate this issue in two ways: by estimating an upper bound of how much of the effect of child gender on investments may work through anticipated family size and by directly controlling for proxies of anticipated family size.

TABLE 9.

ANTICIPATED FAMILY SIZE and ACTUAL FAMILY SIZE. DHS 1992

	# Children	Ever breastfed?	Vitamin A supplement?	Vaccination card?	# months breastfed	log(# months breastfed)
	(1)	(2)	(3)	(4)	(5)	(6)
Panel A: OLS Estimate of the Effect of First Born Boy on Family Size (N=14, 991; mean # children: 4.56)
First Born Male = 1	−0.282 [0.038]***
Panel B: OLS Estimate of the Effect of Family Size on Investments
# Children		0.001 [0.001]*	−0.019 [0.001]***	−0.032 [0.002]***	0.397 [0.044]***	0.029 [0.003]***
Obs		32070	30911	32183	31119	31119
Panel C: How much of the effect of male is accounted by anticipated family size?
Panel A * Panel B		0.000	0.005	0.009	−0.112	−0.008
% of (male=1) in Panel D		−6%	38%	21%	−153%	−63%
Panel D: OLS Estimate of the Effect of Boy Youngest on Investments
Male = 1		0.005 [0.004]	0.014 [0.007]**	0.043 [0.009]***	0.073 [0.095]	0.013 [0.017]
Obs		11578	11226	11586	11043	11043
Panel E: Estimate of the Effect of Boy Youngest on Investments Controling for Proxies of Anticipated Family Size
Male = 1		0.001 [0.005]	0.009 [0.007]	0.045 [0.010]***	0.111 [0.100]	0.019 [0.018]
Mom Pregnant = 1		0.024 [0.013]*	0.108 [0.029]***	0.11 [0.035]***	3.392 [0.251]***	0.569 [0.035]***
Mom/Dad Sterilized = 1		0.007 [0.006]	0.015 [0.024]	−0.036 [0.029]	−0.763 [0.223]***	−0.138 [0.035]***
Mom More Kids = 1		0.016 [0.006]***	0.032 [0.008]***	0.064 [0.011]***	0.314 [0.109]***	0.069 [0.020]***
Ideal Number of Children		0.002 [0.002]	−0.021 [0.003]***	−0.062 [0.005]***	0.128 [0.048]***	0.023 [0.008]***
Use Contraceptive = 1		0.045 [0.005]***	0.102 [0.019]***	0.201 [0.022]***	2.115 [0.171]***	0.399 [0.026]***
Obs		10318	9998	10323	9851	9851

Notes: Robust standard errors [in brackets]. Panels A-D report regression results with no other controls. In Panel A we regress family size on the gender of the first-born child (coefficient −0.282)--the sample is restricted to mothers ages 38 and above. Results in Panels B and D correspond to a separate linear regression of the dependent variable listed in the column on the independent variables listed in the rows. Panel B presents OLS estimates of the effect of actual family size on investments. Panel C corresponds to the product of Panels A and B, our estimate for the effect of child gender on investments working through family size. In Panel D we reproduce some of the mains results of the boy-girl differences in investments. Panel E shows the same regressions as Panel D but it includes proxies for anticipated family size (namely dummy for being pregnant, dummy for use of some contraceptive method, dummy for sterilization, dummy for whether mother reported wanting more children and the reported ideal number of children) are included as controls. The sample in panels B and D are restricted to live children. Panel D further restricts the sample to youngest 0–15 months old. Survey weights are used for estimation.

^***p<0.01,

^**p<0.05,

^*p<0.1

To compute the upper bound, we estimate the effect of child gender on investments working through actual family size—calculated as the effect of the gender of the firstborn child on completed family size times the effect of family size on investments. Since anticipated family size is hard to measure, we use actual family size instead. There are two reasons why the actual family size mechanism should provide an upper bound to the anticipated family size mechanism. First, the best existing estimates of family size effects suggest that OLS estimates of the actual family size effects overestimate the negative causal effect of family size on children’s outcomes (e.g., Black, Devereux and Salvanes 2005). Second, one might expect the magnitude of the causal effect of anticipated family size on investments to be smaller than the effect of actual family size on investments given the intrinsic uncertainty associated with anticipated family size.

Table 9 shows the results of such an exercise. Panel A shows that mothers whose firstborn child is a boy end up having 0.28 fewer children than their peers—the sample was restricted to women 38 years or older, who have most likely completed their fertility.³¹ Panel B shows the results from OLS estimates of the effect of actual family size on investments. Panel C shows our estimates of the effect of child gender on investments working through actual family size, which correspond to the product of Panels A and B. These estimates can be compared to the figures in Panel D, where we reproduce some of our results of the boy–girl differences in investments shown in Table 2. If our assumptions are correct, these results imply that anticipated family size can account at most for 38% of the effects we observe (in the case of vitamin A), and in fact several estimates are negative.

We also attempt to estimate the bias in our estimates because of anticipated family size by directly controlling for proxies of anticipated family size. Panel E shows results when we include as controls proxies for anticipated family size (namely a dummy for being pregnant, a dummy for use of some contraceptive method, a dummy for mother or mother’s spouse being sterilized, a dummy for whether mother reported wanting more children, and the reported ideal number of children). With the exception of Vitamin A, all the coefficients on the male dummy remain almost identical (or slightly bigger), positive and statistically significant. In fact both methods suggest that for vitamin A there is an upwards bias in OLS and for breastfeeding there is a downward bias.

Other reasons for greater investments in boys

Our results suggest that differential needs and anticipated family size cannot explain all the effects of gender that we observe. Another possible reason for differential treatment is (perceived) lower returns to investments in girls—a hypothesis we do not have enough information to assess. However, there is growing evidence that this is indeed part of the explanation, as suggested in the seminal paper by Rosenzweig and Schultz (1982). Jensen (2012) and Oster and Millet (2011) document that in India, when the returns to schooling for women increase (as a result of the availability of higher-paying jobs in female-oriented call centers), girls stay in school longer. Also Jayachandran and Lleras-Muney (2010) show in a different context that when female adult mortality declines, schooling of girls increases. Relatedly, Qian (2008) shows that in China girls’ mortality and education improve when the price of female-intensive crops and, thus, female income rises. Overall, our findings point to either differences in returns or differences in preferences as the main reasons for lower investments in girls.

IX. Assessing the Bias in Other Estimates of Gender Gaps

We proposed in Section III a novel empirical strategy that addresses the issue that son-biased stopping rules may bias the estimates of differential treatment. To gauge the contribution of our estimator, we attempt to assess the bias in other estimates of gender gaps by comparing our estimates to the estimates that ignore son-biased stopping rules.

We start by comparing estimates for childcare time. Web Appendix Table 8 investigates how the effects of gender vary depending on the strategy used. Panel A reproduces the main results using the empirical strategy we propose, for comparison. This strategy shows large gender differences, with boys receiving on average 14% more childcare time than girls. In Panel B, we show results for all children (not restricting to the youngest child) 5 years old and younger, a strategy similar to what has been used in the literature. We have two main explanatory variables, number of boys under 5 and number of children under 5. While childcare time increases substantially with the number of children, this increase is not larger when these children are boys. In fact, most of the coefficients on the number of boys have the “wrong” sign, which suggests the estimates for the older children are biased because of changes in unobserved characteristics.

However, it may also be that the nature of parental time inputs is different among older children. More generally, comparisons of estimates for different age groups are not straightforward because the nature of investments changes rapidly as a function of age. For example, some investments are acquired at specific ages, often only once when the child is very young (e.g., vaccinations), while others happen throughout the infant’s life (e.g., breastfeeding and childcare). These differences on the age profile of investments will have implications for the bias on estimates of gender differences. For example, we do not expect the gaps in vaccination rates to differ much as children age, because all vaccinations are supposed to be acquired within the first 12 months of life; thus, the “experimental sample” will yield estimates that should be very similar to those one obtains using older children.³² On the other hand, investments that occur at every age, such as time inputs, will be affected.

We assess the bias in other estimates of gender gaps by conducting the following exercise. First, we estimate gender-specific age profiles for the youngest children under 15 months of age. We then use the estimated profiles to predict what the gender gaps among older children would have been if their family characteristics were held constant. Finally, we compare the predicted gaps to the actual gaps observed for all children (not just the youngest) of all ages (pooling ages 0–4). If they are different, the difference is likely because of bias introduced by changing characteristics. The key assumption for this method is that the gender-specific age profile for the older children can be predicted using the gender specific age profile for the youngest under 15 months of age.

For some outcomes in the DHS, this exercise is likely to work well. Figure 6 illustrates the approach for breastfeeding. We first estimate flexible but parametric gender-specific age profiles using the youngest children under 15 months of age. Panel A shows the observed breastfeeding profiles by age and gender. Panel B shows what these profiles look like if we estimate them separately by age and gender for the youngest children under 15 months of age using a quadratic function of age. Then, for each gender, we project the profiles to older ages based on the estimated coefficients for age and age squared. (We also display the profiles for the entire sample for comparison.)

Figure 6. Assessing the bias in gender gaps in breastfeeding.

Notes: Authors’ computation using the 1992 Indian Demographic and Health Survey

These profiles imply different gender gaps; to better observe them, we display these gender gaps directly in Panel C. This shows that our estimates predict gender gaps that would increase with age at greater rates than is observed in the data. This result holds true regardless of the functional form we choose for age. However, the magnitudes do not: Panel D compares the bias in gender gaps implied by linear, quadratic, cubic, and quartic functions of age. The higher-order specifications imply greater bias. We take this as evidence that unobservables correlated with gender generate a downward bias in mean gender gaps, but the magnitude cannot be ascertained with great accuracy, although it appears to grow with age.

Figure 7 shows the results for our anthropometric measures, the other outcomes for which age patterns can be predicted with some accuracy. ³³ For both height and weight, the models predict larger gender gaps than is observed in the data, and the gaps grow with age.

Figure 7. Assessing the bias in gender gaps in anthropometric measures.

Notes: Authors’ computation using the 1992 Indian Demographic and Health Survey

Overall, we find that for many outcomes (time, breastfeeding, height, and weight), gender gaps are typically underestimated. For Vitamin A and having a vaccination card, we cannot properly account for the age profiles; therefore, the method is less useful in analyzing the bias. In all cases however, the exact magnitude of the bias is sensitive to functional-form assumptions.

X. Conclusion

This study asks whether parents treat girls and boys differently in India. Although women in India lag behind men in many domains, there is equivocal evidence about whether these lower outcomes are the result of lower parental investments in girls, particularly because boys and girls live in household with different observed and unobserved characteristics as a result of son-biased stopping rules. We develop a novel empirical strategy to address this problem by looking at children while they are still very young—a situation in which the parents have not had a chance to respond to the gender of the last child by having more children. We then used our identification strategy to look at differential treatment for inputs previously used in the literature. In addition, we examine whether families spend more time with childcare when the baby is a boy than when the baby is a girl. Time investments have not been studied previously in the context of developing countries.

We find evidence that boys receive more investments than girls in rural India. Households with an infant boy under the age of one spend roughly 30 minutes more per day (about 15% more time) on childcare than households with an infant girl. This difference is even larger for one-child households: Households with one boy under age six spend roughly 60 minutes more (30%) per day on childcare than households with one girl under age six. We also find suggestive evidence that the quality of childcare given to boys is higher. Moreover, we find that boys are more likely to be breastfed longer and to be given vitamin supplementation. In general, we find these inputs to be at least 10% higher for boys. Finally we also find that, relative to girls, boys in India fare better than boys in other developing countries with respect to height and weight, consistent with higher parental inputs. We do not find evidence however of higher vaccination rates for boys in objectively collected data, despite maternal reports that boys are more likely to obtain vaccinations.

We also investigate why parents may choose to invest less in girls. We find no evidence of greater needs among boys. We also look at whether girls receive less because families of recently born girls anticipate that they will have to continue having more children. We find that the anticipated family size effect accounts for at most 38% of the effect of child gender on investments (and much less than that for most investments). Thus, in general, we find that these explanations cannot account for the patterns we observe across all outcomes. We conclude that parents invest less in girls because these investments have lower returns (for which there is some evidence in the literature) or because they have a preference for sons, although our study is not conclusive on the ultimate reason for differential treatment.