Measurement of δ¹⁸O, δ¹⁷O, and ¹⁷O-excess in Water by Off-Axis Integrated Cavity Output Spectroscopy and Isotope Ratio Mass Spectrometry

Abstract

Stable isotopes of water have long been used to improve understanding of the hydrological cycle, catchment hydrology, and polar climate. Recently, there has been increasing interest in measurement and use of the less-abundant ¹⁷O isotope in addition to ²H and ¹⁸O. Off-axis integrated cavity output spectroscopy (OA-ICOS) is demonstrated for accurate and precise measurements δ¹⁸O, δ¹⁷O, and ¹⁷O-excess in liquid water. OA-ICOS involves no sample conversion and has a small footprint, allowing measurements to be made by researchers collecting the samples. Repeated (514) high-throughput measurements of the international isotopic reference water standard GISP demonstrate the precision and accuracy of OA-ICOS: δ¹⁸O_VSMOW-SLAP =−24.74 ± 0.07 ‰ (1σ) and δ¹⁷O_VSMOW-SLAP = −13.12 ± 0.05 ‰ (1σ). For comparison, the IAEA value for δ¹⁸O_VSMOW-SLAP is −24.76 ± 0.09 ‰ (1σ) and an average of previously reported values for δ¹⁷O_VSMOW-SLAP is −13.12 ± 0.06 ‰ (1σ). Multiple (26) high-precision measurements of GISP provide a ¹⁷O-excess_VSMOW-SLAP of 23 ± 10 per meg (1σ); an average of previously reported values for ¹⁷O-excess_VSMOW-SLAP is 22 ± 11 per meg (1σ). For all these OA-ICOS measurements, precision can be further enhanced by additional averaging. OA-ICOS measurements were compared with two independent isotope ratio mass spectrometry (IRMS) laboratories and shown to have comparable accuracy and precision as the current fluorination-IRMS techniques in δ¹⁸O, δ¹⁷O, and ¹⁷O-excess. The ability to measure accurately δ¹⁸O, δ¹⁷O, and ¹⁷O-excess in liquid water inexpensively and without sample conversion is expected to increase vastly the application of δ¹⁷O and ¹⁷O-excess measurements for scientific understanding of the water cycle, atmospheric convection, and climate modeling among others.

Introduction

Stable isotopic compositions of water, particularly δ²H and δ¹⁸O, have long been used to improve understanding of the hydrological cycle,¹ catchment hydrology,² and polar climate.^{e.g. 3} The combination of the measurements, d-excess =δ²H − 8δ¹⁸O, roughly describes the degree to which δ²H values vary from what would be expected at low and temperate latitudes if equilibrium processes were solely responsible for the relationship between δ²H and δ¹⁸O values. Kinetic fractionation processes, such as diffusive processes associated with evaporation, are partially responsible for the variation in d-excess which varies as a function of both evaporative temperature and humidity.^{1, 3} Given its sensitivity to environmental conditions of evaporation, d-excess has been used extensively to characterize climate and hydrological conditions today and in the past.^{e.g. 3–6}

Recently, there has been increasing interest in measurement and use of the less-abundant ¹⁷O isotope in addition to ²H and ¹⁸O. Similarly to d-excess, the deviation from an expected relationship between ¹⁷O/¹⁶O and ¹⁸O/¹⁶O ratios has been defined by ¹⁷O-excess = ln(δ¹⁷O + 1) − 0.528ln(δ¹⁸O + 1) and variation in ¹⁷O-excess in waters is dominated by kinetic fractionation effects.⁷ However ¹⁷O-excess is relatively insensitive to temperature and thus can be used as a direct proxy for humidity at the region of evaporation.^{7, 8} Combined measurements of d-excess and ¹⁷O-excess allow researchers to understand more fully the contributions of both temperature and relative humidity to water isotope fractionation, thus improving atmospheric models and understanding of climate processes.^e.g.8 Recent advances using fluorination coupled to isotope ratio mass spectrometry (IRMS) have made possible the precise measurements of ¹⁷O-excess in waters; these measurements have been applied to ice,^{8, 9} meteoric waters,¹⁰ and African precipitation.¹¹

The variation in ¹⁷O-excess in meteoric waters is generally a very small quantity (reported in per meg, parts per million) and meaningful measurements require extremely high precision. Careful studies of ¹⁷O-excess typically cite precisions for ¹⁷O-excess of less than 10 per meg,^{e.g. 8, 12, 13} an order of magnitude smaller than the cited precisions for both δ¹⁸O and δ¹⁷O. While at first glance it seems impossible to measure a derived quantity to better precision that its constituent measurements, the improvement in precision is real and is described in detail by Landais et al.¹⁴ and Luz and Barkan.¹⁰ Briefly, the definition of ¹⁷O-excess is derived from the measured global meteoric water line (GMWL) for δ¹⁸O and δ¹⁷O, so that ¹⁷O-excess values indicate deviations from the GMWL. The GMWL is itself naturally created by the isotopic fractionation of water due to vapor-liquid kinetics and equilibrium and vapor diffusion in air, and thus the slope of 0.528 in the ¹⁷O-excess definition^{12, 15} is extremely close to the liquid-vapor equilibrium fractionation slope of 0.529¹² and reasonably close to the kinetic evaporation slope of 0.518.⁷ The consequence of this is that any measurement errors which result from mass-dependent equilibrium fractionation of a sample will cancel nearly perfectly on calculation of ¹⁷O-excess, provided that δ¹⁸O and δ¹⁷O are measured on the same sample. This cancellation of mass-dependent equilibrium fractionation errors can thus enable measurements of ¹⁷O-excess that are much more precise than the constituent measurements of δ¹⁸O and δ¹⁷O.

All of the previously published measurements of ¹⁷O-excess in water have utilized fluorination of water into O₂ followed by IRMS (see e.g. Baker et al.¹⁶ and Barkan and Luz¹² and references therein). This IRMS method requires chemical conversion using toxic reagents and measurement on sophisticated and expensive equipment with highly-skilled operators; only a handful of laboratories worldwide currently have this measurement capability. In this work we demonstrate for the first time the use of off-axis integrated cavity output spectroscopy (OA-ICOS) to directly measure δ¹⁸O, δ¹⁷O, and ¹⁷O-excess in liquid water. OA-ICOS involves no sample conversion and has a small footprint, allowing measurements to be made by researchers collecting the samples. This study demonstrates by comparison with two independent IRMS laboratories that OA-ICOS measurements of δ¹⁸O, δ¹⁷O, and ¹⁷O-excess in liquid water achieve accuracy and precision comparable to the fluorination and IRMS method.

Experimental

Off-Axis ICOS Analysis

We utilized a commercially-available, OA-ICOS laser absorption spectrometer (Los Gatos Research (LGR) Triple Isotope Water Analyzer (TIWA-45EP)) for simultaneous direct measurement of the ²H/¹H, ¹⁸O/¹⁶O, and ¹⁷O/¹⁶O stable isotope ratios in liquid water. The OA-ICOS instrument employs near-infrared tunable diode laser absorption spectroscopy with the laser coupled off-axis to a high-finesse optical cavity¹⁷ to provide highly accurate quantification of δ¹⁸O, δ¹⁷O, and δ²H in injected water samples. The OA-ICOS instrument is very robust¹⁸ and more compact¹⁹ than the current IRMS configuration. ¹⁷O-excess was calculated from measurements of δ¹⁸O and δ¹⁷O according to the definition ¹⁷O-excess = ln(δ¹⁷O + 1) − 0.528ln(δ¹⁸O + 1).⁷ Water samples were introduced without sample conversion into the OA-ICOS instrument via a PAL HTC-xt autoinjector (CTC Analytics) equipped with a heated (≈85 °C) injector block (LGR), where the water samples were evaporated for isotope analysis directly on the water vapor. Liquid water samples were injected into the injector block using a Hamilton 1.2 μL, zero dead volume syringe (P/N: 203185/01).

Simultaneous measurements of δ¹⁸O, δ¹⁷O and δ²H were completed at a speed of approximately 90 seconds per measurement of an individual injection. In the normal range of natural waters, LGR recommends injecting each sample 6 times and averaging the last four injections to produce a single, high-throughput sample measurement; in this way 128 sample measurements can be completed per day in addition to reference water standards. Because of the use of a large span of primary reference water standards and the desire to measure δ²H, as well as δ¹⁸O and δ¹⁷O, nine preparatory injections (injections which are not measured, designed to eliminate inter-sample memory) followed by 5 measurement injections were run for each sample in this study to overcome memory effects (see discussion below). The last four injections were averaged to produce a single, high-throughput (HT) sample measurement. Multiple HT measurements of the same sample can be averaged to improve measurement precision as described below. δ²H values, while measured throughout this study, are outside the scope of this manuscript and will be discussed in a future manuscript. Primary isotopic reference water standards were interleaved with samples throughout each run; data normalization is described in detail below.

Off-Axis ICOS Data Processing

Processing of raw instrumental OA-ICOS data proceeded in the following steps. First, any injection with measured water number density outside of the manufacturer's suggested range of 2 – 4.5 × 10¹⁶ H₂O moleculess/cm³ was discarded. Second, any injection for which the water had not fully evaporated prior to measurement of the isotope ratios was discarded. Incomplete evaporation can be caused by septum pieces, salts, or other debris inside the injector block. Incomplete evaporation was detected by examining the standard deviation of the measured water number density (σ_nmeas) as reported by the instrument. Injections with a σ_nmeas more than three standard deviations higher than the average σ_nmeas for the analysis were discarded. Any measurement set (typically a 20 hour run sequence of interleaved samples and standards) with more than 2% of injections rejected by the preceding two filters was repeated.

Third, a mathematical injected volume correction was applied similar to that described by Lis et al.²⁰ This type of correction commonly is called a “linearity correction” in IRMS data reductions. A single isotopic reference water was measured on the analyzer at varying injected volumes between 600 and 1200 nL. The measured water number density (n_meas) was then normalized, N= (n_meas-n*)/n*, where n* = 3 × 10¹⁶ molecules/cm³. For each isotope, the measured isotope ratios of the isotopic reference water, R(¹⁸O/¹⁶O) and R(¹⁷O/¹⁶O), were plotted versus the normalized injected volumes and a linear least-squares fit was utilized to determine the slope of the injected volume effect. The slopes, one for each isotope, remained relatively constant over the six month analysis period. For each measurement injection, the measured water number density was normalized and then multiplied by the previously-determined slopes to establish the ratio correction. The injected volume correction was applied separately for each isotope to each injection in an analysis before further processing. After the above processing, the isotope ratios of the final four injections of each sample were averaged to produce raw isotope ratios, R(¹⁸O/¹⁶O) and R(¹⁷O/¹⁶O), which were then normalized as described below. The average of the last four injections of each sample produced the final, measured value for that sample and is herein referred to as an individual high-throughput (HT) sample measurement. Multiple HT measurements can be averaged to improve measurement precision of all isotope analyses, as is described below for averages of 20 HT measurements, herein referred to as high-precision (HP) sample measurements.

Isotope Ratio Mass Spectrometric Analysis

Isotope ratio mass spectrometric (IRMS) analyses were performed at both the Laboratoire des Sciences du Climat et l'Environnement (LSCE) and Johns Hopkins University (JHU). The analytical approaches at both laboratories are based on methods outlined by Baker et al.¹⁶ and modified by Luz and Barkan. ¹² Briefly, 2–3 μL of water was fluorinated using CoF₃ under helium flow to quantitatively produce O₂. O₂ was separated from helium on a molecular sieve trap immersed in liquid nitrogen and finally trapped by liquid helium for mass spectrometric analysis. Mass Spectrometry was performed on a dual-inlet Thermo MAT 253 mass spectrometer which allows simultaneous measurements of m/z 32, 33, and 34.

IRMS measurements at JHU used a modified fluorination line similar to that described by Schoenemann et al.¹³ All JHU IRMS measurements were run against a working O₂ reference gas during 7 sequences of 10 dual inlet runs. The working O₂ reference was routinely calibrated by analyzing the International Atomic Energy Agency (IAEA) primary reference water standards Vienna Standard Mean Ocean Water 2 (VSMOW2) and Standard Light Arctic Precipitation 2 (SLAP2)²¹ as part of the analytical sequence. Using this procedure, a maximum of 8 total waters (including references) can be processed and measured per day at JHU.

IRMS measurements at LSCE were run against a working O₂ isotopic reference standard during 2 sequences of 16 dual inlet runs. The working O₂ standard was calibrated by analyzing VSMOW2 and SLAP2. Every day, one or two isotopic reference waters, themselves also calibrated against VSMOW2 and SLAP2, were processed together with the samples. In order to avoid any memory effects, blanks were run between samples any time their δ¹⁸O differences exceed 3 ‰. Using this procedure, 4 to 5 duplicate samples were processed and measured per day at LSCE in addition to isotopic reference waters.

Data Normalization

In order to make meaningful comparisons of isotope measurements between laboratories, a common data normalization scheme is necessary. All three laboratories involved in this comparison have utilized the primary isotopic reference water standards VSMOW2 and SLAP2 with the normalization proposed by Schoenemann et al.¹³ Specifically, VSMOW2 values of δ¹⁸O_VSMOW-SLAP = 0 ± 0.02 ‰²¹ and δ¹⁷O_VSMOW-SLAP = 0 ± 0.02 ‰²² and SLAP2 values of δ¹⁸O_VSMOW-SLAP = −55.5 ± 0.02 ‰²¹ and ¹⁷O-excess_VSMOW-SLAP = 0 (δ¹⁷O_VSMOW-SLAP ≈ −29.6986 ‰)¹³ were used in all calculations. The ¹⁷O-excess_VSMOW-SLAP values for both VSMOW2 and SLAP2 were taken to be defined as zero and thus considered to have no uncertainty for propagation of errors.¹³ The uncertainty of the δ¹⁷O_VSMOW-SLAP of SLAP2 was calculated from the uncertainty of δ¹⁸O_VSMOW-SLAP and ¹⁷O-excess_VSMOW-SLAP and determined to be 0.02 ‰. In all cases, the uncertainties of the measured δ¹⁸O and δ¹⁷O values have been convolved with the uncertainties of the reported VMSMOW2 and SLAP2 values to report values on the VSMOW-SLAP scale. No convolution has been used in the case of ¹⁷O-excess as the standard values are taken to have zero uncertainty.

The OA-ICOS instrument outputs raw data as isotope ratios; conversion to δ-values utilized the VSMOW isotope ratios R(¹⁸O/¹⁶O) = 2005.20 × 10^{−6 23} and R(¹⁷O/¹⁶O) = 379.9 × 10⁻⁶. ²⁴ Note that while these ratios were measured on VSMOW, measurements of VSMOW and VSMOW2 show that they have indistinguishable δ¹⁸O and δ¹⁷O values,²² and thus indistinguishable R(¹⁸O/¹⁶O) and R(¹⁷O/¹⁶O) values. Normalization was completed on ratios after which normalized ratios were converted into normalized δ-values vs VSMOW-SLAP. Normalization in ratio space is algebraically identical to normalization in δ-value space; the order of operations is insignificant. Dual-inlet IRMS instruments output raw data in both ratios and δ-values relative to an internal O₂ working isotopic reference standard; normalization was completed on raw δ-values to produced normalized δ-values vs. VSMOW-SLAP.

For OA-ICOS measurements, the primary isotopic reference water standards VSMOW2 and SLAP2 were interleaved throughout each measurement set, typically > 10 measurements of each standard in an approximately 20 hour run. In order to minimize the effects of instrumental drift, a spline calibration was used. Specifically, for each standard, a cubic spline function was used to interpolate between measurements of that standard to produce a local value of each standard for every measurement (either standard or sample). For each standard or sample measurement, the local values of SLAP2 and VSMOW2 were fitted to the accepted values for the standards using the `traditional linear' method as described by Schoenemann et al.¹³ This produced a local slope and intercept that were used to normalize the measurement to the VSMOW-SLAP scale. This procedure was completed separately for each measured isotope ratio.

Results and Discussion

Sample-to-sample memory

Many researchers have noted with laser-based measurements of water isotopes that there is a sample-to-sample memory effect between samples (e.g. ^{20, 25–27}). This memory effect is likely due to a combination of factors, including mixing of waters and carryover by the sampling syringe²⁸ as well as the tendency of water to adhere to the internal surfaces of the instrument.²⁰ Sample-to-sample memory is particularly apparent for large changes in isotope ratio and for the ²H isotope. Figure 1a illustrates the memory observed (from all causes) with the TIWA instrument for the transition from SLAP2 to VSMOW2 (−55.5 ‰ to 0 for δ¹⁸O), which is among the largest differences encountered between natural waters. Fourteen injections of VSMOW2 were performed directly after 14 injections of SLAP2. The solid line is at 0, the known value for VSMOW2, and the dashed lines are at ± 0.2 ‰, approximately the 1σ measurement uncertainty of a single injection (as noted above, four injections are generally averaged to produce a single, HT measurement with the factor of two improvement in precision). For the SLAP2 to VSMOW2 transition, for δ¹⁸O (black squares), the first four injections and for δ¹⁷O (red circles) the first two injections fall outside of the ± 0.2 ‰ band. In contrast, for δ²H (see inset) the first 6 injections fall outside of the 1σ uncertainty band for a single injection of 1.0 ‰. For smaller isotopic composition changes in the common range of natural waters, < 25 ‰ change in δ¹⁸O and < 13 ‰ change in δ¹⁷O, two or fewer injections fall outside of the 1σ uncertainty band for all three isotopes. Figure 1b illustrates this case on VSMOW2 measured immediately after Greenland Ice Sheet Precipitation (GISP), a transition from −24.76 ‰ to 0 ‰ for δ¹⁸O.²⁹ Note that the scales on both panels are the same to facilitate comparison. These data suggest that for measurements of δ¹⁸O, δ¹⁷O, and ¹⁷O-excess, depending on the largest isotope step encountered, memory can be addressed using 1 – 4 preparatory injections on the TIWA instrument followed by 4 measurement injections. If δ²H measurements are also desired, a larger number of preparatory injections may be necessary. It is also possible to utilize mathematical memory corrections (see e.g. ^25–27); these are outside the scope of this manuscript and will be discussed in a future manuscript. The accuracy and precision of the isotope measurements described herein demonstrate the suitability of this procedure to effectively handle sample-to-sample memory.

Figure 1.

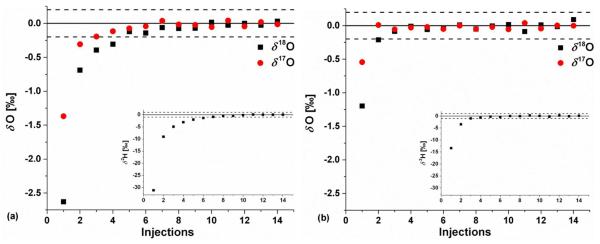
a) Sample-to-sample memory for the transition from SLAP2 to VSMOW2 for δ¹⁸O (black squares), δ¹⁷O (red circles), and δ²H (inset). b) Sample-to-sample memory for the transition from GISP to VSMOW2. The solid lines show the known VSMOW2 values of 0 ‰; the dashed lines show the approximate single injection 1σ uncertainty band for δ¹⁸O and δ¹⁷O of ± 0.2 ‰ and for δ²H of ± 1.0 ‰. Note that the scales on both panels are the same to facilitate comparison.

Measurement Precision and Accuracy of δ¹⁸O and δ¹⁷O

The international isotopic reference water standard GISP was analyzed on the OA-ICOS instrument to produce 514 HT measurements over a 6 month period. Each instrumental analysis was constructed as described above, with VSMOW2 and SLAP2 interleaved throughout the analysis. All data was processed with the injected volume correction and normalized with the spline calibration as described above. Figure 2 shows the excellent measurement precision and accuracy for these HT measurements, with an average δ¹⁸O_VSMOW-SLAP = −24.74 ± 0.07 ‰ (1σ) and δ¹⁷O_VSMOW-SLAP = −13.12 ± 0.05 ‰ (1σ). The best-fit normal distribution for δ¹⁸O_VSMOW-SLAP shows a center value of −24.74 ‰ with a half width half max (HWHM) of 0.06 ‰. The IAEA reported value for δ¹⁸O_VSMOW-SLAP in GISP is −24.76 ± 0.09 ‰ (1σ).²⁹ The best-fit normal distribution for δ¹⁷O_VSMOW-SLAP shows a center value of −13.12 ‰ with a HWHM of 0.04 ‰. For comparison, the collected average of 5 previously reported IRMS measurements of δ¹⁷O_VSMOW-SLAP in GISP was −13.12 ± 0.06 ‰ (1σ).¹³ Allan deviation analyses³⁰ (not shown) for both δ¹⁸O and δ¹⁷O show that averaging improves the precision of the measurements to an instrumental noise floor of approximately 0.02 ‰ in δ¹⁸O and 0.01 ‰ in δ¹⁷O. This precision is achieved by averaging 20 HT measurements to produce a single high-precision (HP) measurement as described below. Throughout this manuscript, these values, convolved with the uncertainties of the primary isotopic reference water standards, are reported as the measurement uncertainties for high-precision measurements of δ¹⁸O_VSMOW-SLAP and δ¹⁷O_VSMOW-SLAP in any case where using the standard error of the mean would result in an error lower than these noise floors.

Figure 2.

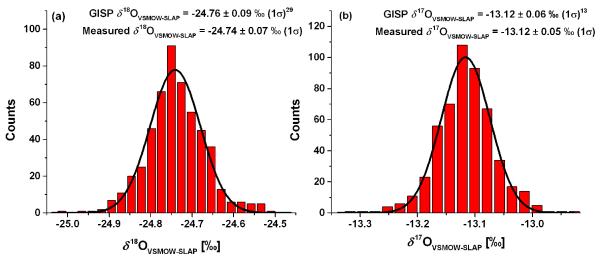
Measurement precision for 514 HT OA-ICOS measurements of GISP calibrated against VSMOW2 and SLAP2 with injected volume correction and spline calibration. Histograms with overlaid normal distribution fit for (a) δ¹⁸O_VSMOW-SLAP and (b) δ¹⁷O_VSMOW-SLAP. The average and standard deviation of the measured values are noted along with the IAEA accepted value for δ¹⁸O_VSMOW-SLAP²⁹ and a published average value of δ¹⁷O_VSMOW-SLAP¹³ (IAEA does not list a value for δ¹⁷O).

Instrumental accuracy was further demonstrated by measuring GISP and four commercially-available United States Geological Survey (USGS) isotopic reference waters^31–34 by OA-ICOS and by IRMS as described above. The data are summarized in Table 1. Figure 3 shows the measurement accuracy of measurements by OA-ICOS and IRMS for GISP and the four USGS isotopic reference waters. For δ¹⁸O, measurements are plotted as the difference between each measurement and the published δ¹⁸O value.^{29, 31–34} Neither IAEA nor USGS publishes values for δ¹⁷O of reference waters. For this reason, δ¹⁷O values for GISP are shown as the difference between each measurement and an average of collected previously reported values.¹³ δ¹⁷O values for the USGS isotopic reference waters are shown as the difference between each measurement and the average of the three experimental measurements inversely weighted by the uncertainty. Error bars shown represent the standard error of the mean for IRMS measurements and the measured limit of instrumental precision as described above for OA-ICOS. The correlation of measurement errors between δ¹⁸O and δ¹⁷O described in the introduction is clearly evident in Figure 3.

Table 1.

OA-ICOS and IRMS measurements of GISP and commercially available USGS isotopic reference waters. Averages are weighted by the inverse of the listed precision of the measurements. Uncertainties listed are standard errors of the mean for IRMS measurements, weighted standard deviations for the weighted averages of the three reported experimental measurements, the published standard deviation for GISP, and the published 95-percent confidence intervals for the USGS values. Uncertainties for OA-ICOS are listed as the standard error of the mean for ¹⁷O-excess and as the convolved measured limit of instrumental precision for δ¹⁸O and δ¹⁷O.

		# of HP measurements	δ18 OVSMOW-SLAP [‰]	δ17 OVSMOW-SLAP [‰]	17O-excessVSMOW-SLAP [per meg]
GISP	OA-ICOS	26	−24.74 ± 0.03	−13.12 ± 0.02	23 ± 2
	IRMS (LSCE)	3	−24.69 ± 0.08	−13.08 ± 0.06	32 ± 6
	IRMS (JHU)	9	−24.79 ± 0.08	−13.14 ± 0.04	25 ± 3
	Wt. Average		−24.74 ± 0.03	−13.12 ± 0.02	25 ± 3
	IAEA29		−24.76 ± 0.09
USGS45	OA-ICOS	4	−2.25 ± 0.03	−1.17 ± 0.02	13 ± 9
	IRMS (LSCE)	5	−2.25 ± 0.03	−1.18 ± 0.03	12 ± 4
	IRMS (JHU)	14	−2.39 ± 0.07	−1.25 ± 0.04	12 ± 1
	Wt. Average		−2.27 ± 0.05	−1.19 ± 0.03	12 ± 1
	USGS31		−2.238 ± 0.011
USGS46	OA-ICOS	3	−29.80 ± 0.03	−15.83 ± 0.02	17 ± 6
	IRMS (LSCE)	3	−29.85 ± 0.04	−15.86 ± 0.03	20 ± 5
	IRMS (JHU)	5	−29.93 ± 0.16	−15.90 ± 0.09	22 ± 3
	Wt. Average		−29.83 ± 0.04	−15.85 ± 0.02	20 ± 2
	USGS34		−29.80 ± 0.02
USGS47	OA-ICOS	3	−19.81 ± 0.03	−10.47 ± 0.02	39 ± 6
	IRMS (LSCE)	5	−19.77 ± 0.03	−10.45 ± 0.03	42 ± 6
	IRMS (JHU)	10	−19.86 ± 0.07	−10.49 ± 0.04	40 ± 3
	Wt. Average		−19.80 ± 0.03	−10.47 ± 0.02	40 ± 1
	USGS33		−19.80 ± 0.02
USGS48	OA-ICOS	3	−2.25 ± 0.03	−1.16 ± 0.02	28 ± 7
	IRMS (LSCE)	3	−2.22 ± 0.03	−1.15 ± 0.03	22 ± 3
	IRMS (JHU)	5	−2.19 ± 0.21	−1.13 ± 0.11	28 ± 2
	Wt. Average		−2.23 ± 0.02	−1.15 ± 0.01	26 ± 3
	USGS32		−2.224 ± 0.012

Figure 3.

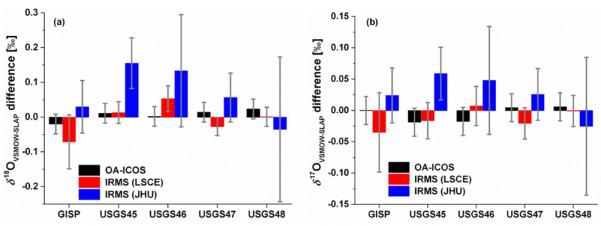
Measurement accuracy demonstrated by measurements of GISP and four commercially-available USGS isotopic reference waters by OA-ICOS and IRMS. Measurements of δ¹⁸O_VSMOW-SLAP (a) are shown as differences from the values published by IAEA²⁹ and USGS^32–34 as appropriate. Neither IAEA nor USGS publishes values for δ¹⁷O of reference waters. Measurements of δ¹⁷O_VSMOW-SLAP (b) for GISP are shown as the difference between each measurement and an average of previously reported values¹³. Measurements of δ¹⁷O_VSMOW-SLAP (b) for USGS isotopic reference waters are shown as the difference between each measurement and the average of the three experimental measurements inversely weighted by the uncertainty. Error bars shown represent the standard error of the mean for IRMS measurements and the measured limit of instrumental precision for OA-ICOS.

Measurement Precision and Accuracy of ¹⁷O-excess

¹⁷O-excess was calculated from the aforementioned OA-ICOS measurements of the international isotopic reference water standard GISP. In order to reach the extremely high precision needed for meaningful measurements of ¹⁷O-excess by either IRMS or OA-ICOS, averaging of multiple individual measurements is required. The precision achieved as a function of the number of averaged OA-ICOS HT measurements is shown in Figure 4(a). This Allan deviation³⁰ plot clearly demonstrates that averaging improves the measurement precision; the solid line shows the case of perfect white noise averaging, which reduces the standard deviation by the square root of the number of averaged measurements. Typical IRMS measurements average 70 –100 individual dual-inlet measurements of O₂ gas from a water sample to produce a single, high-precision measurement of ¹⁷O-excess and typically report a measurement precision of 5 – 10 per meg (1σ).^{e.g. 8, 12, 13} Individual HT measurements on the OA-ICOS instrument are averages of 4 injections; therefore, averaging of 20 HT OA-ICOS measurements produces a high-precision (HP) measurement which is based on 80 measured injections of the water sample, comparable to the IRMS technique. Using this procedure, 6 – 7 HP sample measurements in the normal range of natural waters can be completed per day in addition to standards. Figure 4(b) shows the excellent measurement precision achieved with HP OA-ICOS measurements of ¹⁷O-excess, with an average ¹⁷O-excess_VSMOW-SLAP = 23 ± 10 per meg (1σ). The best-fit normal distribution for ¹⁷O-excess_VSMOW-SLAP of GISP shows a center value of 23 per meg with a half width half max of 9 per meg. For comparison, the collected average of 3 previously reported IRMS measurements of ¹⁷O-excess_VSMOW-SLAP in GISP was 22 ± 11 per meg (1σ).¹³

Figure 4.

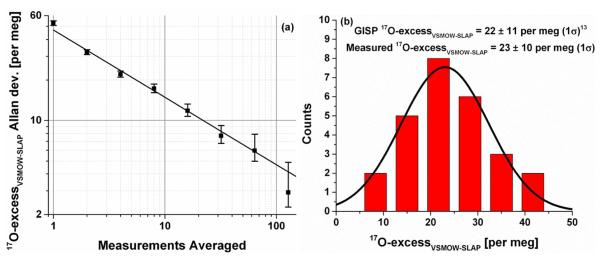
a) Allan deviation plot showing precision as a function of number of HT OA-ICOS measurements averaged. The solid line represents perfect averaging of white noise. b) Histogram with overlaid normal distribution fit for HP OA-ICOS measurements (averages of 20 HT measurements) of ¹⁷O-excess_VSMOW-SLAP of GISP calibrated against VSMOW2 and SLAP2 with injected volume correction and spline calibration. The average and standard deviation of the measured values are noted, along with a published average value.¹³

Figure 5 shows the excellent measurement agreement among ¹⁷O-excess measurements by OA-ICOS and IRMS for GISP and the four USGS isotopic reference waters. Error bars represent the standard error of the mean for multiple HP measurements of each sample. The line behind the GISP columns shows the collected average of 3 previously reported IRMS measurements.¹³ These data all illustrate the utility of ¹⁷O-excess measurements in distinguishing among natural waters; note that USGS45 (Biscayne Aquifer Drinking Water) and USGS48 (Puerto Rico Precipitation) have essentially identical δ¹⁸O and δ¹⁷O values, but significantly different ¹⁷O-excess values. The exceptional precision for ¹⁷O-excess measurements among different laboratories and between methods makes it possible to differentiate the ¹⁷O-excess composition of these two waters. Table 1 summarizes all IRMS and OA-ICOS measurements of GISP and the USGS isotopic reference waters. Averages are weighted by the inverse of the listed precision of the measurements. Uncertainties listed are standard errors of the mean for IRMS measurements, weighted standard deviations for the averages of the three reported experimental measurements, the published standard deviation for GISP, and the published 95-percent confidence intervals for the USGS values.

Figure 5.

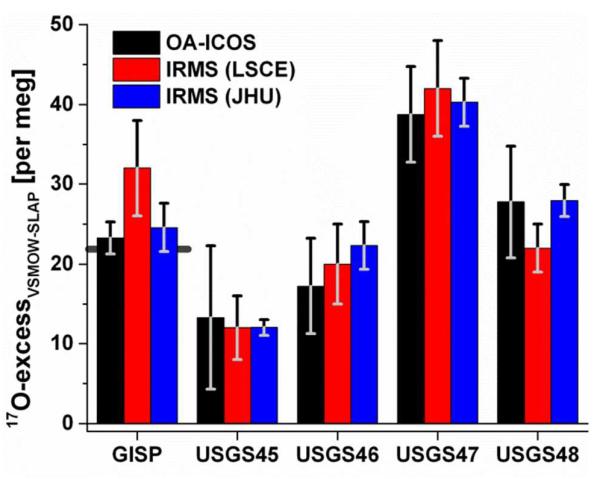
Measurement accuracy for ¹⁷O-excess_VMSOW-SLAP demonstrated by measurements of GISP and four commercially-available USGS isotopic reference waters by OA-ICOS and two independent IRMS labs. Error bars represent one standard error of the mean. The line behind the GISP columns shows the collected average of 3 previously reported IRMS measurements.¹³

Uncertainties for OA-ICOS are listed as the standard error of the mean for ¹⁷O-excess and as the measured limit of instrumental precision for δ¹⁸O and δ¹⁷O as described above.

Conclusions

In this work we demonstrate for the first time the use of off-axis integrated cavity output spectroscopy (OA-ICOS) to measure δ¹⁸O, δ¹⁷O, and ¹⁷O-excess in liquid water. OA-ICOS involves no sample conversion and has a small footprint, allowing measurements to be made by researchers collecting the samples. Repeated (514) high-throughput measurements of the international standard isotopic reference water GISP made over a 6 month period demonstrate the precision and accuracy of the OA-ICOS instrument: δ¹⁸O_VSMOW-SLAP = −24.74 ± 0.07 ‰ (1σ) and δ¹⁷O_VSMOW-SLAP = −13.12 ± 0.05 ‰ (1σ). For comparison, the IAEA reported value for δ¹⁸O_VSMOW-SLAP in GISP is −24.76 ± 0.09 ‰ (1σ)²⁹ and the average of 5 previously reported measurements of δ¹⁷O_VSMOW-SLAP in GISP is −13.12 ± 0.06 ‰ (1σ).¹³ To achieve the high precision needed for meaningful ¹⁷O-excess measurement, we average 20 high-throughput OA-ICOS measurements to get a single, high-precision measurement. In this way we measure the ¹⁷O-excess_VSMOW-SLAP of GISP as 23 ± 10 per meg (1σ); the average of 3 previously reported measurements of ¹⁷O-excess_VSMOW-SLAP in GISP is 22 ± 11 per meg (1σ).¹³ For OA-ICOS measurements of δ¹⁸O, δ¹⁷O, and ¹⁷O-excess, precision can be enhanced further by additional averaging. OA-ICOS measurements are compared with two independent IRMS measurements of commercially available GISP and USGS isotopic reference waters and shown to have comparable accuracy and precision as fluorination followed by IRMS. The ability to measure accurately δ¹⁸O, δ¹⁷O, and ¹⁷O-excess in liquid water inexpensively and without sample conversion is expected to increase vastly the application of δ¹⁷O and ¹⁷O-excess measurements for understanding of the water cycle, atmospheric convection, and climate modeling among others.