Assessing Calibration of Prognostic Risk Scores

Abstract

Current methods used to assess calibration are limited, particularly in the assessment of prognostic models. Methods for testing and visualizing calibration (e.g., the Hosmer-Lemeshow test and calibration slope) have been well thought out in the binary regression setting. However, extension of these methods to Cox models are less well-known, and could be improved. We describe a model-based framework for assessment of calibration in the binary setting that provides natural extensions to the survival data setting. We show that Poisson regression models can be used to easily assess calibration in prognostic models. In addition, we show that a calibration test suggested for use in survival data has poor performance. Finally, we apply these methods to the problem of external validation of a risk score developed for the general population when assessed in a special patient population (i.e., patients with particular comorbidities, such as rheumatoid arthritis).

1. Introduction

Risk prediction tools are increasingly being used to estimate individuals' risks of developing disease in the clinical setting. This has led to increased interest in methods used to validate (or assess the accuracy of) risk prediction tools. ^1,2 Validation of risk prediction tools in different study populations than those used to develop the risk prediction tool (e.g., different countries, different races, or subpopulations of patients with specific comorbidities) is necessary to determine the generalizability of the risk prediction tools. The two primary measures used to assess the performance of a risk prediction tool are calibration and discrimination. Calibration is the ability to accurately predict the absolute risk level, and discrimination is the ability to accurately rank individuals from low to high risk. The primary method used to assess discrimination is the concordance statistic, which corresponds to the area under the receiver operating characteristic curve in the binary outcome setting. The concordance statistic was extended to the Cox model setting by Harrell, and this extension is now a standard part of many statistical packages. ³ In contrast, while methods for testing and visualizing calibration have been well thought out in the binary regression setting, we found a wide misunderstanding in the medical literature of how to assess calibration in the Cox model setting.

In this article, we consider the problem of assessing calibration in prognostic models. First, we review concepts of calibration assessment in the binary setting, including the very well-known Hosmer-Lemeshow test. We then recast these concepts in a model-based framework, as 3 very simple models that relate observed to predicted values. We then demonstrate how a natural extension of the model-based framework to Cox and Poisson models is a useful way to simplify the assessment of calibration for survival data. Then we review the literature regarding assessment of calibration and goodness-of-fit in the survival data setting. Next, we demonstrate the application of these methods to assess the calibration of the Framingham risk score for cardiovascular disease in a population-based cohort of patients with rheumatoid arthritis.^4,5 Finally, we address the issue of how to recalibrate when the calibration is found to be poor.

2. Calibration Concepts for a Binary Outcome

Commonly used methods to assess calibration include calibration-in-the-large, the Hosmer-Lemeshow goodness-of-fit test and the calibration slope, which were developed in the logistic and linear regression model settings.^6-8 Calibration-in-the-large is a basic measure of agreement between the observed and predicted risks, which is computed as the difference between the mean observed risk and the mean predicted risk. The mean observed and predicted risks will definitely agree when assessed in the data set used to build the risk model, but agreement is less certain when applying a risk score to a new data set.

The Hosmer-Lemeshow test is computed by partitioning the study population into k groups based on the predicted probability of an event obtained from the risk prediction model (usually k=10). Then the expected number of events in each group of patients is computed as the sum of the predicted probabilities for the patients in that group, and the observed number of events is computed as the sum of the number of events observed in that group. A chi-square statistic is then used to compare the observed and expected events. When assessing the calibration of a risk score using the data set it was developed on, one degree of freedom is lost in defining the groups, so the chi-square statistic is assessed using k-2 degrees of freedom. When assessing calibration on a new data set, this is not a problem and k-1 degrees of freedom are used for the chi-square test. Limitations of the Hosmer-Lemeshow test are well-known and include its dependence on arbitrary groupings of patients, poor power in small data sets, as well as the fact that it only results in a p-value.^1,9

A calibration plot is sometimes described as a visual representation of the Hosmer-Lemeshow test, because it categorizes patients into groups according to predicted risk, similar to the groups used for the Hosmer-Lemeshow test.¹ The observed risk is calculated for each group and the predicted risk is plotted against the observed risk for each group of patients. In the binary outcome setting, the observed risk is simply the proportion of patients with an event and the predicted risk is the average risk score for patients in each group. Confidence intervals for the observed risk estimates are sometimes included. The identity line is usually included for reference, and a smoother line or a regression line may also be included. (We suspect that some users have estimated this trend test by fitting linear regression to the data points for each group shown on the plot, which is clearly not a good approach). See figure 1 for an example of a calibration plot.

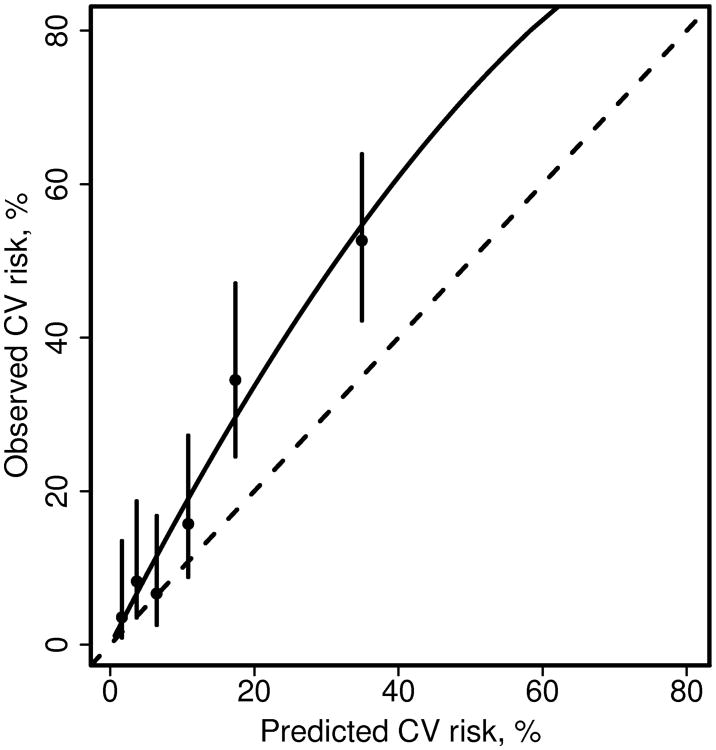
Figure 1.

Calibration plot comparing predicted and observed cardiovascular (CV) disease risk for patients with rheumatoid arthritis. Patients were grouped into 6 groups of predicted risk (obtained from the Framingham risk score). Observed 10 year risk of CV events for each group of patients and confidence intervals were estimated from a Poisson regression model including covariates for each group (model 3). The dashed line is the identity line. The solid line was estimated from a Poisson regression model including only an intercept with an offset for the log of the expected number of events (model 1).

The calibration slope, which is calculated by regressing the observed outcome on the predicted probabilities, does not suffer from the limitations of the Hosmer-Lemeshow test, as it does not require grouping patients and the estimated slope obtained from the regression model provides a measure of effect size and a confidence interval, in addition to a p-value. For these reasons, the calibration slope is more informative and is the preferred method for assessing calibration.² It might be more prevalent were it not for the prominence of the Hosmer-Lemeshow test in many statistical packages.

3. A Model-based Framework for Calibration

To generalize these concepts for use in multiple types of models, the unifying idea is to think of the calibration methods in a regression context. Let (Y_i, X_{i j}) be the outcomes and predictors for the ith subject in some new data set to which we wish to apply a target risk model, and let β₀, β₁,… be the coefficients of this model, where β₀ is the intercept, β₁, β₂,… are coefficients for various risk predictors. Let p_i be the linear predictor for each subject using the original coefficients (e.g., p_i = β₀ + β₁ x_i1 + …). Then consider fitting a set of regression models to the new data:

1. E(y) = f(ɣ₀+ p)

2. E(y) = f(ɣ₀+ ɣ₁p)

3. E(y) = f(ɣ₁ group₁ + ɣ₂ group₂ +…+ ɣ_k group_k + p)

In models 1 and 3, the coefficient for p is forced to be 1, and is referred to as an offset in generalized linear models. The function f depends on the type of y variable, and hence the type of regression model to be fit. For a binary outcome, y, models 1 - 3 would naturally be fit using logistic regression. Assume that data0 contains the original data used to create the model which had 3 variables x1, x2 and x3, and that data1 is the new data set with which we will validate said model. Then in R we can fit the 3 models as:

fit0	<- glm(y ∼ x1 + x2 + x3, family=binomial, data=data0) #reprise the fit
p	<- predict(fit0, newdata=data1) #default type is the linear predictor
group	<- cut(p, c(-Inf, quantile(p,(1:9)/10), Inf))
fit1	<- glm(y ∼ offset(p), family=binomial, data=data1)
fit2	<- glm(y ∼ p, family=binomial, data=data1)
fit3	<- glm(y ∼ −1 + group + offset(p), family=binomial, data=data1)

(Appendix 1 shows the same example using SAS).

The value of ɣ₀ from model 1 is the calibration-in-the-large or the recalibration constant. The value of ɣ₁ from model 2 is the calibration slope. Model 3 includes a set of grouping variables, and a common choice for creating the groups is to categorize p into deciles of predicted risk. A test for group effect (i.e., ɣ₁ = ɣ₂ = _… = ɣ_k =0) in model 3 is asymptotically equivalent to the Hosmer-Lemeshow goodness-of-fit test, though not precisely identical for finite samples. ^6,10 A score test for group effect in model 3 is the goodness-of-fit test that was first proposed by Tsiatis. ^6,10

One advantage of the model-based approach for the goodness-of-fit test is that it automatically provides further information, namely the estimated risk level (i.e., coefficient) for each group, along with confidence intervals for each, if desired. This facilitates production of the calibration plot. The regression framework also makes the relationship between the calibration slope ɣ₁ and the Hosmer-Lemeshow test clearer. The calibration slope will be related, but clearly not equivalent, to a linear trend test on the group coefficients of model 3.

Another advantage of the regression approach to assessing goodness-of-fit is that it suggests clear extensions, such as the use of other grouping variables in model 3, non-linear extensions of model 2, and the translation of these ideas to other types of models. The use of other grouping variables, particularly assessing whether calibration is similar within groups based on patient characteristics that were not included in the original score has been suggested previously, but is rarely explored.^8,10-12 This is probably because calibration is usually assessed soon after developing a risk score, and there are more direct ways to assess subgroup characteristics during the model development process. Finally, non-linear extensions, such as the use of smoothers to assess calibration, instead of arbitrary groups, have also been suggested.³

4. Extension to Survival Data

The most common model for survival data is the Cox model which relates the cumulative hazard function Λ_i for each subject to an overall baseline rate and the covariates Λ_i (t) = Λ₀ (t) exp(η_i) where η _i = β₁ x_i1 + β₂ x_i2 + … is the linear predictor, without an intercept term. The individual coefficients exp(β) capture the relative risk of death associated with each covariate. When computing absolute predictions from a Cox model the estimated log baseline hazard log(Λ̂₀) plays the role of the intercept β₀ in other models. Unfortunately the baseline hazard is neither printed as a standard part of the output from Cox model fitting routines nor is it normally included in the reported results for a paper. (This has led to a common misconception that absolute risk prediction is not possible from a Cox model). However, many programs will compute the martingale residuals m_i = y_i – e_i where y_i is the status variable 1=death/0=censored and e_i = Λ₀ (t) exp(η_i) is the expected number of events. ^13,14 Thus the value of p which we require for validation, that with the baseline included, can be obtained as p_i = log(e_i). However, since this expected number of events incorporates each patient's follow-up time, it cannot be used to create the groups to be assessed in model 3. Instead, the linear predictor must be used to define the groups, as shown in the sample R code in the next section.

4.1 When the original data is available

In R the prior code for models 1-3 is hardly changed:

fit0	<- coxph(Surv(futime, status) ∼ x1 + x2 + x3, data=data0)
p	<- log(predict(fit0, newdata=data1, type=“expected”))
lp	<- predict(fit0, newdata=data1, type=“lp”)
logbase	<- p − lp
fit1	<- glm(y ∼ offset(p), family=poisson, data=data1)
fit2	<- glm(y ∼ lp + offset(logbase), family=poisson, data=data1)
group	<- cut(lp, c(-Inf, quantile(p,(1:9)/10, Inf))
fit3	<- glm(y ∼ −1+ group + offset(p), family=poisson, data=data1)

(Appendix 1 shows the same example using SAS).

The only surprise is the use of Poisson regression rather than a Cox model for the fits. A Cox model with pre-fixed baseline hazard is exactly equivalent to a Poisson regression. ^15,16 If we were instead to invoke a Cox model regression at this stage, the program would estimate a new baseline hazard behind the scenes, confounding the assessment of absolute risk.

Assessment of calibration in the large is based on the intercept term ɣ₀ from fit1. The value exp(ɣ₀) estimates the ratio of observed events in the new data set to the number predicted by the risk model. Models of this form have long been used in epidemiology to compare observed to expected numbers of events; the o / e values are referred to as standardized incidence ratios (SIR). This is commonly done in cancer research where incidence rates of cancer obtained from the Surveillance, Epidemiology, and End Results (SEER) database are used to calculate the expected number of cancer events.¹⁷ These methods are also common in occupational health literature, where observed health risks related to exposure to environmental agents are often compared to population standards.¹⁸

4.2 When the baseline hazard is only available at specific time points

When the baseline hazard Λ₀(t) or equivalently the baseline survival S₀(t) = exp(-Λ₀(t)) is provided in a paper, it usually is given at only a limited number of time points. Sometimes, as in the case of the Framingham score, only a single time point (e.g., 10 years) is provided. In this case one must interpolate the baseline hazard function to obtain the value appropriate to the actual follow-up time for each subject, i.e., the value that would have been used in computing the martingale residual. An obvious candidate is simple linear interpolation, e.g., if the reported value in manuscript were Λ₀ = .34 a subject with 2.1 years of follow up would use Λ₀(2.1) ∼ 0.34(2.1/10), and then p = log(0.34(.21) + β₁ x_i1 + β₂ x_i2 + …). However, in some settings, such as mortality after myocardial infarction, which is very high in the first 30 days and then drops subsequently, this assumption may not be valid. In this case, it would be helpful for published risk scores to provide baseline survival values at multiple time points.

An alternative which has sometimes been proposed to assess calibration without requiring an assumption in the face of limited information regarding the baseline hazard function is to extrapolate each subject forward in time. This is done by estimating the risk score using the baseline hazard at the provided time point (e.g., 10 years) and comparing it to the estimated number of observed events if all patients had 10 years of follow-up, instead of the actual number of events observed with the true available follow-up. We show in section 5.2 that this approach is flawed.

4.3 When the baseline hazard is not available

If neither the original data nor the baseline hazard are available, unfortunately a not uncommon situation, calibration in the large is not possible. In models 2 and 3, however, an estimated intercept term is not the primary focus of the fit, and we can often successfully proceed by using the approximate value P̃_i = η_i, i.e.; the prediction omitting the baseline hazard; the original baseline is “absorbed” into the intercept term of the model. In this case it is also advisable to replace the Poisson regression with a Cox model fit, since the former implicitly assumes that the baseline hazard function of the original fit was constant.

5. Relationship to previous work

5.1 Previous work on calibration in the survival data setting

Several variations of the Hosmer-Lemeshow test have been proposed for use in the Cox model setting. Some of the earliest tests created groupings based on time intervals, in addition to or instead of the usual groups based on partitioning the predicted risks.^19-23 The primary reason for partitioning time in these tests was to assess the proportional hazards assumption of the Cox model. Goodness-of-fit tests applied to assessment of calibration include variations of the Hosmer-Lemeshow test proposed by Grønnesby and Borgan and by D'Agostino and Nam. The test proposed by Grønnesby and Borgan is equivalent to the score test for group effect in model 3, a fact which was demonstrated by May and Hosmer.^14,24

D'Agostino and Nam proposed comparing the observed Kaplan-Meier percentages with the average risk predictions across groups of patients using a small variation to the usual Hosmer-Lemeshow test statistic. Here is the original Hosmer-Lemeshow formula along with the D'Agostino and Nam variation:

$$\begin{array}{c}{\mathrm{X}}_{\mathit{\text{HL}}}^2=\sum _{j=1}^M\frac{{(O_j-E_j)}^2}{E_j(1-E_j/n_j)}\\ {\mathrm{X}}_{\mathit{\text{DN}}}^2=\sum _{j=1}^M\frac{n_j{({\mathit{\text{KM}}}_j-{\overline{p}}_j)}^2}{{\overline{p}}_j(1-{\overline{p}}_j)}\end{array}$$

Their work focused on deriving the test to assess calibration in the same data set used to develop the model. In the binary setting it is customary to simply subtract an extra degree of freedom due to defining the groups on the same data set that is used to assess the group effect. D'Agostino and Nam discovered assessment of calibration in the original data set was more complicated in the Cox model setting than simply subtracting an extra degree of freedom.²⁵ Steyerberg also recommended the same test proposed by D'Agostino along with a subtraction of the extra degree of freedom when assessing calibration on the original data set, but he did not provide any references for his recommendations.¹ Comparing the D'Agostino and Nam suggestion to the original Hosmer-Lemeshow formula, they have replaced the observed events with a pseudo-observed n_jKM_j for each group, where n_j is the starting sample size. This results in a larger number of events than actually seen, especially when there is extensive censoring. The estimated number of observed events is effectively an estimate of the number of events that would have been observed if all the study subjects had been followed to the time point of the Kaplan-Meier estimate. Of note, this approach is similar to that proposed for calculation of expected mortality by Hartz,²⁶ which was also based on probabilities that inadvertently resulted in pseudo-events rather than the actual observed events, and was later refuted by several others.^27-29 Henceforth, we will refer to this approach as the extrapolation approach.

5.2 Problem with extrapolation approach to test calibration

The problem with the extrapolation approach is that the test statistic ignores censoring, leading to an incorrect variance. For example, two studies with identical event rates, but one with a low censoring rate and the other with a high censoring rate, would yield the same test statistic despite the fact that the study with a higher censoring rate contained less information.

To demonstrate the problem with the extrapolation approach, we performed a simulation to determine the empirical size of the extrapolation approach compared to our model-based approach. For the simulation, we used an exponential baseline hazard function, along with Framingham risk scores sampled with replacement from our real-data example used in the next section. We performed 1000 replications dividing the risk score into 6 risk groups (to match our real-data example). Censoring was uniform, mimicking a study with uniform accrual over a fixed time period and a fixed analysis date with a 10 year study period. We varied the amount of censoring from 10% to 50%.

The extrapolation approach performed reasonably well with 10% censoring, but the empirical size worsened progressively as the amount of censoring increased. With 50% censoring the empirical size of a “0.05” test was nearly 60%, meaning the null hypothesis was incorrectly rejected 60% of the time. In contrast, our model-based approach demonstrated a consistent size of about 3%, showing it to be slightly conservative (Table 1). This result may be due to our use of 5 degrees of freedom to assess the group effect for our 6 groups. In these simulations of the null case, we could argue that we are defining the groups on the same data set we are assessing, so we would obtain less conservative results if we used 4 degrees of freedom. May and Hosmer also performed extensive simulations on the Grønnesby and Borgan test, which is equivalent to our model-based approach, and they demonstrated that this test has incorrect size for studies with small sample size or when the test is performed using too many groups.³⁰ However, it is still a vast improvement over the extrapolation approach, which demonstrated severely inflated false positive rates.

Table 1. Simulation comparing empirical size of the goodness-of-fit test obtained using our model-based approach and the extrapolation method with 6 risk score groups and α=0.05 for an exponential baseline hazard function.

n	Censoring %	Type 1 error: Model-based approach	Type 1 error: Extrapolation approach	Mean observed events	Mean projected events in extrapolation approach
500	10%	0.031	0.054	314	338
500	20%	0.035	0.080	301	338
500	30%	0.018	0.161	272	338
500	40%	0.028	0.276	256	338
500	50%	0.030	0.591	232	338
200	10%	0.025	0.063	124	134
200	20%	0.026	0.088	119	134
200	30%	0.026	0.213	108	134
200	40%	0.038	0.329	101	134
200	50%	0.031	0.573	92	134

^*results based on 1000 replications for each simulation

6. Application to assessment of cardiovascular disease risk in patients with rheumatoid arthritis

6.1 Description of example data set and calculation of Framingham risk score

Patients with rheumatoid arthritis (RA) are known to have an increased risk of cardiovascular disease (CVD). Rheumatoid arthritis is characterized by chronic inflammation, and inflammation has also been associated with the development of CVD. Thus, it is not clear whether CVD risk scores developed for use in the general population, such as the Framingham risk score, will accurately predict the risk of CVD in patients. If the increased risk of CVD in patients with RA is mediated by traditional risk factors (e.g., leading to more hypertension and increased lipid levels), then the standard tools may accurately predict the increased CVD risk in these patients. However, if other factors unrelated to the traditional risk factors are precipitating the increased CVD risk or if the traditional risk factors work differently (i.e., require different weights) then the standard tools may not perform well in patients with RA. Our research question is whether the Framingham risk score, which was designed to predict the risk of CVD in the general population, accurately predicts the risk of CVD in patients with RA.^4,5

To examine this question, we make use of a data set of 525 patients aged 30+ years with incident RA and no prior CVD from a population-based cohort. During an average of 8.4 years of follow-up per patient, 84 patients had a CVD event. For each patient the 10 year risk of CVD is computed using the Framingham risk score with risk factor data obtained at the time of RA diagnosis. Because we only had information about the baseline hazard at the 10 year time point for the Framingham risk score, we then prorated this 10 year risk to the variable follow-up of our cohort assuming the baseline hazard, Λ₀, is linear over the 10 years (i.e., constant hazard), as described earlier. In the case of CVD in patients with RA, this constant hazard assumption is reasonable.

6.2 Assessing calibration using the model-based approach

Using Poisson models, the estimated calibration-in-the-large expressed as an SIR is 1.84 (95% confidence interval [CI]: 1.49, 2.28) (obtained from model 1 using Poisson regression). This estimated SIR is identical to dividing the observed number of events by the expected number of events (84 / 45.6 = 1.84). This result indicates the Framingham risk score is poorly calibrated among patients with RA, as RA patients have on average an 84% higher risk for CV events than would be expected given their age and risk factors (i.e., than predicted by the Framingham risk score). The calibration slope expressed as an SIR is 1.17 (95% CI: 0.99, 1.38)(obtained from model 2), which states that each unit increase in the risk score may have a larger effect within this population than in the Framingham reference population. Therefore, it may be worthwhile to examine each of the risk factors in the Framingham risk score individually to see if their weights (i.e., coefficients) should be modified to better predict CV risk in the RA population.

The goodness-of-fit test can be generated using model 3 in the Poisson regression setting. Using the common approach, we first defined deciles, but we found that 5 of them had less than 5 patients with events. Since the typical goodness-of-fit tests are based on chi-square statistics and general sample size guidelines for discrete data problems recommend at least 80% of groups should have counts of 5 or more, we reduced the number of groups to 6 in order to comply with these recommendations.²³

Table 2 shows both the observed (o) number of events and the expected (e) number of events obtained from model 3 for each of the 6 groups. The ratio o / e for each group is the same as exp(ɣ_j) from the Poisson regression of model 3, since it is the maximum likelihood estimator in this simple case. Exclusive use of the multiplicative measures of risk, such as the SIR, has been rightly criticized because it can inflate our perception of low absolute risks. For example, a doubling of risk from 1 in 100,000 to 2 in 100,000 is less cause for real alarm than the 25% change from 20 in 100 to 25 in 100. For this reason including both the absolute numbers as well as the risks, as was done in table 2, is recommended.

Table 2. Demonstration of group-based goodness-of-fit test for rheumatoid arthritis example.

			Goodness-of-fit test*
Group	FRS, %	N	o	e	SIR	z score	p-value
1	<2.58	88	2	0.84	2.38	1.22	0.22
2	2.59 – 4.79	88	5	2.14	2.34	1.89	0.058
3	4.80 – 8.20	87	4	3.81	1.05	0.10	0.92
4	8.21 – 13.59	88	10	6.63	1.51	1.30	0.19
5	13.60 – 21.96	87	23	10.28	2.24	3.86	<0.001
6	>21.96	87	40	21.93	1.82	3.80	<0.001
Total		525	84	45.63	1.84

o=observed number of events; e= expected number of events; SIR= standardized incidence ratio (o/e); KM=Kaplan-Meier estimate; FRS=Framingham risk score

^*Overall deviance=28.94, df=5, p<0.001

6.4 Obtaining the calibration plot

The Poisson regression of model 3 can also be used to generate the calibration plot. For plotting we want to return to an absolute risk scale, e.g., 10 year probability of an event. To do so, we need to return to a common time scale, since each of the groups in table 2 has a slightly different average follow-up time, which would confuse the visual perception. This is easily remedied by creating a dummy data set with one observation for each group, using the average 10 year Framingham risk for subjects in that group to define the expected events, and then obtaining the predictions and standard errors for each group. This is shown in Figure 1. An advantage of the model based approach is the ability to create confidence bars for each point. An alternative method to create the calibration plot is to use the Kaplan-Meier method to estimate the 10 year risk of CVD for each group of patients, and to plot these estimates along with their confidence intervals based on Greenwood standard errors against the average 10 year Framingham risk for each group.

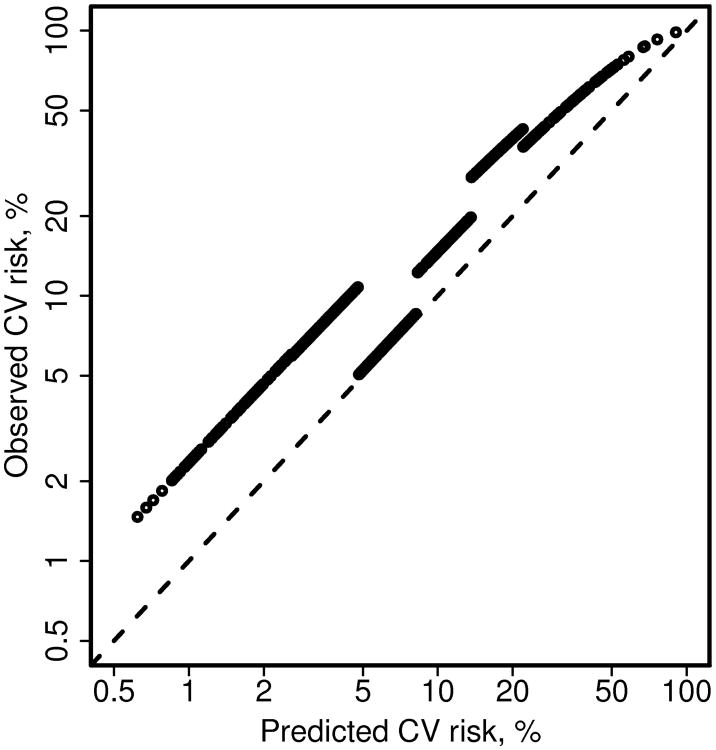
Figure 2 shows the Poisson regression estimates of model 3 for each patient, instead of just one estimate per group. The estimated risks for each group of patients are nearly parallel to the identity line when plotted on a log scale, reflecting the single coefficient for each group. The lines would be perfectly parallel if we plotted the complementary probabilities (i.e., freedom from CV events, or 1-p). A natural extension of this model is to replace the groups, which are defined somewhat arbitrarily, with a smoothing spline as shown in Figure 3. In this case, the offset for the Poisson model was the log of the person-years of follow-up instead of the log of the expected number of events. This approach made it easy to obtain 10 year estimates of the CVD risk.

Figure 2.

Alternate depiction of the calibration plot comparing predicted and observed cardiovascular (CV) disease risk for patients with rheumatoid arthritis. The dashed line is the identity line. This figure demonstrates that the slope for each group obtained from model 3 using Poisson regression is parallel to the identity line when plotted on a log scale. This does not appear to be true for the highest group, but would be if we plotted the complementary probabilities (i.e., freedom from CV events, or 1-p).

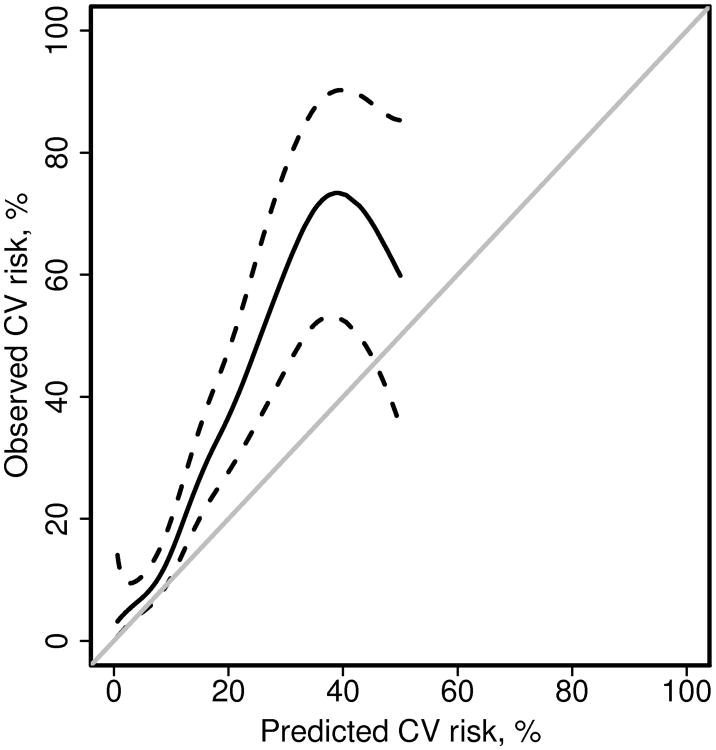
Figure 3.

Alternate calibration plot comparing predicted and observed cardiovascular (CV) disease risk for patients with rheumatoid arthritis. Poisson regression with a smoothing spline was used to estimate observed risk from the predicted risk (obtained from the Framingham risk score). The grey line is the identity line. Dashed lines are 95% confidence intervals for the fit. There were only 4 events with predicted CV risk >50%, so the fit is not displayed beyond this point.

6.5 Assessing calibration using patient characteristics

The model-based Poisson regression approach also allows assessment of subgroups with different characteristics, as recommended by Le Cessie.¹¹ In a well-calibrated model, the observed and predicted risks should agree for any subgroup of patients. In our example, assessment of subgroups of RA patients with different disease characteristics could help us determine if the Framingham risk score performs poorly among all patients with RA, or only in certain subsets. For example, ∼60% of patients with RA have a positive rheumatoid factor, which is associated with disease severity. Using Poisson regression and changing group in model 3 to an indicator for rheumatoid factor positivity revealed that the observed and predicted CVD risks differ greatly among patients with positive rheumatoid factor (observed events: 63; expected events: 25.8; SIR: 2.45; 95% CI: 1.91, 3.13). In contrast, the Framingham risk score appeared to adequately predict the CVD risk among patients with negative rheumatoid factor (observed events: 21, expected events: 19.9; SIR: 1.06; 95% CI: 0.69, 1.62). This finding is consistent with previous findings that patients with negative rheumatoid factor typically have milder disease, and they may not suffer from increased risks for CVD or mortality. ³¹

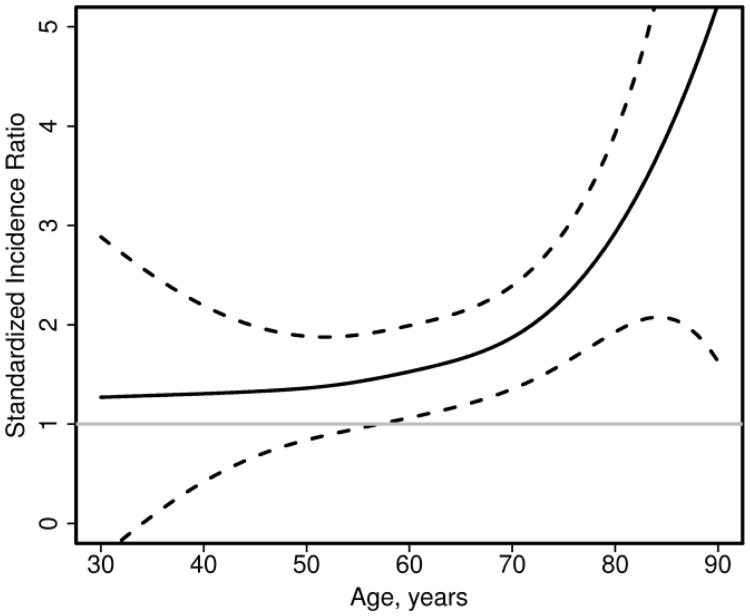
For continuous variables, such as age, a smoothing spline can be used in the Poisson regression model to examine potential non-linear effects. Figure 4 shows that the Framingham risk score works reasonably well for younger patients with RA (e.g., age <60 years), but the SIR increases with age demonstrating the observed risk of CVD exceeds the predicted risk from the Framingham risk score by larger amounts at older ages. This information could then be used to identify characteristics that could be added to an RA-specific CV risk score to improve prediction of CVD among patients with RA.

Figure 4.

Plot of standardized incidence ratio comparing observed to predicted cardiovascular events in patients with rheumatoid arthritis according to age. Standardized incidence ratios > 1 indicate the observed risk is higher than the predicted risk. Dashed lines are 95% confidence intervals for the fit.

7. Recalibration

Another issue that often arises when validating a risk prediction model in a new study population is recalibration. If calibration is found to be poor when assessing a risk score in an external population with a different underlying event rate, recalibrating may be necessary or useful. In the setting of a binary outcome when the assessment of calibration shows that the predicted risks are consistently higher (or lower) than the observed risks, a simple adjustment to the intercept of the model without re-weighting the risk factors may be sufficient to improve performance of the risk score in the new population. ^32,33 Note that the adjustment to the intercept, which we will call the recalibration constant, is the same as the calibration-in-the-large.

In the survival data setting, recalibration involves updating the baseline hazard (or the baseline survival rate in the risk score formula), which plays the same role as the intercept in the binary outcome setting. Fitting a Cox model including the linear predictor part of the risk score as a covariate would allow estimation of the appropriate baseline hazard for the new data set. Note that fitting the linear predictor as an offset term would force the weights for the risk factors in the score to remain the same, which is often the preferred approach to recalibration.

8. Discussion

We found a wide misunderstanding in the medical literature of how to assess calibration in the Cox model setting. This is perhaps not surprising, since we also found numerous methods in the statistical literature to assess goodness-of-fit in the survival data setting. We found that recasting calibration concepts in a model-based framework provided natural extensions to Cox and Poisson models, which simplified the assessment of calibration for survival data. In addition, we discovered that one of the recommended ways to assess calibration in the survival data setting demonstrated extremely poor performance (i.e., severely inflated false positive rates).

Furthermore, our model-based approach provides estimates and confidence intervals, which improves interpretation compared to a lone p-value from a goodness-of-fit test. P-values alone rarely contain all the information in any statistical analysis, and calibration is no exception. Regardless of whether the p-value for the Hosmer-Lemeshow test is significant or not, it is useful to have a measure of how discrepant the calibration is (i.e., how inaccurate the predicted risks are) with a confidence interval to aid in interpretation. Another advantage is that it is possible to assess subgroups of patients with certain characteristics, which may help inform efforts to improve risk prediction.

Additionally, these methods could be used to compare observed risk in a special disease population to predicted risk in the general population without use of a comparison group. For example, once it is demonstrated that the Framingham risk score is well calibrated to observed CVD risk among Olmsted County, Minnesota residents, then observed CVD risk can be compared to predicted risk obtained from the Framingham risk score for patients in Olmsted County with RA or systemic lupus erythematosus or psoriasis, or any number of other diseases of interest. However, it would be necessary to first demonstrate that the risk score is well calibrated in the community of interest, especially in the case of the Framingham risk score, which has been shown to over-estimate CVD risk in the Women's Health Initiative data.³⁴ In addition, it is important to ensure that the observed events are defined in the same way as the events used to develop the original risk score, as calibration involves absolute risks, so comparing observed and expected events with different definitions is nonsensical and will surely result in poor calibration. While demonstrating good calibration in the community of interest may seem like the same amount of work as assembling a comparison cohort, it could save effort and money over time if there was more than one special population of interest.

In conclusion, as risk prediction models become more common, so will assessment of whether these models accurately predict risk in various populations of interest. Careful thought regarding methods to assess goodness-of-fit in the survival data setting is important and has been lacking in the medical literature. Meaningful assessments of calibration can, in turn, be used to inform ways to improve risk score predictions.

Appendix 1.

sample code

1. Sample SAS code for binary outcome

**trick to get predicted values on a new data set that is not included in the fit**;

**use case weights of zero for the new data set**;

data databoth; set data0(in=in0) data1(in=in1);

if in0 then wt=1;

else if in1 then wt=0;

proc logistic des data=databoth;

model y=x;

weight wt;

output out=pred1 xbeta=p;

**model 1**;

data data1;set pred1;

if wt=0; **subset to new data**;

proc logistic des data=data1;

model y= /offset=p;

**model 2**;

proc logistic des data=data1;

model y=p;

**model 3**;

data data1;set data1;

group=p;

proc rank data=data1 out=data2 groups=10;

Var group;

proc logistic des data=data1;

Class group;

Model y=group p /noint;

**alternative: newer syntax to get predictions on a new data set**;

proc logistic des data=data0 outmodel=model0;

model y=x;

proc logistic inmodel=model0;

score data=data1 out=pred1;

**convert predicted probability to linear predictor**;

data pred1;set pred1;

p=log(p_1/(1-p_1));

See the SAS manuals for more information on the outmodel, inmodel and score options in proc logistic. ³⁵

2. Sample SAS code for survival outcome

**trick to get predicted values on a new data set that is not included in the fit**;

data dataall; set data0(in=in0) data1(in=in1);

if in0 then wt=1;

else if in1 then wt=0;

proc phreg data=dataall;

model time*event(0)=x;

weight wt;

output out=pred1 resmart=resmart xbeta=lp;

**convert martingale residual into expected number of events**;

data pred1;set pred1;

p=event -resmart;

logp=log(p);

logbase= logp − lp;

**model 1**;

data data1;set pred1;

if wt=0; **subset to new data**;

proc genmod data=data1;

model event= /offset=logp dist=poisson link=log;

**model 2**;

proc genmod data=data1;

model event= logp / offset=logbase dist=poisson link=log;

**model 3**;

data data1;set data1;

group=lp;

proc rank data=data1 out=data2 groups=10;

var group;

proc genmod data=data2;

model event= group /offset=logp dist=poisson link=log noint;

See the SAS manuals for more information on obtaining the Martingale residuals for new observations. Our proposed approach of using weights of 0 used to work in previous versions of SAS. The current documentation (SAS version 9.2 and 9.3) mentions you can also do this by including a freq statement with a freq variable set to missing for the new observations or by setting the censoring variable to missing for the new observations. ³⁵ However, we were unable to get any of these options to work in SAS version 9.2. or 9.3.