A conceptual review on systems biology in health and diseases: from biological networks to modern therapeutics

Abstract

Human physiology is an ensemble of various biological processes spanning from intracellular molecular interactions to the whole body phenotypic response. Systems biology endures to decipher these multi-scale biological networks and bridge the link between genotype to phenotype. The structure and dynamic properties of these networks are responsible for controlling and deciding the phenotypic state of a cell. Several cells and various tissues coordinate together to generate an organ level response which further regulates the ultimate physiological state. The overall network embeds a hierarchical regulatory structure, which when unusually perturbed can lead to undesirable physiological state termed as disease. Here, we treat a disease diagnosis problem analogous to a fault diagnosis problem in engineering systems. Accordingly we review the application of engineering methodologies to address human diseases from systems biological perspective. The review highlights potential networks and modeling approaches used for analyzing human diseases. The application of such analysis is illustrated in the case of cancer and diabetes. We put forth a concept of cell-to-human framework comprising of five modules (data mining, networking, modeling, experimental and validation) for addressing human physiology and diseases based on a paradigm of system level analysis. The review overtly emphasizes on the importance of multi-scale biological networks and subsequent modeling and analysis for drug target identification and designing efficient therapies.

Introduction

Studies in human system in the past several decades have generated qualitative understanding of the biochemical and molecular interactions that contribute to human physiology. Typically reductionist approaches were used to deduce these interactions constituting a large biological network. Biological networks comprise of interactions between genes, proteins and metabolites that co-ordinate in the regulation of cellular processes. While interactions between several cells contribute to a tissue level response, different organs comprised of different tissue types further synchronize to elicit a physiological response. These interactions form the basis for a network structures that codes for the inherent design principle that governs the dynamics of the physiological response. The network structures constitute regulatory motifs at multiple levels that help the system to elicit a desired phenotype in a regulated fashion. Feedback regulations prevalent in these networks are key mechanisms that give rise to the functional properties of the network (Ferrell 2002; Brandman et al. 2005). However, the quantification of these networks is essential to understand the design and deduce the functional properties of the system (Kholodenko et al. 2002). Computational and systems biological techniques can be employed to study the cellular and organ level networks that mediate physiological system dynamics. The main goal of system biology is to understand the integrative nature of the biological systems which nature has engineered through evolution, and deduce the fundamental principles that govern them (Kitano 2002a, b). Till now it has successfully decoded some of the circuit architectures and reproducibly demonstrated their functioning with respect to the design. Specific sub-networks present in prokaryotic and eukaryotic systems (Przytycka and Kim 2010), such as, chemotaxis in bacteria, cell cycle and osmotic adaptation in yeast, growth factor signaling pathways in mammals have been well characterized (Rao and Arkin 2001; Csete and Doyle 2002; Milo et al. 2002; Alon 2003, 2007). Extending such an analysis of biological network for human diseases and further complementing it with physiological states will help in obtaining valuable insights on the behavior of a healthy phenotypic response and its disrupted state in diseases.

Systems biology for physiology and diseases

Characterizing disease in the mammalian systems is challenging due to the inherent complexity in the system. Molecular studies help in deciphering the information at the bio-molecular interaction level, which is not sufficient to correlate the physiological response. Although the conventional techniques are being used in systems biology, their applications to biological complexity draws up new challenges and provides new openings. For example, it has been pointed out that mere use of biochemistry and molecular biology is no more useful for diseases such as cancer which are found to be multi-factorial and nonlinear (Wang 2010). This puts forth a greater challenge in developing techniques and methodologies through a paradigm shift from the conventional ways of research. Systems biology which has emerged in the last decade has accepted this challenge and provides a newer way to tackle such a problem.

Traditionally, the way in which medical sciences would approach a problem is quite different than the engineering sciences would do. Systems biology strives to fill this gap and synchronizes both the approaches to address the issues in linking genotype to phenotype. Therefore, there is a growing need to understand the relationship between the network structure at multiple spatio-temporal scale and the resulting physiological states (Butler 1999; Hartwell et al. 1999; Tyson et al. 2001; Ge et al. 2003; Wolf and Arkin 2003). A system level analysis of biological networks by linking regulatory structure to dynamical properties is required to study the emergent properties of the network such as robustness, adaptation, bistability and oscillations, which enables the cell to respond in a controlled and specified fashion (Barkai and Leibler 1997; Bhalla and Iyengar 1999; Papin et al. 2005; Kholodenko 2006).

The current challenge for systems biology is to bring together genetic, signaling and metabolic networks to create a complete in silico cell for patho-physiological applications (Herrgård et al. 2004; Cho et al. 2007). Understanding the design principles of biological network can help in modifying and constructing biological networks with desired properties. The review emphasizes on approaches to build and analyze networks and briefly focus on extending the mathematical models to disease analysis that will help in modern therapeutics. This approach has higher potential in biomedical research to study the functioning of human body on the molecular and modular levels treating it as a whole operating system. Hence, in case of diseases, it tends to address it as a system defect rather than defect in the single component.

Disease as a systemic defect

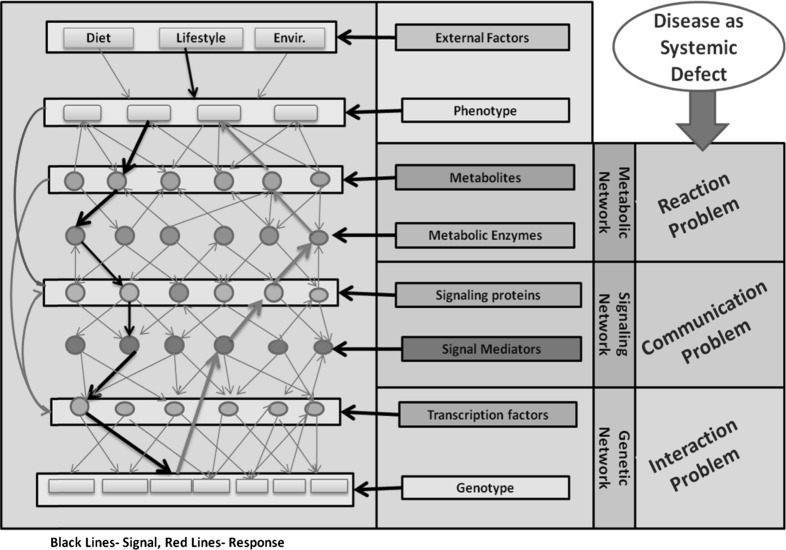
Typically engineering systems are bottom-up designs and precise design manual is available for the operation of these systems which can be referred to diagnose faults in the system. Unlike this, a biological system is a top-down design and manuals are not available for the same. In physiological systems disease is analogous to the fault in engineered systems which need to be diagnosed. The complexity has to be quantified and the design properties known, to identify the perturbation that may result into faulty phenotype. Bio-Systems analysis provides a platform for deciphering the biological process design, which can be further referred in case of diseases diagnosis. Cellular systems are akin to operating systems where various unit operations at different level are coordinated to accomplish certain function. Different networks in cellular organization orchestrate together to exhibit specific phenotypes (Kholodenko et al. 2012). The environmental cues are typically sensed at the metabolic/signaling level which activate or deactivate certain signaling mechanisms that will eventually influence transcriptional factors. The signal input to the transcriptional factors triggers the gene expression event from where a phenotypic response is generated. This response is then carried by the signaling pathways to bring out certain metabolic changes via metabolic pathways to respond to a signal. Figure 1 shows how such kind of information processing is carried out by the cell with the precise coordination of the genetic, signaling and metabolic networks.

Fig. 1.

Schematic diagram showing the typical coordination of genetic, signaling and metabolic networks for generating a phenotypic response. The figure shows the schematic of the typical information processing in a cellular network. Any defect at either of these levels of information process can lead to disruption in the adequate response leading to disease states

Diseases and interactome (interaction networks)

The functional interactions between various biomolecules such as DNA, RNA, transcription factors, enzymes, proteins and metabolites form the basis of the components for an interaction network (Tiffin et al. 1980; Mayer 1999). The data and information regarding such molecular interaction and their regulation from molecular to organism level is called as interactome, (Tiffin et al. 1980; Botstein et al. 1980; Perez-Iratxeta et al. 2002; Macé et al. 2005; Sam et al. 2007). The analysis of the interactome enables to obtain insights into the link between genotype and phenotype in terms of bio-molecular interactions.

Disturbances in these bio-molecular interactions can lead to emergence of various diseases. Hence it is necessary to investigate various interacting partners and analyze the network for proper diagnosis of disease along with its mechanisms (Houtman et al. 2005; Terentiev et al. 2009). Intrinsic and Extrinsic factors such as mutations in certain genes and environmental cues respectively, perturb network behavior leading to disease states (Stelling et al. 2004; del Sol et al. 2010). The robust characteristics of the network is traded off due to impact of perturbations on the native network leading to changes in phenotypic response thereby exhibiting pathological states (Kitano et al. 2004). The knowledge of the dynamic regulatory properties of the integrated network would be essential in performing perturbation analysis to characterize the disease states. There are some disease phenotypes that are monogenic, that arise due to mutations in single genes while most of them are multigenic, where mutation in multiple genes are involved leading to failure of regulatory cascades. To tackle multigenic disease, knowing protein–protein interaction networks is extremely essential to relate the cause and effect mechanisms (Zhu et al. 2007). Furthermore, protein interaction networks are increasingly being used for identifying new genes, study network properties, identify sub-networks related to disease and classification of network based diseases (Dunker et al. 2001). This approach provides better understanding of the complex mechanisms of systemic diseases such as tumor development, neurodegenerative, cardiovascular, autoimmune diseases and metabolic syndromes.

By implementation of high-throughput techniques, researchers have gathered huge amount of biological data and developed various interaction networks and are available on various protein network databases. One of the great achievement is the development of human interactome which contains maps of over 70,000 interactions between 6,231 human proteins (van Driel et al. 2005) and statistically estimated interactions range up to 650,000 (Safran et al. 2003). Studies have also identified large number of disease associated proteins and genes (Scriver and Waters 1999; Kahraman et al. 2005).

Diseasome and disease networks

The disease states can be understood as a resultant network property rather than a single protein or gene defect. The defects in regulatory interaction networks collectively define a disease phenotype (Jordán et al. 2012). The pathogenesis of most multi-genetic diseases involves interactions and feedback loops across multiple temporal and spatial scales, from cellular to organism level (Klipp et al. 2010). Hence it is observed that the organism and the phenotypes are the emergent properties of the interaction networks of all the individual cells without which process like tissue repair, immunity or homeostasis would not be possible. Thus the errors in the cellular information processing are responsible for diseases such as cancer, autoimmunity, and diabetes (Klipp et al. 2010). Recent studies on various diseases and the corresponding physiological disorders have led to enormous data on the defects in proteins and genes associated with specific function. The efforts have been made to relate the disease phenome to corresponding genome. The Online Mendelian Inheritance in Man (OMIM) (Hamosh et al. 2005) is the repository of such information where 1,284 disorders and 1,777 disease genes are listed and are being added continuously as newer gene—disease linkages are discovered. The collective information of most of the disease disorders and their corresponding mutations in the genes or disease genes is termed as diseasome (Goh et al. 2007).

Furthermore, the diseasome information is represented (Goh et al. 2007) by constructing two kinds of networks namely ‘Human disease Network (HDN)’and ‘Disease gene Networks (DGN)’. In HDN, nodes represent the disorders and are linked by two disorder nodes if both the disorders share a common gene defect. While in DGN, nodes represent genes and two genes are linked to each other if they are responsible for the same disorder. The HDN analysis revealed that among 1,284 disorders, 867 have at least one link to other disorders, while 516 belonged to giant component, suggesting that most of the diseases have their genetic origin from other diseases. Whereas in DGN, among 1,777 disease genes 1,377 are connected to other disease genes while 903 genes belong to a giant component. It infers that the protein products of the genes that are involved in common disorders tend to interact with other proteins via interactome. Moreover these genes express together in certain tissues with synchronized and high expression levels, which implies their higher interconnectivity leading to the cluster of disease hubs. This shows the global functional relatedness in various diseases leading to a network organization of diseasome (Park et al. 2009). Some common examples of such network diseases are diabetes, obesity and cancer which are precursors for various other physiological disorders.

By topological analysis it was established that majority of the disease genes are nonessential and do not have high degree in protein–protein interaction network and lie at the periphery of the network, whereas essential genes encoding most of the hubs lie centrally to the network (Goh et al. 2007; Qi and Ge 2006). These observations reveal the existence of disease specific functional modules. Such network information provides insight into various diseases that are interlinked and inter-originated along with their modular nature. The network measures and topological analysis will significantly help in deriving fruitful information from the complex network such as degree, shortest path connectivity, clustering, centrality and hubs in the network. This information further helps in designing experiments for perturbation analysis experimentally or by simulation (Erler and Linding 2010). Thus construction and analysis of disease networks from protein–protein interaction and diseasome data lays a concrete foundation for modeling diseases (Goh et al. 2007).

Network approach to identification of disease genes

The network based approach is being used extensively to identify the candidate genes responsible for various diseases and syndromes (Chen et al. 2012). In a outstanding work by Lage et al. (2007), the authors applied such kind of analysis to construct the interactions network of various genes and proteins for human diseases. Based on the network analysis and Bayesian predictor they found a total of 669 linkages out of which 298 correctly ranked the disease-causing proteins as top candidates. About 870 linkages with no disease causing genes were found which can provide novel candidates for investigation of diseases like Type II diabetes, (Miyatsuka et al. 2008) coronary heart disease, Alzheimer’s Retinitis pigmentosa, cancer (Wang et al. 2007), inflammatory bowel disease, and amyotrophic lateral sclerosis disease. Similar studies were carried out by various researchers to identify the genes and interaction network for different obscure diseases such as obesity, metabolic syndrome, ageing and cancer (Wang et al. 2007). This approach of network reconstruction and analysis has great potential to identify large number of genes and proteins responsible for diseases and help in identification of better drug targets (Cuccato et al. 2009).

Disease modeling and model integration

Although network development and graph based analysis are useful in understanding the inter-relations between different diseases and identification of disease candidates, intuitively it is difficult to understand the dynamic nature of these networks (Kann 2007). Networks are static representations of the systems and are unable to provide the time evolution of the system state with respect to changes in various governing conditions such as mutations and environmental effects (Maayan 2011). Thus modeling the interactions and mechanisms is essential to extract dynamical behavior of network characterizing diseases (Chandra 2009; Liu and Thagrajan 2012).

The mathematical representation of a disease mechanism from molecular to physiological level can be described as disease modeling (Tegnér et al. 2009). Modeling of disease states is essential for computational analysis of the disease process which essentially involves translating the biological data into quantifiable terms (Cho et al. 2006). Kinetic equations are formulated using first principles, law of mass action, Michalis-Menten and Hill equations based upon the types of reactions and interactions involved in the pathways. Since these mechanisms are also stochastic in nature, various stochastic modeling approaches such as Monte-carlo simulations, Foker-Plank formulations and rule based approaches to study the dynamics of the disease pathways proves to be helpful. The effects of feedback mechanisms are mathematically incorporated to represent the underling dynamics. These models are required to obtain the mechanistic insights and predict the outcomes for the set of parameters in terms of different conditions or perturbations (Vicini 2008; del Sol et al. 2010). So far kinetic modeling and flux balance analysis approaches have been typically used to model the dynamical and steady state response of the network systems respectively (Moreno-Sánchez et al. 2008; Chen et al. 2010b). Moreover, rule based and compartmental modeling approaches and several modeling software tools are now available to reduce the computational effort. The choice of modeling approach is based on the quantum of data available, scale of the model and the representation of the perturbation leading to disease. Table 1 lists various network modeling tools and databases used for biological modeling and drug discovery (Karp et al. 2005; Chandra 2009; Klipp et al. 2010).

Table 1.

Pathway and protein interaction databases

S. No.	Database
1	KEGG (Kyoto Encyclopedia of Genes and Genomes)
2	BioCyc Pathway/Genome Databases
3	EMP (The Enzymes and Metabolic Pathways Database)
4	aMAZE (Molecular function, Interaction and biochemical process database)
5	BRENDA (Comprehensive Enzyme Information System)
6	Pathway Hunter Tool
7	Reactome
8	WikiPathways
9	NCI/Nature Pathway Interaction Database
10	BioCarta (Pathway database)
11	Pathway commons
12	HPRD (Human Protein Reference Database)
13	MINT (Molecular INTeraction database)
14	DIP (Database of Interacting Proteins)
15	BIND (Biomolecular Interaction Database)
16	STRING (Functional Protein–Protein Interaction database)
17	Panther (Genes, Proteins and pathway database)

These databases can be resorted to obtain the information on various cellular pathways and biomolecular interactions. The information thus obtained can be used to reconstruct the integrated network

Indeed, one needs to perform immense data mining to construct the detailed multi-scale network. Relevant experimental data and various databases can be resorted for system parameters. The increasing research and availability of more reliable data and knowledge of interaction networks will provide refinement to these models. Table 2 lists various databases for the pathway and protein interaction databases (Ogata et al. 1999; Le Novère et al. 2006; Chandra 2009; Gehlenborg et al. 2010; Bauer-Mehren et al. 2009; Klipp et al. 2010).

Table 2.

Database and tools for network modeling and target identification

S. No.	Database
1	COBRA (Constraint-based reconstruction and analysis)
2	Cell Designer
3	Cytoscape (Software tool for analyzing networks)
4	JDesigner (Graphical modeling for biochemical networks)
5	COPASI—COmplex PAthway SImulator
6	iPATH—Interactive Pathways Explorer
7	SABIO-RK (Relational Database for Biochemical Kinetics)
8	SYCAMORE (Computational Modeling and simulation tool)
9	TIde: Target Identification (Scanning drug targets in network models)
10	Drugbank (drug and drug target database)
11	Matador (Drug target database)
12	PDTD (Potential Drug Target Database)
13	DIP (Database of Interacting Proteins)
14	STITCH (Chemical Association networks)
15	SuperTarget (Web source for analyzing drug-target interaction)
16	TDR: Targets Database
17	TTD: Therapeutic Targets Database
18	Biomodels.net (Biological Modeling tool)
19	CellML (XML markup language and Model Repository)

These databases and tools can be resorted for simulating the models and analysis of the biological networks for drug target identification. Some of the database enlisted here also provide information on several diseases and drugs

Hierarchical model development at various network levels is another essential task in efficient disease modeling (Kirouac et al. 2010, Werner et al. 2013, Heiner and Gilbert 2013). Based on the disease pathway deduced from the protein–protein interaction and metabolic networks one can perform a hierarchical regulation analysis to understand the transcriptional, signaling and metabolic contributions to the disease phenotype (Sharan 2008, Handorf and Klipp 2012). The idea is to construct the models for individual networks and analyze the dynamics at respective levels (Terentiev et al. 2009; Koschorreck et al. 2009). Integration of these models of sub-networks with difference in the timescales and heterogeneity in the cellular environment puts forth another challenge for analyzing the dynamics of specific phenotype (Przytycka and Kim 2010; Shahrezaei and Swain 2008, Wilkinson 2009, Chandra 2009). Since different types of modeling techniques provide different perspectives, their integration into a combined framework is helpful in improving the ability of target identification (Heiner and Gilbert 2013). Appropriate assumptions which do not override the mechanistic details can aid in resolving this issue. It is interesting and quite challenging to build the disease models which track every event in the disease process with integration of network models embedded in physiological models (Kumar et al. 2006, Koshiyama et al. 2010). However, models are just the precise approximation of the system which delivers the asymptotic behavior of a disease process.

Disease dynamics analysis: Network perturbations

Based on the quantitative analysis of network systems and integration of different types of data, it is possible to understand the dynamics of these networks using the disease models which will enable to derive various predictions about the physiological systemic response (Janes and Yaffe 2006; Kumar et al. 2006; Jørgensen and Linding 2008). By conducting perturbation analysis one can explore for various possibilities of the dynamics of the network (Maayan 2011). Perturbation analysis such as variations in system parameters, protein concentration, node sizes, edge sizes, strengths of interactions and nodal knock-outs can be performed to monitor the system response under various scenarios. This can lead to hefty computation where enormous range of parameter space has to be analyzed against system’s phenotypic response. Nevertheless, the parameters space should be in physiologically feasible ranges. The system response for single parameter variation at a time, keeping other parameters constant that are native to the system, can also give better insight in the disease dynamics. Such an analysis can yield a matrix of sensitive parameters that define the healthy and disease phenotypes. Parametric sensitivity forms a foundation for drug target analysis enabling the quantification of the impact of each node and edge on the network dynamics along with identification of the functional modules in the network (Zanzoni et al. 2009; Chautard et al. 2009). Further by such analysis, the nodes that are essential for structural and dynamic integrity of the network can be deciphered (Koster et al. 2009). Once the essential and dominant interactions are revealed one can optimize the network performance by tweaking the network parameters and identifying the precise target. Moreover this kind of analysis forms a fundamental basis for synthetic biology interventions to control diseases. Flux control analysis is another potential approach that can be used in perturbation analysis and quantify the governance of system parameter on the network performance (Moreno-Sánchez et al. 2008). Recently such approaches have been applied in proteome of Mycobacterium tuberculosis to identify the possible drug targets (Verkhedkar et al. 2007).

The set of probable drug targets are further screened by hit and lead optimization studies. Once the targets are identified, these targets are studied for their biological properties and the corresponding (antagonist/or modulating) molecules are designed so as to control the target and subsequent network dynamics. The drug acts as an experimental perturbation to the system. In the clinical trials the effectiveness of the drugs are studied at different levels of patho-physiology essentially by monitoring the progression of the disease (Chan and Holford 2001; Lesko and Atkinson 2001; Post et al. 2005). Analyzing these models for disease progression with respect to drugs is essential to obtain co-relation between the effectiveness of a drug on diseases response. Furthermore, the drug target assessment in clinical studies can yield data at various points in the network, which can be fed back into the model to refine its predictability. These models help in predicting the time course progression of the disease state with respect to drug usability. Moreover these models can be used to predict the time courses of allied disorders in particular disease such as diabetes (De Gaetano et al. 2008) and cardiovascular events by evaluating the morbidity and mortality associated with diseases. This prediction will help in designing the therapeutic regimes that can be applied in advance to combat the risk.

Physiological and immunological models

The network models have their limitations in clearly translating their response in terms of physiologically measurable output. Due to difference in the scales of models there is large gap in synchronization of molecular models with the tissue and organ level dynamics (Kumar et al. 2006). Research in tissue engineering and physiological engineering are trying hard to bridge this gap. Physiome project is one such endeavor (Hunter et al. 2005). For the success of physiological models, the extensive understanding of the system with high level of abstraction from molecular to physiological level is essential. It includes understanding the physiological system with all its properties i.e. biophysical, chemical, electro-mechanical, signal processing, cellular and tissue geometry along with various layers of system information processing (Butcher et al. 2004). These models, if build successfully, have high level of predictive ability and can precisely simulate the physiological behavior. Physiological models have been implemented with excellent results in various disease such as tumor progression, Parkinson’s disease, Alzheimer’s disease, respiratory disease, diabetic nephropathy, and osteoporosis.

Apart from this, there is high demand for the immunological models that can describe host–pathogen interactions, especially for deadly infectious diseases like AIDS (Bertoletti et al. 2010). The properties of host pathogen interactions have their own distinct peculiarities (since the pathogens i.e. bacteria, fungi, viruses are the foreign entities to the native physiology) which are to be addressed during building the models. Such immunological models help in identifying the appropriate drug targets that are specific antagonists for pathogens without disturbing the immune system. These models have the potential to describe the dynamics of the infection inside the body and design better therapies to combat infections.

By advent of detailed disease network modeling, disease progression modeling and physiological modeling, the concepts of virtual humans and virtual patient are emerging (Ghosh et al. 2007; Hunter et al. 2013). Virtual patient is the combination of all these mathematical models that represent the disease state from all its structural and dynamic aspects (Klinke 2008; Koyutürk 2010). This strives to represents human physiology and disease in its completeness. The virtual human models can be used as the platform to carry out the studies like perturbation analysis, drug trials, clinical trials and simulate the corresponding physiological states.

Networks as drug target

The interaction network comprising of marker bio-molecules for diseases which influence the network function towards disease phenotype is known as disease network (Yildirim et al. 2007; Butcher et al. 2004). The inherent complexity in the interaction networks results in multiple components yielding a emergent property essential for normal functioning. Identification of the components required for these specific properties and perturbation of which results in alterations in the phenotypic response resulting in diseases, are essential to identify targets. This indicates that multiple component nodes may be involved in a disease state which further affect the functional modules that are multigenic in nature. The diseases like cancer and metabolic syndrome are not single target diseases but are manifested due to multiple players to yield phenotypic disorders.

Conventional therapies for these diseases have hardly helped to cure them. Thus the network based approach where instead of targeting single node, the network sub circuits can be targeted to bring down the disease effects (Zanzoni et al. 2009). There can be multiple targets or a single target that governs the network dynamics (Neduva and Russell 2006; Wells and McClendon 2007). It has been noticed that in complex diseases the hub genes/proteins are affected and targeting them can yield monotonous response which can be undesirable leading to several side effects. Therefore, the strategy in target selection should be to minimize the side effects. Yildirim et al. (2007), have developed the Drug-Target network based upon US-FDA approved drugs by linking them with their specific protein target. It is revealed that the topological signatures of drug targets are different from the essential proteins and they occupy certain regions in the interactome networks (Yildirim et al. 2007). Based on topological analysis of disease network it has been shown that disease genes lie on periphery of the network which can effectively be targeted without much side effects (Hase et al. 2009; Zhu et al. 2009). There can be multiple targets (i.e. in diabetes and cancer) at different network levels which can be identified by network dynamic analysis (Moller 2001). Therefore, identifying the target and designing the drug molecules that can modulate the network response could be better option than the drugs that just alter functioning of the disease genes (Pujol et al. 2010; Arrell and Terzic 2010).

The task of network targeting becomes more difficult than targeting single genes/biomolecules (Barabási 2007). This requires an in depth knowledge of the regulatory dynamics of the network and availability of the exact system parameters. The dynamic simulations of network response can be carried out by performing perturbation analysis as described above. The optimum set of parameters that give the healthy (non diseased) system response can be set as the benchmark for target identification for the network. This will essentially track how the system response changes with the strength of each node and edge in the network. Since the disease states are robust in nature and can even utilize the redundant pathways for maintaining their state, it is important to identify the target such that redundant pathways are blocked or restricted (Kitano 2007). These approaches are still in their infancy and are continuously evolving with immense potential to discover more rational drug targets. Table 2 enlists various databases and tools for target identification.

Systemic approach to insulin resistance and metabolic homeostasis

To illustrate some of the ideas of modeling listed in the sections above, we present a systemic view on insulin resistance leading to defective metabolic homeostasis. Metabolic syndrome is one of the most studied diseases which have massively affected the world population. Since its complexity and multigenic in nature it demands systems biological approach to analyze the disease. Complications at multiple network level are observed in insulin resistance such as defects in several gene expressions (e.g. PPAR, SREBP gene) at genetic level, signaling level (e.g. insulin, mTOR, glucagon signaling) and metabolic level (e.g. fat, glucose and amino acid metabolism). The systemic approach involves reconstruction of the disease network with genes, signaling proteins and metabolites as nodes and their mutual interactions represented as edges (Becker et al. 2007; Bajikar and Janes 2012). This essentially will provide with the disease map which can be used for modeling various interactions.

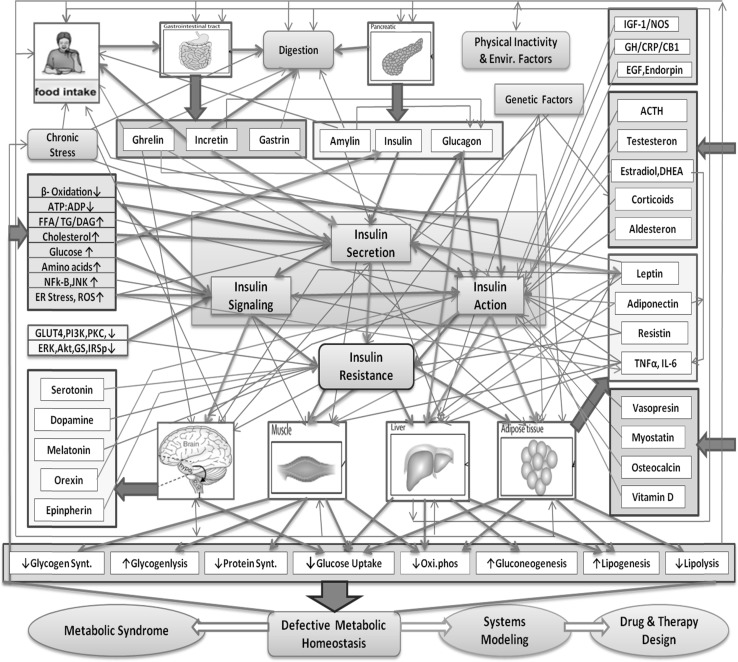
To characterize the complexity in commencement of insulin resistance, we have developed a component map that highlights various factors that are responsible for this disease. The map also depicts the cycle of events that lead to metabolic defects and in turn aggravate metabolic syndrome. It is observed that, metabolic syndrome is a systemic response to the complex interplay of several hormones (GI track, Pancreas, stress and sex), statins, sterols, adipokines, metabolites, signaling molecules, genetic mutations, inflammation, lifestyle (diet, exercise, sleep, digestive disorder and behavior). This involves a multi-scale problem which ranges from genetic to whole body physiological level. These levels are inter/intra-connected with various feedbacks and crosstalk that are essential for regulation of coordinated response of the systems. Moreover, the timescales at each level are different ranging from seconds–minuets–hours to days which are precisely coordinated to elicit the required dynamics of the metabolic system. The overall system roughly constitutes of around 155 inter-scale (pertaining to different levels) interaction, in which around 32 are positive and 41 negative feed forward/feedback interactions (see Fig. 2). Apart from this there are several feedback and feed forward interaction at biological network levels (transcriptional, signaling and metabolic networks) which constitutes the intra-scale interaction (see Fig. 3a). The complex interaction map shows that each network is a sub module of another higher network which depicts the inherent modularity and hierarchy in the regulation of metabolic systemic response.

Fig. 2.

A systemic map of the complex nature of insulin resistance and defective metabolic homeostasis. The factors affecting insulin secretion, signaling and action in liver, muscle, adipose and brain are shown in the figure. The bold lines represent the modeled interactions. The green and red lines show positive and negative effects of corresponding factors on insulin, respectively, whereas the blue lines show the general flow of the processes. (Color figure online)

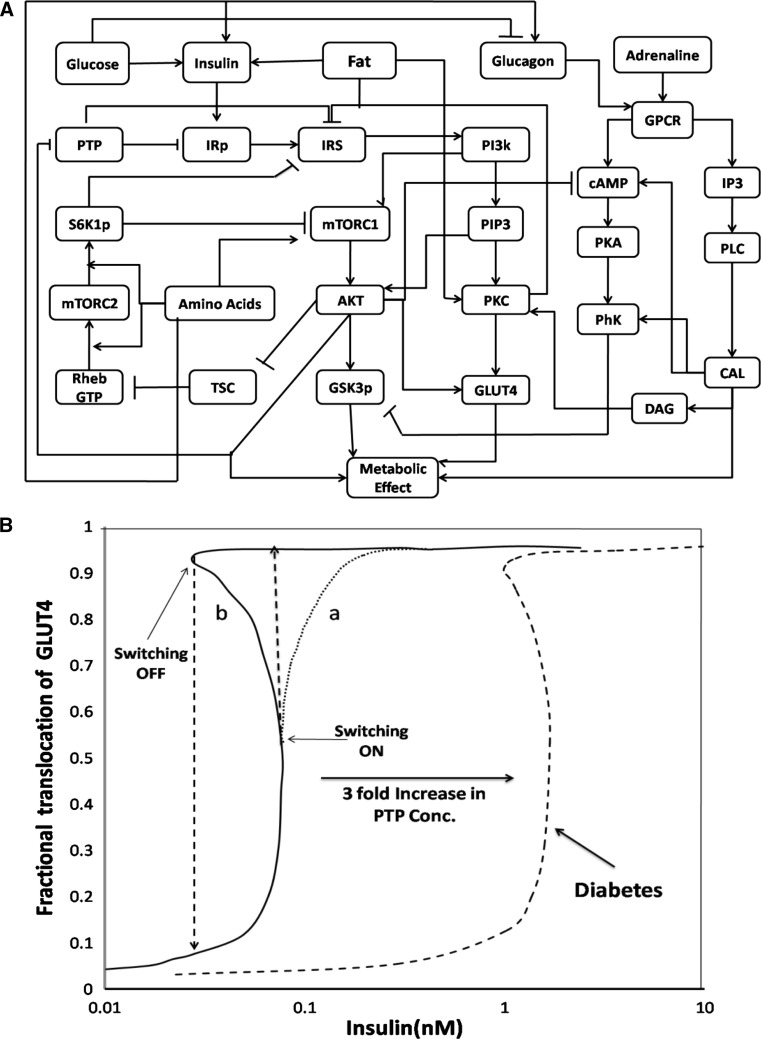
Fig. 3.

a The integrated network of metabolic signaling regulation and the interplay of insulin, mTOR, glucagon and calcium signaling pathways. The interplay depicts the regulation of these signaling pathways on glucose, amino acids and fat metabolism. b Dose response curve for a sub module of integrated network, i.e. insulin stimulated fractional GLUT4 on plasma membrane. Curve ‘a’ is sigmoidal dose–response curve obtained in absence of positive feedback loop. Curve ‘b’ represents a bistable response in insulin-stimulated fractional GLUT4 on plasma membrane in presence of feedback loop. Simulated type 2 diabetic conditions represented by dose–response curve of insulin-stimulated fractional GLUT4 on membrane at threefold higher PTP concentration. Note that the input–output relationship is perturbed for high PTP concentration leading to higher requirement of insulin above the physiological levels

When we look at the components that are responsible for the defects in insulin secretion, signaling and action on the metabolic regulation, it is found that multiple factors affect at each levels which when impaired can lead to insulin resistance and defective metabolic homeostasis (see Fig. 2). This is further responsible to mediate other diseases such as cardiovascular diseases, hyperglycemia, dyslipidimia and diabetic complications such as nephropathy, retinopathy and neuropathy. To brief some of these factors, Fig. 2 depicts several defects that are known to alter insulin signaling such as altered ratios of IRS isoform A and IRS isoform B, decreased receptor binding affinity, impaired phosphorylation of IR and IRS-I, enhanced PKC-ζ activity, impaired GLUT4 expression, distribution, translocation and recruitment to plasma membrane, Serine phosphorylation of IRS-I by inflammatory cytokines and excessive fatty acid metabolites. In case of insulin secretion there is decrease in β-cell mass and function due to various factors such as lipotoxicity, glucotoxicity, genetic mutations, deregulation of β-cell apoptosis/α-cell proliferation, endoplasmic reticulum stress and decreased incretin effect. Whereas in case of insulin action, the sensitivity of insulin is affected due to mitochondrial dysfunction, polymorphisms in PPAR-γ and PGC1α gene and β-3 adrenergic receptor, increase in triglycerides, diacylglycerol, fatty acyl-coenzyme and ceramides, and endoplasmic reticulum stress (Sesti 2006; Tripathy and Chavez 2010).

Network modeling and analysis for diabetes and cancer

Network modeling, analysis and subsequent target and therapy identification approach appear more promising in characterizing diseases such as the pathogenesis of diabetes and cancer (Mardinoglu and Nielsen 2012). These diseases involve multilevel defects comprising of several players such as hormones, growth factors, inflammatory molecules that increases the complexity of modeling these diseases. To address such a complexity and quantify the relative contributions of various factors in development of disease, network modeling becomes inevitable. Efforts in this direction have led to development of different mathematical models that attempt to describe various molecular and physiological interactions and serve the basis for target identification using network approach. Since last decade several attempts have been made to identify various disease signatures and understand its mechanisms. This has led to generation of enormous data that can stand as the basis for quantification of the disease state (Kim et al. 2012).

Tremendous research in this area have led to minimal models and PK-PD models to depict the glucose insulin dynamics at the physiological level (Bergman 1997; Vicini et al. 1999; Bergman 2001; Roy and Parker 2006; Dalla Man and Rizza 2007; Makroglou et al. 2006). However, the minimal models do not provide the clear picture of the disease mechanisms. Hence, the extensive mathematical modeling of insulin signaling including subsystem models such as insulin receptor binding kinetics, receptor recycling and GLUT4 translocation are developed. An integrated model was developed by including these subsystems and also post receptor signaling, which now serve as a tool for studying insulin signaling (Sedaghat et al. 2002; Giri et al. 2004; Sriram et al. 2005). Moreover, the integrated models with higher mechanistic details including dynamics of insulin signaling pathway, glucagon signaling and glucose regulation are also developed (Topp et al. 2000; Chen et al. 2010a; Chew et al. 2009; Liu et al. 2009). Models have been developed for energy homeostasis and whole body metabolic homeostasis which illustrate the metabolism of fat, carbohydrates and amino acids based on the regulations by key regulatory hormones such as insulin and glucagon (Sangar et al. 2012; Kim et al. 2007; Pattaranit and van den Berg 2008; de Graaf 2009; Smith et al. 2009). The efforts have been made to build and validate the disease progression models (Meeting 2007; Klinke 2008) for diabetes (Zelezniak et al. 2010). Given the detail information of the patients clinical data, these models can effectively predict the rate of disease progression (De Gaetano et al. 2008) and the key information such as time course evolution of insulin sensitivity, β-cell mass and hyperglycemia. Such information will further help in predicting the vulnerability of the patient to other allied diseases which in turn will help in advanced preventive therapeutic regimes.

To illustrate a network analysis, here we choose a sub-module of a complex interplay of the signaling pathways that regulate metabolic homeostasis (see Fig. 3a). The an analysis of insulin signaling pathway demonstrates bistability in response to GLUT4 translocation (Giri et al. 2004) to the plasma membrane with respect to insulin concentration (see Fig. 3b). The bistable response arises due to the positive feedback of Akt on the signaling pathway. Any modification to robust setting either due to over activation of the positive feedback or negative feedback can result in a disease state such as diabetes, as illustrated by overexpression of PTP concentration. PTP is a negative regulator of the pathway, and increasing its concentration can shift the activation threshold for GLUT4 towards right (see dotted curve in Fig. 3b), which implies higher dose of insulin. However, administering higher dose of insulin has its own side effect on the system. Therefore, the rational target would be to reduce the inhibitory effect of PTP on signaling pathway rather than increasing insulin dose. This kind of non-linear analysis of networks provides insights into the conditions that lead to onset of insulin resistance, which further aid in decision making in lifestyle interventions (diet, fasting and exercise plans) to maintain insulin sensitivity and cure diabetes.

Similarly, cancer is also identified as a network disease (Azmi et al. 2010; Cloutier and Wang 2011). Owing to its complexity, networks and the corresponding models to explain tumerogenesis (Andasari et al. 2011; Comen et al. 2012; Zheng et al. 2013), angiogenesis (Duda et al. 2013; Wang et al. 2013), cell proliferation, differentiation, cell migration and apoptosis (Cheng et al. 2012; Zinovyev et al. 2012; Schleich and Lavrik 2013; Zheng et al. 2013) have been developed to study the mechanisms of the disease. Alike diabetes, cancer also involves multilevel defects at genetic, signaling and metabolic pathways (Edelman et al. 2010; Cloutier and Wang 2011; Deisboeck et al. 2011; Hageman et al. 2012).

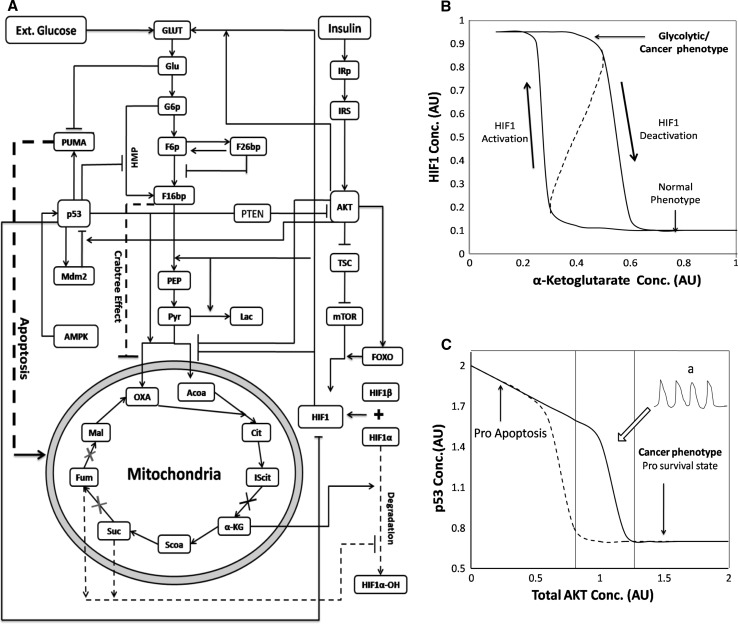
As an example, here we elaborate on the network behavior that can lead to Warburg effect observed in cancerous cells wherein aerobic glycolysis is more prominent with the reduction in the fluxes of TCA cycle leading to the lactate accumulation (Resendis-Antonio et al. 2010; Folger et al. 2011). Figure 4a shows the integrated network of signaling and metabolic pathways that are responsible for Warburg effect. Higher levels of Hypoxia inducible factor (HIF1) have been found to be responsible for the shift of fluxes towards aerobic glycolysis by reducing oxidative phosphorylation. Hypoxia or α-ketoglutarate is known to regulate the activity of HIF1. It is found that the activation of HIF1 is sensitive to the varying levels of or α-ketoglutarate which attributes to metabolic plasticity (Bhat et al. 2011) due to the possible bistability in the network (see Fig. 4b). Once the cell gets lock in the glycolytic phenotype, it further enhances the HIF1 activity by the role of AKT-PTEN-p53 interaction with respect to insulin. This formulates a positive feedback in AKT signaling which transform a cell state leading towards the Warburg effect. Moreover, the AKT-p53-MDM2 interaction loop also elicit bistability with respect to total AKT concentration, switching between pro-survival and apoptotic states (see Fig. 4c) (Zinovyev et al. 2012). These are network dynamics that may happen irrespective of the mutations just due to varying component concentrations in the network and may further prone the cells towards mutative consequences leading to tumerogenesis. Furthermore these interactions along with crab-tree effect leads to multiple positive feedback loop which provides the fitness benefit of growth and survival to cancerous cells. If cancer is due to such metabolic plasticity, instead of chemotherapeutic treatments, increasing the oxygen supply or enhancing the TCA flux in the cell can regain the normal cellular state. On the other hand decreasing the growth factor mediated Akt activation can also pave the way for p53 activity thereby initiating apoptosis. Such analysis provides insights on the kind of therapies that can be implemented in cancer.

Fig. 4.

a Integrated network of metabolic and signaling pathways involved in warberg effect in cancerous cells. The network consists of the interplay of growth factor (insulin) signalling, p53-Mdm2-PTEN signaling and the HIF1 signalling that regulates central metabolism. The apoptosis, crab-tree effect and the degradation of HIF1 by metabolites is shown by dotted lines. b The dose response curve for a submodule of the integrate network for HIF1 with respect to varying α-ketoglutarate concentration. The system elicit bistability with two distinct states i.e. glycolytic phenotype and normal TCA functioning state. c The dose response curve for another submodule of the integrate network for p53 activation with respect to total Akt concentration. Due to mutual inhibitory loop the AKT-p53 signaling system also elicit bistability with respect to varying AKT concentrations leading to prosurvival/cancerous phenotype and pro apoptotic states. In the normal range of Akt, p53 shows oscillatory behaviour (curve ‘a’) in the dynamic scale which enables the cell to frequently decide between survival and apoptotic cellular fate

Systems engineering in health and disease

Human health is an intricately designed natural system. Alike physical systems, we hypothesize that human physiological systems also follow the first principles and laws with greater complexity of its organization and operations (Menolascina et al. 2012). The physical and engineering principles that explain the design of the physical systems can be applied to physiological systems to study and analyze the underlying mechanisms and fault diagnosis (Imms et al. 2011). Therefore, the process of systemic analysis of the disease mechanisms from molecular interactions to the network dynamics with application of modeling and analysis techniques to quantify patho-physiological states for drug discovery and assessment can be called as Health/Disease systems engineering.

Basic research on disease systems and target Identification costs about 20–25 % of total drug development cost. Only 2–5 targets per 1,000 targets reach the final stage of drug development (Butcher et al. 2004). Huge amount of work, time and money is consumed in identification of efficient and safer targets. The efficiency of the identified target, therapies and the drug entirely depends upon the well understood network and rational modeling. It can be noted that network modeling and analysis forms the crux of target identification, wherein poor/insufficient network can lead to inefficient targets. Hence, the knowledge of complete network and appropriate parameterization of individual interactions is the inevitable information for a rational target identification. Moreover, there are sever ethical constrains on the clinical studies on human systems which makes it difficult to arrive at the effective conclusions based on the limited data. Therefore, modeling and analysis mitigates the efforts required for clinical studies and economizes the process of drug discovery.

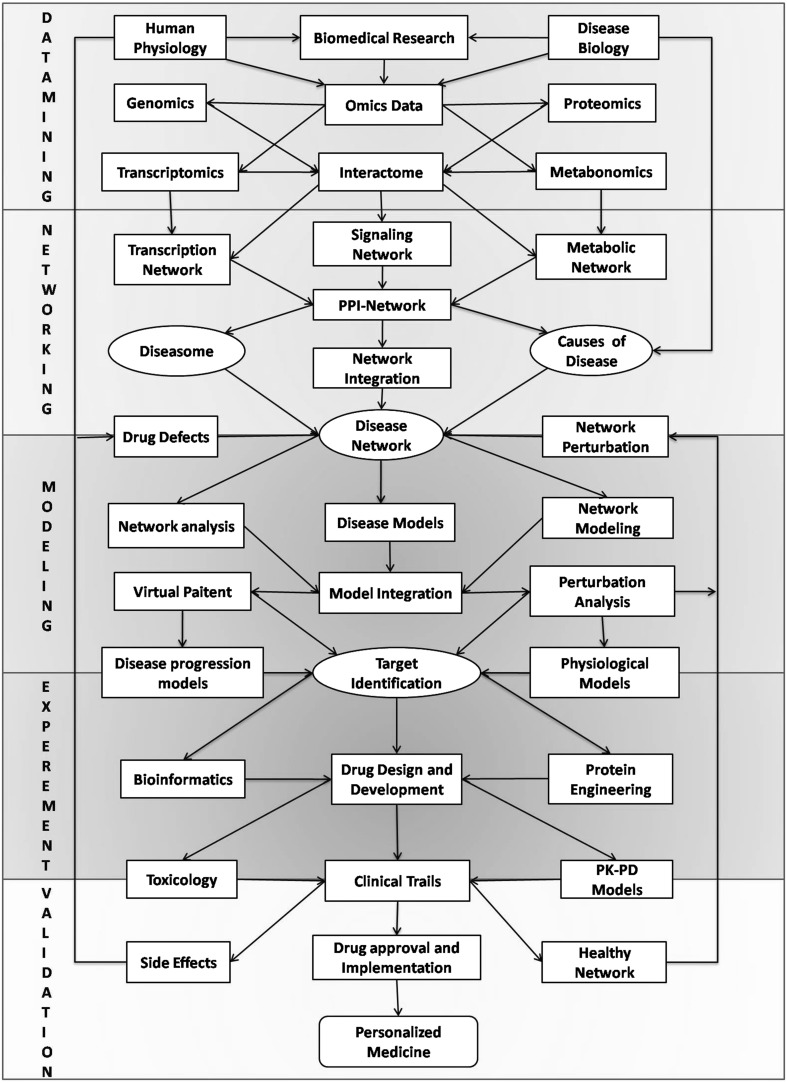
Biomedical researchers in past decade have applied different paradigms to analyze disease systems and the ideas of systems medicine and computational drug discovery are being put forth (Arrell and Terzic 2010; Bogle et al. 2010; Eissing et al. 2011; Kolodkin et al. 2012). Based on the advances in the knowledge of human systems biology, we propose a “Cell-to-Human” approach to address human diseases. We outline a framework for the application of network modeling approach towards personalized medicine. The framework consists of five basic modules i.e.—(1) data mining module, (2) networking module, (3) modeling and analysis module (4) experimental cum development module and (5) validation cum Implementation module. Figure 5 shows the schematic for this framework of network modeling and analysis in disease systems for personalized medicine.

Fig. 5.

Shematic framework for application of network modeling in disease systems and drug development. The framework illustrates the flow and interconnections of the five modules viz. data mining, networking, modeling and analysis, experimental and drug development, validation and drug implementation processes

In the data mining module it starts with a hypothesis or a predefined research problem and acquisition of the high throughput multi-scale omics data at genomics, proteomics, metabolomics and transcriptomics levels (Kim et al. 2010). While genomic and transcriptomics data refers to the gene expression and transcriptional interactions at the DNA level, proteomics and metabolomics data refers to the interactions of various protein, enzyme, signaling and metabolic pathways respectively. The relevant omics data are gathered together to link functional components and an interactome is formulated.

In the networking module, based on the interactome, the network for protein–protein interaction can be build comprising of genetic and signaling network (Langley et al. 2013). The regulations from interaction network are further integrated to appropriate metabolic reactions in the metabolic network to form an overall integrated network (Oberhardt et al. 2009; Kirouac et al. 2010). The integrated network essentially comprises of several signaling and metabolic pathways interconnected through feedbacks and crosstalk. Further, based on the disease biology the network is annotated for the defective interactions in the integrated network that are responsible for the pathological conditions, which can be termed as disease networks (Przytycka and Kim 2010; Rolfsson et al. 2011).

In the modeling and analysis module, the overall network forms the basis for the kinetic modeling of the network interactions (Pfau et al. 2011). The multi-scale models are formulated based on the experimental and literature data. These models are optimized and parameterized for the desired phenotypic response using flux balance and pathway analysis methods (Orth et al. 2010; Walpole et al. 2013). Moreover the network can further be particularized to include the person specific genetic and metabolic data based upon the clinical investigations of the patient’s genetic and metabolic profiles. Thereafter, network perturbation are simulated and analyzed to obtain the key interactions and the parameter space that characterize the disease and healthy phenotypes (Koyutürk 2010; Rees et al. 2011). The key interactions that can alter the overall diseased network response to healthy response can be identified as the potential drug targets.

In the experimental cum drug development module, once the theoretical targets are identified, these targets are further screened and studied for their viability assessments in the pharmacological settings. Hits and lead target optimization studies are performed to screen the potential targets (Renner et al. 2011). A typical drug discovery pipeline is followed which comprises of bioinformatics and protein engineering approaches that are used to formulate effective drugs/ligands to modulate the target (Schenone et al. 2013). The structures of the targets are identified and corresponding compounds (biological or chemical) are designed so as to influence these targets for the desired network response (Duffy et al. 2012). The effectiveness of these drugs is further assessed in animal studies to check their physiological impacts (Mizushima 2012). This helps to refine the physiologically feasible targets with least side effects and maximum therapeutic value.

In the validation module, the experimental results are validated with the desired theoretical response that has been in sighted by the modeling studies (Smith 2003). Moreover, physiological and pharmaco-kinetic/pharmaco-dynamic models are then applied to quantify the effects of these drugs and identify the most potential drug for certain ailment. Furthermore, the drugs are subjected to their toxicological assessments and possible side effects. The potential drug is then subjected through preclinical and clinical trials before approved by FDA (Schenone et al. 2013). This overall process can be reiterated unless the optimum healthy response is achieved (with least side effects and optimum cure), wherein the experimental data thus obtained can be used to refine the available data and subsequent improvements in the mathematical models. This will essentially enable the final drug to tune the diseased network response towards the sustained healthy state.

Significance of systems engineering for disease systems

Implementing the systems engineering perspective for the complex diseases will help in understanding how these networks are integrated into a whole system and work collectively to represent a specific phenotype. By knowing this, the entire trajectory of the response can be traced out right from its root to the top. (i.e. genotype to phenotype). This will provide us with the information about the cause and effect mechanisms at various system levels. In most diseases it is observed that once a cause is triggered it gives certain effect which in turn acts as the cause for another effect and so on. On the other hand, single cause is responsible for multiple effects which run in parallel to each other. This kind of phenomena makes the system output more complex to comprehend the system mechanism and its design principles. Thus, the engineering approach towards disease systems will help in addressing fundamental challenges such as (1) precisely tracing the exact cause to a certain effect (disease target); (2) finding the mechanism by which the cause generate effects (disease mechanisms); (3) understanding how the cause leads to multiple effects (disease networks); (4) controlling the causative mechanism at source or preventing the cause (preventive medicine); (5) controlling the effect of one cause by introducing the counteractive cause (drug target); (6) breaking the link between cause and effect (therapy design); (7) eradicate the effect without disturbing the system (no side effect) (drug design). Systems biology hopes in providing the basis to deal with such issues by engineering analysis of the diseases (Nielsen 2012; Winslow et al. 2012).

Conclusion

The network modeling and analysis for targeting network diseases (systemic diseases) becomes inevitable to find cures for these diseases. This approach has several advantages such as identification of rational drug targets, effective drug design with least side effects, effective therapeutic strategies, diagnosis of actual source of disease state, treatment on disease source rather than symptoms, early and reliable diagnosis of diseases using predictive models, rational toxicological and drug safety assessments leading to improved healthcare. Such an approach has got tremendous potential in biomedical research and pharmaceutical industries wherein the efforts of clinical trial studies can be drastically minimized. Hence, the concept of disease systems engineering that emerges from system biology will definitely revolutionaries the human health with invention of modern therapeutics and personalized medicine. Nevertheless, it requires global collaboration in research and academics to collectively address these issues and arrive at fruitful ends in shorter times. Indeed, with advancements in computational systems biology and in conjunction with other interdisciplinary sciences and technological developments, the advent of highly efficient ‘in silico Clinic’ is in the horizon.