Abstract
Protein networks, describing physical interactions as well as functional associations between proteins, have been unravelled for many organisms in the recent past. Databases such as the STRING provide excellent resources for the analysis of such networks. In this contribution, we revisit the organisation of protein networks, particularly the centrality–lethality hypothesis, which hypothesises that nodes with higher centrality in a network are more likely to produce lethal phenotypes on removal, compared to nodes with lower centrality. We consider the protein networks of a diverse set of 20 organisms, with essentiality information available in the Database of Essential Genes and assess the relationship between centrality measures and lethality. For each of these organisms, we obtained networks of high-confidence interactions from the STRING database, and computed network parameters such as degree, betweenness centrality, closeness centrality and pairwise disconnectivity indices. We observe that the networks considered here are predominantly disassortative. Further, we observe that essential nodes in a network have a significantly higher average degree and betweenness centrality, compared to the network average. Most previous studies have evaluated the centrality–lethality hypothesis for Saccharomyces cerevisiae and Escherichia coli; we here observe that the centrality–lethality hypothesis hold goods for a large number of organisms, with certain limitations. Betweenness centrality may also be a useful measure to identify essential nodes, but measures like closeness centrality and pairwise disconnectivity are not significantly higher for essential nodes.
Electronic supplementary material
The online version of this article (doi:10.1007/s11693-013-9123-5) contains supplementary material, which is available to authorized users.
Keywords: Protein–protein interactions, Lethality, Centrality, Network biology
Introduction
Protein networks, describing functional associations as well as physical interactions between proteins, have been unravelled for several organisms in the recent past. A number of methods have been developed to identify protein–protein interactions, using both experimental (Shoemaker and Panchenko 2007a) and computational techniques (Shoemaker and Panchenko 2007b). Databases such as the DIP (Xenarios et al. 2002) and STRING (Szklarczyk et al. 2011) provide excellent resources for building and analysing networks of proteins. The organisation of these protein networks have been studied in the past, particularly examining the importance of highly connected proteins, or ‘hubs’, in terms of their essentiality, or lethality (Batada et al. 2006; He and Zhang 2006; Jeong et al. 2001; Ning et al. 2010; Rodrigues et al. 2011; Song and Singh 2013). Previous studies have also addressed how complex networks can be attacked, by targeting specific nodes, based on centrality properties (Holme et al. 2002). Many of the previous studies (Batada et al. 2006; He and Zhang 2006; Jeong et al. 2001) have focussed on budding yeast, Saccharomyces cerevisiae, as the model organism, while some focus on yeast and Escherichia coli (Ning et al. 2010).
In this contribution, we revisit the organisation of protein networks, particularly the centrality–lethality hypothesis (He and Zhang 2006; Jeong et al. 2001), assessing the importance of a set of network parameters and centrality measures, for protein networks of a diverse set of 20 organisms. The networks we consider are functional association networks from the STRING database; however, we consider only the interactions and associations reported with high confidence. We analyse various network parameters, such as degree centrality, betweenness centrality, closeness centrality and pairwise disconnectivity index.
In particular, we seek to answer the following questions, across a diverse set of 20 organisms: How are protein networks organised, structurally, in terms of the connectivity of essential and non-essential proteins? Does the centrality–lethality hypothesis hold good for different types of organisms? Do essential proteins hold a special position in the network organisation? What are the important network metrics that can decide if a protein is likely to be essential?
Methods
Data
We obtained the protein networks for 20 organisms from the STRING database (STRING version 9.0; http://string.embl.de/; file protein.links.v9.0.txt.gz). We chose these 20 organisms, because they had essentiality data available from the Database of Essential Genes (see below). The STRING database (Szklarczyk et al. 2011) includes interactions from published literature describing experimentally identified protein interactions, as well as functional associations from genome sequence analysis using many well-established methods based on phylogenetic profiling, domain fusion and gene neighbourhood concepts. For each organism, we considered only the high-confidence interactions, i.e. interactions with a STRING score greater than 700.
Data on essential genes were obtained from the Database of Essential Genes (DEG version 5.0; http://tubic.tju.edu.cn/deg/). While the DEG indexes proteins using the NCBI GI numbers (GenInfo Identifiers), the STRING indexes proteins using RefSeq/ENSEMBL identifiers. We translated the DEG identifiers to STRING identifiers, using the aliases file provided in the STRING database (file protein.aliases.v9.0.txt.gz). Based on the data in the DEG, we annotated proteins in the networks derived from STRING as essential or non-essential. Some essential proteins may not have high-confidence interactions; this leads to a small discrepancy in the number of proteins listed as essential in DEG for an organism, and the number in the third column of Table 1. The table also lists all the organisms considered in this study, along with statistics on network size, number of essential proteins, as well as the total number of interactions considered.
Table 1.
Summary of the networks considered in this study
| Organism (NCBI taxonomy ID) | Nodes (proteins) | Essential nodes | (%) | Edges (interactions) |
|---|---|---|---|---|
| Acinetobacter baylyi (62977) | 2,546 | 468 | (18.4 %) | 12,996 |
| Arabidopsis thaliana (3702) | 7,090 | 195 | (2.8 %) | 69,603 |
| Bacillus subtilis (224308) | 3,347 | 219 | (6.5 %) | 20,728 |
| Caenorhabditis elegans (6239) | 5,184 | 192 | (3.7 %) | 46,737 |
| Escherichia coli (511145) | 3,789 | 672 | (17.7 %) | 25,784 |
| Francisella novicida (401614) | 1,415 | 362 | (25.6 %) | 7,587 |
| Haemophilus influenzae (71421) | 1,497 | 592 | (39.5 %) | 8,877 |
| Helicobacter pylori (85962) | 1,352 | 298 | (22.0 %) | 7,915 |
| Mycobacterium tuberculosis (83332) | 3,295 | 587 | (17.8 %) | 18,445 |
| Mycoplasma genitalium (243273) | 446 | 363 | (81.4 %) | 3,376 |
| Mycoplasma pulmonis (272635) | 616 | 288 | (46.8 %) | 3,111 |
| Pseudomonas aeruginosa (208963) | 4,556 | 296 | (6.5 %) | 21,818 |
| Saccharomyces cerevisiae (4932) | 5,477 | 1,109 | (20.2 %) | 105,429 |
| Salmonella enterica serovar typhi (209261) | 3,491 | 344 | (9.9 %) | 19,650 |
| Salmonella typhimurium (99287) | 3,712 | 204 | (5.5 %) | 20,985 |
| Staphylococcus aureus NCTC (93061) | 2,127 | 328 | (15.4 %) | 9,500 |
| Staphylococcus aureus subsp. aureus N315 (158879) | 1,966 | 296 | (15.1 %) | 9,207 |
| Streptococcus pneumoniae (170187) | 1,718 | 109 | (6.3 %) | 8,597 |
| Streptococcus sanguinis (388919) | 1,801 | 215 | (11.9 %) | 8,315 |
| Vibrio cholerae (243277) | 2,958 | 537 | (18.2 %) | 15,644 |
The table lists the organisms considered in this study along with their NCBI taxonomy ID, the number of nodes (proteins), the number of essential nodes (as obtained from DEG), and the number of high-confidence interactions between the nodes (as obtained from STRING)
Network analyses
A number of biological networks have been analysed using concepts from graph theory in computer science. An excellent introduction to network biology, the science of analysing biological networks, can be found elsewhere (Barabási and Oltvai 2004). For the protein networks we discuss here, the nodes are proteins, and the interactions between proteins comprise edges. Nodes in networks can be characterised by several parameters, which evaluate their importance in the network’s structure, from different perspectives. We here describe only few of the important network parameters, which we have used in our study. A more comprehensive review of networks and network parameters can be found elsewhere (Boccaletti et al. 2006; Newman 2003b).
Degree centrality
Degree centrality, or degree, represents the number of edges or links that a node has to other nodes in the network.
Betweenness centrality
Betweenness centrality (CB) measures the participation of a node in the shortest parts in a network. For a graph G(V,E) with n vertices (nodes), the betweenness centrality of a vertex v is defined as:
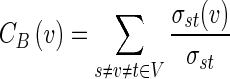 |
Here, σst is the number of shortest paths from s to t, and σst(v) is the number of shortest paths from s to t that pass through the vertex v. Betweenness centrality was first defined by Freeman (1977).
Closeness centrality
Closeness centrality (CC) is defined as the reciprocal of the sum of all geodesic distances from one vertex to all other vertices in the graph (Sabidussi 1966):
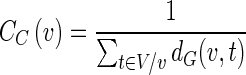 |
Here dG(v,t) represents the distance between v and t in the graph. Note that closeness centrality can generally be computed only for a fully connected graph.
Pairwise disconnectivity index
The pairwise disconnectivity index was defined by Wingender and co-workers earlier (Potapov et al. 2008), as the “fraction of those initially connected pairs of vertices in a network which become disconnected if vertex v is removed from the network”:
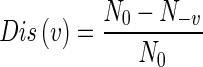 |
Here, N0 is the total number or vertex pairs in the network that are connected by a path of any length in the network, and N-v is the number of vertex pairs that remain connected following the removal of vertex v. We computed these values for every node in each of the networks, using MATLAB and the Boost Graph Library for MATLAB (http://dgleich.github.io/matlab-bgl/).
Assortativity
Newman (2003a) defined a measure to quantify the assortativity of networks with discrete types of nodes. In our networks, we have two types of nodes—essential and non-essential. We compute the assortativity coefficient as defined by Newman:
 |
where e is a 2 × 2 matrix indicating the fraction of edges between nodes of different types (essential and non-essential). eij in the matrix represents the fraction of edges in the network between a node of type i and a node of type j. The trace of a matrix is the sum of the main diagonal elements, while 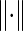 denotes the sum of all the elements in the corresponding matrix.
denotes the sum of all the elements in the corresponding matrix.
Results
We analysed the relationships between essentiality and network parameters such as degree centrality, betweenness centrality, closeness centrality and pairwise disconnectivity index. We performed these analyses for 20 organisms with data available in the DEG. While Arabidopsis thaliana had the smallest fraction of essential genes, some of the very small organisms had very large fractions of essential genes, viz. Mycoplasma genitalium (81.4 %) and M. pulmonis (46.8 %). This is understandable, given that these organisms have very small genomes, and that a large number of genes in their genomes might not be redundant, but rather have very important functions for the survival of the organism. S. cerevisiae has its 5,477 proteins connected through a large number of high confidence interactions. About 20 % of the proteins in S.cerevisiae are essential. E. coli has 3,789 proteins in its network, with about 18 % of its nodes being essential.
Protein networks are predominantly disassortative/essential proteins tend to connect to non-essential proteins
We observe that nearly all of the protein networks studied here show low assortativity. Table 2 illustrates the distribution of various edge types (essential–essential, non-essential–non-essential and essential–non-essential) as well as the assortativity coefficients, computed according to Newman (2003a). If a network is assortative, then a vast majority of the edges must connect like nodes. In the protein network of S. typhi, which has an assortativity coefficient of 0.55, we observe that 85 % of the connections are between like nodes. In all the other networks, the assortativity coefficient is less than 0.5; even though a number of edges connect non-essential nodes amongst themselves, relatively few edges connect essential nodes amongst themselves, leading to low overall assortativity.
Table 2.
Assortativity coefficients for the networks considered in this study
| Organism | Nodes (proteins) | Fractions of edges of different types | Total edges | Assortativity (r) | ||
|---|---|---|---|---|---|---|
| EE | NE | NN | ||||
| Arabidopsis thaliana | 7,090 | 0.002 | 0.066 | 0.932 | 69,603 | 0.034 |
| Caenorhabditis elegans | 5,184 | 0.005 | 0.100 | 0.895 | 46,737 | 0.041 |
| Helicobacter pylori | 1,352 | 0.105 | 0.390 | 0.505 | 7,915 | 0.071 |
| Streptococcus pneumoniae | 1,718 | 0.019 | 0.171 | 0.810 | 8,597 | 0.084 |
| Mycoplasma genitalium | 446 | 0.825 | 0.158 | 0.017 | 3,376 | 0.088 |
| Haemophilus influenzae | 1,497 | 0.249 | 0.454 | 0.296 | 8,877 | 0.090 |
| Salmonella typhimurium | 3,712 | 0.020 | 0.145 | 0.836 | 20,985 | 0.135 |
| Saccharomyces cerevisiae | 5,477 | 0.193 | 0.371 | 0.436 | 105,429 | 0.212 |
| Pseudomonas aeruginosa | 4,556 | 0.047 | 0.168 | 0.785 | 21,818 | 0.265 |
| Mycobacterium tuberculosis | 3,295 | 0.141 | 0.294 | 0.565 | 18,445 | 0.284 |
| Escherichia coli | 3,789 | 0.149 | 0.261 | 0.590 | 25,784 | 0.352 |
| Bacillus subtilis | 3,347 | 0.068 | 0.159 | 0.773 | 20,728 | 0.367 |
| Mycoplasma pulmonis | 616 | 0.658 | 0.216 | 0.126 | 3,111 | 0.397 |
| Vibrio cholerae | 2,958 | 0.176 | 0.251 | 0.573 | 15,644 | 0.404 |
| Streptococcus sanguinis | 1,801 | 0.184 | 0.252 | 0.565 | 8,315 | 0.411 |
| Staphylococcus aureus subsp. aureus N315 | 1,966 | 0.235 | 0.274 | 0.491 | 9,207 | 0.413 |
| Acinetobacter baylyi | 2,546 | 0.263 | 0.278 | 0.459 | 12,996 | 0.422 |
| Francisella novicida | 1,415 | 0.360 | 0.287 | 0.353 | 7,587 | 0.426 |
| Staphylococcus aureus NCTC | 2,127 | 0.245 | 0.238 | 0.517 | 9,500 | 0.486 |
| Salmonella enterica serovar typhi | 3,491 | 0.137 | 0.149 | 0.714 | 19,650 | 0.554 |
EE Essential–Essential, NE Non-essential–Essential, NN Non-essential–Non-essential
The table lists the different organisms along with the fraction of different types of edges and the assortativity coefficient, computed as indicated in the text. The list is sorted in increasing order of the assortativity coefficient (r)
Do essential nodes differ significantly in certain metrics?
Many previous studies have highlighted the critical roles played by ‘hubs’, or highly connected proteins in protein networks (He and Zhang 2006; Jeong et al. 2001); the centrality–lethality hypothesis essentially implies that proteins essential for an organism’s survival are likely to have a higher degree (Jeong et al. 2001). We here examine multiple metrics, in addition to degree, as to whether essential proteins in the networks differ in terms of metrics such as betweenness centrality, closeness centrality and pairwise disconnectivity index. We address this question by means of a simple statistical test: our null hypothesis is that essential nodes have the same average value of a metric (degree, betweenness centrality, etc.) as the entire set of nodes in the network. We consider the set of essential nodes (E) as a particular subsample of the entire set of nodes (N). Following this, we create 106 random subsamples of size |E| from N. We then compute a p-value, as the probability of observing a mean value of the metric (in these random subsamples) greater than equal to that of E. Table 3 lists these values for degree, betweenness centrality, closeness centrality and pairwise disconnectivity index, for each of the 20 organisms. For example, in S.cerevisiae, we observe that the degree and betweenness centrality are significantly higher for essential nodes, vis-à-vis the entire network (p < 10−6). Indeed, it can be clearly seen that the average degree for essential nodes is significantly higher than the network average, for each of the 20 organisms considered. Interestingly, in addition to degree centrality, betweenness centrality also is significantly higher (p < 0.01), for 15 of the 20 organisms considered here.
Table 3.
p-values for the significance of deviation of the mean of different metrics for the set of essential nodes vis-à-vis all nodes in a network
| Organism | p (degree) | p (Betweenness centrality) | p (Closeness centrality) | p (Pairwise disconnectivity index) |
|---|---|---|---|---|
| Acinetobacter baylyi | < 10−6 | < 10−6 | 0.22 | 0.14 |
| Arabidopsis thaliana | 8.52 × 10−3 | 0.05 | 0.18 | 0.15 |
| Bacillus subtilis | < 10−6 | < 10−6 | 0.89 | 0.40 |
| Caenorhabditis elegans | 8.40 × 10−5 | 0.25 | 0.10 | 0.01 |
| Escherichia coli | < 10−6 | < 10−6 | 0.92 | 0.98 |
| Francisella novicida | < 10−6 | < 10−6 | 0.50 | 0.49 |
| Haemophilus influenzae | < 10−6 | 0.26 | 0.22 | 0.36 |
| Helicobacter pylori | < 10−6 | 6.55 × 10−4 | 0.86 | 0.03 |
| Mycobacterium tuberculosis | < 10−6 | < 10−6 | 0.20 | 0.07 |
| Mycoplasma genitalium | < 10−6 | 0.05 | 0.76 | 0.18 |
| Mycoplasma pulmonis | < 10−6 | < 10−6 | 0.87 | 0.00 |
| Pseudomonas aeruginosa | < 10−6 | < 10−6 | 0.14 | 0.05 |
| Saccharomyces cerevisiae | < 10−6 | < 10−6 | 0.28 | 0.09 |
| Salmonella enterica serovar typhi | < 10−6 | < 10−6 | 0.92 | 0.06 |
| Salmonella typhimurium | < 10−6 | 0.0163 | 0.85 | 0.15 |
| Staphylococcus aureus NCTC | < 10−6 | < 10−6 | 0.24 | 0.18 |
| Staphylococcus aureus subsp. aureus N315 | < 10−6 | < 10−6 | 0.96 | 0.05 |
| Streptococcus pneumoniae | 2 × 10−6 | 7.14 × 10−4 | 0.57 | 0.11 |
| Streptococcus sanguinis | < 10−6 | < 10−6 | 0.61 | < 10−6 |
| Vibrio cholerae | < 10−6 | < 10−6 | 0.57 | 0.89 |
Poor p values (p > 0.01) have been shown in bold. The table clearly shows that metrics such as closeness centrality and pairwise disconnectivity index cannot be used to selectively delineate essential nodes
In stark contrast, closeness centrality and pairwise disconnectivity index for yeast are not significantly different for essential nodes compared to the entire network (p = 0.28 and p = 0.09 respectively). It is clear from the table that metrics such as closeness centrality and pairwise disconnectivity index do not vary significantly for essential nodes, for all of the organisms considered here.
Degree and betweenness centrality correlate with lethality in many organisms
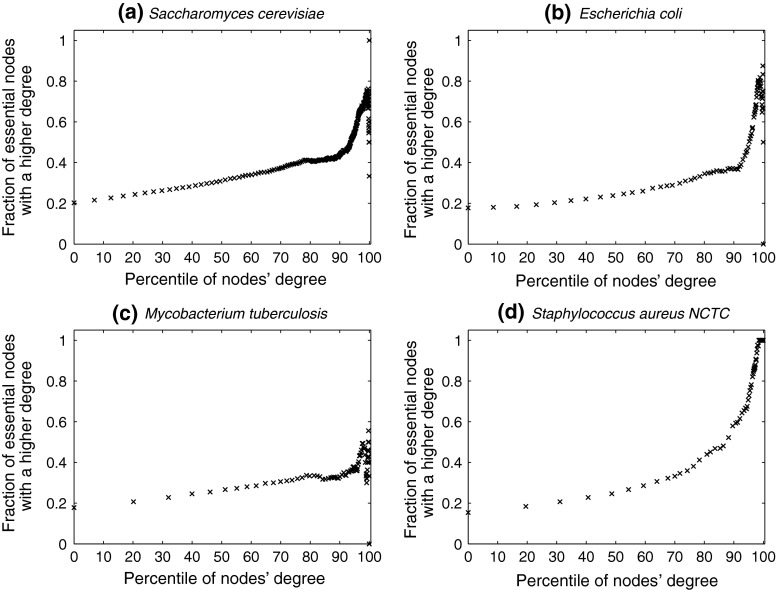
Does degree or betweenness centrality form a strong indicator of lethality? To address this, we computed the fraction of nodes that are essential, in a set of proteins having a degree greater than a specified value. Figure 1 shows a plot to this end for S. cerevisiae, E. coli, Staphylococcus aureus NCTC and Mycobacterium tuberculosis: the horizontal axis represents increasing node degrees, indicated as percentiles (x); such a representation also hints at the degree distribution. The vertical axis indicates the fraction of essential nodes in Nx ∈ N, where Nx is the set of nodes with degrees in the xth percentile and above, i.e. 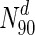 is the set of nodes with degrees (indicated by the superscript d) in the 90th percentile and above (top 10 % of nodes with highest degrees). In S.cerevisiae, we see that for
is the set of nodes with degrees (indicated by the superscript d) in the 90th percentile and above (top 10 % of nodes with highest degrees). In S.cerevisiae, we see that for 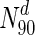 , 43.8 % nodes are essential, compared to 20.2 % in the entire network (also see Table 4). A similar plot for betweenness centrality is shown in Fig. 2. For
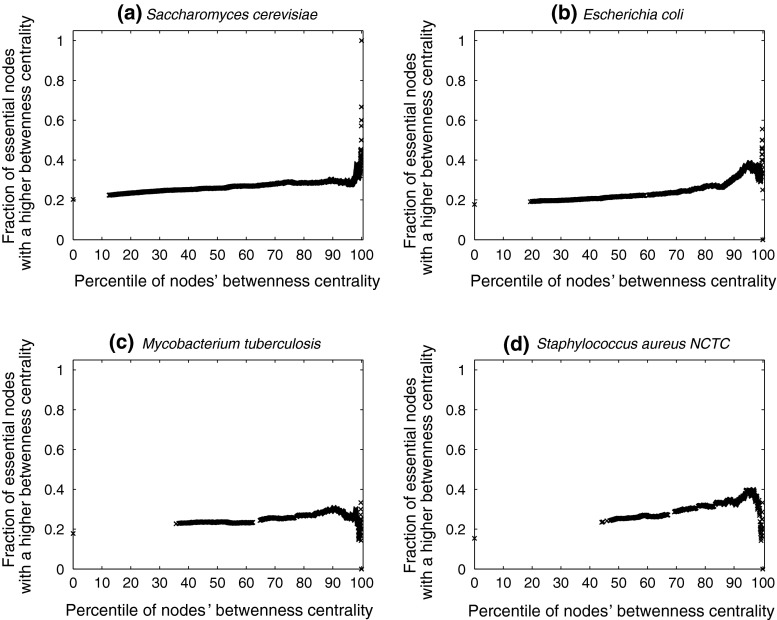
, 43.8 % nodes are essential, compared to 20.2 % in the entire network (also see Table 4). A similar plot for betweenness centrality is shown in Fig. 2. For 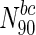 (the superscript bc denotes betweenness centrality), 29 % of the nodes are essential. Online Resources 1 and 2 show similar plots for the remaining organisms. Table 4 summarises the N90 data for degree and betweenness centrality. Overall, we observe that, for most organisms, there is a clear increase in the fraction of essential nodes (albeit gradual), with increase in degree or betweenness centrality.
(the superscript bc denotes betweenness centrality), 29 % of the nodes are essential. Online Resources 1 and 2 show similar plots for the remaining organisms. Table 4 summarises the N90 data for degree and betweenness centrality. Overall, we observe that, for most organisms, there is a clear increase in the fraction of essential nodes (albeit gradual), with increase in degree or betweenness centrality.
Fig. 1.
Variation in fraction of essential nodes, with increase in degree. The horizontal axis represents increasing node degrees, indicated as percentiles (x), while the vertical axis indicates the fraction of essential nodes in 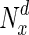 , the set of nodes with degrees in the xth percentile and above. For simplicity, four example organisms are shown: a
S. cerevisiae, b
E. coli, c
S. aureus NCTC and d
M. tuberculosis. To illustrate, in panel (d), M.
tuberculosis, about 31 % the nodes with the highest 30 % of degrees (nodes in
, the set of nodes with degrees in the xth percentile and above. For simplicity, four example organisms are shown: a
S. cerevisiae, b
E. coli, c
S. aureus NCTC and d
M. tuberculosis. To illustrate, in panel (d), M.
tuberculosis, about 31 % the nodes with the highest 30 % of degrees (nodes in 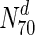 ) are essential. This increases to 33 % in
) are essential. This increases to 33 % in 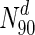 . In panel (a), S. cerevisiae, about 37 % of the nodes in
. In panel (a), S. cerevisiae, about 37 % of the nodes in 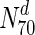 are essential, which rises to 44 % in
are essential, which rises to 44 % in 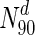 . For further details, see text
. For further details, see text
Table 4.
Fraction of essential proteins in the top 10 % of nodes (by degree, by betweenness centrality)
| Organism | Nodes (proteins) |N0| | Essential nodes in N0 | (%) |
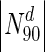
|
Essential nodes in 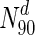
|
(%) |
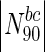
|
Essential nodes in 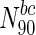
|
(%) |
|---|---|---|---|---|---|---|---|---|---|
| Acinetobacter baylyi | 2,546 | 468 | (18.4) | 258 | 138 | (53.5) | 257 | 101 | (39.3) |
| Arabidopsis thaliana | 7,090 | 195 | (2.8) | 717 | 29 | (4.0) | 710 | 24 | (3.4) |
| Bacillus subtilis | 3,347 | 219 | (6.5) | 338 | 71 | (21.0) | 335 | 53 | (15.8) |
| Caenorhabditis elegans | 5,184 | 192 | (3.7) | 519 | 34 | (6.6) | 519 | 27 | (5.2) |
| Escherichia coli | 3,789 | 672 | (17.7) | 407 | 150 | (36.9) | 379 | 118 | (31.1) |
| Francisella novicida | 1,415 | 362 | (25.6) | 147 | 102 | (69.4) | 142 | 63 | (44.4) |
| Haemophilus influenzae | 1,497 | 592 | (39.5) | 160 | 89 | (55.6) | 150 | 62 | (41.3) |
| Helicobacter pylori | 1,352 | 298 | (22.0) | 140 | 48 | (34.3) | 136 | 40 | (29.4) |
| Mycobacterium tuberculosis | 3,295 | 587 | (17.8) | 330 | 109 | (33.0) | 330 | 99 | (30.0) |
| Mycoplasma genitalium | 446 | 363 | (81.4) | 45 | 45 | (100.0) | 46 | 40 | (87.0) |
| Mycoplasma pulmonis | 616 | 288 | (46.8) | 63 | 61 | (96.8) | 62 | 45 | (72.6) |
| Pseudomonas aeruginosa | 4,556 | 296 | (6.5) | 468 | 77 | (16.5) | 456 | 61 | (13.4) |
| Saccharomyces cerevisiae | 5,477 | 1,109 | (20.2) | 548 | 240 | (43.8) | 548 | 159 | (29.0) |
| Salmonella enterica serovar typhi | 3,491 | 344 | (9.9) | 355 | 103 | (29.0) | 350 | 66 | (18.9) |
| Salmonella typhimurium | 3,712 | 204 | (5.5) | 395 | 45 | (11.4) | 372 | 37 | (9.9) |
| Staphylococcus aureus NCTC | 2,127 | 328 | (15.4) | 221 | 128 | (57.9) | 213 | 72 | (33.8) |
| Staphylococcus aureus subsp. aureus N315 | 1,966 | 296 | (15.1) | 200 | 115 | (57.5) | 197 | 68 | (34.5) |
| Streptococcus pneumoniae | 1,718 | 109 | (6.3) | 180 | 25 | (13.9) | 172 | 22 | (12.8) |
| Streptococcus sanguinis | 1,801 | 215 | (11.9) | 181 | 80 | (44.2) | 181 | 58 | (32.0) |
| Vibrio cholerae | 2,958 | 537 | (18.2) | 314 | 130 | (41.4) | 296 | 83 | (28.0) |
The table lists all organisms considered in this study, along with the numbers and fraction of essential nodes in the entire network, as well as for sets of nodes with the highest degree or betweenness centralities. The table clearly illustrates the enrichment of essential nodes in the N90 sets: in all cases, there is an increase in the fraction of essential proteins in the N 90 sets, more so in some organisms compared to others
Fig. 2.
Variation in fraction of essential nodes, with increase in betweenness centrality. The horizontal axis represents increasing node betweenness centralities, indicated as percentiles (x), while the vertical axis indicates the fraction of essential nodes in 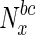 , the set of nodes with betweenness centralities in the xth percentile and above. For further details, see text
, the set of nodes with betweenness centralities in the xth percentile and above. For further details, see text
Closeness centrality and pairwise disconnectivity index are not strong indicators of essentiality
We computed closeness centrality for every node in the 20 different networks. Online Resource 3 indicates the variation of the fraction of essential nodes in the 20 organisms with increasing closeness centrality. Clearly, we observe that with increasing closeness centrality, there is no appreciable change in the fraction of essential nodes. In most cases, we can observe that the fraction of essential nodes remains unaffected, for instance, when one compares 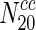 and
and 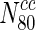 .
.
We also computed the pairwise disconnectivity index (Potapov et al. 2008) for every node in each of the organisms. Online Resource 4 indicates the variation of the fraction of essential nodes in the 20 organisms with increasing pairwise disconnectivity indices. The sparse plots and the large gaps between successive points in the plots indicate that a very large fraction of nodes share the same pairwise disconnectivity index; further, the fraction of essential nodes does not increase very much with an increase in pairwise disconnectivity index, suggesting that this is not a very powerful metric to evaluate the lethality of a node. These observations reiterate the statistical tests illustrated in Table 3, which showed that the set of essential nodes do not differ significantly from the set of all nodes in the network, in terms of metrics such as closeness centrality or pairwise disconnectivity index.
Discussion
Understanding the structural organisation of protein networks holds the key to understanding biological function, as well as the design principles of biological networks. As several protein networks have become readily available, it is now possible to ask several questions about the structural organisation of these networks, and examine the roles played by different proteins in such networks. The identification and analysis of essential proteins in an organism serves more than one purpose: (1) such proteins may be functionally very important, and mediate a number of biological processes (Batada et al. 2006), (2) such proteins, particularly in a pathogenic organism, may be of particular interest as drug targets (Flórez et al. 2010; Verkhedkar et al. 2007). The identification of essential genes/proteins in an organism experimentally is a challenging, expensive and time-consuming task. Therefore, it is important to identify likely essential proteins in organisms through computational analyses. It is already possible to identify important metabolic enzymes through computational techniques such as flux balance analysis (Joyce and Palsson 2008; Kauffman et al. 2003). While such methods are powerful, they also require data on the stoichiometry of individual reactions, and are restricted to enzymes/metabolic genes. Protein networks, on the other hand, encompass the entire proteome of an organism—therefore, an analysis of protein network structure may provide a better picture of essential proteins in an organism.
Although there are many metrics commonly used in graph theory and network biology, there is no clear understanding of the best metric to predict essentiality/lethality in biological systems. For example, even though betweenness centrality has been suggested as an important metric to identify critical nodes in a network (Holme et al. 2002), other researchers have argued that betweenness centrality may be less informative in many cases (Potapov et al. 2008).
Following our analysis of multiple network measures in this study, we make three broad observations, for a set of diverse organisms. Firstly, we observe that nearly all the protein networks considered in this study are disassortative; this is in agreement with previous studies by Newman (2002). Also, most interactions happen amongst non-essential proteins, or between essential and non-essential proteins; interactions amongst essential proteins are much rarer. Secondly, we observe that essential nodes have a significantly higher average degree compared to the network average in all organisms; the centrality–lethality hypothesis thus appears to hold for a larger set of organisms. However, the rate at which the fraction of essential nodes increases, with increase in degree is slow. For example, in M.tuberculosis, about 31 % the nodes with the highest 30 % of degrees (nodes in 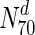 ) are essential. This increases to only 33 % in
) are essential. This increases to only 33 % in 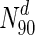 . Only at much higher degrees (top 2 %), does the fraction of essential nodes near 49 %. Even in S. cerevisiae, about 37 % of the nodes in
. Only at much higher degrees (top 2 %), does the fraction of essential nodes near 49 %. Even in S. cerevisiae, about 37 % of the nodes in 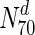 are essential, which rises to 44 % in
are essential, which rises to 44 % in 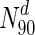 ; only in
; only in 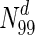 do we observe nearly 73 % essential nodes. Therefore, while higher degree may be an indicator of lethality in general, high degree does not automatically imply lethality. The average betweenness centrality for essential proteins is significantly higher compared to the network average in most organisms considered here; however, similar to degree, high betweenness centrality does not automatically imply essentiality. Perhaps, it would be fruitful to explore combinations of metrics, which may have a stronger association with lethality. Finally, we observe that metrics such as closeness centrality and pairwise disconnectivity index, while useful to predict/analyse critical nodes in complex networks, are insufficient to predict lethality of proteins in the networks.
do we observe nearly 73 % essential nodes. Therefore, while higher degree may be an indicator of lethality in general, high degree does not automatically imply lethality. The average betweenness centrality for essential proteins is significantly higher compared to the network average in most organisms considered here; however, similar to degree, high betweenness centrality does not automatically imply essentiality. Perhaps, it would be fruitful to explore combinations of metrics, which may have a stronger association with lethality. Finally, we observe that metrics such as closeness centrality and pairwise disconnectivity index, while useful to predict/analyse critical nodes in complex networks, are insufficient to predict lethality of proteins in the networks.
Our work does have its limitations. Firstly, we consider protein networks that are composed not only of physical interactions, but also functional associations. However, we consider only the high-confidence associations reported in the STRING database, which should considerably limit any false positive associations in our networks. The advantage, however, is that, these interactions present a more complete view of protein function within a cell, in comparison with networks composed merely of physically interacting protein pairs. While we have considered more organisms than some of the previous studies, it is possible that our results could be altered if we were to consider a much larger and even more diverse set of organisms. Here, we are quite limited by the availability of data on gene essentiality in various organisms. Further, we are also currently limited by the gaps in our existing knowledge of essential genes in the organisms considered; in particular, we would be limited by any gaps in the DEG.
Overall, the major contribution of this study is that the identification of hubs or highly connected proteins is insufficient to identify essential proteins in networks. Importantly, we perform an extensive analysis of protein networks of 20 diverse organisms, which, to our knowledge, has not been carried out before. These organisms differ substantially in the number of proteins, the fraction of essential proteins, the density of interactions and so on. Therefore, our analysis across this diverse set of organisms scrutinises the centrality–lethality hypothesis more critically, and enables us to make general statements about the associations between centrality and lethality for different organisms. Although degree centrality, betweenness centrality and lethality are correlated in many organisms, it is still not possible to predict lethal nodes in an organism to a large degree of accuracy using merely degree/betweenness. Further, we observe that metrics like pairwise disconnectivity index are much poorer indicators of essentiality in protein networks, despite the fact it is a useful metric to analyse critical nodes in complex networks (Potapov et al. 2008). Indeed, our results reiterate the observation by Roy and others (Roy 2012; Roy and Filkov 2009) that individual metrics may not be sufficient to analyse the phenotypes of an organism. Our results warrant a further exploration of the organisation of protein networks; a mere analysis of hubs in a network may not completely explain the complex organisation of protein networks.
Electronic supplementary material
Supplementary material Variation in fraction of essential nodes, with increase in degree. The horizontal axis represents increasing node degrees, indicated as percentiles (x), while the vertical axis indicates the fraction of essential nodes in 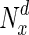 , the set of nodes with degrees in the xth percentile and above. (PDF 38 kb)
, the set of nodes with degrees in the xth percentile and above. (PDF 38 kb)
Supplementary material Variation in fraction of essential nodes, with increase in betweenness centrality. The horizontal axis represents increasing node betweenness centralities, indicated as percentiles (x), while the vertical axis indicates the fraction of essential nodes in 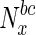 , the set of nodes with betweenness centralities in the xth percentile and above. (PDF 299 kb)
, the set of nodes with betweenness centralities in the xth percentile and above. (PDF 299 kb)
Supplementary material Variation in fraction of essential nodes, with increase in closeness centrality. These plots are similar to those in Online Resources 1 and 2. (PDF 466 kb)
Supplementary material Variation in fraction of essential nodes, with increase in pairwise disconnectivity index. These plots are similar to those in Online Resources 1 and 2. (PDF 26 kb)
Acknowledgments
Funding from IIT Madras and the seed grant BIO/12-13/579/NFSC/KARH is gratefully acknowledged. KR wishes to thank Dr. Saketha Nath (IIT Bombay) for several useful discussions.
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Nandita Damaraju and Govind Krishna Joshi have contributed equally to this article.
References
- Barabási A-L, Oltvai ZN. Network biology: understanding the cell’s functional organization. Nat Rev Genet. 2004;5:101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- Batada NN, Hurst LD, Tyers M. Evolutionary and physiological importance of hub proteins. PLoS Comput Biol. 2006;2:e88. doi: 10.1371/journal.pcbi.0020088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boccaletti S, Latora V, Moreno Y, et al. Complex networks: structure and dynamics. Phys Rep. 2006;424:175–308. doi: 10.1016/j.physrep.2005.10.009. [DOI] [Google Scholar]
- Flórez AF, Park D, Bhak J, et al. Protein network prediction and topological analysis in Leishmania major as a tool for drug target selection. BMC Bioinformatics. 2010;11:484. doi: 10.1186/1471-2105-11-484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman LC. A set of measures of centrality based on betweenness. Sociometry. 1977;40:35–41. doi: 10.2307/3033543. [DOI] [Google Scholar]
- He X, Zhang J. Why do hubs tend to be essential in protein networks? PLoS Genet. 2006;2:e88. doi: 10.1371/journal.pgen.0020088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holme P, Kim B, Yoon C, Han S. Attack vulnerability of complex networks. Phys Rev. 2002;E65:056109. doi: 10.1103/PhysRevE.65.056109. [DOI] [PubMed] [Google Scholar]
- Jeong H, Mason SP, Barabási AL, Oltvai ZN. Lethality and centrality in protein networks. Nature. 2001;411:41–42. doi: 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
- Joyce AR, Palsson BØ. Predicting gene essentiality using genome-scale in silico models. Methods mole biol (Clifton, NJ) 2008;416:433–457. doi: 10.1007/978-1-59745-321-9_30. [DOI] [PubMed] [Google Scholar]
- Kauffman KJ, Prakash P, Edwards JS. Advances in flux balance analysis. Curr Opin Biotechnol. 2003;14:491–496. doi: 10.1016/j.copbio.2003.08.001. [DOI] [PubMed] [Google Scholar]
- Newman M. Assortative mixing in networks. Phys Rev Lett. 2002;89:208701. doi: 10.1103/PhysRevLett.89.208701. [DOI] [PubMed] [Google Scholar]
- Newman MEJ (2003a) Mixing patterns in networks. Phys Rev E 67:026126. doi: 10.1103/physreve.67.026126 [DOI] [PubMed]
- Newman MEJ. The structure and function of complex networks. SIAM Rev. 2003;45:167–256. doi: 10.1137/S003614450342480. [DOI] [Google Scholar]
- Ning K, Ng H, Srihari S, et al. Examination of the relationship between essential genes in PPI network and hub proteins in reverse nearest neighbor topology. BMC Bioinformatics. 2010 doi: 10.1186/1471-2105-11-505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potapov AP, Goemann B, Wingender E. The pairwise disconnectivity index as a new metric for the topological analysis of regulatory networks. BMC Bioinformatics. 2008;9:227. doi: 10.1186/1471-2105-9-227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodrigues FA, da Costa LF, Barbieri AL. Resilience of protein–protein interaction networks as determined by their large-scale topological features. Mol BioSyst. 2011;7:1263–1269. doi: 10.1039/c0mb00256a. [DOI] [PubMed] [Google Scholar]
- Roy S. Systems biology beyond degree, hubs and scale-free networks: the case for multiple metrics in complex networks. Syst Synth Biol. 2012;6:31–34. doi: 10.1007/s11693-012-9094-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Filkov V. Strong associations between microbe phenotypes and their network architecture. Phys Rev. 2009;E80:040902. doi: 10.1103/PhysRevE.80.040902. [DOI] [PubMed] [Google Scholar]
- Sabidussi G. The centrality index of a graph. Psychometrika. 1966;31:581–603. doi: 10.1007/BF02289527. [DOI] [PubMed] [Google Scholar]
- Shoemaker BA, Panchenko AR. Deciphering protein–protein interactions. Part I. experimental techniques and databases. PLoS Comput Biol. 2007;3:e42. doi: 10.1371/journal.pcbi.0030042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoemaker BA, Panchenko AR. Deciphering protein–protein interactions. Part II. computational methods to predict protein and domain interaction partners. PLoS Comput Biol. 2007;3:e43. doi: 10.1371/journal.pcbi.0030043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song J, Singh M. From hub proteins to hub modules: the relationship between essentiality and centrality in the yeast interactome at different scales of organization. PLoS Comput Biol. 2013;9:e1002910. doi: 10.1371/journal.pcbi.1002910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szklarczyk D, Franceschini A, Kuhn M, et al. The STRING database in 2011: functional interaction networks of proteins, globally integrated and scored. Nucleic Acids Res. 2011;39:D561–D568. doi: 10.1093/nar/gkq973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verkhedkar KD, Raman K, Chandra NR, Vishveshwara S. Metabolome Based Reaction Graphs of M. tuberculosis and M. leprae: a Comparative Network Analysis. PLoS ONE. 2007 doi: 10.1371/journal.pone.0000881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xenarios I, Salwínski L, Duan XJ, et al. DIP, the Database of Interacting Proteins: a research tool for studying cellular networks of protein interactions. Nucleic Acids Res. 2002;30:303–305. doi: 10.1093/nar/30.1.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material Variation in fraction of essential nodes, with increase in degree. The horizontal axis represents increasing node degrees, indicated as percentiles (x), while the vertical axis indicates the fraction of essential nodes in 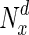 , the set of nodes with degrees in the xth percentile and above. (PDF 38 kb)
, the set of nodes with degrees in the xth percentile and above. (PDF 38 kb)
Supplementary material Variation in fraction of essential nodes, with increase in betweenness centrality. The horizontal axis represents increasing node betweenness centralities, indicated as percentiles (x), while the vertical axis indicates the fraction of essential nodes in 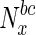 , the set of nodes with betweenness centralities in the xth percentile and above. (PDF 299 kb)
, the set of nodes with betweenness centralities in the xth percentile and above. (PDF 299 kb)
Supplementary material Variation in fraction of essential nodes, with increase in closeness centrality. These plots are similar to those in Online Resources 1 and 2. (PDF 466 kb)
Supplementary material Variation in fraction of essential nodes, with increase in pairwise disconnectivity index. These plots are similar to those in Online Resources 1 and 2. (PDF 26 kb)