Abstract
Metabolism forms an integral part of all cells and its study is important to understand the functioning of the system, to understand alterations that occur in disease state and hence for subsequent applications in drug discovery. Reconstruction of genome-scale metabolic graphs from genomics and other molecular or biochemical data is now feasible. Few methods have also been reported for inferring biochemical pathways from these networks. However, given the large scale and complex inter-connections in the networks, the problem of identifying biochemical routes is not trivial and some questions still remain open. In particular, how a given path is altered in perturbed conditions remains a difficult problem, warranting development of improved methods. Here we report a comparison of 6 different weighting schemes to derive node and edge weights for a metabolic graph, weights reflecting various kinetic, thermodynamic parameters as well as abundances inferred from transcriptome data. Using a network of 50 nodes and 107 edges of carbohydrate metabolism, we show that kinetic parameter derived weighting schemes 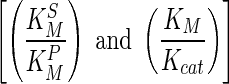 fare best. However, these are limited by their extent of availability, highlighting the usefulness of omics data under such conditions. Interestingly, transcriptome derived weights yield paths with best scores, but are inadequate to discriminate the theoretical paths. The method is tested on a system of Escherichia coli stress response. The approach illustrated here is generic in nature and can be used in the analysis for metabolic network from any species and perhaps more importantly for comparing condition-specific networks.
fare best. However, these are limited by their extent of availability, highlighting the usefulness of omics data under such conditions. Interestingly, transcriptome derived weights yield paths with best scores, but are inadequate to discriminate the theoretical paths. The method is tested on a system of Escherichia coli stress response. The approach illustrated here is generic in nature and can be used in the analysis for metabolic network from any species and perhaps more importantly for comparing condition-specific networks.
Electronic supplementary material
The online version of this article (doi:10.1007/s11693-013-9128-0) contains supplementary material, which is available to authorized users.
Keywords: Biochemical networks, Weighted networks, Alternate paths, Transcriptomics, Metabolomics
Introduction
Metabolites are the end products of cellular regulatory processes and their levels can be regarded as the ultimate response of biological systems to the environmental changes, thereby making it essential to study metabolism. The significance of understanding metabolic behaviour for identifying drug targets or drug design strategies have long been established (Cornish-Bowden and Cárdenas 2003). Given that about a thousand different enzymes exist even in a typical prokaryotic cell, which catalyse numerous biochemical conversions, that are well orchestrated through many inter-connections and extensive cross-talk, comprehending metabolism as a whole requires a systems biology approach. Cellular metabolism is often altered in diseases, leading to an increased recognition of the importance of metabolic analysis in drug discovery (Flight 2010; Tennant et al. 2010). Metabolic fluxes can be seen as fundamental determinants of cellular physiology as they quantitatively show the contributions of various pathways to overall cellular functions. Analysing metabolic fluxes serves as a useful method to relate a cell’s genotype to its phenotype. This information can also be exploited to identify targets for drug discovery or to enhance the performance of a pathway of commercial importance.
Elucidation of biological pathways has been said to be one of the biggest challenges in the systematic analysis of a genome (Palsson 2000). Metabolic pathways can be defined as a series of consecutive enzymatic reactions that produce specific products in a living system. Abstracting these as networks, provide useful insights into the mechanistic and topological behaviour of the system. Compound–compound, reaction–reaction or enzyme–enzyme graphs have been used widely (Arita 2012; Hawick 2011; Ma’ayan 2009). Bipartite graphs between compounds or reactions and enzymes are also used (Acuña et al. 2011). Flow of biochemical information under different conditions and therefore the dynamics of a network are commonly studied by analysing shortest paths between pairs of nodes (Pitkänen et al. 2009; Verkhedkar et al. 2007). Lately, attention has been shifting to construction of weighted networks (Croes et al. 2005, 2006; Ideker et al. 2001; Scott et al. 2005; Zien et al. 2000). However the complexity in metabolic networks are typically high, due to the scale as well as extensive inter-connections in the networks, posing challenges to the problem of identifying biochemical routes. It is particularly difficult to identify alternate routes or alterations that may occur in a disease condition or upon other types of perturbations. With an increase in the amount of genomic data and subsequent increase in the availability of reconstructed metabolic network data for different organisms, the need to analyse them is also increasing rapidly. It is therefore necessary to explore development of newer and improved methods for mining biologically useful information from such networks.
Graphs provide an elegant method of abstraction and analysis of biochemical reactions and their interactions. In this work we have explored weighting the graphs with kinetic, thermodynamic parameters or inferred molecular abundances as edge weights and compare different weighting schemes to infer biologically meaningful biochemical routes. Earlier reports in literature where graphs are weighted include parameters such as connectivity information of the metabolites and centrality of nodes (Aittokallio and Schwikowski 2006; Ideker et al. 2002; Noirel et al. 2008). It is important to explore different parameters for deriving the weights and to perform a systematic comparison of different weighting schemes, so that the weights capture biologically meaningful information and hence will provide paths that are biologically significant.
In this study, large-scale experimental data as well as datasets of kinetic parameters are used to study the dynamics of carbohydrate metabolism by integrating kinetic and thermodynamic data to the metabolic network. Towards this goal, five major pathways of carbohydrate metabolism have been captured as a network and weighted using different weighting schemes. These weighting schemes are a function of kinetic and thermodynamics parameters and mimics the biological system nicely. Metabolic networks integrated with these weighting schemes are investigated to study the significance of adding weights to the networks. Furthermore, the developed methodology is also used to compare large networks from pairs of phenotypic states so as to identify differences in metabolic routes and further larger shifts if any, in the metabolic focus of the cell in a perturbed state. An example test case of lactose shift in Escherichia coli has been analysed for this purpose.
Methods
Two networks are used in this study. The first consists of five major pathways from carbohydrate metabolism, Glycolysis, Kreb’s Cycle, Pentose Phosphate Pathway, Pyruvate metabolism and Gluconeogenesis from E. coli. These pathways were chosen since they are well characterized biochemically and also their kinetic and thermodynamic parameters as well as abundances of enzymes and metabolites are available. Thus, 51 nodes/metabolites and 107 edges are in this network, which is referred to as Network-1. The second (Network-2) is an extension of Network-1 and includes additional pathways to capture the entire carbohydrate metabolism. Network-2 thus contains 250 nodes/metabolites and 331 edges. Kinetic parameters are not available for all reactions in this network; however transcriptome and metabolome data are available, which are incorporated into it. Network-1 is used for comparing weighting schemes where as Network-2 is used for analyzing a case scenario of lactose stress response.
Network reconstruction
For metabolic network reconstruction, the substrates and products involved in the reactions formed nodes and an edge was drawn between them, if they shared a substrate-product relationship. The network so generated was a directed network to emphasize the direction of the fluxes. In case of a reversible reaction, connections were made in both directions. The chemical compounds involved in each reactions and the respective reversibility information was obtained from KEGG database (Ogata et al. 1999).
Weighting schemes
Six different weighting schemes based on the kinetic, thermodynamic and transcriptome data for all the reactions have been used in this study. The kinetic parameters were obtained from BRENDA (Scheer et al. 2011), BioNumbers (Milo et al. 2010) for each enzyme at pH = 7 and 298 K where available and through literature survey for the remaining (parameters listed in Table S1). The details of the weighting schemes are provided below:
Scheme 1 [sc1]:
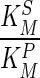 : Ratio between the Michaelis-Menton [MM] kinetic constant of the substrate and the product. For irreversible reaction, we assume
: Ratio between the Michaelis-Menton [MM] kinetic constant of the substrate and the product. For irreversible reaction, we assume 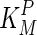 to be very high (very low affinity for the product) with a default value of 0.1.
to be very high (very low affinity for the product) with a default value of 0.1.Scheme 2 [sc2]:
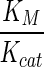 : Inverse of catalytic efficiency i.e.; the efficiency with which an enzyme converts a substrate into product.
: Inverse of catalytic efficiency i.e.; the efficiency with which an enzyme converts a substrate into product.Scheme 3 [sc3]: ΔG: The thermodynamic feasibility of any reaction can be established by calculating the ΔG value for the formation of the product. ∆G was calculated for each reaction using the ‘Group contribution method' (GCM) (Mavrovouniotis 1990; Dreyfuss et al. 2013; Liebermeister and Klipp 2006).
Scheme 4 [sc4]:
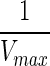 : Inverse of the maximum velocity was taken as the edge weight between any two metabolites.
: Inverse of the maximum velocity was taken as the edge weight between any two metabolites.Scheme 5 [sc5]:
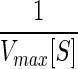 : Similar to sc4, but with an added constraint of metabolite availability. The metabolite concentrations were obtained from ordinary differential equation (ODE) based kinetic model of carbohydrate metabolism. This model consisted of 64 reactions, of which all reactions were assumed to follow Michaelis–Menton kinetics, except those describing metabolite transports. The model was simulated using Teranode Design Suite (www.teranode.com).
: Similar to sc4, but with an added constraint of metabolite availability. The metabolite concentrations were obtained from ordinary differential equation (ODE) based kinetic model of carbohydrate metabolism. This model consisted of 64 reactions, of which all reactions were assumed to follow Michaelis–Menton kinetics, except those describing metabolite transports. The model was simulated using Teranode Design Suite (www.teranode.com).Scheme 6 [sc6]:
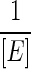 : where [E] is the molecular abundance of the enzyme responsible for driving the reaction, obtained from transcriptomic experiments.
: where [E] is the molecular abundance of the enzyme responsible for driving the reaction, obtained from transcriptomic experiments.
Implementation of weights
To maintain the stoichiometric information of the reaction, parameters were calculated by taking the average of all the substrates and products. For a reaction: A + 2B → C + D, the different weighting schemes were implemented as follows:
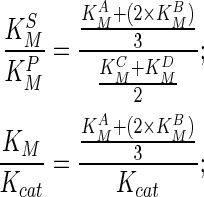 |
ΔG was calculated for complete reaction using GCM;
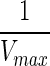 = Every reaction and therefore edges connecting the substrates and products have same value of Vmax, since it is common for a reaction;
= Every reaction and therefore edges connecting the substrates and products have same value of Vmax, since it is common for a reaction;
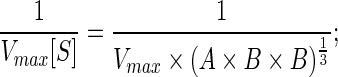 |
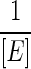 = constant for a given reaction.
= constant for a given reaction.
Finally, a total of 7 networks (6 weighted and 1 unweighted) were generated to analyse and compare the different weighting schemes. It should be noted here, that since our analysis involves calculating shortest paths, the weighting schemes have been formulated such that a lower edge weight and a lower path score implies higher biological relevance. The path score is calculated by summing the edge weights.
Network analysis
Floyd–Warshall algorithm (Floyd 1962) is used to calculate shortest paths between all pairs of nodes. The algorithm was implemented in MATLAB-BGL (Batenkov 2011; Gleich 2009). Cytoscape (Shannon et al. 2003) was used for the purpose of visualizations.
Results
In this study, a weighted biochemical network of carbohydrate metabolism (Network-1) is reconstructed and weighted based on the different kinetic and thermodynamic parameters and the abundances of the enzyme responsible for driving the reactions. Shortest paths between all pairs of nodes are calculated and compared with reference paths to study the impact of weights on the network and further more to compare the different weighting schemes. The transcriptome and metabolome based weighting scheme is further used for identifying alterations in biochemical routes in E. coli upon stress induction using Network-2.
Network reconstruction
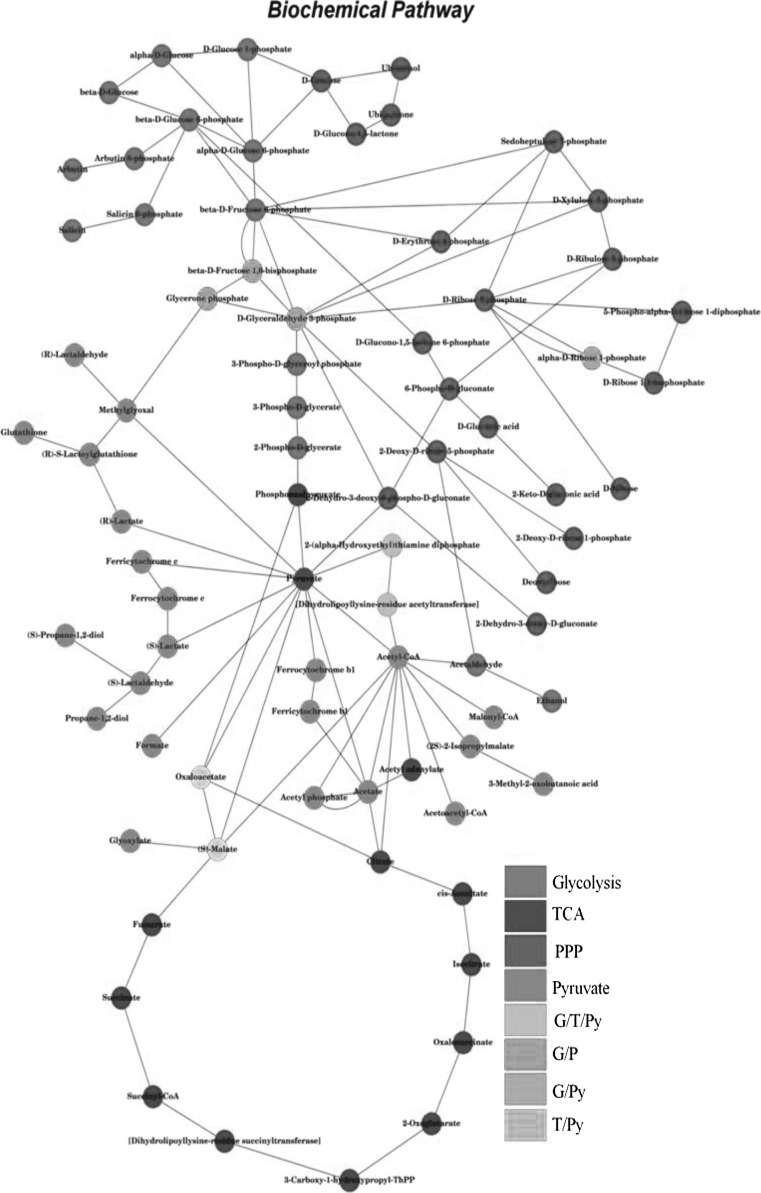
Five major pathways of the carbohydrate metabolism, (a) Glycolysis, (b) Kreb’s cycle, (c) Pentose Phosphate pathway, (d) Pyruvate metabolism and (e) Gluconeogenesis in E. coli as provided in KEGG (Ogata et al. 1999) is used to reconstruct the network (Network-1). The network consists of 51 nodes and 107 edges, capturing a total of 64 reactions, of which 23 are reversible. Figure 1 shows the complete view of the biochemical network used in this study. Edges in the network are weighted using six different weighting schemes, (1) 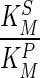 , (2)
, (2) 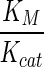 , (3) ΔG, (4)
, (3) ΔG, (4) 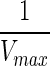 , (5)
, (5) 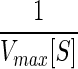 and (6)
and (6) 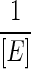 .
.
Fig. 1.
Cytoscape view of the complete metabolic network used in this study. The nodes/metabolites are colour coded according to the pathway it belongs to. (Color figure online)
Comparison of weighting schemes
This study required comparison between independent weighting schemes lying in different value ranges and therefore it was important to normalize the data before carrying out any analysis. Standard data normalization procedure was carried out using the following equation:
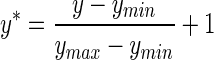 |
1 |
Once the data was processed, different weighting schemes are compared by calculating all pair shortest paths using Floyd–Warshall algorithm. A total of 1,892 shortest paths were calculated. Initially, the basic topological properties such as path length distribution and network diameter are calculated to check for any resultant topological variations upon adding weights. In all the 7 networks as expected, the length of the shortest path mostly occur in the range of 5–7 with the length of the longest shortest path (network diameter) being 15.
We next analysed the influence of adding weights to the flow of information by comparing the shortest path scores and routes between the different weighting schemes. For this, we describe two terms: (a) Reference paths (RPs) are a list of biochemical paths that are experimentally well characterized metabolic conversions. These paths were obtained from standard text-books and KEGG; (b) Theoretical paths (TPs) are the set of all possible shortest paths calculated between any two nodes from the network. This does not include the RPs. We obtained a total of 86 RPs (listed in Table S2) with each path having at least 2 intermediates, excluding the source and destination. Of the 1,806 TPs calculated, 1,272 paths had at least two intermediates. Based on the path length score distribution, it was observed that a very small percentage of paths exceeds path length = 10. Therefore, amongst the 1,272 TPs, those with more than 8 intermediate steps (>length 10) were not included for this analysis to remove any bias that may arise due to high scores obtained as a result of longer path length. Finally, for each weighting scheme, the scores of the computed paths corresponding to the 86 RPs were compared to those of the remaining 1,066 TPs. It must be noted that TPs reflect a set of all possible biochemical conversions between all pairs of metabolites, under the directional constraints of the network, if all conversions were equally possible. Clearly, this is not the case, since in the network considered, only 86 conversions are known to be present. A good weighting scheme should be able to discriminate among them and provide top ranks (lower path costs) to the experimentally proven RPs.
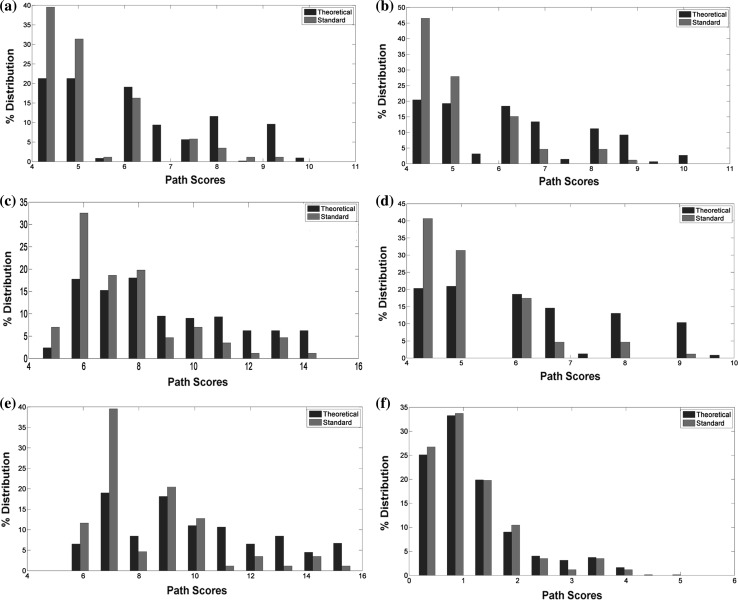
Figure 2 plots the percentage distribution of the path scores obtained after using different weighting schemes for the 86 RPs as compared to the 1,066 TPs. The figure clearly indicates that use of weights in general improve the scores, with the paths corresponding to the 86 RPs having higher scores (lower weights/lower cost) while the 1,066 TPs having much poorer scores (higher weights/higher cost). It must be noted that from an unweighted graph, all 1,066 TPs and the 86 RPs score the same (if path length is same) and hence it is difficult to discriminate RPs from TPs. Among the weighting schemes, sc1 and sc2 perform best in identifying RPs as the best biochemical routes. The significance of using weights is thus clear from this analysis, of which the kinetic parameters 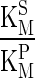 and
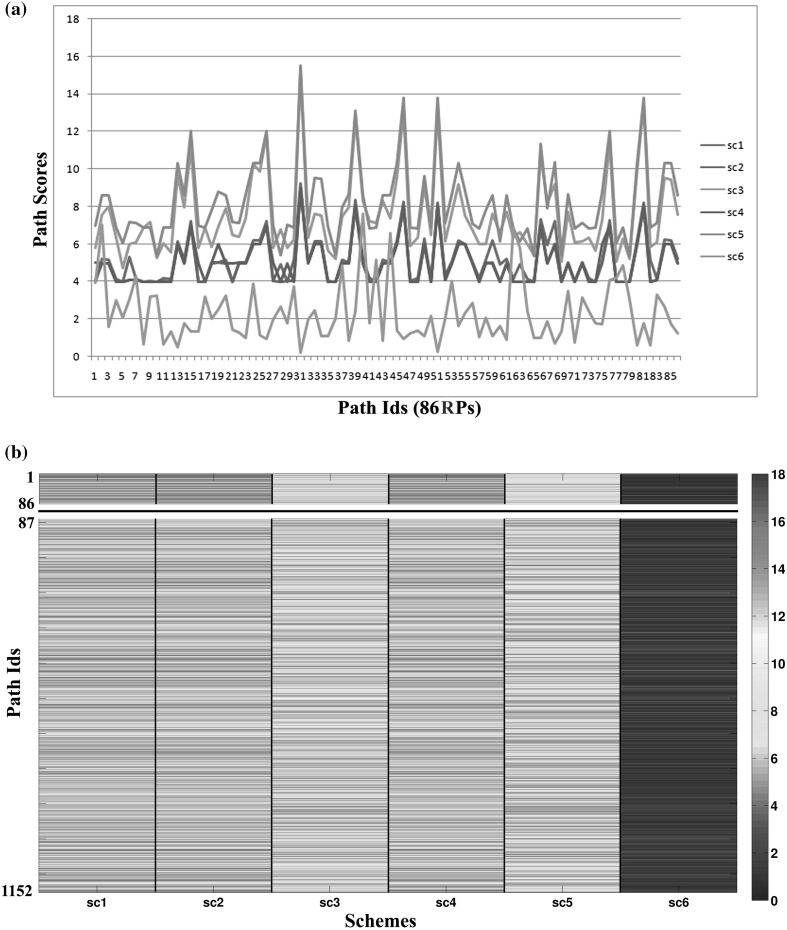
and 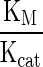 present the best weighting schemes with sc1 scoring 70.8 % of RPs with high ranking scores (lower path scores) and sc2 scoring 74.4 %. On the other hand, sc3/4/5 although have lesser percentage of RPs in the low-scoring region; they are higher when compared to TPs. Infact, as can be seen in Fig. 3(a, b), sc3 and sc5 consistently display higher path scores as compared to its counterparts. Another interesting observation that is evident from Fig. 2f as well as Fig. 3(a, b) is that transcriptome derived weighting schemes gives the lowest scores for a given path, amongst all other schemes. However, it is inadequate to distinguish the TPs from the RPs (Figs. 2f, 3b). Figure 3b shows the heat map of the distribution of the scores for all the 1,152 paths (86 RPs + 1,066 TPs). In case of sc1 and sc2, it is clearly visible that the paths belonging to RPs (top panel) have lower scores as compared to other TPs (lower panel). It should be pointed out here that few TPs do exist that have lower path scores, indicating that alternate routes with marginally lower scores exist for many reactions suggesting that subtle change in the kinetic parameters and/or molecular abundances at key positions in the network could be sufficient to bring about alterations in biochemical routes, indicating a means of achieving robustness of the biological network from random perturbations. These are the paths that must be investigated thoroughly and should be considered during therapeutic interventions. Overall, it is clear from this analysis that scoring schemes do add to the dynamicity of the network and hence important to consider for inferring biologically significant routes.
present the best weighting schemes with sc1 scoring 70.8 % of RPs with high ranking scores (lower path scores) and sc2 scoring 74.4 %. On the other hand, sc3/4/5 although have lesser percentage of RPs in the low-scoring region; they are higher when compared to TPs. Infact, as can be seen in Fig. 3(a, b), sc3 and sc5 consistently display higher path scores as compared to its counterparts. Another interesting observation that is evident from Fig. 2f as well as Fig. 3(a, b) is that transcriptome derived weighting schemes gives the lowest scores for a given path, amongst all other schemes. However, it is inadequate to distinguish the TPs from the RPs (Figs. 2f, 3b). Figure 3b shows the heat map of the distribution of the scores for all the 1,152 paths (86 RPs + 1,066 TPs). In case of sc1 and sc2, it is clearly visible that the paths belonging to RPs (top panel) have lower scores as compared to other TPs (lower panel). It should be pointed out here that few TPs do exist that have lower path scores, indicating that alternate routes with marginally lower scores exist for many reactions suggesting that subtle change in the kinetic parameters and/or molecular abundances at key positions in the network could be sufficient to bring about alterations in biochemical routes, indicating a means of achieving robustness of the biological network from random perturbations. These are the paths that must be investigated thoroughly and should be considered during therapeutic interventions. Overall, it is clear from this analysis that scoring schemes do add to the dynamicity of the network and hence important to consider for inferring biologically significant routes.
Fig. 2.
Percentage distribution of the path scores for the different weighting schemes, a sc1, b sc2, c sc3, d sc4, e sc5 and f sc6. Red bar represents the 86 RPs (Reference/Standard) while the blue bar represent 1,066 TPs (Theoretical). Percentage distribution was calculated to normalize the discrepancy of the number of data points in the two sets. (Color figure online)
Fig. 3.
a Path scores of the different weighting schemes for the 86 RPs. Sc3 and sc5 show consistent higher values, while sc6 consistently shows lower values. b Heat map showing the scores obtained by each path by the different weighting schemes (sc1, sc2, sc3, sc4, sc5, sc6); top panel represents the 86 RPs and the bottom panel shows 1,066 TPs. Higher density of blue is seen for sc1 and sc2 in the top panel. It should also be noted that sc6 shows lower scores for all the paths. (Color figure online)
Analysis of alternate paths
In the previous section, we discussed about the pool of TPs that can form alternate paths under diseased or perturbed conditions. To probe further into this aspect, we performed a detailed analysis and compared the different weighting schemes on the basis of the routes taken up by the shortest paths. Table 1 shows the number of different routes taken up by the different scoring schemes. Overall, it is observed that the different networks majorly tend to follow the same route, with a small percentage (~4–5 %) of shortest paths showing different routes.
Table 1.
Different path routes taken up by the same pair of nodes due to the different weighting schemes
| unw | Sc1 | Sc2 | Sc3 | Sc4 | Sc5 | Sc6 | |
|---|---|---|---|---|---|---|---|
| unw | 0 | 80 | 234 | 158 | 190 | 156 | 134 |
| Sc1 | 0 | 258 | 118 | 295 | 206 | 136 | |
| Sc2 | 0 | 299 | 295 | 238 | 140 | ||
| Sc3 | 0 | 120 | 258 | 141 | |||
| Sc4 | 0 | 187 | 128 | ||||
| Sc5 | 0 | 125 |
An example of an alternate path is observed when one considers the traversal from acetyl-CoA to malate, wherein the different weighting schemes suggest two routes, one via citrate, and another via oxaloacetate. Considering that the reactions are reversible, both the routes are feasible and can be taken under different dynamic states of the system. Such examples strongly indicate the presence of alternate routes that may turn out to be important under certain abnormal conditions.
Overall, it is seen that for a given pair of nodes, different weighting schemes can yield different routes, highlighting the fact that each weighting scheme adds its own perspective to the network and thus integrating these weighting schemes, where parameters are available, could lead to much more useful networks. Often, all weighting schemes cannot be applied to specific networks being studied, due to the paucity of data. For example, Vmax, KM and Kcat are available for some enzymes, whereas transcriptomics and metabolomics data is available for some other enzymes. A more useful approach would then be to combine different parameters that may be available for the system under consideration, so as to obtain integrated weights. This becomes even more important in light of the omics data that is now increasingly becoming available in large quantities. Moreover, choosing a particular weighting scheme would depend on the question being asked. For e.g.: in cases such as environmental shifts or non-availability of preferred nutrient source, weights derived from biochemical parameters may not be useful, but metabolomics and transcriptomics data, if available, may prove to be useful to understand the various hidden adjustments being undertaken by the cell to adapt to a particular condition.
To illustrate this, we combine transcriptomic and metabolomics data, which is equivalent to integrating sc5 and sc6 and apply network analysis (using Network-2) to understand stress response. As an example, we choose E. coli, a well studied bacterial system for which omics data and other biochemical and molecular data are readily available. This approach lends for ready adaptation in other networks as well.
E. coli stress response
Escherichia coli cells are known to best grow on glucose medium and undergo stress when the medium is shifted to lactose (Kayser et al. 2005). This phenomenon is known as glucose–lactose shift, under which the bacteria alters its metabolism to adapt to the new environmental conditions. Given this information and the network approach described above, it was interesting to study the changes that the bacteria achieve upon lactose shift (Jozefczuk et al. 2010). This network (Network-2) consists of 250 nodes/metabolites and 331 edges/interconnections. The experimental data (transcriptome and metabolomics data) are available for two time points (OD = 0.6 and 0.7) before the induction of stress and 4 time points, after every 10 min of stress induction. Metabolomics data is also available for 90, 140 and 210 min after stress. The first time point (t0) at OD = 0.6 represents the control and is abstracted as an unweighted network. For the other time points (t1–t8), the fold change of metabolite and enzyme concentrations are combined as shown in Eq. 2 to weight the networks.
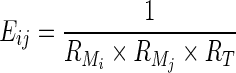 |
2 |
where, 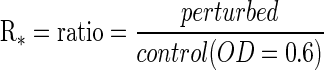 ; Mi = metabolite i, Mj = metabolite j; T = enzyme involved in the reaction; Eij = edge weight.
; Mi = metabolite i, Mj = metabolite j; T = enzyme involved in the reaction; Eij = edge weight.
It should be mentioned here that since this stress response involved metabolic alteration and not genetic defects or mutations, the kinetic and thermodynamic parameters would not alter and hence, using weighting schemes derived from only the omics data was sufficient to understand the metabolic shifts.
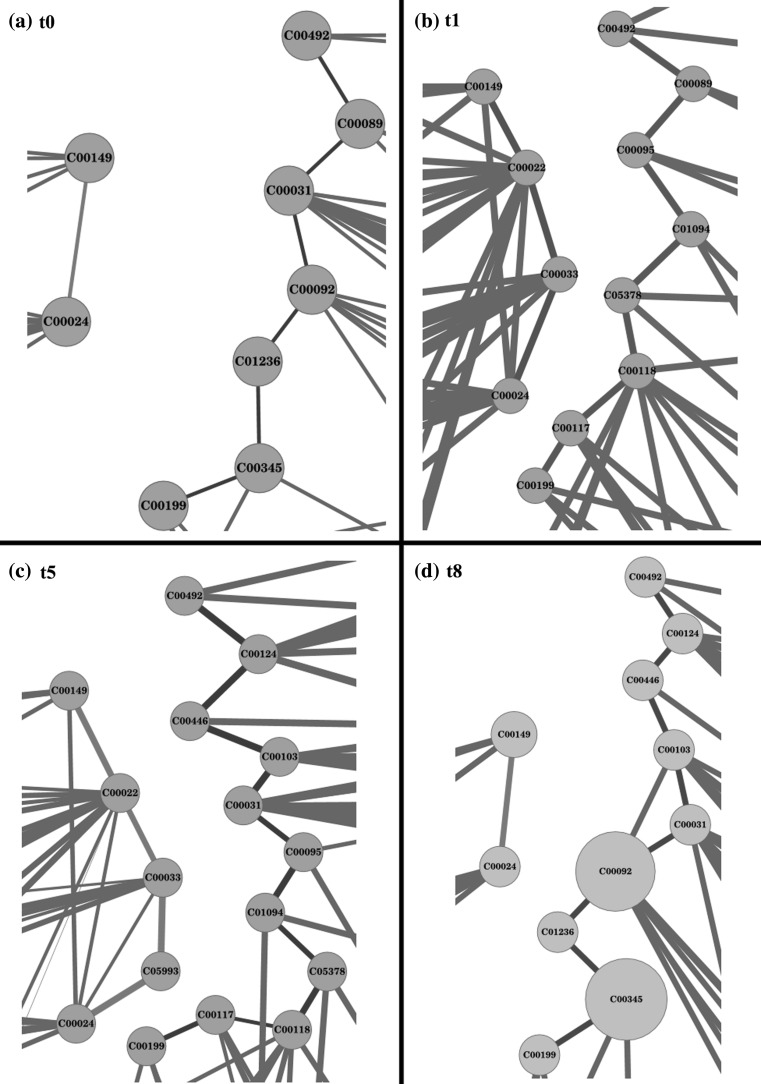
Nine different networks representing the different time points are generated. To study how information is processed, shortest paths between all node pairs are analysed and compared between the networks. Table 2 gives the number of alternate routes and therefore metabolic adjustments that are taken up as the system shifts to different time points. Transition of the system upon perturbation and attainment of altered steady state behaviour is clearly seen. Pairs that show more than 20 % alternate routes are in bold values while those showing lower percentage of alternate routes are in italicized values. In general, networks generated after stress induction show high similarity amongst themselves as compared to the time points before the induction of stress. Higher percentage of dissimilarity between t0 and t1 highlights the dynamics that occur at the transcriptomics as well as the metabolomics data as the bacteria shifts from a log phase (OD = 0.6) to stationary phase (OD = 0.7). However, upon introducing stress the cell dynamics changes rapidly to obtain a new altered steady state that best suits the environmental conditions. Initially, at t3 (10 min after stress) the network shows higher similarity to the unperturbed network and slowly transition away from the unperturbed state. It is interesting to note that 38.8 % of the metabolic pathways are altered between the initial steady state (t0) and the altered steady state (t8). Experimental data suggests that upon inducing stress, bacterial growth is arrested for 40 min after which it resumes growth. Based on this and the data described in Table 2, it seems that although alterations start occurring immediately after stress induction, cell growth is resumed only after a particular threshold of alterations have been successfully manifested. Infact, the average difference is seen to be lowest for the network at t5 (40 min) suggesting the majority of changes required for adaptation have been accomplished at this stage. Based on the above network analysis, one can easily gather that upon stress induction, the organism immediately starts preparing itself to deal with stress and hence we observe major metabolic shifts immediately after the stress response. Once, the system is stabilized it resumes growth and even the number of metabolic shifts, as obtained from network analysis, decreases. This highlights the importance of such studies for interpretation of experimental data, since we now know how and where these metabolic alterations occur. Figure 4 shows example of the different shortest paths taken up by the same pair of nodes as a function of time.
Table 2.
Percentage of altered routes between the different networks representing the time dependent response of the E. coli cell under carbon stress condition
| OD 0.6 | OD 0.7 | 10 min | 20 min | 30 min | 40 min | 90 min | 140 min | 210 min | |
|---|---|---|---|---|---|---|---|---|---|
| (t0) | (t1) | (t2) | (t3) | (t4) | (t5) | (t6) | (t7) | (t8) | |
| (t0) | 0 | 24.1 | 19.3 | 42.2 | 39.5 | 41.5 | 39.6 | 40.6 | 38.9 |
| (t1) | 0 | 15.3 | 35.5 | 39.8 | 36.6 | 39.3 | 35.7 | 39.5 | |
| (t2) | 0 | 36.7 | 29.5 | 30.3 | 29.9 | 32.6 | 36.4 | ||
| (t3) | 0 | 9.8 | 14.2 | 11.5 | 12.6 | 19.4 | |||
| (t4) | 0 | 5.9 | 2.3 | 9.1 | 15.4 | ||||
| (t5) | 0 | 4.7 | 3.2 | 10.1 | |||||
| (t6) | 0 | 7.9 | 14.8 | ||||||
| (t7) | 0 | 7.3 |
Fig. 4.
Illustration of the different metabolic routes taken up by the network at different time points, highlighting the change in dynamics of the cell. Paths for two pairs of nodes are shown in different colours at a time point t0, b time point t2, c time point t5 and d time point t8, highlighting the different phases of the system. (Color figure online)
Discussion
In this study, the problem of pathway identification has been approached using network analysis, but after refining the networks with thermodynamic and kinetic parameters and protein abundances. Six different weighting schemes based on the kinetic, thermodynamic and transcriptomic data were used and compared using shortest path analysis. It is observed that the schemes derived from kinetic data fared best and could easily differentiate reference paths from theoretical paths. Detailed analyses suggest that adding weights, add to the information content of the network and makes the network biologically more meaningful. It is also noted that each weighting scheme, adds its own perspective to the network and therefore combining these weighting schemes would make the network much more realistic. This was further tested using E. coli stress response, wherein transcriptomic and metabolomics data are integrated to derive a weighting scheme.
A unique and important feature of this approach is that it makes available a pool of potential alternate paths that can be taken up by the system under different conditions. Interestingly, even with the normal network topology, the different weights can give rise to alternate routes. An example of such routes that are feasible but not considered standard is also provided. We believe that due importance should be given to these low-scoring and feasible alternate routes, which can then form a pool of possible paths that can be targeted therapeutically under abnormal conditions.
The use of network makes it easier to perform such analysis on large scale genomic data. Further, unlike other methods of route identification such as flux balance analysis (FBA), this method does not need prior information to define the objective function. Moreover, conditions that mimic latency require down-regulation of fluxes, which is difficult to capture via FBA, since minimizing the objective function would lead to zero fluxes, therefore providing no information about the system. Such conditions, however, can be easily mimicked using the approach explained in this study. When new data pertaining to enzyme or metabolite abundances or even the variations in kinetic parameters due to mutants or comparison of homologous proteins become available, they can be easily incorporated into the network. Studies providing insights about gene knockouts, genetic defects, growth under nutrient deprived conditions or anaerobic conditions can be easily performed using this method.
An important limitation of the study is the availability of kinetic, thermodynamic, transcriptomic and metabolomics data for the same condition. Depending upon the origin of the disease, a suitable weighting parameter that best describes the abnormality can be used. For disease that involve alterations in enzyme activity, weighting schemes based on kinetic and thermodynamic parameters in combination with transcriptomic and metabolomics data would be useful, while for those abnormal conditions where shift in metabolite concentration occurs (lactose shift), only using transcriptomic and metabolomics data should be sufficient to understand the flow of information in altered condition.
We believe that with the increasing availability of high throughput data, this approach can be successfully used to understand the hidden metabolic changes that a cell undergoes during perturbations which can be then exploited for many applications including drug discovery.
Electronic supplementary material
References
- Acuña V, Ferreira C, Freire A, Moreno E (2011) Solving the maximum edge biclique packing problem on unbalanced bipartite graphs. Discret Appl Math. doi:10.1016/j.dam.2011.09.019
- Aittokallio T, Schwikowski B. Graph-based methods for analysing networks in cell biology. Brief Bioinform. 2006;7(3):243–255. doi: 10.1093/bib/bbl022. [DOI] [PubMed] [Google Scholar]
- Arita M. From metabolic reactions to networks and pathways. Bact Mol Netw, Springer. 2012;804:93–106. doi: 10.1007/978-1-61779-361-5_6. [DOI] [PubMed] [Google Scholar]
- Batenkov D. Boosting productivity with the boost graph library. XRDS Crossroads ACM Mag Stud. 2011;17(3):31–32. doi: 10.1145/1925041.1925054. [DOI] [Google Scholar]
- Cornish-Bowden A, Cárdenas ML. Metabolic analysis in drug design. C R Biol. 2003;326(5):509–515. doi: 10.1016/S1631-0691(03)00117-3. [DOI] [PubMed] [Google Scholar]
- Croes D, Couche F, Wodak SJ, van Helden J. Metabolic PathFinding: inferring relevant pathways in biochemical networks. Nucleic Acids Res. 2005;33(suppl 2):W326–W330. doi: 10.1093/nar/gki437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croes D, Couche F, Wodak SJ, van Helden J. Inferring meaningful pathways in weighted metabolic networks. J Mol Biol. 2006;356(1):222–236. doi: 10.1016/j.jmb.2005.09.079. [DOI] [PubMed] [Google Scholar]
- Dreyfuss JM, Zucker JD, Hood HM, Ocasio LR, Sachs MS, Galagan JE. Reconstruction and validation of a genome-scale metabolic model for the filamentous fungus Neurospora crassa using FARM. PLoS Comput Biol. 2013;9(7):e1003126. doi: 10.1371/journal.pcbi.1003126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flight MH. Drug screening: shifting energy metabolism. Nat Rev Drug Discov. 2010;9(4):272. doi: 10.1038/nrd3146. [DOI] [PubMed] [Google Scholar]
- Floyd RW. Algorithm 97: shortest path. Commun ACM. 1962;5(6):345. doi: 10.1145/367766.368168. [DOI] [Google Scholar]
- Gleich DF (2009) Models and algorithms for pagerank sensitivity. Stanford University
- Hawick KA. Applying enumerative, spectral and hybrid graph analyses to biological network data. Small. 2011;15:16. [Google Scholar]
- Ideker T, Thorsson V, Ranish JA, Christmas R, Buhler J, Eng JK, Bumgarner R, Goodlett DR, Aebersold R, Hood L. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science. 2001;292(5518):929–934. doi: 10.1126/science.292.5518.929. [DOI] [PubMed] [Google Scholar]
- Ideker T, Ozier O, Schwikowski B, Siegel AF. Discovering regulatory and signalling circuits in molecular interaction networks. Bioinformatics. 2002;18(suppl 1):S233–S240. doi: 10.1093/bioinformatics/18.suppl_1.S233. [DOI] [PubMed] [Google Scholar]
- Jozefczuk S, Klie S, Catchpole G, Szymanski J, Cuadros-Inostroza A, Steinhauser D, Selbig J, Willmitzer L. Metabolomic and transcriptomic stress response of Escherichia coli. Mol Syst Biol. 2010;6(1):364. doi: 10.1038/msb.2010.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayser A, Weber J, Hecht V, Rinas U. Metabolic flux analysis of Escherichia coli in glucose-limited continuous culture. I. Growth-rate-dependent metabolic efficiency at steady state. Microbiology. 2005;151(3):693–706. doi: 10.1099/mic.0.27481-0. [DOI] [PubMed] [Google Scholar]
- Liebermeister W, Klipp E. Bringing metabolic networks to life: integration of kinetic, metabolic, and proteomic data. Theor Biol Med Model. 2006;3(1):42. doi: 10.1186/1742-4682-3-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma’ayan A. Insights into the organization of biochemical regulatory networks using graph theory analyses. J Biol Chem. 2009;284(9):5451–5455. doi: 10.1074/jbc.R800056200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mavrovouniotis ML. Group contributions for estimating standard gibbs energies of formation of biochemical compounds in aqueous solution. Biotechnol Bioeng. 1990;36(10):1070–1082. doi: 10.1002/bit.260361013. [DOI] [PubMed] [Google Scholar]
- Milo R, Jorgensen P, Moran U, Weber G, Springer M. BioNumbers—the database of key numbers in molecular and cell biology. Nucleic Acids Res. 2010;38(suppl 1):D750–D753. doi: 10.1093/nar/gkp889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noirel J, Ow SY, Sanguinetti G, Jaramillo A, Wright PC. Automated extraction of meaningful pathways from quantitative proteomics data. Brief Funct Genomic Proteomic. 2008;7(2):136–146. doi: 10.1093/bfgp/eln011. [DOI] [PubMed] [Google Scholar]
- Ogata H, Goto S, Sato K, Fujibuchi W, Bono H, Kanehisa M. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 1999;27(1):29–34. doi: 10.1093/nar/27.1.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palsson B. The challenges of in silico biology. Nat Biotechnol. 2000;18(11):1147–1150. doi: 10.1038/81125. [DOI] [PubMed] [Google Scholar]
- Pitkänen E, Jouhten P, Rousu J. Inferring branching pathways in genome-scale metabolic networks. BMC Syst Biol. 2009;3(1):103. doi: 10.1186/1752-0509-3-103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheer M, Grote A, Chang A, Schomburg I, Munaretto C, Rother M, Söhngen C, Stelzer M, Thiele J, Schomburg D. BRENDA, the enzyme information system in. Nucleic Acids Res. 2011;39(suppl 1):D670–D676. doi: 10.1093/nar/gkq1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott MS, Perkins T, Bunnell S, Pepin F, Thomas DY, Hallett M. Identifying regulatory subnetworks for a set of genes. Mol Cell Proteomics. 2005;4(5):683–692. doi: 10.1074/mcp.M400110-MCP200. [DOI] [PubMed] [Google Scholar]
- Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, Amin N, Schwikowski B, Ideker T. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13(11):2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tennant DA, Durán RV, Gottlieb E. Targeting metabolic transformation for cancer therapy. Nat Rev Cancer. 2010;10(4):267–277. doi: 10.1038/nrc2817. [DOI] [PubMed] [Google Scholar]
- Verkhedkar KD, Raman K, Chandra NR, Vishveshwara S. Metabolome based reaction graphs of M. tuberculosis and M. leprae: a comparative network analysis. PLoS ONE. 2007;2(9):e881. doi: 10.1371/journal.pone.0000881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zien A, Kuffner R, Zimmer R, Lengauer T (2000) Analysis of gene expression data with pathway scores. Proceedings of the 8th international conference intelligent systems molecular biology (ISMB) 8:407–417 [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.