FFAS-3D: improving fold recognition by including optimized structural features and template re-ranking

Abstract

Motivation: Homology detection enables grouping proteins into families and prediction of their structure and function. The range of application of homology-based predictions can be significantly extended by using sequence profiles and incorporation of local structural features. However, incorporation of the latter terms varies a lot between existing methods, and together with many examples of distant relations not recognized even by the best methods, suggests that further improvements are still possible.

Results: Here we describe recent improvements to the fold and function assignment system (FFAS) method, including adding optimized structural features (experimental or predicted), ‘symmetrical’ Z-score calculation and re-ranking the templates with a neural network. The alignment accuracy in the new FFAS-3D is now 11% higher than the original and comparable with the most accurate template-based structure prediction algorithms. At the same time, FFAS-3D has high success rate at the Structural Classification of Proteins (SCOP) family, superfamily and fold levels. Importantly, FFAS-3D results are not highly correlated with other programs suggesting that it may significantly improve meta-predictions. FFAS-3D does not require 3D structures of the templates, as using predicted features instead of structure-derived does not lead to the decrease of accuracy. Because of that, FFAS-3D can be used for databases other than Protein Data Bank (PDB) such as Protein families database or Clusters of orthologous groups thus extending its applications to functional annotations of genomes and protein families.

Availability and implementation: FFAS-3D is available at http://ffas.godziklab.org.

Contact: adam@godziklab.org

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

One of the most intriguing problems in molecular biology is the extent of homology between genes and proteins. With sequences evolving quickly, many homologs become unrecognizable by simple sequence-sequence comparisons. More sophisticated methods, including sequence-profile and profile-profile methods allow us to recognize statistically significant similarities even between distant homologs. The fold and function assignment system (FFAS) is one of the first programs that introduced using profile-profile alignment (Jaroszewski et al., 2000; Rychlewski et al., 2000) for protein homology detection, and since its inception it is publicly available on the http://ffas.godziklab.org server. Profile-profile methods have been proved to be more accurate and more sensitive than sequence-sequence alignment and sequence-profile alignment methods (Panchenko, 2003), and such methods are now widely used in various types of applications, such as protein structure prediction (Baker and Sali, 2001), function assignment (Kinch and Grishin, 2002), new domain annotation(Jaroszewski et al., 2009) and aiding molecular replacement method of protein crystallography (Schwarzenbacher et al., 2004).

The performance of the profile-profile comparison depends critically on the diversity of sequences included in the profiles. With low diversity, the performance of profile-profile alignment becomes similar to that of the sequence-sequence alignment. Continuous growth of the protein sequence databases partly alleviates this problem. In addition, accuracy of profile-profile algorithms can be improved by using additional information to add more sequences to the profile or by adding other features/descriptors to it. In the former category, one can include sequence fragments with similar structure in the profile calculation, as done in the SP³ method (Zhou and Zhou, 2005), or incorporate more distant homologs in the profile calculation by using a higher E-value cutoff in Position-Specific Iterated Basic Local Alignment Search Tool (PSI-BLAST) (Altschul et al., 1997) searches as done by MUlti-Sources ThreadER (MUSTER) (Wu and Zhang, 2008). In the latter category, one can expand scoring by including real or predicted structural features such as secondary structure (SS) type, solvent accessibility (SA) and torsion angles (Wu and Zhang, 2008; Yang, et al., 2011). This strategy recently became increasingly effective because of the improving accuracy of methods for predicting local structural features. It is important to note that using local structural features predicted from sequence allows comparison of profiles of proteins neither of which has an experimentally determined structure.

In this study, we tested various predicted local structural features in the context of the FFAS scoring, including SS, residue–type-independent SA and residue depth (RD). Besides testing the new composite score, we predict the accuracy of each alignment by neural network trained on various parameters of the alignment. All new features were tested on benchmarks independent from the training set.

2 METHODS

FFAS-3D contains several features of the original FFAS (Rychlewski et al., 2000), such as the collection and weighting of sequences in the multiple sequence alignments used for profile calculation and normalization of profile matching matrix between two sequences. The modifications of the profile-profile matching score added after original FFAS publication (Rychlewski et al., 2000) are described in Section 2.1.

The most important scoring terms added to FFAS-3D include the SS matching score, solvent exposure matching score and template re-ranking. The derivation of residue-size independent SA, the direct comparison of RD and the re-ranking score using different sources of information were not used in similar profile-profile methods before. These features are described in Sections 2.2–2.4. Implementation of dynamic programing, calculation of the final Z-score and template re-ranking are described in Sections 2.5–2.7.

2.1 Sequence profile derivation

Current implementation of FFAS first runs PSI-BLAST (Altschul et al., 1997) on a non-redundant sequence database clustered using CD-HIT (Li and Godzik, 2006) with sequence identity cutoff 85% to obtain the multiple sequence alignments. The E-value threshold of 0.005 and the maximum number of five iterations are used as a default. At most 750 alignments are saved in each round. The profile is built from alignments from the last PSI-BLAST round and all alignments from previous rounds, if aligned sequences were not included in the last round [in the original FFAS (Rychlewski et al., 2000) all the alignments from five PSI-BLAST iterations were included but then aligned proteins were purged by removing ones with >97% sequence identity to other proteins].

Unlike the Henikoff–Henikoff weighting scheme (Henikoff and Henikoff, 1994) used for balancing the sequences in multiple sequence alignments found by PSI-BLAST, the weight of each sequence in FFAS profile is based on the diversity of this sequence as compared with all the other sequences, which is calculated using the BLOSUM62 mutation matrix as described in Rychlewski et al. (2000).

The sequence-profile score sp(i,j) for matching two residues in two sequences is the product of the corresponding two profile vectors and the BLOSUM62 matrix [see Equation (1)]. The multiplication by the BLOSUM62 matrix was introduced after year 2000, and it is a logical equivalent of the transformation of profiles used in Rychlewski et al. (2000).

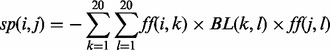(1)

We then calculate the average μ(sp) and standard deviation σ(sp) of sp(i,j) score over all residue pairs in the two compared profiles and transform sp(i,j) into a normalized scoring matrix, which is then used by dynamic programing algorithm [see Equation (2)] [the same approach was used in Rychlewski et al. (2000)].

(2)

The rationale behind this step is that raw (not normalized) profile-profile comparison matrices show large differences in average values and standard deviations resulting from factors such as similarity of amino acid composition and number and diversity of sequences included in the profiles. These factors are not related to specific similarity between two proteins represented by these profiles. As confirmed by benchmark tests, the normalization step improves prediction accuracy by reducing unspecific score differences and enhancing specific sequence similarity signal related to the optimal alignment found by dynamic programing.

2.2 Secondary structure type

The three-state SS type (helix, sheet, coil) of each residue is predicted by PSIPRED (Jones, 1999) for the query sequence. For each template structure, we group the eight SS types as assigned by Define Secondary Structure of Proteins (DSSP) (Kabsch and Sander, 1983) into three states. The SS matching score (used in the alignment scoring matrix) for two residues depends on the agreement of aligned SS types and the confidence score provided by PSIPRED [see Equation (3)]. The PSIPRED’s confidence is in the range of 0–9. For templates whose SS was calculated using DSSP, we assumed confidence score of 9.

(3)

We have also tested a scoring function using negative logarithm of the SS probability (Soding, 2005), but it did not improve the prediction accuracy.

2.3 Residue-type independent solvent accessibility

The real-value SA of each residue was predicted by a back propagation neural network (Rumelhart et al., 1986) with two hidden layers for the query sequence (Xu and Zhang, 2012). The input features are 20 frequencies of residue types extracted from the checkpoint file generated by PSI-BLAST and three probabilities of SS types as predicted by PSIPRED.

For template structures, solvent accessible surface area (SASA) was calculated by EDTSurf (Xu and Zhang, 2009) and then normalized by dividing it by the maximum solvent accessible surface area (MSASA). However, we found that this kind of SA is residue-type dependent, e.g. smaller residues usually have smaller SA values despite the fact that they have lower values of MSASA (see Supplementary Table S1 in Supplementary Materials) used for normalization. This is because small residues tend to be buried by the neighboring bigger residues. It results in the smaller values of average SA for small residues as compared with bigger residues even if they have similar hydrophobicity values. This dependence on the residue type does not cause problems if the predicted and real SA values are compared for the same residue type (Xu and Zhang, 2012). However, it introduces discrepancies when we align residues and compare their SA values for different residue types.

To make the SA normalization residue-type independent, we introduced the reference solvent accessible surface area (RSASA) and used it for normalization of SA. We downloaded a non-redundant set of 3922 protein chains provided by Protein Sequence Culling Server (PISCES) (Wang and Dunbrack, 2003) server (pairwise sequence identity < 0.30) and calculated all-to-all structure alignment using Template Modeling Score Alignment (TM-align) (Zhang and Skolnick, 2005). Then we selected protein pairs that have TM-score > 0.5, which means they have the same fold (Xu and Zhang, 2010). We only considered pairs of aligned residues with distances <5 Å after the optimal superposition of each protein pair. Then we calculated RSASA iteratively. In the first step, RSASA of each residue type is set to its MSASA. Then we sum the SA values for residue types a and b separately when they are aligned and then calculate their ratio RAT^k(a,b) in the k-th iteration. We divide the RSASA by the average ratio ARAT^k(a) for each residue type to get the new RSASA. After ∼5 iterations, the RSASA of each residue type becomes stable and most of the ratios between the 400 residue pairs get closer to 1. The final 20 values of RSASA are listed in Supplementary Table S1 [they can also be used for the normalization of SA values calculated with DSSP, as SASA values calculated by EDTSurf and DSSP are highly correlated (Xu and Zhang, 2013)]. The iterative procedure is described formally by Equation (4). The average absolute difference of solvent accessibilities normalized with RSASA for the aligned residue pairs is equal to 0.113 as compared with 0.120 difference of solvent accessibilities normalized with MSASA.

(4)

The SA matching score [given in Equation (5)] used in the alignment scoring matrix is the absolute difference of solvent accessibilities between any two residues in two sequences.

(5)

2.4 Residue depth

RD evaluates the position of each residue in the protein structure relative to the closest point of the solvent accessible surface (Chakravarty and Varadarajan, 1999). When residues are completely buried inside of the protein, their solvent accessibilities are all equal to zero, but depth values are different. Hence, RD can be considered as a complementary term to SA. It was used before for generating structure profile to help find remotely homologous protein pairs (Zhou and Zhou, 2005).

Here, RD of a template structure is calculated by EDTSurf, whereas for the query sequence it is predicted by a separate neural network with two hidden layers. Input features for each residue are the same as that used for the SA prediction. The window size is 33, which results in 23 × 33 = 759 nodes in the input layer. Each of the two hidden layers contains 70 nodes and the output layer (consisting of one node) predicts the real-value RD. Similar to SA, we normalize the depth value dv(i) to a value between 0 and 1 as shown in Equation (6). We then directly use the absolute difference of RDs as the matching function in the alignment scoring matrix [see Equation (7)].

(6)

(7)

The inclusion of predicted structural features into profiles improves profile-profile comparison only if these predictions are sufficiently accurate. For instance, the accuracy of SS prediction is relatively high (Q₃ accuracy >0.80) and it is known to provide a useful contribution to profile-profile alignment. The prediction errors of SA and RD are listed in Supplementary Table S2. For SA, hydrophobic residues such as CYS, ILE, LEU and VAL, often have smaller prediction errors, as they are usually buried and have small values of SA. For hydrophilic residues such as ASP, GLU, LYS, ASN, GLN and ARG, SA is harder to predict, as they are on the surface region and real SA values of those residues vary in a broad range. On the contrary, hydrophilic residues often have small values of RD, which are easier to predict with neural networks. In summary, the values listed in Supplementary Table S2 suggest that by using both RD and SA one may reduce errors related to inaccuracies in solvent exposure prediction.

2.5 Dynamic programing

FFAS carries out Smith–Waterman dynamic programing algorithm (Smith and Waterman, 1981) to obtain the optimum local-local alignment (because FFAS uses local-local alignment, it is not necessary to introduce a separate step of splitting sequences into domains). The gap opening and gap extension penalties are constant, set to 6.0 and 0.3, respectively. The complete matching score in Equation (8) is the linear combination of the four terms described earlier in the text with weighting factors w₁ = 1.25, w₂ = 2.15 and w₃ = 2.05.

(8)

The weighting factors were optimized on the targets of the ninth Critical Assessment of protein Structure Prediction (CASP9) compared with the template library consisting of 29 301 protein chains from the Protein Data Bank (PDB) (Berman, et al., 2000) released before CASP9. For every pair of sequences q and t, the final raw score raw_ score(q,t) that is found by dynamic programing corresponds to the optimal local alignment between the two sequences. Average Global Distance Test-High Accuracy (GDT-HA) score for all targets was used as an objective in the optimization.

2.6 Calibration of raw profile-profile alignment scores

Raw profile-profile alignments scores for a given protein are obviously correlated with protein’s length, but they also show less trivial biases toward higher or lower average scores. They may also have wider or narrower distribution when compared with profiles of unrelated proteins. These differences, related to amino acid composition and diversity of sequences included in the profile, are difficult to predict from the profile itself. Therefore, FFAS calibrates raw alignment score using actual distribution of scores obtained by comparing each sequence profile with a library of profiles representing 1195 different folds from Structural Classification of Proteins (SCOP) (Murzin et al., 1995) database. The profiles representing SCOP structures are assigned to four bins based on their lengths (bins correspond to length ranges: <100aa, 100–200aa, 200–300aa, >300aa), and median value and average absolute deviation of the raw scores are then calculated for alignments between query profile and profiles from each bin. Subsequently, linear regression is used to interpolate the median value and the average absolute deviation values (we then denote intercept and slope parameters for median raw score and absolute deviation α_μ, β_μ, α_σ and β_σ, respectively). The expected median value and average absolute deviation of raw score for proteins with any sequence length can be then estimated using these four parameters. These expected values are then used to calibrate the raw score.

For each alignment of two sequences q and t, raw score raw_score(q,t) can be calibrated in two ways leading to two different Z-scores. The first calibration is based on the parameters of the expected median and average absolute deviation for sequence q, and the second is calculated using analogous values for sequence t [see Equation (9)]. High value of Z₁(q,t) indicates that protein t may be a significant hit among all proteins with similar lengths, when they are aligned with protein q. At the same time, high value of Z₂(q,t) means that protein q may be a significant hit among all proteins with similar lengths, when they are aligned with protein t.

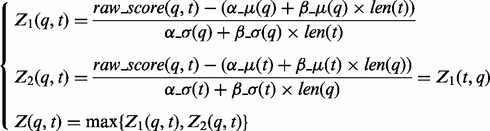(9)

We assumed that a significant hit should fulfill both of the above criteria. Hence, we used the maximum of Z₁(q,t) and Z₂(q,t) as the final value of the calibrated score (because FFAS scores are negative, maximum corresponds to the less outstanding of the two Z-scores). Note that raw_score(q,t) is symmetrical with respect to q and t.

Template t may be a significant hit to query q based on the low Z₁(q,t), but on the contrary, q may be not an outstanding hit to t based on the high Z₂(q,t). Hence by using a maximum, we eliminate cases when raw score is significant as compared with only one ‘baseline’ distribution. As we show later, this approach improves template selection. The comparisons between the three possible ways of Z-score calculation for two example query sequences and representatives of the 1195 folds from SCOP database are shown in Supplementary Figure S1. Interestingly, more pairs between the first query sequence and the SCOP folds have Z₂(q,t) > Z₁(q,t) than vice versa especially in cases of higher homology. For more remotely related sequences (i.e. in the high Z-score region), Z₂(q,t) is more often lower than Z₁(q,t). In this example, Z(q,t) = Z₂(q,t) for the closest SCOP fold assigned to this query sequence (see the bottom-left point in Supplementary Fig. S1b). For the second example shown in Supplementary Figure S1d–f, more pairs have Z₁(q,t) > Z₂(q,t) and Z-score of the closest SCOP fold assigned to this query sequence comes from Z₁(q,t).

2.7 Re-ranking of the templates based on the predicted alignment accuracy and structural fitness

To further optimize the selection of templates, we predict the accuracy of each alignment using neural network. The neural network input features include the Z-score, sequence identities and coverage of alignments, agreement of SS, Pearson’s correlation coefficients of SA and RD between the aligned residues and the average matching score per residue pair (total raw score divided by the number of aligned pairs). The output is the predicted MaxSub score (Siew et al., 2000) of the alignment (in the range between 0 and 1).

We used the CASP9 targets as the training set and selected 75 top scoring alignments for each target. We tested different numbers of hidden nodes and hidden layers and found that the best accuracy comes from the neural network with 13 hidden nodes and 2 hidden layers. The average error of the predicted MaxSub score was 0.067 as compared with the real MaxSub score of the same alignment applied to the two corresponding structures. [We have tested neural networks trained on MaxSub, TM-score (Zhang and Skolnick, 2004), Global Distance Test-Total Score (GDT-TS) and GDT-HA scores (Zemla, 2003), and MaxSub score yielded optimal benchmark results].

Given the alignment between the query sequence q and the template t, we obtain the unrefined backbone structure for the query q, by replacing template residues with aligned query residues. We then evaluate the fitness of the query sequence in the template structure by using pairwise Cα potential E_Cα(q,t) implemented in the Distance-scaled, Finite-Ideal gas REference (DFIRE) method (Zhou and Zhou, 2002). In the final step, the MaxSub score MS(q,t) predicted by the neural network as well as the energy of the initial backbone structure are combined with the original FFAS-3D Z-score Z(q,t) and the original sequence–profile-based Z-score Z_sp(q,t) by FFAS and used as a score for template selection [see Equation (10)] with weights optimized empirically using grid search. Z_sp(q,t) has a higher correlation with the alignment accuracy especially when its value is low, hence it helps the ranking if we include it in the equation. (If the templates structure is unknown, the scoring function only includes the first three terms).

(10)

3 RESULTS

3.1 Overall accuracy of alignment

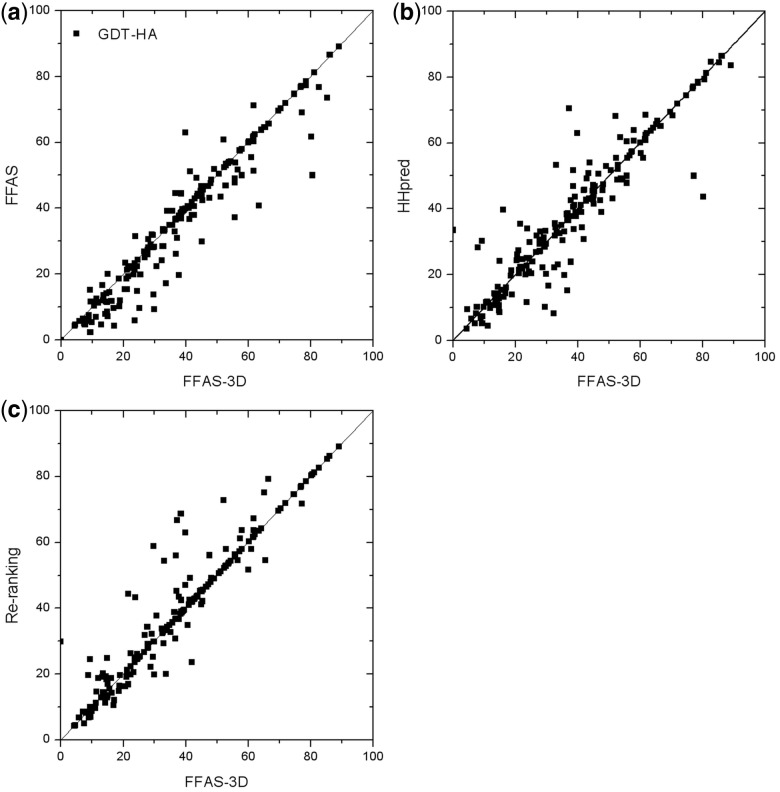
We selected a test set of 367 single-domain protein chains with <30% sequence identity to each other from the pre-calculated list available from the PISCES server (Wang and Dunbrack, 2003). This set does not include any homologs of the CASP9 targets, which were used as the training set. We used queries from the test set in searches against library of profiles of PDB structures and evaluated the alignment coverage, GDT-HA and GDT-TS scores (Zemla, 2003) of the top-scoring alignment and the Modeller (Sali and Blundell, 1993) model based on that alignment. The incremental effects of adding structural features to the scoring function are shown in Table 1. The addition of the SS to the scoring function improved the accuracy of the GDT-HA of the top-scoring alignment by 4% as compared with the original version that used only profile-profile comparison. However, it may be partly attributed to the 4% increase of the average alignment length. Matching terms for SA and RD contributed another 2 and 1% to the accuracy, respectively, without increasing the average alignment length. Finally, the re-ranking of the templates based on the alignment accuracy predicted with neural network improved average GDT-HA score by another 4% leading to the cumulative improvement of 11% as compared with the original FFAS. At the same time, the average alignment length increased by 10%. The improvement of the accuracy of the top-scoring alignments as compared with the original FFAS program is illustrated by Figure 1a. The new program improved the alignments for 59% of the targets in the test set, the accuracy of 18% alignments did not change and the accuracy of 23% decreased, as compared with the original FFAS method.

Table 1.

Comparison of alignment accuracy on the 367 test proteins

Method	First threading alignment			Modeller model
	COV	GDT-HA	GDT-TS	COV	GDT-HA	GDT-TS
sp (FFAS)	0.81	35.02	47.34	0.85	34.33	47.31
sp + ss	0.84	36.42	49.07	0.88	35.67	49.07
sp + ss + sa	0.84	37.19	49.97	0.90	36.68	50.30
sp + ss + sa + rd	0.85	37.52	50.47	0.90	37.00	50.77
Re-ranking	0.89	39.08	52.42	0.94	38.19	52.40
HHpred	0.83	37.54	50.47	0.89	37.05	50.84

Note: COV, coverage; sp, sequence profile; ss, secondary structure; sa, solvent accessibility; rd, residue depth.

Fig. 1.

Comparison of the GDT-HA of the top alignments selected by different methods. (a) FFAS-3D and FFAS; (b) FFAS-3D and HHpred; (c) FFAS-3D and re-ranking by the combined score

To evaluate the impact of the modeling step, we compared the accuracy of the Modeller model with the accuracy of the initial alignment. As show in Table 1, the average GDT-TS score of the models is slightly higher than GDT-TS score of the corresponding alignments but the opposite is true for the average GDT-HA score. Because GDT-HA takes into account only the most accurate parts of the model (Cα-Cα distances < 4 Å), whereas GDT-TS score also includes less accurately predicted regions (Cα-Cα distances < 8 Å), it means that the modeling step improved the overall completeness of the model at the expense of the accuracy of most reliably predicted regions.

We also compared the performance of FFAS-3D with HHpred (Soding, 2005), a leading Hidden Markov Model-Hidden Markov Model (HMM-HMM) local-local alignment program. HHpred uses hidden Markov models, which can be viewed as a special type of profiles that include probabilities of insertions and deletions and SS matching score based on confidence-dependent conditional probability. We built HHpred HMM profiles for the same template library of 29 301 protein chains that was used to evaluate FFAS-3D. The average alignment accuracy and alignment coverage of HHpred are close to those of the FFAS-3D before the template re-ranking step (Table 1). The distribution of differences in accuracy of the top-scoring alignments between FFAS-3D and HHpred is illustrated by Figure 1b. Both programs yield similar results for easy benchmark targets with highly accurate alignments (GDT-HA > 75). Similarly, for difficult cases, where there is probably no accurate template in the library, the top hits by both programs have low accuracy (GDT-HA < 20). However, most benchmark queries fall into the region between these two extremes and, in this region, alignment results are significantly different. In fact, the top-scoring templates from FFAS-3D and HHpred are different for 231 of 367 queries, suggesting that despite similar overall accuracy, there are significant differences between these two local-local alignment programs.

3.2 Fold recognition rate

To evaluate fold recognition independently from the overall prediction accuracy assessed as described in the previous section, we tested FFAS-3D on the Lindahl benchmark set (Lindahl and Elofsson, 2000), consisting of 976 domains from the SCOP library. The benchmark contains 555, 434 and 321 targets with at least one similar structure at the family, superfamily and fold levels, respectively. We evaluated the success rates in terms of ranking any of the similar structures as the first and among top five hits. The comparison of FFAS-3D with HHpred and SPARKS-X is shown in Table 2. SPARKS-X conducts a semi-global alignment and tends to yield longer alignments (on average ∼9% higher coverage than HHpred and FFAS-3D).

Table 2.

Family, superfamily and fold recognition rates of different programs on the Lindahl benchmark set

Method	Family (%)		Superfamily (%)		Fold (%)
	First	Top 5	First	Top 5	First	Top 5
FFAS	82.3	87.7	60.4	67.5	15.0	28.3
HHpred	82.9	87.1	58.8	70.0	25.2	39.4
SPARKS-X	84.1	90.3	59.0	76.3	45.2	67.0
FFAS-3D	84.9	91.2	66.6	79.5	35.8	55.1
FFAS-3Dp	86.3	91.9	65.7	77.0	33.0	53.9
FFAS-3Dr	87.2	93.9	71.0	81.8	42.7	63.9

Note: In each level, the program succeeds in recognizing the target if the structure with the same SCOP family, superfamily or fold classification is ranked as the first or as one of the top 5.

FFAS-3D^p, using the matching of predicted structural features in the scoring function; FFAS-3D^r, using the matching of real structural features in the scoring function.

FFAS-3D has better recognition rates than the other two programs at the family and superfamily levels, even without template re-ranking. Because SPARKS-X is specifically designed with focus on the remote homologs, it has the highest success rate at the fold level. Although FFAS-3D fold detection rate is ∼25% lower than that of SPARKS-X, it is 40% better than HHpred’s. The lower performance of local-local alignment programs at the fold level as compared with semi-global programs such as SPARKS-X is probably linked to the fact that for remote homologs they either yield short alignments or do not yield any alignment at all and, thus, do not provide any meaningful score. In other words, semi-global algorithm, which ‘forces’ the alignment of apparently dissimilar pairs, makes it possible to choose the closest of these marginally similar templates.

FFAS-3D uses predicted structural features of the query sequence and real structural features of template structures. However, using experimental structures significantly limits the range of potential applications of the method, as thousands of protein families have no structural coverage. Thus, to detect remote homologies to such families, we evaluated the version of the program that uses predicted structural features for both the query and the template (denoted FFAS-3D^p in Table 2). For reference, we also checked the performance of the program where real structural features were used for the query and the template (denoted FFAS-3D^r in Table 2). To maintain simplicity, we used the same weighting parameters of the scoring terms as that in the default version, even that they could be re-optimized for predicted features to achieve better results. Surprisingly, the performance of the version using only predicted features is similar to that of FFAS-3D at the superfamily level and surpasses FFAS-3D at the family level. It is understandable because at the family level sequences are highly similar and the differences between their predicted structural features obtained with the same SS prediction method are smaller than the differences between predicted and real structural features. At the fold level where sequences are more distantly homologous, the recognition rate is only 8% worse. As expected, when we use the real features for both the target and the template, the performance is much better than the default FFAS-3D at all the SCOP levels indicating the potential gain from improving the accuracy of predicted features.

3.3 Symmetrical Z-score improves template ranking

We compared the ranking result by the symmetrical Z-score Z(q,t) (see Section 2) with results obtained with individual Z-scores calculated for query and the template (Z₁(q,t) and Z₂(q,t)). Based on the test set, the first alignments selected by the latter two yield average GDT-HA scores 36.82 and 37.03, respectively, which are 1.7 and 1.2% worse than average GDT-HA obtained with the symmetrical Z-score (Fig. 2). There are many targets that have the same GDT-HA if ranked by Z(q,t) and Z₂(q,t) (Fig. 2b), suggesting that Z₁(q,t) is usually smaller than Z₂(q,t). This also makes Z₁(q,t) versus Z₂(q,t) in Figure 2c similar to that in Figure 2a, except that Z(q,t) provides better prediction than Z₂(q,t) for many hard proteins shown in the bottom-left region. Because the top templates selected by Z₁(q,t) and Z(q,t) are often quite different, both of them could be used as independent methods in the future FFAS metaserver.

Fig. 2.

Comparison of the GDT-HA of the top alignments selected by different types of Z-scores. (a) Z-score calculated using calibration parameters for the query versus symmetrical Z-score; (b) Z-score calculated using calibration parameters for the templates versus symmetrical Z-score. (c) Z-score calculated using calibration parameters for the query versus Z-score calculated using calibration parameters for the template

As an example we analyzed test target 3s8sA, which is a medium-sized alpha + beta protein with many good modeling templates. Top values of Z₁(q,t) are higher than top values of Z₂(q,t), which is related to the higher standard deviation of the distribution of the raw scores of the query. The top template picked by the symmetrical Z-score Z(q,t) 1p27B is ranked in the sixth place by Z₁(q,t) and on position 27th by Z₂(q,t). It has GDT-HA score of 54.21, that is 0.24 and 12.62 higher than the top ranking templates picked by Z₁(q,t) and Z₂(q,t) scores, respectively.

Better performance of the symmetrical Z-score can be understood, as it conservatively ‘picks’ the template whose raw score is outstanding as compared with the baseline distributions of both compared profiles.

It is important to note that here the full FFAS-3D score (raw_score(q,t)) was normalized using distributions of raw scores of the profile-profile term only. Interestingly, using the distribution of the complete raw score for calibration did not improve the ranking of templates. This can be rationalized by the fact that our descriptors of SSs and solvent exposure and related comparison terms fall into well-defined numerical ranges, while there are huge differences between characteristics of sequence profiles.

3.4 Adding structural features to the scoring function improves ranking of the templates and alignment accuracy

Because structural features are used in the scoring function, they do not only affect the ranking of templates, but also influence the alignments between the query and templates. As illustrated by the Figure 1a, structural features added in FFAS-3D did not change the alignments of highly similar protein pairs whose accuracy was already high in the original FFAS. However, the differences between the alignments calculated with these two programs become larger for more distantly related pairs (as indicated by lower GDT-HA values).

For instance, for target 3ndqA, which is an alpha protein with six short helices, the first and second templates as ranked by FFAS-3D are 2dmeA and 1enwA (see Supplementary Fig. S2a). The correlation coefficients of SA and RD, agreement of SS, raw score of profile-profile alignment are also listed in the figure. The alignment accuracy is 59.53 for 2dmeA and 27.84 for 1enwA. Because the profile-profile matching score is slightly lower for 1enwA than 2dmeA (−45.836 versus −45.310), the first template selected by the original FFAS program is 1enwA and the alignment is the same as that by FFAS-3D. However, based on the structural features in the alignment, 2dmeA has much higher correlation coefficient of SA and agreement of SS, which result in better Z-score in FFAS-3D. This example illustrates the situation where matching of structural features improves template selection.

Target 2y9wC is one chain of Agaricus bisporus mushroom tyrosinase (shown as cartoon in Supplementary Fig. S3). This protein chain has a globular shape, which is covered by many beta-strands. Both FFAS and FFAS-3D correctly picked the same top-scoring template 2e4mC (shown as line in Supplementary Fig. S3). However, the alignments calculated with FFAS and FFAS-3D are significantly different with most differences in the coil regions between beta-strands. As illustrated by Supplementary Figure S2b, only the terminal part of the alignment is identical for both programs. The alignment from FFAS-3D has four small gaps, whereas that by FFAS has two long gaps. GDT-HA score is 35.84 for the FFAS-3D alignment, which is much higher than GDT-HA of 19.30 of the FFAS alignment. This example illustrates how incorporating structural features can improve the alignment accuracy. We also show the structure alignment of these two structures (see Supplementary Fig. S2c, residue pairs with Cα-Cα distances < 5 Å are connected by dots). As expected, structural alignment would result in the most accurate template-based model, with GDT-HA = 53.68. However, this alignment requires introducing 14 gaps, which would have prohibitive cost in dynamic programing alignment of remotely similar proteins.

3.5 Improved template ranking using neural network

The effect of template re-ranking is illustrated by Figure 1c. Although the average accuracy of the prediction after template re-ranking increases, there are still many targets for which it decreases. The re-ranking procedure does not change the order of top templates for ∼39% of targets (these are usually cases when one template is significantly better than others). Most of the situations when templates are re-ranked fall into two categories: (i) there are many templates with low Z-scores; (ii) all the top-scoring templates have high Z-scores. In such cases, the predicted Maxsub score and the backbone potential provide information complementary to the Z-score and help to differentiate between the templates with similar Z-scores.

Because the predicted structural features have only limited accuracy, they may sometimes become closer to the structural features of the wrong template than to the correct one. The calculation or prediction of SA/depth for a protein is also likely to be inaccurate for the surface regions where it binds to cofactors or other proteins. In other cases, correct templates with good matching of structural terms are not on the top of the scoring list because of the high raw profile-profile score or high normalization factor— i.e. denominator in Equation (9). Neural network re-ranking can account for these situations and effectively filter out at least some erroneous templates.

The first situation may be illustrated by the example 2y0mB, which is a small domain consisting of one helix. Z-scores of the top templates are high (>−15.0), suggesting that it is a hard target and the original template ranking may be incorrect. Generally, the neural network predictions of Maxsub scores are higher than the actual Maxsub scores, as illustrated by the top part of Table 3. Because neural network correctly infers that the first template has low Maxsub score (possibly due to the low sequence identity in the alignment region), this template drops to the fourth place. The template 2o98P is predicted to have the highest accuracy (due to the high sequence identity to the query sequence). Although this template is not the optimal choice (as indicated by real Maxsub scores of the predictions), it still gives the much higher Maxsub score than the top template in the original ranking.

Table 3.

Top five templates before and after re-ranking for targets 2y0mB(top) and 3rjpA(bottom)

R	Temp	ID	cSA	cRD	aSS	Z	MSp	MSr	R′
1	1undA	0.09	0.56	0.10	0.85	−14.1	0.43	0.30	4
2	2kesA	0.15	−0.03	0.07	0.97	−13.9	0.79	0.60	2
3	2rmfA	0.25	0.21	−0.03	1.00	−13.9	0.62	0.58	3
4	2o98P	0.31	0.08	0.26	0.96	−13.3	0.81	0.55	1
5	3a1qC	0.11	0.21	−0.01	0.94	−13.0	0.42	0.67	5
1	2jzyA	0.38	0.44	0.35	0.78	−84.1	0.69	0.59	2
2	2pmuA	0.35	0.65	0.55	0.87	−80.8	0.75	0.79	1
3	2hqnA	0.27	0.50	0.44	0.81	−75.2	0.70	0.66	4
4	1gxpA	0.37	0.58	0.55	0.84	−71.4	0.75	0.80	3
5	1ys6A	0.41	0.58	0.60	0.90	−69.2	0.73	0.76	5

R, order before re-ranking; Temp, template name; ID, sequence identity in the alignment region; cSA, correlation coefficient of solvent accessibility in the alignment region; cRD, correlation coefficient of residue depth in the alignment region; aSS, agreement of secondary structure in the alignment region; Z, original Z-score; MSp, predicted MaxSub score; MSr, real MaxSub score of the alignment; R′, order after re-ranking.

The second type of situation where templates re-ranking may lead to substantial improvement can be exemplified by predictions for target 3rjpA, an alpha + beta protein, with a lot of highly homologous templates in the library. Here, the predicted Maxsub scores are highly correlated with the real Maxsub scores (see the bottom of Table 3). The best template 1gxpA has the highest predicted score, but it is only in the third place after re-ranking due to the much lower Z-score. The second best template 2pmuA now becomes the first template, which has Maxsub score 0.20 higher than the original first template 2jzyA.

Table 3 illustrates only the re-ranking of the top five templates. After testing several values for the number of templates included in the re-ranking process, we found that the best improvement is achieved if top 10 templates are re-ranked.

4 CONCLUSIONS

We have performed an extensive upgrade of a FFAS profile-profile alignment method, bringing its sensitivity and accuracy on par to the leading programs in the field, while maintaining its unique features. This was achieved by incorporating three local structural features into FFAS: SS type and solvent exposure term consisting of complementary SA and RD terms. The combination of these terms improves the average alignment accuracy of the program by ∼7% as compared to the original version of FFAS, which only conducts profile-profile alignments. The next step of predicting the alignment accuracy of the top templates by neural network and re-ranking the templates adds another 4% in accuracy as evaluated by the GDT-HA score. The new FFAS-3D program is comparable with the current state-of-the-art programs as evaluated on the independent test set of structures deposited after CASP9 targets (which served as our training set). We have also tested FFAS-3D on the test set consisting of CASP10 targets obtaining an average GDT-HA of 41.65, which would rank FFAS-3D among the most accurate homology recognition methods. FFAS-3D was also tested on the Lindahl benchmark set for fold recognition and showed superior success rate on the family and superfamily levels.

The individual predictions obtained with FFAS-3D and predictions from other programs often show significant differences in template selection suggesting that they are complementary and thus FFAS-3D would contribute to the accuracy of meta-servers and other jury-based prediction methods.

Because the accuracy of the predicted structural features is crucial to the alignment accuracy and template ranking, the future improvements of the performance of FFAS-3D may depend on the development of the more accurate programs for predicting structural features. Such new added structural features should provide non-redundant information to the scoring function. For instance, SS description schemes with >3 SS types may improve prediction accuracy if they can be accurately predicted from protein sequence.

Another possible direction of development is linked to the observation that optimal parameters for the alignment of close homologues are probably significantly different from the optimal method for aligning remotely homologous pairs and pairs for which similarity can only be predicted based on structural features. In particular, the optimal detection of such remote homologs may require different values of gap penalties, higher weights of structural features or even switching to semi-global alignments. To address this issue, the alignment program may evaluate the difficulty of the prediction in the initial search and then adjust alignment parameters and perform another search in the template library.

Funding: National Institute of Health (GM087218 and GM101457).

Conflict of Interest: none declared.