Determination of parameter identifiability in nonlinear biophysical models: A Bayesian approach

A Bayesian approach can be used to determine the reliability of estimated parameters in biophysical models.

Abstract

A major goal of biophysics is to understand the physical mechanisms of biological molecules and systems. Mechanistic models are evaluated based on their ability to explain carefully controlled experiments. By fitting models to data, biophysical parameters that cannot be measured directly can be estimated from experimentation. However, it might be the case that many different combinations of model parameters can explain the observations equally well. In these cases, the model parameters are not identifiable: the experimentation has not provided sufficient constraining power to enable unique estimation of their true values. We demonstrate that this pitfall is present even in simple biophysical models. We investigate the underlying causes of parameter non-identifiability and discuss straightforward methods for determining when parameters of simple models can be inferred accurately. However, for models of even modest complexity, more general tools are required to diagnose parameter non-identifiability. We present a method based in Bayesian inference that can be used to establish the reliability of parameter estimates, as well as yield accurate quantification of parameter confidence.

INTRODUCTION

A major goal of biophysics is to understand the physical mechanisms of biological molecules and systems. The general approach to rigorously evaluate mechanistic hypotheses involves comparison of measured data from well-controlled experiments to the predictions of quantitative physical models. A candidate model (and the mechanism that it implies) is rejected if it does not quantitatively fit all available data. For models that agree with the data, the fits provide estimates for the model parameters, which represent system properties of interest that cannot be measured directly, such as binding affinities, cooperative interactions, kinetic rate constants, etc. An extensive literature exists concerning methods for finding sets of parameter values that provide the “best fit” of model to data (Jennrich and Ralston, 1979; Johnson, 2010; Johnson and Faunt, 1992), but the important issue of determining and characterizing the confidence of parameter estimates in models with several, usually nonindependent, parameters is more challenging and less well developed. Here, by way of examples from fairly simple and common biophysical models, we consider two related issues: (1) For a given model and a given type of data, are the parameters of a model uniquely constrained by the measurements? (2) How confident can one be in the parameter values obtained by fitting a model to data?

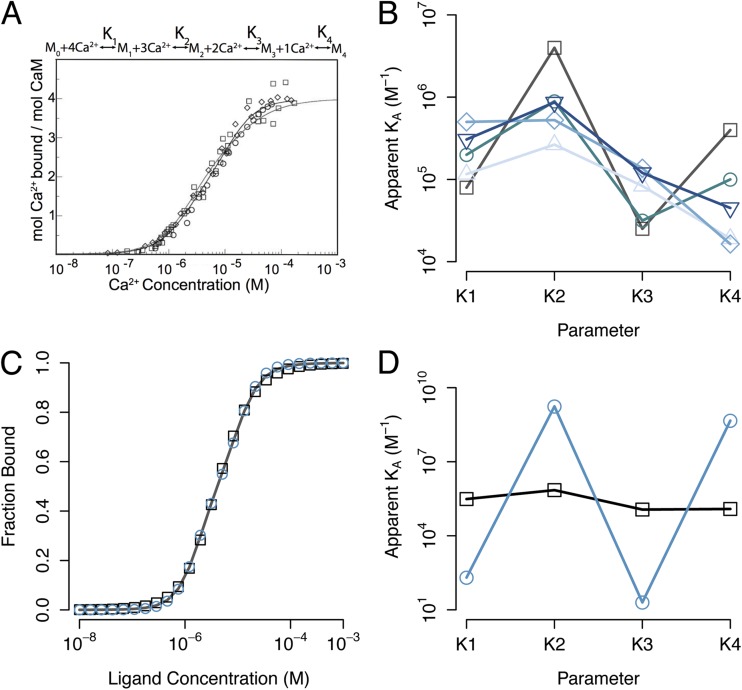
To illustrate the issues of confidence in parameter estimation, we consider ligand activation of the macromolecular receptor calmodulin (CaM). CaM plays a central role in many biological signaling processes and has been studied extensively (Cheung, 1980; Cheung et al., 1978; Hoeflich and Ikura, 2002). This protein has four non-identical EF hand–binding sites for calcium ions. Upon activation by calcium, CaM can interact with over 300 known effector proteins (Crivici and Ikura, 1995; Yap et al., 2000). Calcium-binding data for CaM are commonly analyzed using a four-site sequential binding model (Fig. 1 A, top), in which the ligand-binding events are quantified by the macroscopic equilibrium constants K₁, K₂, K₃, and K₄ for the four binding steps. Mechanistically, these four parameters reflect intrinsic binding affinities and potential cooperative interactions between the sites, as originally proposed by Adair (1925) to describe cooperative oxygen binding to hemoglobin. Fig. 1 A (bottom; adapted from Stefan et al., 2009) shows calcium-binding curves from several studies (Crouch and Klee, 1980; Porumb, 1994; Peersen et al., 1997); Fig. 1 B shows the corresponding estimates for parameters K₁ through K₄ reported by these groups and those from three related studies (Haiech et al., 1981; Burger et al., 1984; Linse et al., 1991). Strikingly, although the data from these groups are in good agreement, the parameter estimates differ significantly: for some parameters, the reported estimates vary >25-fold.

Figure 1.

Estimating the parameters of a four-site binding model. (A) CaM-binding data from multiple experimental groups (adapted from Stefan et al., 2009). M_i refers to CaM with i-bound calcium ions. (B) Parameters obtained by fitting the sequential binding model in A to experimental data from five groups. Parameters are from Linse et al., 1991 (squares), Haiech et al., 1981 (rhombi), Porumb, 1994 (circles), Burger et al., 1984 (triangles), and Crouch and Klee, 1980 (inverted triangles). (C) Synthetic, noiseless binding data (solid curve) calculated using parameters from Linse et al. (1991). (D) Two distinct parameter sets that yield excellent fits to the data. For parameters shown as squares, all binding sites have nearly identical affinity, consistent with weak cooperativity. The parameters shown as circles are consistent with strong cooperative interactions between the binding sites. The binding curves generated from these parameters are plotted in C as circles and squares.

What underlies this large uncertainty in binding parameter estimates? The problem may be intrinsic to data fitting, such that a given binding curve is fit arbitrarily well by many combinations of parameter values, regardless of data quality. Alternatively, it could be a consequence of noise in the data, in which case more precise experimentation may place tighter constraints on the parameter values. We investigated these possibilities using simulated data. A synthetic binding curve with no added noise was generated using the binding parameter estimates from a single study (Linse et al., 1991) (smooth curve in Fig. 1 C). Systematic exploration of the parameter space of the sequential binding model revealed that no single set of parameter values provides a clear best fit to the synthetic data. Rather, many parameter sets, covering a wide range of values for each parameter, fit the data with <1% root-mean-squared (RMS) deviation. (This value is a conservative threshold for identifying “excellent” fits, as real binding measurements are unlikely to surpass this noise criterion.) Two representative excellent fits are shown in Fig. 1 C, and the corresponding parameter values for these fits are shown in Fig. 1 D. Note that the scale of the vertical axis in Fig. 1 D spans nine orders of magnitude, indicating that parameter sets with very different apparent affinities yield similar binding curves. For the set of points shown as squares in Fig. 1 D, the equilibrium constants K₁–K₄ are nearly equal. For the parameter set shown as circles in Fig. 1 D, the apparent affinity for each binding event is very different, consistent with large differences in binding affinity or strong cooperative interactions between the sites. Comparison of the two fits shown in Fig. 1 C indicates that even high quality binding data (1% RMS noise) lack the power to distinguish between mechanisms with very different binding affinity and/or cooperativity. When fitting data, not only the best fit but also the uniqueness of the fit must be determined to understand the confidence one can have in the estimates. Otherwise, the uncertainties in model parameter values may be so large (as in Fig. 1 D) that they preclude even qualitative insights into the mechanism of the process.

If fitting a model to data is to yield accurate and meaningful parameter estimates, the complexity of the model must be commensurate with the constraining power of the data. We show that this requirement is often not met when typical models are used to analyze common types of experimental data such as binding curves and kinetic time series. We present multiple methods for assessing the uniqueness of parameter estimates obtained from fitting experimental data. For some simple models that allow analytical solutions, we describe a method for determining the maximum number of parameters that can be meaningfully quantified by regression analysis. This work builds upon previous investigations (Bellman and Astrom, 1970; Reich, 1974; Straume and Johnson, 2010), and such methods are effective for simple models. However, any biophysically realistic models of protein signaling and conformational change, such as ion channel gating, will not be tractable. Therefore, a general method is needed for estimating parameters accurately regardless of model complexity. To this end, we present a framework based in Bayesian inference that uses Markov chain Monte Carlo (MCMC) sampling. By providing distributions of parameter values consistent with the available data, this method yields accurate estimates of model parameters (and their uncertainties) and can be used to determine whether those estimates are unique. In addition, the method possesses significant computational advantages over approaches that sample error surfaces exhaustively.

MATERIALS AND METHODS

Simulations and figures were generated using Matlab and R.

RESULTS

In the following sections, we explore the reliability of parameter estimates obtained by fitting various models to common types of biophysical data. Experimental data are generally fitted using regression methods. The theory for nonlinear regression assumes that there is a point in the parameter space that yields a minimum local (although hopefully global) error between model and data. Furthermore, it is assumed that the error contours surrounding this point are well approximated by ellipsoids (this geometry stems from a quadratic error function; Seber and Lee, 2003; Seber and Wild, 2003). When these conditions hold, we have strong statistical guarantees that the true parameter value is located within some bounded interval from our estimated value. A variety of optimization methods can then be used to obtain a best-point estimate for the parameters and to construct confidence intervals defining the uncertainty in the parameters. For many models of biophysical interest, however, multiple parameter combinations (often with very different values) produce nearly identical observables. In these cases, the assumptions of nonlinear regression theory do not hold, and we lose the statistical assurance that our point estimates of the parameters are close to the true values. We next use simple example models to investigate when such issues arise and to demonstrate that this problem may occur frequently in biophysical investigations.

Two-site, three-parameter binding model: A case of structural non-identifiability

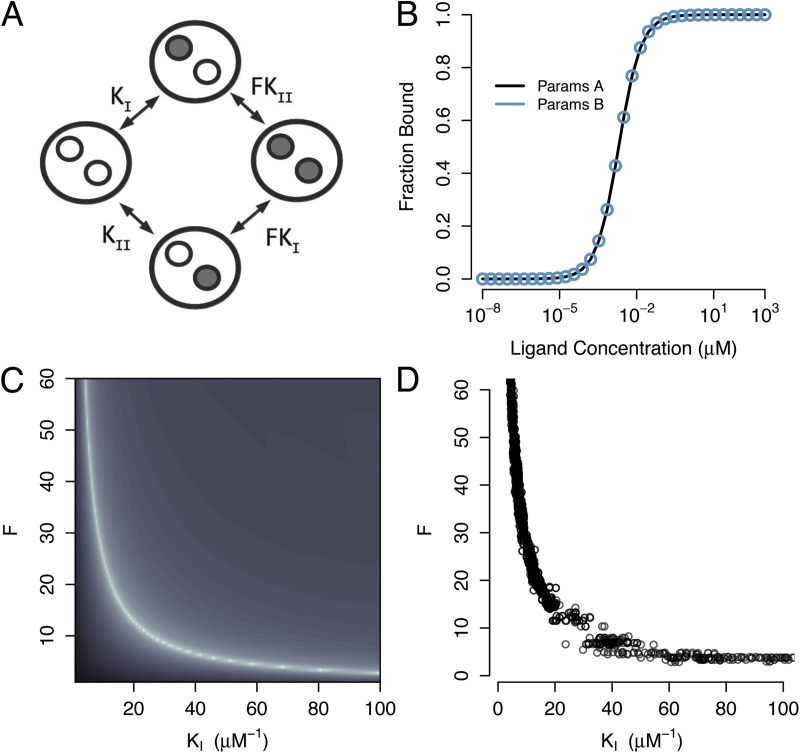
Consider a cooperative model of ligand binding to a receptor with two inequivalent binding sites (Fig. 2 A). The microscopic association equilibrium constants of the sites are denoted K_I and K_II, and an additional cooperativity parameter (F) quantifies the degree to which binding events at one site can enhance (or hinder) binding at the other site. Note that there is only one free parameter for cooperativity because of the detailed balance constraint. A simulated binding curve is shown in Fig. 2 B, which was generated with parameters {K_I, K_II, F} = {500 µM⁻¹, 500 µM⁻¹, 1}. A second binding curve is also shown, generated with parameters {K_I, K_II, F} = {997.5 µM⁻¹, 2.5 µM⁻¹, 100}. Although these curves were generated from very different parameter values, they overlay exactly. How is it that multiple points in the parameter space of this model can yield identical binding curves?

Figure 2.

Parameter estimation for a two-site cooperative binding model. (A) Diagram of a model that assumes two binding sites with microscopic association constants K_I and K_II, and cooperativity factor F. (B) Two parameter sets with very different values yield identical simulated binding curves. Parameter set A: {K_I, K_II, F } = {500 µM⁻¹, 500 µM⁻¹, 1}; parameter set B: {K_I, K_II, F } = {997.5 µM⁻¹, 2.5 µM⁻¹, 100}. For parameters A, the binding sites have identical affinity and weak cooperativity, whereas for parameters B, the binding sites have distinct affinities and strong positive cooperativity. (C) Log-error surface of a region of the F-K_II parameter space. The curve generated from parameters A was used as a reference curve. Binding curves were calculated for various points in the parameter space, and the total error between the two curves was computed. Areas of lighter shading correspond to areas of less error. The minimum error estimate of the parameters defines a curve through the parameter space and not a point estimate. (D) MCMC samples drawn from the joint posterior distribution of K_I and F. The curved structure of the posterior distribution indicates that the model’s parameters are not identifiable using this binding data.

We used the smooth curve in Fig. 2 B as simulated data (without added noise) and explored the values of parameters F and K_I systematically (Fig. 2 C). For every point in this grid, the values of F and K_I were fixed, and the third parameter (K_II) was varied to generate the best fit to the reference curve using nonlinear least-squares regression (Levenberg, 1944; Marquardt, 1963). The residual sum-squared-error between the model and the data were then determined for each {F, K_I} pair. This error surface is represented in Fig. 2 C, with lighter shading corresponding to lower total error. No single combination of parameter values in this surface provides a best fit to the reference curve. Rather, a vast contour through the parameter space yields equally good fits to the synthetic data. The minimum error contour (lightest color in Fig. 2 C) extends infinitely in both directions of the parameter space, even as the total error approaches zero. The shape of this contour illustrates how the parameter values compensate systematically over wide ranges to fit the data. (Note that the true value of K_I [500 µM⁻¹] is far to the right of the plot shown at this scale.) An experimental scientist confronted with the error surface in Fig. 2 C would reach several discouraging conclusions: (a) finding a good fit of the cooperative model to typical binding data provides no guarantee that the inferred parameter values are close to the correct values; (b) the range of parameter values consistent with an exact fit to an experimental binding curve is infinite; and (c) more careful experimentation to reduce the noise in the data will not improve matters.

Situations in which fitting a model to data does not yield unique and optimal parameter estimates are well-documented in the control theory literature (Bellman and Astrom, 1970; Cobelli and DiStefano, 1980; Walter and Pronzato, 1997). The parameters of the model in Fig. 2 are not structurally identifiable: there is not enough constraining power, even in noiseless data, to enable a unique estimate of their true values. It is easy to imagine that correlations between the numerous parameters in complex models could yield non-unique fits to data. However, the results in Fig. 2 illustrate that interactions between the three parameters in a very simple model can be so effective that fitting of high quality data provides little meaningful constraint on the parameter values. How can we determine whether a model’s parameters are structurally identifiable when constrained by a measurement?

Rank-deficient regression

When the experimental observables of a system can be expressed analytically in terms of the model parameters, the data fitting problem can be cast in closed form, and simple methods can be used to test for parameter identifiability (Seber and Lee, 2003). Returning to the model of Fig. 2 A, we define a parameter vector with components a₁ = K_I, a₂ = K_II, and a₃ = FK_IK_II. If our observable signal (y) is the fraction of sites occupied by ligand at concentration x, then

$$y\left(x\right)=\frac{a_{1}x+a_{2}x+2a_3{x}^2}{2(1+a_{1}x+a_{2}x+a_3{x}^2)}.$$ (1)

If we can cast the observable as a linear system of the model parameters, then we can simply use linear regression for parameter inference. Multiplying both sides of Eq. 1 by the denominator of the right-hand side linearizes the parameters:

$$2y+2a_{1}xy+2a_{2}xy+2a_3{x}^{2}y=a_{1}x+a_{2}x+2a_3{x}^2.$$

We proceed to find a*, an optimal estimate of the parameters, by minimizing the error between the model and the data. For our cost function, S, we use the sum of the squared error between observations y_i and model predictions y(x_i):

$$S={\displaystyle \sum _i{\left(y_i-y\left(x_i\right)\right)}^2.}$$

Substituting in the expression for y(x_i) yields,

$$S={\displaystyle \sum _i{\left(a_1{x}_i\left(2y_i-1\right)+a_2{x}_i\left(2y_i-1\right)+2a_3{x_i}^2\left(y_i-1\right)+2y_i\right)}^2.}$$

The optimal estimate of the parameters is obtained by minimizing S. The partial derivatives of S with respect to the components of the parameter vector a are:

$$\frac{\partial S}{\partial a_1}={\displaystyle \sum _i\left(\begin{array}{l}{a}_1{x_i}^2{\left(2y_i-1\right)}^2+a_2{x_i}^2{\left(2y_i-1\right)}^2\\ +2a_3{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)+2x_i{y}_i\left(2y_i-1\right)\end{array}\right)}$$

$$\frac{\partial S}{\partial a_2}={\displaystyle \sum _i\left(\begin{array}{l}{a}_1{x_i}^2{\left(2y_i-1\right)}^2+a_2{x_i}^2{\left(2y_i-1\right)}^2\\ +2a_3{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)+2x_i{y}_i\left(2y_i-1\right)\end{array}\right)}$$

$$\frac{\partial S}{\partial a_3}={\displaystyle \sum _i\left(\begin{array}{l}2a_1{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)+2a_2{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)\\ +4a_3{x_i}^4{\left(y_i-1\right)}^2+4{x_i}^2{y}_i\left(y_i-1\right)\end{array}\right).}$$

Setting all of these derivatives to zero and rearranging yields a linear system in a:

$$\mathit{X}{a}^{*}=R,$$ (2)

where

$$R^T=\left\{{\displaystyle \sum _{i}2x_i{y}_i\left(1-2y_i\right),}{\displaystyle \sum _{i}2x_i{y}_i\left(1-2y_i\right),}{\displaystyle \sum _{i}4{x_i}^2{y}_i\left(1-y_i\right)}\right\}.$$

Here, R^T refers to the transpose of vector R. The design matrix, X, is given by

$$\mathit{X}=\left(\begin{array}{ccc}{\displaystyle \sum _i{x_i}^2{\left(2y_i-1\right)}^2}& {\displaystyle \sum _i{x_i}^2{\left(2y_i-1\right)}^2}& {\displaystyle \sum _{i}2{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)}\\ {\displaystyle \sum _i{x_i}^2{\left(2y_i-1\right)}^2}& {\displaystyle \sum _i{x_i}^2{\left(2y_i-1\right)}^2}& {\displaystyle \sum _{i}2{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)}\\ {\displaystyle \sum _{i}2{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)}& {\displaystyle \sum _{i}2{x_i}^3\left(2y_i-1\right)\left(y_i-1\right)}& {\displaystyle \sum _{i}4{x_i}^4{\left(y_i-1\right)}^2}\end{array}\right).$$ (3)

The solution of this linear system (Eq. 2) should yield a*, the optimal point estimate of the parameters given the data. However, the first and second columns of the design matrix (Eq. 3) are identical (and therefore linearly dependent). In general, the rank of a matrix is the number of linearly independent rows (or columns), and a matrix whose rank is less than the total number of rows or columns is called rank deficient. A rank-deficient matrix defines a linear system with an infinite number of solutions (Seber and Lee, 2003). In this example model, the design matrix is rank deficient, and therefore Eq. 2 specifies not a point estimate, but rather all combinations of the parameters that are optimal fits to the data. By indicating that a unique estimate of the model parameters is not possible, this test of the design matrix for rank deficiency is effectively a structural identifiability test. This method of assessing parameter identifiability is similar to other proposed methods that use sensitivity matrices or Fisher information (Cobelli and DiStefano, 1980), and can be generally applied to any model where the observable can be expressed as a linear system of the model parameters.

Two-site, two-parameter binding model: A case of practical non-identifiability

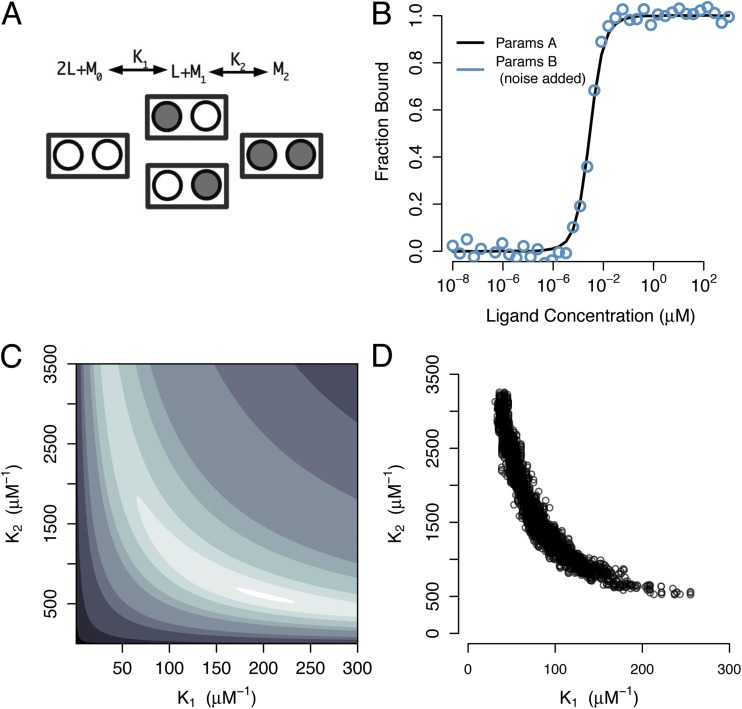
Demonstrating that a system’s design matrix is full-rank is a necessary, but not sufficient, condition for ensuring that the model’s parameters can be uniquely estimated from experimental data (Jacquez and Greif, 1985; Faller et al., 2003; Raue et al., 2009). Consider the model depicted in Fig. 3 A for a two-site receptor. This sequential binding model (which is a reduced version of the four-site model in Fig. 1 A) assumes that the two singly occupied binding configurations are equivalent, and has only two macroscopic affinity parameters, which quantify the first and second binding steps. It is straightforward to show that the design matrix for the model in Fig. 3 A is full-rank. Therefore, we might be tempted to conclude that the parameters of this model can be inferred uniquely from binding data.

Figure 3.

Parameter estimation for a two-site sequential binding model. (A) Diagram of model in which macroscopic binding constants K₁ and K₂ quantify the affinities of the first and second binding steps, respectively. M_i refers to receptor with i-bound ligands, and L refers to ligand. (B) Simulated binding curves for two different parameter sets. Parameter set A is consistent with weak cooperativity between the binding sites (K₁ = 200 µM⁻¹ and K₂ = 600 µM⁻¹). Parameter set B is consistent with strong binding cooperativity (K₁ = 75 µM⁻¹ and K₂ = 1,500 µM⁻¹). Gaussian noise was added to the curve for parameter set B to mimic experimental variability. Although these parameter sets (and their mechanistic interpretations) are quite different, they produce nearly identical observables. (C) Log-error surface in K₁–K₂ parameter space with respect to the noiseless data curve in B. For visualization, log-error values are contoured at levels {−8.5, −8, −5, −4, −3, −2.5, −1.5, −1, 0, 1, 2}. Although this error surface is bounded, large ranges of parameter values produce very similar binding curves. (D) MCMC samples of joint posterior distribution of the parameters when constrained by the noisy curve in B.

Fig. 3 B shows two simulated datasets that were calculated using the model in Fig. 3 A with distinct parameter values. For parameter set A, K₁ = 200 µM⁻¹ and K₂ = 600 µM⁻¹. For parameter set B, K₁ = 75 µM⁻¹ and K₂ = 1,500 µM⁻¹. To one of the curves (shown as circles), Gaussian noise of 2.5% variance has been added to mimic the variability of experimental data. Although the curves were generated from very different parameter values, they produce similar curves (apart from the added noise). The error surface (Fig. 3 C) was computed as the difference between a noiseless reference curve (the solid curve in B) and the model predictions for a large region of the parameter space of the model. The error contours are curved, and thus, as for the models in Figs. 1 and 2, parameter compensations can occur so that disparate parameter values yield the same error. However, unlike those in Fig. 2 C, the error contours in Fig. 3 C are bounded, with the lowest-error contours approaching perfect ellipses. Thus, for data with infinite signal-to-noise ratio (no added noise), the two-site, two-parameter sequential model is uniquely identifiable, and fitting of such data would yield accurate parameter estimates. However, the inevitable presence of experimental noise in real data (even at low levels of 2.5% variance) would prevent a unique determination of this model’s parameters. Previous authors have documented this phenomenon (Jacquez and Greif, 1985; Vajda et al., 1989; Raue et al., 2009) and distinguish between structural non-identifiability (as in Fig. 2), in which even noiseless data cannot yield unique parameter estimates, and practical non-identifiability (as in Fig. 3), in which a model’s parameters are identifiable only if data are available with sufficient signal-to-noise.

These examples demonstrate the dangers one incurs when only point estimates or best fits are considered. It is of vital importance to establish not only the best fit to the data but also the full range of parameters that yield good fits. The typical approach when fitting data to nonlinear models relies on maximum likelihood (ML) theory to estimate parameters (Cramer, 1946). The ML estimate (MLE) of a parameter is the point in parameter space that yields the optimum of the likelihood of observing the data given a particular value of the parameters. Asymptotically, the MLE is an efficient and unbiased estimate of a parameter. As an example, if the data are assumed to be normally distributed, then minimizing the sum-squared-error between model and data provides the MLE (Seber and Wild, 2003). Once an optimal point estimate is found, ML theory prescribes that confidence regions can be calculated by identifying the range of parameters that yield likelihoods consistent with the noise in the data (see Colquhoun et al., 2003, for a description of properties of ML estimators for common biophysical systems). For low dimensional models, a grid of the entire likelihood surface might be computed (as in Figs. 2 and 3 C), but this becomes infeasible for larger models (see Discussion). Because of this constraint, it is typically assumed that the likelihood surface is approximately quadratic around the MLE. Therefore, efficient algorithms can be used to identify the MLE and to numerically approximate the local curvature of the likelihood to construct a confidence ellipsoid around the MLE. In cases of non-identifiability, this elliptical approximation around the MLE can be quite inaccurate. Take, for example, the likelihood surface of the two-parameter binding model when constrained by the noiseless binding curve in Fig. 3 C (K₁ = 200 µM⁻¹ and K₂ = 600 µM⁻¹). The MLE would indeed be the true parameter values, and the lowest error contour surrounding this point would be well approximated by an ellipse (lightest color contour in Fig. 3 C). However, in the face of realistic experimental noise, our estimate of parameter confidence must take into account all parameter combinations that are consistent with any particular level of error. Such error contours are no longer elliptical but are curved (because of practical non-identifiability). If we use a quadratic likelihood approximation around the MLE in Fig. 3 C, we would vastly underestimate our parameter uncertainty. It might be the case that the likelihood surface near the MLE is relatively flat in the direction of one (or more) of the parameters, and this would suggest non-identifiability. However, we will be unable to distinguish between structural and practical non-identifiability without directly assessing all the regions of parameter space that yield high likelihood. Because exhaustive exploration of parameter space will not be feasible for most realistic models (see Discussion), we next describe a computationally efficient method of exploring parameter spaces.

Bayesian inference

The previous section demonstrated that in the face of realistic experimental noise, analysis of the design matrix does not provide a sufficient condition for establishing whether the parameters of a model are uniquely constrained by the available data. Therefore, a more general method is needed for determining whether the parameters of a model are both structurally and practically identifiable. In Figs. 2 C and 3 C, we explored the entirety of parameter spaces to identify which regions led to low error between model predictions and data. If the parameter values in best agreement with the data are confined to a small region of the parameter space, then the model parameters are identifiable. This approach moves us away from the idea of accepting a single best fit to the data, and instead identifies all regions of the parameter space that are in agreement with the observations. In the language of Bayesian inference, what we seek is called the posterior distribution of the parameters: a probability distribution on the parameter space that assigns higher probability to areas that are in better agreement with the observations. Here, we demonstrate that a Bayesian approach provides accurate estimates of model parameters and their uncertainty and provides a direct and general method of diagnosing parameter identifiability.

Assume that we have gathered N observations, y_N, to infer the “true” values of m parameters {θ₁,θ₂, …,θ_m}, comprising the vector θ. In Bayesian terms, we seek to know p(θ|y_N), the posterior probability distribution of the parameters, which is the probability (over the entire parameter space) of a particular value of θ having given rise to the observations y_N. To estimate this distribution, we apply Bayes’ rule,

$$p\left(\theta \hspace{0.17em}|\hspace{0.17em}{y}_N\right)\propto p\left(y_N\hspace{0.17em}|\hspace{0.17em}\theta \right)p\left(\theta \right),$$

which states that the posterior distribution of the parameters is proportional to the likelihood of observing the data, $p\left(y_N\hspace{0.17em}|\hspace{0.17em}\theta \right),$ multiplied by the prior distribution of the parameters, p(θ). If the observations y_i are independent, then the total posterior probability is the product of the posterior probability of each observation,

$$p\left(\theta \hspace{0.17em}|\hspace{0.17em}{y}_N\right)\propto {\displaystyle \prod _{i}p\left(y_i\hspace{0.17em}|\hspace{0.17em}\theta \right)}p\left(\theta \right).$$ (4)

For a particular model and some observed data, it is straightforward to compute p(θ|y_N). The structure of the posterior distribution indicates whether the region of highest posterior probability (the “best fits”) is localized or extends over a significant fraction of the parameter space, and is thus an indicator of parameter identifiability.

As with the direct calculation of error surfaces (Figs. 2 C and 3 C), computing posterior distributions over an entire parameter space by brute force is possible for low dimensional problems but quickly becomes infeasible for even modestly sized models. Fortunately, posterior distributions can be computed efficiently using an existing numerical method from the statistics literature called Markov chain Monte Carlo (MCMC) sampling. The theory of MCMC is described elsewhere (Tierney, 1994; Robert and Casella, 2010), and we provide only a brief description. Consider a high dimensional system for which the brute force computation of posterior probabilities over the entire parameter space is not practical. If we can draw a finite number of independent and identically distributed (iid) samples from the corresponding posterior distribution, then the properties of this finite sample will approximate the properties of the posterior. To generate these iid samples, we simulate a Markov chain whose limiting distribution is the posterior distribution of interest. Generating a Markov chain with a desired limiting distribution can be achieved by several methods. Here, we rely on one of the simplest: the Metropolis Random Walk algorithm (Metropolis et al., 1953). For iteration i of the algorithm, the Markov chain is in position θ_i in the parameter space. A potential transition to a new point, θ^* is generated by a random walk according to the following rules. The posterior probability of this potential point, p(θ^*|y_N), is computed and compared with the posterior probability of the current position of the chain, p(θ_i|y_N). If the proposal point has greater posterior probability than the current point, then it is accepted as a sample from the posterior distribution. If it has lower posterior probability, then it is rejected with probability proportional to the decrease in posterior probability. Thus, transitions of the Markov chain are accepted with probability α, where

$$\alpha =\text{min}\left(1,\frac{p\left({\theta }^{*}\hspace{0.17em}|\hspace{0.17em}{y}_N\right)}{p\left({\theta }_i\hspace{0.17em}|\hspace{0.17em}{y}_N\right)}\right).$$

This rule allows the chain to move efficiently toward areas of high posterior probability, but it also provides a mechanism to move away from local minima in the posterior distribution by allowing transitions to regions of lower posterior probability. The Markov chain produced by this algorithm explores the parameter space in proportion to the posterior probability and provides a finite number of iid samples from the posterior distribution. This method can be used to efficiently approximate posterior distributions of arbitrarily high dimension. The next section illustrates the use of MCMC to assess parameter identifiability for some common biophysical models.

Applications

A common form of parameter inference involves fitting a candidate model to observations drawn from a controlled experiment. Although the Bayesian framework presented here is general, we focus primarily on curve-fitting applications because of their prevalence in experimental science. We assume that each observation, y_i, is a function of some independent variables, x_i, and that the model of interest defines the function, f(x_i, θ), which depends on the model parameters, θ. We seek to identify the values of θ that lead to the best agreement between y_N and f(x_N, θ).

Our probability model considers that each observation y_i is the result of f(x_i, θ) plus some experimental noise, which is assumed to be normally distributed (although this assumption is not necessary). Each observation is drawn from a normal distribution $\mathcal{N}(m,{\sigma }^2)$, whose mean, m, is equal to the model prediction, f(x_i, θ), for some particular values of the parameters, and whose variance, σ², is caused by noise of any kind:

$$y_i\sim \mathcal{N}\left(f\left(x_i,\theta \right),{\sigma }^2\right).$$

The posterior probability distribution (Eq. 4) then becomes,

$$p\left(\theta |y_N\right)\propto {\displaystyle \prod _i\mathcal{N}\left(y_i\hspace{0.17em}|\hspace{0.17em}f\left(x_i,\theta \right),{\sigma }^2\right)}p\left(\theta \right).$$

In the following applications, the prior distribution, p(θ), is a flat distribution (a truncated uniform distribution). Although this form of the prior works well for the simulated datasets we use for illustration, it is in general an improper prior and more thoughtful prior distributions should be used in practice. By using MCMC, we generate a Markov chain that preferentially explores regions of the parameter space that lead to high posterior probability (i.e., the best fits to the data).

Binding models

We showed earlier, using algebraic techniques, that the three-parameter binding model of Fig. 2 A is not structurally identifiable. Consistent with this finding, the error surface (Fig. 2 C) revealed an unbounded zero-error contour through the parameter space of this model. MCMC samples from the joint posterior distribution of F and K_I (Fig. 2 D) show that this distribution is highly curved, indicating that a large range of values of these parameters is in good agreement with the data. The MCMC approach leads to the same conclusion as the error surface, but with a much improved computational efficiency and potential for scalability (see Discussion).

A thorough mapping of the error surface for the two-parameter model of Fig. 3 A, shown in Fig. 3 C, revealed that this model is not practically identifiable. Although unique “best-fit” parameters can be obtained in theory, this is not possible for data with a realistic signal-to-noise ratio. Consistent with this observation, the MCMC approximation to the posterior distribution for this model (Fig. 3 D) revealed that the two parameters of the model can compensate for one another to produce good fits to the data. In this case, the noisy data of Fig. 3 B is used to constrain the model parameters for MCMC. When faced with this level of noise in the data, parameters are able to compensate, as revealed by the curved structure of the posterior distribution. However, in contrast to situations of structural non-identifiability (for which it is impossible to constrain parameter estimates usefully), we would conclude that the true values of the parameter lie within a certain bounded region (by constructing a 95% credible interval), when constrained by this data: parameter K₁ is likely between 50 and 250 µM⁻¹, and parameter K₂ is likely between 500 and 3,500 µM⁻¹. Although this level of confidence is a considerable improvement over the situation of Fig. 2, these large uncertainties may still prevent us from achieving a useful level of mechanistic insight. For example, there are posterior samples corresponding to {K₁, K₂} = {50, 3,000} and {200, 600}, each of which is a valid explanation of the data. Therefore, although we can put reasonable bounds on parameter estimates, we may not be able to draw even qualitative conclusions regarding mechanism.

Kinetic models

Many chemical and biochemical systems can be described by kinetic models (such as in Figs. 4 A and 5 A) comprising systems of coupled differential equations. Typical experimental investigations of these systems involve monitoring the time course of the state populations in response to a perturbation to determine the transition rate constants. Numerous methods have been proposed to assess parameter identifiability in these so-called compartmental systems (Cobelli and DiStefano, 1980; Godfrey et al., 1982), including Laplace transforms (Walter and Pronzato, 1997) and information matrices (Bellman and Astrom, 1970). However, the practical non-identifiability of model parameters for many biological systems may not be detected by matrix methods (Raue et al., 2009). An alternative approach to assess identifiability involves computing low dimensional error surfaces in the relevant parameter space directly (Johnson et al., 2009a,b; Raue et al., 2009). Here, we use the more efficient Bayesian framework to determine whether candidate kinetic models are uniquely constrained by a given observable.

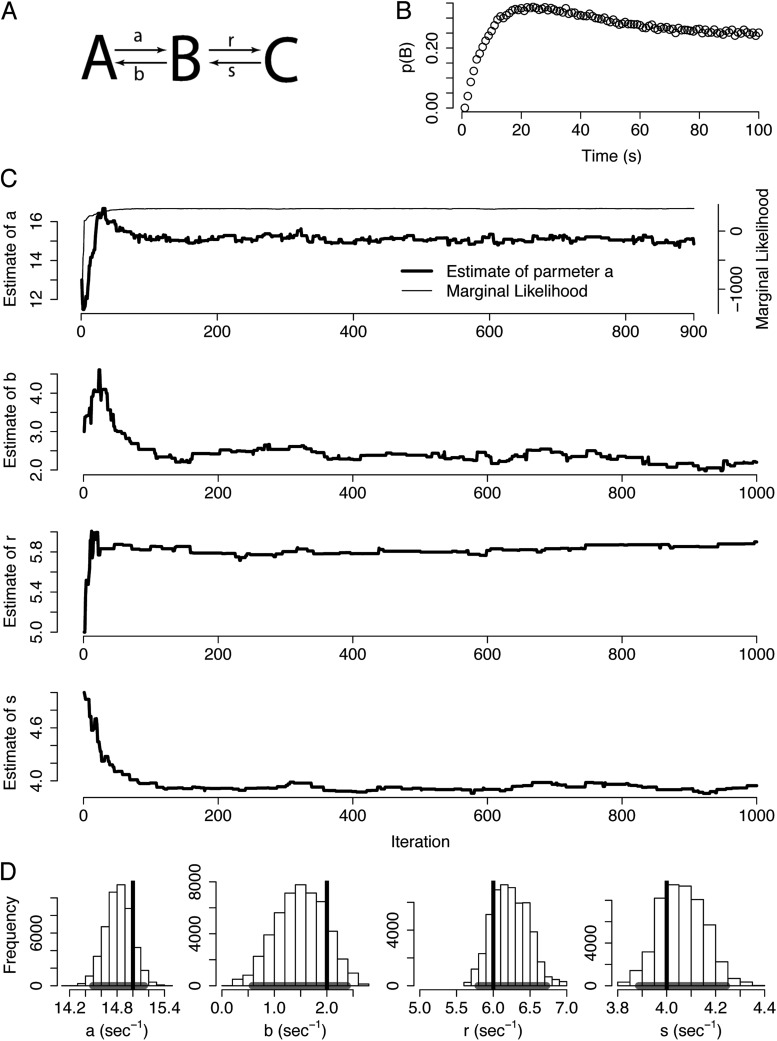
Figure 4.

Application of MCMC to dynamical systems. (A) A kinetic model with three states and four free parameters. (B) Time course of the population of state B. Curve was generated by solving the dynamical system in A with the parameters {a, b, r, s} = {15, 2, 6, 4} (values in s⁻¹). (C) MCMC results when inferring the parameter values from the data in B. Top panel shows one dimension of the Markov chain (corresponding to parameter a) throughout the course of the simulation (thick trace). Thin trace is the corresponding marginal likelihood, which quantifies the total goodness of fit between the model and the data. All movements of the chain after the marginal likelihood settles (∼100 iterations) generate iid samples from the posterior distribution. Lower traces are the corresponding trajectories for the remaining parameters. (D) Histograms of the marginal posterior distribution of each parameter shown along with the true values (vertical lines) and the corresponding 95% credible interval (horizontal line segment).

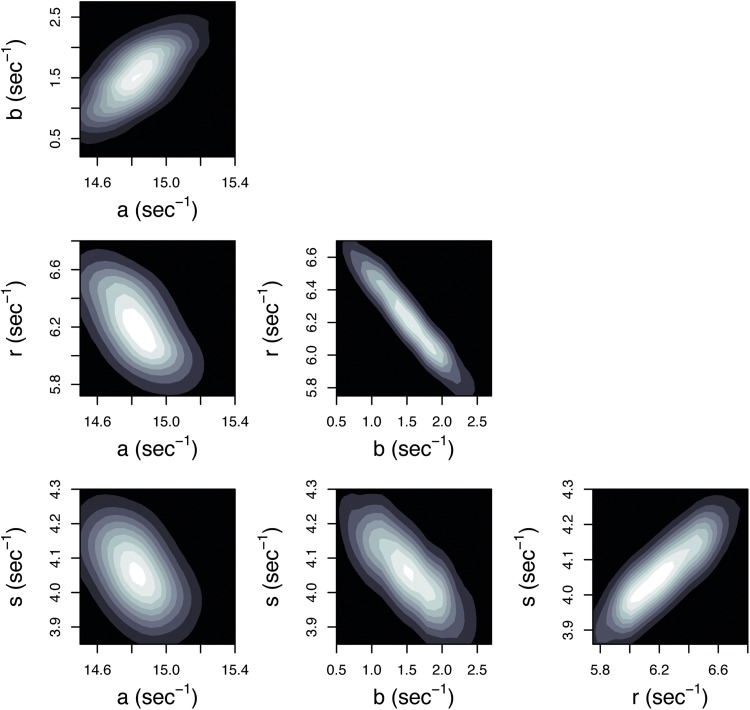
Figure 5.

MCMC can be used to assess parameter correlations. The MCMC trajectories from Fig. 4 C were used to visualize all the pairwise correlations between model parameters. The density of MCMC samples has been used to generate maps where areas of lighter shading correspond to higher posterior probability. In contrast to Figs. 2 and 3 D, the joint posterior distributions of these model parameters are approximately elliptical, indicating that the optimal estimates of the model parameters are contained in a small, bounded region of the parameter space.

The kinetic scheme of Fig. 4 A comprises three states connected sequentially. Suppose that our observable signal is the population of state B over time (Fig. 4 B) with additional Gaussian noise. The independent variable x_i represents time and the model prediction, f(x_i, θ), is the solution to the system of differential equations represented by the diagram in Fig. 4 A with the parameter set, θ. We use these observations to estimate the posterior distribution of the model parameters by generating 50,000 MCMC samples. The structure of the posterior distribution will indicate whether the four transition rates {a, b, r, s} are uniquely constrained by this observable.

At the top of Fig. 4 C, the trajectory of one dimension of the Markov chain is plotted (corresponding to parameter a). The thin trace represents the marginal likelihood throughout the course of the simulation. The marginal likelihood, which quantifies the total goodness of fit between the model and the data, starts at a low value because the simulation is initialized at an arbitrary point in parameter space that is likely a poor fit to the data. As the Markov chain evolves, the marginal likelihood improves and eventually plateaus after ∼100 iterations; this initial period is termed the “burn-in,” and these samples are discarded. After this convergence, the Markov chain has reached stationarity, and all subsequent transitions provide iid samples from the posterior distribution (see Discussion). The estimate of parameter a (thick trace) moves in large jumps initially but eventually settles near the true value of 15. The trajectories of each of the other parameters are also plotted for the first 1,000 iterations in Fig. 4 C. In each case, the chain explores a small region of the parameter space but does not stray far from the optimal estimate, especially after the Markov chain converges. Each of these transitions represents an iid sample from the posterior distribution and is a valid estimate of the parameter. Therefore, the transitions of the Markov chain, taken in aggregate, approximate the total uncertainty in each parameter (called the marginal posterior distributions). Fig. 4 D shows histograms of the estimate of each parameter (after the burn-in) as well as the true values (vertical lines). Such an approximation of the marginal posterior distributions can be used to derive credible intervals for each parameter. Although the peaks of the posterior distributions do not all coincide with the true parameter values, 95% credible intervals (horizontal line segments below the histograms) contain the true values.

Because MCMC samples are drawn from the total joint posterior distribution of the parameters, they can be used to assess any pairwise (or higher order, if desired) correlations between the parameters. Similar to Figs. 2 and 3 D, pairwise joint posterior distributions are shown in Fig. 5, using the same MCMC samples from Fig. 4 C. The density of samples is used to generate a map such that areas of lighter shading correspond to areas of higher posterior probability. In this way, the four-dimensional posterior distribution of this model is projected into each two-dimensional subspace. The ensemble of “good” fits to the data is confined to small regions of the parameter space that contain the true parameter values, and therefore the parameters of this model are identifiable.

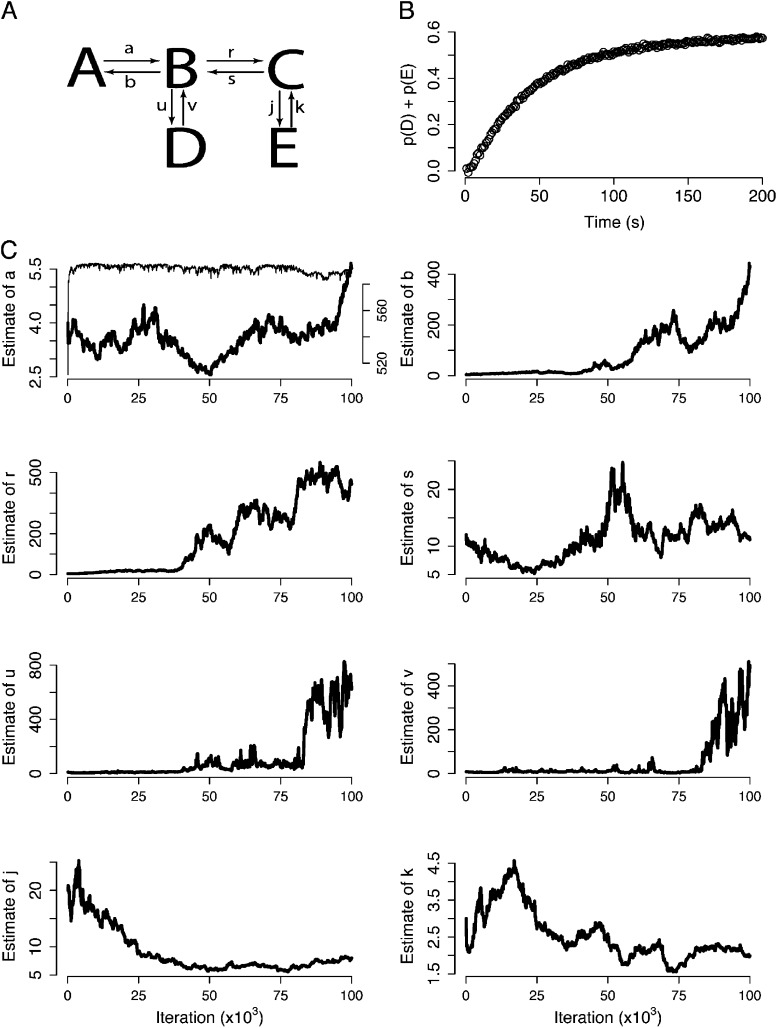
As a counter example, consider the more complex model of Fig. 6 A, which has five states and eight free parameters. In this case, assume that the observable is the combined populations of states D and E (Fig. 6 B) with additional Gaussian noise. The panels in Fig. 6 C show 100,000 samples from the resulting MCMC trajectories for each of the eight parameters. At top left, one dimension of the Markov chain (corresponding to parameter a) is shown along with the marginal likelihood (thin trace). The portions of the trajectories plotted in Fig. 6 C after the marginal likelihood settles represent excellent fits to the data. In nearly every case, a large range of values is sampled, all of which yield comparable marginal likelihood, meaning that they provide excellent fits to the data and can be considered valid estimates. This unbounded exploration of the parameters demonstrates that these parameters are not identifiable when constrained by this data.

Figure 6.

MCMC can detect non-identifiable models. (A) A five-state model with eight free parameters. (B) Time course of the combined populations of states D and E with parameters {a, b, r, s, u, v, j, k} = {3, 3, 5, 10, 9, 9, 20, 4} (values in s⁻¹). (C) Result of using MCMC to infer parameter values. At top left, the thick black trace is one dimension of the Markov chain (corresponding to parameter a) throughout the course of the simulation. The thin trace is the corresponding marginal likelihood. The MCMC trajectories of the other model parameters are also shown. Because the marginal likelihood stabilizes, but most of the parameter estimates do not, this model is not identifiable when constrained by this measurement.

DISCUSSION

Parameter identifiability and model selection

The work described here was motivated by the striking observation that typical binding data place very weak constraints on the magnitudes of affinity parameters for multisite receptors. We showed that many parameter sets, with affinity values varying by over four orders of magnitude for each of the steps in a sequential binding model for CaM, produced binding curves differing by <1% RMS (Fig. 1). Even if binding data could be obtained with this low noise level, the enormous uncertainties in the derived parameter estimates severely limit the usefulness of this data for developing a quantitative model for calcium activation of CaM. Parameter estimates are not unique even for simple two-site binding models comprising only two or three parameters (Figs. 2 and 3). Similar problems affect parameter estimation for dynamical models used to analyze biochemical kinetic data (Fig. 6).

When model parameters are not identifiable, one has little confidence that estimated values are close to the true values. For some model/data combinations, the data are fit arbitrarily well by many combinations of parameter values, and the uncertainties in the model parameter estimates are unbounded, even for noiseless data. These systems are structurally non-identifiable: the model contains more parameters than can be supported, even by perfect data (Bellman and Astrom, 1970; Cobelli and DiStefano, 1980; Walter and Pronzato, 1997). A structurally non-identifiable system is analogous to an underdetermined system of algebraic equations, which has an infinite number of solutions.

Structural non-identifiability of a model’s parameters can often be detected using algebraic methods, as in our demonstration that the design matrix for the two-site cooperative binding model in Fig. 2 is rank deficient. Identifiability analysis indicates that this model is over-parameterized: we are attempting to extract three model parameters (F, K_I, and K_II) from curve fitting, whereas the rank of the design matrix for this system, which specifies the maximum number of parameters that can be quantified by fitting ideal (i.e., noiseless) total binding data, is two. The parameterization of the cooperative model is designed to address two fundamental questions about a receptor with two binding sites: (1) are the site affinities unequal (i.e., is K_I ≠ K_II?), and (2) does binding at one site influence binding at the other site (i.e., is F ≠ 1?). Because it requires three parameters to quantify these properties, it is not possible to extract site affinities and cooperative interactions from this single type of experiment. Meaningful regression analysis of these data with this model requires a simpler parametrization than that in Eq. 1, such as

$$y\left(x\right)=\frac{b_{1}x+2b_2{x}^2}{2\left(1+b_{1}x+b_2{x}^2\right)}.$$ (5)

One could then make the simplifying assumption that the binding site affinities are equal and define the parameters as {b₁, b₂} = {2K, F*K²}, where K_I = K_II = K. Alternatively, one could assume that the sites do not interact cooperatively and define the parameters as {b₁, b₂} = {K_I + K_II, K_I*K_II}. If both of these options were deemed unsatisfactory, then other types of data would need to be recorded. A new round of structural identifiability analysis would then indicate whether three parameters could be extracted from fitting the enhanced dataset. This example illustrates how structural identifiability analysis can provide an upper limit on what can be learned about a system through experimentation.

It is necessary that the parameters of a model are structurally identifiable with respect to a given type of data for inference to even be possible. However, the uncertainties in the parameters estimated by regression analysis of such a system might still be unacceptably large. For these practically non-identifiable cases, the uncertainty in parameter values is linked to the amount of noise in the data, such that meaningful parameter estimates are obtained only if the noise amplitude is sufficiently small (Jacquez and Greif, 1985; Faller et al., 2003; Raue et al., 2009). Establishing that a system is practically non-identifiable is inherently subjective, because the acceptable parameter uncertainty must be weighed against the difficulty (or impossibility) of improving the signal-to-noise ratio of the data to a specified level. A useful approach, which we have followed here, is to determine by simulation the precision in parameter estimates that is required for gaining useful mechanistic insight into the system under study. If this precision requires data with a signal-to-noise ratio that is not achievable in practice, then the parameters are practically non-identifiable.

Using the algebraic approach described here, it is easily shown that the parameters of the four-site sequential model (Fig. 1 A) are structurally identifiable (i.e., the associated design matrix is full-rank). However, the simulations in Fig. 1 indicate that synthetic binding data with extremely low (1% RMS) noise are not sufficient to constrain the values of the affinity parameters K₁–K₄ to within less than four orders of magnitude. Thus, the four-site model parameters are practically non-identifiable when constrained by this type of data. The large parameter uncertainties prevent even qualitative insights about cooperative interactions in CaM.

For the examples in Figs. 1–6, we explored the uniqueness of parameter estimation by fitting an assumed model to data. However, in real-world experimental investigations, the “correct” model is usually not known. There are often several different competing schemes for describing a given biophysical phenomenon, and thus identifying a satisfactory model is an important aspect of the overall modeling process. Although there is no way to confirm a model structure definitively, unsuccessful models can be eliminated from consideration by their inability to fit the available data for any set of parameters. Because models and parameters are tested simultaneously, the MCMC method for diagnosing parameter non-identifiability may also be useful for model selection (Siekmann et al., 2012). When the available data lack the power to constrain one model’s parameters significantly, it is likely that many other models of comparable complexity will also easily fit that data. Therefore, diagnosing identifiability comes as a first step in the model selection process whereby potential models are discarded from consideration if they cannot be constrained by the data. Detecting when model parameters are not identifiable can indicate situations in which model selection is also compromised.

Relationship to previous work

The strong interrelationships between experimental design, model selection, and parameter estimation have been rediscovered in many fields, including econometrics (Koopmans, 1949; Rothenberg, 1971), process industries (Gustavsson, 1975;Chappell and Godfrey, 1992), systems and control engineering (Lee, 1964), and, more recently, systems biology (Audoly et al., 2001; Chis et al., 2011). These ideas have been rigorously systematized into a unified discipline called “system identification” (Eykhoff, 1974; Goodwin and Payne, 1977; Ljung, 1987; Walter and Pronzato, 1997). The parameter identifiability aspect of system identification has been explored extensively in the control theory literature (Bellman and Astrom, 1970; Grewal and Glover, 1976; Cobelli and DiStefano, 1980). Recently, there has been a surge of interest in questions of parameter identifiability for models of large biological systems, such as genetic, metabolic, biochemical, and ecological networks, and signal transduction, cell cycle, and pharmacodynamic pathways (Audoly et al., 2001; Hengl et al., 2007; Chis et al., 2011; Cheung et al., 2013). For these complex interconnected systems, the parameter compensations that result in non-identifiability are possible because of the large number of parameters required to model them.

There is a large body of literature on fitting binding curves of single- and multisite receptors using models such as the Hill model and the Adair model (Hill, 1913; Adair, 1925; Klotz, 1997; Wyman and Gill, 1990; Forsén and Linse, 1995) However, there has been relatively little treatment of identifiability for simple biochemical systems (Kienker, 1989; Bruno et al., 2005; Johnson et al., 2009a; Raue et al., 2009; Hines, 2013). We show here that the parameters of even extremely simple models are often not identifiable, suggesting that this problem may be more widespread than is generally appreciated. Parameter non-identifiability in biochemical systems was investigated by J.G. Reich and colleagues in the 1970s (Reich, 1974; Reich and Zinke, 1974; Reich et al., 1974a,b). In this work, the authors address difficulties when analyzing ligand binding data as well as kinetic data. They proposed methods of calculating parameter sensitivity to detect redundant parameters (non-identifiability) and used these methods to compare various binding models (such as those shown in Fig. 1) to quantify the information content in a binding curve. Their work predates modern computing power and the widespread use of efficient sampling algorithms such as MCMC.

Although we have focused on curve-fitting applications, the MCMC method can be applied to any model for which posterior probabilities can be calculated. For example, stochastic process models are commonly used for modeling the dynamics of molecules. Markov models and hidden Markov models have been used to understand the conformational dynamics of ion channels (Qin et al., 1997), molecular motors (Müllner et al., 2010), and ligand-binding proteins (Stigler and Rief, 2012). In these settings, the stochastic properties of single molecule time series are used to constrain model parameters (transition rates between states). The model parameters are estimated by maximizing the likelihood of the data (or the posterior probability). Commonly, a point estimate of the parameters of a candidate model is calculated (Rabiner, 1989), but such an approach does not indicate whether these parameters are uniquely constrained by a particular time series. In contrast, MCMC samples the full posterior distributions and thus provides an indication of non-identifiability. This approach has been applied to the study of ion channel gating (Siekmann et al., 2012) and may become a powerful method for developing useful models of molecular processes.

Computational advantages of MCMC

The Bayesian framework presented here has clear advantages over alternative methods of diagnosing parameter identifiability. One approach might be to examine the sensitivity of the fit to changes in the parameters, using a variety of matrix-based methods. We showed that this approach can only be applied in special cases and can even misleadingly suggest reasonable parameter estimates in the presence of realistic experimental noise. It is necessary to directly explore the full range of the parameter space that leads to good agreement with the data. Therefore, an alternative approach might be to directly compute the error between the data and model for an entire parameter space. This approach works well for simple problems but is not feasible for large models. For a K-dimensional model, computation of N points for each parameter requires $\mathcal{O}\left(N^K\right)$ error calculations (here the notation $\mathcal{O}\left(f\left(N,K\right)\right)$ specifies that as a function of N and K, the number of computations is on the order of f(N, K)). Obviously, this exponential explosion makes larger models impractical. An alternative is to consider just the pairwise parameter correlations for all model parameters and compute the total error. This approach was taken in Figs. 2 C and 3 C and has been used previously (Johnson et al., 2009a,b). This method is limited, as errors are calculated on a large joint-error-surface, and therefore computational effort is wasted in regions of parameter space that yield poor fits to the data. In addition, each total-error computation involves finding the best-fit point of the other parameters and thus entails $\mathcal{O}\left(N^2{K}^2\right)$ repetitions of some optimization algorithm, which itself might involve many iterations to reach convergence. In contrast, MCMC focuses computational effort in the region of parameter space that is relevant to the data. Further, posterior estimation requires only $\mathcal{O}\left(NK\right)$ repetitions of a simple calculation of posterior probability. Such Bayesian methods have recently been embraced by the systems biology community, where inference is routinely conducted on models containing >70 free parameters (Battogtokh et al., 2002; Klinke, 2009; Eydgahi et al., 2013). Using MCMC to sample posterior distributions yields not only accurate parameter estimates in high dimensional spaces but also provides information regarding identifiability and nonlinear parameter correlations. Our MCMC implementations use the Metropolis–Hastings algorithm, which is conceptually simple but not optimal for high dimensional problems. Fortunately, more sophisticated MCMC algorithms have been developed (Neal, 2010; Girolami and Calderhead, 2011).

We briefly mention some of the practical considerations that must be noted when using MCMC to estimate posterior distributions. Fig. 4 C shows the parameter trajectories of MCMC samples from an identifiable model. Each of the parameters is initialized at an arbitrary value, and these trajectories visualize how parameter estimates move toward regions of high posterior probability. Once these large movements of the parameters cease, the chain makes transitions only in proportion to the posterior probability, and the Markov chain is said to have reached stationarity (or converged). After convergence, all subsequent transitions of the chain produce iid samples from the posterior and can be used for parameter estimation. The iterations preceding convergence are termed the “burn-in period,” and these values are discarded. The MCMC samples visualized in Figs. 2 D and 3 D, the histograms of Fig. 4, and in Fig. 5 have excluded the burn-in samples. It is important to determine when the Markov chain has reached stationarity, and many methods can be used. Most simply, one could assess convergence by visual inspection: the trajectories in Fig. 4 C seem to have converged by 200 iterations. More rigorous methods are desirable, and many have been developed; we point the reader to Gelman and Rubin (1992) and Geweke (1992). We also direct the reader to Gilks et al. (1996a) for a discussion of chain mixing efficiency and the effect on burn-in time. For nonspecialists and those interested in implementing MCMC sampling, there are two excellent introductory handbooks by Brooks et al. (2011) and Gilks et al. (1996b) that provide practical advice and guidance, and include numerous case studies of MCMC applied in diverse fields such as epidemiology, genetics, archeology, ecology, and image analysis.

Parameter identifiability and experimental design

The tools described here for diagnosing parameter identifiability can be a useful component of the experimental design process. Figs. 4 and 6 present potential signals that might be used to constrain different kinetic schemes. Although previous work has addressed model discrimination with macroscopic kinetic time series (Celentano and Hawkes, 2004), a Bayesian approach provides a direct assessment of identifiability. By sampling the posterior distribution using MCMC, we showed that the model with four parameters (Fig. 4) is uniquely constrained by the data. Conversely, the model with eight parameters (Fig. 6) is non-identifiable when constrained by the data, and inferences about the properties of this model would be meaningless. In the latter case, we may reject the initial model in favor of one with fewer parameters, although the parameters of the simpler model may lack the required mechanistic significance. Alternatively, if this model is motivated by specific phenomenological considerations, then we may be resistant to reject it. To derive meaningful mechanistic conclusions from this system, we must then redirect our experimental efforts in one of three ways: (1) by performing the same experiment, but collecting data with sufficiently higher signal-to-noise ratio (in the case of practical non-identifiability); (2) by collecting other types of data using existing approaches; or (3) by devising novel experiments that generate observable signals with greater constraining power.

Many examples exist to illustrate the power that new types of data bring to our ability to quantitatively model biophysical phenomena. For example, it is particularly difficult to differentiate binding events from conformational changes in ligand-gated ion channels when only macroscopic ionic current measurements are available (Colquhoun, 1998). Recently, Benndorf’s group has pioneered an approach in which channel opening is measured electrophysiologically, while ligand-binding events are detected simultaneously by fluorescence methods (Kusch et al., 2012). A second example is the role that single-channel recording has had on the development of mechanistic models of ion channel gating. For example, we demonstrated that the parameters of the model in Fig. 6 are non-identifiable when constrained by macroscopic current relaxations. However, single-channel recordings can be used to constrain models of this complexity (Colquhoun and Sakmann, 1985; Sakmann and Neher, 1995). Another example is the transformative role of gating current measurements in elucidating mechanisms in voltage-gated ion channels (Armstrong and Bezanilla, 1973; Keynes and Rojas, 1974). Complementing ionic current measurements with gating currents can reveal parts of a model’s state space that are difficult to distinguish with ionic currents alone. The constraining power of the additional data reduces compensation in the model parameters and results in an identifiable model. Returning to the problem of calcium binding to CaM, we showed that the parameters of the four-site sequential model (Fig. 1 A) are not identifiable when constrained by measurements of the net occupancy of CaM’s four metal binding sites. Our analysis indicates that enormous parameter uncertainties will result from fitting typical binding data, even data with noise that is lower than is practically achievable. However, this barrier may be overcome by performing experiments that quantify the site-specific occupancy of the four binding sites in CaM as a function of calcium concentration (Di Cera, 1995). Our results indicate that, given the frequent occurrence of non-unique parameter estimation, analyzing parameter identifiability should become a standard component of the experimental design process.