Life tables adjusted for comorbidity more accurately estimate noncancer survival for recently diagnosed cancer patients

Abstract

Objective

To provide cancer patients and clinicians with more accurate estimates of a patient’s life expectancy with respect to non-cancer mortality, we estimated comorbidity-adjusted life tables and health-adjusted age.

Study Design and Setting

Using data from the SEER-Medicare database, we estimated comorbidity scores that reflect the health status of people 66 years of age and older in the year prior to cancer diagnosis. Non-cancer survival by comorbidity score was estimated for each age, race and sex. Health-adjusted age was estimated by systematically comparing the non-cancer survival models with US life tables.

Results

Comorbidity, cancer status, sex and race are all important predictors of non-cancer survival; however, their relative impact on non-cancer survival decreases as age increases. Survival models by comorbidity better predicted non-cancer survival than the US life tables. The health-adjusted age and national life tables can be consulted to provide an approximate estimate of a person’s life expectancy, e.g., the health-adjusted age of a black man aged 75 with no comorbidities is 67, giving him a life expectancy of 13 years.

Conclusions

The health-adjusted age and the life tables adjusted by age, race, sex and comorbidity, can provide important information to facilitate decision-making about treatment for cancer and other conditions.

Introduction

Accurate and reliable survival estimates are of great importance to newly diagnosed cancer patients and the physicians treating them. Patients and physicians must balance the benefits of cancer therapy with its potential toxicity and other adverse effects as well as with the patient’s life expectancy and health status. Furthermore, advances in early diagnosis and screening have increased the proportion of cancer patients diagnosed with early stage diseases (1). Accurately predicting life expectancy for these patients is important because they may be at a higher risk of dying of other causes than of their cancer; this is especially true for older patients. For some patients, therapy may represent overtreatment, unnecessarily adding to treatment costs, complications, side effects, early and late morbidities and treatment-related mortality. Overtreatment is considered to occur when patients die of non-cancer causes prior to dying of cancer.

Estimating an individual’s life expectancy is notoriously difficult, and subjective predictions tend to be inaccurate and overly optimistic (2–5). General US life tables (6) have limited ability to predict life expectancy for cancer patients (7). Tools have been developed to calculate life expectancy adjusted for health status; however, most of these are specific to a cancer site, stage or particular treatment and are not derived from population-based data (7–14). Better prediction tools are needed to more precisely estimate the risk of death due to other health-related conditions (15).

For people diagnosed with cancer, two competing causes of death can determine survival: cancer and non-cancer (other cause). A patient’s cancer prognosis is usually estimated using relative survival (16) or cancer-specific survival. Both represent net survival measures in a hypothetical world in which cancer is the only cause of death. In this study, we estimate the counterpart of net cancer survival, i.e., the net non-cancer survival representing the probability of surviving non-cancer causes of death in the absence of a cancer death. Thus, the non-cancer survival models developed in this study represent the chance of dying of other causes of death, eliminating cancer as a cause of death and taking into account the patient’s comorbidity in the year prior to cancer diagnosis. This type of information may be useful for weighing the potential benefits against the potential adverse effects of cancer therapy to help in treatment decision-making.

The objective of the current study was to use population-based data to provide improved estimates of non-cancer survival for patients recently diagnosed with cancer, taking into account their chronological age, sex, race and comorbidity score prior to their diagnosis. Comparing these non-cancer survival estimates with US life tables by age provided the basis for calculating the health-adjusted age of an individual with a specific comorbidity profile. Health-adjusted age represents the age of an average person in the US with the same life expectancy as the cancer patient based on the patient’s chronological age and comorbidity profile. For example, a healthy, 75-year-old person with no comorbidity is likely to have a better life expectancy than that given by the corresponding US life table, which was calculated using the entire 75-year-old US population and includes healthy people as well as people with comorbidities. The non-cancer survival by comorbidity and health-adjusted age provides a more precise estimate of the risk of dying of non-cancer causes.

Crude probabilities of dying of cancer, dying of other causes and survival, calculated taking into account the risks of dying of all causes (competing risks) (17), provide a more complete picture of a patient’s prognosis. However, some patients may not want to learn about their overall chances of survival. Instead, they may prefer to know their life expectancy with respect to other causes of death, independent of their cancer diagnosis. In addition, the net non-cancer survival can be integrated with net cancer survival under the assumption of independence to provide crude probabilities of death (18, 19). In fact, the non-cancer survival developed in this study will be integrated with cancer prognosis for colorectal and prostate cancers using the competing risk framework in the Cancer Survival Query System (CSQS)(19). The independent modeling of cancer and non-cancer survival methods allows for estimation using the best data sources and covariates for each component (18).

Methods

Methods Overview

A three-step approach was used to develop non-cancer life tables by comorbidity score and to calculate health-adjusted age. We will use the terms “non-cancer survival” and “non-cancer life tables” interchangeably. We first identified comorbid conditions that existed in the year prior to the cancer diagnosis, and calculated a comorbidity score (20, 21). Next, we estimated non-cancer survival based on specific comorbidity profiles and single ages from 66 to 94 years. In the last step, we estimated health-adjusted age by matching the non-cancer survival estimates for each age, comorbidity profile and race with the corresponding US life table.

Data Sources

The comorbidity score was estimated using Surveillance Epidemiology and End Results (SEER) program data on cancer patients linked to Medicare claims, which represents 14% of the US population (22). Data from a 5% sample of Medicare beneficiaries residing in the SEER areas who do not have cancer were added to the SEER-Medicare cancer data to improve precision and to provide sufficient data at each age group for estimation of age-specific non-cancer life tables. More information on the linked SEER-Medicare data and the 5% non-cancer sample is available at http://healthservices.cancer.gov/seermedicare/. Medicare claims are available for cancer and non-cancer individuals in the same format. Only individuals that were not in health maintenance organizations (HMO) and were continuously enrolled in both Parts A and B of Medicare between 1992 and 2005 were included. Comorbid conditions were identified using Part A hospitalization, Part B physician/supplier, and outpatient facility claims.

Cancer patient cohort

The cancer patient cohort consisted of 1,108,085 patients who were diagnosed with cancer between 1992 and 2005 in the SEER-11 areas. To ensure that comorbid conditions in the year prior to diagnosis could be identified, only data from Medicare beneficiaries 66 years of age or older were included in the data analysis. Patients whose cancer was diagnosed by death certificate or autopsy were excluded from data analysis.

Estimating the comorbidity score

Claims during the 12-month period before cancer diagnosis were used to detect incidences of 16 comorbid conditions that had been previously identified by Charlson et al. (23) and used in other scores (20, 21). These comorbid conditions include: acute myocardial infarction, AIDS, cerebrovascular disease, chronic renal failure, congestive heart failure (CHF), chronic obstructive pulmonary disease (COPD), dementia, diabetes, moderate/severe liver disease, history of myocardial infarction, paralysis, rheumatologic disease, ulcer disease, cirrhosis and/or chronic hepatitis and vascular disease. Diabetes (ICD-9: 250) and diabetes with sequelae (ICD-9: 5712, 5714, 5715, and 5716) were grouped together. We did not capture the diagnostic codes corresponding to solid tumors and lymphoma/leukemia because we were specifically studying non-cancer comorbidity and non-cancer mortality in cancer patients. Conditions that were reported during the month of diagnosis were excluded to avoid misclassifying complications potentially related to cancer as comorbid conditions. Consistent with prior work (20, 21), a rule-out algorithm was used so that only conditions appearing on more than one physician claim were included, thereby ensuring diagnoses recorded only in Part B claims were not transient episodes.

Condition indicators were created to reflect whether the patient received care for a comorbid condition from either an inpatient hospital or outpatient setting. We used a Cox proportional hazards model to estimate the effects of comorbid conditions on non-cancer death. The dependent variable in the model was time from diagnosis to death due to non-cancer causes, and censoring events included loss to follow-up, end of study (12/31/2005) or cancer death. Age, sex and race were included as additional variables in the model to control for their independent effects on non-cancer death. Interactions with the most prevalent conditions, diabetes, COPD and CHF, were included in the model. The final model included interactions and terms that were significant at the 0.001 confidence level. Each patient received a comorbidity score calculated as the sum of the coefficient estimated from the Cox model multiplied by their condition indicators.

Combined study cohort: cancer patient cohort and the non-cancer sample

For each individual in the non-cancer sample of SEER residents, comorbid conditions were identified in the year prior to each birthday occurring between 1992 and 2005 using the same algorithm as for the cancer cohort. Individuals from the non-cancer sample were utilized multiple times, but only once in the calculation of an age-specific non-cancer life table. For example, an individual who turned age 66 on 7/15/1998 and died at age 70 on 3/28/2003 would be included in 5 survival model calculations (from age 66 to 70), using a comorbidity score based on the comorbid conditions present in the year before each birthday. The non-cancer sample has 3,099,833 records and contains multiple records per individual.

Estimating life tables by comorbidity score

Comorbidity scores, as previously described, were calculated as the sum of the coefficient estimated from the Cox model multiplied by their condition indicators for individuals with and without cancer from the combined data set. The Cox proportional hazard method was used to estimate 58 non-cancer age-conditional life tables, one for each sex and index age (66 through 94) combination. Comorbidity score, race (white, black and other) and cancer status (Yes/No) were modeled as covariates. For the non-cancer sample, each individual contributes once to the model and his or her survival time was the index age to either age at all causes of death (cancer death cannot occur) or age at one of the following censoring events: loss to follow-up or end of study date (12/31/2005). For cancer patients, survival time was age at cancer diagnosis (which corresponds to the index age) to either age at non-cancer death or age at one of the following censoring events: loss to follow-up, end of study date (12/31/2005) or cancer death. The comorbidity score was entered in the model as a restricted cubic spline function linear at the tails (24). The inclusion of the comorbidity score as a spline function allows for more flexibility and does not assume linearity, i.e., that each increment in comorbidity incurs the same increment in risk of non-cancer death. For more details, see the Appendix. The proportional hazards assumption was tested by analyzing scaled Schoenfeld residuals (25).

Estimating the health-adjusted age

Decennial US 2000 life tables (6) are available by sex (male, female) and race (white and black, but not other races) from the National Center for Health Statistics (NCHS). The decennial US 2000 life table for other races was estimated using mortality data from NCHS and can be obtained from the SEER*Stat software (http://seer.cancer.gov/Seerstat).

The health-adjusted age was calculated by searching the US life table that provides the closest survival experience to the estimated non-cancer life table for the specific chronological age, sex, race (white, blacks and other races) and comorbidity score. For each survival model given by a fixed age, sex, race and comorbidity score (which ranges from 0.0 to 3.0 in 0.001 increments), we calculated distance to the US 2000 life table using several different ages, but the same sex and race. Distance was calculated as the absolute difference between the two survival curves, and the US life table age that minimizes this distance represents the health-adjusted age for a person with the same sex, race and comorbidity score. For more details, see Appendix.

Model validation

To assess the discrimination ability of the model, the area under the receiver operating characteristic curve (AUC) was constructed as a function of follow-up time based on methods used by Heagerty et al., 2005 (26). The AUCs were plotted as a function of time to characterize the ability of our model to discriminate between those observed to die of non-cancer death (cases) and those observed to survive non-cancer death (controls).

To evaluate potential bias in the predictions, we calculated observed and estimated non-cancer survival (calibration plots) for the following subsets of cancer patients: men and women diagnosed at age 66 with no comorbidity, and with comorbidity scores between 0.5 and 1.0. Estimated survival probabilities were calculated by averaging the covariates and then estimating survival, similar to conditional marginal survival probabilities. Observed survival probabilities were calculated using Kaplan-Meier estimates. To evaluate the benefit of using our modeled life tables by comorbidity compared to US life tables, we also calculated the averaged survival probabilities obtained from the US life tables for the selected cohorts. Calibration plots are shown in the appendix.

Results

Demographics and prevalence of individual comorbid conditions

Cancer patients and the non-cancer sample had similar distributions with respect to age and race (Table 1). However, compared to the non-cancer sample, cancer patients were more likely to be men (53% vs. 37%) and to have more comorbid conditions (40% vs. 31.4%). For both cancer patients and the non-cancer sample, the most prevalent comorbid conditions were diabetes (15.9% cancer patients vs. 13.6% non-cancer sample), COPD (15.3% vs. 9.0%), congestive heart failure (9.6% vs. 6.7%) and cerebrovascular disease (5.9% vs. 5.2%).

Table 1.

Data characteristics. For cancer patients, comorbidities were identified in the year prior to the cancer diagnosis; for the cancer-free Medicare beneficiaries in the SEER areas, comorbidities were identified before each birthday. Denominators for the cancer patients represents people, while denominators for the non-cancer sample include all records (birthdays) per person (SEER-Medicare 1992–2005).

	Cancer		Non-cancer sample
	Patients		Multiple records
Age	No.	%	No.	%
66–69	211,849	19	673,786	22
70–74	293,324	26	821,570	27
75–79	269,384	24	689,356	22
80–84	188,485	17	486,045	16
85–89	99,993	9	273,705	9
90+	45,050	4	155,371	5
Sex
Females	524,625	47	1,966,271	63
Males	583,460	53	1,133,562	37
Race
White	978,633	88	2,713,051	88
Black	79,921	7	223,353	7
Other	49,531	4	163,429	5
Life Status
Alive	897,368	81	2,249,854	73
Dead	210,717	19	849,979	27
Comorbidity
Diabetes	176,308	15.9	421,279	13.6
COPD	169,780	15.3	277,638	9.0
Congestive heart failure	106,067	9.6	207,307	6.7
Cerebrovascular disease	65,711	5.9	159,874	5.2
Vascular Disease	47,195	4.3	101,248	3.3
Chronic renal failure	22,952	2.1	43,948	1.4
Rheumathologic disease	22,606	2.0	59,259	1.9
History myocardial infarction	22,270	2.0	44,584	1.4
Ulcer disease	20,218	1.8	37,923	1.2
Dementia	16,305	1.5	60,806	2.0
Acute myocardial Infarction	14,466	1.3	30,653	1.0
Paralysis	8,000	0.7	19,456	0.6
Cirrhosis, chronic hepatitis	6,430	0.6	7,475	0.2
Mod./severe liver disease	2,171	0.2	2,407	0.1
AIDS	279	0.0	430	0.0
No Comorbidity	665,135	60.0	2,125,944	68.6
Only 1 comorbidity	278,749	25.2	649,227	20.9
2 or more	164201	14.8	324,662	10.5
Total	1,108,085	100	3,099,833	100

Comorbidity score

Cancer patients who were diagnosed with CHF, chronic renal failure, cirrhosis and/or chronic diabetes, dementia and COPD prior to their cancer diagnosis had the highest risk of dying of non-cancer causes, the risk being 2 to 2.5 times higher compared to people with no comorbidities (Table 2). Being black, older and male increased the risk of non-cancer mortality, while being neither black nor white (other races) decreased the risk of non-cancer mortality. People diagnosed with CHF, chronic renal failure, cirrhosis and/or chronic diabetes, dementia and COPD have the highest comorbidity score, i.e. between 0.7 and 0.9. People with 2 or more conditions tended to have comorbidity scores that exceeded 0.9 (Table 2).

Table 2.

Results of the Cox proportional hazard me thod on 13 years non-cancer survival for cancer patients diagnosed between 1992 and 2005 (SEER-Medicare 1992–2005). Conditions are listed by increasing comorbidity score. The shaded areas corresponds to comorbidity score being <0.4, 0.4 to <0.6, 0.6 to <0.8, 0.8 to <1.0 and >=1.0.

	Variables		Hazard Ratio	Comorbidity Score	Coefficient	Std. Err.	p-value
	Age		1.09		0.088	0.0003	<0.0001
Sex	Female	-			Ref.	-	-
	Male		1.25		0.224	0.0045	<0.0001
Race	White		-		Ref.	-	-
	Black		1.16		0.151	0.0083	<0.0001
	Other		0.91		−0.090	0.0113	<0.0001
Conditions		No comorbidity	-	0.00	Ref.	-	-
		History MI	1.08	0.08	0.079	0.0135	<0.0001
		Acute MI	1.17	0.15	0.155	0.0173	<0.0001
		Ulcer	1.18	0.17	0.168	0.0153	<0.0001
	Rheumathologic disease		1.45	0.37	0.369	0.0189	<0.0001
		Paralysis	1.49	0.40	0.399	0.0199	<0.0001
		Vascular	1.53	0.42	0.424	0.0127	<0.0001
		Diabetes	1.59	0.47	0.466	0.0072	<0.0001
		AIDS	1.68	0.52	0.516	0.1544	0.0008
		CVD	1.70	0.53	0.532	0.0110	<0.0001
	Mod./severe liver disease		1.94	0.66	0.662	0.0426	<0.0001
		COPD	2.03	0.71	0.707	0.0073	<0.0001
		Dementia	2.08	0.73	0.731	0.0133	<0.0001
	Cirrhosis, chronic hepatitis		2.43	0.89	0.889	0.0263	<0.0001
	Chronic renal failure		2.46	0.90	0.900	0.0172	<0.0001
		CHF	2.49	0.91	0.913	0.0091	<0.0001
		Interactions	Hazard Ratio*	Comorbidity score	Interaction Coefficient	Std. Err.	p-value
		Diabetes & Rheum.	1.93	0.66	−0.176	0.0361	<0.0001
		CHF & Ulcer	2.43	0.89	−0.178	0.0302	<0.0001
		Diabetes & CVD	2.53	0.93	−0.071	0.0171	<0.0001
		COPD & Diabetes	2.56	0.94	−0.233	0.0141	<0.0001
		COPD & Rheum.	2.62	0.96	−0.114	0.0336	0.0007
		COPD & CVD	2.71	1.00	−0.241	0.0179	<0.0001
		COPD & Vascular	2.88	1.06	−0.072	0.0196	0.0002
		CHF & Rheum.	3.12	1.14	−0.146	0.0351	<0.0001
		CHF & Vascular	3.13	1.14	−0.195	0.0199	<0.0001
		CHF & CVD	3.16	1.15	−0.296	0.0176	<0.0001
		CHF & Diabetes	3.71	1.31	−0.068	0.0134	<0.0001
		COPD & Renal	4.13	1.42	−0.190	0.0256	<0.0001
		CHF & COPD	4.23	1.44	−0.179	0.0129	<0.0001
		CHF & Renal	5.06	1.62	−0.192	0.0237	<0.0001

^†Myocardial infarction (MI), cerebrovascular disease (CVD), congestive heart failure (CHF), chronic obstructive pulmonary disease (COPD).

^*Hazard ratio calculated using main effect and interaction coefficients, e.g. HR(COPD & CVD)=exp(COPD +CVD+COPD*CVD)

Non-cancer survival by comorbidity

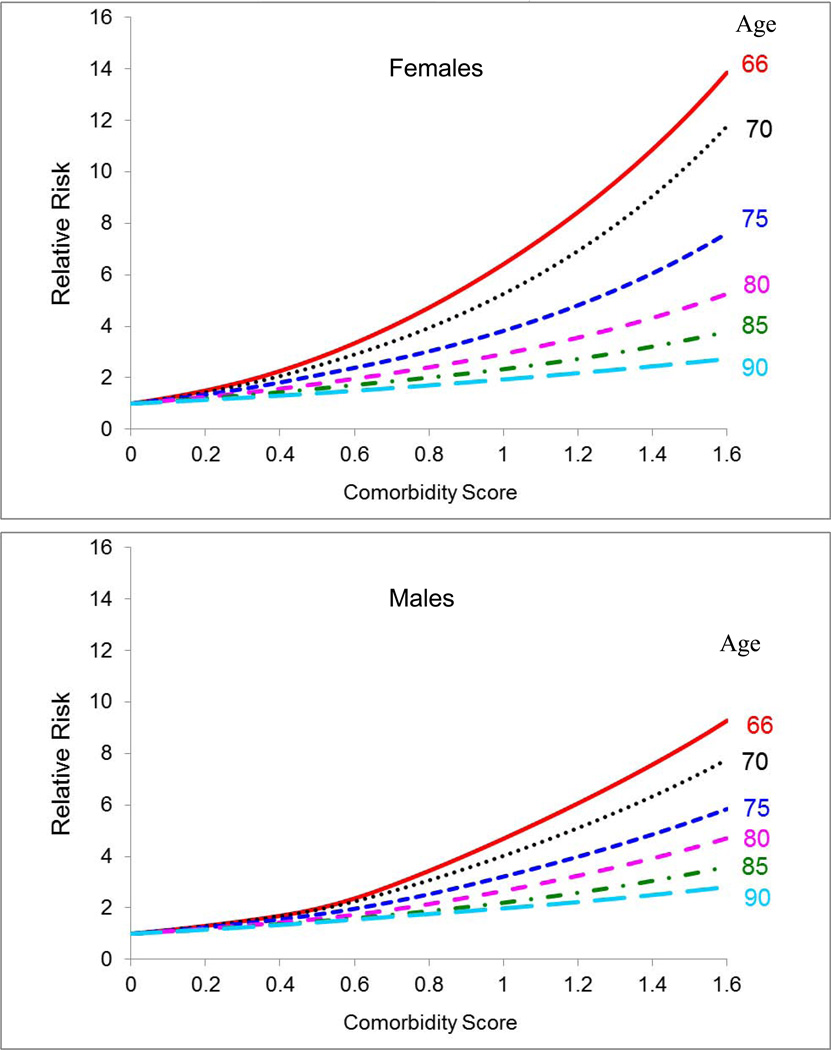
Survival models were estimated for each combination of age and sex using race, cancer status and comorbidity score as covariates. The risk of non-cancer mortality increases substantially with greater comorbidity (Figure 1). It increases more for women than for men. For women aged 66 and 80 with high comorbidity (score=1.0), the risk of non-cancer death is 6.4 fold and 2.9 fold higher, respectively, compared to healthy women of the same age. For men aged 66 and 80, the risk of non-cancer death is 4.7 fold and 2.7 fold higher, respectively, relative to the healthy population (Figure 1). Cancer patients have a higher risk of non-cancer mortality than the cancer-free population (Appendix, Table I). Compared to whites, blacks have a higher risk of non-cancer mortality at younger ages, but a lower risk at older ages. The “other races” group has a lower risk of non-cancer death compared to whites (Appendix, Table I).

Figure 1.

Relative risk of dying of other causes of death by comorbidity score for selected ages. Reference category is people with no comorbidity (comorbidity score 0). Estimates from the Cox proportional hazard model are fitted to people without cancer from the non-cancer sample of Medicare beneficiaries residing in the SEER areas (1992–2005).

Appendix Table I.

Estimates of hazard ratio (standard errors; s.e.) of race and cancer status from the Cox proportional hazard model by sex and selected ages. Model fitted to cancer patients and people without cancer from the non-cancer sample of Medicare beneficiaries residing in the SEER areas (1992–2005).

	Hazard ratios (s.e.)
	Females				Males
Age	66	70	80	90	66	70	80	90
No comorbidity/No Cancer/White (Reference)	1	1	1	1	1	1	1	1
Cancer	1.60	1.45	1.23	1.14	1.27	1.19	1.15	1.17
	(0.04)	(0.03)	(0.02)	(0.03)	(0.03)	(0.02)	(0.02)	(0.04)
Black	1.33	1.20	0.97	0.84	1.51	1.40	1.09	0.80
	(0.04)	(0.03)	(0.02)	(0.03)	(0.04)	(0.04)	(0.03)	(0.04)
Other races	0.92	0.85	0.83	0.81	1.03	0.87	0.82	0.86
	(0.05)	(0.03)	(0.03)	(0.04)	(0.05)	(0.03)	(0.03)	(0.05)

Health-adjusted age

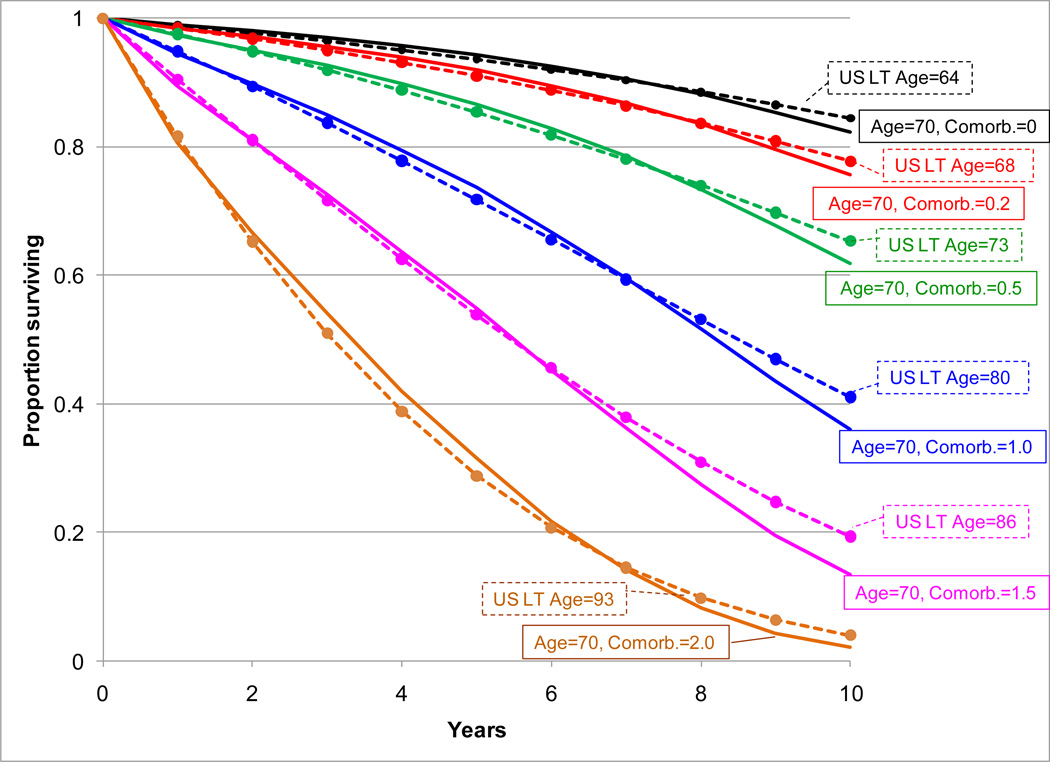
Figure 2 shows an example of the calculation used to obtain health-adjusted age. The modeled non-cancer survival for white women diagnosed with cancer at age 70 with comorbidity scores of 0.0, 0.2, 0.5, 1.0, 1.5 and 2.0 are compared to the age-specific US life table that best fit each modeled survival. The US life table age that best fits the modeled survival provides the health-adjusted age. For example, a white woman diagnosed with cancer at age 70 has a health-adjusted age of 64 when she has no comorbidities, but has a health-adjusted age of 73 when she has a comorbidity score of 0.5. Note that a comorbidity score of 0.5 is similar to the comorbidity score for a cancer patient with diabetes (0.466; Table 2).

Figure 2.

Fit of estimated net other-cause survival for white women diagnosed with cancer at 70 years old and selected comorbidity scores (plain lines) to the best-fit US life table (dashed lines). The age of the best-fit US life table is the health-adjusted age corresponding to a 70-year-old female white cancer patient with the given comorbidity.

Table 3 shows the mapping of comorbidity score to health-adjusted age by sex and race for people at age 66, 70, 75, 80 and 85. The health-adjusted ages of patients diagnosed with cancer at age 66 and no comorbidity are 60 (white men and women), 59 (black men and women), 66 (men of other races) and 64 (women of other races). Table 3 also shows the 10-year expected survival. For cancer patients diagnosed at age 66 with no comorbidity, the expected 10-year non-cancer survival is higher for women (84%–88%) than for men (74%– 82%), with the lowest non-cancer survival expected for black men (74%). For cancer patients diagnosed at age 66 with more severe comorbidity (comorbidity score 1.0), their 10-year non-cancer survival is between 32%–45% for women and 24%–39% for men.

Table 3.

Health-adjusted age and respective 10-year non-cancer survival for selected age at diagnosis and comorbidity scores.

		Female								Male
		White			Black			Other		White		Black		Other
	Como rbidity score	health-adj. age	10-yr non-cancer		health-adj. age	10-yr non-cancer surv.		health-adj. age	10-yr non-cancer surv.	health-adj. age	10-yr non-cancer surv.	health-adj. age	10-yr non-cancer surv.	health-adj. age	10-yr non-cancer surv.
Age
66	0.0	60	87%	23.3	58	84%	22.7	64	88%	60	82%	59	74%	66	81%
	0.2	65	82%	19.2	63	77%	19.0	69	83%	63	77%	62	67%	68	76%
	0.4	69	74%	16.2	68	67%	15.7	73	76%	66	71%	66	60%	71	70%
	0.6	73	64%	13.4	73	55%	12.6	76	66%	69	62%	70	49%	74	61%
	0.8	76	53%	11.4	77	43%	10.4	79	56%	73	50%	75	35%	78	49%
	1.0	79	42%	9.6	81	32%	8.5	82	45%	77	39%	79	24%	81	38%
	1.2	81	32%	8.5	84	22%	7.3	85	35%	79	29%	83	16%	84	28%
	1.4	84	23%	7.0	87	15%	6.1	87	26%	82	22%	86	10%	86	21%
70	0.0	64	82%	20.0	61	79%	20.5	67	85%	63	76%	62	68%	67	79%
	0.2	68	76%	16.9	66	71%	17.0	71	79%	66	70%	65	61%	69	74%
	0.4	71	67%	14.8	70	62%	14.4	74	71%	69	63%	68	53%	72	67%
	0.6	75	57%	12.0	74	51%	12.0	77	62%	72	54%	72	42%	75	59%
	0.8	77	46%	10.8	78	40%	9.9	80	52%	75	43%	76	31%	78	48%
	1.0	80	36%	9.0	81	29%	8.5	83	42%	78	33%	80	21%	81	38%
	1.2	83	26%	7.5	84	20%	7.3	85	32%	80	25%	83	14%	83	30%
	1.4	85	17%	6.6	87	12%	6.1	87	22%	83	18%	86	9%	85	22%
75	0.0	70	70%	15.5	67	68%	16.3	73	74%	69	63%	67	56%	71	69%
	0.2	73	61%	13.4	71	60%	13.8	76	67%	71	56%	70	48%	74	62%
	0.4	76	52%	11.4	74	50%	12.0	78	58%	73	48%	73	40%	76	56%
	0.6	78	42%	10.2	77	40%	10.4	81	49%	76	40%	76	32%	78	48%
	0.8	80	33%	9.0	80	31%	9.0	83	40%	78	31%	79	23%	81	38%
	1.0	83	25%	7.5	83	23%	7.7	85	32%	81	22%	83	15%	83	30%
	1.2	85	18%	6.6	86	16%	6.5	87	24%	83	16%	86	10%	85	22%
	1.4	87	11%	5.8	88	10%	5.8	89	16%	85	10%	88	6%	87	16%
80	0.0	76	51%	11.4	74	52%	12.0	79	57%	75	41%	73	38%	78	49%
	0.2	78	43%	10.2	76	44%	11.0	81	49%	77	35%	75	32%	79	42%
	0.4	80	35%	9.0	79	36%	9.4	83	41%	79	28%	78	25%	81	36%
	0.6	82	27%	8.0	81	28%	8.5	85	33%	81	22%	80	19%	83	29%
	0.8	84	20%	7.0	84	21%	7.3	86	26%	83	15%	83	13%	85	21%
	1.0	86	14%	6.2	86	15%	6.5	88	19%	85	10%	86	8%	87	15%
	1.2	88	9%	5.4	88	10%	5.8	90	13%	87	6%	89	4%	89	10%
	1.4	90	5%	4.7	90	6%	5.2	93	9%	89	3%	91	2%	92	6%
85	0.0	82	28%	8.0	81	31%	8.5	85	35%	81	20%	79	23%	84	27%
	0.2	84	22%	7.0	83	25%	7.7	86	28%	83	16%	81	18%	85	22%
	0.4	86	16%	6.2	85	19%	6.9	88	22%	85	11%	83	13%	87	17%
	0.6	87	11%	5.8	87	14%	6.1	89	16%	86	8%	85	9%	88	12%
	0.8	89	8%	5.0	89	10%	5.5	91	12%	88	5%	88	6%	90	9%
	1.0	90	5%	4.7	91	7%	4.9	94	8%	90	3%	90	4%	93	6%
	1.2	92	3%	4.0	92	4%	4.6	96	5%	91	2%	92	2%	95	3%
	1.4	93	2%	3.8	94	2%	4.1	98	3%	93	1%	94	1%	98	2%

Model validation

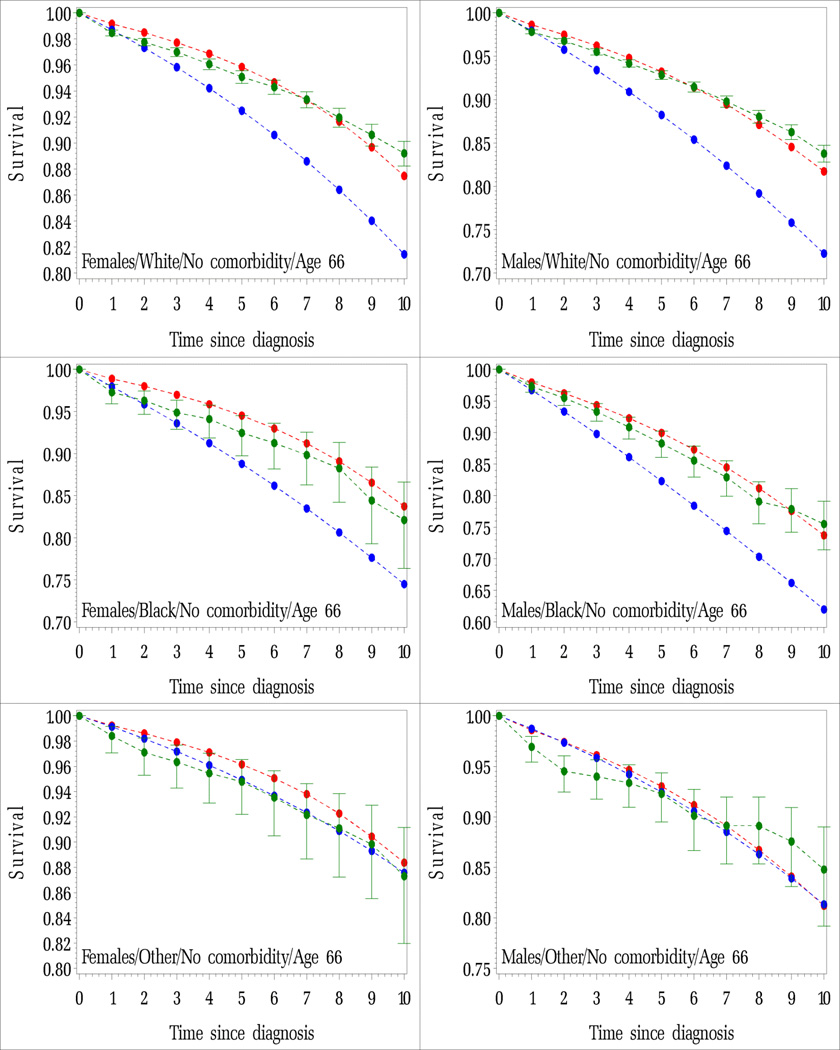
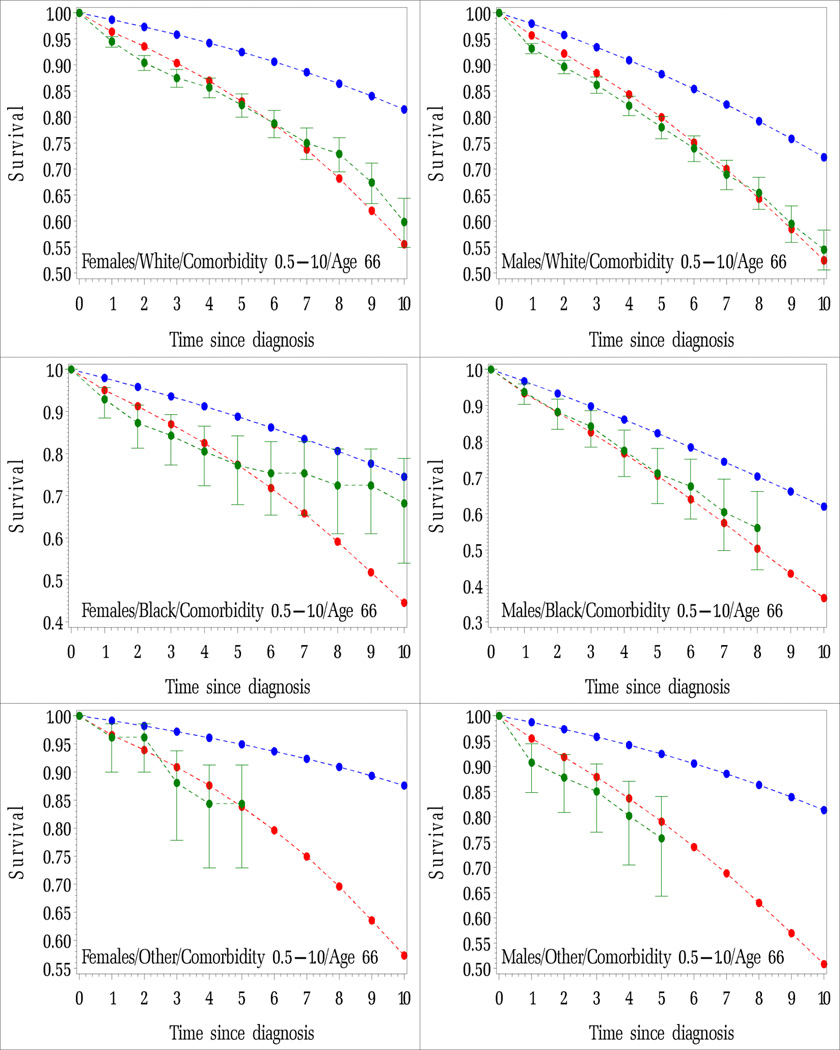
Our survival models by comorbidity better predict non-cancer survival than the US life tables (Appendix, Figure IA and IB). There were some discrepancies between the averaged modeled and observed survival probabilities, especially after 5 years of follow up. This likely stems from variability in the observed survival probabilities for the black and other races cohorts, which each had relatively small sample populations. However, even in these cases, the modeled survival probabilities provided a good fit to the observed data up to 4 years of follow-up. The distance between the US life table estimates and the observed survival probabilities provides a measure of the average bias when using the US life tables to predict non-cancer survival.

Figure IA.

Average probability of surviving non-cancer death for cancer patients diagnosed by years since diagnosis. Cancer patients diagnosed at age 66 with no comorbidity and comorbidity scores between 0.5 and 1.0 by race and sex. Modeled (red lines), observed and 95% confidence intervals (green lines), estimated using 2000 US life tables (blue lines). Figures are by sex and by race.

A. Age 66 and No comorbidity

B. Age 66 and Comorbidity score between 0.5 and 1.0

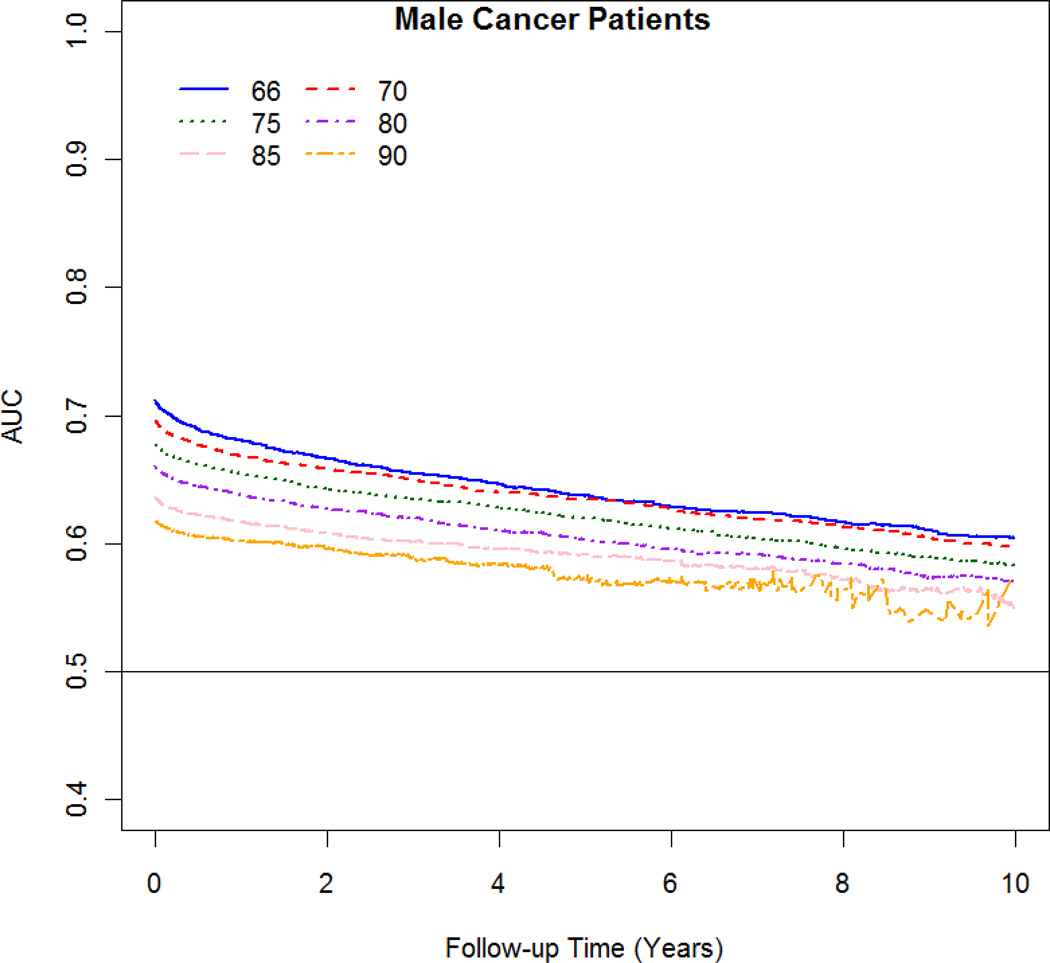
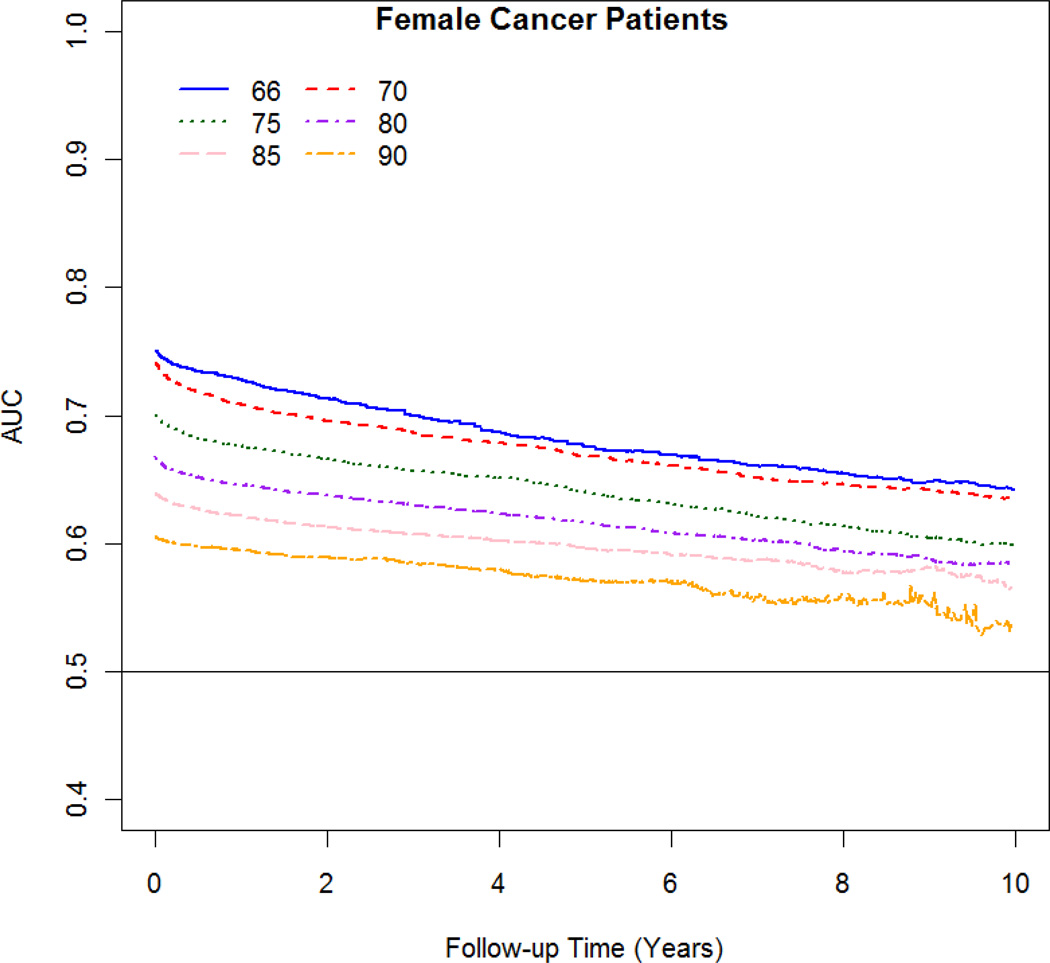
The AUC varied with follow-up time and age. The best discrimination occurred at 1 year after the cancer diagnosis and at younger age at diagnosis (Figure 3 A–B). For women diagnosed at age 66 and 80, the discrimination changes from 0.73 and 0.65, respectively; at 1 year after diagnosis to 10 years after diagnosis from 0.64 to 0.58, respectively. For men diagnosed at age 66 and 80, the discrimination changes from 0.68 and 0.64, respectively; at 1 year after diagnosis to 10 years after diagnosis from 0.60 to 0.57, respectively.

Figure 3.

AUC against survival time at follow-up for male and female cancer patients by age at diagnosis (66 to 90).

Discussion

In this study, we developed life tables by comorbidity score using a large population-based claims dataset, taking into account each individual’s comorbidity profile in the year prior to cancer diagnosis. A health-adjusted age was estimated by systematically comparing non-cancer survival models with US life tables. While comorbidity scores have been used to measure health status (20, 21, 23), the current study represents the first time – to our knowledge – that comorbidity scores have been used to estimate life tables for cancer patients as well as their health-adjusted age. We found that the comorbidity life tables better predicted competing non-cancer survival up to 10 years than did the standard US life tables. Because a patient’s cancer history and comorbidities compete for overall survival estimates, the non-cancer survival by comorbidity score and the health adjusted age may help in making cancer-treatment decisions.

The non-cancer survival models developed in this study provide a partial picture of cancer patient survival. Our models, which specifically represent life expectancy in the absence of cancer death, are being integrated with cancer prognosis using a competing risk framework (17) in the Cancer Survival Query System (CSQS)(19). Given a patient’s age, race, comorbidity score and stage at diagnosis, the CSQS can calculate the individualized crude probabilities of dying of cancer and of causes other than cancer. The CSQS was initially developed for prostate and colorectal cancer, but two other sites, breast and head and neck cancer, will be added in the future. The non-cancer survival algorithm and estimates could be integrated to other prognostic models, and will be made available by request.

Age, race, sex, cancer status and comorbidity are all important non-cancer survival predictors, and their effect on survival decreases as age increases due to the increasing frailty of older patients regardless of existing comorbid conditions. After age, comorbidity is the most important predictor of non-cancer mortality. In our study, comorbidity was measured as a continuous score, with higher scores representing a greater burden of comorbidity. The models also showed adequate discriminatory ability (65% to 75%), with the best discrimination occurring for short term predictions (1-year) and for younger patients. The models were better at predicting non-cancer survival than the general US life tables for patients both with and without comorbidities.

We developed the non-cancer life tables and health-adjusted age for all cancer sites combined in order to produce one set of life tables that could be used for people diagnosed with any type of cancer. In addition, modeling all cancer sites combined allowed for a more precise calculation of life tables by single year of age, sex and race. While cancer survival varies substantially by cancer type, non-cancer survival adjusted by health status is less dependent on cancer site. While previous work has shown that cancer site affects the comorbidity score; however, differences in the comorbidity score based on cancer site, while significant, were small (20). Other work has also shown that non-cancer survival varies by cancer site, especially for cancers that share common risk factors (i.e., smoking) with other diseases, such as lung cancer (27). Nonetheless, the non-cancer survival was not adjusted for health status and/or comorbidity score in this previous study. Although non-cancer survival may vary by cancer site, after adjusting for comorbidity score, the differences based on cancer site are small. For instance, we have compared simple Kaplan-Meier non-cancer survival curves for male colorectal and prostate cancer patients (66–69 years old) diagnosed with diabetes only and COPD only (data not shown). Non-cancer survival for prostate cancer patients was slightly higher than for colorectal cancer patients, but confidence intervals overlapped and the difference was smaller than 5% points in survival. For COPD non-cancer survival was very similar 7 years after diagnosis. Modeling single cancer sites requires a large cohort of patients, and is possible for the most common cancer sites. In future research, we plan to develop cancer-specific life tables for prostate, breast and colorectal cancers.

The findings in this study are subject to a few limitations. Life tables by comorbidity were only estimated for populations aged 66 and older. However, while comorbidity does predict non-cancer survival better for younger cancer patients, fewer people under age 66 actually have comorbid conditions. Comorbidities were identified through claims data; however, the algorithms we used have been extensively tested and validated (20, 21). The results are based on comorbidity scores estimated in the year prior to cancer diagnosis and survival using 10 years of follow-up. Thus, the models are valid up to 10 years survival predictions and do not directly model conditions cancer patients may develop after diagnosis. In order to estimate comorbidity progression and integrate it with survival, complex models that incorporate correlation between multiple measurements and temporal modeling are needed and beyond the scope of this work. The comorbidity score included 2 level interactions with the three most prevalent comorbidities: diabetes, COPD and congestive heart failure. This allows for a more accurate estimation of the score for people with two or more conditions. Nevertheless, estimating more complicated multivariate survival models for each specific age using individual comorbid conditions rather than a single comorbidity summary score would be difficult because of sparse data, especially at older ages. While the models took into account age, sex, race and comorbidity score, other factors may also impact mortality risks, including smoking status, occupation, and socio-economic class. However, comorbidity likely provides a better predictor of non-cancer survival than these other risk factors given that they potentially contribute to the comorbidities (although this might not be true for comorbidities not yet expressed). Because other race populations are not large enough to allow reliable estimation, we have only modeled whites, blacks and other races.

Health-adjusted age was calculated by mapping comorbidity-adjusted non-cancer survival models onto the US life tables. The health-adjusted age of individuals just diagnosed with cancer reflects how they compare to the average US population matched for sex and race. Matching to the US life tables is useful because these represent the gold standard estimates of life expectancy for the US population. Given a health-adjusted age, US life tables can be consulted to provide an approximate estimate a persons’ life expectancy. For example, using the decennial US 2000 life table (6), a black man aged 75 has a life expectancy of 9.07 years, and is thus expected to live on average to age 84 (75+9). However, if the same man has no comorbidities, his health-adjusted age is 67, giving him a life expectancy of 12.99 years, and is thus expected to live on average to age 88 (75+13). However, because the matching was done by comparing 10 years of survival, these life expected calculations are an approximation, since we don’t know how the models fit the US life tables beyond 10 years. Instead, Table 3 provides a direct estimate of an individual’s 10-year non-cancer survival and can be used to compare people with different comorbidity levels to healthy people with no comorbidity. For example, the 10-year expected survival of a black man aged 75 with no comorbidity (comorbidity score = 0.0) is 56%, while the expected survival of a black man aged 75 with moderate comorbidity (comorbidity score = 0.6) is 32%.

In summary, our estimates of comorbidity-adjusted non-cancer survival and health adjusted age provide a more accurate expected survival than the US life tables and may be valuable for helping to make clinical decisions for cancer patients. Medical research may be far from developing “personalized medicine” in which each person’s disease and treatment course can be uniquely individualized. Nevertheless, one step towards the goal of “personalized medicine” for cancer patients is developing treatment recommendations tailored to both the patient’s cancer prognosis and their life expectancy with respect to non-cancer mortality.

Appendix

Estimating life tables by comorbidity score

For each age a and sex g, the Cox proportional hazard model is specified as

$$S_{a,g}(t,x|\beta )={[S_{a,g}(t)]}^{\text{exp}(\beta x)}$$ [1]

where x is a vector of the covariates race (white, black and other), cancer indicator (0=non-cancer and 1=cancer) and comorbidity score as a restricted cubic spline function linear at the tails.

In mathematical terms

$$\beta x={\beta }_1\mathit{\text{cancer}}+{\beta }_2\mathit{\text{black}}+{\beta }_3\mathit{\text{other race}}+\mathit{\text{CI spline}}$$

The comorbidity score spline term is modeled with a restricted cubic spline with 4 knots at the 5%, 35%, 65% and 95% percentile of each individual age : k₁, k₂ k₃, and k₄ and can be expressed as CI spline = α₁ CI + α₂ CI₁ + α₃ CI₂ where CI₁ and CI₂ are functions of the comorbidity score variable CI and knots.

$$C{I}_j={(CI-k_j)}_{+}^3-\frac{{(CI-k_3)}_{+}^3(k_4-k_j)}{(k_4-k_3)}+\frac{{(CI-k_4)}_{+}^3(k_3-k_j)}{(k_4-k_3)},j=1,2.u_{+}=\{\begin{array}{cc}0\hfill & \mathit{\text{if}}u\le 0\hfill \\ u\hfill & \mathit{\text{if}}u>0\hfill \end{array}.$$

Estimating age adjusted for comorbidity: health-adjusted age

The age adjusted for health status is calculated by searching the US life table that provides the closest survival experience to the estimated life table with a specific chronological age and comorbidity score. The following S_a,g (t | Cancer = 1, r, x) was the net probability of surviving other causes of death up to age a + t for individuals diagnosed with cancer at age a, comorbidity score x, gender g and race r, estimated using the Cox proportional hazard model [1]. The terms $S_{a,g,r}^{US}(t)$ represented the cumulative probability of surviving up to age a + t for a person in the US alive at age a, gender g and race r, calculated using annual probabilities of death provided in the US life table. To estimate the health-adjusted age of an individual aged a with comorbidity score x, we calculated the absolute difference between the estimated individual survival and the US survival for a range of ages. The health-adjusted age B was the age of the US survival closest to the estimated survival. In mathematical terms, the absolute difference was calculated for a range of ages b as

$$\mathit{\text{ABSD}}(b|a,g,r,x)=\sum _{t=1}^{10}\{|S_{a,g}(t|\mathit{\text{cancer}}=1,r,x)-S_{b,g,r}^{US}(t)|\}.$$

The health-adjusted age was given by B = min{b, ABSD(b | a, g, r, x) | 50 ≤ b ≤ 110}. Although the data allow for a maximum of 13 years of follow-up, we limited the comparisons to 10 years of follow-up because most data estimates have more variability at longer follow-up dates.