Escaping the snare of chronological growth and launching a free curve alternative: General deviance as latent growth model

Abstract

Researchers studying longitudinal relationships among multiple problem behaviors sometimes characterize autoregressive relationships across constructs as indicating “protective” or “launch” factors or as “developmental snares.” These terms are used to indicate that initial or intermediary states of one problem behavior subsequently inhibit or promote some other problem behavior. Such models are contrasted with models of “general deviance” over time in which all problem behaviors are viewed as indicators of a common linear trajectory. When fit of the “general deviance” model is poor and fit of one or more autoregressive models is good, this is taken as support for the inhibitory or enhancing effect of one construct on another. In this paper, we argue that researchers consider competing models of growth before comparing deviance and time-bound models. Specifically, we propose use of the free curve slope intercept (FCSI) growth model (Meredith & Tisak, 1990) as a general model to typify change in a construct over time. The FCSI model includes, as nested special cases, several statistical models often used for prospective data, such as linear slope intercept models, repeated measures multivariate analysis of variance, various one-factor models, and hierarchical linear models. When considering models involving multiple constructs, we argue the construct of “general deviance” can be expressed as a single-trait multimethod model, permitting a characterization of the deviance construct over time without requiring restrictive assumptions about the form of growth over time. As an example, prospective assessments of problem behaviors from the Dunedin Multidisciplinary Health and Development Study (Silva & Stanton, 1996) are considered and contrasted with earlier analyses of Hussong, Curran, Moffitt, and Caspi (2008), which supported launch and snare hypotheses. For antisocial behavior, the FCSI model fit better than other models, including the linear chronometric growth curve model used by Hussong et al. For models including multiple constructs, a general deviance model involving a single trait and multimethod factors (or a corresponding hierarchical factor model) fit the data better than either the “snares” alternatives or the general deviance model previously considered by Hussong et al. Taken together, the analyses support the view that linkages and turning points cannot be contrasted with general deviance models absent additional experimental intervention or control.

Longitudinal research projects involving problem behaviors frequently attempt to detect time-bound linkages or “turning points” between level or onset of one behavior and subsequent level or onset of another behavior. Turning points are frequently viewed as external events or behaviors that provoke or inhibit change (Rutter, 1996). To cite a few typical examples, Hussong, Curran, Moffitt, Caspi, and Carrig (2005), proposed that early onset of substance abuse hindered decline in subsequent antisocial behavior during middle adulthood. Vazsonyi and Huang (2010) analyzed data from a 3-year longitudinal sample of third to fifth graders via a parallel linear growth curve models and found that self-control and deviance were both negatively associated overall and that the patterns of growth between the two constructs were negatively associated. Similarly, Welte, Barnes, Hoffman, Wieczorek, and Zhang (2005) found that alcohol use and dependence were associated with a greater increase in delinquency in adolescence, whereas drug use was negatively associated with a declining trajectory of delinquency. In two large-scale Monte Carlo studies designed to simulate the magnitude of turning points in developmental research, Kwok, Lou, and West (2010) argued that modification indices could be successfully used to identify turning points in longitudinal data. In a general discussion of criteria for identification of time-bound linkages and turning points, Rutter (1996) stressed that research into turning points must necessarily involve the measurement of intraindividual change over time and that studies must rule out heterotypic continuity (which posits that the manifestation of a given behavior has changed but its presence had not) as an alternative explanation.

The existence of turning points and linkages in longitudinal data has been established by comparing models with and without such turning point components. Sterba and Bauer (2010) survey several person-oriented developmental statistical models that could serve as base models for such investigations. They note, however, that the variety of statistical models is impressive and that such models often invoke implicit, untestable assumptions about the nature of interindividual differences in intraindividual change over time. This sheer variety of statistical models often means that a given data set can be used to identify linkages under one statistical model but not another. As a result, it is difficult to definitely conclude that particular turning points exist, whether alternate explanations involving heterotypic continuity hold or whether the model comparison is simply invalid because the data fail to meet implicit assumptions about change over time. Such limitations of substantive inference due to the selected statistical model have been noted in other areas of longitudinal developmental research: Partridge and Lerner (2007), for example, note in their review of infant temperament that researchers using repeated measures multivariate analysis of variance (MANOVA) often conclude that temperament is stable and traitlike, whereas those using growth curve models found that it changed systematically over time. Similarly, although some researchers may argue for the presence of turning points or linkages (e.g., by comparing linear growth curve models with and without turning points), a reasonable skeptic may counter that the analysis is unconvincing because an inappropriate model of growth over time was used.

The multiplicity of statistical models for testing turning point hypotheses leaves researchers with four general alternatives: a clearly superior choice is to use a statistical model based on substantive considerations that all reasonable qualified experts would agree upon. Unfortunately, this happy state of affairs does not often attain. A less appetizing alternative is to abandon claims to conclusiveness based on any given model and note that “other techniques may yield other conclusions.” Such an admission raises questions about the probative value of the analysis or, worse, raises the suspicion that the model used has been “cherry-picked” to serve the desired conclusion. Still other researchers entertain a variety of statistical models and tally those that do and do not favor the turning point hypothesis of interest in an effort to test the “robustness” of proposed findings. Unfortunately, such “elections” are suspect on two grounds: first, “voters” in the election are determined based on their publication in statistical or related journals with no evaluation of whether the model is appropriate to the data at hand; and second, such comparisons do not take into account that some models may make restrictive or unreasonable assumptions of the data or, alternatively, may lack parsimony to such a degree that the statistical power for testing hypotheses is greatly reduced. A final approach, which is the one outlined in this paper, is to consider and evaluate the suitability of models in terms of the dual criteria of their parsimony and fit to the data. Given that general deviance may constitute an alternative explanation for observed time-bound associations, it is necessary to explore and evaluate the models of general deviance that a reasonable skeptic might propose as counterarguments to models that posit time-bound associations between constructs.

The simultaneous inductive and deductive processes implicit in model building were first discussed by Cattell (1988) and more recently by Rodgers (2010) as a “quiet methodological revolution” in which researchers shift away from using a statistical procedure within a particular rule-based framework to building and comparing models informed by both substantive questions and the data at hand. Although it may be initially tempting to choose models that make the fewest assumptions of the data or that involve estimation of the smallest number of parameters, Rodgers argues that choosing the “best” mathematical model involves sometimes conflicting trade-offs based on parsimony, theoretical reasonableness, and fit with the observed data. We now turn to a discussion of these trade-offs and explore alternative substantive explanations involving heterotypic continuity and third-variable explanations.

Problems With Linear/Polynomial Growth Models

The examples of turning point research cited in the introductory paragraph of this article are similar in that linear or polynomial growth curve models (or their hierarchical linear model equivalents) were assumed as base models for identification of turning points. This is not atypical of most longitudinal analysis, given the popularity and ease of specification of such models. Analytic and substantive reservations have been expressed, however, as to whether such models are appropriate on substantive and empirical grounds. Liu, Rovine, and Molenaar (2012) argue against use of the linear growth curve model as a primary model and point out that autoregressive, moving average, or Toeplitz structures may be more appropriate. They point out that the tail probabilities associated with the linear model may be very inaccurate, even when the predicted means of the model fall on a straight line. Some substantive reasons for caution also seem appropriate. In developmental psychology, for example, no psychologist has proposed a theory in which changes in personality traits or problem behaviors are necessarily linear (or quadratic) as a function of elapsed time. Periods of developmentally limited growth, stasis, and decline are often hypothesized instead, the precise form of which is unknown to the researcher beforehand. Others have criticized whether linear or polynomial form of growth is appropriate. Browne (1993) and Ram and Grimm (2007), for example, note that such models may not recover abrupt nonlinear changes and do not recover plateaus or short-term periods of elevation such as those observed in problem behaviors, which are normatively developmentally limited to a specific period of the lifespan. Free curve models of growth (McArdle & Anderson, 1990; Meredith & Tisak, 1990; Ram & Grimm, 2007; Wood, 2011) entail no constraints on the form of growth over time and may readily recover such nonlinear change. Other, more parsimonious models may also be appropriate, including confirmatory factor models, which model both mean level and patterns of covariation (e.g., McArdle & Epstein, 1987; McDonald, 1967), as well as more familiar longitudinal models such as repeated measures analysis of variance (Liu et al., 2012). To our knowledge, no studies of developmental psychopathology have compared the suitability of such alternative models against the more traditional linear and polynomial curve growth curve or HLM model.

Heterotypic Continuity as Third-Variable Explanation

If heterotypic continuity is to be taken as a possible alternative explanation for time-bound associations between constructs, it is first necessary to show how a model of heterotypic continuity might be operationalized. The term is often taken to mean that an individual possesses a constant level of (underlying) impairment over time. If the manifest level of impairment over time due to heterotypic continuity is also constant, heterotypic continuity may then be modeled as a general intercept factor with unit loadings. In addition, if equal measurement error variance over time is assumed, conditions of compound symmetry are met and hypotheses regarding change over time can be used using traditional repeated measures analysis of variance (Liu et al., 2012; Wood, 2011).

It is possible, however, that the manifest level of impairment may vary from occasion to occasion, even though individuals’ underlying levels of impairment are constant over time. For example, although a given level of alcohol use may be considered moderate consumption during adulthood, the same level of use may, in younger individuals, indicate a high level of problematic consumption. Such differences may typify normative shifts in consumption across ages. In addition, stable interindividual differences in the construct of interest may manifest themselves differently across a developmental period due to changes in general environment (e.g., living at home versus on a college campus) or in response to developmentally graded tasks and roles. These factors may also cause assessments of behaviors to be differentially reliable across measurement occasions. If heterotypic continuity takes this more subtle form, it is better modeled as a latent variable with factor loadings that vary over measurement occasions. Although such a factor model with mean level effects was proposed by McArdle and Epstein (1987) to model intellectual development, it has not, to our knowledge, been used to typify heterotypic continuity.

Other Third-Variable Explanations

Heterotypic continuity is not the only common process or trait that may underlie behaviors over time. For example, a common factor of substance use vulnerability or a common genetic mechanism has been proposed to account for abuse across different substances as well as comorbidity with antisocial behavior (Jessor & Jessor, 1977; Krueger, Markon, Patrick, & Iacono, 2005; McGue, Iacono, & Krueger, 2006). State-trait factor models that account for substance use via general traits spanning time as well as time-specific associations have also been proposed (e.g., Jackson, Sher, & Wood, 2000). Hussong et al. (2008) tested a “general deviance” or “common propensity” factor across constructs using a hierarchical linear slope growth model and used the poor relative fit of this model to argue for the existence of “developmental snares” and “launches” involving antisocial behavior and substance use. Although it is not possible to disambiguate these constructs from the general notion of heterotypic continuity, it bears noting that these related constructs also involve invocation of some common causal construct modeled using one or more latent variables that span time. When the longitudinal studies under consideration involve multiple constructs (of different problem behaviors), models involving a general deviance factor may be structurally analyzed as single-trait multimethod designs in which the single trait constitutes general deviance or propensity and the distinct “methods” are the specific problem behaviors under investigation.

Nested Model Comparisons of Growth and Change

In order to make systematic comparisons of structural models of heterotypic continuity and time-bound associations, we propose that researchers make nested comparisons of structural models of general deviance or common propensity that vary in terms of their assumptions about the nature and form of growth/change in individual problem behaviors over time. When sufficient measurement occasions exist, the free curve slope intercept growth model is proposed as the most general model because it makes no assumptions about the form of growth over time and need not necessarily require assumptions of equality of measurement error over time. By imposing constraints or redacting elements of this model entirely, it is possible to generate structural models for the data that may more parsimoniously characterize the general nature of heterotypic continuity and related systematic interindividual differences in intraindividual change. These special cases include the linear slope intercept growth model (used by Hussong et al., 2008), hierarchical linear models, and multivariate repeated measures analysis of variance as well as other models, such as McDonald’s (1967) linear factor model. Because many of these models are nested comparisons, it is then possible to evaluate the degree to which model components (such as the existence of both random intercept and factor mean [FM] models described above) or model assumptions (such as the assumption that growth is typified by a straight line or that measurement error variability is constant over time) appear warranted by the data.

As an example of this model comparison approach, we reconsider two analyses originally presented in Hussong et al.’s (2008) original analysis of data from the Dunedin Multidisciplinary Health and Development Study (Silva & Stanton, 1996). In the first analysis, the single construct of antisocial personality is considered. Although Hussong et al.’s original analysis concluded that the data were poorly fit by a linear growth model and therefore that general deviance did not explain the construct of antisocial personality over time, we find that the data are well fit by a free curve slope intercept model and, based on incremental fit indices, better fitting than both repeated measures analysis of variance and the linear growth curve model originally proposed by Hussong et al.

In order to examine whether a single construct (such as general deviance or propensity) can explain comorbidity patterns across problem behaviors as well as interindividual variability over time within constructs, we then reconsider an analysis of antisocial personality, alcohol, and marijuana use in the Dunedin data. Specifically, we propose fitting a single-trait model of general deviance or propensity along with multimethod factors corresponding to the individual problem behaviors of antisocial personality: alcohol and marijuana use. These models, expressed in both bifactor and hierarchical factor form, fit the data well and better than the hierarchical linear growth model proposed in Hussong et al.’s (2008) original analysis. Although Hussong et al. argued that additional developmental linkages exist in these data because their linear slope model of general deviance fit the data poorly relative to substance-specific linkage models, our reanalysis suggests that general deviance adequately accounts for patterns of comorbidity and that no time-bound associations exist across these constructs. It is not the goal of this paper to contrast the deviance model with alternate launch and snare models tested by Hussong et al. A direct comparison of the launch and snare alternatives is difficult, given that the launch and snare modes considered by Hussong et al. are either not nested or based on a different subset of variables than the general deviance models. Our goal here is to show that decisions based on the poor fit of the deviance model should be revisited in light of our reanalysis of the Dunedin data, which operationalizes deviance via factor models as opposed to linear growth models.

Notation for Factor Model With Means

In order to specify the candidate statistical models and to highlight nested relationships between them, it is necessary to briefly introduce the relevant notation. Because the interest conceptually is in growth or change over time and degree of impairment, the structural models under consideration are simultaneously statements of both mean level of functioning and covariation between variables. Accordingly, the score matrix to be modeled consists of the raw scores to which a unit column has been adjoined (or, in summary form as for the data reported in Hussong et al., 2008, and reanalyzed here, the average adjoined sum of squares and cross-products matrices). Using Sörbom’s (1974) notation (with a minor modification so that rows represent individuals and columns represent variables), the factor model including mean effects is given by

$$X=\mathrm{\mu }+\mathrm{\xi }\mathrm{\Lambda }+\mathrm{\epsilon }$$ (1)

and

$$\mathrm{\xi }=\mathrm{\theta }+\mathrm{\eta },$$ (2)

where X is a matrix of n individual scores on k manifest variables. Assuming f factors, μ is an n×k column scalar matrix (i.e., a matrix composed of column identical elements) composed of k intercepts corresponding to each manifest variable that scales each variable to its zero point, Λ is a f×k matrix of factor loadings,ε is an n×k matrix of errors of measurement, θ is an n×f column scalar matrix of factor means, and η is an n×f matrix of latent variable scores expressed as deviations from their respective factor means. The variance/covariance matrix Σ based on this model is given as (Sörbom, 1974, p. 230)

$$\mathrm{\sum }=E[{(X-\mathrm{\mu }-\mathrm{\theta }\mathrm{\Lambda })}^{\prime }(X-\mathrm{\mu }-\mathrm{\theta }\mathrm{\Lambda })]={\mathrm{\Lambda }}^{\prime }\mathrm{\Phi }\mathrm{\Lambda }+{\mathrm{\Psi }}^2,$$ (3)

where Φ represents the variance/covariance matrix of the latent variables and Ψ² is a (generally diagonal) matrix of variances of the uniquenesses. The expected values of the observed manifest variables are given by

$$E(X)=\mathrm{\mu }+\mathrm{\theta }\mathrm{\Lambda }.$$ (4)

As noted by Sörbom (1974), the factor model outlined in Equations 1 and 2 is not identified unless boundary conditions are imposed on the variance components and intercepts. Although discussed in more detail in Sörbom (1974) and Jöreskog (1971), at a minimum, f ² restrictions across Λ and Φ must be imposed to secure an identified solution. For a given factor, this may be accomplished by fixing a factor variance or factor loading associated with each factor to 1. In the case of multiple factors, however, additional care must be taken that each factor is identified distinctly. This may be accomplished in a variety of ways and may involve setting some or all factor covariances to zero, setting selected loadings to equality, or setting some factor loadings to zero, depending on the substantive and design characteristics of the study. In addition, the mean matrices μ and θ can accommodate at most k freely estimated parameters.

Factor Models for Means for Prospective Data

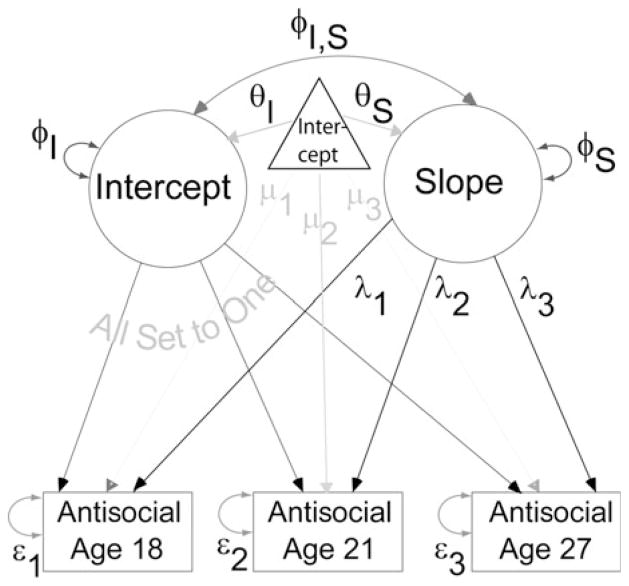
Using this notation, we can now formally present a variety of structural models for growth and change over time. These models include the free curve slope intercept model (FCSI; Meredith & Tisak, 1990), as well as several popular alternatives as special cases including the chronometric slope intercept (CSI) growth model considered by Hussong et al. (2008), hierarchical linear models (HLMs), repeated measures MANOVA, FM models (e.g., McArdle & Epstein, 1987), and FM models with shift (FM shift; Wood, Jackson, & Steinley, 2013). When viewed as structural models, the relative fits of these alternatives may be compared and, in some situations, tested as nested alternatives. Figure 1 shows, in path diagram form, the general growth curve model, which includes these models as special cases. In this model, both intercept and slope factors for the case of three measurement occasions are assumed. The slope factor is specified with either free or fixed loadings (λ), and loadings for the intercept factor are fixed at 1. The FMs for the intercept and slope factors are defined as θ_I and θ_S, respectively, and Φ, the variance covariance matrix of factors mentioned in Equation 3, is composed of the intercept factor variance φ_I, the slope factor variance, φ_S, and covariance between the intercept and slope factors, φ_I,S. Finally, diagonal elements of the Ψ matrix discussed in Equation 3 are estimated via ε_i, where i indexes the measurement occasion.

Figure 1.

The slope intercept growth curve model for a single construct.

For didactic purposes, we test and evaluate models with the data used by Hussong et al. (2008), which were drawn from the Dunedin Multidisciplinary Health and Development Study, a longitudinal study of health and behavior in a complete birth cohort in New Zealand (Silva & Stanton, 1996). The study included 1,037 children (52% male) who participated in an age 3 assessment; participants were followed roughly every 2 years through late adolescence. The sample used in Hussong et al. included 461 men who were assessed at ages 18, 21, and 26 and had complete data across at least two waves.

Symptoms of alcohol abuse and marijuana abuse were assessed using the Diagnostic Interview Schedule (Robins, Helzer, Cottler, &, Goldring, 1989). A count was taken across the 19 alcohol abuse/dependence symptoms and 10 marijuana abuse/dependence symptoms. Antisocial behavior was assessed using the total number of items endorsed from a list of eight different antisocial acts (e.g., arson and robbery).

CSI models

For purposes of comparison with proposed alternatives, it is helpful to begin with the CSI model, as considered in Hussong et al.’s (2008) original analysis and frequently used in research in developmental psychopathology. In this model, slope loading values are fixed numerical values corresponding to elapsed time relative to a measurement occasion (usually the initial occasion; for a more detailed presentation of the model, see Bollen & Curran, 2006). As shown in the CSI column in Table 1, for the summary Dunedin data reported in Hussong et al., these factor loadings are fixed to 0, 3, and 8 for the three measurement occasions. Consonant with Hussong et al.’s original analysis (p. 92) based on full information maximum likelihood estimates taking into account missing data patterns, χ² (1) = 9.31, p = .002, comparative fit index (CFI) = 0.98, fit of the CSI model to the summary data reported in Hussong et al. is poor as shown in the bottom of Table 1, χ² (2) = 11.44, p < .001, Tucker–Lewis index (TLI) = 0.96, CFI = 0.97, root mean square error of approximation (RMSEA) = 0.10, 95% confidence interval (CI) = 0.05–0.16.¹

Table 1.

Linear and free curve models of growth

	Model
Variable	CSI	HLM	FCSI	Orthogonal CSI	FCSI Rotated to Age 18	FCSI Rotated to Age 26
Slope Factor Loadings (λ)
Age 18	0	18	0.69***	0.63***	0	0.90***
Age 21	3	21	0.12	0.32***	0.57***	0.33***
Age 26	8	26	−0.21	−0.19	0.90***	0
Factor Means (θ)
Intercept	1.89***	2.86***	1.58***	1.57***	1.94***	1.48***
Slope	−0.05***	−0.05***	0.51***	0.52***	−0.51***	0.51***
Covariance Between Intercept and Slope Factors (φI,S )
Covariance	−0.065***	−0.26***	0	0	−0.69***	−0.21
Correlation	r = −.48	r = −.91			r = −.51	r = −0.18
Variances (φ and εi)
Intercept	1.72***	7.53***	1.35***	1.32***	1.83***	1.40***
Slope	0.011	0.01	1	1	1	1
E1	0.79***	0.79***	0.73***	0.79***	0.73***	0.73***
E2	1.49***	1.49***	1.49***	1.49***	1.49***	1.49***
E3	0.79***	0.79***	0.73***	0.79***	0.73***	0.73***
Selected Fit Measures
χ2 (df)	11.44 (2)	11.44 (2)	3.71 (1)	11.44 (2)	3.71 (1)	3.71 (1)
TLI	0.96	0.96	0.98	0.96	0.98	0.98
CFI	0.97	0.97	0.99	0.97	0.99	0.99
RMSEA	0.10	0.10	0.08	0.10	0.08	0.08
90% CI	0.05–0.16	0.05–0.16	0.00–0.17	0.05–0.16	0.00–0.17	0.00–0.17

Note: Corresponding intercept factor loadings are fixed to unity. CSI, chronometric slope intercept; HLM, hierarchical linear model; FCSI, free curve slope intercept; E1, Estimate 1; E2, Estimate 2; E3, Estimate 3; TLI, Tucker–Lewis index; CFI, comparative fit index; RMSEA, root mean square error of approximation; CI, confidence interval.

^***p < .001.

HLMs

Given the multiple random effects often present in prospective data, HLMs have often been proposed as an attractive model for such data. As noted by Rovine and Molenaar (2000), from a structural equation modeling perspective, such HLMs are equivalent to corresponding CSI models. When error variances are assumed to be unequal (equivalent to the type UN in Proc Mixed), the fit of this model is identical to that obtained with the CSI model, although, as noted by Rovine and Molenaar, estimated factor variances and covariances as well as FMs are different, due to the change in scale imposed by the different sets of linear loadings (i.e., the intercept latent variable in HLM is scaled to represent variability at birth rather than variability at age 18).

Conceptually, it seems odd to adopt either the CSI or the HLM model as a default growth curve model for problem behaviors across many years of development because, as mentioned above, periods of developmentally limited growth as well as periods of stasis and precipitous decline are often hypothesized to occur. Unfortunately, although these life-stage specific phenomena are theoretically expected, their presence in the data is not a certainty. Even when the presence of such phenomena are agreed upon, the precise timing of these phenomena is often not known. In the case of three measurement occasions such as these data, the failure of the CSI and HLM models appears largely due to the models’ failure to replicate means across the three measurement occasions, given that the number of factor loadings and error variances is equal to the number of variances and covariances in the data. However, in a more general sense, the CSI and HLM models may in many occasions be simultaneously too “complex” in that they assume the existence of separate intercept and slope functions over time that may not exist and too “simple” in that they assume that prospective patterns of change must assume a linear or quadratic form. These difficulties would appear compounded when the CSI model is used as a component of a larger general deviance model because patterns of stasis may occur in some behaviors but not others, resulting in poor model fit, even though interindividual differences could still be well explained by a single general deviance factor.

FCSI models

As noted by Meredith and Tisak (1990), a “free curve” growth models results when all slope loadings (λ) are freely estimated, assuming a Slope factor variance (φ_S) of 1 and no covariance between the Intercept and Slope factors. In this model, the FCSI model includes estimates of means for the Intercept (θ_I) and Slope (θ_S) factors, as well as a variance component for the Intercept factor (φ_I ). Errors of measurement for the mth manifest variable (ε_m) are estimated as well. In terms of assumptions about the continuously measured manifest variables, the FCSI is similar to the CSI in that it assumes a common interval level measurement of manifest variables and the intercept variable but a ratio level of measurement of the slope latent variable. Differences in the rate of change in growth in the free curve model can be estimated by the difference between adjacent slope factor loadings (e.g., McArdle & Epstein, 1987). For the Dunedin data, fit of FCSI model is very good, χ² (1) =3.71, p =.054, TLI = 0.98, CFI = 0.99, RMSEA = 0.08, 90% CI = 0–0.17.

Relationship of FCSI to CSI

If the freely estimated loadings of the FCSI model were constrained to be linear over time, the model that results has an identical fit to the original CSI model. In terms of nested model comparisons, researchers can compare the FCSI with a constrained model to assess if the assumption of linearity is warranted. Although it is easier for researchers to specify these linear constraints by fixing slope loadings to chronological age or elapsed time relative to a measurement occasion, an orthogonal linear growth model can also be fit by fitting the FCSI model with constraints on the loadings intermediary between the first and last measurement occasion to secure the desired linear form. For these data, the loading corresponding to age 21 is fixed to be equal to (5/8)×λ₁₈ + (3/8)×λ₂₆ and results in the estimates reported in the Orthogonal CSI column in Table 1. A χ² difference test between the orthogonal CSI and FCSI models finds the FCSI model is preferable, χ² (1) = 7.73, p < .01.

Examining the FCSI column in Table 1, the Slope factor loading of only the age 18 measurement occasion loading is significant (λ = 0.69) corresponding to a standardized loading value of .43. Means for the Intercept (θ_I = 1.59) and Slope (θ_S = 0.51) factors are both statistically significant, as is the Intercept factor variance (φ_I = 1.35). The pattern of statistical significance in the orthogonal solution indicates that the FCSI model describes a decline from age 18 measurement occasion to other ages, but that no significant normative decrease in antisocial personality was found from ages 21 to 26. Further, the proportion of variability in the construct of antisocial personality accounted for by the tau-equivalent model can be calculated by the proportion of variability accounted for by the intercept factor divided by the variability accounted for by both the intercept and slope factors. When this is done, for example, it can be seen that 99% and 98% of the variability in ages 21 and 26 can be accounted for by the tau equivalent factor model, compared to only 74% of the variability at age 18, suggesting that the change observed in the data appears limited to a developmentally graded increase in antisocial personality assessed at age 18.

Rather than asking whether evidence exists for growth or change above and beyond a tau-equivalent trait model, researchers may be interested in knowing whether a relationship exists between interindividual variability associated with a particular measurement occasion and a trajectory of (subsequent or antecedent) change relative to that time of measurement. For example, similar to the CSI model, researchers may be interested in determining if interindividual variability at age 18 is related to subsequent course of change and whether general level of response at age 18 is related to the subsequent trajectory of change. This rotation of the original FCSI model is accomplished by setting the loading associated with age 18 to zero and freeing the covariance between the intercept and slope factors. The resulting parameters are shown in Table 1 in the FCSI Rotated to Age 18 colulmn. Seen from this perspective, the same normative decline in antisocial personality is estimated (calculated by multiplying the negative slope mean by each loading and adding the result to the mean of the intercept factor), but via a process that posits that age 18 is unrelated to the growth curve of interest (accomplished by setting the slope loading to zero). Factor loadings for the slope factor are statistically significant, consonant with the orthogonal FCSI model, which found that the age 18 loading was dramatically different than the remaining two measurement occasions. Variability in growth, (operationalized as the implied decreases in scores as indicated by loadings of the slope factor), is negatively (r = −.51) related to variability at age 18, as was also found in the linear CSI.

Other researchers (e.g., Demetriou & Raftopoulos, 2004), following Wohlwill (1973), have argued for teleological models of development in which a retrospective focus is employed. Under these models, the desire is to understand the route by which the individual arrived at the last assessed occasion rather than prospectively linking the first measurement occasion to subsequent growth. These models seek to ascertain, for example, the process by which individuals with a given level of antisocial personality at age 26 came to it based on earlier assessments, consistent with the idea of equifinality (Cicchetti & Rogosch, 1996), which posits that the same level of psychopathology may result in different individuals via different earlier developmental processes and risk factors. This model is the same FCSI model but this time rotated relative to the last measurement occasion, age 26. Estimates from this model are shown in the FCSI Rotated to Age 26 column in Table 1. As can be seen, this equally well-fitting model produces a non-significant negative estimated correlation between prior growth (slope) and level of antisocial personality at age 26.

In summary, these analyses suggest that a FCSI growth model fit the data well and that the assumption of linear change over time adopted by the CSI and HLM models is unwarranted, given the data. Although the FCSI is one growth model for these data, it may be that other more parsimonious models of growth may account for the data as well. As mentioned earlier, these models are variants of the FCSI model and involve selective redaction of components associated with the intercept and slope factors of the FCSI model. As such, though some submodels are not nested with other submodels, all are nested within the FCSI model.

FM and FM-shift models

It may be that the FCSI model is unparsimonious because it stipulates the existence of two factors rather than one; specifically, it positsthat an Intercept factorexists as well as a Slope factor. Two such redactions of the FCSI growth model have been proposed as more parsimonious alternatives: the FM model (McArdle & Epstein, 1987) and the FM-shift model (Wood et al., 2013). These two models are similar in that they estimate variance components of only the slope factor. Although chronometric FM models for data have also been proposed (see McArdle & Epstein, 1987), the more generally used FM model estimates free factor loadings at all measurement occasions.

In the FM model, only Slope factor loadings (λ), slope FM (θ_s), and error variances (ε_i) are estimated. The slope variance (φ_s ) is fixed to 1 for identification purposes, and the remaining parameters associated with the Intercept factor are fixed to zero or redacted from the model specification entirely. Table 2 shows the estimated parameters of the FM model and associated fit measures, which are generally poor relative to the FCSI model, χ² (3) = 11.83, p < .01, CFI = 0.97, TLI = 0.97, RMSEA = 0.08, 95% CI = 0.04–0.13.² The χ² difference test between the FM and the FCSI model reveals that the FCSI model has demonstrably better fit, χ² (2) = 8.15, p = .02.

Table 2.

Comparison of prospective univariate antisocial personality models

	Model
Variable	FM	FM Shift	FCSI	MANOVA	τ Equiv.
Slope Factor Loadings (λ)
Age 18	1.29***	1.22***	0.69***	0	0
Age 21	1.11***	1.12***	0.12	−0.38***	0
Age 26	1.02***	1.09***	−0.21	−0.45***	0
Factor Means (θ)
Intercept	0	−2.50	1.58***	1.95***	1.67***
Slope	1.48***	3.64	0.51***	1	0
Covariance Between Intercept and Slope Factors (φI,S)
Covariance	0	0	0	0	0
Variances (φ and εi)
Intercept	0	0	1.35***	1.34***	1.32***
Slope	1	1	1	0	0
E1	1.06***	1.06***	0.73***	1.18***	1.24***
E2	1.45***	1.43***	1.49***	1.18***	1.24***
E3	1.06***	1.06***	0.73***	1.18***	1.24***
Selected Fit Measures
χ2 (df)	11.86 (3)	8.09 (2)	3.71 (1)	15.72 (4)	58.33 (6)
TLI	0.97	0.97	0.98	0.97	0.92
CFI	0.97	0.98	0.99	0.97	0.85
RMSEA	0.08	0.08	0.08	0.08	0.14
90% CI	0.03–0.13	0.03–0.15	0.00–0.17	0.04–0.13	0.11–0.17

Note: Corresponding intercept factor loadings are fixed to unity. FM, factor mean; FCSI, free curve slope intercept; MANOVA, multivariate analysis of variance; E1, Estimate 1; E2, Estimate 2; E3, Estimate 3; TLI, Tucker–Lewis index; CFI, comparative fit index; RMSEA, root mean square error of approximation; CI, confidence interval.

^***p < .001.

As noted in Wood et al. (2013), the FM model has a rather serious practical limitation in that it requires the assumption that all variables (manifest and latent) are measured at the ratio level. More recently, the FM-shift model has been proposed as a more general extension of the FM model, requiring only the assumption that manifest variables are measured at a common interval (as opposed to ratio) level of measurement. This is accomplished by the addition to the FM model of a mean parameter for the intercept factor (θ_I), but absent variance or covariance components (φ_I = φ_IS = 0). The estimated θ_I acts as a “shift” operator to bring the (commonly measured) interval assessments to the ratio level values assumed by the FM model. Although adding or subtracting a uniform constant to all manifest variables in the FM model would affect model fit, in the FM-shift model, such a change would affect only the estimated shift. Given that the psychological nature of many variables used in growth curve modeling, the assumption of a common interval scale for such variables seems more reasonable than requiring ratio level measurement (i.e., measurement with a meaningful zero point) as assumed in the FM model.

Parameter estimates and model fit shown in the FM Shift column in Table 2 appears close to that for the CSI model originally proposed, χ² (2) = 8.08, p = .003, TLI = 0.97, CFI = 0.98, and indicates a slightly better general level of model fit than the CSI and HLM models. Although just failing statistical significance when compared to the base FM model ${\mathrm{\chi }}_{\text{diff}.}^2(1)=3.77$, p = .05, it may be preferred in model construction to the FM model for these data because of its less restrictive measurement assumptions. When the FM-shift model is compared to the FCSI model (shown in the FCSI column in Table 2), the fit of the FCSI model is significantly better, ${\mathrm{\chi }}_{\text{diff}.}^2(1)=4.38$, p = .04. It is also worth noting, however, that the FM-shift model, which assumes only a single slope factor, generally accounts for the data better than the CSI and HLM models although this comparison is not nested.

Tau-equivalent FM models

Rather than redacting the intercept factor from the model, researchers may also begin by redacting the slope factor from the model. For example, it is possible to specify a strictly tau-equivalent factor model for the data by specifying an intercept factor with estimated mean and variance as well as equal measurement errors over time. Although the tau-equivalent model is usually expressed by factor variances fixed at unity with estimated and equal factor loadings, the fit of this model is equivalent to the usual specification because the models are equivalent via the tracing rules. As can be seen from the model fit of the τ Equiv. column in Table 2, the overall fit of this model is poor; however, this model may be used as a null model against which repeated measures analysis of variance may be compared. Specifically, this model estimates a common mean (of the intercept factor) across all measurement occasions and, if measurement errors are assumed equal, the assumption of compound symmetry is made of the data.³

MANOVA models

Some researchers choose to describe growth and change using repeated measures analysis of variance, attractive because of its wide use by researchers and the ease with which means across measurement occasions may be compared. Partridge and Lerner (2007) note, for example, that researchers who argue for the stability of temperament in longitudinal data frequently do so on the basis of repeated measures analyses of variance. As noted previously (Meredith & Horn, 2001; Meredith & Tisak, 1990), MANOVA models can also be expressed within the general framework for growth curves as well, enabling researchers to evaluate the merits of a MANOVA model to other structural models such as the FCSI. Estimated parameters for a repeated measures MANOVA for these data are shown in the MANOVA column in Table 2 in which the error variances are fixed to equality, the slope factor variance and covariance between slope and intercept factors are fixed to 0, the slope FM is fixed to 1, a reference loading for the slope factor (in this case the loading associated with age 18) is fixed to 0, with the remaining intercept FM and variance, as well as the remaining slope factor loadings freely estimated. The mean of the intercept variance in this model corresponds to the mean the initial measurement occasion. Slope factor loadings for the remaining measurement occasions are equal to the mean contrasts of each measurement occasion relative to the reference measurement occasion. As shown in the MANOVA column in Table 1, slope factor loadings associated with ages 21 and 26 are statistically significant, and a χ² difference test of the FCSI model relative to the MANOVA model favors the FCSI model, χ² (3) = 12.01, p < .001, suggesting that evidence exists for variability in the slope factor and for inequality of measurement error over time.⁴

To summarize the models presented in Tables 1 and 2, when viewed as structural equation models, the FCSI model appears to fit better than linear slope intercept models, hierarchical linear models, and traditional repeated measures analysis of variance. Three chains of nested comparisons with the FCSI were described, involving the linear growth, FM, and null model MANOVA. Heuristically, fit of the FM-shift model was better than the CSI model (Akaike information criterion and Bayesian information criterion values not reported here also favored the FM-shift model slightly), suggesting that model comparisons beginning with a general factor model may be a more reasonable strategy for fitting general models of deviance than an hierarchical CSI model of problem behaviors such as that considered by Hussong et al. (2008). We turn now to such general factor models as models involving a single construct of general deviance that spans multiple problem behaviors.

Estimation of general deviance factor

Earlier hierarchical CSI models

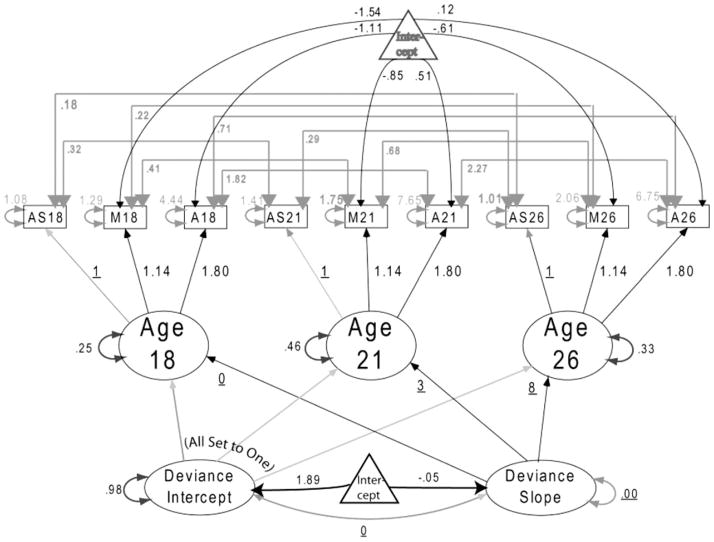
In Hussong et al.’s (2008) study, the original model for general deviance was a multiconstruct version of the CSI model, except that the three problem behaviors at each measurement occasion were modeled as “proneness” factors as shown in Figure 2. As can be seen in Figure 2, “proneness factors” at each measurement occasion were then modeled as a CSI using higher order intercept and slope factors. Means of each “proneness” factor were assumed to be a function of the higher order intercept and slope factors. When this model is fit to the data by us in the present study using the summary data reported in Hussong et al., fit of the model is poor, χ² (20) = 69.18, p < .001; TLI = 0.94, CFI =0.97, RMSEA =0.07, 90% CI =0.06–0.09, and, consonant with Hussong et al.’s (2008, p. 99) analysis, we found the variance of the slope factor was near zero (φ_s = .02). Following their analysis, we refit the model fixing both the φ_S and φ_IS to zero. As with Hussong’s analysis, the fit of the resulting model remained poor, χ² (22) = 88.44, p < .001; TLI = 0.93, CFI = 0.96, RMSEA = 0.08, 90% CI = 0.07–0.10).

Figure 2.

The Hussong et al. (2008) chronometric slope intercept model.

Monotrait multimethod factor models

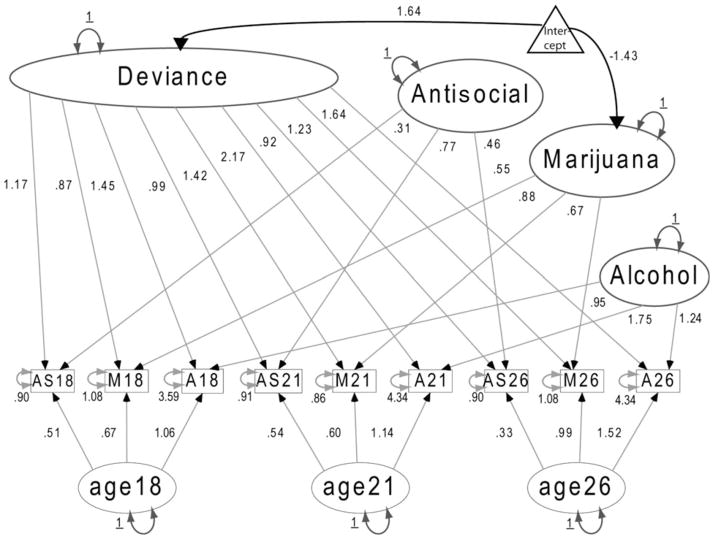
As an alternative, the construct of general deviance can be viewed as a monotrait multimethod factor model with estimated FMs. As such, a single trait factor of Deviance (as indicated by latent variable D in the model) is estimated with both FM θ_s and factor variance φ_s set to 1. This factor has, as indicators, all manifest variables in the study. Orthogonal method factors corresponding to antisocial behavior, marijuana, and alcohol are estimated, which include FMs as well with factor variances fixed to unity for identification purposes. Because data were assessed at three measurement occasions, factors corresponding to age assessments at 18, 21, and 26 factors were also specified with freely estimated FMs and variances fixed to 1. Following Hussong’s et al.’s (2008) approach, error variances associated with each problem behavior were constrained equal across their respective measurement occasions. Manifest variable intercepts μ are fixed to zero. As for the single construct analysis of antisocial personality, confidence intervals of estimated manifest variable error variances were examined to determine whether it was reasonable to assume equality of measurement error over time. Based on this, error variances for ages 18 and 21 were constrained to equality for both the antisocial personality and marijuana variables. Error variances for alcohol use at ages 21 and 26 were constrained to equality, perhaps reflecting differential alcohol consumption effects due to achieving the age of majority. The resulting fit of the model is quite good, χ² (14) =14.62, p =.40; TLI = CFI = 1, RMSEA = 0, 90% CI = 0–0.05. Because this model had fewer degrees of freedom than that proposed by Hussong et al. (2008), we examined pattern of statistical significance in the estimated parameters and found that the FMs associated with the age factors, as well as the antisocial and alcohol factors, were nonsignificant. We reestimated the model fixing these to zero, and parameter estimates for the standardized and unstandardized solution are shown in Table 3 and shown in diagram form in Figure 3. The fit of this model, χ² (19) = 26.72, p = .11; TLI = 0.99, CFI = 1, RMSEA = 0.03, 90% CI = 0–0.06, is within commonly accepted standards for acceptable fit.

Table 3.

Monotrait, multimethod parameter estimates for the Dunedin data

		Factor
Age	Measure	Deviance	Age 18	Age 21	Age 26	Antisoc. Pers.	Marijuana	Alcohol	Unique.
Standardized Factor Loadings (λ)
18	Antisoc. pers.	0.72	0.31			0.19			0.34
	Marijuana	0.54	0.44				0.34		0.33
	Alcohol	0.52	0.35					0.34	0.44
21	Antisoc. pers.	0.59		0.33		0.46			0.33
	Marijuana	0.71		0.28			0.44		0.22
	Alcohol	0.59		0.33				0.48	0.27
26	Antisoc. pers.	0.64			0.23	0.32			0.46
	Marijuana	0.61			0.49		0.34		0.27
	Alcohol	0.50			0.48			0.38	0.40
Unstandardized Factor Loadings (λ)
18	Antisoc. pers.	1.17	0.51			0.31			0.90
	Marijuana	0.87	0.67				0.55		1.07
	Alcohol	1.46	1.06					0.96	3.59
21	Antisoc pers.	0.99		0.54		0.76			0.91
	Marijuana	1.42		0.60			0.88		0.86
	Alcohol	2.17		1.14				1.75	4.34
26	Antisoc. pers.	0.92			0.33	0.46			0.90
	Marijuana	1.23			0.99		0.67		1.08
	Alcohol	1.64			1.52			1.23	4.34
	Factor means (θ)	1.64	0.00	0.00	0.00	0.00	−1.43	0.00

Note: Refer to Figure 3.

Figure 3.

The monomethod multitrait factor model with means (unstandardized solution).

When interpreted as a factor model with means, the estimated parameters from this solution are conceptually interpretable. Most problem behaviors over the developmental period of interest in this study appear to reflect a general deviance factor; and based on examination of the standardized loadings in Table 3, it appears that this deviance factor explains most of the variability, as evidenced by the standardized loadings of the deviance factor. Of these loadings, the standardized loading for alcohol use was generally lower than for the variables corresponding to marijuana and antisocial personality.

General deviance as hierarchical factor model

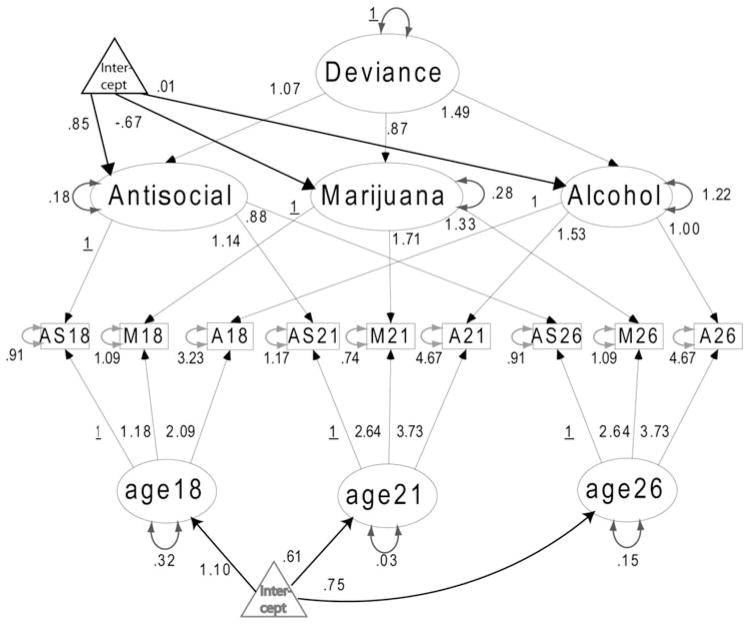
The monotrait multimethod approach described here has mathematical affinities with the hierarchical factor model in much the same way that the Schmid–Leiman decomposition of factor structure has relationships with a corresponding hierarchical factor model. As noted by the Cattell–White theorem (Cattell, 1978, chap. 9) factor solutions can be equivalently expressed between Schmid–Leiman and hierarchical factor representations of the data. The models considered in the Cattell–White theorem apply to structured exploratory factor models, and the fit of the corresponding hierarchical factor model as shown in Figure 4 is worth mentioning. In this figure, the three problem behaviors, antisocial personality, marijuana, and alcohol, are indicators of a general trait associated with their respective constructs. As with the previous model, individual age-specific method factors can be specified as well and the same equality constraints imposed across error variances as for the earlier deviance model. Fit of the model is acceptable, χ² (21) = 22.48, p = .37; TLI = CFI = 1.00, RMSEA = 0.01, 90% CI = 0.00–0.04. As can be seen, the three problem behaviors are substantial indicators of a general deviance factor (standardized loadings = 0.80–0.93), with only modest to moderate loadings associated with measurement occasion factors at ages 18 and 21 (standardized loadings = 0.09–0.52). The fit of the model appears a substantial improvement on the originally proposed linear hierarchical model, χ² (22) = 88.44, p < .001; TLI = 0.93, CFI = 0.96, RMSEA = 0.08, 90% CI = 0.07–0.10.

Figure 4.

The hierarchical factor model with means for the Dunedin data. The intercept is shown twice in the diagram for convenience of presentation.

Discussion

Developmental psychopathology takes a life course perspective to the study of psychological disorders such as antisocial behavior and substance use and misuse. Researchers in this field have frequently drawn on models of growth to examine their research questions. In the past few decades, researchers have moved beyond statistical techniques such as repeated measures analyses of variance to a variety of models of change, which include additional interindividual differences in change over time via latent variables with patterned factor loadings, such as the growth curve models considered here.

However, we may be at the point where researchers are not sufficiently critical of these models of growth. Although advances in statistical software make a variety of analytic techniques more accessible to the applied researcher, often some of these statistical models may involve assumptions about the data that are not warranted. Specifically, researchers should not necessarily blindly select chronometric models, because many of the phenomena of interest are not expected to increase or decrease linearly as a function of elapsed time. For example, nationally representative data sets have shown consistently that alcohol consumption (particularly heavy drinking) rapidly increases up to age 20 or 21 and gradually declines thereafter, leveling off in the 30s (e.g., Johnston, O’Malley, Bachman, & Schulenberg, 2011; Johnstone, Leino, Ager, Ferrer, & Fillmore, 1996). Unfortunately, many studies characterizing alcohol involvement over time use latent growth models to model growth in drinking as a linear trend. Even those that incorporate quadratic or “piecewise” growth factors may be making assumptions about growth that do not reflect reality.

Although in our example we specifically argue that researchers should consider competing models of growth when comparing a common underlying factor (deviance) model with time-bound models, our take-home message is more universal. We encourage researchers to use caution when applying models of growth. Our paper provides guidance on selection of appropriate models by comparing several structural models for growth and change over time, and we specifically offer the FCSI model as a general model that can be compared to more parsimonious alternatives. Future research should examine the extent to which different fixed and time-bound associations vary across these different models of growth and evaluate to what extent making erroneous assumptions about the data can alter substantive conclusions.

Specifically, we have stressed the need for researchers to formally compare candidate statistical models in terms of their characterization of interindividual differences over time before testing longitudinal hypotheses of interest. To the extent that these candidate models, when expressed in terms of structural questions, are nested, researchers can defend their rationale for selection of one or another longitudinal statistical model. For example, if a MANOVA model of the data fits poorly relative to other alternatives, a researcher may justify the more elaborate model on grounds of better fit. The examples considered in this paper raise questions about use of the MANOVA and the CSI model (and, by extension HLM and the hierarchical CSI model) as default frameworks for studying growth and change. These structural model comparisons of MANOVA, HLM, CSI, and FCSI growth models echo earlier sentiments expressed in more technical fora (e.g., Meredith & Horn, 2001). Although not all prospective models can be compared as nested comparisons when nested model comparisons are possible, they permit the researcher to more accurately specify the form of heterotypic continuity (or other traitlike constructs) for the constructs of interest. If a particular statistical model does not appear to meet its statistical assumptions, this does not mean that it must necessarily “lose” to more complex models. It may be, for example, that poor fit may be indicative of psychometric deficiencies in measurement or the presence of influential observations or outliers. Researchers making these adjustments, however, must be willing to defend their choices in this regard and to explore whether proposed effects are robust when, alternatively, models that make fewer assumptions of the data are considered. Even if, however, the mean levels of change over time appear to conform to polynomial or linear growth, researchers should examine whether individual-level change patterns actually conform to the model (as described by Liu et al., 2012, pp. 7–8). In sum, although a researcher cannot “carve nature at its joints” with selection of one model, such model comparisons seem far preferable to simply assuming heterotypic continuity be described using a particular model such as the linear growth model considered by Hussong et al. (2008) or repeated measures MANOVA.

On a more general methodological note, it was found here that the general factor model fit as well as or better than autoregressive alternatives in which earlier levels of one problem behavior were associated with later levels of some other problem behavior. This finding is not an accident or idiosyncratic characteristic of this particular data set. Rovine and Molenaar (2005) used Granger and Morris’s (1976) addition rules to show that covariance pattern can be constructed as a sum of autoregressive and moving average components. This is also a methodological parallel to Molenaar’s (2003) observation that longitudinal factor models of growth (such as a general deviance model) are “moving average models” that can be equivalently rewritten as equally well-fitting autoregressive models (e.g., a model involving “developmental snares”). Kuljanen, Brown, and DeShon (2011) make a similar point that HLM models assuming linear trend over time can be expressed as stochastic trend models. Our point in showing these issues in reverse (i.e., that autoregressive models may also be fit as moving average models) is that researchers may mistakenly believe that multiwave data can be used to detect time-bound causal relationships in data when, from a statistical perspective, the fit of autoregressive “launch” models or moving average “general deviance” models such as longitudinal factor growth models is equivalent and adjudication between such models is not possible using prospective observational data. As an example of Molenaar’s point, in the example data considered here, fit of the multitrait multimethod and hierarchical factor models was superior to even the time-bound launch and snare models considered by Hussong et al. (2008). As such, it appears premature to elevate the constructs of alcohol and marijuana use to a particularly critical status in description of the development of problem behavior and psychopathology over the developmental period considered here when any proposed link (autoregressive) model can be equivalently expressed as a general (moving average) model.

However, some argument can be made for the primacy of the antisocial personality measure assessed at age 18 within a general factor model: the standardized deviance factor loading associated with antisocial personality at age 18 appears slightly larger than standardized coefficients associated with antisocial personality assessed at other measurement occasions or for other constructs at any measurement occasion. Similarly, the standardized loading associated with antisocial personality in the hierarchical model shown in Table 4 is also the largest of the three problem behaviors, suggesting that it is more closely associated with general deviance. There is, however, no reason to conclude from this that problematic alcohol and marijuana use at age 18 are necessarily developmental “snares” for antisocial personality. It may be that antisocial personality assessed at age 18 is simply the most reliable indicator of general deviance and that other measurement occasions and behaviors are less accurate indicators of the general deviance factor.

Table 4.

Hierarchical deviance factor model

			Substance Use Subfactors
Depend. Variable	Independ. Variable	Unstand. Est.	Antisocial	Marijuana	Alcohol	Error Variance ( εi)	Uniqueness
Antisocial	Deviance	1.07 (0.93)				0.17	0.13
	Variance = 1
	Mean = 0
Marijuana		0.86 (0.85)				0.28	0.28
Alcohol		1.49 (0.80)				1.22	0.36
Age 18	Age 18
Antisocial	Variance = 0.32	1 (0.36)	1 (0.72)			0.91	0.36
	Mean = 1.10
Marijuana		1.18 (0.42)		1 (0.63)		1.09	0.42
Alcohol		2.09 (0.42)			1 (0.65)	3.23	0.40
Age 21	Age 21
Antisocial	Variance = 0.03	1 (0.09)	1.14 (0.77)			1.17	0.40
	Mean = 0.61
Marijuana		3.65 (0.29)		1.71 (0.86)		0.74	0.18
Alcohol		5.80 (0.25)			1.53 (0.77)	4.67	0.34
Age 26	Age 26
Antisocial	Variance = 0.15	1 (0.27)	0.88 (0.70)			0.91	0.43
	Mean = 0.75
Marijuana		2.64 (0.52)		1.33 (0.68)		1.09	0.27
Alcohol		3.73 (0.46)			1.00 (0.58)	4.67	0.45
Subfact intercept			0.85	−0.67	0.01

Note: Refer to Figure 4. The underscored values denote values fixed for identification reasons, and the numbers in parentheses are standardized values.

Implications for future research

Mixture models

Other approaches to the identification of linkages have involved use of factor mixture models to identify different subgroups of at-risk, or differentially linked subpopulations because these models are based on factor models (frequently CSI models). Care must be taken, however, to correctly parameterize the factor structure underlying the data and to correctly identify the factor model parameters that differentiate subgroup membership, and even then such identified subgroups are at best suggestive of the existence of an at-risk or “hardy” subpopulation or are perhaps only an artifact of distributional properties of the data (see, e.g., Bauer & Curran, 2003; as well as a commentary in response, Muthén, 2003).

State-space models

However, it may be that identification of linkages and turning points may be entirely an idiosyncratic function of the trajectory of change at the individual level. This has been highlighted in earlier conceptual articles dealing with the “loss” of the individual in developmental data, particularly as it applies to the study of psychopathology (Bergman & Magnusson, 1997; von Eye & Bergman, 2003). There is some reason to believe that individual change patterns may not be generalizable across individuals, thus invalidating the use of a common growth curve (or any factor model, for that matter). There is some reason to believe that this may be the case, and state-space models have been proposed to test such propositions and to introduce alternatives to common factor structural equation models for such data (Molenaar, 2004; Molenaar, Huizenga, & Nesselroade, 2003; Schmitz, 2000). Although the technical aspects of conducting such analyses can be daunting, such analyses may provide new insights into the dynamics of at-risk individuals (Kuljanen et al., 2011). Such analytic models hold promise for the identification of bifurcations in performance at the individual level, permitting researchers to identify developmental turning points that may be idiosyncratic to each individual (e.g., for a discussion of how individual-level bifurcations can be thought of as a third source of variability in behavior genetic models, see Kan, Boomsma, Dolan, & van der Maas, 2012).

Causal inference based on instrumental variables and controlled experiment

Given that the equivalence of general factor and autoregressive models proves again the old adage that “correlation does not imply causality,” it seems appropriate to suggest some directions for better assessing whether turning points and linkages exist in the data. One clear possibility is to conduct controlled experiments in which the researcher employs an intervention designed to affect one problem behavior at a given measurement occasion and then observes subsequent changes in the trajectory and level of other constructs. Such models could include general factors of general deviance and could include specific components designed to assess change and elevation effects subsequent to the intervention. It may be, in some situations, that researchers may all reasonably agree on “instrumental variables” (Bollen, 1989) in which one manifest variable is viewed as indisputably causing a latent variable in the model. For example, controlled experiments constitute one such instrumental variable within a prospective structural model given that participants have been randomly assigned to condition.