Abstract
Tumor selective, replication competent viruses are being tested for cancer gene therapy. This approach introduces a new therapeutic paradigm due to potential replication of the therapeutic agent and induction of a tumor-specific immune response. However, the experimental outcomes are quite variable, even when studies utilize highly inbred strains of mice and the same cell line and virus. Recognizing that virotherapy is an exercise in population dynamics, we utilize mathematical modeling to understand the variable outcomes observed when B16ova malignant melanoma tumors are treated with vesicular stomatitis virus in syngeneic, fully immunocompetent mice. We show how variability in the initial tumor size and the actual amount of virus delivered to the tumor have critical roles on the outcome of therapy. Virotherapy works best when tumors are small, and a robust innate immune response can lead to superior tumor control. Strategies that reduce tumor burden without suppressing the immune response and methods that maximize the amount of virus delivered to the tumor should optimize tumor control in this model system.
Keywords: cancer gene therapy, virotherapy, initial conditions, heterogeneity, mathematical modeling, nonlinear least square fitting
INTRODUCTION
Patients with cancer have variable outcomes—they respond differently to therapy and they survive for variable periods of time from diagnosis.1 There are many explanations for this variability, including host-specific factors (for example, susceptibility to the specific tumor, pharmacogenomics, general health, physiologic state) as well as tumor-specific features (collectively known as the ‘biology’ of the tumor and include the specific mutations that lead to tumor development, resistance to therapy).2–4 However, experiments in animal models using closely inbred strains of mice (for example, C57BL/6) that are implanted with tumor forming cells derived from the same cell culture and treated identically (for example, with a replicating virus such as vesicular stomatitis virus (VSV)) also result in significant differences in outcome.5–14 The differences are unlikely to be due to host genetic factors or the behavior of the implanted cells since they are often from the same culture, as is the batch of virus used for attempted control of the tumor. Therefore, the reasons behind this difference must lie elsewhere.
Tumor therapy with replicating viruses is unlike any other form of cancer therapy since (i) the therapeutic agent (virus) can be amplified by the cancer cells,15–17 (ii) the virus can be armed to induce a bystander effect18–21 and (iii) the virus may alert the immune system to induce, or enhance, an attack against the tumor.7,11–14,20 One can consider tumor virotherapy as an exercise in population dynamics due to the complex interactions between the virus, tumor and immune system. As a result, dynamic modeling is required to understand these interactions and provide rational predictions about the optimal way to utilize these exciting novel cancer therapeutics. Various groups have developed mathematical and computational models to understand the dynamics of tumor virotherapy. These models relate to a variety of tumor types as well as viruses that kill cells via different mechanisms.15,22–39 In the following analysis, we utilize our modeling approach to try and understand the diverse outcomes observed with tumor virotherapy in a seemingly homogenous host and tumor cell population. We utilize data on VSV therapy of B16ova melanoma tumor cells that are syngeneic to C57BL/6 mice with a fully competent immune response making them a realistic model for the translation of these novel therapeutics into humans. Our results illustrate the critical importance of initial conditions on the outcome of therapy and suggest ways in which these conditions can be optimized to improve therapeutic outcomes.
RESULTS
Growth of untreated tumor cells
In order to determine the growth characteristics of B16ova in immunocompetent C57BL/6 mice, we fitted serial tumor growth data to the generalized logistic as well as to its special case, the Gompertz model. Data from untreated tumors as well as tumors injected with heat-inactivated (HI) VSV were both considered. Both models led to good fits (Figure 1); however using the model selection criteria, we chose the preferred model for each data set. Note that growth of tumors treated with the HI virus was the same as in the control mice treated with phosphate-buffered saline (PBS), and therefore, some virus replication is necessary for any anti-tumor effect.12
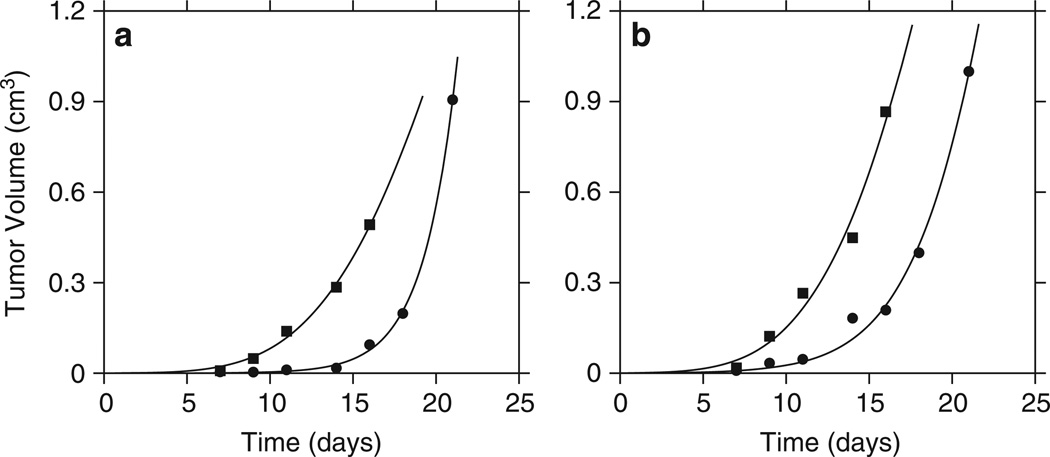
Figure 1.
Fitting of tumor growth models to in vivo data. Each curve represents serial data on one tumor with a total of four tumors represented. (a) The tumors were injected with PBS. (b) The tumors were injected with HI virus. The square symbols represent fitting of data by the Gompertz model, which was preferred according to the used model selection criteria (ΠA=0.0028; ΠB=0.011). The circles correspond to data fitting using the generalized logistic model (ΠA=0.0026; ΠB=0.024).
Initial tumor size and outcome
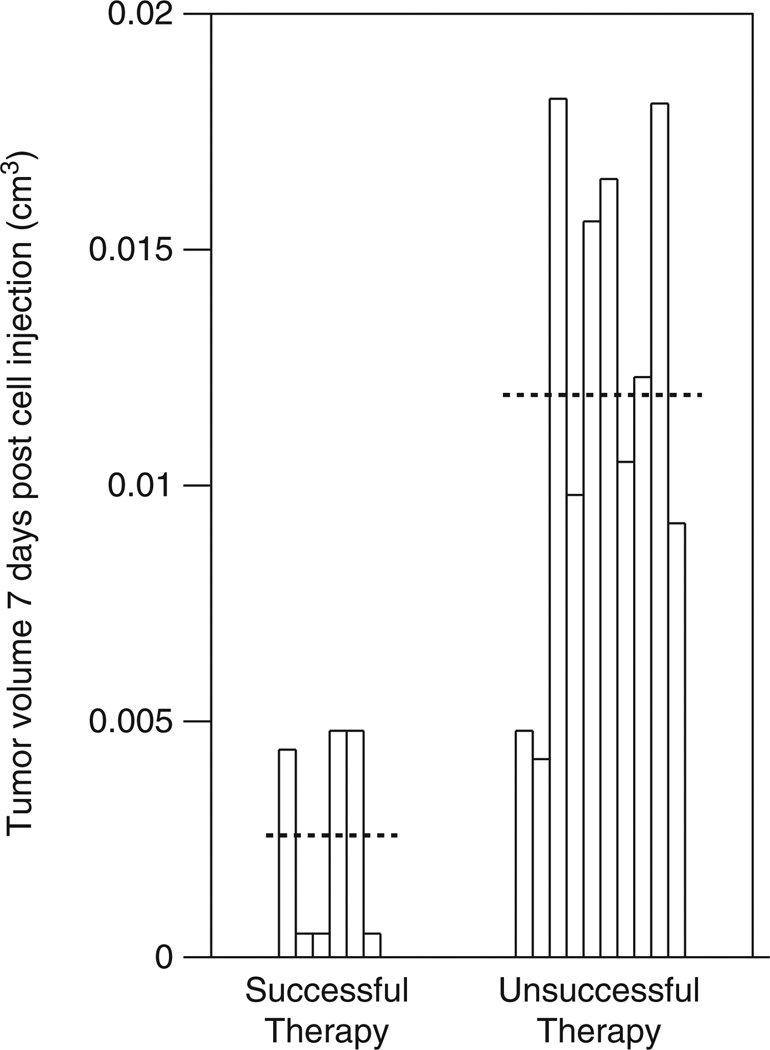
Mass action kinetics would suggest that treating a larger tumor could lead to superior results due to a higher probability of infecting tumor cells. Therefore, we initially determined whether there were any significant differences in tumor size at the time of initiation of therapy. Using the F-test, we determined that tumor volume 7 days after cell line injection (before the injection of the virus or control) was not significantly different between the four experimental groups: PBS injected control, HI group and the two intervention groups injected with 8 or 17 doses of virus (P=0.4070). However, therapy with the virus led to better overall survival: while overall survival was not significantly different among the PBS and HI groups (P=0.4597) nor among the two treated groups (P=0.9464) by the log-rank test, there was a significant difference between the control groups and the treated groups (P=0.0019). We next determined whether the individual tumor size at the initiation of therapy impacted the outcome of the mice treated with the virus. Using the effect likelihood ratio test, the tumor volume 7 days after tumor cell injection had no impact on overall survival in the two control cases (P=0.2611), but had significant influence in the viral-treated groups (P=0.009) (Figure 2). As the tumor increases in volume, the risk of death increases: an increase of 0.01 cm3 increased the risk of treatment failure and death by a factor of 3.92. Therefore, treating smaller tumors appears to lead to better outcomes and tumor size at the initiation of therapy (y(0)) is a critical initial condition.
Figure 2.
The tumor burden at the time of initiation of therapy determines outcome. The mice were separated into two groups based on the outcome of therapy. The horizontal dotted line represents the mean volume.
Variability in the virus dose available for infection
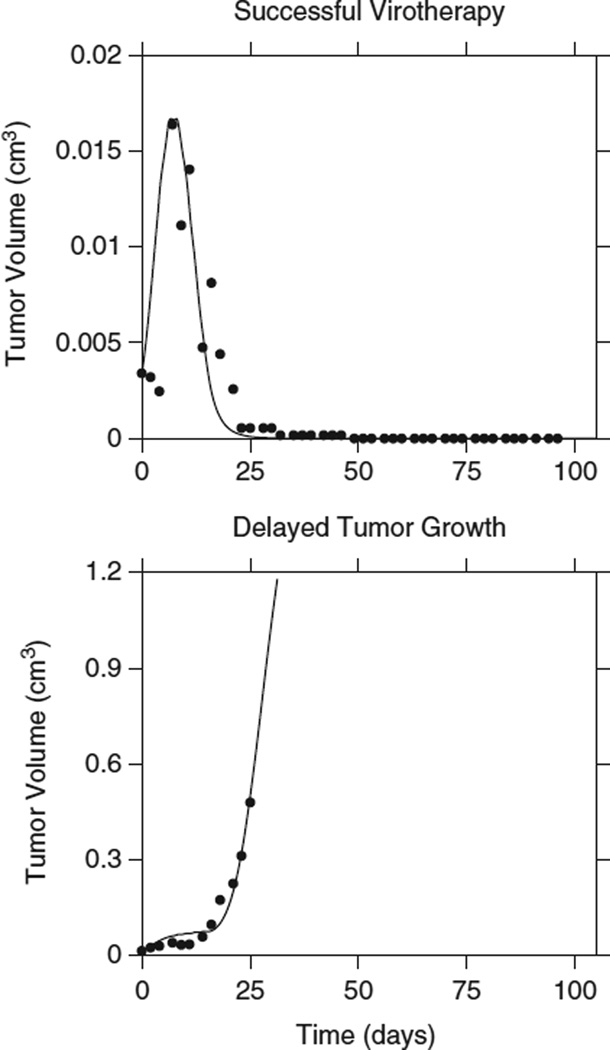
We observed that there were three general patterns of tumor behavior in response to virotherapy with VSV: mice that were cured of their disease, mice where the tumor was controlled while on therapy but grew once therapy was stopped and mice where virotherapy had no impact at all on tumor growth (Figure 3). Tumor growth and response data from these three groups were combined and we fitted the model to the averaged tumor growth data for each group. Having established the importance of the initial tumor size on the outcome of therapy, we attempted to simultaneously fit tumor growth curves for the three groups of mice, while keeping the growth parameters the same. Our goal was to consider the initial tumor size as the only variable that influenced the outcome. This approach did not lead to good fits, implying that y(0) is not the only parameter that influences the outcome (Figure 4).
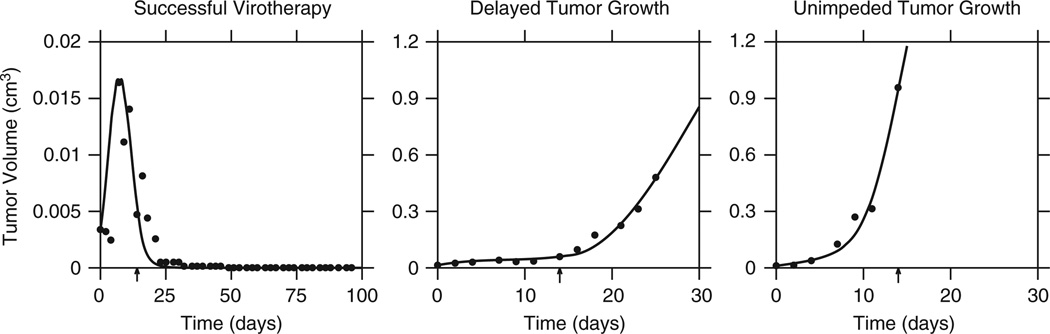
Figure 3.
Tumors treated with VSV exhibited three behaviors: cure, delayed growth and unimpeded growth. The data were fitted by the model given by Equations (1–5). The arrow on the time scale indicates the end of therapy (Πcure=0.33; Πdelayed=0.023; Πunimpeded=0.02).
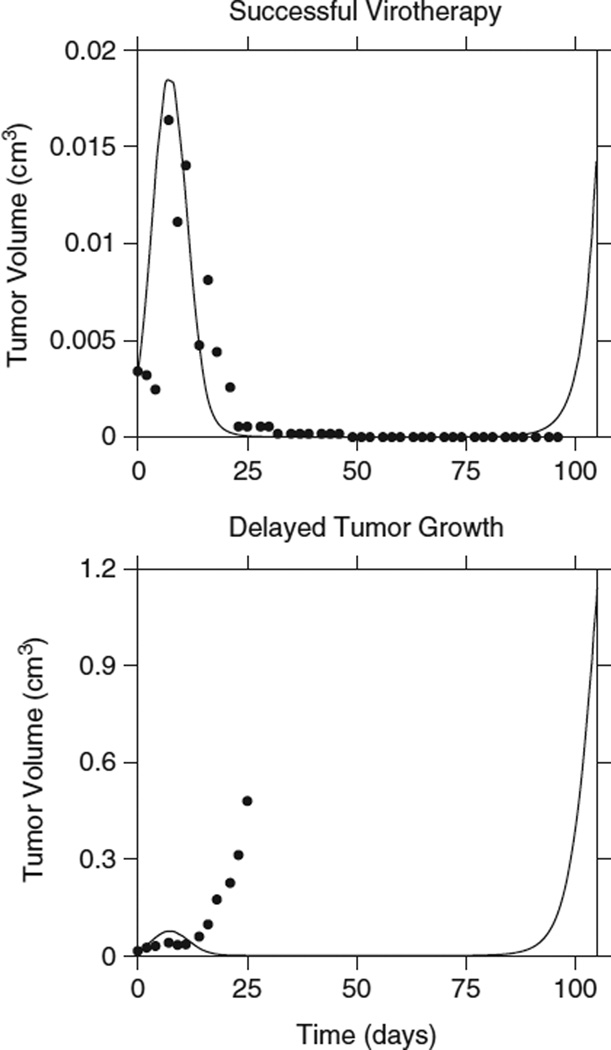
Figure 4.
Initial tumor burden and the outcome of virotherapy. Data from a successfully treated tumor is fitted using the same parameters for a tumor that is transiently slowed. The initial tumor sizes differ: for successful virotherapy it is 0.0034 cm3, while for delayed growth it is 0.0146 cm3. However, this difference in initial tumor size alone is not enough to explain the outcome of virotherapy (Πcure=0.402; Πfailed=1.79).
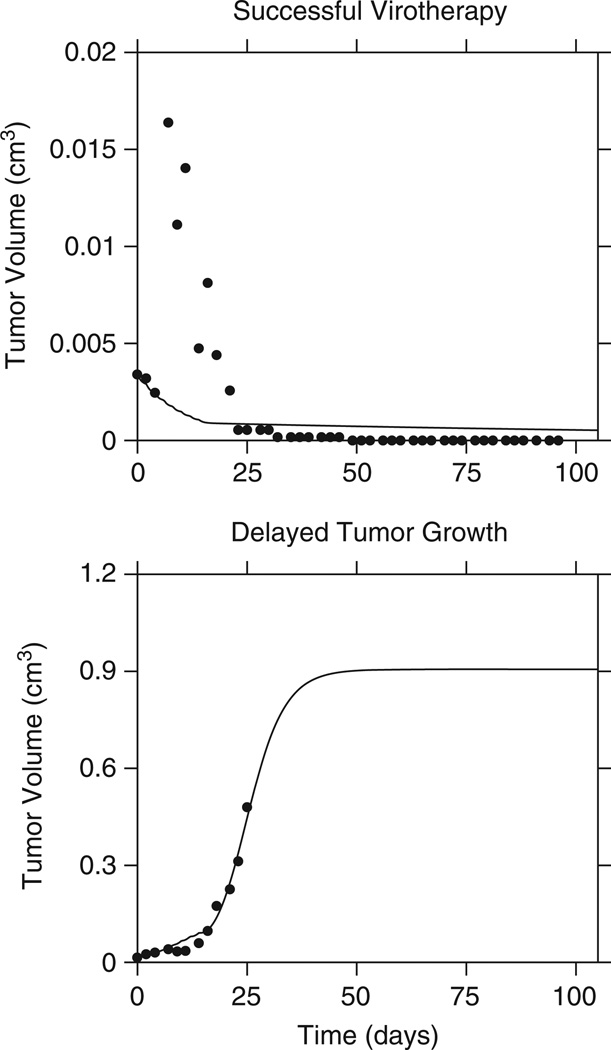
We therefore proceeded to consider the impact of v(0) on the outcome, using the estimated average value of y(0) for each group. Although the virus was administered intratumorally and the total dose injected was known (kept constant at 5×108 PFU in 50 µl PBS), we reasoned that it was unlikely that all the virus particles that were injected remained in the vicinity of the tumor and could successfully infect tumor cells. Therefore, we introduced a correction parameter c that estimated the fraction of each dose of virus that is effectively present at the tumor site after injection. With this maneuver, the simultaneous fitting of cured versus controlled versus uncontrolled tumors improved substantially (Figure 5). Surprisingly, we found that the fraction of the effective dose size was invariably small and generally <15% of the injected dose. Note that we assumed that this fraction was constant for a given mouse despite repeated injections and therefore it represents an ‘average’ fraction of injected virus for a given mouse. This parameter was reasonably consistent across all mice.
Figure 5.
The injected dose of virus is a variable. Treated tumor growth data simultaneously fitted as in Figure 4. However, here the fraction c of the total dose injected is introduced as a free parameter fitted for each set of data, yielding c=0.0958 for successful therapy and c=0.1201 for delayed growth (Πcured=0.33; Πfailed=0.043).
The antiviral immune response
Another potential variable that can influence the outcome is the size of the immune cell population that can respond to the infected cell population40 (resulting in a bystander killing of uninfected tumor cells7). Therefore, we introduced in a model a variable number z0 of immune cells available at the time of virus administration (see Equations (1–5)). Again, we determined that there is variability in the size of this population of cells; mice with a higher number of innate immune cells that can recognize VSV-infected cells tended to have a superior outcome. However, the impact of this variable on the fit was not as strong as that of the initial virus dose (Figure 6). This of course makes sense, since one does not expect significant variability in the innate immune response to the same antigens in these closely inbred mice.
Figure 6.
Preexisting immunity and the outcome of therapy. Treated tumor growth data were simultaneously fitted as in Figure 4. However, here z0 (see text) is introduced as a free parameter fitted for each set of data, yielding z0=108 for successful therapy and z0=5×107 for delayed growth (Πcured=0.924; Πfailed=0.026).
Simulations
In our prior work to understand the dynamics of tumor therapy with measles virus, simulations often led to the appearance of population oscillations where the virus and the tumor cells oscillate out of phase with each other in the absence of an immune response.28,32,33,37 This dynamic behavior has been observed in immunodeficient animal models.41 Other models of tumor virotherapy with lytic viruses also suggest such oscillatory behavior.22,23 However, this behavior has not been observed with VSV oncotherapy. With the inclusion of an effective initial population of virus, our model is able to describe nonoscillatory behavior.
DISCUSSION
Tumor virotherapy offers exciting prospects for the field of oncology and many patients have been enrolled in clinical trials that have shown the safety of the approach as well as tantalizing evidence of efficacy in various tumor types.42–44 However, the outcomes of therapy are quite variable and the reasons for these differences must be understood in order to optimize the use of such novel therapies. Although the outcomes may be due to heterogeneity in host and tumor related genetic factors, these explanations ostensibly are not present in highly inbred strains of mice and in vitro cell culture systems, especially when experiments are performed using a single cell and virus stocks. Here, we show how mathematical modeling can illustrate and provide biologically plausible explanations for the variability in outcomes.
In this work, we have demonstrated that the initial conditions have a determining role on the outcome of therapy, as suggested by other investigators in the field.45–47 It appears that tumor cytoreduction before the introduction of the oncolytic virus may lead to superior results, in the sense that the initial conditions could be stacked in favor of the virus. Perhaps, this is one mechanism by which alkylating agents such as cyclophosphamide can improve the success of oncolytic virotherapy.6,48 However, such therapy ideally should not interfere with the immune response since it is clear that, at least in this model, the bystander killing of uninfected tumor cells by the immune response is of some relevance for cure.7 Some tumors are amenable to intralesional injection of the virus. Although this is expected to improve the rate of infection of tumor cells, our analysis suggests that only a small fraction of the virus actually infects the tumor. Methods that can reduce the wastage of virus outside the tumor microenvironment should help to improve disease control rates. It has been shown that hydrodynamic forces may have an important role on the distribution of the virus in the tumor environment.34,49,50 Therefore, strategies that optimize the delivery of the virus are urgently required to also improve on this important initial condition.
The maxim in cancer therapy has been that it is better to treat a smaller tumor rather than a larger one and in general smaller tumors are associated with a superior outcome. This is the basis of the TNM classification of tumors and its impact on prognosis. However, the field of cancer virotherapy has provided the impression that, given the potential amplification of the therapeutic agent due to local new virion production from infected tumor cells, that perhaps this oncologic paradigm may be broken. Unfortunately, it appears that even with virotherapy, a smaller tumor is a better therapeutic target and indeed, we have a race between the tumor, the virus and the immune system.27
One criticism of mathematical modeling of virotherapy has been the prediction of oscillatory behavior across the various populations. This behavior is well known in population dynamics and ecology and it was such an observation that ushered in the era of mathematical biology almost 100 years ago. However, most tumors do not appear to oscillate in size although this depends on the scales at which tumors are measured (both time scales and geometry). However, in in vivo studies with other oncolytic viruses (MV-Edm-based derivatives), clear oscillations have been observed, perhaps due to the lack of an immune response.33,41 It is possible that such behavior will not be observed in the presence of an immune response to the virus. To our knowledge, such oscillations have not been observed with VSV-treated tumors. Interestingly, the introduction of the correction term c that accounts for the variable fraction of virus particles that actually infect tumor cells essentially eliminated this ‘problem’ in our model while maintaining biological plausibility.
One can postulate that other explanations may exist for the variable outcomes observed in the experiments and certainly no model can be comprehensive enough to include all possibilities. However, our model provides biologically plausible explanations that also make fitting of the data significantly better. The conclusion that the initial tumor size, the extent of innate immune response to the administered virus and the actual dose of virus available to infect the tumor cell population all influence the outcome is mathematically logical and also biologically.45–47 and clinically relevant. Overall, our analysis suggests that attempts to improve the outcomes of therapy will be more successful if these observations are taken into consideration: the dice could finally be skewed in favor of therapy rather than the tumor!
MATERIALS AND METHODS
Cell line
The murine B16ova melanoma cell line (H2-Kb) was derived from B16 cells by transduction with a cDNA coding for the chicken ovalbumin gene.51 The cells were grown in Dulbecco’s modified Eagle’s medium with glucose (4.5 g l−1) and l-glutamine without sodium pyruvate (Mediatech, Herndon, VA, USA) supplemented with 10% (v/v) fetal bovine serum (Life Technologies, Carlsbad, CA, USA) and maintained in a humidified incubator at 37 °C with 5% CO2.
Virus
VSV Indiana strain, engineered to express the green fluorescent protein (VSVGFP)52 was a gift from G Barber (University of Miami School of Medicine, Miami, FL, USA). The virus was amplified by infection of BHK-21 cells at a multiplicity of infection of 0.01 for 24 h. The culture supernatants were filtered and purified by sucrose gradient centrifugation. The virus pellet was resuspended in PBS, aliquoted and stored at −80 °C. The virus titer was determined by a standard plaque assay on BHK-21 cells.7
Mouse work and monitoring
All procedures were approved by the Mayo Clinic Institutional Animal Care and Use Committee. C57BL/6 mice were purchased from The Jackson Laboratory (Bar Harbor, ME, USA) at 6–8 weeks of age. To establish subcutaneous tumors, 5×105 B16ova cells in 100 µl of PBS were injected into the right flank of mice. The virus was injected intratumorally (5×108 PFU in 50 µl PBS) every other day starting on day 7 after implantation of the cells in all mice. Each group was composed of eight mice. HI virus was also used as a control, apart from a cohort of tumor bearing mice that were injected with PBS alone. The duration of therapy was variable depending on the protocol (see Results section). Mice were monitored daily for tumor burden and overall health. Caliper measurements of subcutaneous tumors were taken three times a week with the animals being killed when tumor size was ~1.0×1.0 cm2 in two perpendicular directions.
Statistical analysis
We grouped the mice according to the therapeutic intervention and analyzed the distribution of tumor sizes at the time of initiation of therapy. The purpose was to determine whether there was any correlation between tumor size at the initiation of therapy and treatment outcome (cure versus failure) as well as overall survival. We used the F-test, to determine whether there was any difference in tumor volume at the start of therapy. Overall survival was defined as the number of days of observed follow-up and not as a function of tumor volume at a particular time. Mice that survived for the full duration of the experiment have a follow-up value equal to that amount of time (103 days). Mice that died before the end of the experiment were uncensored while those that survived were censored accordingly. Differences in overall survival were tested with the log-rank test. The impact of tumor size at the time of therapy on outcome was determined using the Cox proportional hazards model. For all statistical analysis, a P<0.05 was considered statistically significant.
Mathematical modeling
The dynamic description has to consider growth of uninfected tumor cells (y), the population of infected tumor cells (x), the free virus population (v) and the cellular immune response (against virus-infected tumor cells as well as uninfected tumor cells, z). We start by modeling the growth of untreated tumors that can follow either a Gompertz model or a generalized logistic model (see the first term on the right-hand side of Equations (1) and (2), below). Both models have been shown to adequately describe untreated tumor growth under a variety of conditions.53 For each untreated tumor, either model was chosen based on the best fit for that specific tumor33 according to model selection criteria (Akaike, Bayesian28,32). Both models impose a maximum size that the tumor can reach, known as the carrying capacity (K) with tumor growth slowing as this value is approached. This leads to the familiar sigmoidal curves for tumor growth.54
Tumor virotherapy is modeled by the following system of differential equations:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where y represents the population of noninfected tumor cells, x is the population of infected tumor cells, v is the population of free virus present and z is the effective immune response.
Introduction of the virus leads to infection of some of the tumor cells at a rate βyv. Whenever a dose of virus is injected at time t>0, the functions are updated to accommodate the fact that the virus population at that time (due to production of new virions from infected tumor cells) is augmented by the addition of exogenous virus and this larger virus population is now available to infect additional tumor cells. The infected cells produce virus at a rate αx and die at a rate δx. Not all of the virions produced are infectious and there are nonimmune mechanisms of virus inactivation. These mechanisms eliminate free virus at rate ωv. With respect to the immune response, we consider that the animals already have immune cells that can recognize the virus but these cells are amplified in the presence of virus-infected tumor cells. This is compatible with the clonal selection theory of immunity—cells that recognize the epitopes are present even before exposure to the antigen and they replicate in response to the antigen.40 The immune response is also able to keep tumor growth in check (to some extent)—hence the term λ(z+z0)y in Equations (1) and (2). In the presence of a therapeutic virus, this immune control on tumor growth can become more prominent as postulated for VSV previously.7,11–14,20 Initially, we introduced different rate parameters (λ1 and λ2) to describe the immune response against tumor cells and virus-infected tumor cells, respectively, assuming that λ2≥λ1. However, data fitting repeatedly showed that these two parameters were essentially the same in value. Hence, we simplified the model and consider that the rate of the immune response is the same for infected versus uninfected tumor cells (λ).
We impose a limit on the size of the immune response to both the viral infection as well as the tumor, compatible with most other physiological processes. This is achieved by introducing the factor (1−z/ξ). Moreover, immune cells die at a rate yz. The initial conditions are y(0)=y0, x(0)=0, v(0)=cvi (where vi is the injected dose and c is a variable from 0 to 1 that captures the fact that only a fraction of the injected dose of virus is able to infect tumor cells), z(0)=0. Collectively, these considerations lead to the above set of nonlinear differential equations with equilibrium points, which can be analyzed along the lines similar to those described in Dingli et al.28 and Bajzer et al.32 A fundamental assumption of the model is that we have mass action kinetics and the populations are homogenously mixed. Alternative models based on partial differential equations are more complex and ultimately lead to similar results.15,24–27,29–31,34,35 Although stochastic models may be used to understand these dynamics,35,39 with large populations, the deterministic and stochastic models give very similar results (at least on average) and the former are much simpler to analyze.
Model fitting and parameter estimation
The available experimental data were in the form of serial tumor diameters in two dimensions. This was used to determine tumor volume (given by a2b/2, where a is the shorter diameter), and then converted to cell population assuming that 1 mm3 ≈1×106 tumor cells. In order to determine the best tumor growth model for a specific tumor, we fitted the generalized logistic or its limiting case, the Gompertz model (for which explicit expressions are known53,54) to serial growth data for tumors that were injected with PBS alone. We performed nonlinear least squares fitting with the use of custom software together with a powerful minimizer based on the simplex-induction hybrid algorithm that has been described previously.55 The preferred model was determined by using several model selection criteria including the modified Akaike and Bayesian selection criterion as previously described.28,32
Since the tumor cell population injected across mice is similar and the mice are syngeneic, we expect limited variability in the growth characteristics of the tumor cells (r, K, ε). However, the results suggested that the tumor size at the initiation of therapy was a major determinant of the outcome (see the Results section). Moreover, tumor growth was variable across the mice. Presumably, this variability could be due to differences in the actual number of cells injected and the intrinsic variability in tumor forming potential of the injected cells as well as other unquantifiable parameters. In order to account for this variability, when fitting the growth function to the untreated tumor cohort, we allowed y(0) to vary by imposing a maximum value based on the number of cells that were injected, that is, y(0)∈[1,5×105]. Subsequently, we divided the mouse data into outcome groups: cured tumors, delayed tumor growth and unimpeded tumor growth (based on the dynamics of tumor growth). For each group, the average growth curve was calculated, which included the average tumor size at the start of virotherapy. To compare the behavior of the established groups, data from the group of cured mice were simultaneously fitted with data for unimpeded growth assuming the parameters α, β, γ, δ, η, λ, ξ, ω to be the same for both groups (Figure 4). When we performed the pairwise comparisons, for the nonlinear least squares fitting, each curve was weighted by the respective mean tumor volume as determined experimentally. Given that not all of the virus population injected at any time was available to infect tumor cells, we introduced a variable c that can range from 0 to 1. The value of this parameter was determined by fitting and was different for each group. Initially, we considered that the level of preexisting immunity to the virus was the same across all mice and therefore z0 was held constant (estimated to be 104 cells). Four fits were performed assuming four sets of available tumor growth parameters (r, K, ε) obtained from fitting tumor growth curves for nontreated mice. The best among those fits was retained (Figure 5). Similar fits were performed assuming c=1 and z0∈[0,108], which was different for each group (Figure 6). The same procedure has been adopted when comparing the group of cured mice with the group in which tumor growth was only delayed by therapy. Throughout the fitting process, we determined the ratio of model error variance to data variance and report this value as Π for the parameter fits (see Supplementary Table S1).
Supplementary Material
ACKNOWLEDGEMENTS
This work was supported by R01 CA130878 and R01 CA107082 (RGV) and the Minnesota Partnership for Biotechnology and Medical Genomics (DD and ZB). Technical support from J Thompson and T Kottke is greatly appreciated.
Footnotes
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Supplementary Information accompanies the paper on Gene Therapy website (http://www.nature.com/gt)
References
- 1.Jemal A, Siegel R, Ward E, Hao Y, Xu J, Thun MJ. Cancer statistics, 2009. CA Cancer J Clin. 2009;59:225–249. doi: 10.3322/caac.20006. [DOI] [PubMed] [Google Scholar]
- 2.Vogelstein B, Kinzler KW. Cancer genes and the pathways they control. Nat Med. 2004;10:789–799. doi: 10.1038/nm1087. [DOI] [PubMed] [Google Scholar]
- 3.Sjoblom T, Jones S,Wood LD, Parsons DW, Lin J, Barber TD, et al. The consensus coding sequences of human breast and colorectal cancers. Science (New York, NY) 2006;314:268–274. doi: 10.1126/science.1133427. [DOI] [PubMed] [Google Scholar]
- 4.Greenman C, Stephens P, Smith R, Dalgliesh GL, Hunter C, Bignell G, et al. Patterns of somatic mutation in human cancer genomes. Nature. 2007;446:153–158. doi: 10.1038/nature05610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Qiao J, Wang H, Kottke T, Diaz RM, Willmon C, Hudacek A, et al. Loading of oncolytic vesicular stomatitis virus onto antigen-specific T cells enhances the efficacy of adoptive T-cell therapy of tumors. Gene Therapy. 2008;15:604–616. doi: 10.1038/sj.gt.3303098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Qiao J, Wang H, Kottke T, White C, Twigger K, Diaz RM, et al. Cyclophosphamide facilitates antitumor efficacy against subcutaneous tumors following intravenous delivery of reovirus. Clin Cancer Res. 2008;14:259–269. doi: 10.1158/1078-0432.CCR-07-1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Diaz RM, Galivo F, Kottke T, Wongthida P, Qiao J, Thompson J, et al. Oncolytic immunovirotherapy for melanoma using vesicular stomatitis virus. Cancer Res. 2007;67:2840–2848. doi: 10.1158/0008-5472.CAN-06-3974. [DOI] [PubMed] [Google Scholar]
- 8.Vile R, Ando D, Kirn D. The oncolytic virotherapy treatment platform for cancer: unique biological and biosafety points to consider. Cancer Gene Ther. 2002;9:1062–1067. doi: 10.1038/sj.cgt.7700548. [DOI] [PubMed] [Google Scholar]
- 9.Kottke T, Diaz RM, Kaluza K, Pulido J, Galivo F, Wongthida P, et al. Use of biological therapy to enhance both virotherapy and adoptive T-cell therapy for cancer. Mol Ther. 2008;16:1910–1918. doi: 10.1038/mt.2008.212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lun X, Senger DL, Alain T, Oprea A, Parato K, Stojdl D, et al. Effects of intravenously administered recombinant vesicular stomatitis virus (VSV(deltaM51)) on multifocal and invasive gliomas. J Natl Cancer Inst. 2006;98:1546–1557. doi: 10.1093/jnci/djj413. [DOI] [PubMed] [Google Scholar]
- 11.Galivo F, Diaz RM, Thanarajasingam U, Jevremovic D, Wongthida P, Thompson J, et al. Interference of CD40L-mediated tumor immunotherapy by oncolytic vesicular stomatitis virus. Hum Gene Ther. 2010;21:439–450. doi: 10.1089/hum.2009.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Galivo F, Diaz RM, Wongthida P, Thompson J, Kottke T, Barber G, et al. Single-cycle viral gene expression, rather than progressive replication and oncolysis, is required for VSV therapy of B16 melanoma. Gene Therapy. 2010;17:158–170. doi: 10.1038/gt.2009.161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wongthida P, Diaz RM, Galivo F, Kottke T, Thompson J, Melcher A, et al. VSV oncolytic virotherapy in the B16 model depends upon intact MyD88 signaling. Mol Ther. 2010;19:150–158. doi: 10.1038/mt.2010.225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wongthida P, Diaz RM, Galivo F, Kottke T, Thompson J, Pulido J, et al. Type III IFN interleukin-28 mediates the antitumor efficacy of oncolytic virus VSV in immune-competent mouse models of cancer. Cancer Res. 2010;70:4539–4549. doi: 10.1158/0008-5472.CAN-09-4658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kirn D, Martuza RL, Zwiebel J. Replication-selective virotherapy for cancer: biological principles, risk management and future directions. Nat Med. 2001;7:781–787. doi: 10.1038/89901. [DOI] [PubMed] [Google Scholar]
- 16.Russell SJ. RNA viruses as virotherapy agents. Cancer Gene Ther. 2002;9:961–966. doi: 10.1038/sj.cgt.7700535. [DOI] [PubMed] [Google Scholar]
- 17.Russell SJ, Peng KW. Viruses as anticancer drugs. Trends Pharmacol Sci. 2007;28:326–333. doi: 10.1016/j.tips.2007.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Aghi M, Chou TC, Suling K, Breakefield XO, Chiocca EA. Multimodal cancer treatment mediated by a replicating oncolytic virus that delivers the oxazaphosphorine/rat cytochrome P450 2B1 and ganciclovir/herpes simplex virus thymidine kinase gene therapies. Cancer Res. 1999;59:3861–3865. [PubMed] [Google Scholar]
- 19.Dingli D, Peng KW, Harvey ME, Greipp PR, O’Connor MK, Cattaneo R, et al. Image-guided radiovirotherapy for multiple myeloma using a recombinant measles virus expressing the thyroidal sodium iodide symporter. Blood. 2004;103:1641–1646. doi: 10.1182/blood-2003-07-2233. [DOI] [PubMed] [Google Scholar]
- 20.Kim JH, Oh JY, Park BH, Lee DE, Kim JS, Park HE, et al. Systemic armed oncolytic and immunologic therapy for cancer with JX-594, a targeted poxvirus expressing GM-CSF. Mol Ther. 2006;14:361–370. doi: 10.1016/j.ymthe.2006.05.008. [DOI] [PubMed] [Google Scholar]
- 21.Luo C, Mori I, Goshima F, Ushijima Y, Nawa A, Kimura H, et al. Replication-competent, oncolytic herpes simplex virus type 1 mutants induce a bystander effect following ganciclovir treatment. J Gene Med. 2007;9:875–883. doi: 10.1002/jgm.1085. [DOI] [PubMed] [Google Scholar]
- 22.Wodarz D. Viruses as antitumor weapons: defining conditions for tumor remission. Cancer Res. 2001;61:3501–3507. [PubMed] [Google Scholar]
- 23.Wodarz D. Gene therapy for killing p53-negative cancer cells: use of replicating versus nonreplicating agents. Hum Gene Ther. 2003;14:153–159. doi: 10.1089/104303403321070847. [DOI] [PubMed] [Google Scholar]
- 24.Wein LM, Wu JT, Ianculescu AG, Puri RK. A mathematical model of the impact of infused targeted cytotoxic agents on brain tumours: implications for detection, design and delivery. Cell Proliferation. 2002;35:343–361. doi: 10.1046/j.1365-2184.2002.00246.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wein LM, Wu JT, Kirn DH. Validation and analysis of a mathematical model of a replication-competent oncolytic virus for cancer treatment: implications for virus design and delivery. Cancer Res. 2003;63:1317–1324. [PubMed] [Google Scholar]
- 26.Wu JT, Byrne HM, Kirn DH, Wein LM. Modeling and analysis of a virus that replicates selectively in tumor cells. Bull Math Biol. 2001;63:731–768. doi: 10.1006/bulm.2001.0245. [DOI] [PubMed] [Google Scholar]
- 27.Wu JT, Kirn DH, Wein LM. Analysis of a three-way race between tumor growth, a replication-competent virus and an immune response. Bull Math Biol. 2004;66:605–625. doi: 10.1016/j.bulm.2003.08.016. [DOI] [PubMed] [Google Scholar]
- 28.Dingli D, Cascino MD, Josic K, Russell SJ, Bajzer Z. Mathematical modeling of cancer radiovirotherapy. Math Biosci. 2006;199:55–78. doi: 10.1016/j.mbs.2005.11.001. [DOI] [PubMed] [Google Scholar]
- 29.Friedman A, Tian JP, Fulci G, Chiocca EA, Wang J. Glioma virotherapy: effects of innate immune suppression and increased viral replication capacity. Cancer Res. 2006;66:2314–2319. doi: 10.1158/0008-5472.CAN-05-2661. [DOI] [PubMed] [Google Scholar]
- 30.Karev GP, Novozhilov AS, Koonin EV. Mathematical modeling of tumor therapy with oncolytic viruses: effects of parametric heterogeneity on cell dynamics. Biol Direct. 2006;1:30. doi: 10.1186/1745-6150-1-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Novozhilov AS, Berezovskaya FS, Koonin EV, Karev GP. Mathematical modeling of tumor therapy with oncolytic viruses: regimes with complete tumor elimination within the framework of deterministic models. Biol Direct. 2006;1:6. doi: 10.1186/1745-6150-1-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bajzer Z, Carr T, Josic K, Russell SJ, Dingli D. Modeling of cancer virotherapy with recombinant measles viruses. J Theor Biol. 2008;252:109–122. doi: 10.1016/j.jtbi.2008.01.016. [DOI] [PubMed] [Google Scholar]
- 33.Dingli D, Offord C, Myers R, Peng KW, Carr TW, Josic K, et al. Dynamics of multiple myeloma tumor therapy with a recombinant measles virus. Cancer Gene Ther. 2009;16:873–882. doi: 10.1038/cgt.2009.40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mok W, Stylianopoulos T, Boucher Y, Jain RK. Mathematical modeling of herpes simplex virus distribution in solid tumors: implications for cancer gene therapy. Clin Cancer Res. 2009;15:2352–2360. doi: 10.1158/1078-0432.CCR-08-2082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Paiva LR, Binny C, Ferreira SC, Jr, Martins ML. A multiscale mathematical model for oncolytic virotherapy. Cancer Res. 2009;69:1205–1211. doi: 10.1158/0008-5472.CAN-08-2173. [DOI] [PubMed] [Google Scholar]
- 36.Wodarz D, Komarova N. Towards predictive computational models of oncolytic virus therapy: basis for experimental validation and model selection. PLoS ONE. 2009;4:e4271. doi: 10.1371/journal.pone.0004271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bieseker M, Kimn JH, Lu H, Dingli D, Bajzer Z. Optimization of virotherapy for cancer. Bull Math Biol. 2010;72:469–489. doi: 10.1007/s11538-009-9456-0. [DOI] [PubMed] [Google Scholar]
- 38.Komarova NL, Wodarz D. ODE models for oncolytic virus dynamics. J Theor Biol. 2010;263:530–543. doi: 10.1016/j.jtbi.2010.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Reis C, Pacheco JM, Ennis MK, Dingli D. In silico evolutionary dynamics of tumour virotherapy. Integr Biol. 2010;2:41–45. doi: 10.1039/b917597k. [DOI] [PubMed] [Google Scholar]
- 40.Cohn M, Mitchison NA, Paul WE, Silverstein AM, Talmage DW, Weigert M. Reflections on the clonal-selection theory. Nat Rev Immunol. 2007;7:823–830. doi: 10.1038/nri2177. [DOI] [PubMed] [Google Scholar]
- 41.Peng KW, Hadac EM, Anderson BD, Myers R, Harvey M, Greiner SM, et al. Pharmacokinetics of oncolytic measles virotherapy: eventual equilibrium between virus and tumor in an ovarian cancer xenograft model. Cancer Gene Ther. 2006;13:732–738. doi: 10.1038/sj.cgt.7700948. [DOI] [PubMed] [Google Scholar]
- 42.Reid T, Galanis E, Abbruzzese J, Sze D, Wein LM, Andrews J, et al. Hepatic arterial infusion of a replication-selective oncolytic adenovirus (dl1520): phase II viral, immunologic, and clinical endpoints. Cancer Res. 2002;62:6070–6079. [PubMed] [Google Scholar]
- 43.Pecora AL, Rizvi N, Cohen GI, Meropol NJ, Sterman D, Marshall JL, et al. Phase I trial of intravenous administration of PV701, an oncolytic virus, in patients with advanced solid cancers. J Clin Oncol. 2002;20:2251–2266. doi: 10.1200/JCO.2002.08.042. [DOI] [PubMed] [Google Scholar]
- 44.Galanis E, Hartmann LC, Cliby WA, Long HJ, Peethambaram PP, Barrette BA, et al. Phase I trial of intraperitoneal administration of an oncolytic measles virus strain engineered to express carcinoembryonic antigen for recurrent ovarian cancer. Cancer Res. 2010;70:875–882. doi: 10.1158/0008-5472.CAN-09-2762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Martinez-Quintanilla J, Cascallo M, Fillat C, Alemany R. Antitumor therapy based on cellular competition. Hum Gene Ther. 2009;20:728–738. doi: 10.1089/hum.2008.144. [DOI] [PubMed] [Google Scholar]
- 46.Martinez-Quintanilla J, Cascallo M, Gros A, Fillat C, Alemany R. Positive selection of gene-modified cells increases the efficacy of pancreatic cancer suicide gene therapy. Mol Cancer Ther. 2009;8:3098–3107. doi: 10.1158/1535-7163.MCT-09-0350. [DOI] [PubMed] [Google Scholar]
- 47.Luo R, Cannon L, Hernandez J, Piovoso MJ, Zurakowski R. Controlling the evolution of resistance. J Process Control. 2011;21:367–378. doi: 10.1016/j.jprocont.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li H, Zeng Z, Fu X, Zhang X. Coadministration of a herpes simplex virus-2 based oncolytic virus and cyclophosphamide produces a synergistic antitumor effect and enhances tumor-specific immune responses. Cancer Res. 2007;67:7850–7855. doi: 10.1158/0008-5472.CAN-07-1087. [DOI] [PubMed] [Google Scholar]
- 49.Nagano S, Perentes JY, Jain RK, Boucher Y. Cancer cell death enhances the penetration and efficacy of oncolytic herpes simplex virus in tumors. Cancer Res. 2008;68:3795–3802. doi: 10.1158/0008-5472.CAN-07-6193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Stohrer M, Boucher Y, Stangassinger M, Jain RK. Oncotic pressure in solid tumors is elevated. Cancer Res. 2000;60:4251–4255. [PubMed] [Google Scholar]
- 51.Linardakis E, Bateman A, Phan V, Ahmed A, Gough M, Olivier K, et al. Enhancing the efficacy of a weak allogeneic melanoma vaccine by viral fusogenic membrane glycoprotein-mediated tumor cell-tumor cell fusion. Cancer Res. 2002;62:5495–5504. [PubMed] [Google Scholar]
- 52.Fernandez M, Porosnicu M, Markovic D, Barber GN. Genetically engineered vesicular stomatitis virus in gene therapy: application for treatment of malignant disease. J Virol. 2002;76:895–904. doi: 10.1128/JVI.76.2.895-904.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bajzer Z, Marusic M, Vuk-Pavlovic S. Conceptual frameworks for mathematical modeling of tumor growth dynamics. Math Comput Modelling. 1996;23:31–46. [Google Scholar]
- 54.Spratt JA, von Fournier D, Spratt JS, Weber EE. Decelerating growth and human breast cancer. Cancer. 1993;71:2013–2019. doi: 10.1002/1097-0142(19930315)71:6<2013::aid-cncr2820710615>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 55.Offord C, Bajzer Z. A hybrid global optimization algorithm involving simple and inductive search. Lecture Notes Comput Sci. 2006;2074:680–688. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.