Evaluation of Stochastic Adjustment for Glucose Sensor Bias During Closed-Loop Insulin Delivery

Abstract

Background: In outpatient studies of closed-loop insulin delivery systems, it is not typically practical to obtain blood glucose measurements for an outcome measure. Using a continuous glucose monitoring (CGM) device as both part of the intervention and as the outcome in a clinical trial can give a biased estimate of the treatment effect. A stochastic adjustment has been proposed to correct this problem.

Materials and Methods: We performed Monte Carlo simulations to assess the performance of the stochastic adjustment in various scenarios where the CGM device was used passively and when it was used to inform insulin delivery. The resulting bias for using CGM to estimate the percentage of glucose values inside a target range was compared with and without the proposed stochastic adjustment.

Results: CGM bias for estimating the percentage of glucose values 70–180 mg/dL ranged from −6% to +4% in the various scenarios studied. In some circumstances, stochastic adjustment did indeed reduce this CGM bias. However, in other circumstances, stochastic adjustment made the bias worse. Stochastic adjustment tended to underestimate the true percentage of glucose values in range for most, but not all, scenarios considered in these simulations.

Conclusions: Stochastic adjustment is not a general solution to the problem of CGM bias. The proposed adjustment relies on an implicit assumption that usually does not hold. The appropriate level of adjustment depends on how efficacious the closed-loop system is, which is not typically known in practice.

Introduction

As clinical trials of closed-loop insulin delivery systems progress from the inpatient to outpatient setting, it becomes less practical to use blood glucose (BG) measurements as an outcome measure.^1,2 Continuous glucose monitoring (CGM) is a practical means of obtaining a representative profile of glucose values but is less accurate than BG measurements.^1–6 Furthermore, a bias may occur if the same CGM device used as part of the closed-loop system is also used to assess outcome. Because the system aims to put the observable CGM in a desired target range rather than acting on the true (unobserved) BG, the CGM device will tend to overestimate the percentage of true glucose values in range when a true treatment effect is present.

Hovorka et al.⁷ propose a stochastic adjustment for CGM data to correct for this bias by integrating over an assumed error distribution. The proposed adjustment implicitly assumes that the measurement error (CGM – BG) is independent of the observed CGM value. This assumption in general is not true and only holds in a specific circumstance that is unlikely to occur in actual practice. In certain circumstances stochastic adjustment is approximately equivalent to adding a second layer of measurement error, which exacerbates the CGM bias rather than correcting it.

In this study, we look at the performance of the proposed stochastic adjustment in various situations. We show some situations where the adjustment does indeed mitigate the CGM bias and other situations where it makes the bias worse. An alternate adjustment can be used in some circumstances to correct this problem, but in general the appropriate adjustment depends on how efficacious the closed-loop system is. Simulation studies are presented to illustrate the performance of adjusted and unadjusted CGM outcomes in various situations.

CGM Bias

Scenario I: passive CGM

Let us first consider the simpler case where the CGM data are not used to drive insulin delivery. Hovorka et al.⁷ assume that CGM=BG+error, where the error is known to have a normal distribution with zero mean and SD 15% of the true BG. As an approximation to better understand why stochastic adjustment often fails in this scenario, suppose instead that the error distribution had a constant SD independent of the BG. Suppose further that the BG values also had a normal distribution. Then the CGM distribution could be taken by integrating that of the BG values over the error distribution, which would result in another normal distribution with

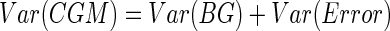The stochastic adjustment proposed by Hovorka et al.⁷ is to integrate the observed CGM reading over the presumed error distribution (Supplementary Fig. S1; Supplementary Data are available online at www.liebertpub.com/dia). This results in another normal distribution with

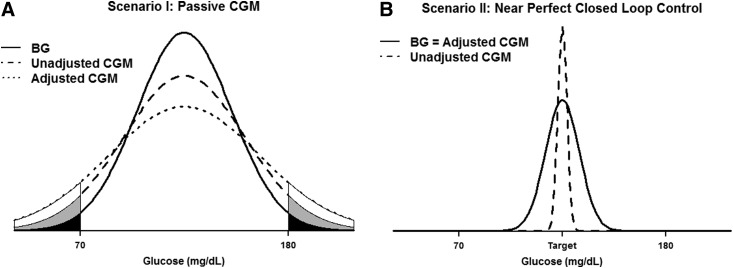
This situation is depicted in Figure 1A with

FIG. 1.

Comparison of continuous glucose monitoring (CGM) versus blood glucose (BG) glucose values. (A) An example where passive CGM is not used to inform insulin delivery (Scenario I). Measurement error increases the variance of CGM values, which is further increased by stochastic adjustment so that Var(BG)<Var(unadjusted CGM)<Var(adjusted CGM), resulting in more probability allocated in the tails of the distribution. CGM therefore tends to underestimate the percentage of glucose values in range, and stochastic adjustment exacerbates this bias. (B) An example where an ideal closed-loop controller puts nearly 100% of CGM values at the desired target (Scenario II). Because of measurement error, the true BG values fluctuate more around the target so that Var(BG)=Var(adjusted CGM)>Var(unadjusted CGM)≈0. In this case, CGM overestimates the percentage of glucose values in range, and stochastic adjustment reduces this bias.

The increased variance with CGM pushes more of the probability outside the interval 70–180 mg/dL, resulting in an underestimation of the percentage in range. The stochastic adjustment exacerbates the CGM bias in this scenario by essentially adding a second error term.

The above approximation is not exact because Hovorka et al.⁷ assume that the SD of the measurement error is 15% of the BG so that the resulting CGM values no longer have a normal distribution. This has little effect on the performance of stochastic adjustment during passive CGM, as shown by the simulations presented in Results.

Scenario II: near-perfect closed-loop control

Now let us consider the opposite extreme, where CGM data are used to drive insulin delivery and an ideal controller puts all of the CGM readings at the target value so that the measured percentage in range is 100%. In this scenario, the only source of variation in the true BG values comes from CGM measurement error. Because of this measurement error, the occasional BG value will fall outside the target range even though the CGM device reads at the target value. The CGM therefore overestimates the true percentage in range under this scenario (Fig. 1B). Here we have

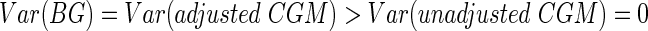so the implicit assumption of independence between measurement error and observed CGM holds true. This is the only scenario where the stochastic adjustment of Hovorka et al.⁷ is theoretically valid.

Intermediate scenarios

In most practical applications reality will likely be somewhere in between the two extreme scenarios described above. Studies of closed-loop systems often use a crossover design where each subject is observed in separate sessions with and without closed loop.^8–13 The session without closed loop represents Scenario I above where passive CGM tends to underestimate the percentage in range and the stochastic adjustment exacerbates this bias. The session with closed loop is likely somewhere intermediate. Whether stochastic adjustment improves or worsens the CGM bias in this case depends on how well the closed loop is able to shift the distribution of CGM values closer to the target range. The closer the closed loop comes to Scenario II above with 100% CGM values at target, the better the proposed stochastic adjustment performs.

Materials and Methods

To observe how CGM bias behaves in the various scenarios described above and how this bias is impacted by stochastic adjustment, some simple Monte Carlo simulations were run to mimic the effect of a controller acting on the CGM readings rather than the true BG values. The BG level at time t was simulated as

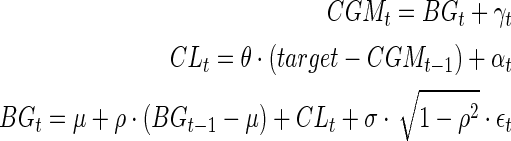where CL_t denotes the impact of the closed loop at time t, θ is a parameter between 0 and 1 that represents how aggressively the controller treats to target, and {γ_t}, {α_t}, and {ɛ_t} are mutually independent sequences of normally distributed error terms with autoregressive correlation structures. The parameter μ represents the baseline mean glucose value in the absence of a closed-loop controller (i.e., when the CL term is zero).

The key factor here is that the CL term above is only allowed to depend on the observed CGM reading rather than the BG value, which would be unknown in actual practice. Note that when the previous CGM reading is above target, a negative term is added to the CL effect (to drop glucose toward the target), and when the previous CGM is below target, a positive term is added to CL. No change is made (except for random drift) when the CGM reading is at the desired target. The target value was taken to be 125 mg/dL. For each simulation, the percentage of values in the range 70–180 mg/dL was calculated for the true BG values as well as the adjusted and unadjusted CGM values. The parameters σ and ρ denote the standard deviation and autocorrelation for the BG process.

Simulations were run under various combinations of the parameters μ, θ, and the variances and correlations of the three error sequences listed above (Supplementary Table S1). The SD of measurement error (γ_t) was taken to be 15% of the true BG as assumed by Hovorka et al.⁷ Simulations were also run with CL_t=0 (Scenario I with passive CGM). For each combination of parameters, 1,000 independent chains of 1,000 values each (1 million total simulations) were generated.

Bias for both unadjusted and adjusted CGM was defined as the CGM percentage in range (70–180 mg/dL) minus the corresponding percentage for the BG values. The treatment effect (δ) was taken as the percentage in range when the controller was active minus the percentage in range with passive CGM. Bias for the treatment effect was defined as the δ estimated by CGM minus the corresponding δ using the BG values. Results were similar for other typically used glycemic indices such as percentage in hypo- and hyperglycemic range and hypo-/hyperglycemic area under the curve (data not shown).

Additional simulations were run using the University of Virginia–University of Padova (UVA-Padova) type 1 diabetes simulator¹⁴ that models real-world CGM sensor behavior, subcutaneous insulin delivery kinetics, and the human metabolic system using a system of differential equations. One hundred virtual subjects were each run for 10 days, giving a total of 1,440,000 simulated BG–CGM pairs during open loop with near-optimal basal-bolus therapy and an additional 1,440,000 pairs using a sample model predictive control-based closed-loop algorithm.

Results

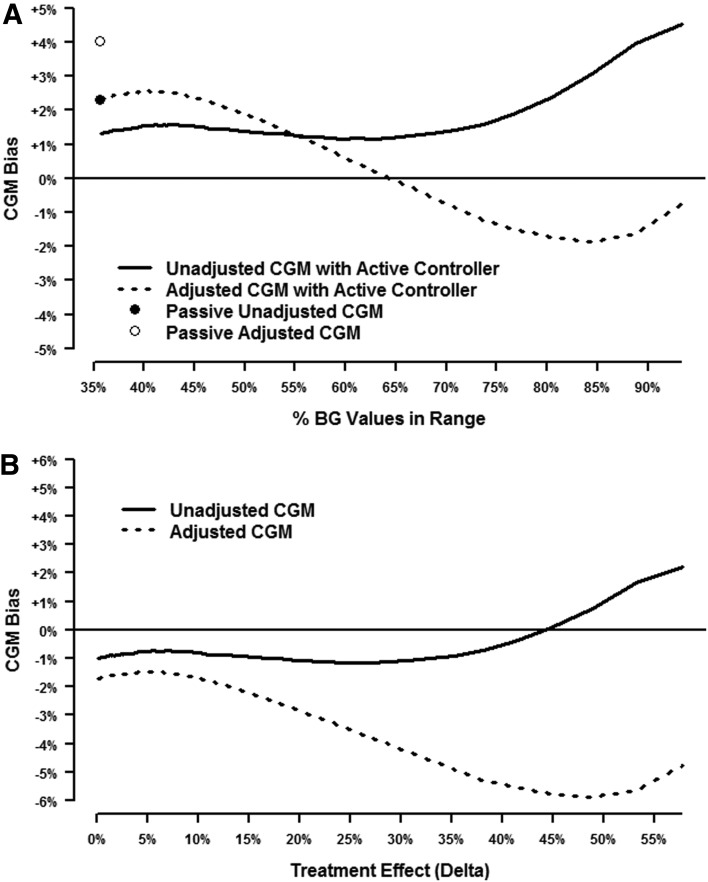
Figure 2 shows the results of a simulation where the baseline (without closed-loop intervention) mean BG was 130 mg/dL and the SD was 50 mg/dL. Each curve represents 100 different scenarios with varying levels of controller efficacy, and each of those 100 points represents the mean of 1 million simulations. Figure 2A shows the bias from an individual session for both unadjusted and adjusted CGM. The points correspond to passive CGM, and the lines denote scenarios with an active controller. The horizontal axis starts at 72% on the far left, which represents the true percentage of BG values in range without closed-loop intervention (Scenario I above). Figure 2A indicates an unadjusted CGM bias of approximately −3% (i.e., CGM averages 69% instead of the true 72%) compared with −5% for the adjusted CGM. In this example, the CGM underestimates the true percentage in range, and the stochastic adjustment exacerbates this bias.

FIG. 2.

Simulation results for a hypothetical subject with baseline mean glucose level of 130 mg/dL and SD of 50 mg/dL. (A) Simulations of a single session when a closed-loop controller is active. The points correspond to passive continuous glucose monitoring (CGM), and the lines denote scenarios with an active controller. A positive bias indicates that CGM overestimates the true percentage of glucose values in range, and a negative bias indicates the CGM underestimates the percentage in range. (B) Simulation results from two sessions, one with and one without a closed-loop controller, using a typical crossover design. The difference in the percentage between these two sessions gives an estimate of the treatment effect (δ). A positive bias denotes a situation where the CGM either overestimates the percentage in range during the closed-loop session and/or underestimates the percentage during the comparison session without closed loop. BG, blood glucose.

As the closed loop becomes more effective and the percentage of true BG values in range increases (moving toward the right side of Fig. 2A), the bias for the unadjusted CGM switches from negative to positive (i.e., overestimates rather than underestimates the true percentage in range), whereas the bias for adjusted CGM becomes less negative, ending up at zero. The far right side of Figure 2A represents Scenario II described above, where the implicit assumption of independence in the stochastic adjustment is valid and the bias for adjusted CGM is therefore zero. Note the slight downturn in the unadjusted CGM curve toward the right end of Figure 2A. As the percentage of unadjusted CGM values in range approaches the ceiling of 100%, it cannot get much larger, whereas the percentage of true BG values in range still has more room to continue rising. This results in the bias (CGM percentage minus BG percentage) decreasing slightly.

Figure 2B shows simulation results for the estimated treatment effect (δ), which is defined as the difference in the percentage in range from a session when the controller is active minus the percentage in range from a session without a controller. The bias for the treatment effect in Figure 2B is therefore given by the difference between the line and the corresponding point in Figure 2A. Under the null hypothesis of no treatment effect (left side of Figure 2B), both unadjusted and adjusted CGM have a negligible positive bias. As the true treatment effect increases, unadjusted CGM shows a positive bias, whereas adjusted CGM shows a negative bias. For δ values greater than 20%, adjusted CGM also shows a positive bias but smaller than that for unadjusted CGM. Ironically, the positive bias from CGM comes not from overestimating the percentage in range when the controller is active, but from underestimating the percentage during the comparison session without a controller. In this example, the adjusted CGM seems preferable because it has a smaller bias for most values of the treatment effect, but the following example shows this is not always the case.

Consider Figure 3, where baseline BG has a mean of 200 mg/dL with an SD of 70 mg/dL. In Figure 3A for a single session unadjusted CGM shows a positive bias that increases with the percentage of true BG values in range. Adjusted CGM goes from a positive to a negative bias. The net effect from two sessions (one with and one without closed loop) in Figure 3B is for both unadjusted and adjusted CGM to underestimate the true treatment effect in most scenarios. The exception is when the true δ is greater than 45% (highly effective controller), where unadjusted CGM overestimates the true δ slightly. Note that adjusted CGM can underestimate the true δ by as much as 6% on average (i.e., report 44% when the true δ is 50%), whereas unadjusted CGM has an average value within±2% of the true δ in this example.

FIG. 3.

Simulation results for a hypothetical subject with baseline mean glucose level of 200 mg/dL and SD of 70 mg/dL. (A) Simulations of a single session when a closed-loop controller is active. The points correspond to passive continuous glucose monitoring (CGM), and the lines denote scenarios with an active controller. A positive bias indicates that CGM overestimates the true percentage of glucose values in range, and a negative bias indicates the CGM underestimates the percentage in range. (B) Simulation results from two sessions, one with and one without a closed-loop controller, using a typical crossover design. The difference in the percentage between these two sessions gives an estimate of the treatment effect (δ). A positive bias denotes a situation where the CGM either overestimates the percentage in range during the closed-loop session and/or underestimates the percentage during the comparison session without closed loop. BG, blood glucose.

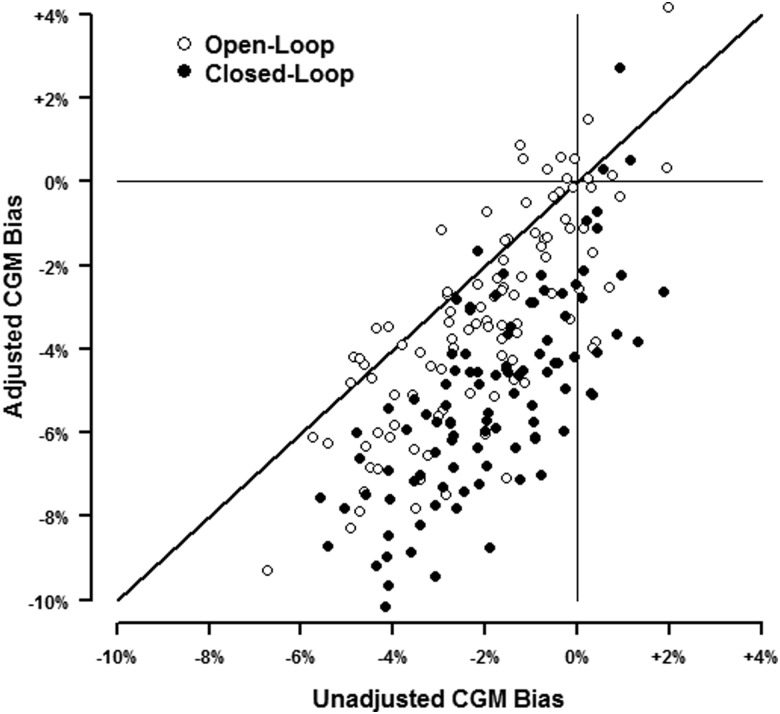
Results from the UVA-Padova T1DM simulator¹⁴ are shown in Figure 4. The SD of the relative error was 16.3% in these simulations during open loop and 16.9% during closed loop, approximating the 15% assumed by Hovorka et al.⁷ The mean±SD percentage in range for the 100 simulated subjects was 70±11%, ranging from 40% to 95%, during open loop and 83±10%, ranging from 54% to 98%, when using the closed-loop emulator. During open-loop simulations unadjusted CGM tended to underestimate the true percentage of BG values in range with a mean bias of −2.1% (95% confidence interval [CI]: −2.4% to −1.7%). This bias was exacerbated by the stochastic adjustment (mean bias −3.3%; 95% CI: −3.8% to −2.8%). These trends were also observed from the closed-loop simulations (mean bias −1.9% [95% CI: −2.2% to −1.5%] for unadjusted CGM vs. −5.1% [95% CI: −5.5% to −4.6%] for adjusted CGM).

FIG. 4.

Ten days of blood glucose and continuous glucose monitoring (CGM) data were simulated for each of 100 virtual subjects using the University of Virginia–University of Padova type 1 diabetes mellitus simulator.¹⁴ The bias for CGM compared with blood glucose percentage of glucose values in range is plotted for each virtual subject. Most of the points below the line of identity denote cases where the stochastic adjustment results in a greater negative bias compared with unadjusted CGM.

When looking at the estimated treatment effect (closed-loop vs. open-loop), unadjusted CGM overstated the true δ 52% of the time compared with 25% for adjusted CGM. However, adjusted CGM was not always more conservative: for 8% of the simulated subjects, it gave a more optimistic estimate of δ compared with unadjusted CGM.

Discussion

Using CGM as both part of the intervention (closed-loop controller) and the outcome measure in a clinical trial can result in a biased estimate of the treatment effect. We have shown by simulation that stochastic adjustment is not a universal solution to this problem. The implicit assumption of independence between measurement error and the observed CGM only holds in an ideal circumstance (Scenario II described above) that is unlikely to occur in actual practice. Simulation results demonstrate that stochastic adjustment can either mitigate or exacerbate the bias depending on the situation. In the case of passive CGM, stochastic adjustment is essentially equivalent to doubling the measurement error. One attractive feature of the stochastic adjustment is that it gives a more conservative estimate of the treatment effect compared with unadjusted CGM in most (but not all) of our simulations.

An alternate stochastic adjustment could be derived, for example, based on the assumption that CGM measurement error is independent of the true BG values (Scenario I). In this case the observed distribution of CGM values is a convolution of the BG distribution and measurement error. Because the error distribution is presumed known, some technique (e.g., the expectation-maximization algorithm¹⁵) could be used to deconvolve the probability distributions and give an estimate of the underlying BG distribution. This version of stochastic adjustment would essentially work in the opposite direction of that proposed by Hovorka et al.,⁷ tending to increase rather than decrease the estimated percentage in range. As such, it would have the opposite problem of what we have demonstrated in these simulations. Namely, it would do well when the CGM is used passively (Scenario I) and would do poorly as we approached ideal control by a closed-loop system (Scenario II).

From a statistical viewpoint, the problem is that using CGM to inform the closed-loop controller induces a correlation between the measurement error and the true BG that does not exist with passive CGM. The closer we get to Scenario II described above, the stronger this correlation becomes. The appropriate stochastic adjustment depends on the magnitude of this correlation, which in turn depends on how effective the closed-loop controller is. Because this is not typically known in advance (the purpose of closed-loop studies is to learn how effective it is), application of stochastic adjustment in practice is problematic.

Over the course of a single study, stochastic adjustment may happen to give a percentage closer to that for the true BG just by chance. It is only when looking at a large number of outcomes that can be generated through simulation that we can see how the overall bias is impacted by stochastic adjustment in various scenarios.

The simulations performed in this study were done under favorable conditions assuming that the specified error distribution was exactly correct. In actual practice CGM measurement error is more complicated than being 15% of the true glucose. Relative error is not typically constant over the range of BG values, with accuracy studies often reporting higher relative absolute differences during hypoglycemia compared with during hyperglycemia.^3,16–18 Furthermore, the true error distribution likely varies among subjects and different sensors. Misspecification of the true error distribution can add further bias to the stochastic adjustment.

Another complicating issue is that the stochastic adjustment proposed in Hovorka et al.⁷ also implicitly assumes that CGM has a slope of 1 and an intercept of 0 relative to the BG (i.e., CGM=BG+error). It is often the case that CGM=intercept+(slope ċ CGM)+error where slope≠1 and intercept≠0. If the slope and intercept are known, then we can simply rescale CGM*=(CGM – intercept)/slope, and the resulting CGM* will have the desired unit slope and zero intercept. However, in practice, the slope and intercept would need to be estimated, and the resulting misspecification could also add further bias to stochastic adjustment.

The first set of simulations performed in this study are admittedly simplistic as they do not incorporate complex glucose dynamics within the human body, the effect of meals, exercise, etc., or any notion of lag between blood and interstitial fluid. BG and CGM error are simply modeled as normally distributed autoregressive time series with a controller informed by noisy CGM data rather than the true BG. However, the stochastic adjustment also does not consider the factors listed above and is based only on the presumed normal distribution of CGM error. Results from the UVA-Padova type 1 diabetes simulator¹⁴ that do take into account the factors mentioned above (except exercise) also demonstrate that stochastic adjustment can exacerbate the bias from CGM.

Another possible strategy would be to have study subjects wear two CGM devices: one to inform closed-loop insulin delivery and another to assess the outcome. Some closed-loop systems may already use multiple glucose sensors to drive insulin delivery, so requiring an additional CGM device to assess outcome may not be feasible. Even when it may be practical to have a separate CGM system for outcome assessment, it is likely that measurement error between the sensors would be correlated (e.g., lag in the interstitial fluid), so this may not entirely remove the bias. Using available BG measurements to retrospectively recalibrate the CGM device may be another possibility to mitigate the bias.⁷

In terms of hypothesis testing as opposed to point estimation, CGM error will not inflate the type I error rate under the strong null hypothesis that the intervention has no effect on the glucose distribution. Under this assumption, any CGM bias would be the same for the sessions with and without closed-loop insulin delivery and would cancel out in the comparison. It is theoretically possible that an intervention could alter the glucose distribution without changing the overall percentage in range (weak null hypothesis). As demonstrated in the far left side of Figures 2B and 3B, the CGM bias may not exactly cancel out in these situations, resulting in a small net bias that can either slightly overestimate or underestimate the actual δ.

It is worth noting that measurement error does not result in an overall bias when mean glucose is the outcome (assuming the CGM slope with the true BG is unity). Cases where the CGM overestimates the true glucose would tend to cancel out on average with cases where the CGM underestimated the true glucose. This is not the case, unfortunately, for nonlinear measures such as percentage in range or percentage hypo-/hyperglycemic. We obtained similar results in our simulations for percentage of time hypoglycemic (below 70 mg/dL) or hyperglycemic (above 180 mg/dL) as well as hypo- and hyperglycemic area under the curve. Hovorka et al.⁷ note that stochastic adjustment does not work well for measures of glycemic variation such as the SD or the coefficient of variation.

In summary, using CGM to serve as both part of the intervention and to assess outcomes can exaggerate a true treatment effect. Stochastic adjustment, as has been proposed,⁷ does not entirely solve this problem and in some cases can make the bias worse. For early-stage proof-of-concept studies in the outpatient setting, CGM may be the only practical way to assess whether closed-loop systems are improving glycemia over a relatively short term of a few days or weeks.

Acknowledgments

Jaeb Center for Health Research support was provided by the JDRF, Inc. (grant 22-2011-643).

The authors collectively wrote the manuscript and vouch for the data. The investigators had complete autonomy to analyze and report the simulation results. There were no agreements concerning confidentiality of the data between the National Institute of Diabetes and Digestive and Kidney Diseases, the authors, or their institution. The Jaeb Center for Health Research takes responsibility for the integrity of the data and the accuracy of the data analysis.

Author Disclosure Statement

C.K. reports having received consulting fees from Medtronic MiniMed, Inc. P.C., J.L., W.S. and R.W.B. declare no competing financial interests exist.