The Influence of Spatial Variation in Chromatin Density Determined by X-Ray Tomograms on the Time to Find DNA Binding Sites

Abstract

In this work, we examine how volume exclusion caused by regions of high chromatin density might influence the time required for proteins to find specific DNA binding sites. The spatial variation of chromatin density within mouse olfactory sensory neurons is determined from soft X-ray tomography reconstructions of five nuclei. We show that there is a division of the nuclear space into regions of low-density euchromatin and high-density heterochromatin. Volume exclusion experienced by a diffusing protein caused by this varying density of chromatin is modeled by a repulsive potential. The value of the potential at a given point in space is chosen to be proportional to the density of chromatin at that location. The constant of proportionality, called the volume exclusivity, provides a model parameter that determines the strength of volume exclusion. Numerical simulations demonstrate that the mean time for a protein to locate a binding site localized in euchromatin is minimized for a finite, nonzero volume exclusivity. For binding sites in heterochromatin, the mean time is minimized when the volume exclusivity is zero (the protein experiences no volume exclusion). An analytical theory is developed to explain these results. The theory suggests that for binding sites in euchromatin there is an optimal level of volume exclusivity that balances a reduction in the volume searched in finding the binding site, with the height of effective potential barriers the protein must cross during the search process.

1 Introduction

What mechanisms drive the process by which regulatory proteins and transcription factors search for specific DNA binding sites? It is usually assumed that in the absence of any interactions, within an “empty” nucleus a protein will move by Brownian motion and bind upon getting sufficiently close to a target site. This corresponds to the well-known diffusion-limited reaction model of Smoluchowski (1917). A number of theoretical and experimental studies suggest proteins may experience facilitated diffusion, allowing them to find specific binding sites faster than the diffusion limit predicted by the Smoluchowski theory (Halford 2009; Normanno et al. 2012). Whether facilitated diffusion occurs in any meaningful way in vivo, allowing proteins to find binding sites significantly faster than the diffusion limit, is very much an active area of investigation and debate (Halford 2009; Normanno et al. 2012; Svetlov and Nudler 2013; Veksler and Kolomeisky 2013). In the present paper, we consider the possible influence of volume exclusion caused by spatial heterogeneity in chromatin density on the time needed for a protein to find a target by diffusion.

There are many different interactions that have been proposed that could in principle decrease the mean time required for regulatory proteins and transcription factors to find specific DNA binding sites, relative to the diffusion limited reaction model. These include nonspecific DNA binding interactions, electrostatic interactions between proteins and binding sites, one-dimensional diffusion of proteins along DNA, and jumping of proteins between different regions of DNA fibers (Halford 2009; Normanno et al. 2012). The relative contribution of these (possible) interactions is still being assessed by both experimental and theoretical studies. Perhaps the most popular of these mechanisms is the possibility that proteins may exploit nonspecific DNA binding interactions to allow diffusion or sliding along DNA. In the classic study of Berg et al. (1981), a model was developed in which proteins could undergo a mixed search process involving periods of three-dimensional diffusion, coupled to periods of one-dimensional diffusion along DNA fibers when the proteins were non-specifically bound. A large number of theoretical studies have investigated how this mechanism might influence the search process for specific DNA binding sites (for example, see Berg et al. 1981; Li et al. 2009; Malherbe and Holcman 2008; Slutsky and Mirny 2004; Mirny et al. 2009; Halford 2009). Recently, several single-molecule imaging studies have demonstrated that sliding of lac repressor can occur in vivo (Elf et al. 2007; Hammar et al. 2012). The theoretical estimates in Hammar et al. (2012) suggest this mechanism may allow a significant decrease in the mean time required for a protein to find a specific binding site, in comparison to the diffusion limited reaction model. Most of the existing studies have focused on prokaryotic cells, and it remains to be seen whether sliding along chromatin in eukaryotic cells can noticeably reduce the time required for regulatory proteins to locate specific binding sites in vivo. More complete references for both theoretical models and previous experimental work can be found in the reviews (Halford 2009; Normanno et al. 2012).

The nucleus of a eukaryotic cell is a complex spatial environment, containing chromatin fibers with spatially-varying compaction levels, nuclear bodies, and fibrous filaments (such as the nuclear lamina). Spatial inhomogeneity of the nuclear space provides another possible mechanism that may influence the search process of proteins for specific binding sites. In Bancaud et al. (2009), the impact of spatial variation in chromatin density on the movement of proteins within the nucleus was investigated. Using a combination of single-particle tracking experiments, photo-activation experiments and computational modeling, the authors concluded that chromatin dense regions, such as heterochromatin, exhibited noticeable volume exclusion compared with less dense regions, such as euchromatin. It was observed that similar fluorescence activation curves were found in photo-activation experiments within heterochromatin and euchromatin, when each of the two curves was normalized to the steady-state fluorescence level of its own region. The authors inferred from these experiments that heterochromatin is not substantially more difficult for proteins to enter than euchromatin, but that heterochromatin has a smaller amount of free space in which proteins can accumulate. In contrast, the supplemental movies of Vargas et al. (2005) demonstrate that individual mRNAs that are able to move freely within nuclei appear restricted to regions of low histone-GFP fluorescence. These mRNAs seem to have difficultly moving into regions of heterochromatin, as identified by regions of high histone-GFP fluorescence.

In Isaacson et al. (2011), we developed a mathematical model to investigate how the spatially varying density of chromatin within eukaryotic cell nuclei might influence the time required for proteins to find specific binding sites. Our model assumed that regions of higher chromatin density were more difficult for proteins to move into. Protein motion was approximated as diffusion within a volume-excluding potential. The model was constructed from the 3D structured illumination microscopy fluorescence imaging data of Schermelleh et al. (2008). In that work, mouse myoblast cell nuclei were chemically fixed, and both antibody labeled nuclear pores and DAPI stained DNA were imaged. From these data, we reconstructed a nuclear membrane surface to determine the nuclear space. The normalized DAPI stain intensity within a given voxel of the imaging data was assumed proportional to the density of chromatin within that voxel. Based on this assumption, we constructed a volume exclusion potential, with the value of the potential within a given voxel chosen to be proportional to the normalized DAPI stain intensity of that voxel. The constant of proportionality, which we called the volume exclusivity, was a model parameter that set the overall strength of volume exclusion. By varying the volume exclusivity, we studied how the time to find specific DNA binding sites varied when there was no volume exclusion (i.e., the volume exclusivity was zero and the protein simply diffused), weak volume exclusion, and strong volume exclusion from chromatin dense regions. Numerical simulations of the protein’s search process suggested that for binding sites localized in regions of low DAPI stain intensity, such as the 20th to 30th percentile of intensity values, the median time for proteins to find a specific binding site was minimized for non-zero values of the volume exclusivity. That is, as the volume exclusivity was increased from zero the median binding time initially decreased to a minimum, beyond which the median time increased to infinity. After randomly shuffling the values of the DAPI stain intensity among the voxels of the nucleus, we observed that this effect was lost and the median binding time simply increased as a function of the volume exclusivity. Based on these results, we concluded that the spatial organization of chromatin played a role in the observed minimum of the median binding time for nonzero volume exclusivity. For binding sites localized in regions of high DAPI stain intensity, such as the 70th to 80th percentile of the DAPI stain intensity distribution, the median time to find the binding site increased monotonically as the volume exclusivity was increased from zero.

In this work, we expand upon the studies begun in Isaacson et al. (2011). To determine chromatin density fields, we now use 3D soft X-ray tomography (SXT) reconstructions of cell nuclei (McDermott et al. 2009; Clowney et al. 2012; Le Gros et al. 2013). SXT provides several advantages over fluorescence imaging in assessing the spatial variation of chromatin density. Foremost, the measured linear absorption coefficient (LAC) of a voxel within SXT reconstructions is linearly related to the density of organic material within that voxel by the Beer–Lambert law (McDermott et al. 2009). Our simulations in Isaacson et al. (2011) made use of imaging data from one mouse myoblast cell nucleus, raising the question of whether the observed dependence of the binding time on the volume exclusivity and binding site localization was simply an artifact of the particular cell we studied. In this work, we repeat the computational studies of Isaacson et al. (2011) within five mouse olfactory sensory neuron cell nuclei obtained by SXT imaging. We observe the same qualitative behavior of the mean binding time on volume exclusivity and binding site localization as was observed for the median binding time in Isaacson et al. (2011). In addition, we now give a theoretical explanation why the mean binding time has this qualitative behavior.

We begin in the next section by summarizing the SXT imaging data we use in constructing our mathematical models. It is shown that the distribution of LACs within each nucleus is bimodal, indicating a division of the nuclear space into regions with high densities of material and low densities of material. We infer that the lower mode corresponds to the most likely regions of euchromatin, less-compact DNA comprised of the majority of active genes, while the higher mode corresponds to the most likely regions of heterochromatin, more-compact DNA thought to contain most silenced genes (Alberts et al. 2007).

In Sect. 3, we summarize the mathematical model we developed in Isaacson et al. (2011). The protein is assumed to diffuse in a volume-excluding potential. Since the underlying SXT imaging data is a 3D grid of voxels, we assume the protein’s motion can be approximated by a Markovian continuous-time random walk. The volume exclusion potential within a given voxel is chosen proportional to the normalized LAC of that voxel. The protein moves by hopping between neighboring voxels of the 3D grid with jump rates determined by the protein’s diffusion constant and the strength of the potential difference between the two voxels. Section 4 summarizes the underlying stochastic simulation algorithm (SSA) we use to simulate the protein’s search for the binding site.

In Sect. 5, we repeat the studies of Isaacson et al. (2011) using volume exclusion potentials reconstructed from SXT imaging of five cell nuclei. We verify that the conclusions of Isaacson et al. (2011) still hold in each of the five nuclei, and demonstrate that for binding sites localized in euchromatin, i.e., regions of low chromatin density, volume exclusion can lead to decreases in the mean binding time of 23 % to 34 % when compared to simulations with no volume excluding potential (zero volume exclusivity). Finally, in Sect. 6, we develop an analytical theory to explain the observed dependence of the mean binding time on the volume exclusivity and binding site localization. The theory suggests that for binding sites in euchromatin there is an optimal level of volume exclusivity that balances a reduction in the volume searched in finding the binding site, with the height of effective potential barriers the protein must cross during the search process.

2 Nonuniformity of Nuclear Chromatin Distribution

To measure the spatial variation in chromatin density within nuclei, we make use of soft X-ray tomographic (SXT) reconstructions of cells. For an overview of SXT imaging, we refer the reader to McDermott et al. (2009). In this work, we use reconstructions of mouse olfactory sensory neurons, including several mature cells and one immature cell taken from the data of Le Gros et al. (2013). The experimental protocol for obtaining these reconstructions was the same used in Clowney et al. (2012). SXT is similar in concept to medical X-ray CT imaging, but uses soft X-rays in the “water window,” which are absorbed by carbon and nitrogen dense organic matter an order of magnitude more strongly than by water (McDermott et al. 2009). As the absorption process satisfies the Beer–Lambert law, the measured linear absorption coefficient (LAC) of one voxel of a 3D reconstruction is linearly related to the density of organic material within that voxel (McDermott et al. 2009). In practice, SXT reconstructions are able to achieve high resolutions of 50 nm or less. For all reconstructions used in this work, the underlying voxels were cubes with sides of length 32 nm. Another advantage of SXT is in the minimal preprocessing of cells that is required before imaging. Cells are cryogenically preserved, but no segmentation, dehydration, or chemical fixation is necessary. In the Appendix, we comment on the measurement error of the SXT imaging process.

As chromatin is the primary organic material within the nuclei of cells, we subsequently assume the LACs from SXT reconstructions are directly proportional to the density of chromatin within each voxel of the reconstruction. For this reason, in the rest of this paper when we discuss regions of low or high chromatin density we are, more precisely, discussing regions with low or high densities of organic material. In Fig. 1, we show two image plane slices through a 3D reconstruction of a cryogenically preserved mature mouse olfactory sensory neuron within a glass capillary. Each image shows the underlying reconstructed LACs within a given voxel, with smaller LACs appearing darker (see colorbars for LAC range). In both images, the cell completely fills the capillary, and the cell nucleus is clearly visible as a circular structure within the cell. The full 3D reconstruction of the LACs within the nucleus are shown in Fig. 2. Voxels denoting the boundary of the nucleus were hand traced in Amira.¹ From these traces, a mask was produced to label voxels within the nucleus. In the rest of this paper, the nuclear membrane is assumed to be given by the collection of voxel faces that are shared by a voxel within and a voxel outside the nucleus. It is readily apparent that the nucleus is comprised of regions of low LAC values interspersed with regions of high LAC values. We subsequently identify regions of smaller LACs, corresponding to regions of low density, as euchromatin (regions of less compact DNA, where most active genes are typically located Alberts et al. 2007). Regions of higher density are identified as heterochromatin (more compact DNA, often containing silenced genes Alberts et al. 2007).

Fig. 1.

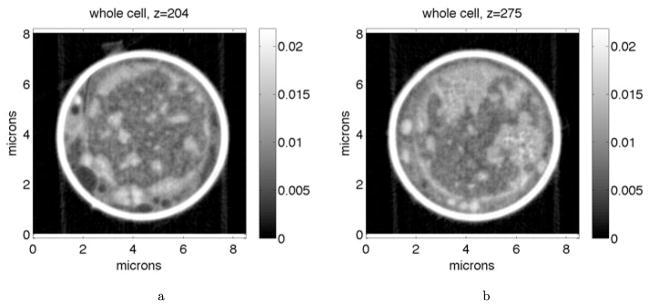
Reconstructed linear absorption coefficients of a mature mouse olfactory sensory neuron. The cell was cryogenically preserved, and then imaged within a glass capillary (the white ring). (a) and (b) show two z-plane slices through the underlying three-dimensional reconstruction. The cell completely fills the capillary in both images. The cell’s nucleus is visible as the circular structure with large regions of lower LAC values (darker pixels). The full 3D reconstruction of this nucleus is shown in Fig. 2. In the figures, LACs have units of per voxel. Each LAC value divided by the voxel length of 32 nm would have the more standard units of nm⁻¹ (Color figure online)

Fig. 2.

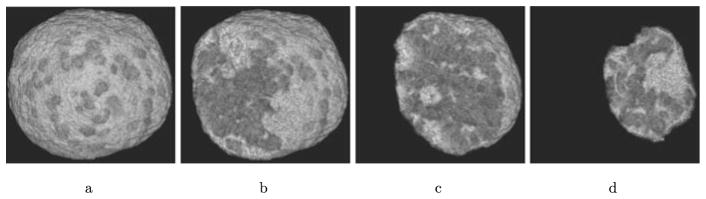
Nucleus of the cell from Fig. 1 (subsequently labeled by “09”). This volume rendering shows the LACs of each voxel of the reconstruction. Lighter colors correspond to larger LACs. (b)–(d) use clipping planes to reveal the interior of the nucleus along the same axis as used for the full cell and glass capillary reconstructions shown in Fig. 1. Movie S1 shows this reconstruction as the clipping plane is moved across the nucleus (Color figure online)

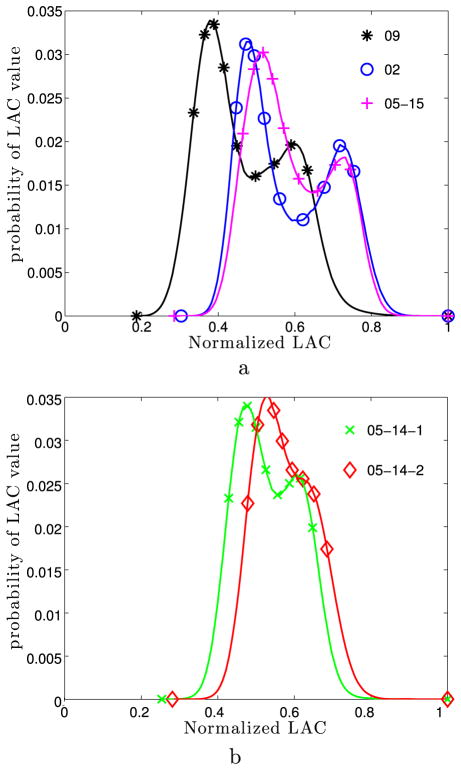
Figure 3 provides further motivation for this labeling. There we plot histograms of the normalized LAC distribution within the nuclei of five cells. (By normalized, we mean that the LACs have been rescaled so that the maximum LAC within each nucleus is one.) For each nucleus, the normalized LAC distribution is bimodal, illustrating the division of the nucleus into regions of euchromatin and heterochromatin. Moreover, we see that the first mode of the distribution occurs between the 20th and 30th percentiles of the normalized LAC distribution, while the second mode occurs between the 70th and 90th percentiles. We therefore interpret these percentile ranges as the most likely LACs for euchromatin and heterochromatin, respectively. Note the bimodal LAC distribution observed in each nucleus is fundamentally different than the unimodal DAPI stain fluorescence distribution we saw in Isaacson et al. (2011) (which was peaked at zero intensity, see Fig. 1C of Isaacson et al. 2011).

Fig. 3.

Histograms of normalized LAC distribution in the nuclei of five cells. Legends give the label subsequently used to identify each nucleus. For each histogram, the LAC values were normalized by the maximum value within that nucleus. Histograms use 100 equally spaced bins between the minimum and maximum normalized LAC values. Markers label every tenth percentile, beginning with the zeroth. Each nucleus is from a mature mouse olfactory sensory neuron, except the 05–15 dataset, which was from an immature mouse olfactory sensory neuron. The label for each histogram corresponds to the dataset from Le Gros et al. (2013) from which that nucleus was extracted. The 05–14 dataset contained two cells, with the corresponding nuclei labeled by 05-14-1 and 05-14-2 (Color figure online)

3 Mathematical Model

We are interested in studying the statistics of the time required for a diffusing regulatory protein to find specific binding sites within the nucleus of a eukaryotic cell. The mathematical model and biological assumptions we describe in this section are based on the model we developed in Isaacson et al. (2011). For completeness, we summarize them here, but refer the reader to Isaacson et al. (2011) for further detail.

We assume that in the absence of chromatin, inside the nucleus the protein would move by Brownian motion with a fixed diffusivity. Volume exclusion caused by the varying spatial density of chromatin is modeled by a repulsive potential that imparts drift to the protein’s movement. The strength of the potential is assumed to be proportional to the density of chromatin at a given point in space. Regions of higher chromatin density will therefore be more volume excluding, i.e., more difficult for proteins to enter, than regions of low density. Note there are many other possible interactions that may influence the protein’s search process. These include nonspecific DNA binding interactions, trapping caused by such interactions or local chromatin structure, and the possibility of protein diffusion along DNA (Halford 2009; Elf et al. 2007). The model we describe focuses on how the search process for specific binding sites is influenced by the assumption that regions of high DNA density are more difficult to enter.

As described in the previous section, the measured soft X-ray tomography (SXT) linear absorption coefficients (LACs) are directly proportional to the density of organic matter within a given voxel. We assume here that the LAC gives a direct measure of the density of chromatin in a voxel. Let I ⊂ ℤ³ denote the set of voxels from a SXT reconstruction that comprise the nucleus of a cell. For i ∈ I, a given voxel within the nucleus, we denote by ℓ_i the normalized LAC for that voxel. By normalized, we mean that the ℓ has been rescaled so that max_i∈I ℓ_i = 1. We assume the potential of the ith voxel is given by

$${\phi }_{\mathit{i}}={\phi }_{max}{\ell }_{\mathit{i}},$$ (1)

where the potential maximum φ_max, subsequently called the volume exclusivity, is a parameter of our model. When φ_max = 0, the particle will simply diffuse, while as φ_max → ∞ it will become increasingly difficult for the protein to enter regions of high chromatin density.

As the imaging data are defined by a mesh of voxels, we approximate the diffusion of the protein within the nucleus as a Markovian continuous-time random walk among these voxels. The protein moves by hopping between neighboring voxels. The probability per unit time that the protein hops from one voxel to a neighbor is determined by the diffusion constant of the protein, the edge length of the voxels, and the strength of the potential barrier crossed in hopping from one voxel to another. Let P_i(t) label the probability the protein is in the ith voxel at time t. In what follows, we assume the DNA binding site is given by one specific voxel of the mesh, i_b, and that upon reaching this voxel the protein immediately binds. Using this condition, our model can be interpreted as an approximation of the search process by the protein for a small region containing the binding site (i.e., the voxel i_b). The binding reaction then gives the reactive boundary condition that

$$P_{{\mathit{i}}_{\mathrm{b}}}(t)=0.$$ (2)

Note this choice of boundary condition assumes the protein is immediately removed from the system upon hopping into the voxel containing the binding site. This is equivalent, insofar as the rest of the system is concerned, to the assumption that the protein stays at the binding site once it has arrived there. It is purely a matter of bookkeeping whether we say that the protein is removed from the system upon arrival at the binding site or remains at the binding site once it has arrived there.

Let α_ij label the probability per unit time the protein will hop to voxel i when within voxel j. The master equation for the probability the protein is in the ith voxel at time t is then the linear system of ODEs

$$\frac{d{P}_{\mathit{i}}}{dt}(t)=\sum _{\mathit{j}\in I}{\alpha }_{\mathit{ij}}{P}_{\mathit{j}}(t)-{\alpha }_{\mathit{ji}}{P}_{\mathit{i}}(t),\forall \mathit{i}\in I-\{{\mathit{i}}_{\mathrm{b}}\},$$ (3)

where I − {i_b} denotes the set of voxels, I, with the i_b voxel removed. Note this model implicitly enforces the no-flux boundary condition that the protein cannot leave the nucleus.

The spatial hopping rates α_ij were derived in the supplement to Isaacson et al. (2011). They are chosen so that in the absence of the reactive boundary condition (2), the master equation (3) would converge as the voxel size approaches zero to a Fokker–Planck partial differential equation (PDE) describing the drift-diffusion of the protein. Let D denote the diffusion constant of the protein, h the edge length of each voxel, k_B Boltzmann’s constant, and T the temperature of the nucleus. We found in Isaacson et al. (2011) that when i and j are nearest neighbor voxels along a coordinate axis the choice

$${\alpha }_{\mathit{ij}}=\frac{2D}{h^2}\frac{1}{exp(({\phi }_{\mathit{i}}-{\phi }_{\mathit{j}})/k_{\mathrm{B}}T)+1},$$ (4)

with α_ij = 0 for all other voxel pairs, provides a second order spatial discretization of the corresponding Fokker–Planck PDE. As the potential barrier to hop from voxel j to i grows (φ_i − φ_j → ∞), we see that α_ij → 0. As the potential becomes constant (φ_i − φ_j → 0), we recover a discretization of the standard discrete Laplacian with the corresponding jump rates

$${\alpha }_{\mathit{ij}}=\frac{D}{h^2}.$$

Note the not-quite-obvious consequence of (4) that

$$\frac{{\alpha }_{\mathit{ij}}}{{\alpha }_{\mathit{ji}}}=e^{-({\phi }_{\mathit{i}}-{\phi }_{\mathit{j}})/k_{\mathrm{B}}T}.$$

This ensures that the steady state solution to (3), in the absence of the reactive boundary condition (2), is the discrete Gibbs–Boltzmann distribution

$$P_{\mathit{i}}^{\text{SS}}=\frac{e^{-{\phi }_{\mathit{i}}/k_{\mathit{B}}T}}{{\sum }_{\mathit{j}\in I}{e}^{-{\phi }_{\mathit{j}}/k_{\mathrm{B}}T}}.$$ (5)

This steady-state will be used in Sect. 6 to estimate the explicit dependence on φ_max of the mean time for the protein to find the binding site, i_b.

We assume that the protein begins its search for the binding site from a nuclear pore within the nuclear membrane. As nuclear pores are not explicitly visible by soft X-ray tomography, we make the approximation that each voxel on the border of the nucleus contains the same fraction of the total number of nuclear pores. Instead of studying the protein’s search from one specific pore (voxel), at the start of each individual simulation we choose the protein’s initial position from a uniform distribution among all voxels on the border of the nucleus. The corresponding initial condition for the master equation (3) is therefore

$$P_{\mathit{i}}(0)=\{\begin{array}{ll}\frac{1}{N_{\text{bnd}}},\hfill & \mathit{i}\in I_{\text{bnd}},\hfill \\ 0,\hfill & \mathit{i}\notin I_{\text{bnd}},\hfill \end{array}$$ (6)

where I_bnd labels the set of voxels on the boundary of the nucleus and N_bnd denotes the number of voxels in this set.

We shall also investigate an extension of the preceding model where i_b is allowed to be a random variable. To understand the difference in binding times for binding sites localized in euchromatin versus heterochromatin, we allow i_b to be chosen from a uniform distribution among all voxels with LACs between two specified percentiles of the nuclear LAC distribution. Binding sites placed in euchromatin were chosen from low percentiles, usually the 20th to 30th, near the first mode of the LAC distribution (see Fig. 3). For the fluorescence imaging data we used in Isaacson et al. (2011), this percentile range corresponded to the first in which there was a non-zero fluorescence level. For the SXT data, this range represents the most likely LAC values for euchromatin containing voxels. (It is unknown if voxels with sufficiently low LAC values actually contain chromatin. Similarly, it has yet to be determined experimentally if there is a precise LAC value above which voxels may be assumed to contain heterochromatin.) To model heterochromatin, we used higher percentiles near the second mode, such as the 70th to 80th.

4 Numerical Solution Method

For a specified value of i_b, the master equation (3) with boundary condition (2) and initial condition (6) is a linear system of ODEs. A typical reconstruction of a nucleus contains on the order of 2.7 million voxels (slightly more than would be contained in a 128 by 128 by 128 Cartesian mesh). While such a system of ODEs can be solved directly, allowing i_b to be a random variable would potentially require the system to be solved many times to obtain good statistical estimates of the binding times. For this reason, we simulated the underlying continuous-time random walk of the protein between the voxels instead of directly solving (3). In these simulations, the protein hops from voxel i to neighbor j with probability per unit time α_ji. When the protein hops into the voxel containing the binding site, i_b, the simulation is terminated and the time the protein entered the voxel recorded. Exact realizations of this stochastic process can be generated by the stochastic simulation algorithm (SSA), also known as the Gillespie method or Kinetic Monte Carlo (Gillespie 1977; Bortz et al. 1975; Gibson and Bruck 2000).

Our numerical simulation algorithm can be summarized as follows:

1. Precalculate the jump rates, α_ij.

2. Choose the binding site location, i_b. This is either specified, or sampled from voxels within specified percentiles of the LAC distribution (i.e., euchromatin or heterochromatin regions).

3. Sample the initial position of the protein from P_i(0).

4. Use the SSA to simulate the motion of the protein until the time, τ, that it hops into the voxel i_b.

5. Repeat from step 2 until the desired number of simulations have been run.

5 Mean Time to Find a DNA Binding Site

We now investigate the statistics of the first passage time, τ, for the protein to find the binding site, and how these statistics depend on the binding site position and volume exclusivity, φ_max. We focus on the survival probability that the protein has not found the binding site by time t,

$$Pr[\tau >t]=\sum _{\mathit{i}\in I}{P}_{\mathit{i}}(t),$$

and the mean binding time

$$\mathbb{E}[\tau ]={\int }_0^{\infty }Pr[\tau >t]dt.$$

For all reported simulations, Pr[τ > t] and associated 95 % confidence intervals were estimated using MATLAB’s ecdf routine. 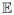[τ] and associated confidence intervals were estimated using MATLAB’s mean routine, while the standard error was estimated using standard deviations determined by MATLAB’s std routine.

In the following, we choose D = 10 μm² s⁻¹, and report φ_max in units of k_BT. For each SXT reconstruction, the voxels were cubic with edge length 32 nm. In all simulations, spatial units were in μm, so that h = 0.032 μm, and time had units of seconds.

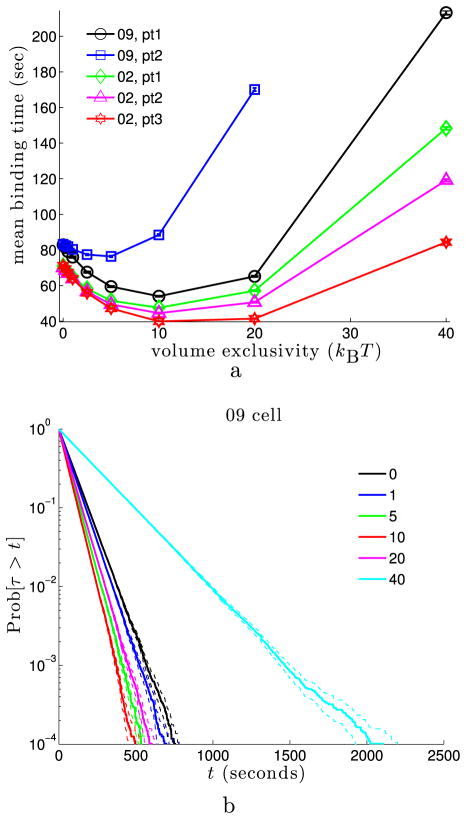
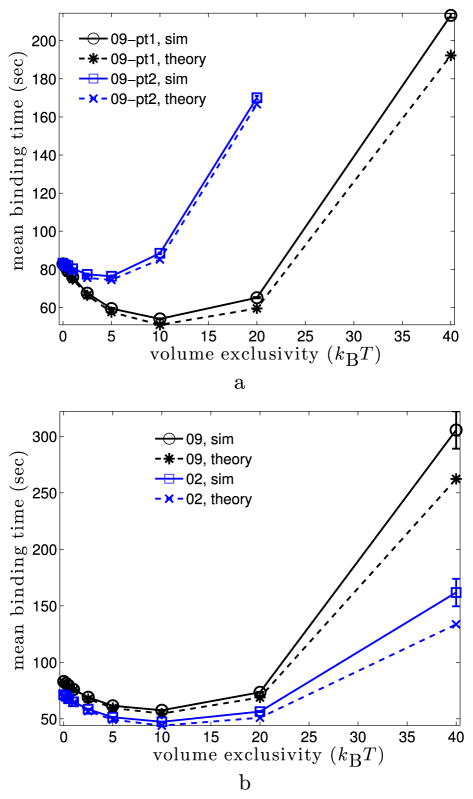
We first examined the time to find a fixed binding site within regions of euchromatin. Several voxels within the euchromatin regions of the 09 and 02 cell nuclei were sampled randomly from all voxels in the 20th to 30th percentiles of the nuclear LAC distribution (see Fig. 3). For each fixed binding site, 128,000 simulations were run, and the time that the protein first encountered the binding site was recorded. In Fig. 4, we examine the statistics of the binding time, τ, for five different binding sites within two cell nuclei (labeled by “09, pt1”, “09, pt2”, “02, pt1”, “02, pt2”, and “02, pt3”). Figure 4(a) shows the mean binding time as a function of φ_max for each of the five binding sites. We see that as the volume exclusivity is increased from zero the mean binding time decreases to a minimum. As the volume exclusivity is further increased, the mean binding time then increases dramatically. This behavior can also be seen in Fig. 4(b), where we show the survival time distribution for the binding site “pt1” from the 09 cell nucleus as the volume exclusivity, φ_max, is increased. Notice that each curve is linear with a logarithmic y-axis, suggesting that the time to find the binding site is approximately an exponential random variable.

Fig. 4.

Mean binding time and survival time distribution for binding sites at fixed locations in euchromatin. (a) Mean binding time as the volume exclusivity, φ_max, is varied. Inset gives the cell nucleus and target point label for each curve. Each data point was obtained from 128,000 simulations. 95 % confidence intervals are shown for each point, but often smaller than the marker size. As φ_max is increased, we see each curve initially approaches a minimum before diverging to ∞. (b) Survival time distribution for the “pt1” binding site from the 09 cell nucleus. The inset gives the volume exclusivity, φ_max, in units of k_BT. Each curve was generated from binding time statistics for 128,000 simulations. The dashed lines about each solid curve give 95 % confidence intervals. Linearity of Pr[τ > t] with the logarithmic y-axis suggests the binding time is approximately exponential (Color figure online)

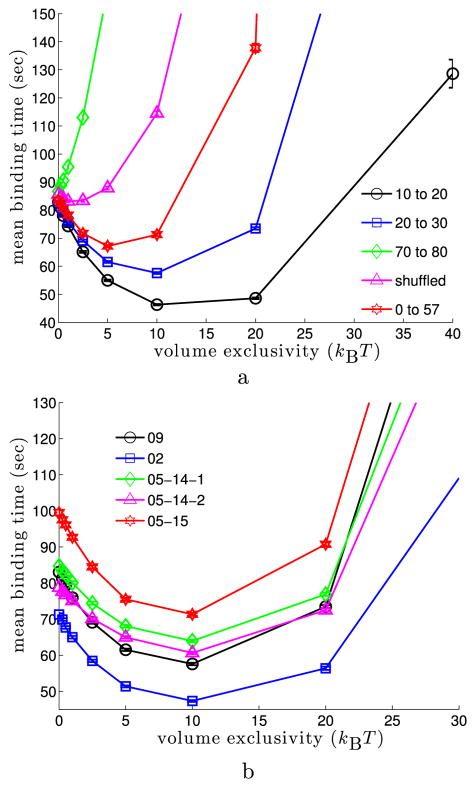
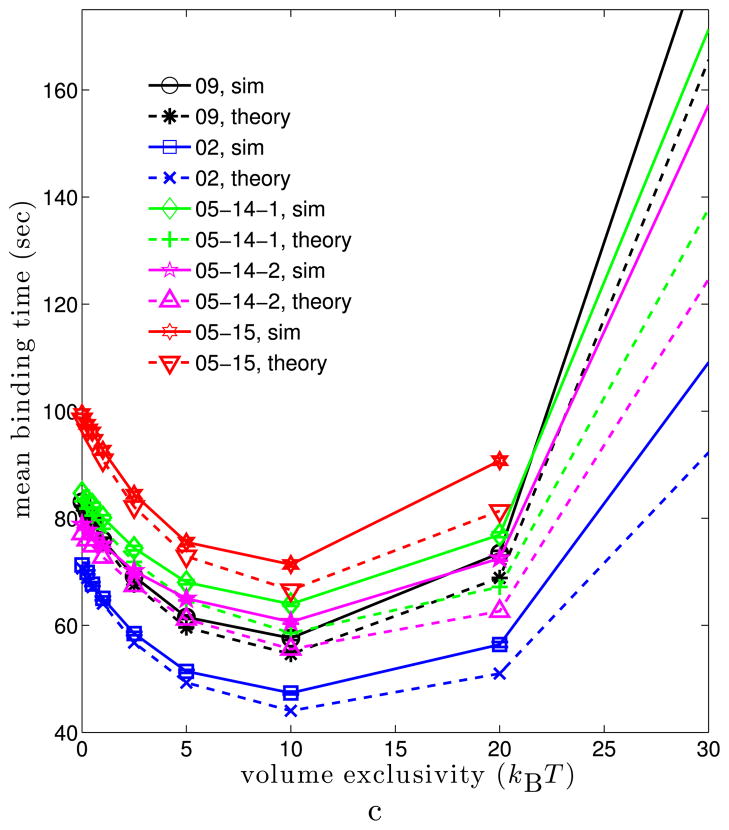
Figures 5 and 6 show how the binding time varies when the binding site is localized in different subregions of the nucleus. For each value of φ_max, a percentile range of the LAC distribution was specified and 128,000 simulations were run. At the beginning of each simulation, the binding site was sampled from a uniform distribution among all voxels within the percentile range. As such, the figures illustrate the average of the mean binding time and survival probability distribution over binding sites localized in different percentile ranges of the LAC distribution. Figure 5(a) illustrates how the mean binding time varies in the 09 nucleus as a function of φ_max when binding sites were localized in euchromatin (the 10th to 20th and 20th to 30th percentile ranges) versus heterochromatin (the 70th to 80th percentile range). When the binding site was localized in regions of higher chromatin density, the mean binding time increased. Moreover, while localizing the binding site within euchromatin leads to a minimum in the mean binding time for nonzero volume exclusivity (about 10 k_BT), this behavior is lost for binding sites localized in heterochromatin. For the latter, the mean binding time simply increases as φ_max increases. Figure 5(b) illustrates that the appearance of a minimum for nonzero volume exclusivity when binding sites are in regions of euchromatin (20th to 30th percentile range) persists across all five of the nuclei we studied. Moreover, for each nucleus the minimum appears at φ_max ≈ 10 k_BT.

Fig. 5.

Mean binding time for binding sites randomly localized in subsets of the nucleus as the volume exclusivity is varied. For each simulation, the target binding site was sampled from a uniform distribution among all voxels within fixed percentile ranges of the nuclear LAC distribution. Each data point was calculated from 128,000 simulations. (a) Mean binding times in the 09 cell. The inset gives the percentile range used for each curve. The black (10 to 20) and blue (20 to 30) curves localized binding sites in regions of euchromatin; see Fig. 3(a). The red (0 to 57) curve localized binding sites anywhere before the LAC value giving the minimum between the two modes of the LAC distribution. The green (70 to 80) curve localized binding sites in heterochromatin. For the magenta curve, the values of the LAC distribution were randomly shuffled among the voxels of the nucleus. Binding sites were then chosen from a uniform distribution among voxels with LAC values in the 20th to 30th percentiles of the LAC distribution. For binding sites in heterochromatin, or when using the shuffled potential, the mean binding time diverges as the volume exclusivity is increased. (b) Mean binding times for binding sites randomly chosen at the start of each simulation within the 20th to 30th percentile of the LAC distribution for five different cell nuclei. For each cell, binding sites in euchromatin were found fastest when φ_max ≈ 10 k_BT (Color figure online)

Fig. 6.

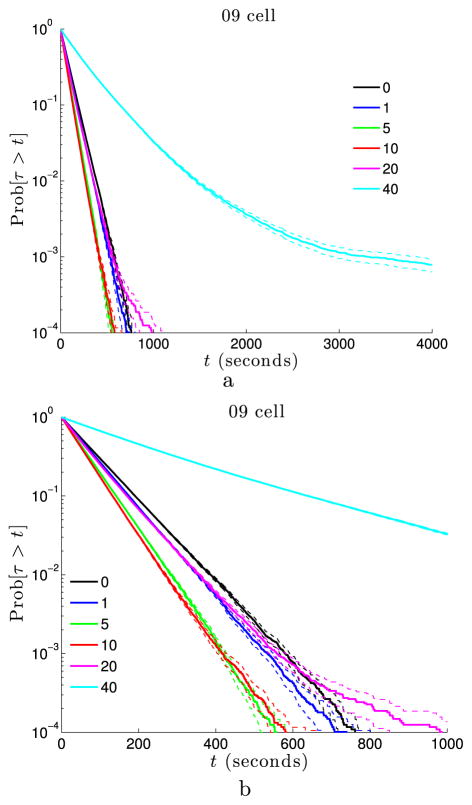
Survival time distributions for binding sites randomly localized in euchromatin. For each simulation, one voxel in euchromatin (the 20th to 30th percentile of the LAC distribution) is randomly chosen to represent the binding site. Each curve is then estimated from 128,000 such simulations. Insets give the volume exclusivity, φ_max, for every curve. (a) For large values of the volume exclusivity, the survival probability is no longer well-approximated by an exponential distribution for all times. (b) Reducing the scale of the t-axis we can see that as φ_max is increased the survival distribution initially shifts to the left, leading to faster binding times. As φ_max → ∞, the distribution shifts back to the right (Color figure online)

The preceding simulations focused on binding sites localized near the most likely regions of euchromatin and heterochromatin. We also examined the behavior of the binding time for binding sites localized in broader regions. The zeroth to 57th percentile curve in Fig. 5(a) corresponds to localizing the binding site anywhere before the minimum located between the two modes of the LAC distribution of the 09 cell; see Fig. 3(a). This minimum was defined to be the center of the bin between the two modes of the 09 nucleus histogram in Fig. 3(a) that had the smallest height, approximately the 57th percentile of the LAC distribution. In Le Gros et al. (2013), the transition point between euchromatin and heterochromatin was assumed to be given by averaging the LAC values at the two modes. For the 09 nucleus, this transition point differs from the location of the minimum between the two modes by less than 0.1 %. Figure 5(a) shows that within this broader region a minimal mean binding time still occurs for a nonzero value of the volume exclusivity, but the overall decrease in the mean binding time relative to that when the volume exclusivity is zero is smaller than for binding sites localized near the mode (20th to 30th percentile). In particular, for sites sampled from the zeroth to 57th percentile range, we observe that the smallest mean binding time is 20 % faster than that when the volume exclusivity is zero, while for sites sampled from the 20th to 30th percentile range the smallest mean binding time is 31 % faster. This decrease in the observed speed-up of the mean binding time arises from the substantially longer time needed to find binding sites within voxels having the highest LAC values. The smallest median binding time, which is less sensitive to outliers, is 27 % faster than the median binding time with zero volume exclusivity for binding sites in the zeroth to 57th percentile range (compared to 31 % faster for the 20th to 30th percentile range).

To test whether the minimum for binding sites in euchromatin regions was dependent on the spatial structure of the LAC distribution we randomly shuffled the values of the LAC distribution among the voxels of the 09 cell nucleus. This preserved the overall distribution of LAC values, shown in Fig. 3(a), while removing all spatial correlations between the values in neighboring voxels. As seen in Fig. 5(a), for binding sites in euchromatin (the 20th to 30th percentile range), the occurrence of a minimum mean binding time for non-zero volume exclusivity is lost (magenta curve). We discuss this result further in the next section, where we show the appearance of a minimum is to be expected if the potential is slowly varying relative to the length scale of the binding site.

In Fig. 6 we show the survival distributions, Pr[τ > t], for the 09 cell nucleus when for each simulation the binding site was randomly localized in regions of euchromatin (20th to 30th percentile range). Note that for large values of the volume exclusivity the survival probability is no longer well-approximated by an exponential distribution, in contrast to the case in which the binding site was fixed across all simulations (as in Fig. 4(b)). This non-exponential behavior arises because the binding site location is now itself a random variable. Figure 6(b) uses an expanded t-axis from Fig. 6(a) to illustrate how the survival distribution shifts as the volume exclusivity is increased. We see that initially the distribution shifts to the left, leading to faster binding times, but that as φ_max → ∞ the distribution rapidly shifts rightward.

The results of this section are consistent with those we found when studying a single cell in Isaacson et al. (2011) using a chromatin density field reconstructed from fluorescence imaging of DAPI stained DNA. Our new simulations illustrate that across several cells of different phenotypes these results persist. The use of X-ray tomography provides a more direct measure of chromatin density since each voxel’s LAC is directly proportional to the density of organic material within that voxel (McDermott et al. 2009). Thus, we would expect the present results to capture more accurately the true spatial distribution of chromatin within each nucleus. Across the five nuclei of this paper, we see that for binding sites localized in euchromatin volume exclusion can lead to 23 % to 34 % lower (i.e., faster) mean search times. The maximum observed speedups are summarized in Table 1.

Table 1.

Percent difference between mean binding time with no volume exclusion (φ_max = 0) and the smallest mean binding time as φ_max is varied (from Fig. 5(b)). The last column gives the percent speed up in the median binding time we found for a single mouse myoblast cell nucleus reconstructed from structured illumination microscopy (SIM) of DAPI stained DNA (Isaacson et al. 2011). The corresponding speedup in median binding times for the X-ray tomography data we study here was comparable to the values reported for the means above

Nucleus	09	02	05-14-1	05-14-2	05–15	SIM nucleus
Percent speedup	31 %	34 %	24 %	23 %	28 %	33 %

6 Why Does the Mean Binding Time Exhibit a Minimum for Binding Sites in Euchromatin?

In this section, we investigate why, for binding sites localized in regions of euchromatin, the mean binding time has a minimum as φ_max is increased from zero to infinity. Our analysis is based on the assumption that near the binding site the volume exclusion potential varies sufficiently slowly that it is well-approximated by a constant.

To estimate the solution to (3), we make several assumptions:

1. There exists a collection of voxels, I′, about and including the binding site where the potential can be approximated as constant.

2. The portion of the nucleus given by the voxels in I′ is large in diameter relative to the length of one voxel, but small relative to the diameter of the entire nucleus.

3. The initial position of the protein is outside I′, that is P_i (0) = 0 for i ∈ I′.

4. The solution to (3) reaches a quasisteady state in space within I′ faster than the binding time scale. We therefore assume that for i ∈ I′, $\frac{d{P}_{\mathit{i}}}{dt}\approx 0$.

5. The time for the protein to find the binding site is sufficiently large that the solution to (3) outside I′ is essentially in equilibrium before the protein locates the binding site. In particular, all memory of the initial position is lost.

Using these assumptions, we construct two solutions to (3), an inner solution valid near i_b, $P_{\mathit{i}}^{\text{in}}(t)$, and an outer solution valid outside I′, $P_{\mathit{i}}^{\text{out}}(t)$. The last assumption above implies that

$$P_{\mathit{i}}^{\text{out}}(t)=A(t)e^{-{\phi }_{\mathit{i}}/k_{\mathrm{B}}T},\mathit{i}\in I-I^{\prime },$$ (7)

where A(t) is a decreasing function of time, to be determined later. Since, by assumption 1, φ_i is nearly constant on I′, we can use (7) to extend the definition of $P_{\mathit{i}}^{\text{out}}$ so that

$$P_{\mathit{i}}^{\text{out}}(t)=A(t)e^{-{\phi }_{{\mathit{i}}_{\mathrm{b}}}/k_{\mathrm{B}}T},\mathit{i}\in I^{\prime }.$$ (8)

The second, third, and fourth assumptions imply

$$\sum _{\mathit{j}\in I}{\alpha }_{\mathit{ij}}{P}_{\mathit{j}}^{\text{in}}(t)-{\alpha }_{\mathit{ji}}{P}_{\mathit{i}}^{\text{in}}(t)=0,\forall \mathit{i}\in I^{\prime }-\{{\mathit{i}}_{\mathrm{b}}\},$$ (9)

with the boundary condition $P_{{\mathit{i}}_{\mathrm{b}}}^{\text{in}}=0$. The assumption that the potential is constant in I′ then simplifies (9) to

$$D{\mathrm{\Delta }}_h{P}_{\mathit{i}}^{\text{in}}(t)=\frac{D}{h^2}\sum _{d=1}^3\left[P_{\mathit{i}+{\mathit{e}}_d}^{\text{in}}(t)+P_{\mathit{i}-{\mathit{e}}_d}^{\text{in}}(t)-2P_{\mathit{i}}^{\text{in}}(t)\right]=0,\mathit{i}\in I^{\prime }-\{{\mathit{i}}_{\mathrm{b}}\},$$ (10)

where Δ_h denotes the discrete Laplacian and e_d is a unit vector along the dth coordinate axis of ℝ³. This equation is coupled to the boundary condition that $P_{{\mathit{i}}_{\mathrm{b}}}^{\text{in}}(t)=0$. Finally, we make the standard inner solution assumption (see Kevorkian and Cole 1996; Cheviakov and Ward 2011) that I′ is sufficiently large that the solution to this equation can be approximated by the solution when I′ = ℤ³. If A(t) were known, a unique solution to (10) when I′ = ℤ³ could be obtained by specifying the matching condition that

$$\underset{\mid \mathit{i}\mid \to \infty }{lim}{P}_{\mathit{i}}^{\text{in}}(t)=P_{{\mathit{i}}_b}^{\text{out}}(t).$$ (11)

This condition assumes that I′ looks like a single voxel on length scales of relevance to the outer solution. We note that all time-dependence in (10) arises from this matching condition.

To solve (10), we consider a related problem where the absorbing boundary condition $P_{{\mathit{i}}_{\mathrm{b}}}^{\text{in}}(t)=0$ is replaced with an explicit sink. Let C_i (t) satisfy

$$D{\mathrm{\Delta }}_h{C}_{\mathit{i}}(t)=K(t){\delta }_{\mathit{i}\mathbf{0}},\mathit{i}\in {\mathbb{Z}}^3,$$ (12)

with lim_|i|→∞ C_i (t) = 0. Here, K(t) denotes the probability per time the protein is removed from the origin at time t. The choice $P_{\mathit{i}}^{\text{in}}(t)=C_{\mathit{i}-{\mathit{i}}_{\mathrm{b}}}(t)-C_{\mathbf{0}}(t)$ satisfies (10) with the boundary condition $P_{{\mathit{i}}_{\mathrm{b}}}^{\text{in}}(t)=0$. Note that C_i (t) ≤ 0, with its most negative value at i = 0. Therefore, $P_{\mathit{i}}^{\text{in}}(t)\ge 0$, as required. The matching condition (11) then gives

$$\underset{\mid \mathit{i}\mid \to \infty }{lim}{P}_{\mathit{i}}^{\text{in}}(t)=-C_{\mathbf{0}}(t)=A(t)e^{-{\phi }_{{\mathit{i}}_{\mathrm{b}}}/k_{\mathrm{B}}T},$$

so that solving for A(t), and substituting the result into (7) and (8) we find

$$P_{\mathit{i}}^{\text{out}}(t)=-C_{\mathbf{0}}(t)e^{({\phi }_{{\mathit{i}}_{\mathrm{b}}}-{\phi }_{\mathit{i}})/k_{\mathrm{B}}T}.$$ (13)

C₀(t) can be determined using Fourier transforms. Let B = [−π, π]³ denote the cube centered at the origin with edges of length 2π. Then for ξ = (ξ₁, ξ₂, ξ₃) labeling a point in B,

$$C_{\mathit{i}}(t)=\frac{1}{{(2\pi )}^3}{\int }_B\widehat{C}(\mathit{\xi },t)e^{i(\mathit{i}·\mathit{\xi })}d\mathit{\xi },$$

where Ĉ(ξ, t) denotes the Fourier transform of C_i (t) and $i=\sqrt{-1}$. The solution to (12) in Fourier space is easily found to be

$$\widehat{C}(\mathit{\xi },t)=-\frac{K(t)h^2}{4D}\frac{1}{{\sum }_{d=1}^3{sin}^2(\frac{{\xi }_d}{2})},$$

so that

$$\begin{array}{l}{C}_{\mathbf{0}}(t)=-\frac{K(t)h^2}{32{\pi }^{3}D}{\int }_B\frac{1}{{\sum }_{d=1}^3{sin}^2(\frac{{\xi }_d}{2})}d\mathit{\xi }\\ =-\frac{2K(t)h^2}{{\pi }^{3}D}{\int }_{\stackrel{\sim }{B}}\frac{1}{{\sum }_{d=1}^3{sin}^2({\xi }_d)}d\mathit{\xi },\end{array}$$ (14)

where $\stackrel{\sim }{B}={[0,\frac{\pi }{2}]}^3$. We note that the singularity of the integrand in (14) is like |ξ|⁻², and hence integrable.

To find the distribution of binding times, and in particular the mean binding time, we make the approximation that the survival probability at any given time t can be found from the outer solution alone, i.e., we assume that

$$Pr[\tau >t]=\sum _{\mathit{i}\in I}{P}_{\mathit{i}}^{\text{out}}(t)=-C_{\mathbf{0}}(t)e^{-{\phi }_{{\mathit{i}}_{\mathrm{b}}}/k_{\mathrm{B}}T}Z,$$

where Z is the partition function

$$Z=\sum _{\mathit{i}\in I}{e}^{-{\phi }_{\mathit{i}}/k_{\mathrm{B}}T}.$$

If we substitute C₀(t) as given by (14) into the above equation, and if we also recall that K(t) is the probability per unit time of binding and, therefore, that

$$K(t)=-\frac{d}{dt}Pr[\tau >t]$$

we get

$$Pr[\tau >t]=-\mathbb{E}[\tau ]\frac{d}{dt}Pr[\tau >t],$$ (15)

where

$$\mathbb{E}[\tau ]=\frac{2}{{\pi }^{3}Dh}\left(\sum _{\mathit{i}\in I}{e}^{({\phi }_{{\mathit{i}}_{\mathrm{b}}}-{\phi }_{\mathit{i}})/k_{\mathit{B}}T}{h}^3\right){\int }_{\stackrel{\sim }{B}}\frac{1}{{\sum }_{d=1}^3{sin}^2({\xi }_d)}d\mathit{\xi }.$$ (16)

Equation (15) shows that the distribution of binding times is exponential, and (16) gives an explicit formula for the mean binding time, 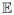[τ]. Note that the theoretical estimate (16) involves no unknown parameters. No parameter fitting is necessary to compare the predicted mean binding time (16) to the simulation results of the previous section.

As the voxel size approaches zero, 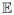[τ] → ∞ like h⁻¹. This is consistent with the well-known fact that it takes an infinite amount of time for a point particle to find a point target by diffusion in a three-dimensional space. (Recall that our target is one voxel in all of the computations reported here.) As we approach the limit h → 0, the last of our simplifying assumptions becomes more and more valid, since there is more and more time for $P_{\mathit{i}}^{\text{out}}$ to equilibrate before binding occurs. Related to this, the assumption that the initial position of the protein does not matter also becomes better and better as h → 0.

In Fig. 7(a), we compare the mean time to find a target binding site predicted by (16) to the empirical mean times found from the simulations in Fig. 4(a). The solid curves in Fig. 7(a) show the simulated mean binding times for the two target locations in the 09 cell that were used in Fig. 4(a). The dashed curves show the estimated mean binding times using (16). The theory gives very good agreement in the predicted mean binding time, particularly for smaller values of the volume exclusivity, φ_max.

Fig. 7.

Theoretical mean binding times (16) and (19) versus those from simulations. Note that both theoretical mean binding times involve no fitting to the simulated times, and are completely determined by known parameters. In all figures, solid lines give the mean binding times from simulations, while dashed lines give the corresponding theoretical prediction. (a) 09 cell for the two fixed targets used in Fig. 4(a). Theoretical mean binding times are from (16). (b) 09 and 02 cells with binding sites randomly localized in euchromatin (20th to 30th percentile of LAC distribution). Simulated means are those from Fig. 5(b), while theoretical are from (19). (c) All five nuclei when binding sites are randomly localized in regions of euchromatin (20th to 30th percentile of the LAC distribution). Simulated means are the same is in Fig. 5(b), while theoretical are from (19) (Color figure online)

To see why the mean binding time has a minimum for binding sites in euchromatin regions, we look at the behavior of 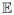[τ] as φ_max is increased from zero. Let

$$\tau =\frac{2h^2}{{\pi }^{3}D}{\int }_{\stackrel{\sim }{B}}\frac{1}{{\sum }_{d=1}^3{sin}^2({\xi }_d)}d\mathit{\xi }.$$

Using (1), we have that

$$\mathbb{E}[\tau ]=\widehat{\tau }\sum _{\mathit{i}\in I}{e}^{{\phi }_{max}({\ell }_{{\mathit{i}}_{\mathrm{b}}}-{\ell }_{\mathit{i}})/k_{\mathrm{B}}T},$$ (17)

where ℓ_i denotes the normalized LAC in voxel i. We now consider the mean binding time as a function of φ_max, 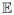[τ](φ_max). Taking the derivative in φ_max,

$$\frac{d}{d{\phi }_{max}}\mathbb{E}[\tau ]({\phi }_{max})=\frac{\widehat{\tau }}{k_{\mathrm{B}}T}\sum _{\mathit{i}\in I}({\ell }_{{\mathit{i}}_{\mathrm{b}}}-{\ell }_{\mathit{i}})e^{{\phi }_{max}({\ell }_{{\mathit{i}}_{\mathrm{b}}}-{\ell }_{\mathit{i}})/k_{\mathrm{B}}T}.$$

At φ_max = 0, 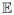[τ](φ_max) will be decreasing when ℓ_ib is smaller than the mean of the nuclear LAC distribution, and increasing when ℓ_ib is above the mean. Examining the second derivative, we see

$$\frac{d^2}{d{{\phi }_{max}}^2}\mathbb{E}[\tau ]({\phi }_{max})=\frac{\widehat{\tau }}{{(k_{\mathrm{B}}T)}^2}\sum _{\mathit{i}\in I}{({\ell }_{{\mathit{i}}_{\mathrm{b}}}-{\ell }_{\mathit{i}})}^2{e}^{{\phi }_{max}({\ell }_{{\mathit{i}}_{\mathrm{b}}}-{\ell }_{\mathit{i}})/k_{\mathrm{B}}T}>0$$

if the LAC values are nonconstant. We therefore find that the first derivative is a strict monotone increasing function.

Note that

$$\underset{{\phi }_{max}\to \infty }{lim}{e}^{{\phi }_{max}({\ell }_{{\mathit{i}}_{\mathrm{b}}}-{\ell }_{\mathit{i}})/k_{\mathrm{B}}T}=\{\begin{array}{ll}0,\hfill & {\ell }_{{\mathit{i}}_{\mathrm{b}}}<{\ell }_{\mathit{i}},\hfill \\ 1,\hfill & {\ell }_{{\mathit{i}}_{\mathrm{b}}}={\ell }_{\mathit{i}},\hfill \\ \infty ,\hfill & {\ell }_{{\mathit{i}}_{\mathrm{b}}}>{\ell }_{\mathit{i}}.\hfill \end{array}$$ (18)

If ℓ_ib ≠ min_i∈I ℓ_i, there is at least one term in the sum (16) for which ℓ_ib − ℓ_i > 0. As such,

$$\underset{{\phi }_{max}\to \infty }{lim}\mathbb{E}[\tau ]({\phi }_{max})=\infty .$$

The preceding results allow for a possible explanation of the dependence on φ_max of the mean binding times observed in our simulations. For binding sites in regions below the mean of the LAC distribution, the mean binding time will always decrease to a minimum as φ_max is increased from zero. Beyond this minimum the mean binding time will increase to infinity as φ_max → ∞. In contrast, for binding sites above the mean of the LAC distribution the mean binding time will simply increase as φ_max is increased. By (13) we see that $P_{\mathit{i}}^{\text{out}}(t)\propto exp[{\phi }_{max}({\ell }_{{\mathit{i}}_{\mathrm{b}}}-{\ell }_{\mathit{i}})/k_{\mathrm{B}}T]$. Combined with (18), this suggests that as φ_max is increased from zero the effective volume the protein must explore is decreased, while the potential barriers provided by regions of high LACs the protein must cross to move between two regions of low LAC become higher and higher. For binding sites in euchromatin, there is a balance between the two effects at which the mean binding time is minimized. In contrast, for binding sites in heterochromatin the latter effect wins out, and the mean binding time simply increases as φ_max increases.

We now consider how the mean binding time behaves when the binding site is itself randomly localized within subregions of the nucleus. Let 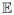[τ_euc] denote the mean binding time when the binding site position is chosen from a uniform distribution among voxels within a region of euchromatin, I_euc ⊂ I. We will subsequently take I_euc to be the collection of all voxels of a nucleus containing euchromatin within the 20th to 30th percentiles of the nuclear LAC distribution. If V_euc denotes the total volume of the voxels within I_euc,

$$\begin{array}{l}\mathbb{E}[{\tau }_{\text{euc}}]=\frac{1}{V_{\text{euc}}}\sum _{{\mathit{i}}_{\mathrm{b}}\in I_{\text{euc}}}\mathbb{E}[\tau ]h^3\\ =\frac{2}{{\pi }^3{\mathit{DhV}}_{\text{euc}}}\left(\sum _{\mathit{i}\in I}\sum _{{\mathit{i}}_{\mathrm{b}}\in I_{\text{euc}}}{e}^{({\phi }_{{\mathit{i}}_{\mathrm{b}}}-{\phi }_{\mathit{i}})/k_{\mathrm{B}}T}{h}^6\right){\int }_{\stackrel{\sim }{B}}\frac{1}{{\sum }_{d=1}^3{sin}^2({\xi }_d)}d\mathit{\xi }.\end{array}$$ (19)

As in (16), we see that (19) completely specifies 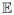[τ_euc] in terms of known parameters.

Figure 7(b) compares (19) to the mean times from simulations in the 09 and 02 cell nuclei, while Fig. 7(c) compares (19) to simulations for all five cell nuclei (see Fig. 5(b)). In every nucleus, we see that for φ_max ≤ 10 k_BT the theory gives good estimates of the mean binding time within the nuclei. As φ_max → ∞ the theoretical formula (19) appears to underestimate the mean binding time found by the SSA simulations. This breakdown could arise for several reasons. Foremost, as φ_max is increased the difference between potential values in neighboring voxels increases. The assumption that the potential is approximately constant near the target binding site can therefore break down.

It should be noted that both (16) and (19) depend only on the value of the target binding site LAC relative to the mean LAC, and not on the detailed spatial structure of the LAC distribution. Based on this observation, one might wonder why we do not observe the same dependence of the mean binding time on φ_max when the values of the LAC distribution are randomly shuffled among voxels (see Fig. 5(a)). The answer is that the conditions under which (16) and (19) were derived no longer hold. After randomly shuffling the LAC distribution, the potential can no longer be approximated as constant near a binding site.

7 Conclusions

We have applied the model we developed in Isaacson et al. (2011) to study how the time required for proteins to find a specific binding site varies as a function of volume exclusion by dense regions of chromatin and binding site localization. Linear absorption coefficients from soft X-ray tomography reconstructions of five mouse olfactory sensory neurons were used to determine the spatial variation of chromatin density within nuclei. The distribution of LACs within each of the nuclei was observed to be bimodal, demonstrating the spatial separation of nuclear space into regions of euchromatin, where most active genes are localized, and denser heterochromatin, where silenced genes are typically located.

Numerical simulations of our model suggest that for binding sites localized in regions of euchromatin there exists a non-zero volume exclusivity at which the mean binding time is minimized. As the volume exclusivity was increased beyond this minimum the mean binding time simply increased to infinity. Across the five nuclei used in this study, the minimal mean binding time was found to be 23 to 34 % faster than that observed in simulations where the volume exclusivity was zero (i.e., the protein simply diffused, experiencing no volume exclusion). Randomly shuffling the LAC values among the voxels of the nucleus led to a loss of this minimum, suggesting that the spatial distribution of the chromatin plays a roll in the existence of a minimal mean binding time for nonzero volume exclusivity. For binding sites localized in heterochromatin, the mean binding time simply increased as the volume exclusivity was increased from zero.

The observed behavior for binding sites localized in either euchromatin or heterochromatin can be explained by the analytical formulas (16) and (19). These approximations to the mean binding time were derived under several assumptions, including that the LAC values in voxels near a binding site are approximately constant and that the time to find the binding site is sufficiently large that the distribution of the protein’s position is proportional to the equilibrium Gibbs–Boltzmann distribution (5). Assuming these conditions hold, both (16) and (19) suggest that the observed dependence of the mean binding time on the volume exclusivity is determined by whether the binding site LAC is below or above the mean LAC within the nucleus. For binding sites with LACs below the mean, such as those localized in euchromatin, the theory predicts the appearance of a minimum mean binding time for non-zero values of the volume exclusivity. It appears that increasing the volume exclusivity from zero helps speed up the search process by decreasing the effective volume that must be searched to find the binding site. Beyond the value that minimizes the mean binding time, further increasing the volume exclusivity leads to increased binding times as the protein becomes trapped in regions surrounded by steep potential barriers. For binding sites localized in regions above the mean, such as heterochromatin, the theory agrees with the observed dependence in our simulations, predicting the mean binding time will simply increase as the volume exclusivity increases from zero.

It should be noted that our theory does not give an explanation for the dependence of the mean binding time on the volume exclusivity when the LAC values are shuffled. In this case, the assumption that the LAC values near the binding site are approximately constant is violated, so that (16) and (19) no longer hold. The simulations with the shuffled LAC values, combined with our analytical theory, suggest that a key aspect of the macroscopic spatial distribution of chromatin that could lead to a decreased mean binding time caused by volume exclusion is a slow variation in chromatin density in the neighborhood of binding sites localized in euchromatin.

Appendix: Soft X-ray Tomography Measurement Error

The X-ray microscope employs monochromatic X-rays and, therefore, the values obtained from computed tomography measurements are equal to the LAC values calculated from the atomic composition of the specimen. The SXT technique avoids the beam hardening effects commonly found in polychromatic tomographic imaging (see Tsuchiyama et al. 2005). The measurement error for each pixel of a single projection image is of order 3 %, determined by photon shot noise. The LAC value of each 32 nm voxel is obtained from tomographic reconstruction of many such projections and is typically less than 1 %. LAC measurement errors are insignificant compared to the observed cell-to-cell variation.