Mechanistic insights into hypothermic ventricular fibrillation: the role of temperature and tissue size

Abstract

Aims

Hypothermia is well known to be pro-arrhythmic, yet it has beneficial effects as a resuscitation therapy and valuable during intracardiac surgeries. Therefore, we aim to study the mechanisms that induce fibrillation during hypothermia. A better understanding of the complex spatiotemporal dynamics of heart tissue as a function of temperature will be useful in managing the benefits and risks of hypothermia.

Methods and results

We perform two-dimensional numerical simulations by using a minimal model of cardiac action potential propagation fine-tuned on experimental measurements. The model includes thermal factors acting on the ionic currents and the gating variables to correctly reproduce experimentally recorded restitution curves at different temperatures. Simulations are implemented using WebGL, which allows long simulations to be performed as they run close to real time. We describe (i) why fibrillation is easier to induce at low temperatures, (ii) that there is a minimum size required for fibrillation that depends on temperature, (iii) why the frequency of fibrillation decreases with decreasing temperature, and (iv) that regional cooling may be an anti-arrhythmic therapy for small tissue sizes however it may be pro-arrhythmic for large tissue sizes.

Conclusion

Using a mathematical cardiac cell model, we are able to reproduce experimental observations, quantitative experimental results, and discuss possible mechanisms and implications of electrophysiological changes during hypothermia.

What's new?

• Mechanistic insights into the effects of temperature and size on the dynamics of fibrillation.

• Modelling based on macroscopic experimental data that then is used to study and compare in tissue dynamics.

• Use of interactive graphic processor unit programing to study spatiotemporal dynamics of a cardiac model in large tissue sizes for tens of seconds within minutes.

Introduction

Understanding the role of thermal effects in cardiac dynamics has been of interest for over 50 years beginning with the pioneer work of Bigelow et al.¹ where the clinical use of hypothermia during intracardiac surgeries was demonstrated. Unfortunately, while hypothermia facilitates surgeons to perform intracardiac operations, it has been shown to be rather hazardous as it has the major risk of inducing ventricular fibrillation (VF)^2–5 and for the core temperatures below 30°C, fibrillation can be more resistant to both electrical defibrillation and anti-arrhythmic therapy.⁶ Furthermore, there is evidence that sudden cardiac death occurs more often during the winter time^7,8 and recently it has been shown a correlation between lower outdoor ambient temperatures and VF, with the risk of VF increasing by as much as 11% for every 1°C decrease in temperatures below 2°C.⁹ On the other hand, hypothermia has been used as a resuscitation treatment for adult victims of VF since 1950s,^10,11 but has increased in popularity in recent years following the results of two landmark studies^12,13 that demonstrated improved survival and neurological outcomes after therapeutic mild-hypothermia (32–34°C) in patients who survived cardiac arrest due to VF. Since 2005, therapeutic hypothermia has become one of the guidelines by the American Heart Association for out of hospital victims of VF. Because of the combined benefits^12–14 and risks^3,15 of hypothermia, it is crucial to understand in a quantitative manner¹⁶ the effects that temperature has on cardiac dynamics.

The heart, as a biological excitable media, is well known to support rotating spiral waves^17–19 and it is now well accepted that they are the underlying mechanism for fibrillation and for some forms of tachycardia.^20,21 Excitable systems are highly non-linear and are very sensitive to temperature changes that can affect spiral wave behaviour.²² The heart is no exception, in fact, since the 1960s it has been suspected that spiral waves were the mechanism behind VF in hypothermia.³

From the electrophysiological point of view, it is well known that temperature affects many characteristics of the action potential (AP) wave: amplitude, duration, conduction velocity, dispersion of repolarization and alternans in AP duration (APD),^3,16,23–26 as well as the directionality in the AP diffusivity due to tissue anisotropy and vascularization.^16,27 From a modelling point of view, excitable media are usually modelled as reaction–diffusion (RD) systems^28,29 based on the Hodgkin–Huxley formalism. Temperature effects are usually introduced in these systems via van't Hoff and Arrhenius equations, together with Pennes bioheat transfer model.^30–33 Most of the models developed for cardiac dynamics, however, do not reproduce well such experimentally observed changes,³⁴ therefore we consider a recent experimentally based phenomenological minimal model (MM) of cardiac tissue,²⁶ which is able to quantitatively reproduce the measured AP shapes, restitution curves, and conduction velocities, respectively, for the right ventricular (RV) canine preparations at different thermal conditions.

In this computational study, we use the previously developed single cell models²⁶ to investigate the effects of temperature and tissue size on the dynamics and stabilities of spiral waves. The paper is organized as follows. In the Methods section, we describe the mathematical model adopted and the numerical simulations performed. In the Results section, we characterize the dynamics of spiral waves for different tissue sizes and temperatures, and in the Discussion section, we discuss our findings and present limitations and future perspectives.

Methods

Mathematical model

In this work, we adopt the four-variable MM for cardiac AP propagation³⁵ fine-tuned on experimental fluorescent optical mapping recordings of canine ventricular electrical activity for different thermal conditions.²⁶ Such choice allows us to correctly reproduce the experimentally measured AP and conduction velocity restitution properties to be simulated in two-dimensional (2D) large domains, both for EPI and ENDO surfaces.

Model equations follow the classical RD formalism:

(1)

(2)

(3)

(4)

where 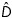is the 2D diffusion tensor. The total transmembrane density current, J_ion = (J_fi + J_so + J_si), is defined through a fast inward, a slow outward and a slow inward currents as:

(5)

(6)

(7)

and the voltage-dependent time constants are

In the previous equations, H(x) represents the standard Heaviside step function; u is the dimensionless membrane potential, rescaled to transmembrane potential dimensions of mV by V_m = (85.7u – 84) mV; ν, w, and s are the three local gating variables. Finally, the temperature-dependent factors are expressed by

(8)

(9)

The above contributions assume T_a = 37°C as the tissue reference temperature and their effects act on both the kinetics of the gating variables Eqs. (2–4) and the ionic currents Eqs. (5–7).

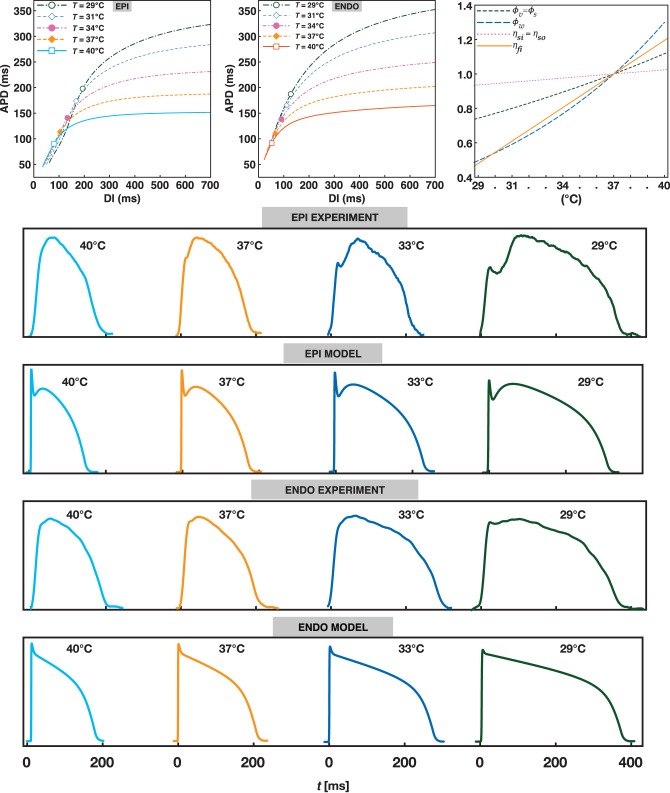
Complete model parameters are referred to Fenton et al.²⁶ Temperature-dependent factors and AP restitution curves obtained from the mathematical model are shown in Figure 1 for the five simulated temperatures. For reference, in the restitution curves, we have added a point that indicates slope one; however it is important to note that the destabilizing effects of slope >1 on the restitution curve is only valid for a 1D map and not necessary when memory or electrotonic effects are considered.^36–38

Figure 1.

(Top row left-centre) Restitution curves for EPI, ENDO tissue models were obtained using 1D cables of 4 cm in length at five different temperatures: 29, 31, 33, 37, 40°C. Symbols indicate where the curves' slope becomes >1. (Top row right) Variation of temperature-dependent factors multiplying the ionic currents and the gating variables as reported in Eqs. (8) and (9). The x-axis highlights the simulated temperatures for both ENDO and EPI. (Bottom four rows) Representative experimental and numerical traces for APs at 900 ms CL stimulation for epicardial and endocardial surfaces at T = 40, 37, 33, 29°C. Differences in shapes are due to various effects such as optical signal average from full 3D experiments in the presence of heterogeneity and fibre rotation anisotropy. Simulations refer to 2D homogeneous and isotropic domains.

Optical mapping

The signals obtained from the numerical simulations during fibrillation are compared with experimental optical mapping signals obtained in canine RV wedge preparations at different temperatures. The tissue preparation has been previously described,^21,39 as well as the optical mapping setup.⁴⁰ Briefly, high-performance light-emitting diodes illuminated the epicardium and endocardium simultaneously and the images were stored using two synchronized cameras. The fluorescence emission light was collected for each camera by a Navitar lens, passed through a long-pass filter, and imaged by a 128 × 128 back-illuminated electron-multiplied charge-coupled device array. The signal was digitized with a 16-bit analogue/digital converter at a frame rate of 511 Hz with a spatial resolution of 600 µm per pixel for a grid size of 7.7 × 7.7 cm².

Data were analysed with a custom-built interactive Java program removing signal drift and fluorescence noise; normalization was conducted on a pixel-by-pixel basis, time averages of length 7 (3 forward and 3 backward) and weighted Gaussian space averages (8 neighbour pixels) of the signal were performed.

Data for the mathematical model were obtained using simultaneous optical mapping recordings from canine RV sections as described in Gizzi et al.⁴¹ that have been separated from the left ventricle resulting in a thin flat slab with effectively zero-flux boundary conditions.

Steady-state APD restitution curves were measured by pacing the tissue at twice diastolic current. Pacing cycle length (CL) was applied starting from long CL (typically 1000 ms) and decreasing by 50 ms until reaching a pacing of 250 ms, after such a value CL was shortened by 10 ms. The protocol ended until capture was lost or VF was induced. This procedure ensures that no alternans is present in the tissue at the starting point of the restitution curve. Pacing was applied at each CL for 1 min before recording for 5–15 s. Action potential duration and diastolic interval (DI) were measured at 25% repolarization threshold (APD₇₅).

Numerical simulations

Simulations are performed using WebGL, which allows solving large number of differential equations in parallel on the computer's graphic processor unit (GPU) and, for some reaction diffusion models, to obtain a simulation time faster than real time.⁴² While GPU simulations allow to run cardiac cell models in tissue at near-real-time speeds without the need of super computers,⁴³ WebGL implementations allow to run models in GPU from a web-browser without the need of pre-compiling and independent of the operating system, in a similar way as Java applets⁴⁴ but at a speed of parallel computing.

Numerical simulations were solved on 2D squared domains adopting a uniform spatial discretization, Δx = 0.125 mm. Four different domain sizes of dimensions 100 × 100 Δx (S1), 256 × 256 Δx (S2), 512 × 512 Δx (S3), and 1024 × 1024 Δx (S4) were analysed. For time integration, a constant time step δt = 0.1 ms was adopted. Calculations were performed on a NVIDIA Quadro FX 580 and on a GTX670 (with 1344 cores) for no <5 min of real time, obtaining a solution timing in frame per second (fps) of 120 fps for S1 (with peak of 180 fps), 60 fps for S2, 60 fps for S3, and 60 fps for S4, respectively. In our simulations, we consider sustained fibrillation when spiral wave activity persisted for >5 min of real time. We performed 64 simulations for a total of 320 real-time minutes.

Results

Using the adaptation of the MM^35,45,46 to the canine electrophysiology described in the Optimal mapping section, we investigate the spatiotemporal dynamics of the epicardial and endocardial models as a function of tissue size, temperature, and initial conditions.

Initiation of fibrillation as a function of tissue size and temperature

For each of the five different temperatures of the EPI and ENDO models, we simulated four different tissue sizes: 2.5 × 2.5 cm², 3.2 × 3.2 cm², 6.4 × 6.4 cm², and 12.8 × 12.8 cm² (corresponding to grid sizes of 200 × 200, 256 × 256, 512 × 512, and 1024 × 1024). As common initial conditions, we started all simulations with two protocols. The first with a single spiral wave initiated from a broken planar wave in the centre of an isotropic and homogeneous domain that was originally at resting initial conditions (RIC), therefore, it produced a spiral wave with the maximum APD. The second consisted of two contra rotating spiral waves initiated at the centre of the domain that simulated previous activations by fast periodic pacing (PFPP) and therefore produced smaller APDs.

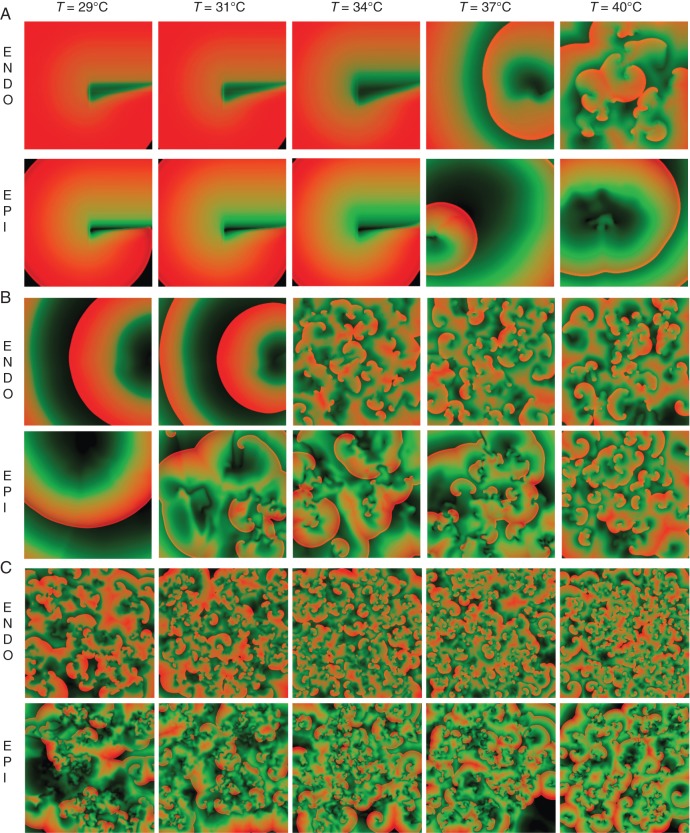
For the first protocol (RIC), we found that the spiral waves were not sustained at smaller tissue sizes for both the EPI and ENDO models as the spiral wave disappeared after a few rotations by collision with the tissue boundaries. Furthermore, the number of rotations before disappearing decreased with the decreasing temperatures to the point that for the smallest tissue sizes of 2.5 × 2.5 cm² the spiral waves initiated at all temperatures could not produce even one full rotation before colliding with a boundary, similarly, a reentry could not be induced for tissue sizes of 3.2 × 3.2 cm² below temperatures of 35°C as shown in Figure 2A. For larger tissue sizes where the induced spiral wave could rotate without colliding with the boundaries, breakup of the spiral always occurred after a few rotations for all temperatures. However, the development of multiple spiral waves arose faster for lower temperatures. Figure 2B shows that in tissue sizes of 6.4 × 6.4 cm² fibrillation (spiral wave breakup) was sustained only at higher temperatures (>31°C), while Figure 2C shows that fibrillation was sustained with very complex dynamics for the larger tissue sizes of 12.8 × 12.8 cm² at any temperature.

Figure 2.

Examples of the dynamics in 2D for the EPI and ENDO models after initiation of a spiral wave in the centre of the tissue following the RIC protocol. Five different temperatures (29, 31, 34, 37, 40°C) and three domain sizes (A) 3.2 × 3.2 cm², (B) 6.4 × 6.4 cm², (C) 12.8 × 12.8 cm² are shown. Non-dimensional AP colour code: black for 0, red for 1.

For the second protocol (PFPP), the spiral waves induced in these cases had smaller wavelengths (due to the shorter APDs generated by this procedure) and unlike in the RIC protocol, they could always fit even in the smaller domains. Therefore, spiral breakup was always present under PFPP for all tissue sizes and temperatures. However, similar to the RIC protocol, breakup was not always sustained and the tissue size at which transient fibrillation occurred was dependent on temperature. Overall, for both protocols, lower temperatures required a larger tissue to sustained fibrillation as described in Table 1.

Table 1.

Simulation results of sustained fibrillation for different tissue size models at different temperatures

Tissue model	40°C	37°C	34°C	31°C	29°C
EPI 2.5 × 2.5 cm2	NS	NS	NS	NS	NS
EPI 3.2 × 3.2 cm2	NS	NS	NS	NS	NS
EPI 6.4 × 6.4 cm2	S	S	S	NS	NS
EPI 12.8 × 12.8 cm2	S	S	S	S	S
ENDO EPI 2.5 × 2.5 cm2	S	NS	NS	NS	NS
ENDO 3.2 × 3.2 cm2	S	S	NS	NS	NS
ENDO 6.4 × 6.4 cm2	S	S	S	NS	NS
ENDO 12.8 × 12.8 cm2	S	S	S	S	S

S, sustained fibrillation; NS, non-sustained fibrillation.

A clear transition between sustained and non-sustained fibrillation can be observed, with a slight difference for the EPI and ENDO tissues.

Persistence and frequency of fibrillation as a function of tissue size and temperature

As defined in the Methods section, we consider sustained fibrillation when complex spatiotemporal dynamics continued for >5 min. Under this criteria, fibrillation was not sustained in the epicardial model for tissue sizes of 3.2 × 3.2 cm² and below any temperature, in fact, the spiral wave activity terminated in less than a few seconds for most of these cases. For the endocardial model, however, sustained breakup could be obtained for the smaller sizes at high temperatures (see Table 1). Sustained fibrillation was possible for both models at all temperatures as long as the tissue size was large (12.8 × 12.8 cm²) as shown in Figure 2C. For tissue sizes of 6.4 × 6.4 cm², fibrillation was sustained in the epicardial and endocardial models for temperatures above 33 and 36°C, respectively.

Temperature not only had an effect on the tissue size at which sustained fibrillation occurred but also had an effect on the frequency of the sustained fibrillation. In the epicardial and endocardial models simulated at the larger tissue sizes, where fibrillation was sustained for all temperatures, the dominant frequency was larger for higher temperatures and decreased for lower temperatures.

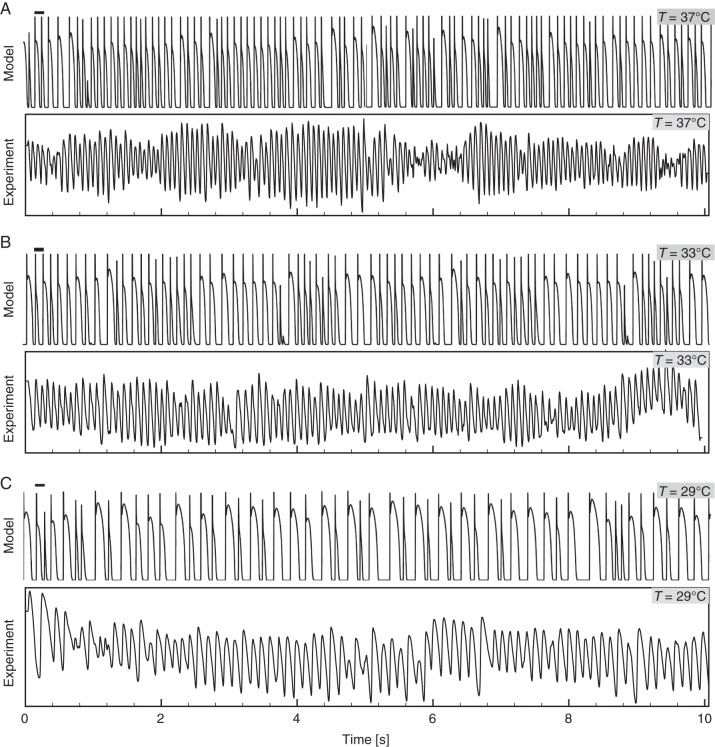
Figure 3 shows the AP from one pixel in the epicardium tissue simulations for three different temperatures (37, 33, and 29°C). The dominant frequency decreased from 10.4 to 8.5 to 6.3 Hz. For comparison, Figure 3 also includes optical traces from one pixel of experimentally recorded fibrillation in RV canine EPI preparations at the same temperatures showing similar trend of frequency change with temperature with dominant frequencies decreasing from 13 to 10 to 8 Hz. Differences in the shapes of the signals are due to the optical mapping space averaging by photon diffusion and pixel size recording both of which decrease the time of the upstroke and smoothing of the AP shape (compare the optical and numerical AP in Figure 1), the minimum DI in the optical signal is also smoothed-out during fibrillation leading to the well-known effect of varying the position of the resting membrane potential.

Figure 3.

Numerical and experimental AP traces from epicardial tissue during VF at T = 37, 33, 29°C. The y-axes represent the normalized membrane voltage AP for the mathematical model and the optically recorded tissue, respectively; the x-axis is time in seconds.

Effects of regional cooling on fibrillation

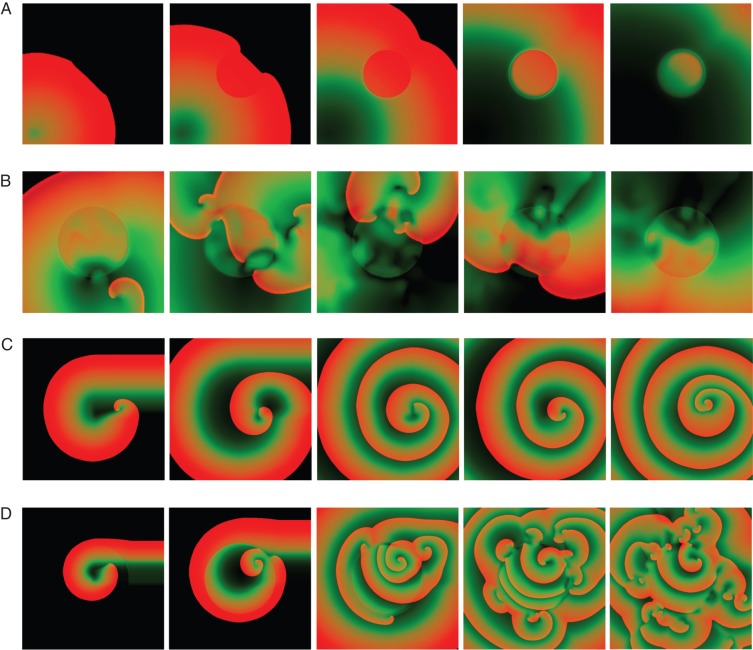
To investigate the effects of regional cooling, we simulated tissues at 40 and 37°C with a centre region at a lower temperature, on the line of Yamazaki et al.⁴⁷ Figure 4A contains five snap shots of a propagating wave illustrating how regional cooling can affect the dynamics of the wave. It is easy to see how the wavelength increases at the centre of the tissue which is cooler (29°C) compared with the outer side (37°C). Our simulations suggest that regional cooling could be anti-arrhythmic for smaller tissue sizes but pro-arrhythmic for large tissue sizes. As shown in Figure 2 and Table 1, fibrillation could be sustained in small tissue sizes of 3.2 × 3.2 cm² of endocardial tissue at 37°C, however, by simulating a cooled down region at (29°C) in the centre of the tissue (Figure 4B), fibrillation could become non-sustained. Conversely, for a tissue size of 6.4 × 6.4 cm² or larger, not only fibrillation could not be terminated but it could be initiated even sooner making it more pro-arrhythmic (Figure 4C and D). Figure 4C shows the starting and evolution of a spiral wave in a 6.4 × 6.4 cm² endocardial tissue at 40°C, while this spiral wave eventually destabilizes and produces a continuous breakup (Table 1); when a cooler region at 29°C is included (Figure 4D) the fibrillation develops at a much faster pace.

Figure 4.

(A) Action potential wavelength variation on a 2D ENDO tissue of size 2.5 × 2.5 cm² at T = 37°C with a central region with temperature of T = 29°C. (B) Anti-fibrillation effect of cooling a small tissue size. A sustainable fibrillation on an endocardial tissue of size 3.2 × 3.2 cm² becomes non-sustainable when a cooling central circular domain at T = 29°C with diameter equal to 1/2 of the square length is included. (C) Spiral wave evolving in endocardial tissue of size 6.4 × 6.4 cm² at T = 40°C and (D) pro-arrhythmic effect of cooling a large tissue size. Simulations is as in (C) however a cooled central region at T = 29°C with diameter 1/2 of the domain is included. Non-dimensional AP colour code: black for 0, red for 1.

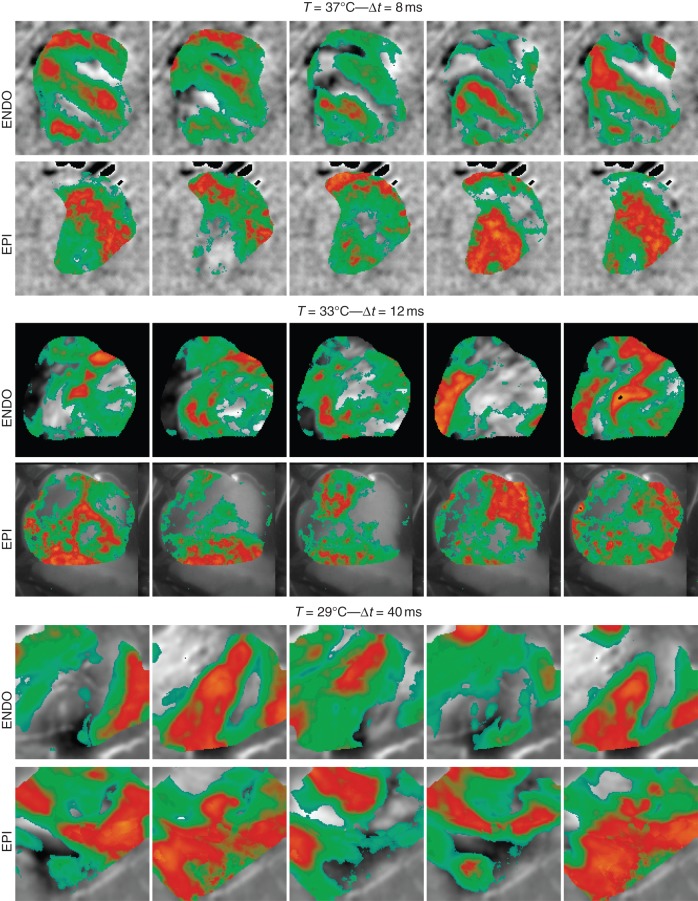
These findings are further enhanced in Figure 5 in which we show simultaneous optical mapping recordings from the epicardium and the endocardium during sustained VF at three different temperatures (37°, 31°, and 29°C). While the optical traces as a function of time from Figure 3 show quantitative correlation between simulations and experiments, the spatial complex dynamics seems only qualitative, with the number of fractionated waves during VF increasing with decreasing temperature.⁴⁸ There are several restrictions in the numerical simulations, discussed in the limitation section, which can explain some of the difference observed in spatiotemporal patterns between simulations and experiments. Nevertheless it is important to notice that the large fractionation shown in Figure 2C is due to the large tissue size. The experimental RV tissues of Figure 5 have an average area of about 4 × 3 cm² therefore the number of waves correlates with those in between Figure 2A and B.

Figure 5.

Experimental optically recorded AP maps during sustained fibrillation at T = 37, 31, 29°C. Endocardial and epicardial synchronous frames are reported. Normalized AP colour code are drawn upon the tissue structure in grey scale: light blue for 0, orange for 1. Average tissue size for the RV preparations shown are 4 cm along the long axes and 3 cm along the short axes.

Discussion

Spiral waves breakup is often associated with a serious pro-arrhythmic state in cardiac tissue particularly with fibrillation.^17,20,21,49 Moreover, thermal effects on biological tissues can induce numerous effects ranging from severe sickness^50,51 to sudden cardiac death.⁵² Therefore, as outlined in the introduction, understanding the non-linear spatiotemporal mechanisms is of crucial importance for medical and clinical practice. Although previous theoretical and experimental studies have discussed the role of spiral waves in relation with arrhythmias, and their relation with tissue size,⁵³ we are not aware of any computational study on the effects of temperature on the spatiotemporal dynamics and stabilities of waves in 2D or 3D tissues. In this work, we present a computational study accounting for physiological changes due to different temperatures by using a previously published minimal phenomenological model of RV epicardial and endocardial cardiac cells.²⁶

Effects of tissue size and temperature on ventricular fibrillation

When temperature is decreased in cardiac tissue, many effects take part such as the slowing of the time constants of the ionic channels which leads to many non-linear changes in the dynamics of the AP and its propagation. Most notably, for mammals other than hibernators,¹⁶ there is a large decrease in conduction velocity, a large increase in QRS intervals, APD alternans, the susceptibility to fibrillation,^3,23,26 and resistance to defibrillation.⁶ While conduction velocity reduces and QRS increases (due to grow of the APD as shown in Figure 1), the net effect on the wavelength is to widen as the temperature is decreased.⁵⁴ However, this only happens at a long CLs where the large growth in APD (Figure 1) overcompensates for the decrease in CV, this is the reason why, at low temperatures, it is not possible to induce a reentry in small tissues with the RIC protocol (Figure 2). Nevertheless, it is possible to induce spiral waves if the tissue is previously paced at short CLs so the wavelength actually decreases. Figure 1 shows that while the APD at long DIs (equivalent to long CLs) dramatically increases with decreasing temperatures, it tends to remain the same at short DIs (the short CLs) therefore, the wavelength actually decreases at low temperatures during fast rates, therefore it is possible to initiate spiral waves in all domains by using the PFPP protocol. The effects of short-term memory and pre-conditioning tissue to produce smaller wavelengths and allow the reentrant waves to be formed in small domains have been previously described for normal physiological temperatures in simulations and experiments in the rabbit ventricles.^55,56

The fact that at lower temperatures and fast pacing the wavelength decreases, explains why hypothermia is pro-arrhythmic,^1–6 being much easier to induce reentries when the wavelength is smaller. However, as Covino and D'Amato³ first described (and since then many other groups), small normal mammalian hearts do not fibrillate (such as rats and rabbits) and/or fibrillation is not sustained (such as in cats) even during severe hypothermia. Our results show similarly (Table 1) that even at low temperatures where fibrillation is easier to induce, fibrillation is not sustained if the tissue size is small. The mechanism for spiral wave self-termination is due to the large increase in APD during a relatively short window of DIs at the lower temperatures as shown in Figure 1. This produces an oscillation of wavelengths during breakup that can be too large to fit in small domains and thus eventually spiral waves annihilate with the boundaries. At higher (more physiological) temperatures, there is still the steep change of APD vs. DI necessary for breakup but not enough to create large wavelengths and thus fibrillation can remain sustainable.

The oscillations of wavelength sizes during fibrillation at low temperatures can further be detected by the dominant period and by AP recordings. Figure 3 shows that during physiological temperatures (37°C) fibrillation has a high dominant frequency (13 Hz for experiments, and 10.5 Hz for simulations) and the AP trace shows many complex activations with very short durations; however, as the temperature is decreased not only the dominant frequency decreases but the differences in duration for the activations increases. At low temperatures, the APD and DI of the signal from fibrillation can vary substantially from as few as 10 ms to as much as 100 ms. The numerical results of the simulated canine VF are consistent with the experimental optical recordings obtained in canine RV preparations during fibrillation for the same temperatures, also shown in Figure 3 and in the optically recorded VF maps in Figure 5. While the frequencies are slightly smaller for the simulations compared with the experimental data, they have similar trends as the temperature decreases going from 13 and 10.5 Hz at 37°C to 10 and 8.5 Hz at 33°C and to 8 and 6.3 Hz at 29°C, respectively. Some of the differences in frequencies can be attributed to the fact that our simulations are only 2D and fail to include 3D effects such as rotational anisotropy, intramural coupling, APD dispersion, and optical smoothing effects.

Regional cooling

Regional heterogeneities such as electroelastic¹⁹ or cooled regions⁴⁷ have recently been proposed as potential methods to defibrillate, in particular, to unpin reentrant spiral waves. In principle, a cool down region can make difficult to initiate a reentry at large activation sequences as the wavelength would be large as shown in Figure 4A; however, at short CLs the wavelength may be too small and could induce reentry. Yamazaki et al.⁴⁷ have shown that reentrant spiral waves can be terminated in a rabbit heart when a circular region is cooled down. In our numerical simulations, a similar situation can be observed when a small tissue of endocardium (3.2 × 3.2 cm²) at 37°C, which can support stable fibrillation as shown in Figure 2 and Table 1, includes a circular region at a lower temperature of 29°C (Figure 4). In this case, fibrillation is no longer sustained as the cooled region produces oscillations in wavelengths that are too large to be sustained in the short tissue. However, a similar simulation but in larger tissue sizes result pro-arrhythmic (in few cases a pinned spiral outside surrounded an inner region with no electrical activity). Figure 4C, for example, shows the dynamics of a reentrant wave initiated in a tissue size of 6.4 × 6.4 cm² at a temperature of 40°C, in this case, when a spiral wave is initiated in the centre of the domain (RIC protocol) the spiral wave will trace a few rotations before a breakup occurs; however, if a circular domain with a lower temperature (29°C) is included in the same simulation, a breakup will start much sooner leading to fibrillation as shown in Figure 4D. In this larger domain, the oscillations of wavelength during breakup can survive and would not terminate the arrhythmia. Therefore, it seems that regional cooling could be anti-arrhythmic for small tissue sizes but pro-arrhythmic when done in larger tissues.

Limitations

It is important to mention that the numerical simulations we present here have several limitations that prevent full comparison with experiments. Most notably the fact that simulations are performed in homogeneous 2D slices of tissue and thus there are no anisotropic effects, dispersion, 3D coupling between epi, endo, and mid-myocardium, curvature, rotational anisotropy,^17,57–59 or temperature changes on the gap junctions dynamic^16,60–62 all of which can affect the dynamics and patterns. In addition, the cable equation as used currently in numerical simulations fails to reproduce some spatiotemporal dynamics observed experimentally^41,63–65 and modifications are starting to be proposed to account for some of these effects^66,67 and which may be needed in addition to the detailed tissue structure to obtain better agreements between simulations and experiments.

Conclusions

Low temperatures have a profound effect on the excitability and the dynamics of electrical waves in the heart. In this work, using a physiologically fitted MM of cardiac AP, we propose mechanisms responsible for some of the dynamics observed in cardiac tissue during hypothermia. We have shown that while fibrillation is easier to induce at lower temperatures, in order for it to be sustained it requires a minimum size of tissue that depends on the temperature. We have also described why the frequency of fibrillation decreases with decreasing temperature and shown that regional cooling can be anti-arrhythmic in small tissues but may actually be pro-arrhythmic in large tissues.

Funding

This work was support from the International Center for Relativistic Astrophysics Network (ICRANet); Italian Istituto Nazionale di Alta Matematica (INdAM) and Gruppo Nazionale per la Fisica Matematica (GNFM); National Science Foundation (NSF) grant CMMI-1028261; National Institutes of Health grant R01HL089271 and the European Community Seventh Framework Program FP7/20072013 under grant agreement No.HEALTH-F2-2009-241526, EUTrigTreat.

Conflict of interest: none declared.