The Physical and Linear Viscoelastic Properties of Fresh Wet Foams Based on Egg White Proteins and Selected Hydrocolloids

Abstract

The aim of this work was to evaluate the physicochemical properties of fresh foams based on egg white proteins, xanthan gum and gum Arabic. The distributions of the size of gas bubbles suspended in liquid were determined, as well as density and volume fraction of gas phase of the generated foams. Additionally, the viscoelastic properties in the linear range were measured, and the results were analyzed with the use of the fractional Zener model. It was shown, that foam supplementation with hydrocolloids considerably decreased their volume fraction of gas phase in comparison to pure egg white protein-based foams. Application of gum Arabic did not cause an increase in the size of foam bubbles when compared to pure white egg foam, whereas application of xanthan gum significantly decreased the size of the bubbles. Application of the fractional Zener model allowed to determine the relaxation times, their intensity in analyzed suspensions and also equilibrium module (G _e). The increase in the concentration of xanthan gum resulted in the prolongation of the relaxation time and increased its intensity. Gum Arabic, when added, weakened the viscoelastic properties of the mixture as a viscoelastic solid.

Introduction

Foams are heterogenic systems of gas–liquid type, where liquid is a continuous phase and gas is a dispersed phase [1]. Such systems are commonly used in food technology as raw materials or final products. The most common substrates for production of industrial foams are proteins of animal origin, mainly egg white and whey protein derivates (as a concentrate or isolate) [2]. However, foams obtained in this way are not stable. This is a consequence of a situation when proteins, that underwent unfolding due to their exposure to larger amounts of aeration-associated mechanical energy, start to regenerate their initial conformation. Macroscopically, this phenomenon is manifested by foam vanishing and drainage [3]. In order to impede these processes, appropriate low- and large molecular mass substances are commonly used in food industry. The foam stabilization can be achieved by changing the ionic strength or pH of the system [4, 5] however, for sensory reasons this kind of stabilization is only occasionally applied in food processing. Other way is application of low molecular chemicals, mostly mono- and disaccharides [6, 7]. Until recently they were the most popular systems used in foam stabilization. Nowadays, however, due to an increasing interest of the consumers in low-sugar and so called light food products, alternative stabilizing agents are taken into considerations. Polysaccharides have become the most popular compounds. Their application, however, can cause a modification of the gas bubble distribution in liquid, resulting in the alteration of volume fraction of gas phase and density of the system. Additionally, changes in the rheological properties have also been observed [8]. This is because the polysaccharide solutions have many non-Newtonian rheological characteristics (viscoelasticity, thixotropy), and in the mixture of proteins, these phenomena may be enhanced. Thus, the knowledge of basic physical and rheological properties, particularly of viscoelastic ones, allows to predict foam structure and enables the appropriate way of foam processing.

Mechanical models, which employ dashpots and springs, representing viscous and elastic effects respectively, are applied to the analysis of viscoelastic phenomena [9]. These elements are combined into larger units, which reflect properties of real materials. The type of a given model depends on the type of the performed experiment. The most commonly used models are the Zener (extended Maxwell model for stress relaxation) and the Burger model (retardation) [10]. In the case, when number of contributions creating relaxation or retardation effects is large, it is easier to operate on continuous relaxation and retardation spectra. However, application of discrete or continuous models requires a complex calculation methods, such as the non-linear least square method with inequality constraints or regularization, and it involves large numbers of estimated parameters [11]. Therefore it could be interesting to employ fractional models, which are based on the fact that derivatives in differential equations for viscoelastic properties are of non-integer order [12]. Assuming this, the fractional Zener model can be presented as follows:

$$\tau \left(t\right)+{\lambda }^{\alpha -\beta }\frac{d^{\alpha -\beta }\tau \left(t\right)}{d{t}^{\alpha -\beta }}=h\cdot {\tau }^{\alpha }\frac{d^{\alpha }\gamma \left(t\right)}{d{t}^{\alpha }}+G_e$$ 1

It means that the stress derivative after time has the order which is (α−β), and the deformation derivative has the order which is α. Assuming in the equation that α = 1 and β = 0, a classical Zener model can be obtained. In order for the Eq. (1) to have a physically interpretable solutions, values must reach α, β ∈ 〈0,1〉 and α > β [12, 13] The values λ, h, G _e have the physical interpretation. λ represents relaxation time, h corresponds with intensity of this time, whereas G _e is described as equilibrium module. The parameter specifies the value of the module of elasticity for the time seeking to infinity. For viscoelastic liquids the parameter takes a value of zero. Possibility of estimation of G _e parameter indicates that from rheological point of view the system behaves like a viscoelastic solid material [9, 10].

Although frequently present in the literature [14], such description of viscoelastic phenomena is only occasionally applied to food systems [15]. The main advantage of fractional models includes a small amount of estimated parameters and no requirement for sophisticated calculation methods. Moreover, the obtained data can be interpreted in a similar way as for models with integer derivatives. At present, it is only the interpretation of derivatives orders that causes a problem. However, the literature reports clearly indicate that the derivatives orders are closely related to the fractal dimension [16].

This paper focuses on the analysis of the physicochemical properties of fresh wet foams based on egg white proteins and selected non-starch hydrocolloids. Particular emphasis was placed on the influence of xanthan (XG) and gum Arabic (AG) (individually and combined) on the viscoelastic properties of the investigated foams as well as on the diameter distribution of the air bubbles suspended in the continuous phase.

Materials and Methods

Materials

The commercially available food egg white (Ovopol, Poland) and the following food additives: gum Arabic (AG) (Regis, Poland) and xanthan gum (XG) (Hortimex, Poland) were used in this research.

The protein content in egg white determined by the method of Kjeldahl was (83.87 ± 0.10)%.

Molecular Characterization of Hydrocolloids

Molecular weights and dispersity of hydrocolloids were determined chromatographically.

Analyses of average molecular masses as well as their distributions were performed by means of gel permeation chromatography (GPC). The system of three columns: Ultrahydrogel-2000 (Waters, USA), Ultrahydrogel-500 (Waters), and Ultrahydrogel-120 (Waters) connected in a series with RI detector (Knauer, Germany) were used. As an eluent a mixture of 0.1 M NaNO₃ and 0.02 % NaN₃ solution in water was applied. Flow rate was set to 0.6 mL/min and sample volume was 100 μL. The sample concentration was 5 mg · mL⁻¹. Samples were prepared by dissolution in NaOH (1 M) and neutralization with addition of 1 M HCl in the presence of phenolphthalein as an indicator. A calibration using pullulan standards (Shodex, Japan) was performed [17].

For xanthan gum there were obtained: weighted molecular mass M _w = (19.6 ± 0.9) · 10⁵ g · mol⁻¹, number molecular mass M _n = (0.022 ± 0.001) · 10⁵ g · mol⁻¹, polydispersity 871 ± 40, and for gum Arabic respectively: M _w = (12.4 ± 0.4) · 10⁵ g · mol⁻¹, M _n = (0.52 ± 0.08) · 10⁵ g · mol⁻¹, polydispersity 16 ± 3.

Foam Preparation

According to the manufacturer’s instructions, the reference pure egg white foam should be obtained by using water and protein at the ratio of 9:1. In the examined foams the part of the protein was replaced by structure-forming hydrocolloids, so the dry matter content remained constant. For this purpose, the weighed amount of protein and hydrocolloids (Table 1) was dissolved in the required amount of distilled water, and subsequently whipped in a industrial planetary mixer (FCM Stalgast, Poland) at the rotation speed of 300 rpm. Foams were prepared in container (20 L capacity) using rotor with changing diameter from 100 to 200 mm. Both container and rotor were supplied by producer. Initial volume of all mixtures subjected to foaming was 2 L. The value of pH of all proteins and proteins-hydrocolloids mixtures was 6.

Table 1.

Concentration of egg white (w/w) in studied foams as a function of hydrocolloid concentration (w/w)

	XG
AG		0 %	0.3 %	0.6 %	0.9 %
	0 %	9.1 %	8.8 %	8.5 %	8.2 %
	0.3 %	8.8 %	8.6 %	8.2 %	7.9 %
	0.6 %	8.5 %	8.2 %	7.9 %	7.6 %
	0.9 %	8.2 %	7.9 %	7.6 %	7.3 %

Within the preliminary tests, the whipping time of 120 s was chosen. This time was based on volume fraction of gas phase (ϕ) measurements. The criterion was set as maximum gas volume fraction during whipping.

Density

Foam density was determined by weighing a fixed foam volume (100 ml) placed in the graduated cylinder. For each experiment measurements were performed in ten repetitions at 23 °C.

Volume Fraction of Gas Phase

Volume fraction of gas phase was determined using the following equation:

$$\phi =\frac{V_f-V_l}{V_f}$$ 2

The value of ϕ was determined by measuring the foam volume and the volume of liquid contained therein. In order to determine the amount of continuous phase (liquid) in foam, the foam disintegration was performed in a laboratory centrifuge at the rotation of 9,000 rpm. Centrifugation was carried out at 23 °C until the complete destruction of the foam occurred. The centrifugation was performed for 10 min and was independent from the composition of the continuous phase. For each foam sample this measurement was made in ten repetitions.

The Size Distribution of Gas Bubbles Suspended in Liquid

Analyses of the size distribution of air bubbles suspended in the liquid phase were carried out with the use of an inverted optical microscope (Kozo, China). The obtained images were recorded with a digital camera and stored on the computer as TIFF (with a resolution of 1,280 × 1,024 pixels).

The image analysis was performed using the ImageJ software [18], using home build macro. The data obtained in this way referred to the cross-section of air bubbles. In order to convert the results to the diameter value, the calculation of the surface given in pixel was performed on a reference object. The calculations of equivalent diameter (d_k) were performed assuming perfect circularity of air bubbles [19]:

$$\begin{array}{c}\hfill d_k=\sqrt{\frac{4\mathit{Sk}}{\pi }}\hfill \\ \hfill k=1,\dots n\hfill \end{array}$$ 3

Based on that equation the size distributions (histograms) of gas bubbles suspended in the liquid were constructed and mean equivalent diameter (d _e) (4) and mean Sauter diameter (d ₃₂ ) (5) were calculated according to equations:

$$d_e=\frac{1}{n}{\displaystyle \sum _{k=1}^n{d}_k}$$ 4

$$d_{32}=\frac{{\displaystyle \sum _{k=1}^n{d}_k^3}}{{\displaystyle \sum _{k=1}^n{d}_k^2}}$$ 5

One hundred fifty images were collected for each foam sample allowing for obtaining a representative population sample of about 1,000 bubbles [20].

The collected data allowed for obtaining values, which enable more precise description of the size of foam bubbles. The following equations were used for further characterisation:

$$\begin{array}{ll}\mathrm{Asymmetry}\mathrm{coefficient}\left(\mathrm{skewness}\right):\hfill & g_1=\frac{M_3}{{\sigma }^3}\hfill \end{array}$$ 6

This factor determines the degree of skewness of the distribution, its value for symmetric distribution is equal to zero. For left-sided asymmetric distributions is negative and the positive for right-asymmetric ones.

$$\mathrm{Concentration}\mathrm{coefficient}\left(\mathrm{kurtosis}\right)K=\frac{M_4}{{\sigma }^4}-3$$ 7

This value characterizes flattening of distribution (width of distribution) relative to a normal distribution. For a normal distribution kurtosis has a value of 0. Values greater than zero indicate on smaller width of the analyzed distribution with respect to the normal distribution. Values below zero indicate on blur in the distribution compared to a normal distribution.

$$\mathrm{Coefficient}\mathrm{of}\mathrm{variation}\nu =\frac{\sigma }{\mu }\cdot 100\%$$ 8

This ratio determines the relative measure of the diversification of obtained distributions of diameter of gas bubbles suspended in a liquid.

Rheological Studies

The measurements were conducted using the RS6000 rheometer (Haake, Germany). A cone-plate geometry was used with the following parameters: diameter 60 mm, angle 1°. A gap size of 3 mm was selected for foams on the basis of preliminary studies. The properties of proteins solutions and hydrocolloids were performed using the same set of sensors, and gap size was set to 0.105 mm. This was the highest value, at which reproducibility of 95 % was achieved. The size of the gap is important in the measurement of the properties of dispersed foam-type systems and has to be carefully selected in order to prevent from crushing and destruction of gas bubbles.

Rheological studies comprised the measurement of the complex module G* as a function of frequency, in the range from 0.1 to 10 Hz at 23 °C. First step was to determine the area of linear viscoelasticity [9, 10]. This test relies, in case of frequency domain measurements, on measurements of the absolute value of complex module as |G*(γ _o )| function of deformation amplitude at constant frequency. Linear viscoelasticity region determines the range of deformation amplitude (γ _o), for which G*(γ _o ) values are parallel to axis of abscissa (γ _o axis). Analyzed for all systems, the measurements of linear viscoelasticity range were done at 0.1Hz and 10Hz. It allowed to determine, common for all systems, the value of γ _o = 0.01 which was used in the following investigations. For each foam sample G’(ω) and G”(ω) measurements were performed in triplicate at 23 °C.

The obtained results of rheological tests were used to calculate the parameters of the fractional Zener model (Eq. 1). The Fourier transformation was applied, assuming sinusoidal deformation constraints, and the following expressions were received, which describe the real (storage) part G’(ω) and imaginary (loss) part G”(ω) of the complex spring module:

$$G\prime \left(\omega \right)=G_e+h\frac{{\left(\mathit{\omega \lambda }\right)}^{\alpha }cos\left(\pi \frac{\alpha }{2}\right)+{\left(\mathit{\omega \lambda }\right)}^{2\alpha -\beta }cos\left(\pi \frac{\beta }{2}\right)}{1+{\left(\mathit{\omega \lambda }\right)}^{2\left(\alpha -\beta \right)}+2{\left(\mathit{\omega \lambda }\right)}^{\alpha -\beta }cos\left(\pi \frac{\alpha -\beta }{2}\right)}$$ 9a

$$G\prime \prime \left(\omega \right)=h\frac{{\left(\mathit{\omega \lambda }\right)}^{\alpha }sin\left(\pi \frac{\alpha }{2}\right)+{\left(\mathit{\omega \lambda }\right)}^{2\alpha -\beta }sin\left(\pi \frac{\beta }{2}\right)}{1+{\left(\mathit{\omega \lambda }\right)}^{2\left(\alpha -\beta \right)}+2{\left(\mathit{\omega \lambda }\right)}^{\alpha -\beta }cos\left(\pi \frac{\alpha -\beta }{2}\right)}$$ 9b

The estimated parameters were α, β, λ, h, and G _e. The objective function in sense of the least square method was defined as follows:

$$s={\displaystyle \sum _{i=1}^N\left\{{\left[G_{{}_{exp}}^{\prime }\left({\omega }_i\right)-G_{\mathit{cal}}^{\prime }\left({\omega }_i\right)\right]}^2+{\left[G_{exp}^{\prime \prime }\left({\omega }_i\right)-G_{\mathit{cal}}^{\prime \prime }\left({\omega }_i\right)\right]}^2\right\}}\underset{\alpha ,\beta ,\lambda ,h,G_e}{\to }min$$ 10

Minimisation of the objective function (Eq. 10) was performed using the Levenberg-Marquardt method. Due to the presence of periodic functions in Eq. (10), the objective function contained large amounts of the local minima. Consequently, accuracy of the fitting was verified with the help of the coordinate system, where the experimental values G’ _exp and G” _exp were plotted on the X axis, and the values calculated from the estimated G’_cal and G”_cal were plotted on the Y axis. The fitting was accepted if its points for set of data were located within the error limit of ±10 %. The exemplary plot is presented in Fig. 1.

Fig. 1.

Accuracy of the fitting fractional Zener model (G’ (black triangle), G” (black circle))

In order to compare other parameters (λ, h, G _e), fixed values for parameters α = 1 and ß = 0.2 were established and they were accepted as the averages resulting from the individual fittings obtained for each analyzed system and were the base for performing specific minimisation.

Surface Tension of Un-Whipped Solutions

Surface tension was measured with Sinterface STA-1 tensiometer (Berlin, Germany) equipped with a platinum du Noüy ring with radius r = 9.55 mm. A surface tension value of 72.1 ± 0.1 mN · m⁻¹ was measured for distilled and degassed water. All analyses were performed at 23 °C (in controlled conditions of temperature and humidity) in three separate series, five repetitions for each solution. All the measurements were carried out for 1 h. The values of surface tensions were calculated using SINTERFACE software.

Statistical Analysis

A classical t-Student’s test was applied to assess significant differences (p-value = 0.05) between the properties of foams obtained from egg white protein, not containing hydrocolloids, and systems that contain one or two hydrocolloids. Additionally, a analysis of the variance (one and two way ANOVA, significance level p = 0.05) in relation to the content of gum Arabic in foam and in relation to the content of xanthan gum was performed. If the ANOVA null hypothesis was rejected, further analysis was carried out on the basis of HSD-Tukey test. It allowed to assess the impact of a specified amount of selected hydrocolloid on the value of the corresponding parameter. The calculations were carried out with the help of R software [21].

Results and Discussion

Results

For all analyzed foams the G’ and G” dependence on frequency (Fig. 2) in log-log scale is comparable with the slow relaxation modes, typical for soft glassy materials [22]. Such moduli behaviour provides an evidence for a formation of a spatial structure. It is visible from the row in Fig. 2, which illustrates increase of XG concentration, that the difference in the distance between G’ and G” remains almost constant. It is observed a slight approaching of G’ and G” curves with increasing frequency. The phenomenon causes a slight increase in phase angle δ = arctan(G”/G’) as a function of frequency. This means, that the investigated foams response to an applied deformation and is moving toward viscous behavior as the frequency increases. This points to the fact that the increase in XG concentration is accompanied by a rise in factors triggering viscoelasticity. The analysis of the columns in Fig. 2 does not confirm this phenomenon. Supplementation with gum Arabic does not change the course of the dependence of G’ and G” in the function of frequency. However, in foams containing only egg white proteins and gum Arabic, a clear decrease by about a decade of both G’ and G” values can be observed. This indicates that xanthan gum is the most potent factor consolidating viscoelastic properties of foams. Further investigations on the impact of AG on foam viscoelasticity show diminished elastic properties of xanthan, particularly for high level of XG (Fig. 2, last column).

Fig. 2.

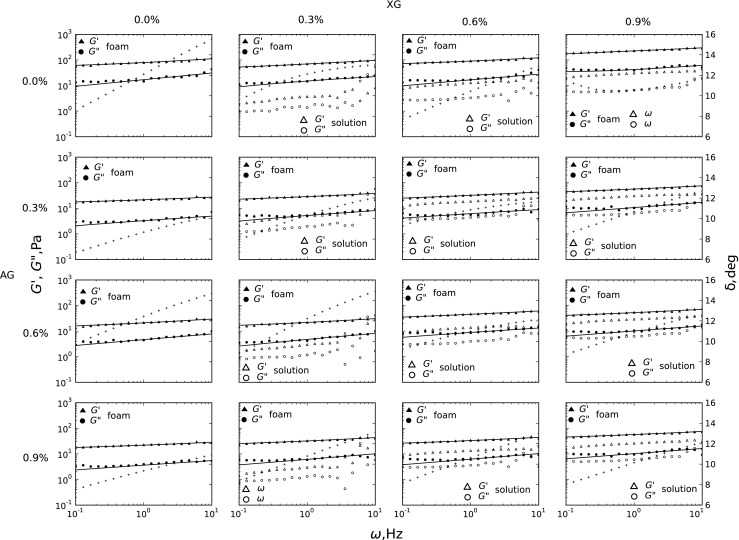
The storage module (G’) and loss module (G”) as frequency function for fresh egg white - hydrocolloids foams and un-whipped solutions(− fractional Zener model) at 23 °C. Phase angle (+) for foams

This phenomenon can be explained by the entirely different behaviour of both xanthan gum and gum Arabic solutions. While XG forms weak gel-like spatial networks [23], which are able to store mechanical energy, AG creates very viscous solutions [24] that are more prone to dissipate the mechanical energy than to accumulate it. These observations are confirmed by rheological study carried out on egg protein solution containing XG and/or AG (Fig. 2). Solutions containing only protein as well as supplemented with AG exhibit only the viscous behavior. It was not possible to obtain interpretable values of G’ and G” in the range of linear viscoelasticity in this case. Addition of XG increases the viscoelastic nature of the solution. For the highest XG concentrations the shape of G’ and G” curves as a function of frequency resembles the courses for the foams, but the module values are smaller. This testifies, that introduction of air into the system creates a viscoelastic structure in the case of foams containing AG, and a reinforcement of the structure in the case of XG addition. In the case of the mixed solution, containing both AG and XG, G’ and G” values are significantly lower than, those in the foam.

The fitted curves presented in Fig. 2 show that the fractional Zener model is more suitable for assessment of real part of the stress relaxation module G’ than G”. For G” the discrepancy within low frequencies are visible as the experimental points and the estimated curve diverge. Table 2 summarizes parameters, that were obtained by fitting of the fractional Zener model (1) to the experimental data. The analysis and interpretation of the derivates orders α and β from Eq. (1) remains the most complicated part.

Table 2.

Parameters of fractional Zener model Eq. (9) fitted to experimental data in studied foams

	XG
		0 %	0.3 %	0.6 %	0.9 %
AG	0 %	h = 27 ± 3 Pa λ = 40 ± 2 s G e = 23 ± 3 Pa	h = 24 ± 2 Pa λ = 42 ± 1 s G e = 21 ± 1 Pa	h = 26 ± 1 Pa λ = 51 ± 4 sa G e = 36 ± 3 Paa	h = 56 ± 3 Paa λ = 83 ± 4 sa G e = 94 ± 2 Paa
	0.3 %	h = 5 ± 1 Paa λ = 49 ± 3 sa G e = 11 ± 1 Paa	h = 10 ± 2 Paa λ = 26 ± 2 sa G e = 11 ± 2 Paa	h = 12 ± 2 Paa λ = 28 ± 1 sa G e = 13 ± 3 Paa	h = 18 ± 1 Paa λ = 34 ± 4 sa G e = 22 ± 2 Pa
	0.6 %	h = 6 ± 2 Paa λ = 47 ± 2 sa Ge = 9 ± 2 Paa	h = 8 ± 1 Paa λ = 29 ± 2 sa G e = 6 ± 1 Paa	h = 14 ± 2 Paa λ = 36 ± 4 sa G e = 17 ± 1 Paa	h = 17 ± 1 Paa λ = 32 ± 2 sa G e = 20 ± 2 Pa
	0.9 %	h = 6 ± 1 Paa λ = 49 ± 4 sa G e = 10 ± 2 Paa	h = 10 ± 2 Paa λ = 26 ± 3 sa G e = 12 ± 2 Paa	h = 10 ± 1 Paa λ = 28 ± 2 sa G e = 13 ± 1 Paa	h = 17 ± 3 Paa λ = 31 ± 1 sa G e = 24 ± 3 Pa

^aSignificant difference between pure egg white foam and foams contain hydrocolloids (t-Student test)

Pure egg white foam possesses a high value of equilibrium modulus (G _e = 23 Pa). Row 1 shows that XG, when added, causes increase to G _e = 94 Pa at XG content of 0.9 %. Similar changes were observed for the relaxation time (λ). The presence of xanthan leads to the establishment of a structure that stably binds air bubbles and forms foams which constitute relatively strong viscoelastic solids. Foams supplemented with gum Arabic (column 1) are characterized by a much lower value of equilibrium modul amounting to G _e∈(9, 11) Pa and the mixtures begin to develop properties of viscoelastic liquid. This is manifested not only by a decreasing equilibrium module when AG concentration rises but also by insignificant alteration in relaxation time (λ). The values of the relaxation time (λ) obtained for the foams with XG are considerably higher in comparison to the values λ for foams stabilized with AG.

Particularly important is the relaxation time intensity h, which grows in the protein-XG system, as the hydrocolloid concentration rises (rows, Table 2). The foam containing protein and AG showed lower values of h in comparison to the pure egg white foam (columns, Table 2). These observations are related to presence of gum Arabic and its ability to change the foam structure towards viscoelastic liquid.

The foams, which contain a mixture of hydrocolloids, display noticeable effects of the presence of both XG and AG. The presence of XG causes increase in relaxation time and its intensity. The presence of gum Arabic in foam leads to a significant decrease in equilibrium module and to formation of foam of nearly viscoelastic liquid structure as a consequence. This effect is visible in the columns in Table 2, which displays values for the spectrum intensity, relaxation time and equilibrium module.

Table 3 shows data on density and volume fraction of gas phase of the obtained foams. The starting foam is characterised by low density (ρ = 54 kg∙m⁻³) and high volume fraction of gas phase (ϕ = 0.951). Enrichment of foam with either XG or AG increases density more than two-fold, while the volume fraction becomes significantly decreased. Further increase in the XG or AG concentration enhances the effect mentioned above. In both cases hydrocolloids bind large amounts of water. Rise in XG concentrations at fixed AG levels (analysis as per the row) intensifies the changes in density and volume fraction. The foams obtained in this way display high density and low volume fraction.

Table 3.

Density and volume fraction of gas phase of egg white and hydrocolloids foams

	XG
		0 %	0.3 %	0.6 %	0.9 %
AG	0 %	ρ = 54 ± 15 kg m−3 ϕ = 0.95 ± 0.02	ρ = 115 ± 15 kg m−3 ϕ = 0.90 ± 0.01	ρ = 126 ± 1 kg m−3 ϕ = 0.87 ± 0.01	ρ = 133 ± 2 kg m−3 ϕ = 0.89 ± 0.01
	0.3 %	ρ = 128 ± 17 kg m−3 ϕ = 0.88 ± 0.02	ρ = 186 ± 4 kg m−3 ϕ = 0.82 ± 0.01	ρ = 190 ± 4 kg m−3 ϕ = 0.82 ± 0.01	ρ = 232 ± 3 kg m−3 ϕ = 0.79 ± 0.01
	0.6 %	ρ = 138 ± 5 kg m−3 ϕ = 0.87 ± 0.01	ρ = 146 ± 3 kg m−3 ϕ = 0.86 ± 0.01	ρ = 154 ± 2 kg m−3 ϕ = 0.85 ± 0.01∙	ρ = 157 ± 2 kg m−3 ϕ = 0.85 ± 0.01
	0.9 %	ρ = 153 ± 5 kg m−3 ϕ = 0.85 ± 0.01	ρ = 165 ± 1 kg m−3 ϕ = 0.84 ± 0.01	ρ = 192 ± 4 kg m−3 ϕ = 0.82 ± 0.01	ρ = 199 ± 2 kg m−3 ϕ = 0.81 ± 0.01

Table 4 shows the values of surface tension (σ) for the discussed systems. In case of solutions containing only AG there are a small changes in the value of surface tension as compared to a solution of pure egg protein. However, for solutions containing protein and XG there is a increase in values of σ. For mixed systems protein—AG - XG the changes in the value of the surface tension take place, resulting from the increase in the XG concentration. The increase in surface tension observed with the increasing amount of xanthan in solution could be related to the increase of viscosity and decrease of protein diffusion [27]. As a result decreasing of gas phase volume faction (Table 3) can be observed.

Table 4.

Surface tension σ (mN · m⁻¹) of un-whipped mixtures at pH = 6 and 23 °C. For 1 % XG and 1 % AG: 60.2 ± 1.4 and 54.0 ± 1.5 mN · m⁻¹

	XG
		0 %	0.3 %	0.6 %	0.9 %
AG	0 %	44.9 ± 1.4	47.1 ± 1.4	49.9 ± 1.3	63.9 ± 1.7
	0.3 %	46.5 ± 1.5	49.1 ± 1.4	53.8 ± 1.5	63.5 ± 1.7
	0.6 %	45.1 ± 1.5	48.3 ± 1.4	55.0 ± 1.5	61.0 ± 1.5
	0.9 %	44.0 ± 1.4	48.9 ± 1.4	57.4 ± 1.5	59.3 ± 1.4

Figure 3 shows histograms of air bubble diameters for individual foam samples. For all analyzed cases, the distributions are unimodal and asymmetric with a tendency to decrease from the side of large bubble diameters. The maximum is located within the range of 0.01–0.1 mm.

Fig. 3.

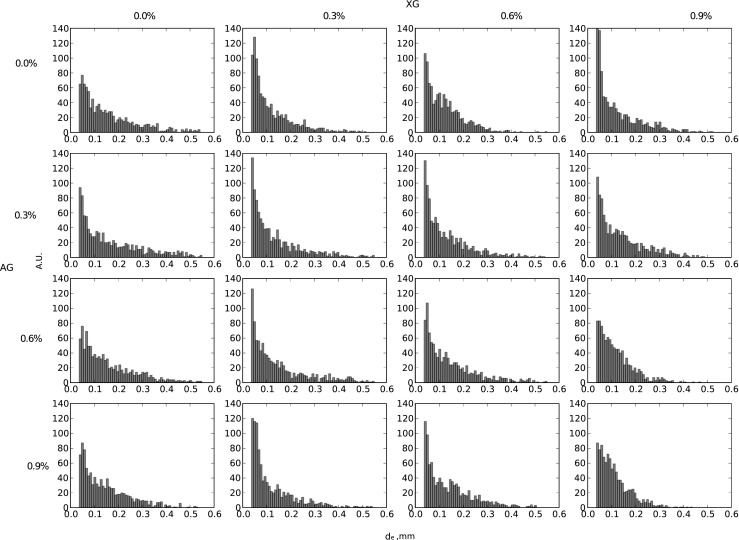
Histograms of bubbles diameters of egg white and hydrocolloids foams

A histogram presenting bubble distribution for foam obtained from pure egg white protein shows an obvious peak. Beginning with the highest values, the amount of bubbles in compartments increases slightly, and then rapidly, to reach its maximum and suddenly drops down. The amount of bubbles with diameter below 0.035 mm in individual compartments is negligible and is not visible due to the applied scale. This shows that foam hosts a differentiated population of air bubbles (a high value of coefficient of variation ν, Table 5) and foam supplemented with xanthan gum significantly differs from the pure egg white foam (row 1, Table 5). Histograms for such foams show increase in the amount of small bubbles (diagram below 0.1 mm, double-fold) and a decrease in large bubbles with a diameter of 0.3 mm. It is manifested in the change of kurtosis value (K).

Table 5.

Bubbles parameters of egg white and hydrocolloids foams

		XG
		0 %	0.3 %	0.6 %	0.9 %
AG	0 %	d = 0.165 ± 0.126 mm d 32 = 0.460 ± 0.022 mm g 1 = 1.7 K = 6.6 ν = 76 %	d = 0.122 ± 0.097 mm d 32 = 0.415 ± 0.020 mm g 1 = 2.3 K = 10.9 ν = 79 %	d = 0.115 ± 0.074 mm d 32 = 0.278 ± 0.016 mm g 1 = 1.6 K = 7.2 ν = 64 %	d = 0.120 ± 0.086 mm d 32 = 0.303 ± 0.010 mm g 1 = 1.6 K = 5.8 ν = 71 %
	0.3 %	d = 0.184 ± 0.153 mm d 32 = 0.538 ± 0.024 mm g 1 = 1.6 K = 6.0 ν = 83 %	d = 0.141 ± 0.120 mm d 32 = 0.509 ± 0.011 mm g 1 = 2.3 K = 10.7 ν = 85 %	d = 0.138 ± 0.104 mm d 32 = 0.373 ± 0.026 mm g 1 = 1.6 K = 6.2 ν = 75 %	d = 0.140 ± 0.092 mm d 32 = 0.307 ± 0.021 mm g 1 = 1.2 K = 4.4 ν = 65 %
	0.6 %	d = 0.163 ± 0.117 mm d 32 = 0.400 ± 0.014 mm g 1 = 1.4 K = 5.1 ν = 72 %	d = 0.142 ± 0.129 mm d 32 = 0.543 ± 0.029 mm g 1 = 2.2 K = 10.3 ν = 91 %	d = 0.136 ± 0.096 mm d 32 = 0.350 ± 0.012 mm g 1 = 1.6 K = 6.4 ν = 71 %	d = 0.114 ± 0.073 mm d 32 = 0.295 ± 0.009 mm g 1 = 1.9 K = 9.3 ν = 64 %
	0.9 %	d = 0.153 ± 0.114 mm d 32 = 0.428 ± 0.015 mm g 1 = 1.8 K = 7.3 ν = 74 %	d = 0.129 ± 0.098 mm d 32 = 0.360 ± 0.023 mm g 1 = 1.8 K = 6.7 ν = 76 %	d = 0.146 ± 0.100 mm d 32 = 0.326 ± 0.017 mm g 1 = 1.2 K = 4.7 ν = 66 %	d = 0.107 ± 0.061 mm d 32 = 0.221 ± 0.015 mm g 1 = 1.5 K = 5.6 ν = 57 %

Thus, the supplementation with XG results in the formation of air bubble populations that comprise of similar size bubbles and a smaller diameter spread (within a range of large diameters). The ν values are similar and span between 64 % and 79 % (Table 5). The average air bubbles diameter and its standard deviation for XG-added foam significantly varied from the pure egg white foam. Sauter mean diameter is also remarkably smaller. With XG added, firstly an elevation of the kurtosis value (K) and subsequently a monotonic decline was observed. A similar tendency was observed for the asymmetry coefficient (g ₁).

Column 1 displays a different situation when foams containing egg white protein and gum Arabic were analyzed. The histograms presented in Fig. 3 (with an exception of 0.3 % AG) resemble those for pure foam. The asymmetry coefficient values are comparable, however the kurtosis values decline. The obtained air bubble population is diffuse which indicates that there are numerous air bubble fractions of diverse diameters. These data reveal that gum Arabic has an insignificant impact on the distribution of the size of gas bubbles in foam. An additional confirmation is provided in Table 5 which shows that the mean diameters values and standard deviation values are comparable with those for pure egg white foam. The values of other distribution parameters did not undergo any remarkable change, either.

Histograms which illustrate the distributions of air bubble diameters for foams containing protein, XG and AG are similar to histograms illustrating processes within protein-XG system (with an exception of two last foams in column 4). Foams display smaller average diameters of air bubbles and lower standard deviation than the starting foam or foam supplemented with AG only. In all observed cases supplementation with xanthan gum caused a decrease in mean Sauter diameter (d ₃₂) and coefficient of variation (ν). Decrease in the value of the variation coefficient indicates, that as the XG content raises, the differentiation of air bubble size suspended in liquid declines. The values for the air bubble population concentrate around average values, and the shape of the histogram for the analyzed foams confirms this observation (Fig. 3). At the XG concentration of 0.9 % the bars disappear at the diameter of 0.4 mm.

It is worth to notice, that kurtosis monotonously decreases as the XG concentration rises and the minimum is observed at 0.6 % XG. This implicates that for low concentrations of XG, the air bubble diameters are less dispersed (around mean value) in comparison to the normal distribution. The concentration tends to become more diffuse, i.e. more comparable with the normal distribution, as the level of XG increases.

The influence of gum Arabic (column analysis) reveals large heterogeneity of parameters from Table 5. Supplementation with AG does not remarkably influence the size of air bubbles. Merely a visible tendency towards diminishing of the value of the mean Sauter diameter (d ₃₂) can be observed. It is apparent for XG content of 0.6 % and 0.9 %. Similarly, the coefficient of variation decreases (ν) as AG rises. This phenomenon is easily visible for the mixtures which XG level reaches 0.6 % and 0.9 %. The lowest value of variation coefficient is observed for foam containing 0.9 % XG and 0.9 % AG.

Discussion

The presented data allow to determine the influence of selected hydrocolloids on the physical properties of foams (Table 6, Fig. 4). The rheological results clearly demonstrate that a rise in the level of xanthan gum results in forming the foam which has a nature of viscoelastic solid with long relaxation time. Such systems are able to store large amounts of energy in their structures. It is owing to the fact that xanthan macromolecules, which adopt helical conformation, are present [25]. When loaded with mechanical forces, the structures span like typical energy-storing springs. Moreover, high values of equilibrium module indicate, that the whole system in liquid phase is a large spatial structure where the protein molecules and polysaccharides, overlaid with water molecules, interpenetrate one another. Supplementation with xanthan caused more than a two-fold increase in foam density and decrease in volume fraction at the same time. This phenomenon can be explained by a XG’s typical feature, which is water binding [22]. Air bubbles which are formed during whipping become visibly smaller and the mean Sauter diameter reflects this process. Furthermore, the foams with XG reveal more homogenous populations of air bubble diameters than the pure egg white foam. Histograms and the value of standard deviation confirm these data (Table 5). Foams based on egg white protein and AG behave differently than foams containing XG (Table 6, Fig. 4). Supplementation with AG causes changes in the rheological picture, causing the properties to become more similar to those characteristic for viscoelastic solids [9]. It is manifested by decreasing values of the equilibrium module (G _e) and low values of the relaxation time (λ). This phenomenon is associated with the nature of AG, i.e. its ability to form highly viscous aqueous solutions which do not have elastic properties. Moreover gum Arabic belongs to the group of surface active polysaccharides [27]. This hydrocolloid is electrically neutral and in solutions it adopts a conformation of a random coil [26]. Upon whipping, i.e. in the presence of large shear forces, macromolecules (proteins and polysaccharides) undergo a partial unfolding and they interpenetrate one another. The generated foam is stabilized by a physical network of entanglement only. This is the reason of no significant alterations in the distribution mode of the size of the gas bubbles suspended in liquid phase (Table 6). The generated foam is morphologically similar to foam based on pure egg white protein. The bubble population is more diffuse than in structures with XG. Foams are characterized by a large mean Sauter diameter. The systems which contain AG display high density, as AG binds large amounts of water. The situation here is different than in the systems with XG. The liquid phase preserves the initial structure of the foam generated by protein. As volume fraction decreases, foam compaction in the space becomes looser, however, it still maintains its geometric (air bubble diameter) properties. In consequence, the analyzed systems are more prone to flow.

Table 6.

The results of one- and two- ANOVA and HSD-Tukey test for main parameters describing the foam properties

		λ s			G e , Pa			d 32 , mm			ϕ
		0 %	0.3 %	0.6 %	0 %	0.3 %	0.6 %	0 %	0.3 %	0.6 %	0 %	0.3 %	0.6 %
AG	0.3 %	a			a						a
	0.6 %	a			a						a	a
	0.9 %	a			a						a		a
XG	0.3 %										a
	0.6 %							a	a		a
	0.9 %				a	a	a	a	a	a	a
AG:XG			b			b

^aHSD-Tukey test—significant difference

^bTwo way ANOVA—significant difference

Fig. 4.

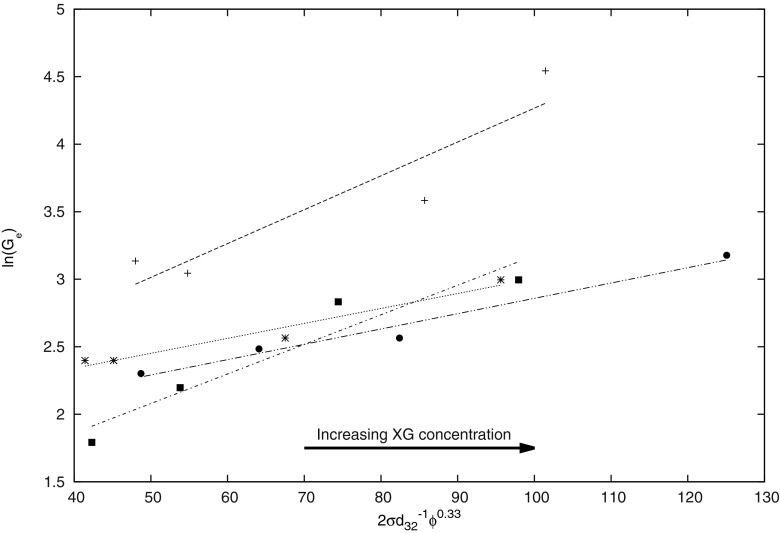
Correlation between physical properties $\left(\frac{2\sigma }{d_{32}}{\phi }^{\frac{1}{3}}\right)$ and G _e for studied foams

Foams which contain protein, XG and AG display a few types of behaviour derived from the applied hydrocolloids. The presence of gum Arabic lowers the numerical values of the parameters in the fractional Zener model. Foams enriched with AG tend to behave as weak viscoelastic solids (Table 2). At the same time, xanthan gum influences the shape of the air bubble population (Fig. 3, Table 5). Histograms are comparable to those, which describe foams containing protein and XG only. Descriptive parameters from Table 4 confirm the data given above. Synergistic effect of XG and AG reflects the density and volume fraction (Tables 5 and 6). The generated foams have a two- or three-fold higher density than the starting foam and it is significantly higher that density in foams treated with either XG or AG. Such behaviour results from the above mentioned functional properties of the applied hydrocolloids. Similar alterations were observed for volume fraction, which has visibly decreased. It corresponds to the reduction of the fractional of the area occupied by gas.

Deeper analysis of influence of selected hydrocolloids on foam properties was described by the correlation between viscoelastic properties represented by G _e values and physicochemical properties $\left(\frac{2\sigma }{d_{32}}{\phi }^{\frac{1}{3}}\right)$ (Fig. 4). In the case of foams, in which XG is only addition, the relationship between equilibrium modulus and physicochemical parameters is R ² = 0.8578. These foams are characterized by the highest values of G _e. The increase of AG content in foams causes the marked/ reduction of G_e values, with essential increase of R² coefficient value, from R ² = 0.9594 up to R ² = 0.9725, for 0.9 % addition of AG (all correlations are significant). Such behaviour means, that with increasing AG addition in foams, the correlation between discussed values becomes strongly linear. The presence of gum Arabic clearly decreases the surface tension of protein solutions, and reduces the elastic effects of foams. Such behaviour results from the possibility of AG adsorption at the interface [27, 28]. Such effects are not exhibited by XG, which belongs to hydrocolloids that do not have adsorbing properties [27, 28]. The application of two hydrocolloids in creating of foam properties seems to be justified, because AG strongly influences the surface properties, and XG is shaping the viscoelastic properties of foams.

Conclusions

In the experiments, various foams based on egg white protein, xanthan gum and gum Arabic were obtained. Foams differ in their physical properties and cannot be dried due to high water content in their structures. Drying of these foams would be not economical, due to consumption of large amounts of energy to evaporate a large quantities of water.

They are, however, a perfect base for light creams, dressings etc. The foams can be also employed to products which require maintaining not only a foam structure but high moisture as well. All examined foams behave like viscoelastic solids (in a linear range). Increase in xanthan gum content caused prolongation of the relaxation time and a rise in its intensity. Supplementation with gum Arabic weakened the properties of the mixture as a viscoelastic solid. Furthermore, higher concentration of xanthan gum resulted in forming foams with visibly smaller spread of the air bubble size. Supplementation with gum Arabic preserved the air bubble populations similar to those obtained from pure egg white protein.

The fractional models appeared to be particularly suitable for a description of the rheological properties of the analyzed foams as the application of the fractional Zener model enabled estimation of their basic viscoelastic properties with relatively high precision. Further research should be carried out on the physical interpretation of the orders of derivatives obtained in Eq. (1).

Nomenclature

D

Diameter, mm

d_e

Equivalent mean diameter, mm

d₃₂

Mean Sauter diameter, mm

G*

Complex relaxation module, Pa

G’

Real part of relaxation module (storage module), Pa

G”

Imaginary part of relaxation module (loss module), Pa

G_e

Equilibrium module, Pa

g₁

Asymmetry coefficient

h

Relaxation time intensity, Pa

K

Kurtosis

M_m

m ^th central moment

S

Square, m²

s

m function in Eq. (10)

V_f

Volume of foam, m³

V_l

Volume of liquid, m³

Greek Letters

α

Exponent in Eq. (1)

β

Exponent in Eq. (1)

γ_o

Deformation

δ

Phase angle

ϕ

Volume fraction of gas phase

λ

Relaxation time, s

μ

Average

ν

Coefficient of variation

ρ

Density, kg∙m⁻³

σ

Surface tension, mN∙m⁻¹

τ

Share stress, Pa

ω

Frequency Hz

Subscripts

Exp

Experimental value

Ca

Calculated value