Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Feb 26;4:4203. doi: 10.1038/srep04203

Quantifying charge carrier concentration in ZnO thin films by Scanning Kelvin Probe Microscopy

C Maragliano 1,a, S Lilliu 2, M S Dahlem 2, M Chiesa 1, T Souier 1, M Stefancich 1
PMCID: PMC3935190  PMID: 24569599

Abstract

In the last years there has been a renewed interest for zinc oxide semiconductor, mainly triggered by its prospects in optoelectronic applications. In particular, zinc oxide thin films are being widely used for photovoltaic applications, in which the determination of the electrical conductivity is of great importance. Being an intrinsically doped material, the quantification of its doping concentration has always been challenging. Here we show how to probe the charge carrier density of zinc oxide thin films by Scanning Kelvin Probe Microscopy, a technique that allows measuring the contact potential difference between the tip and the sample surface with high spatial resolution. A simple electronic energy model is used for correlating the contact potential difference with the doping concentration in the material. Limitations of this technique are discussed in details and some experimental solutions are proposed. Two-dimensional doping concentration images acquired on radio frequency-sputtered intrinsic zinc oxide thin films with different thickness and deposited under different conditions are reported. We show that results inferred with this technique are in accordance with carrier concentration expected for zinc oxide thin films deposited under different conditions and obtained from resistivity and mobility measurements.

In the last century, Zinc Oxide (ZnO) attracted interest within the scientific community. Defined as the future material, ZnO has been widely studied since 1935. Lately a renewed interest for this material had risen. This is mainly due to reports of p-type conduction1, ferromagnetic behavior2 and improvements in epitaxial growth technologies that make this material suitable for the fabrication of optoelectronic3, piezoelectric4 and spintronic devices5. Extensive reviews on ZnO applications are available in the literature6,7. Nano-crystalline ZnO thin films are being widely studied, especially for photovoltaic applications8,9. Due to its inherent transparency in the visible range, ZnO is used as transparent conductive oxide (TCO) on top of thin film solar cell10,11. As an example, in inverted bulk-heterojunction organic solar cells12,13, n-doped ZnO can be used as the electron collector/hole blocking buffer layer14.

ZnO thin films can be either deposited15 or solution processed14. Determination of the doping concentration of ZnO films is a fundamental step for finely tuning ZnO deposition parameters (e.g. for epitaxial growth) and ZnO nanoparticles synthesis (for solution processing). A method able to determine thin films ZnO doping profiles at the nanoscale would allow optimizing its performance in several applications.

Although different techniques to measure the doping concentration in semiconductors have been developed16,17,18, the determination of this property in ZnO thin films still remains challenging19. This is due to the fact that ZnO is intrinsically n-doped, presumably by Zn interstitials, O vacancies and H, that affect the position of the Fermi level within the bandgap20. In this view, ordinary method such as Secondary Ion-Mass Spectroscopy (SIMS) and Electron Holography (EH) can just give an insight of the possible cause of the self-doping effect21,22, without giving accurate quantitative results in terms of charge carrier concentration. Furthermore, these two techniques are destructive and therefore their versatility is limited. Four Probe Method is the most widespread technique to measure the resistivity of thin films23. From this measurement, given the carriers mobility, the effective doping concentration of the material can be recovered. However, several experimental issues have to be taken into account when using this technique. The contact between a metal and a semiconductor can form a Schottky diode24 rather than an ohmic contact. To obtain reliable results, adjustments of the drive current are needed depending of the resistivity of the sample. Due to the reduced thickness of thin films, the measurement can be affected by the presence of the substrate, leading to erroneous results. In this view, a non-contact technique able to measure the position of the Fermi level and to relate it with the effective doping concentration would represent an adequate solution for the aforementioned issues.

Scanning Kelvin Probe Microscopy (SKPM), a modified version of Atomic Force Microscopy (AFM), is a non-destructive non-contact surface technique that allows imaging two-dimensional profiles of contact potential difference (VCPD) i.e. the difference in the work functions of the tip and the sample25,26,27,28. This is true in absence of trapped charges29 or adsorbates on the surface. It is well known that in semiconductors the work function depends on the dopant types and concentrations24. This is because they affect the Fermi level position within the bandgap.

Different attempts to correlate SKPM measurements with doping concentration in semiconductors have been reported in literature since the technique has been proposed27,30. Henning31, Shin32 and Hochwitz33 reported a doping concentration two-dimensional image in silicon microstructures and integrated circuits. Due to its inherent nanometric spatial resolution29, SKPM has been successively used to probe non-uniform doping distribution at the nanoscale. Semenikhin34 reported evidence of local doping inhomogeneity on conducting polybithiophene, while Koren35 measured the doping distribution along single phosphorous-doped silicon nanowires. Although compared with Scanning Capacitance Microscopy (SCP) this technique presents some limitations in terms of accuracy36,37, previously mentioned and other reports38 demonstrate that SKPM can be used to quantitatively measure the doping concentration in semiconductors with high spatial resolution31,33,39. Attempts to correlate SKPM measurements with charge carriers concentration in ZnO have been reported40,41. However, a clear and complete formalism is still lacking.

Measuring the doping concentration of a sample without touching its surface represents a considerable advantage, especially for thin films. This avoids damaging the surface and does not introduce extra effects due to Schottky barrier formation. Compared to Four Probe Method, SKPM can be used to measure the doping profile of semiconducting thin films deposited on metal41. This would prevent from the need to deposit a sample on an insulating substrate just to measure its resistivity. Being a surface technique, SKPM is able to measure carrier concentration on top of the sample. Here, the presence of charges can affect the measurement. To minimize this effect, the sample is scanned in tapping mode while both the tip and the back contact are connected to the ground, before performing the actual experiments. By creating a closed circuit, the surface charges flows towards the electric ground, causing the surface to discharge. This technique has been successfully applied by Jespersen et al.42. While doping concentration is normally associated with bulk intrinsic or extrinsic doping, due to their small thickness, surface defects in thin films have a significant contribution on the overall sample doping43. This has been experimentally demonstrated by photovoltage measurements performed on ZnO nano-“mounds”44. Since SKPM is able to measure the presence of surface defects45, it represents a suitable technique for imaging two-dimensional doping concentration in ZnO thin films.

In this paper, two-dimensional charge carrier concentration images acquired on RF-sputtered intrinsic ZnO thin films are reported. A simple energy band model that correlates work function difference measurements with the effective doping concentration is presented. ZnO samples with different thickness (from 10 to 300 nm) are investigated. To further validate the method, doping concentrations of ZnO samples deposited under different conditions are compared. We show that results inferred with this technique are in accordance with carrier concentration obtained with Four Probe and Hall measurements.

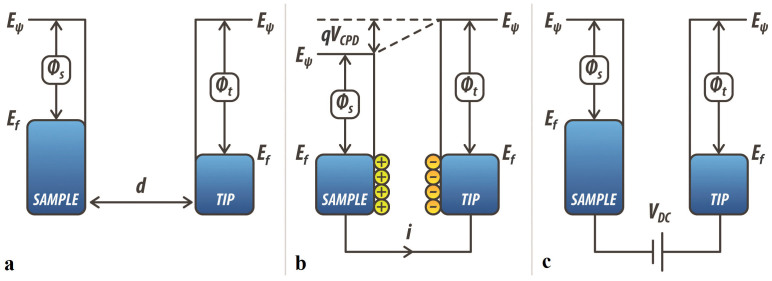
SKPM is an AFM based technique developed by Nonnemacher et al. in 199127,30. As other electrostatic force microscopy techniques39,46, it measures the contact potential difference VCPD between a conductive tip and a sample. The VCPD is defined as:

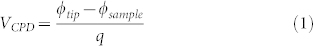graphic file with name srep04203-m1.jpg

where q is the electronic charge, while ϕtip and ϕsample are the work functions of the tip and the sample respectively. Compared to Ultraviolet Photoelectron Spectroscopy (UPS), which measures the kinetic energy of spectra of photoelectrons emitted under ultraviolet excitation, both techniques can be used to quantify the work function of a given material and therefore could be employed to determine the charge carrier concentration. However, UPS has a lower spatial resolution compared to SKPM, being limited by the dimension of the ultraviolet light spot used as excitation47. Thus, in order to quantify the charge carrier concentration with high spatial resolution, we rely on SKPM. In SKPM, when the tip is brought close to the sample and they are both grounded, an electrostatic interaction due to the differences in their Fermi energy levels can be probed. Fig. 1 shows the energy level diagram of the tip and the sample for different ϕtip and ϕsample. When tip and sample are not electrically connected, their vacuum levels are aligned but Fermi energy levels are different (Fig. 1a). Upon electrical contact (for example both grounded), the system reaches equilibrium, and Fermi levels line-up through electron current flow (Fig. 1b). This current flow causes the vacuum energy levels to be no longer the same: the consequence of this is the formation of a contact potential difference VCPD that affects the interaction between the tip and the sample, causing the formation of an electrostatic force between them. As shown in Fig. 1c, this force can be nullified. This is done indeed applying an external bias VDC = VCPD between the tip and the sample. Thus, in this case, the amount of applied external bias is exactly equal to the work function difference between the two.

Figure 1. Electronic energy levels of the tip-sample system for three different cases.

Figure 1

Open in a new tab

(a) tip and sample are separated by a distance d and are not electrically connected; (b) tip and sample are electrically connected. In this case the Fermi energy levels are lined-up; (c) an external bias equal to the contact potential difference VCPD is applied to the tip. This causes the tip-sample electrical force to be nullified.

In SKPM the contact potential difference VCPD between a conductive tip and a sample is measured by applying to the tip an ac voltage (Vac = VACsin(ωt)) and a dc voltage (VDC). The Vac causes the cantilever to oscillate because of the electrical forces between the AFM tip and the sample surface, while the VDC nullifies the oscillating electrical forces that originated from the VCPD. The frequency ω is chosen equal or close to the resonance frequency of the cantilever in order to increase the signal-to-noise ratio. The electrostatic force component measured at frequency ω has the following expression27,30,32:

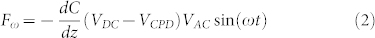graphic file with name srep04203-m2.jpg

where C is the tip-sample capacitance and z is the tip-sample distance. From (2), it is evident that the VCPD can be measured by applying a dc voltage VDC such that the oscillating amplitude at ω is nullified. Equation (2) is strictly valid for metallic samples. However, it has been demonstrated that a similar expression can be derived for semiconductors, provided that the tip-sample capacitance is written as the sum of the air gap and the space-charge capacitor48.

The Fermi energy level in semiconductors depends on the doping concentration24. Fig. 2 depicts the electronic energy level for a tip-semiconductor system when the tip and the back surface of the semiconductor are electrically connected. In the case of a non-degenerate n-doped semiconductor, the Boltzmann approximation for the concentration of electrons (n) reads49:

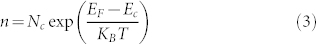graphic file with name srep04203-m3.jpg

where Nc is the effective density of states in the conduction band, Ec and EF are the conduction band energy level and the Fermi energy level, KB is Boltzmann constant and T is the temperature. If the effective donors concentration CD is significantly higher than the intrinsic carriers concentrations ni, the concentration of electrons n can be used to estimate CD by using the following approximation49:

graphic file with name srep04203-m4.jpg

where the effective donors concentration CD is defined as the difference between the ionized concentration of donors 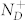Inline graphic and the ionized concentration of acceptors 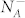Inline graphic. When the n-doped semiconductor surface is electrically connected to the tip through a back contact, the VCPD can be written as32:

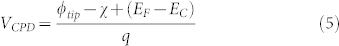graphic file with name srep04203-m5.jpg

where χ is the electron affinity of the semiconductor. Analogous expressions can be derived for a p-doped semiconducting surface. In equation (5) the band bending term ϕB is not explicitly included and its effect on the electrical conductivity of the surface is taken into account by including it in the bulk. Due to their limited thickness, indeed, we expect the presence of defect states at the surface to affect the charge carrier concentration through the entire film. This assumption is supported by Ref. 44, where photovoltage measurements confirm the presence of electrically-active deep levels due to zinc vacancies that affects the surface potential on a scale of hundreds of nanometers.

Figure 2. Electronic energy band line-up for a metallic tip-semiconductor system when the tip and the back surface of the semiconductor are electrically connected.

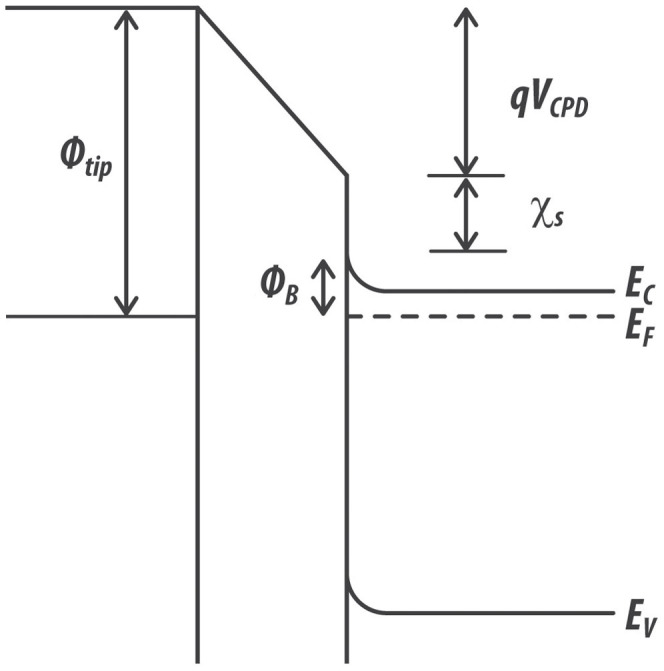
Figure 2

Open in a new tab

The contact potential difference VCPD depends on the tip work function ϕtip, on the electron affinity of the semiconductor χ, as well as on the difference between the bottom energy level of the conduction band Ec and the Fermi level EF in the semiconductor. In this case, the effect of the surface band bending ϕB is included in the bulk.

Finally, by combining equations (3–5), VCPD images probed by SKPM can be mapped into the effective donors concentration CD, which actually corresponds to the effective doping profile:

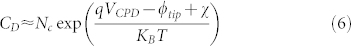graphic file with name srep04203-m6.jpg

While performing SKPM scans, two main sources of errors must be taken into account: stray capacitances from tip geometry, and environmentally mediated water layers presence32. In the ideal case, it is generally assumed that the tip-sample capacitance is essentially due to the effect of the tip apex32. However, the contribution from the tip cone and the cantilever can be significant37,50. Therefore, it is possible that measured SKPM values differ from theoretical ones. Gil et al.51 reported that the standard interpretation of data may be incorrect because the total force is produced not only by the end of the tip, but also by the contributions of the cantilever and the tip cone, which senses a different surface potential than the tip. Jacobs et al.52 demonstrated that reasonable VCPD values can only be obtained by using tips with a long cone and by reducing the lift height during the SKPM interleave scan. In the present work, tips with a long cone (tip height 14 ± 4 μm) and a small tip angle (15 ± 5 degrees) are employed. Moreover, the surface is scanned at a small tip-sample distance (20 nm). This allows minimizing the effect of the tip cone and the lever, which would dominate instead at larger tip-sample separations. We have quantified indeed that at 20 nm away from the surface, for our cantilever (ASYELEC 0.1) the tip contributes to more than 50% of the total electrostatic interaction and its contribution is therefore the most relevant among all. The contributions of the cone and the lever can be further reduced by measuring the gradient of the force instead of the force itself53. Furthermore, scanning at small tip-sample separations allows maintaining a high spatial resolution because the smaller is the distance, the smaller is the area of interaction of the AFM probe54. A small oscillating amplitude (5 nm) is used in this case to maintain the system working in the harmonic regime. This has been verified by looking at the shape of the electrical tuning where no distortions in the Lorentzian function (amplitude vs. frequency) were observed. When a high value of VAC is employed, the tuning curve may present distortions, causing bi-stability in the tip-sample interaction55. Another source of inaccuracy in the measurement of VCPD is the presence of water layers or molecular adsorbates on the sample surface. It has been shown that the presence of a thin layer of water or water vapor in the environment can cause deviations in the measurement of the resistivity of metal-oxide films56. Water molecules are generally chemisorbed and physisorbed by the surface57, and this process increases or decreases the surface electron conductivity depending on the type of the semiconductor (respectively n or p type)58. In the present work, we minimize the effect of water layers and adsorbates by preparing the samples by cycles of Ar+ bombardment at 250°C, followed by annealing at 120°C in a vacuum chamber. Samples are transferred from the sputtering chamber to the AFM in an environmental chamber filled with N2 in order to minimize the exposure to humidity and SKPM measurements are performed in dry and inert atmosphere (N2, relative humidity < 10%).

Results

The experiment consists of three steps. First of all, the back metal (Ag) is connected to the electrical ground and a SKPM scan is performed on top of metal surface (a portion of back metal surface is intentionally not covered with ZnO for this purpose). This is done to measure the metal work function. A calibrated tip (with known work function) is used for this purpose. Depending on the specific sample, small changes in value (±0.1 eV) have been measured. No dependency of Ag work function on relative humidity was found. After that, the same procedure is repeated with another tip in order to measure its work function. By doing so, we are able to calibrate each tip. Secondly, the tip is connected to the ground and the top surface of the ZnO sample is scanned in tapping mode. As previously mentioned, this procedure is done in order to discharge the surface before starting the SKPM measurement. Finally, the same portion of the surface is scanned with SKPM. A positive ac voltage Vac is applied to the tip. In this case, electrons (majority carriers in n-doped semiconductors) are attracted to the top surface of the sample. Thus, the semiconductor is in the accumulation regime and the metal/semiconductor system can be treated in a first approximation as a metal/metal system, allowing for the determination of the VCPD48.

Before starting the experiments on ZnO, SKPM measurements are carried out on silicon and germanium samples with known charge carrier concentration. This is done to validate the model. Samples are etched with HF in order to remove their native oxide. Doping concentrations in accordance with nominal values are recovered, confirming the reliability of this technique. After that, the same experiments are performed on ZnO.

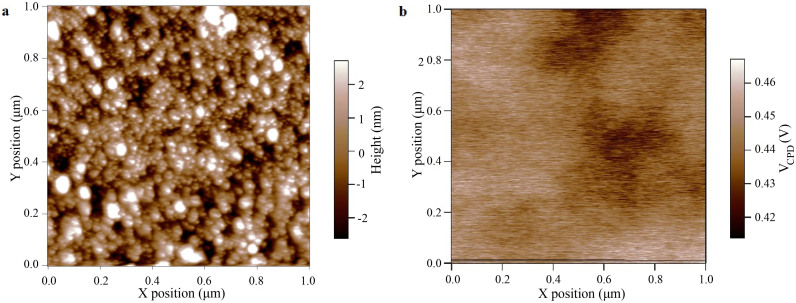
An AFM topography image of the surface of a ZnO thin film with the corresponding contact potential VCPD image, acquired at a distance of 20 nm, is shown in Fig. 3. Fig. 3a shows the typical polycrystalline nature of ZnO sputtered thin film, with small grains of nanometric dimension (tens of nanometers). The contact potential VCPD image in Fig. 3b does not show the same morphological features reported in Fig. 3a. The VCPD value appears almost uniform, varying within 10% of the mean value. Similar VCPD values with a deviation in the order of 5% are recorded after scanning the same portion of the surface for more than 1 hour. This result confirms that no charging phenomena are taking place. The same experiment was repeated one week after the first measurement, keeping in the meanwhile the sample in inert atmosphere. No sensible variation in the VCPD was measured.

Figure 3.

Figure 3

Open in a new tab

(a) Atomic force microscopy topography image of a ZnO thin film deposited by RF sputtering. Small grains with dimensions of tens of nanometers can be observed (b) Two-dimensional contact potential difference VCPD image of the same surface imaged in Fig. 3a. The image is acquired at an equilibrium distance of 20 nm with an oscillation of 5 nm.

In order to relate the VCPD with the effective doping concentration of thin film ZnO, all the parameters in equation (6) have to be recovered. In Table 1, the value of NC and χ for room temperature RF sputtered ZnO as well as the value of ϕ for Ag are reported. While the first two are taken from19, the value of ϕ for Ag is measured for each sample as previously pointed out.

Table 1. ZnO and Ag parameters extracted from experimental results.

Quantity Value and Reference
ZnO effective density of states in the conduction band NC 3.7·1018 cm3 19
ZnO electron affinity χ 4.5 eV19
Ag work function ϕ 4.7 ± 0.1 V
Open in a new tab

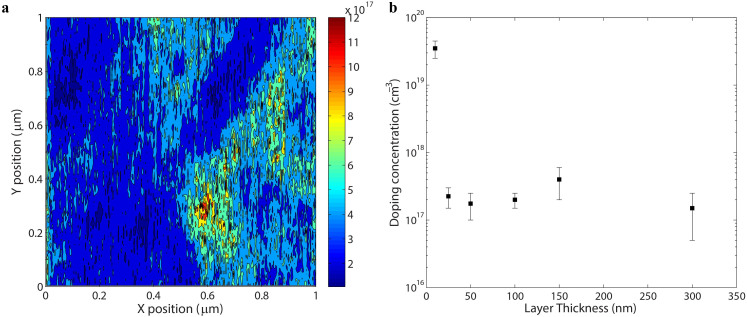
As long as the sample temperature is kept constant, these parameters do not change with thickness and deposition conditions59. Fig. 4a shows a two-dimensional map of the effective doping concentration in a 150 nm thick ZnO layer. In Fig. 4b the charge carrier density is plotted versus the layer thickness (from 10 to 300 nm). Each sample is deposited under the same conditions (deposition rate 0.1 Å/sec, Ar pressure 0.8 mTorr). The average value as well as the standard deviation of the contact potential difference VCPD measured on all the samples is reported in the supplementary material. The uncertainty in the quantification of the free carrier concentration of this technique is given by the calibration process i.e. the quantification of the VCPD between the tip and the Ag surface.

Figure 4.

Figure 4

Open in a new tab

(a) Two-dimensional map of the charge carrier density in a 150 nm thick ZnO film.(b) doping concentration versus layer thickness for a set of ZnO thin films (from 10 to 300 nm). All the samples are deposited under the same conditions (deposition rate 0.1 Å/sec, Ar pressure 0.8 mTorr). The effective doping concentration does not correlate with the layer thickness, except for the 10 nm layer. For each sample, three different regions have been scanned. The standard deviation of the value of the effective doping concentration is reported.

Doping concentrations in the order of 1017 cm−3 are recovered for all the samples. This value is in agreement with Four Probe measurements performed on polycrystalline ZnO samples deposited under the same conditions on an insulating substrate (resistivity ρ = 0.7–1.8 Ωcm, which, given a measured electron mobility of 31 ± 3 cm2/Vs, gives a doping concentration of ~1·1017–3·1017 cm−3). Furthermore, the doping concentration does not correlate with layer thickness. This is valid for layers with a thickness larger than the electron mean free path in ZnO (close to 20 nm)60. Below this limit, the proposed model is not valid since quantum effects become relevant and the transport regime is not diffusive anymore61. Therefore it cannot be applied to quantify the doping concentration in the material.

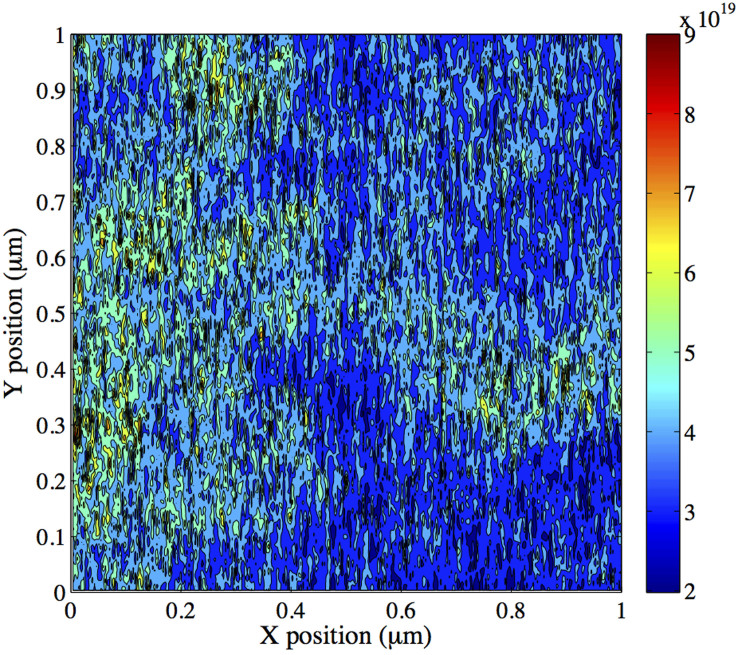
In order to further validate the technique, a thin film ZnO with a thickness of 100 nm, deposited with a higher deposition rate (0.2 Å/sec) and with higher Ar pressure (10 mTorr), is measured. It has been experimentally demonstrated that an increase in the deposition rate as well as in the Ar pressure causes the doping carrier concentration in ZnO thin films to increase62. In this case, we measure an increase in the work function difference (approximately 200 mV, from an average value of 445 mV to 647 mV) between the metal and the ZnO with respect to the previous case. This difference is attributed to a change in the charge carrier concentration because no considerable difference in mean surface roughness (from 4 to 4.2 nm) as well as in electron mobility (from 31 to 40 cm2/Vs) was measured. Fig. 5 shows the sample charge concentration image. An average charge carrier density in the order of 1019 cm−3 is calculated. Therefore, an increase of two orders of magnitude in the doping concentration is achieved by changing the deposition parameters. Being in accordance with experimental results reported in literature62 and with our Four Probe measurements (ρ = 0.9·10−2 Ω·cm), these results confirm the ability of the technique to measure the doping concentration of ZnO thin layers deposited under different conditions.

Figure 5. Two-dimensional map of the charge carrier density in ZnO thin film (thickness 100 nm, deposition rate 0.2 Å/sec, Ar pressure 10 mTorr).

Figure 5

Open in a new tab

Conclusions

We probed the charge carrier density in ZnO thin films with high spatial resolution by using SKPM. A simple electronic energy model is used to correlate the work function of the sample with the effective doping concentration in the ZnO thin films. Limitations of this technique (stray capacitances from tip geometry, water layer presence, surface charges and adsorbates) are discussed and possible solutions are proposed. The technique is experimentally tested on a set of samples deposited by RF sputtering under different conditions. Finally, we showed that results inferred with this technique are in accordance with carrier concentration expected for intrinsic ZnO thin films deposited with two different deposition rate and Ar pressure and obtained with Four Probe and Hall measurements.

Methods

SKPM measurements are performed on ZnO layers deposited by Radio Frequency (RF) sputtering on top of Ag. A set of samples with different thickness (from 10 to 300 nm approximately) is analyzed. The samples are deposited and their surface is pretreated (Ar+ bombardment at 250°C), annealed at 120°C in a vacuum chamber and immediately measured. SKPM measurements are performed in inert atmosphere (N2) with a Cypher (Asylum Research, USA). A Si cantilever coated with Ti-Ir (ASYELEC-01) is used. A cantilever resonant frequency ω0 of ~71 KHz, Q factor of 130 and a spring constant k of 1.5 N/m were measured using a thermal noise method63.

The average value as well as the standard deviation of the contact potential difference VCPD measured on all thin film ZnO samples are reported in the supporting information.

Author Contributions

C.M. and S.L. developed the technique, conducted the experiments, prepared the figures and wrote the manuscript. M.S.D., M.C. and M.S. supervised the project. T.S. and M.S. helped with the theoretical development of the technique.

Supplementary Material

Supplementary Information

Supplementary Material

srep04203-s1.pdf (187.4KB, pdf)

Acknowledgments

We thank Yamila Omar for proofreading the manuscript.

References

  1. Duan L. et al. Stable p-type ZnO films dual-doped with silver and nitrogen. Solid State Commun. 157, 45–48 (2013). [Google Scholar]
  2. Zhang Y., Guo T., Luo Y. D., Lin Y. H. & Nan C. W. Tunable Ferromagnetic Behaviors Observed in Highly Orientated Co-Doped ZnO Thin Films by the Bandgap Engineering. J. Am. Ceram. Soc. 96, 361–364 (2013). [Google Scholar]
  3. Kim Y. H. et al. Realizing the Potential of ZnO with Alternative Non-Metallic Co-Dopants as Electrode Materials for Small Molecule Optoelectronic Devices. Adv. Funct. Mater. 23, 3645–3652 (2013). [Google Scholar]
  4. Dodds J. S., Meyers F. N. & Loh K. J. Piezoelectric characterization of PVDF-TrFE thin films enhanced with ZnO nanoparticles. Sens. Journ., IEEE 12, 1889–1890 (2012). [Google Scholar]
  5. Pearton S. J. et al. ZnO spintronics and nanowire devices. J. Electron. Mater. 35, 862–868, 10.1007/bf02692541 (2006). [Google Scholar]
  6. Ozgur U., Hofstetter D. & Morkoc H. ZnO Devices and Applications: A Review of Current Status and Future Prospects. Proceed. of the IEEE 98, 1255–1268, 10.1109/jproc.2010.2044550 (2010). [Google Scholar]
  7. McGlynn E. ZnO Nanostructures and Their Applications. Contemp. Phys. 1–2, 10.1080/00107514.2013.776113 (2013). [Google Scholar]
  8. Nagata T. et al. Photoelectron spectroscopic study of band alignment of polymer/ZnO photovoltaic device structure. Appl. Phys. Lett. 102, 043302–043302-043304 (2013). [Google Scholar]
  9. Maragliano C., Stefancich M., Rampino S. & Colace L. Realistic simulation of polycrystalline CIGS absorbers and experimental verification. MRS Online Proceedings Library 1493, 10.1557/opl.2013.401 (2013). [Google Scholar]
  10. Repins I. et al. 19.9%-efficient ZnO/CdS/CuInGaSe2 solar cell with 81.2% fill factor. Progr. in Photov.: Research and Applications 16, 235–239, 10.1002/pip.822 (2008). [Google Scholar]
  11. Maragliano C., Colace L., Chiesa M., Rampino S. & Stefancich M. Three-Dimensional Cu(InGa)Se2 Photovoltaic Cells Simulations: Optimization for Limited-Range Wavelength Applications. IEEE Journ. of Photov. http://dx.doi.org/10.1109/JPHOTOV.2013.2258191 (2013). [Google Scholar]
  12. Lilliu S. et al. Dynamics of crystallization and disorder during annealing of P3HT/PCBM bulk heterojunctions. Macromolecules 44, 2725–2734 (2011). [Google Scholar]
  13. Krebs F. C. Fabrication and processing of polymer solar cells: A review of printing and coating techniques. Sol. Energy Mater. Sol. Cells 93, 394–412, http://dx.doi.org/10.1016/j.solmat.2008.10.004 (2009). [Google Scholar]
  14. Huang J., Yin Z. & Zheng Q. Applications of ZnO in organic and hybrid solar cells. Energy & Environm. Science 4, 3861–3877 (2011). [Google Scholar]
  15. Xu W. et al. Low-pressure MOCVD growth of p-type ZnO thin films by using NO as the dopant source. Journ. of Crystal Growth 265, 133–136,http://dx.doi.org/10.1016/j.jcrysgro.2003.12.061 (2004). [Google Scholar]
  16. Ellmer K. in Characterization of Materials (John Wiley & Sons, Inc., 2002). [Google Scholar]
  17. Vickerman J. C. Secondary ion mass spectrometry–basic concepts, instrumental aspects, applications and trends. (Wiley, New York, 1987).
  18. Rau W., Schwander P., Baumann F., Höppner W. & Ourmazd A. Two-dimensional mapping of the electrostatic potential in transistors by electron holography. Phys. Rev. Lett. 82, 2614–2617 (1999). [Google Scholar]
  19. Ellmer K. [Transparent Conductive Zinc Oxide] Springer Series in Materials Science (Springer Berlin Heidelberg, 2008). [Google Scholar]
  20. Coleman V. A. & Jagadish C. Zinc Oxide Bulk, Thin Films and Nanostructures (Elsevier Science Ltd, 2006). [Google Scholar]
  21. Saw K. G., Ibrahim K., Lim Y. T. & Chai M. K. Self-compensation in ZnO thin films: An insight from X-ray photoelectron spectroscopy, Raman spectroscopy and time-of-flight secondary ion mass spectroscopy analyses. Thin Solid Films 515, 2879–2884,http://dx.doi.org/10.1016/j.tsf.2006.08.047 (2007). [Google Scholar]
  22. Müller E. et al. Probing the electrostatic potential of charged dislocations in n-GaN and n-ZnO epilayers by transmission electron holography. Phys. Rev. B 73, 245316 (2006). [Google Scholar]
  23. Schuisky M., Elam J. W. & George S. M. In situ resistivity measurements during the atomic layer deposition of ZnO and W thin films. Appl. Phys. Lett. 81, 180–182 (2002). [Google Scholar]
  24. Sze S. M. & Ng K. K. Physics of semiconductor devices. (Wiley-interscience, 2006). [Google Scholar]
  25. Melitz W., Shen J., Kummel A. C. & Lee S. Kelvin probe force microscopy and its application. Surf. Sci. Rep. 66, 1–27, http://dx.doi.org/10.1016/j.surfrep.2010.10.001 (2011). [Google Scholar]
  26. Nonnenmacher M., O'Boyle M. P. & Wickramasinghe H. K. Kelvin probe force microscopy. Applied Physics Letters 58, 2921–2923 (1991). [Google Scholar]
  27. Nonnenmacher M., O'Boyle M. & Wickramasinghe H. K. Surface investigations with a Kelvin probe force microscope. Ultramicroscopy 42–44, 268–273, 10.1016/0304-3991(92)90278-r (1992). [Google Scholar]
  28. Girard P. Electrostatic force microscopy: principles and some applications to semiconductors. Nanotechnology 12 (2001). [Google Scholar]
  29. Zerweck U., Loppacher C., Otto T., Grafström S. & Eng L. M. Accuracy and resolution limits of Kelvin probe force microscopy. Phys. Rev. B 71, 125424 (2005). [Google Scholar]
  30. Nonnenmacher M., O'Boyle M. P. & Wickramasinghe H. K. Kelvin probe force microscopy. Appl. Phys. Lett. 58, 2921–2923, 10.1063/1.105227 (1991). [Google Scholar]
  31. Henning A. K. et al. Two dimensional surface dopant profiling in silicon using scanning Kelvin probe microscopy. J. Appl. Phys. 77, 1888–1896, 10.1063/1.358819 (1995). [Google Scholar]
  32. Shin H. et al. Measurement and Visualization of Doping Profile in Silicon Using Kelvin Probe Force Microscopy (KPFM). Electronic Mat. Lett. 1, 127–133 (2005). [Google Scholar]
  33. Hochwitz T. et al. Imaging integrated circuit dopant profiles with the force-based scanning Kelvin probe microscope. Journal of Vacuum Science & Tech. B: Microel. and Nanometer Struct. 14, 440–446, 10.1116/1.588491 (1996). [Google Scholar]
  34. Semenikhin O. A., Jiang L., Iyoda T., Hashimoto K. & Fujishima A. Atomic Force Microscopy and Kelvin Probe Force Microscopy Evidence of Local Structural Inhomogeneity and Nonuniform Dopant Distribution in Conducting Polybithiophene. The Journ. Phys. Chem. 100, 18603–18606, 10.1021/jp960844y (1996). [Google Scholar]
  35. Koren E., Rosenwaks Y., Allen J. E., Hemesath E. R. & Lauhon L. J. Nonuniform doping distribution along silicon nanowires measured by Kelvin probe force microscopy and scanning photocurrent microscopy. Appl. Phys. Lett. 95, 092105–092105-092103, 10.1063/1.3207887 (2009). [Google Scholar]
  36. Park S.-E., Nguyen N. V., Kopanski J. J., Suehle J. S. & Vogel E. M. Comparison of scanning capacitance microscopy and scanning Kelvin probe microscopy in determining two-dimensional doping profiles of Si homostructures. J. Vac. Sci. Technol. B 24, 404, http://dx.doi.org/10.1116/1.2162569 (2006). [Google Scholar]
  37. Koley G., Spencer M. G. & Bhangale H. R. Cantilever effects on the measurement of electrostatic potentials by scanning Kelvin probe microscopy. Appl. Phys. Lett. 79, 545–547 (2001). [Google Scholar]
  38. Koren E. et al. Obtaining Uniform Dopant Distributions in VLS-Grown Si Nanowires. Nano Lett. 11, 183–187, 10.1021/nl103363c (2010). [DOI] [PubMed] [Google Scholar]
  39. Maragliano C., Heskes D., Stefancich M., Chiesa M. & Souier T. Dynamic electrostatic force microscopy technique for the study of electrical properties with improved spatial resolution. Nanotechnology 24, 225703 (2013). [DOI] [PubMed] [Google Scholar]
  40. Van Ben C., Cho H. D., Kang T. W. & Yang W. Doping transition of doped ZnO nanorods measured by Kelvin probe force microscopy. Thin Solid Films 520, 4622–4625, http://dx.doi.org/10.1016/j.tsf.2011.10.129 (2012). [Google Scholar]
  41. Lakhwani G. et al. Probing Charge Carrier Density in a Layer of Photodoped ZnO Nanoparticles by Spectroscopic Ellipsometry. The Journ. of Phys. Chem. C 114, 14804–14810, 10.1021/jp104846h (2010). [Google Scholar]
  42. Jespersen T. S. & Nygård J. Charge Trapping in Carbon Nanotube Loops Demonstrated by Electrostatic Force Microscopy. Nano Lett. 5, 1838–1841, 10.1021/nl0505997 (2005). [DOI] [PubMed] [Google Scholar]
  43. Ohring M. Materials science of thin films. (Academic press, 2001). [Google Scholar]
  44. Merz T. A., Doutt D. R., Bolton T., Dong Y. & Brillson L. J. Nanostructure growth-induced defect formation and band bending at ZnO surfaces. Surf. Sci. 605, L20–L23, http://dx.doi.org/10.1016/j.susc.2010.12.021 (2011). [Google Scholar]
  45. Rosenwaks Y., Shikler R., Glatzel T. & Sadewasser S. Kelvin probe force microscopy of semiconductor surface defects. Phys. Rev. B 70, 085320 (2004). [Google Scholar]
  46. Lilliu S. et al. EFM data mapped into 2D images of tip sample contact potential difference and capacitance second derivative. Nat. Scient. Rep. (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Rabalais J. W. & Rabalais J. W. Principles of ultraviolet photoelectron spectroscopy. (Wiley New York, 1977). [Google Scholar]
  48. Hudlet S., Saint Jean M., Roulet B., Berger J. & Guthmann C. Electrostatic forces between metallic tip and semiconductor surfaces. J. Appl. Phys. 77, 3308–3314, 10.1063/1.358616 (1995). [Google Scholar]
  49. Sze S. M. & Kwok K. N. Physics of Semiconductor Devices. Third edn, (Wiley-interscience, 2007). [Google Scholar]
  50. Gómez-Moñivas S., Froufe L. S., Carminati R., Greffet J. J. & Sáenz J. J. Tip-shape effects on electrostatic force microscopy resolution. Nanotechnology 12, 496 (2001). [Google Scholar]
  51. Gil A., Colchero J., Gómez-Herrero J. & Baró A. M. Electrostatic force gradient signal: resolution enhancement in electrostatic force microscopy and improved Kelvin probe microscopy. Nanotechnology 14, 332 (2003). [Google Scholar]
  52. Jacobs H. O., Leuchtmann P., Homan O. J. & Stemmer A. Resolution and contrast in Kelvin probe force microscopy. J. Appl. Phys. 84, 1168–1173 (1998). [Google Scholar]
  53. Colchero J., Gil A. & Baró A. M. Resolution enhancement and improved data interpretation in electrostatic force microscopy. Phys. Rev. B 64, 245403 (2001). [Google Scholar]
  54. Santos S. et al. How localized are energy dissipation processes in nanoscale interactions? Nanotechnology 22, 345401 (2011). [DOI] [PubMed] [Google Scholar]
  55. San Paulo A. & Garcia R. Unifying theory of tapping-mode atomic-force microscopy. Phys. Rev. B 66, 041406 (2002). [Google Scholar]
  56. Dixit S., Srivastava A., Shukla R. K. & Srivastava A. Pulsed laser deposited ZnO films and their humidity sensing behavior. J. Mater. Sci.: Mater. Electron. 19, 788–792, 10.1007/s10854-007-9414-2 (2008). [Google Scholar]
  57. Cox P. The surface science of metal oxides. (Cambridge university press, 1996). [Google Scholar]
  58. Seiyama T., Yamazoe N. & Arai H. Ceramic humidity sensors. Sensors and Actuators 4, 85–96, http://dx.doi.org/10.1016/0250-6874(83)85012-4 (1983). [Google Scholar]
  59. Jacobi K., Zwicker G. & Gutmann A. Work function, electron affinity and band bending of zinc oxide surfaces. Surf. Sci. 141, 109–125, http://dx.doi.org/10.1016/0039-6028(84)90199-7 (1984). [Google Scholar]
  60. Baxter J. B. & Schmuttenmaer C. A. Conductivity of ZnO nanowires, nanoparticles, and thin films using time-resolved terahertz spectroscopy. The Journ. Phys. Chem. B 110, 25229–25239 (2006). [DOI] [PubMed] [Google Scholar]
  61. Alkhatib A., Souier T. & Chiesa M. Morphology dependent electrical transport behavior in gold nanostructures. Thin Solid Films 520, 656–661 (2011). [Google Scholar]
  62. Gao W. & Li Z. ZnO thin films produced by magnetron sputtering. Ceram. Int. 30, 1155–1159, http://dx.doi.org/10.1016/j.ceramint.2003.12.197 (2004). [Google Scholar]
  63. Hutter J. L. & Bechhoefer J. Calibration of atomic-force microscope tips. Rev. Sci. Instrum. 64, 1868–1873 (1993). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Material

srep04203-s1.pdf (187.4KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES