BAYESIAN SEMIPARAMETRIC ANALYSIS FOR TWO-PHASE STUDIES OF GENE-ENVIRONMENT INTERACTION

Abstract

The two-phase sampling design is a cost-efficient way of collecting expensive covariate information on a judiciously selected sub-sample. It is natural to apply such a strategy for collecting genetic data in a sub-sample enriched for exposure to environmental factors for gene-environment interaction (G × E) analysis. In this paper, we consider two-phase studies of G × E interaction where phase I data are available on exposure, covariates and disease status. Stratified sampling is done to prioritize individuals for genotyping at phase II conditional on disease and exposure. We consider a Bayesian analysis based on the joint retrospective likelihood of phase I and phase II data. We address several important statistical issues: (i) we consider a model with multiple genes, environmental factors and their pairwise interactions. We employ a Bayesian variable selection algorithm to reduce the dimensionality of this potentially high-dimensional model; (ii) we use the assumption of gene-gene and gene-environment independence to trade-off between bias and efficiency for estimating the interaction parameters through use of hierarchical priors reflecting this assumption; (iii) we posit a flexible model for the joint distribution of the phase I categorical variables using the non-parametric Bayes construction of Dunson and Xing (2009). We carry out a small-scale simulation study to compare the proposed Bayesian method with weighted likelihood and pseudo likelihood methods that are standard choices for analyzing two-phase data. The motivating example originates from an ongoing case-control study of colorectal cancer, where the goal is to explore the interaction between the use of statins (a drug used for lowering lipid levels) and 294 genetic markers in the lipid metabolism/cholesterol synthesis pathway. The sub-sample of cases and controls on which these genetic markers were measured is enriched in terms of statin users. The example and simulation results illustrate that the proposed Bayesian approach has a number of advantages for characterizing joint effects of genotype and exposure over existing alternatives and makes efficient use of all available data in both phases.

1. Introduction

Case-control studies are popular analytical tools, particularly in cancer epidemiology, for assessing gene-disease association where the allele/genotype frequencies at a bi-allelic single nucleotide polymorphism (SNP) locus are compared between cases and controls. Recent genomewide case-control association studies (GWAS) have been remarkably successful in identifying susceptibility loci for many cancers [Yeager et al. (2007); Hunter et al. (2007); Amundadottir (2009)]. A large fraction of variability in the different cancer traits still remain unexplained, with the identified SNPs contributing modestly to prediction of disease risk [Wacholder et al. (2010); Park et al. (2010)]. In search of the missing heritability, it is thus natural to study the genetic architecture of a cancer phenotype in conjunction with the known environmental risk factors (environmental toxins, dietary exposures, physical activity levels, medication use, and other behavioral risk factors). In the post-GWAS era, more efficient statistical approaches to characterize such complex gene-environment (G × E) interactions, in terms of both design and analytic tools, have become a pressing need in cancer epidemiology research.

Variants of the case-control sampling design have been often employed in epidemiologic studies. Two-phase stratified sampling [Neyman (1938)] is an efficient alternative to the traditional cohort and case-control designs [Cochran (1963)] from cost and resource-saving perspectives. A typical application of two-phase sampling is for collecting expensive covariate information, for example, novel biomarkers or genotype data on a prioritized sub-sample of the initial study base. In particular, we will consider the following set-up: the binary disease outcome or case-control status D, some relatively inexpensive covariates (S) and environmental data (E) are collected at phase I (P₁). At phase II (P₂), genotype data (G) is collected on a subset selected from phase I sample. To select this phase II sub-sample, stratified sampling with strata defined by phase I data (D, E and possibly S) is implemented.

There is a large amount of literature on two-phase designs, using different likelihood based approaches [Horvitz and Thompson (1952); Flanders and Greenland (1991); Breslow and Cain (1988)] or estimating score approaches [Reilly and Pepe (1995); Chatterjee et al. (2003); Robins et al. (1994)]. Maximum likelihood inference for such problems was considered in the pioneering work of Scott and Wild (1997) and Breslow and Holubkov (1997a, b). Lawless et al. (1999) and Breslow and Chatterjee (1999) compare and contrast several approaches for analyzing two-phase data. It has been noted that adding more phases can lead to further efficiency gains, consequently, the two-phase design has been generalized to multiphase designs [Whittemore and Halpern (1997); Lee et al. (2010)]. Haneuse and Chen (2011) propose an intermediate phase between phase I and phase II to reduce participation bias caused by differential participation.

The potential for such sampling designs for G × E studies has been indicated in Thomas (2010). Many GWAS adopt this sampling at the design phase, but little attention is paid at the analysis stage to address the sampling design, thus potentially leading to biased estimates. To the best of our knowledge, literature on two-phase studies of G × E interaction is very limited. Chatterjee and Chen (2007) proposed maximum likelihood inference using a novel regression model for G × E interaction studies where second stage sampling was carried out based on disease outcome and family history. Asymptotic theories were established under the assumption of independence of the genetic and environmental factors in the population.

Multiple papers [Piegorsch et al. (1994); Umbach and Weinberg (1997); Chatterjee and Carroll (2005)] attest the phenomenon of gaining efficiency in studies of G × E by exploiting independence between the genetic and environmental factors under case-control sampling. Under such constraints, it is beneficial to use the retrospective likelihood for estimating interaction parameters instead of standard prospective logistic regression. However, with departures from these constraints, biases in estimating the interaction parameter can occur under retrospective methods. Several researchers have addressed this issue and proposed more robust strategies for testing G × E interaction [Mukherjee et al. (2008, 2010); Mukherjee and Chatterjee (2008); Vansteelandt et al. (2008); Li and Conti (2009); Murcray et al. (2009)]. There is no standard multivariate tool for handling multiple genetic markers simultaneously for G × G and G × E studies that data-adaptively exploits gene-gene and gene-environment independence for gaining efficiency in estimating multiple SNP × E interaction parameters in a potentially high dimensional model.

Bayesian literature on two-phase studies, even beyond the context of G × E studies is also very limited. Haneuse and Wakefield (2007) presented the first hierarchical Bayesian work that closely relate to such data structure. The Bayesian framework presented in this paper appears to be a natural route to explore for multiple reasons. First, Bayesian estimation can lead to efficient computational algorithms as the two-phase likelihood is naturally a missing data likelihood. Second, for G × E studies, Bayesian methods provide data-adaptive shrinkage to leverage the constraints of gene-environment independence by imposing informative priors around this assumption. Third, we incorporate Bayesian variable selection features which help us to handle a potentially high dimensional disease risk model with main effects and interactions of multiple genes and environmental factors simultaneously. Fourth, we use the clever non-parametric Bayesian construction of Dunson and Xing (2009) as a substitute for profile likelihood in the frequentist setting to construct the retrospective likelihood under two-phase sampling. The current paper thus contributes to analysis of G × E studies with multiple markers/environmental exposures under an outcome-exposure stratified two-phase sampling design by offering a new Bayesian treatment of the problem. Our data analysis and simulation studies illustrate that for characterizing sub-group effects of the environmental exposure across genotype categories, our method provides gain in efficiency compared to other alternatives. Moreover, there are no comparable alternatives that can offer the flexibility of our method in terms of multi-marker models and efficient G × E analysis under the two-phase design.

The paper is largely motivated by an example that originates from a population based case-control study of colorectal cancer (CRC) in Israel, namely, the Molecular Epidemiology of Colorectal Cancer (MECC) study. Statins (our environmental factor E) are a class of lipid-lowering drugs used by more than 25 million individuals worldwide for reducing cardiovascular disease risk. The MECC study was the first to establish a chemoprotective association of statins with risk of CRC [Poynter et al. (2005)]. Follow-up individual studies and a meta analysis of 18 studies have confirmed this association [Hachem et al. (2009)]. The benefit of statins for reducing CRC risk has been shown to vary with genetic variations in HMGCR (3-Hydroxy-3-methylglutaryl coenzyme A reductase) gene, a gene involved in cholesterol synthesis [Lipkin et al. (2010)]. To understand the mechanism of effect modification further, investigators measured 294 SNPs in 40 genes, including HMGCR (our set of genetic factors G), selected in the cholesterol synthesis/lipid metabolism pathway. The sub-sample selected for genotyping from the study population of all cases and controls was chosen by stratified sampling conditional on statin use (E) and case-control status (D) where statin users were purposefully oversampled. This sampling strategy was adopted due to limited budgetary resources and DNA samples. Complete statin use (E) data and other basic demographic covariates (S) were available on the entire study base (phase I or P₁), and genetic data on these 294 SNPs were only available for the phase II subsample (P₂).

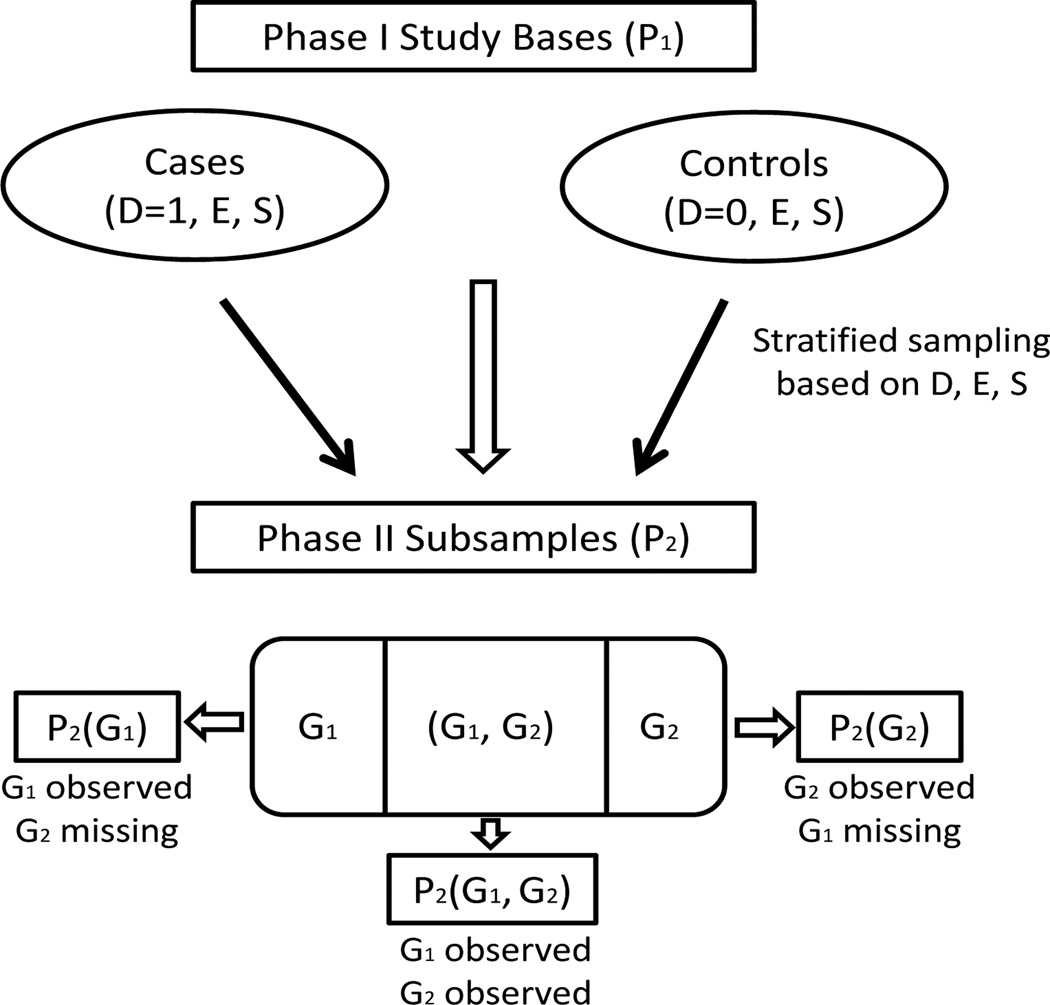
In addition, in the MECC study, due to experimental and laboratory logistics, genotype data were missing on a subset of individuals selected in P₂ on a group of genes (G₁, say) and on a different subset of individuals on another group of genes (G₂, say). This led to a non-monotone missing data structure with some individuals in P₂ having observations on both (G₁, G₂) (subset denoted by P₂(G₁, G₂)) and some only on G₁ (subset denoted by P₂(G₁)) and some only on G₂ (subset denoted by P₂(G₂)). Figure 1 is a flow diagram of the sampling scheme and missingness pattern in the data.

Fig 1.

Data structure under two-phase sampling with partial missingness in phase II genetic covariates from the Molecular Epidemiology of Colorectal Cancer study

The rest of the paper is organized as follows. In Section 2, we present the model ingredients: the likelihood, priors and posteriors. In Section 3, we discuss the analysis of statin × gene interaction in the MECC study. In Section 4, we conduct a simulation study to compare the various maximum likelihood and score based approaches with the Bayesian approach. Section 5 concludes with a discussion.

2. Proposed Methods

2.1. The likelihood

We refer to Figure 1 for understanding the data structure and construction of our likelihood. Let u and D denote the subject indicator and disease status respectively. Here, E is environmental exposure and S are basic demographic covariates as described before. Let W = (E, S). There are N individuals in phase I and M individuals in phase II. To simplify notations we write the retrospective likelihood corresponding to a two-gene model (G₁, G₂), with the understanding that the methods/notations can be directly extended to gene-sets (G₁, G₂) where each contain multiple SNPs. The two-phase likelihood has the following form to capture the sampling phases and the missingness patterns in G (Figure 1),

$${\mathrm{L}}^{\mathrm{T}\mathrm{P}}=\prod _{u\in P_1\backslash P_2}\mathrm{P}(W_u|D_u)\times \prod _{u\in P_2(G_1)}\mathrm{P}(G_{1u},W_u|D_u)\times \prod _{u\in P_2(G_2)}\mathrm{P}(G_{2u},W_u|D_u)\times \prod _{u\in P_2(G_1,G_2)}\mathrm{P}(G_{1u},G_{2u},W_u|D_u).$$

Each term in L^TP can be factorized by using P(G₁, G₂, W|D) = {P(D|G₁, G₂, _W) P(G₁, G₂|W)P(W)}/P(D). This retrospective likelihood is then marginalized over the missing data in each term. We assume missing completely at random [Little and Rubin (2002)] for the genotype data collected at phase II. The likelihood is then expressed as,

$${\mathrm{L}}^{\mathrm{T}\mathrm{P}}=\prod _{u\in P_1\backslash P_2}\sum _{g_1,g_2}\mathrm{P}(D_u|g_1,g_2,W_u)\mathrm{P}(g_1,g_2|W_u)\mathrm{P}(W_u)/\mathrm{P}(D_u)\times \prod _{u\in P_2(G_1)}\sum _{g_2}\mathrm{P}(D_u|G_{1u},g_2,W_u)\mathrm{P}(G_{1u},g_2|W_u)\mathrm{P}(W_u)/\mathrm{P}(D_u)\times \prod _{u\in P_2(G_2)}\sum _{g_1}\mathrm{P}(D_u|g_1,G_{2u},W_u)\mathrm{P}(g_1,G_{2u}|W_u)\mathrm{P}(W_u)/\mathrm{P}(D_u)\times \prod _{u\in P_2(G_1,G_2)}\mathrm{P}(D_u|G_{1u},G_{2u},W_u)\mathrm{P}(G_{1u},G_{2u}|W_u)\mathrm{P}(W_u)/\mathrm{P}(D_u),$$ (2.1)

where P(D_u) = ∑_{g1, g2} ∫_w P(D_u|g₁, g₂, w)P(g₁, g₂|w)P(dw) with the integral replaced by the sum when components of W are discrete. Corresponding to this likelihood, there are three model ingredients:

1. A disease risk model. We assume, P(D = 1|G₁ = g₁, G₂ = g₂, W = w, β) = H[{β₀ + m(g₁, g₂, w, β)}], where H is the logistic function H(u) = {1 + exp(−u)}^𢄡. Typical choice of m involves, say for two genes G₁ and G₂, $m(g_1,g_2,w;\mathit{\beta })={\beta }_{G_1}{g}_1+{\beta }_{G_2}{g}_2+{\beta }_{E}e+{\mathit{\beta }}_S^{\top }\mathit{s}+{\beta }_{G_1{G}_2}{g}_1{g}_2+{\beta }_{G_{1}E}{g}_{1}e+{\beta }_{G_{2}E}{g}_{2}e$, noting that w = (e, s).

2. A model for (G₁, G₂|W = (E, S)). For genotype data at a bi-allelic locus, G_j can take three possible values (‘g₀=aa’, ‘g₁=Aa’ and ‘g₂=AA’). We assume, $\mathrm{P}(G_1=g_j,G_2=g_j^{\prime }|W=w;\mathit{\lambda })=q_{jj\prime }(w;\mathit{\lambda })$, j, j′ = 0, 1, 2. This specification will require a joint model for multivariate categorical data (trinary for SNP data at a bi-allelic locus). Under gene-gene and gene-environment independence, the model can in general be factorized conditional on covariates S, for j, j′ = 0, 1, 2.

$$\underset{\text{under}\mathrm{G}-\mathrm{G}\text{and}\mathrm{G}-\mathrm{E}\text{independence}}{\underbrace{\mathrm{P}(G_1=g_j,G_2=g_j^{\prime }|E=e,\mathit{S}=\mathit{s};\mathit{\lambda })=P(G_1=g_j|\mathit{S}=\mathit{s},{\mathit{\lambda }}_1)P(G_2=g_j^{\prime }|\mathit{S}=\mathit{s};{\mathit{\lambda }}_2),}}$$

Instead of the above fully non-parametric model, we explore a parametric model for the joint distribution P(G₁, G₂|W). We consider a class of log-linear models with linear by linear structure [Agresti, (2002)] for parsimonious modeling of the (G₁, G₂|W) associations,

$$\text{log}\{\mu (G_1=g_j,G_2=g_j^{\prime }|E=e,\mathit{S}=\mathit{s};\mathit{\lambda })\}={\lambda }_0+{\lambda }_{G_1}{g}_j+{\lambda }_{G_2}{g}_j^{\prime }+{\lambda }_{E}e+{\mathit{\lambda }}_S^{\top }\mathit{s}+{\lambda }_{G_1{G}_2}{g}_j{g}_{j\prime }+{\lambda }_{G_{1}E}{g}_{j}e+{\lambda }_{G_{2}E}{g}_{j\prime }e+{\mathit{\lambda }}_{G_{1}S}^{\top }{g}_j\mathit{s}+{\mathit{\lambda }}_{G_{2}S}^{\top }{g}_{j\prime }\mathit{s},$$ (2.2)

where g_j are chosen ordinal scores, typically 0, 1, 2 [Agresti, (2002)]. This is the common allelic dosage coding under a log-additive genetic susceptibility model.

Our method could easily be extended to a co-dominant coding of the genetic factor using two dummy variables. Since log-additivity is often assumed for screening interactions, and for simplicity of presentation in terms of one parameter estimate as opposed to two, we proceed with this additive coding. Additionally, even if the true genetic susceptibility model is co-dominant with the disease-causing allele, for a tagging marker which is correlated to this causal allele, one would not a’priori know the direction of association of the marker allele and causal allele. Pfeiffer and Gail (2003) show that the additive scores are more robust to choice of marker allele and varying correlation scenarios. In case of high dimensional G, we can further reduce the dimensionality of the problem by assuming common association parameters λ_GE and λ_GS between similar functional groups of SNPs. As discussed in Agresti (2002), this Poisson log-linear model has a corresponding multinomial representation. Thus, the probability of ${\mathrm{P}}_{G_1,G_2}(g_j,g_j^{\prime }|\mathit{\lambda })=P(G_1=g_j,G_2=g_j^{\prime }|E=e,\mathit{S}=\mathit{s})$ can be written in terms of the multinomial probabilities,

$$P_{G_1,G_2}(g_j,g_j^{\prime }|\mathit{\lambda })=\frac{\text{exp}({\lambda }_{G_1}{g}_j+{\lambda }_{G_2}{g}_j^{\prime }+{\lambda }_{G_1{G}_2}{g}_j{g}_{j\prime }+{\lambda }_{G_{1}E}{g}_{j}e+{\lambda }_{G_{2}E}{g}_j^{\prime }e+{\mathit{\lambda }}_{{G_1}_S}^{\top }{g}_j\mathit{s}+{\mathit{\lambda }}_{{G_2}_S}^{\top }{g}_j^{\prime }\mathit{s})}{{\sum }_{l=0}^2{\sum }_{l\prime =0}^2\text{exp}({\lambda }_{G_1}{g}_l+{\lambda }_{G_2}{g}_l^{\prime }+{\lambda }_{G_1{G}_2}{g}_l{g}_{l\prime }^{\prime }+{\lambda }_{G_{1}E}{g}_{l}e+{\lambda }_{G_{2}E}{g}_{l\prime }^{\prime }e+{\mathit{\lambda }}_{G_{1}S}^{\top }{g}_l\mathit{s}+{\mathit{\lambda }}_{G_{2}S}^{\top }{g}_{l\prime }^{\prime }\mathit{s})}.$$

Note that, gene-gene and gene-environment independence in the above model (2.2) will imply λ_G1E ≡ λ_G2E ≡ λ_G1G2 ≡ 0.

3. A model for W = (E, S). A non-parametric and flexible model for the distribution of W is desired. Recall that W can be a mixed set of quantitative and categorical variables. For the MECC example W is a set of categorical covariates, which will be our primary focus in this paper. The approach for modeling the joint distribution of a set of categorical variables that we follow for W can also be applied to the the joint distribution of the trinary genotype variables G₁ and G₂ in (2.2) as well. However, reflecting prior faith on the gene-gene and gene-environment independence assumptions through direct priors on parameters λ_G1E, λ_G2E, λ_G1G2 in the log-linear model is more straightforward for a practitioner (2.2). This is the primary reason for using (2.2) for the second component P(G₁, G₂|W = (E, S)).

Let W_u = (E_u, S_u), denote the W data corresponding to subject u, u = 1, …, N. Here W_u is p×1 vector of p categorical variables, i.e. W_u = (w_u1, …, w_up) for a subject u. Assume that the j-th component of W can have d_j values j = 1, ⋯, p. In order to parsimoniously model this (d₁ × d₂ × ⋯ × d_p) joint distribution, DX first note that the joint distribution of two categorical variables can always be expressed as a finite mixture of product-multinomial distributions. Extending this idea DX introduce a latent class index variable z_u ∈ {1, …, k}, such that w_ur, w_ut, r, t ∈ {1, …, p}, r ≠ t, are conditionally independent given z_u. Then the joint distribution for w_u has this finite mixture representation,

$$P_W(w_{u1}=c_1,\cdots ,w_{up}=c_p)=\sum _{h=1}^{k}P(w_{u1}=c_1,\cdots ,w_{up}=c_p|z_u=h)P(z_u=h)=\sum _{h=1}^{k}P(z_u=h)\prod _{j=1}^{p}P(w_{uj}=c_j|z_u=h).$$ (2.3)

For notational convenience, we rewrite (2.3) as

$$P_W(w_{u1}=c_1,\cdots ,w_{up}=c_p)={\pi }_{c_1\cdots c_p}=\sum _{h=1}^k{\nu }_h\prod _{j=1}^p{\psi }_{h{c}_j}^{(j)},\sum _{c_1=1}^{d_1}\cdots \sum _{c_p=1}^{d_p}{\pi }_{c_1\cdots c_p}=1,$$

where ν = (ν₁, …, ν_k)^⊤ is a probability vector with ν_h = P(z_u = h) and ${\psi }_{h{c}_j}^{(j)}=P(w_{uj}=c_j|z_u=h)$, is a d_j × 1 probability vector i.e., the conditional probability of w_uj = c_j, given that subject u is in latent class h for j = 1, …, p. We will discuss the choice of k through a Dirichlet process prior structure on this latent class probability model in the next section.

Remark 1: While Chatterjee and Chen (2007), Chatterjee and Carroll (2005) use profile likelihood for handling the distribution of W non-parametrically, it has been a challenging task in the Bayesian framework to posit a flexible model for W = (E, S) which could be a mixture of categorical and continuous covariates. In this mixed case, Müller et al. (1999) model the joint distribution of the continuous covariates through a Dirichlet Process mixture of normals. Then, conditional on the continuous covariates, the categorical variables have a joint multivariate probit distribution. A recent paper by Bhattacharya and Dunson (2011) extends the above DX construction for categorical data to handle joint distribution modeling of more complex data, including continuous and discrete data. They extend the conditional independence idea and replace the product-multinomial structure in (2.4) by a product of various kernels, such as Gaussian, Poisson and more complex univariate or multivariate distributional kernel. The MECC example does not require going beyond the original DX construction, but with continuous E, this is what we would adopt.

Remark 2: If the phase I sample is a cohort study, with disease endpoint D, then the corresponding likelihood is proportional to:

$${\mathrm{L}}^{\text{cohort},\mathrm{T}\mathrm{P}}\propto \prod _{u\in P_1\backslash P_2}\sum _{g_1,g_2}\mathrm{P}(D_u|g_1,g_2,W_u)\mathrm{P}(g_1,g_2|W_u)\times \prod _{u\in P_2(G_1)}\sum _{g_2}\mathrm{P}(D_u|G_{1u},g_2,W_u)\mathrm{P}(G_{1u},g_2|W_u)\times \prod _{u\in P_2(G_2)}\sum _{g_1}\mathrm{P}(D_u|g_1,G_{2u},W_u)\mathrm{P}(g_1,G_{2u}|W_u)\times \prod _{u\in P_2(G_1,G_2)}\mathrm{P}(D_u|G_{1u},G_{2u},W_u)\mathrm{P}(G_{1u},G_{2u}|W_u),$$ (2.4)

Similarly, if environmental data E is collected in phase II as well, the first term representing the phase I cohort likelihood can also involve an integral over the missing E data with respect to a probability distribution dF(E), exactly as in equation (3) of Chatterjee and Chen (2007). A surrogate measure of E, namely E* may be available in phase I and a measurement error model relating E and E* can also be used to construct a joint likelihood of phase I and phase II data.

2.2. Priors

As mentioned before, for this complex retrospective likelihood formulation, we have three sets of parameters from the above three ingredients of the likelihood. For β in the disease risk model, we use a spike and slab type mixture prior to handle variable selection in a high-dimensional disease risk model with multiple markers. For λ in the multivariate gene model, the Bayesian hierarchical approach provides a flexible way to allow for uncertainty around the assumption of gene-gene and gene-environment independence, through prior on λ_G1G2, λ_G1E, and λ_G2E. When sparsity occurs in a certain configuration of (G₁, G₂, W) or dimension of (G₁, G₂, W) grows, the frequentist profile likelihood estimation may become unstable and the log-linear model with shared parameters across gene-sets and the DX latent mixture construction aids with such situations. We follow the same sequence as in the previous section to describe the prior structure on the parameters.

1. In the presence of multiple genes in G₁ and G₂, the logistic disease risk model can potentially have many pairwise and higher order interaction terms. We implement a scalable variable selection framework via spike and slab type priors [Mitchell and Beaucamp (1988); George and McCullogh (1993)] on the parameters β in the disease risk model P(D|G₁, G₂, W; β). We impose mixture prior distributions on each component of β, say, (β₀, β_G1, β_G2, β_E, β_S, β_G1G2, β_G1E, β_G2E) for a two-gene model. In general we denote this vector by β_nβ×1 = {β_r, r = 1, …, n_β}. Given a latent variable p₀ representing the mixture weight on the “not informative” regression coefficients, we describe the hierarchical prior structure as follows,

$${\beta }_r|f_r,{\tau }_r\stackrel{ind}{~}N(0,f_r{{\tau }_r}^2),r=1,\dots ,n_{\beta },f_r|{\upsilon }_0,p_0\stackrel{iid}{~}{p}_0{\delta }_{{\upsilon }_0}(·)+(1-p_0){\delta }_1(·),{\tau }_r^{-2}|a_1,a_2\stackrel{iid}{~}\mathit{\text{Gamma}}(a_1,a_2),p_0\stackrel{iid}{~}\mathit{\text{Beta}}(a,b).$$

As discussed in Ishwaran and Rao (2003), υ₀ in the above specification is assumed to be a small positive value near 0. Note that f_r can assume two values υ₀ or 1. At each iteration of posterior sampling, f_r takes value 1 if sampled β_r is significantly away from zero, implying that the r-th covariate is potentially informative. Note that a key feature of this prior specification is that the marginal prior variance of β_r is calibrated as var(β_r) = f_rτ_r² and has a bimodal distribution. Large var(β_r) can occur when f_r = 1 and ${\tau }_r^2$ is large, inducing large values of β_r, identifying potentially informative covariates. Small values of var(β_r) occur when f_r assumes value υ₀, leading to values of β_r that are near zero, suggesting that β_r is potentially uninformative. The value of p₀ controls how likely it is for f_r to be υ₀ or 1, thus controlling how many β_r are non-zero or the complexity of the model. The Gamma parameters (a, b) controls the degree of parsimony through the prior on p₀. We set (a, b) = (1, 1), i.e. a uniform prior on p₀, for the analysis we present in the main text. Note that, (a₁, a₂) determines the prior on ${\tau }_r^2$ and thus the variance of β_r. We fix (a₁, a₂) at (5, 50) to allow the possibility of large prior variances on β. The values used for the hyperparameters in the hierarchy are exactly as recommended in Ishwaran and Rao (2003).

2. In the joint log-linear model (2.2), we typically assume vague normal priors with large variance on the parameters (λ_G1, λ_G2, λ_G1S, λ_G2S). In our data example, we have used a N(0, 10⁴) prior. On the other hand, for the G-E pairwise association parameters (λ_G1G2, λ_G1E, λ_G2E) we reflect a priori information on G-G or G-E independence via a normal prior centered at zero but with two different choices for the prior variance. In the first set of priors we reflect the belief that with 95% probability the association parameter lies between log(0.8) and log(1.2). This leads to an approximate SD=0.1 under a normal distribution and thus we assume an informative prior of N(0, 10⁻²). In the second choice, following the empirical Bayes estimation of Mukherjee and Chatterjee (2008), we compute association parameters for G₁–G₂, G₁-E, and G₂-E in the control subjects in the data, say θ̂, and use a data-driven prior N(0, θ̂²) on λ_G1G2, λ_G1E, and λ_G2E.

3. The mixture representation in (2.4) requires determining the number of latent classes k. Following DX, instead of selecting a fixed k, a Bayesian nonparametric approach is carried out through the Dirichlet process prior specification on ν:

$$\pi =\sum _{h=1}^{\infty }{\nu }_h{\psi }_h,{\psi }_h={\psi }_h^{(1)}\otimes \cdots \otimes {\psi }_h^{(p)},h=1,\dots ,\infty ,{\psi }_h^{(j)}~\mathit{\text{Dirichlet}}(a_{j1},\dots ,a_{j{d}_j}),\text{independently for}j=1,\dots ,p,{\nu }_h=\sum _{h=1}^{\infty }{V}_h\prod _{l<h}(1-V_l),V^h~\mathit{\text{Beta}}(1,\alpha ),\alpha ~\mathit{\text{Gamma}}(a_{\alpha },b_{\alpha }).$$

where ⊗ is the outer product. The parameter α is a hyper-parameter that controls the rate of decrease from the stick-breaking process (Sethuraman, 1994). For example, in case of small values of α, ν_h decreases towards zero quickly with increasing h, thus putting most of the weight on first few components, leading to a sparse representation. The hyperprior on α allows one to data-adaptively determine the degree of sparseness or the number of components needed. As discussed in DX (2009), we set (a_α, b_α) = (1/4, 1/4) for a vague prior which implies the probability of independence across components of w in the product multinomial model to be 0.5. We set uniform priors for each category probability ψ with a_j1 = ⋯ = a_jdj = 1, for j = 1, …, p and let the data dominate over priors. To minimize large number of mixture components instead of using infinite mixtures, we truncate the maximum of the number of mixture components k at 30 in real data example [Ahn et al. (2012)]. We study sensitivity with respect to this truncation threshold in Table 1.

Table 1.

(a) Analysis results for the MECC study data with statins (E), G₁ RS1800775 on CETP and G₂ RS1056836 on CYP1B1. The model adjusts age (S₁, ‘¿50’=1, ‘≤ 50’=0), gender (S₂, male=1, female=0), ethnicity (S₃, Ashkenazi=1, Non-Ashkenazi=0), sports activity (S₄, Yes=1, No=0), vegetable consumption (S₅, High=1, Low=0), family history of CRC (S₆, Yes=1, No=0), the use or non-use of NSAID within 3 years(S₇, Yes=1, No=0), the use or non-use of Aspirin within 3 years (S₈, Yes=1, No=0). Under the TPFB method the ‘est.’ corresponds to the posterior mean whereas PSD corresponds to posterior standard deviation. The methods that yield the smallest PSD are in bold font in each row.

	TPFB	TPFBemp	WL	PL	UML	CML	EB
	est.(PSD)	est.(PSD)	est.(se)	est.(se)	est.(se)	est.(se)	est.(se)
Exposure variables
G1	0.04 (0.09)	0.01 (0.09)	0.00 (0.09)	0.00 (0.09)	0.00 (0.09)	0.00 (0.08)	−0.07 (0.08)
G2	−0.04 (0.10)	−0.06 (0.10)	−0.13 (0.10)	−0.13 (0.10)	−0.13 (0.10)	−0.12 (0.08)	−0.12 (0.08)
Statin use	−1.29 (0.30)	−1.32 (0.27)	−1.30 (0.30)	−1.30 (0.30)	−1.40 (0.30)	−1.54 (0.28)	−1.51 (0.29)
G1 × G2	0.01 (0.07)	0.03 (0.05)	0.05 (0.08)	0.06 (0.08)	0.06 (0.08)	0.06 (0.06)	0.06 (0.06)
G1 × Statin use	0.34 (0.17)	0.34 (0.15)	0.25 (0.18)	0.25 (0.18)	0.25 (0.18)	0.38 (0.15)	0.34 (0.17)
G2 × Statin use	0.33 (0.16)	0.33 (0.16)	0.38 (0.18)	0.38 (0.19)	0.38 (0.20)	0.38 (0.18)	0.38 (0.19)
Gene-Statin and Gene-Gene association parameters from P(G1, G2|E, S)
λG1G2	0.02 (0.05)	0.00 (0.05)
λG1E	0.05 (0.07)	0.08 (0.06)
λG2E	0.01 (0.07)	0.01 (0.07)

(b) Sensitivity analysis with respect to the maximum number of allowable mixture components kmax, and the prior on G-G and G-E association parameters λ.
		G1	G2	Statin use	G1 × G2	G1 × Statin use	G2 × Statin use
kmax=10	TPFB	0.05 (0.10)	−0.03 (0.10)	−1.29 (0.30)	0.01 (0.07)	0.36 (0.16)	0.32 (0.17)
	TPFBemp	0.01 (0.09)	−0.06 (0.10)	−1.32 (0.29)	0.03 (0.07)	0.31 (0.15)	0.32 (0.16)
kmax=30	TPFBnon	0.05 (0.11)	−0.03 (0.11)	−1.29 (0.31)	0.01 (0.07)	0.34 (0.19)	0.34 (0.21)

^†TPFB, TPFB_emp, TPFB_non: Two-phase full Bayes (with informative prior N (0, 10⁻²), using empirical estimates for prior variances, with non-informative prior N (0, 10⁴)) on G-E association parameters.

UML: Unconstrained maximum likelihood, CML: Constrained maximum likelihood, EB: Empirical-Bayes, WL: weighted likelihood, and PL: pseudo-likelihood.

2.3. Posterior sampling

In the full likelihood (2.1), we would like to point out that the three components are linked with each other through the sum over each component in the expression for P(D) in the denominator. We denote the two-phase likelihood in (2.1) by L_TP which involves the parameters (β, λ, ψ, V, α). The full conditionals are not reducible to a simpler closed form and are best represented by the following proportionality relations:

$${\beta }_r|·\propto {\mathrm{L}}^{\mathrm{T}\mathrm{P}}\times \text{exp}(-\frac{{{\beta }_r}^2}{2f_r{{\tau }_r}^2}),r=1,\dots ,n_{\beta },{{\tau }_2}^{-2}|·\propto \text{Gamma}(a_1+0.5,a_2+\frac{{{\beta }_r}^2}{2f_r}),f_r|·\propto \{I(f_r={\upsilon }_0)p_0+I(f_r=1)(1-p_0)\}\times \text{exp}(-\frac{1}{2f_r{{\tau }_r}^2}{{\beta }_r}^2)\times {f_r}^{-0.5},p_0|·\propto \text{Beta}(a+\sum _{r=1}^{n_{\beta }}I(f_r={\upsilon }_0),b+\sum _{r=1}^{n_{\beta }}I(f_r=1)),{\lambda }_l|·\propto {\mathrm{L}}^{\mathrm{T}\mathrm{P}}\times \text{exp}(-\frac{{\lambda }_l^2}{2{\sigma }^2}),l=1,\dots ,n_{\lambda },$$

where n_β and n_λ again represent the number of parameters in (β, λ) respectively.

Posterior sampling corresponding toP(W): Let us recapitulate the model structure for W which is essentially a Dirichlet process mixture of discrete Dirichlet kernels. For u = 1, ⋯, N and j = 1, ⋯, p,

$$w_{uj}~\mathit{\text{Multinomial}}(\{1,\dots ,d_j\},{\psi }_{z_u,1}^j,\dots ,{\psi }_{z_u,d_j}^j),z_u~V_h\prod _{l<h}(1-V_l){\delta }_h,V_h~\mathit{\text{Beta}}(1,\alpha ),\alpha ~\mathit{\text{Gamma}}(a_{\alpha },b_{\alpha }).$$

DX present an efficient data-augmented Gibbs sampling algorithm by augmenting the likelihood with latent constructs following Walker (2007). The details of the updating steps are described in the supplemental article [Ahn et al. (2012)].

Note that while the entire likelihood in DX constituted of W data only, in our problem, P(W) is embedded as a component in the joint retrospective likelihood L^TP in (2.1). Thus for updating the parameters involved in P(W), say θ(={ψ, V, α}), we use the Metropolis Hastings algorithm. Only the terms ∏_u P(W_u)/P(D_u) from the full likelihood (2.1) involve θ, where P(D_u) = ∑_{g1, g2} ∑_w P(D_u|g₁, g₂, w) P(g₁, g₂|w)P(w). We draw θ following the DX algorithm and for the proposal density of θ we consider the implied full conditional q(θ^new|W) as determined by this algorithm. Then given λ, β we repeat the following updates of θ.

• At iteration l, sample a vector θ^new from q(θ^new|W) as described in DX (2009) algorithm.

• Compute the acceptance ratio

  $$r({\mathit{\theta }}^{\mathit{\text{new}}},{\mathit{\theta }}_l)=\text{min}[1,\frac{{\prod }_u\mathrm{P}(D_u|{\mathit{\theta }}_l,\mathit{\lambda },\mathit{\beta })}{{\prod }_u\mathrm{P}(D_u|{\mathit{\theta }}^{\mathit{\text{new}}},\mathit{\lambda },\mathit{\beta })}].$$

  In calculating the acceptance ratio, we note that the numerator and denominator ∏_u{P(W_u|θ^new)}p(θ^new) q(θ_l|W)/∏_u{P(W_u|θ_l)}p(θ_l)q(θ^new|W) is canceled out where p(θ) is a prior for θ.

• If r(θ^new, θ_l) < U where U ~ unif(0, 1), we set θ_l+1 = θ^new. Otherwise, the candidate vector θ^new is rejected and θ_l+1 = θ_l.

• Repeat the steps until the posterior chains converge.

Given the full conditionals, we implement the Gibbs sampler [Geman and Geman (1984)] with Metropolis Hastings updates to sample from respective full conditional distributions. For each parameter, we iterate 50,000 times and discard the first 40,000 iterations as ‘burn-in’. We check convergence of the chains using trace plots and the numerical diagnostic statistic ‘potential scale reduction factor’ [Gelman and Rubin (1992)] using the R package CODA [Plummer et al. (2009)]. Auto and cross-correlation checks are performed and a thinning of every tenth observation is carried out. Remaining posterior samples are used to construct estimated posterior summaries needed for Bayesian inference.

3. The Molecular Epidemiology of Colorectal Cancer Study

In this section, we describe the motivating example from the MECC study in detail and present analysis results. We use data on 1,746 cases and 1,853 controls with completely observed response to the question whether statins were used for more than 5 years. The binary variable ‘statin use of at least 5 years’ (E), is the environmental factor of interest with 91% “NO” and 9% “YES”.

We adjust for completely observed confounders and precision variables (S): age (S₁), gender (S₂), ethnicity (S₃), physical activity (S₄), family history of CRC (S₅), vegetable consumption (S₆), NSAID usage within 3 year (S₇), and Aspirin usage within 3 year (S₈). Age and ethnicity variables were dichotomized as Age ≥ or < 50 (94% and 6% respectively), and ‘Ashkenazi’ and ‘Non-Ashkenazi’ (68% and 32% respectively). Gender (S₃) was coded as 1 (50%) for male and 0 (50%) for female. The remaining binary factors (S₄, S₅, S₆, S₇, S₈) are classified to 1 or “YES” with the proportions of (0.36, 0.09,0.31, 0.02, 0.20) respectively.

For genotyping at phase II, stratified-sampling based on the disease status (D) and statin use (E) was carried out. All case-control subjects with statin use (“YES”) were included at phase II sample. We have 1,200 cases and 1,200 controls at phase II with data available on 294 trinary SNPs G = (G₁, …, G₂₉₄). Genotype data are not completely observed even at phase II due to technical genotyping failures for a limited number of SNPs. Among 2,400 case-control subjects at phase II, 56 subjects and 20 had partial genotype information on two subsets of SNPs. We did not have a dense set of markers typed across the genome to successfully impute these missing genotypes, thus we consider a marginalized likelihood as in (2.1).

Among 294 SNPs, we first illustrate our methods with two SNPs on two genes, RS1800775 on CETP (G₁) and RS1056836 on CYP1B1 (G₂) where both SNPs exhibit significant interactions with statin use in an initial single marker interaction analysis. We compare our methods for this simple two SNP model to some of the alternative methods that can only handle single marker interaction analysis. The raw frequencies of the cross-classification of case-control status (D), statins (E), genotypes G₁ and G₂ are shown in online supplementary Table 1 [Ahn et al. (2012)]. Simple logistic regression analysis was carried out to examine G₁-E and G₂-E association among control subjects and yielded odds ratios of 1.11 and 1.01 and corresponding p-values of 0.30 and 0.91 respectively. Based on a chi-squared test for independence G₁–G₂ reveals no association (p-value of 0.90) These tests suggest that the data support G₁-E, G₂-E and G₁–G₂ independence assumption.

We report the results of the multivariate analysis in Table 1. Along with two-phase full Bayes approach (TPFB) we consider five alternative methods. Unfortunately, none of these competing methods use the data in both phases and make use of the independence constraints. The first three use phase II data only (i) Unconstrained maximum likelihood (UML), a retrospective analysis that does not specify any constraints on P(G₁, G₂|E, S), (ii) Constrained maximum likelihood (CML), that imposes the Hardy-Weinberg Equilibrium as well as G₁-E/G₁–G₂ independence, (iii) Empirical-Bayes (EB), using data-adaptive ‘shrinkage estimation’ between the constrained and unconstrained ML estimates. Since methods (ii) and (iii) are developed for single marker analysis, G₂-E independence cannot be enforced in existing software (we used the ‘CGEN’ package by Bhattacharjee, Chatterjee, and Wheeler, 2011). These three methods completely ignore biased sampling at phase II and may thus lead to biased estimation of the main effect of E, particularly if the exposure sampling rates were differential among cases and controls. The next two approaches use information from both phases under a prospective likelihood framework: (iv) a Horvitz-Thompson estimator, typically known as a weighted likelihood (WL) approach [Manski and Lerman (1977); Breslow and Chatterjee (1999)]. This approach uses sampling fractions n_ij/N_ij, where n_ij and N_ij are the number of subjects corresponding to D = i, E = j at phase II and phase I respectively. The sampling fraction serves as weights in the likelihood to adjust for biased sampling (we used the svyglm function in ‘survey’ package in R by Lumley, 2011). Finally (v) a pseudo-likelihood (PL) approach which also adjusts for biased sampling probabilities in a likelihood framework [Schill et al. (1993)]. Briefly, if we denote P_ij = P(D = i|E = j) = exp(iα_j)/{1+exp(α_j)} where α_j is the log-odds for D = 1 when E = j, then pseudo-likelihood is defined as ${\prod }_{i,j}{P}_{ij}^{N_{ij}}{\prod }_{i,j,k}{p}_{ijk}$. Here,

$$p_{ijk}=\frac{n_{ij}\text{exp}\{i({\beta }_0-{\alpha }_j+s_{ijk}\beta )\}}{n_{0j}+n_{1j}\text{exp}({\beta }_0-{\alpha }_j+s_{ijk}\beta )}.$$

where s_ijk denotes covariate values for a subject with D = i and E = j.

Note that all of these five methods use completely observed phase II data on G₁ and G₂ as opposed to our proposed method that includes partially observed data by marginalization of the likelihood in terms of G₁ and G₂ when needed.

As previously explained, we present our method (TPFB) corresponding to two different priors on the G-E and G-G association parameters in model (2.2). First, we consider informative prior N(0, 10⁻²) that enforces fixed prior belief around G-E and G-G independence, we denote this by TPFB. The analysis using an alternative prior where the prior variances on λ_GG and λ_GE are estimated based on observed association in the data is denoted by TPFB_emp. In Table 1, variable selection scheme is excluded in the TPFB and TPFB_emp by assuming all f_r = 1, r = 1, …, n_β so that all covariates are included across all methods. This is done so that the method can be fairly compared to other alternatives which do not have the variable selection feature.

Under all methods, note in Table 1 that the estimated coefficients corresponding to statin-use suggests strong negative association with CRC status. The estimated effect size varies depending on whether the method accounts for biased sampling and/or gene-environment independence. In presence of interactions, we cannot really interpret the main effect estimates and need to combine the model results to present estimated sub-group effects. Recall that G₁-E and G₂-E independence does appear to be plausible in the light of this data. Note that while G₂ × E interaction is detected by all methods, G₁ × E interaction can only be detected by CML, EB, TPFB and TPFB_emp, i.e., methods that use the independence assumption. The TPFB estimates of terms involving E are slightly different in effect sizes with smaller standard errors when compared to the other methods. Smaller standard errors corresponding to interaction parameters are noted in all retrospective methods that explicitly model (G₁, G₂, E) dependence structure.

We also carried out a sensitivity analyses with respect to the choice of threshold to truncate the maximum value of k in the DX construction and the prior on G-E and G-G association. As can be seen from Table 1.(b), the results are almost identical with smaller number (k_max = 10) of components in the mixture distribution for W. This suggests further computational efficiency gain is possible by imposing more parsimonious constraint on k. In another sensitivity analysis, when the prior on G-E association is non-informative N(0,10⁴), we notice TPFB estimates slightly drift toward the estimates from PL and WL while losing some efficiency on the G₁ × E and G₂ × E terms.

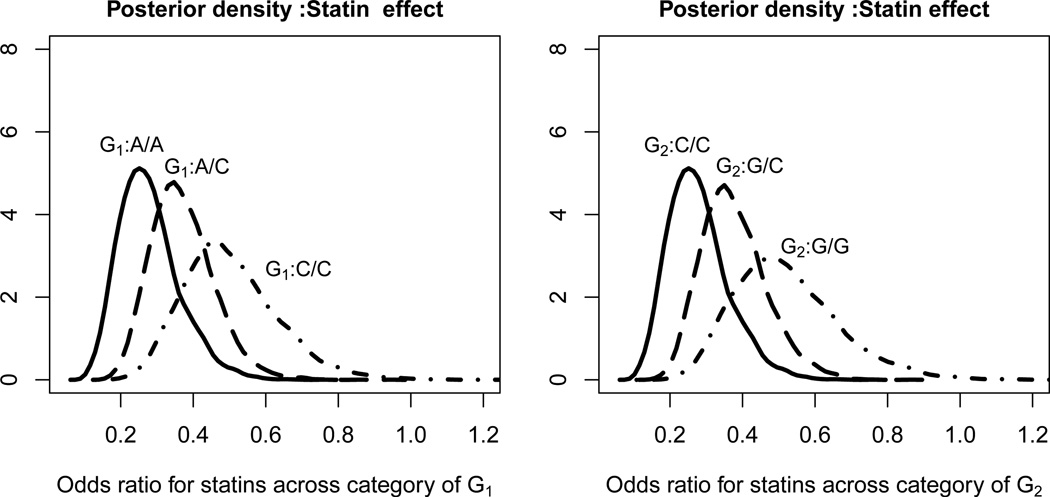
To reflect our main interest in sub-group effects of statin across genotype configurations, we report effects of statin across genotype sub-groups of one SNP, holding the other SNP fixed at the common genotype category for that second SNP (coded as 0). It seems that statin effect is strongly modified by G₁ and G₂. According to TPFB_emp estimates, keeping G₂ genotype fixed at C/C, the benefit of taking statins to reduce the risk of CRC is maximum in the A/A genotype of G₁ with the posterior estimate (and 95% HPD) of the odds-ratios (corresponding to statin users versus non-users) being 0.26 (0.15, 0.42). The corresponding ORs in genotype category A/C and C/C are 0.36 (0.23, 0.45) and 0.49 (0.31, 0.69) respectively. Figure 2 illustrates estimated posterior densities of the odds ratios corresponding to statin-use across each genotype of G₁ (left) or G₂ (right) respectively, while holding the other SNP fixed at the most common category. This figure indicates that the protective effect of statin in CRC are diminishing as the allelic dosage for the minor allele increases in both G₁ and G₂. Overall, the TPFB approaches provide much narrower credible intervals compared to PL and WL by exploiting G₁-E and G₂-E independence. The estimates from methods that use phase II data only, like CML, UML and EB are numerically slightly different.

Fig 2.

The left figure shows the posterior densities of the odds ratio estimates of CRC corresponding to statin users versus non-users across three genotypes in RS1800775 on CETP(G₁), holding the genotype in RS1056836 on CYP1B1 at the most frequent category, i.e., (G₂) = (C/C). Similarly, The right figure shows the posterior densities of the odds ratio estimates corresponding to statin users versus non-users across three genotypes in RS1056836 of CYP1B1(G₂), holding the genotype in RS1800775 of CETP fixed at the most frequent category, i.e., (G₁) = (A/A)

Variable Selection: We explore how variable selection feature performs in this example for the TPFB method. Previous research by Ishwaran and Rao (2003) discussed the performance of spike and slab prior for general variable selection. We introduce three SNPs (RS5925224, RS10174721, RS10077453) and all possible pairwise G × G and G × E interactions to the previous two SNP model as fit in Table 1. The dimension of the disease risk model is now 34. None of the main effects and interactions corresponding to these three additional SNPs were found significant in an initial single marker analysis.

We set f_r = 1 for S₁ through S₈ to always keep the confounders and precision variables in the model. The tuning parameters υ₀ is fixed at 0:0001 for this application with sensitivity analysis results presented for υ₀ = 0:001 in Table 3. We would like to see if the variable selection can still detect a significant G₁ × E and G₂ × E interaction. Moreover, we would like to assess if the three additional SNPs and the corresponding interactions we added (with null effects as observed in our initial analysis) are also identified to be not informative by this process. We tabulate the posterior distribution of f_r = 1 among f = (f₁, …, f_nβ) which indicate ‘in-and-out’ frequencies of the corresponding parameters. These posterior frequencies of f_r = 1 can be used to define a ranking of important predictors. An alternative is to rank the top models (not just the predictors individually). Before implementing the TPFB, we reduced the dimensionality of parameters in the model P(G|W) where G = (G₁, G₂, G₃, G₄, G₅) by assuming common λ_GG and λ_GE association parameters across all SNPs. We use N(0, 0.1²) prior on this common parameter. In addition, we further assume a single common parameter λ_GS for all G-S associations with a vague normal prior N(0, 10⁴). These are assumptions that may be stringent in certain situations, but to reduce estimation burden in the log-linear model, we do need to make these assumptions for the TPFB methods. For SNPs on a same functional pathway like in our example, it may not be too unrealistic to assume a shared association parameter across SNPs.

Table 3.

(a) The top 10 promising models in terms of estimated posterior probabilities of the models. All S adjustment variables are retained in the model by default and variable selection is performed only on the five genetic and environmental factors and all possible pairwise interactions. Bayesian Information Criterion (BIC) is provided for each model. Results in parentheses represent the sensitivity analysis carried out with υ₀ = 0.001.

Model	posterior probability %	BIC
[E][All S][G2 × E]	13.1 % (12.5 %)	43992 (43967)
[E][All S][G1 × E][G2 × E]	9.2 % (6.3 %)	43993 (43978)
[E][All S][G1 × E]	7.7 % (5.1 %)	43994 (43967)
[E][All S]	7.5 % (10.6 %)	43997 (43977)
[E][All S][G2 × E][G3 × E]	3.9 % (4.6 %)	44004 (43977)
[E][All S][G2 × E][G4 × E]	2.4 % (2.2 %)	44002 (43974)
[E][All S][G2 × E][G3 × G4]	2.1 % (1.5 %)	43998 (43971)
[E][All S][G1 × E][G3 × E]	2.1 % (2.2 %)	44,005 (43974)
[E][All S][G1][G2 × E]	1.8 % (0.7 %)	43,996 (43976)
[E][All S][G1 × E][G2 × E][G5 × E]	1.6 % (2.0 %)	44010 (43974)

(b) The estimated posterior probabilities of appearance corresponding to G and E main effects and their interactions are shown under the identical setting as in Table 3.(a). Results in parentheses represent the sensitivity analysis carried out with υ0 = 0.001.
G1	G2	G3	G4	G5	E	E × G1	E × G2	E × G3	E × G4	E × G5
6.7	5.0	4.3	4.1	7.6	100.0	36.8	64.0	18.4	10.1	13.9
(5.6)	(6.8)	(10.6)	(7.3)	(9.4)	100.0	(29.5)	(55.4)	(19.9)	(9.7)	(9.5)

BIC represents Bayesian Information Criterion.

In Table 3, we present numerical results on model and predictor ranking as well as the Bayesian Information Criterion (BIC) corresponding to each model. We only present the top 10 models. According to the result, the model with main effects of E and G₂ × E interactions seems to be the most preferred model (posterior probability 13.1%) followed by the model with E and both G₁ × E and G₂ × E interactions (posterior probability 9.2%). With υ₀ = 0.001, the ranking of predictors is slightly different as the main effects of G₁ through G₅ are now selected more often. The bottom panel of Table 3 shows the frequency of retaining a predictor in the model according to the posterior distribution of f. The main effect of E appears most of the times (100%) with large selection probabilities for G₁ × E and G₂ × E interactions (36.8% and 64.0%) respectively. Overall, non-significant interactions/main effects are well filtered under this variable selection scheme.

4. Simulation study

In this section, we assess the performance of the proposed method by conducting a simulation study. We mainly consider two aspects (i) varying gene-gene/gene-environment association structure and (ii) when phase II sampling is differential between cases and controls. We compare our method with the five alternative methods mentioned before: WL, PL, UML, CML, and EB in terms of the average bias and mean squared errors (MSE), based on 1,000 simulated datasets.

We first describe the data generation procedure. We consider two genes G₁ and G₂, and, one environment factor E, with disease status D, all binary. We generate data from the following log-linear model [Li and Conti (2009)]:

$$\text{log}(\mu |D,G_1,G_2,E)={\gamma }_0+{\gamma }_{G_1}{G}_1+{\gamma }_{G_2}{G}_2+{\gamma }_{E}E+{\gamma }_{D}D+{\lambda }_{G_{1}E}{G}_{1}E+{\lambda }_{G_{2}E}{G}_{2}E+{\lambda }_{G_1{G}_2}{G}_1{G}_2+{\beta }_{G_1}{G}_{1}D+{\beta }_{G_2}{G}_{2}D+{\beta }_{E}ED+{\beta }_{G_{1}E}{G}_{1}ED+{\beta }_{G_{2}E}{G}_{2}ED+{\beta }_{G_1{G}_2}{G}_1{G}_{2}D,$$ (4.1)

where μ denotes expected cell counts corresponding to the (D, G₁, G₂, _E) configuration. Under this model, we are capable of fixing G₁-E, G₂-E, and G₁–G₂ association under controls by setting values of λ_G1E, λ_G2E, and λ_G1G2 respectively. These parameters are approximately equivalent to those in model P(G₁, G₂|W) (2.2) when the disease is rare. Similarly, we can set β_G1E, β_G2E or β_G1G2, corresponding to the G × E or G × G interactions in the disease risk model. The parameters (γ₀, γ_G1, γ_G2, γ_E) controls the marginal frequencies of G₁, G₂ and E in controls. A large negative value of D ensures that the disease is rare.

For the model parameters in (4.1), we fixed (γ₀, γ_G1, γ_G2, γ_E, γ_D) = (−6, −0.5, −0.5, −2.0, −4.5) that produces approximately 2.5% of cases, frequency of G₁ = 1 and G₂ = 1 both at 45% while the prevalence of E = 1 is 15%. We assign (β_G1E, β_G2E, β_G1G2) = (0, log(2), log(2)) in (4.1). For setting parameters corresponding to G-E/G-G association, we set (λ_G1G2, λ_G1E, λ_G2E) = (log(2), 0, log(1.5)) to reflect G₁–G₂ and G₂-E dependence, and (0, 0, 0) for the independence scenario.

Now we turn our attention to the sampling design. We randomly generate 1; 000 cases and 1; 000 controls with complete (D, G₁, G₂, E) data. We then carry out (D, E)-stratified sampling as follows. We select 600 cases and 600 controls in phase II. We consider two scenarios regarding this the stratified sampling strategy: (a) all subjects with a positive E(= 1), in cases and controls, are automatically included in phase II; (b) all subjects with a positive E(= 1) in cases are included in phase II, however, 600 controls for phase II are randomly selected regardless of E status. Finally, information on G₁ and G₂ from phase I subjects, that is, 400 cases and 400 controls, is treated as missing by design. We iterate this step to generate 1,000 replicate datasets under each sampling scheme.

Table 4 and 5 display the simulation results based on two different sampling schemes (a) and (b) respectively. We follow the convention that ⊥ and ~ represent independence and dependence between two variables respectively. Under G₁⊥E, G₂⊥E, and G₁⊥G₂ the CML method yields the smallest MSE with respect to G₁ × E and G₁ × G₂ interaction followed by TPFB, TPFB_emp, and EB while WL, PL, and UML present relatively larger MSE. Here we need to note that the current implementation of CML and EB can only use G₁-E and G₁–G₂ independence, but not G₂-E independence. As phase II sampling becomes differential between cases and controls from scenario (a) (Table 4) to (b) (Table 5), we notice the substantial increase in the bias for estimating the main effect of E from CML, UML, and EB as expected while WL, PL, TPFB, and TPFB_emp provide relatively less biased estimates. This trend remains present in case where G₁⊥E, G₂ ~ E, and G₁ ~ G₂. Beyond the bias in β_E from CML, UML, and EB, we note that under the departure from the independence assumption, namely, G₁⊥G₂, there is a dramatic increase in the bias corresponding to the G₁ × G₂ interaction under CML and to some extent in TPFB. TPFB_emp and EB are more robust to this assumption. Both TPFB show gain in efficiency for interaction estimation compared to PL and WL. Overall, our proposed methods, especially TPFB_emp, yield obvious gain in efficiency compared to PL and WL in terms of the G × E or G × G interactions in the presence of independence. On the other hand, TPFB_emp provides less biased estimates of the E effect compared to UML, CML, and EB which use only phase II data. When sub-sampling ratio is 80%, the pattern remains same as seen in online supplemental Table 2 [Ahn et al. (2012)]. We also provide the sum of the MSEs across all parameters in order to capture the accuracy of estimating sub-group effects defined by different G-E configurations. This summary measure in the last columns of Table 4 and Table 5 clearly suggests that our methods yield more efficient characterization of the joint effect of exposure and genetic factors.

Table 4.

Simulation results under exposure enriched sampling with all E = 1 in phase I data are selected in phase II for both cases and controls. We consider two association scenarios 1) G₁⊥E, G₁⊥G₂, and G₂⊥E association, 2) G₁⊥E, G₁ ~ G₂, and G₂ ~ E. The results are based on 1,000 replicated datasets, each with 1,000 cases and 1,000 controls in phase I and 600 cases and 600 controls in phase II. The approaches listed, TPFB, TPFB_emp, WL, PL, UML, CML, and EB where each represents Two-phase full Bayes (with empirically obtained prior variance), Weighted likelihood, Pseudolikeliohod, Unconstrained Maximum likelihood, Constrained Maximum Likelihood, and Empirical Bayes respectively. The CML imposes G₁-E and G₁–G₂ independence, however, no constraints on G₂-E association. We set (β_E, β_G1G2, β_G1E, β_G2E) = (−1.5, 0, log(2), log(2)) for all scenarios. The rows with smallest two sum(MSE) are in bold.

		G1⊥E, G1⊥G2, G2⊥E					G1⊥E, G1~G2, G2~E
Stratified sampling (a)†		E	G1 × G2	G1 × E	G2 × E	Sum (MSE)¶	E	G1 × G2	G1 × E	G2 × E	Sum (MSE)¶
			(λG1G2, λG1E, λG2E) = (0, 0, 0)				(λG1G2, λG1E, λG2E) = (log(2), 0, log(1.5))
TPFB	Bias	−0.024	−0.017	0.020	−0.017		−0.056	0.166	−0.022	0.119
	(MSE)	(0.093)	(0.044)	(0.120)	(0.135)	(0.392)	(0.117)	(0.081)	(0.091)	(0.122)	(0.411)
TPFBemp	Bias	0.007	−0.019	−0.021	−0.062		−0.033	0.043	−0.029	0.026
	(MSE)	(0.089)	(0.025)	(0.111)	(0.126)	(0.351)	(0.113)	(0.064)	(0.091)	(0.120)	(0.388)
WL	Bias	−0.038	−0.025	0.043	0.009		−0.038	0.011	0.011	0.006
	(MSE)	(0.099)	(0.058)	(0.144)	(0.157)	(0.458)	(0.105)	(0.057)	(0.101)	(0.121)	(0.384)
PL	Bias	−0.038	−0.026	0.043	0.009		−0.038	0.011	0.011	0.006
	(MSE)	(0.098)	(0.056)	(0.144)	(0.157)	(0.455)	(0.105)	(0.056)	(0.101)	(0.121)	(0.383)
UML	Bias	−0.093	−0.026	0.043	0.009		−0.096	0.011	0.011	0.006
	(MSE)	(0.110)	(0.056)	(0.144)	(0.157)	(0.467)	(0.116)	(0.056)	(0.101)	(0.121)	(0.394)
CML	Bias	−0.085	−0.020	0.026	0.003		−0.100	0.700	0.011	0.009
	(MSE)	(0.099)	(0.025)	(0.083)	(0.155)	(0.362)	(0.112)	(0.520)	(0.070)	(0.116)	(0.818)
EB	Bias	−0.087	−0.025	0.036	0.004		−0.099	0.089	0.010	0.008
	(MSE)	(0.099)	(0.036)	(0.099)	(0.155)	(0.389)	(0.112)	(0.069)	(0.075)	(0.116)	(0.392)

^†All subjects with E = 1 in case and control are sub-sampled for phase II.

^¶The combined MSEs as summed over all four parameters.

TPFB uses the informative prior N (0, 10⁻²) on G-G and G-E associations in the model (2.2)

TPFB_emp uses the prior N (0, θ̂²) on G-G and G-E associations in the model (2.2) where θ̂² is empirically estimated G-G or G-E association parameter under controls.

Table 5.

Simulation results under exposure enriched sampling with all E = 1 in phase I data are selected in phase II for cases but a random sample of controls are selected in phase II. We consider two association scenarios 1) G₁⊥E, G₁⊥G₂, and G₂⊥E association, 2) G₁⊥E, G₁ ~ G₂, and G₂ ~ E. The results are based on 1,000 replicated datasets, each with 1,000 cases and 1,000 controls in phase I and 600 cases and 600 controls in phase II. The approaches listed, TPFB, TPFB_emp, WL, PL, UML, CML, and EB where each represents Two-phase full Bayes (with empirically obtained prior variance), Weighted likelihood, Pseudolikeliohod, Unconstrained Maximum likelihood, Constrained Maximum Likelihood, and Empirical Bayes respectively. The CML imposes G₁-E and G₁–G₂ independence, however, no constraints on G₂-E association. We set (β_E, β_G1G2, β_G1E, β_G2E) = (−1.5, 0, log(2), log(2)) for all scenarios. The rows with smallest two sum(MSE) are in bold.

		G1⊥E, G1⊥G2, G2⊥E					G1⊥E, G1 ~ G2, G2 ~ E
Stratified sampling (b)†		E	G1 × G2	G1 × E	G1 × E	Sum (MSE)¶	E	G1 × G2	G1 × E	G2 × E	Sum (MSE)¶
			(λG1G2, λG1E, λG2E) = (0, 0, 0)				(λG1G2, λG1E, λG2E) = (log(2), 0, log(1.5))
TPFB	Bias	0.007	0.022	−0.007	−0.022		−0.105	0.160	0.032	0.128
	(MSE)	(0.081)	(0.040)	(0.113)	(0.124)	(0.358)	(0.125)	(0.073)	(0.106)	(0.128)	(0.432)
TPFBemp	Bias	0.039	0.015	−0.054	−0.073		−0.027	0.036	0.024	0.000
	(MSE)	(0.086)	(0.031)	(0.127)	(0.122)	(0.366)	(0.121)	(0.058)	(0.115)	(0.135)	(0.429)
WL	Bias	−0.012	0.016	0.021	0.024		−0.044	0.004	0.076	−0.014
	(MSE)	(0.098)	(0.059)	(0.165)	(0.167)	(0.489)	(0.133)	(0.056)	(0.150)	(0.147)	(0.486)
PL	Bias	−0.012	0.015	0.020	0.025		−0.046	0.002	0.077	−0.013
	(MSE)	(0.097)	(0.059)	(0.164)	(0.166)	(0.486)	(0.132)	(0.055)	(0.149)	(0.146)	(0.482)
UML	Bias	0.538	0.015	0.020	0.025		0.520	0.002	0.077	−0.013
	(MSE)	(0.395)	(0.059)	(0.164)	(0.166)	(0.784)	(0.407)	(0.055)	(0.149)	(0.146)	(0.757)
CML	Bias	0.544	0.017	−0.002	0.018		0.530	0.699	0.046	−0.013
	(MSE)	(0.384)	(0.030)	(0.088)	(0.161)	(0.663)	(0.399)	(0.515)	(0.073)	(0.141)	(1.128)
EB	Bias	0.543	0.016	0.008	0.018		0.528	0.078	0.059	−0.013
	(MSE)	(0.385)	(0.039)	(0.112)	(0.161)	(0.697)	(0.401)	(0.066)	(0.097)	(0.141)	(0.705)

^†All cases with E = 1 are included in phase II, however, control are randomly selected for phase II.

^¶The combined MSEs over all four parameters.

TPFB uses the informative prior N (0, 10⁻²) on G-G and G-E associations in the model (2.2)

TPFB_emp uses the prior N (0, θ̂²) on G-G and G-E associations in the model (2.2) where θ̂² is empirically estimated G-G or G-E association parameter under controls.

Table 3 in the online Supplement [Ahn et al. (2012)] presents simulation results under the traditional or unstratified case-control design when a random sample of cases and controls are taken irrespective of E status. We can note clear efficiency gains from stratified sampling when comparing Table 4 to Table 3 in the online Supplement for estimating the interaction parameters.

5. Discussion

We presented a flexible Bayesian approach to estimate gene-gene (G × G) and/or gene-environment (G × E) interactions under two-phase sampling with multiple markers. The proposed approach can handle multiple genetic and environmental factors. The method can trade off between bias and efficiency by incorporating uncertainty around gene-environment independence through the hierarchical structure in a data-adaptive way. The underlying ingredients of this hierarchy are the disease risk model, the multivariate gene model, and the joint model for the environment factors/covariates respectively. Our method can also handle potential missingness in genetic information due to technical inconsistency, or due to merging different studies or cohorts, leading to non-monotone missing data structure at phase II sub-sample. This paper is the first Bayesian paper with retrospective modeling for G × E studies under two-phase sampling that can handle multiple markers.

We compared our method to simpler alternatives such as UML, CML, and EB that use gene-environment independence but only based on phase II data, ignoring biased sampling. We also considered methods that account for biased sampling at phase II: weighted likelihood and pseudo likelihood, but do not leverage the independence assumption. Our method provides a framework that integrates both of these features. In a clinical study like the MECC example, where interest lies in estimating the differential effect of statin use across genetic sub-groups for devising targeted prevention strategies, estimates of main effects as well as gene-environment interaction are equally important, thus both estimates need to be assessed. In terms of aggregate MSE our method has superior performance across a wide range of scenarios over competing method.

There are some limitations of the current paper that need to be expanded and explored in future studies. First, we do not fully address the performance of our method in the presence of a truly high-dimensional gene model through simulation studies. The method is scalable to handle up to 294 SNPs and pairwise interactions in our data example, but we have not carried out a simulation study due to computation time. We also need to deal with exponentially increasing number of G × E and G × G interactions in the disease risk model as well as G-E/G-G/G-S associations in the multivariate gene model, as we add more G-variables in the model. We address this by Bayesian variable selection and assuming a common parameter for G-E/G-G/G-S association on genes in the same pathway in the multivariate gene model. The latter is a rather ad-hoc strategy for reducing the dimension and is a limitation of our method. Bias in parameter estimates is expected to arise under departures from this assumption. Calculation of P(D) in the denominator of the likelihood could also pose challenges with truly high-dimensional data. Second, we have not tested the Dunson and Bhattacharya (2011) algorithm for mixed set of discrete and continuous covariates in W. Future research will focus on the higher-dimensional G and E settings, more general structure of the W vector as well as possibility of capturing higher order interactions, not just pairwise interactions.

For practitioners who want to choose a design strategy to enhance the power of screening G × E effects with a relatively rare exposure, exposure enrichment of cases and controls for collecting genotype data is a better strategy than random sampling. The tools we developed in the paper provides a way to account for the biased sampling. The approach also allows one to explore a multivariate model with multiple SNPs and environmental exposure and identify potentially informative predictors. If the interest lies in characterizing sub-group effects of E across different sub-groups defined by G, this design and analysis strategy is particularly powerful. We recommend the use of default prior choices in the codes available at http://www.umich.edu/~jaeil/tp.zip and recommend using TPFB_emp as the analysis to be reported. For prescribing a preventive medicine prophylactically, like use of statins for colorectal cancer, identifying genetic sub-groups that will receive the most benefit from such a therapy is particularly helpful. Characterizing G × E effects further our understanding of such sub-group effects for tailoring targeted prevention strategies.

Table 2.

Odds ratio estimates (confidence interval or credible interval) for CRC corresponding to statin users vs non-users across genotype sub-groups. Under all five methods, a model with main effect of G₁, G₂, E controlling for S was fit as in Table 1. Common allele in G₁ (RS1800775 on CETP) and G₂ (RS1056836 on CYP1B1) are A and C respectively and minor allele in G₁ and G₂ are C and G respectively.

	Statins	Statins	Statins	Statins	Statins
G1	A/A	A/C	C/C	A/A	A/A
G2	C/C	C/C	C/C	G/C	G/G
TPFB	0.27 (0.15, 0.39)	0.35 (0.22, 0.44)	0.48 (0.26, 0.65)	0.38 (0.24, 0.51)	0.48 (0.30, 0.77)
TPFBemp	0.26 (0.15, 0.42)	0.36 (0.23, 0.45)	0.49 (0.31, 0.69)	0.37 (0.23, 0.50)	0.50 (0.31, 0.79)
WL	0.27 (0.15, 0.49)	0.35 (0.22, 0.55)	0.45 (0.26, 0.77)	0.40 (0.26, 0.62)	0.59 (0.34, 1.02)
PL	0.27 (0.15, 0.49)	0.35 (0.22, 0.55)	0.45 (0.26, 0.79)	0.40 (0.25, 0.63)	0.59 (0.33, 1.05)
UML	0.25 (0.14, 0.44)	0.32 (0.20, 0.50)	0.41 (0.23, 0.72)	0.36 (0.23, 0.57)	0.53 (0.29, 0.95)
CML	0.22 (0.12, 0.37)	0.33 (0.21, 0.51)	0.49 (0.29, 0.83)	0.34 (0.20, 0.48)	0.46 (0.26, 0.80)
EB	0.22 (0.13, 0.39)	0.31 (0.20, 0.49)	0.43 (0.24, 0.79)	0.32 (0.21, 0.49)	0.47 (0.27, 0.82)

^†TPFB, TPFB_emp: Two-phase full Bayes (with empirical estimates for prior variances), UML: Unconstrained maximum likelihood, CML: Constrained maximum likelihood, EB: Empirical-Bayes, WL: weighted likelihood, and PL: pseudo-likelihood