Uncertainty about mapping future actions into rewards may underlie performance on multiple measures of impulsivity in behavioral addiction: Evidence from Parkinson’s disease

Abstract

A subset of patients with Parkinson disease (PD) develops behavioral addictions, which may be due to their dopamine replacement therapy. Recently, several groups have been comparing PD patients with and without behavioral addictions on tasks that are thought to measure aspects of impulsivity. Several of these experiments, including information sampling, a bias towards novel stimuli and temporal discounting, have shown differences between PD patients with and without behavioral addictions. We have developed a unifying theoretical framework which allows us to model behavior in all three of these tasks. By exploring the performance of the patient groups on the three tasks with a single framework we can ask questions about common mechanisms that underlie all three. Our results suggest that the effects seen in all three tasks can be accounted for by uncertainty about the ability to map future actions into rewards. More specifically, the modeling is consistent with the hypothesis that the group with behavioral addictions behaves as if they cannot use information provided within the experimental context to improve future reward guided actions. Future studies will be necessary to more firmly establish (or refute) this hypothesis. We discuss this result in light of what is known about the pathology that underlies the behavioral addictions in the Parkinson patients.

Introduction

Recent work has shown that impulsive-compulsive behaviors (ICBs; also referred to as impulse control disorders), which are behavioral addictions, can be a consequence of using dopamine agonists to treat the motor symptoms of Parkinson Disease (Dang, Cunnington, & Swieca, 2011; Gallagher, O’Sullivan, Evans, Lees, & Schrag, 2007; Hassan et al., 2011; Newman-Tancredi et al., 2002; Weintraub et al., 2010). The behavioral addictions, which include pathological gambling, compulsive shopping, compulsive sexual behavior, binge eating and excessive use of dopamine replacement therapy, have devastating consequences for those affected (Leroi et al., 2011). The relationship between dopamine agonists and behavioral addictions is supported by the fact that patients treated with agonists develop addictions about 20% of the time, whereas patients treated with L-dopa monotherapy develop addictions about 7% of the time (Weintraub et al., 2010). Additionally, the behavioral addictions often abate when the agonist dose is decreased (Avila, Cardona, Martin-Baranera, Bello, & Sastre, 2011).

These patients afford a unique opportunity to study a population that may provide insight into the neural mechanism that underlies behavioral, and perhaps drug, addictions in other populations. While treatment with agonists contributes to the development of behavioral addictions, the neural circuits that are affected and core changes in behavior that drive the addictions are not yet known. To examine this in detail, several groups have recently been carrying out behavioral and functional imaging experiments on these groups to explore the underlying mechanisms (Cilia et al., 2011; Djamshidian et al., 2010; Rao et al., 2010; Voon, Gao, et al., 2011). This work has started to provide evidence for core changes in behavior, as well as changes in the neural circuits that control these behaviors in the ICB group.

Several experiments have shown that some tasks that are thought to measure impulsivity do not consistently distinguish PD patients with and without behavioral addictions. These tasks include measures thought to assess motor impulsivity including the Stroop task (Djamshidian, O’Sullivan, Lees, & Averbeck, 2011)and the Eriksen flanker task (Wylie et al., 2012). In addition to these, other tasks which have not shown clear group differences include behavioral economics measures of risk (Djamshidian et al., 2010; Rao et al., 2010; Voon, Gao, et al., 2011) and reinforcement learning or 2-armed bandit tasks (Djamshidian et al., 2010; Djamshidian, O’Sullivan, Lees, & Averbeck, 2012; Djamshidian, O’Sullivan, Wittmann, Lees, & Averbeck, 2011; Housden, O’Sullivan, Joyce, Lees, & Roiser, 2010; Voon, Pessiglione, et al., 2010). Reinforcement learning has, however, revealed interactions between medication (comparing patients on their regular dose of medication vs. acutely off their regular dose of medication) and group such that PD patients with and without behavioral addictions respond to feedback differently on vs. off medication, although these results have been inconsistent (Djamshidian et al., 2010; Voon, Pessiglione, et al., 2010), perhaps due to differences in reward schedules across studies.

Three tasks have emerged that appear to discriminate PD patients with and without behavioral addictions relatively robustly; temporal discounting (Housden et al., 2010; Voon, Reynolds, et al., 2010; Voon, Sohr, et al., 2011), information sampling (Djamshidian, O’Sullivan, Sanotsky, et al., 2012) and novelty preference (Djamshidian, O’Sullivan, Wittmann, et al., 2011). The goal of the present work was to find a unifying explanation that could underlie all 3 of these apparently disparate tasks. Such an explanation can be used to drive hypotheses about a fundamental behavioral process that may give rise to both the clinical features and the behavior across tasks. The framework of sequential decision making (DeGroot, 1970; Puterman, 1994), or Markov Decision processes (MDPs) is sufficiently flexible to model all 3 of these tasks. The MDP framework allows us to model choices that affect future actions. This is important because all 3 of the tasks are structured such that current choices affect the relationship between future actions and rewards. Specifically, in the temporal discounting task, the chosen reward affects the delay until it can be collected. In the information sampling task, the subject is asked if they want to make a decision, or continue to collect information to make a more informed decision in the future. In the novelty task, the subject is occasionally presented a novel choice option. They then have to decide whether they want to choose one of the options with which they already have experience, or the novel option. Choice of the novel option when an alternative good choice option is available suggests that previous evidence is not being strongly weighted. By bringing all of these tasks into a single framework we sought to clarify the relationships between the formal decision making mechanisms that underlie decisions in each of them.

Methods

Data from the 3 experiments analyzed here have been published previously (Djamshidian, O’Sullivan, Sanotsky, et al., 2012; Djamshidian, O’Sullivan, Wittmann, et al., 2011; Housden et al., 2010). All participants provided written informed consent according to the declaration of Helsinki and the studies were approved by the UCLH Trust. Patients were recruited from the National Hospital for Neurology and Neurosurgery London. All patients fulfilled the Queen Square Brain Bank criteria for the diagnosis of PD and were taking L-dopa. Patients who scored under 26/30 points on the MMSE were excluded. For the beads task we analyzed data from 17 healthy controls, 22 patients without behavioral addictions and 26 PD patients with behavioral addictions. In the ICB group, 12 had hypersexuality, 13 pathological gambling (PG), 7 punding, 5 compulsive buying and 3 substance abuse (previous). For the temporal discounting task we analyzed data from 20 healthy controls, 18 PD patients without behavioral addictions and 18 PD patients with behavioral addictions. In the ICB group, 7 had hypersexuality, 9 pathological gambling (PG), 9 had binge eating, 8 punding, 6 compulsive buying and 4 substance abuse (dopamine dysregulation syndrome). For the novelty task we analyzed data from 18 healthy controls, 25 PD patients without behavioral addictions and 23 PD patients with behavioral addictions. In the ICB group 12 had hypersexuality, 11 pathological gambling (PG), 4 punding and 8 compulsive buying. Although the studies were carried out separately, there was overlap in patient recruitment for the PD patients with behavioral addictions, as this is a relatively small patient group. Overall there were 47 separate patients with behavioral addictions. There were 28 patients that did only one study, 17 that did two studies, and 2 that did all 3 studies. Although one large study incorporating all tasks in a single set of subjects would have been more straightforward, our goal is to show similarities between tasks, and heterogeneity between groups should only decrease this similarity. Demographic information is given in Table 1. There were differences in age between the ICB and PD groups in all 3 studies. Controls were matched to the ICBs. The ICB group has a younger age of disease onset, and therefore they are a younger population than PDs without behavioral addictions (Weintraub et al., 2010). The differences in age cannot account for our results as the ICBs did not differ in age from the healthy controls, but behaviorally the ICBs differed from both the controls and the PDs. In the beads experiment for age, the ICBs differed from the PDs (t(46) = 2.49, p = 0.016), but not from the controls (t(41) = 0.09, p = 0.928). In the temporal discounting experiment the ICBs differed from the PDs (t(34) = 2.78, p = 0.008) but not from controls (t(36) = 1.42, p = 0.16). In the novelty task, the ICBs differed from PDs (t(46) = 3.35, p = 0.002) but not from controls (t(49) = 0.634, p = 0.530).

Table 1.

Demographic information across the 3 studies. LEU-DA is levodopa equivalent units for dopamine agonists. In all locations, n is the number of subjects.

	ICB	PD	Controls
Beads – n	26	22	17
Age	58.9 (9.6)	64.8 (5.3)	58.8 (10.9)
Gender (n male)	22	19	14
N on agonist	13	16
LEU – DA	66.7 (91.7)	160.7 (157.2)
L-dopa	865.4 (405.6)	624.4 (338.5)
Temporal Discounting – n	18	18	20
Age	62.3 (7.6)	67.7 (5.5)	65.5 (6.0)
Gender (n male)	11	12	10
N on agonist	11	11
LEU DA – n on DA	248.0 (301.3)	170.5 (159.3)
L-dopa	643.5 (254.1)	634.2 (301.7)
Novelty – n	23	25	18
Age	55.9 (8.7)	64.2 (8.1)	57.9 (11.9)
Gender (n male)	19	21	8
N on agonist	11	11
LEU – DA	99.5 (150.6)	181.7 (207.2)
L-dopa	684.8 (321.5)	626.5 (331.0)

In the temporal discounting study and in the beads study, patients were tested only on their regular dose of medication. In the novelty study they were tested both off and on their regular medication in a counter-balanced order. There were no statistical effects of the medication manipulation in the novelty study (Djamshidian, O’Sullivan, Wittmann, et al., 2011), so we report only group effects in the results. All PD patients had an excellent L-dopa response assessed by UPDRS Part III scores during “off” and “on” state.

Beads task

The beads task is an information sampling task. These tasks are based on an explicit and quantifiable trade-off between the amount of information sampled, and the accuracy of decisions. More sampling in these tasks leads to more accurate decisions. Thus, quick decisions are necessarily less accurate. They are related to the matching familiar figures task (MFFT) which has been used extensively as a measure of reflection impulsivity (Kagan, 1966). However, the MFFT requires both visual attention and information sampling, and therefore it is not a pure measure of the trade-off between sampling and the accuracy of decisions. Subjects can be slow or inaccurate in the MFFT because they have poor visual attention skills. Information sampling tasks have been used previously to measure impulsivity in various clinical groups, and they have consistently shown group differences with controls (Clark, Robbins, Ersche, & Sahakian, 2006; Djamshidian, O’Sullivan, Sanotsky, et al., 2012).

The beads task was performed on a laptop computer, often in the participant’s home or in a quiet room. Participants were required to guess from which of two urns a series of colored beads were being drawn. The cups differed in the proportion of blue and green beads they contained. For example, one of the urns may have contained 80% blue beads and 20% green beads, whereas the other urn may have contained 80% green beads and 20% blue beads. Participants were first shown a bead drawn from one of the urns, which was either blue or green. They were then given the choice of drawing another bead from the same urn, or guessing that the bead had been drawn from the predominantly green or blue urn. This was repeated until they chose to guess one of the urns, or they drew ten beads, at which point they had to guess an urn. Participants completed 4 blocks of 3 trials each in a 2 × 2 design with beads ratio and loss as factors. Specifically, two blocks contained an 80/20 ratio of beads and 2 blocks a 60/40 ratio of beads in each urn. In addition, in two blocks participants lost 10 points if they were wrong, and in two blocks they lost nothing if they were wrong. They were always charged 0.2 points for each additional bead drawn, and they won 10 points if they were correct.

Novelty Task

We performed a three-armed bandit task, modified from a “four armed bandit choice task” used previously in health participants (Wittmann, Daw, Seymour, & Dolan, 2008). This task measures the extent to which subjects select novel choice options, relative to choice options with which they have some experience. We have previously shown that Parkinson’s patients with behavioural addictions are more novelty prone in this task than matched PD patients without behavioural addictions (Djamshidian, O’Sullivan, Wittmann, et al., 2011). Further, imaging studies have shown that novelty preference in this task is driven by the ventral striatum (Wittmann et al., 2008), and data in the PD patients with behavioural addictions also suggests that aberrant processing in their ventral striatum may underlie aspects of their disorder (Cilia et al., 2010; Evans et al., 2006; O’Sullivan et al., 2011; Steeves et al., 2009).

The task was administered on a laptop computer. Participants performed 60 trials of the task in a single block. In each trial three black and white picture post-cards were presented on the screen. After presentation of the pictures, the participant was required to select one of the three pictures using a key press. After the option was selected, they were told whether they had “won” or “lost”. We also provided auditory feedback (5 Khz for winning and 2.5 Khz for losing) to reinforce feedback learning. Following an inter-trial interval, during which the screen was blank, the participants were again presented with the 3 choice options and they could make another decision. The location of each picture was randomized from trial to trial to prevent habituation. The participants were told to pick the most often rewarded picture as many times as possible to maximize their winnings.

During the task, as the participants were making their choices and learning the reward value of the pictures, novel stimuli were introduced. This was done by replacing one of the images from which participants had been choosing with a new image, which was then a novel choice option. A novel choice option was introduced on 20% of trials, or on average every 5 trials. These novel choices were of two types – unfamiliar and familiar. There was no statistical effect of the image familiarity in our original study (Djamshidian, O’Sullivan, Wittmann, et al., 2011) and therefore we do not address that feature of the task here. We treat all novel choice options, whether they were familiar or unfamiliar, as the same.

Temporal Discounting

The Kirby delayed discounting questionnaire, which is a measure of choice impulsivity, was used to examine how participants valued immediate relative to delayed rewards (Kirby, Petry, & Bickel, 1999). Participants were presented a fixed set of 27 choices between smaller, immediate rewards, and larger, delayed rewards. For example, one question asked participants, ‘Would you prefer £54 today, or £55 in 117 days?,’ while another asked, ‘Would you prefer £55 today, or £75 in 61 days?’ A future reward is typically valued less highly than the same reward available immediately. Therefore, delay discounting is the reduction in the present value of a future reward as the delay to that reward increases.

Model fitting

We first discuss features of the algorithms used to model the behaviors that are consistent for all of the models. We then discuss specifics related to each task. All tasks were modeled as discrete state, discrete time, finite-horizon Markov decision processes (MDP). The MDP framework models the utility, u, of a state, s, at time t as

$$u_t(s_t)={\max }_{a\in A_{s_t}}\{r_t(s_t,a)+{\sum }_{j\in s}\gamma p_t(j|s_t,a)u_{t+1}(j)\}$$ (1)

Where, $A_{s_t}$ is the set of available actions in state s at time t, r_t(s_t, a) is the reward that will be obtained in state s at time t if action a is taken. The summation is taken over the set of possible subsequent states, S at time t+1 weighted by the transition probability, or the probability of transitioning into each of those states from the current state, s_t if one takes action a, given by p_t (j|s_t, a). The γ term represents a discount factor, although we set it to 1 for all analyses here. The term inside the curly brackets is referred to as the action value, Q (s_t, a) = r_t(s_t, a) + Σ_j∈s γp_t (j|s_t, a)u_t+1 (j), for each available action.

Utility estimates for these models are given by backward induction. As we model all tasks as finite horizon tasks, at the final state one can only collect a reward. There is no transition to a subsequent state. Therefore, if we start by defining the utilities of the final states, we can work backwards and define the utilities of all previous states. Specifically, the algorithm proceeds as follows (Puterman, 1994), where N is the final state.

1. Set t = N

   $$u_N(s_N)=r_N(s_N)\text{for all}{s}_N\mathit{\in }N.$$
2. Substitute t-1 for t and compute

   $$u_t(s_t)=\underset{a\in A_{s_t}}{\max }\left\{r_t(s_t,a)+{\displaystyle \sum }_{j\in s}\gamma p_t(j|s_t,a)u_{t+1}(j)\right\}$$

   Set

   $$A_{s_t,t}^{\ast }=\mathit{arg}\underset{a\in A_{s_t}}{\max }\left\{r_t(s_t,a)+{\displaystyle \sum }_{j\in s}\gamma p_t(j|s_t,a)u_{t+1}(j)\right\}$$

3. If t = 1 stop, otherwise return to 2.

The beads task

For the beads task there are three possible actions at each time. Specifically, (i) choose the green urn, (ii) choose the blue urn, or (iii) draw another bead. The state is given by the number of draws (n_d), and the number of blue (n_b) beads that have been drawn, s_t{ n_d, n_b}. For guessing the blue urn, a = blue, we have:

$$r_t(s_t,a=\mathit{blue})=C_e{p}_g+C_c{p}_b$$ (2)

where C_e is the cost of an error (0 or −10 points, depending on the condition) and C_c is the reward for being correct (10 points). The probability that we are drawing from the blue urn p_b is given by

$$p_b={\left[1+{\left(\frac{q}{1-q}\right)}^{(n_d-2n_b)}\right]}^{-1},$$ (3)

where q is the fraction of beads in the majority urn. The probability of the green urn is then 1-p_b. The second term in equation 1, which is the value of the next state, is 0 for choosing either blue or green urns, because choosing an urn terminates the sequence. For drawing again, a=draw, we have

$$Q_t(s_t,a=\mathit{draw})=C_d+{\sum }_{j\in s}{p}_t(j|s_t,a)u_{t+1}(j),$$ (4)

where C_d is the cost of drawing (−0.20). From a given state, s_t, if one draws again, one draws either a blue or a green bead, so the two subsequent states are, s_t+1 = n_d+1, n_b+1 if a blue bead is drawn or s_t+1 = n_d+1, n_b if not. And the transition probabilities are

$$p_t(n_d+1,n_b+1|s_t=\{n_d,n_b\},a=\mathit{draw})={\mathit{qp}}_b+(1-q)p_g$$

And

$$p_t(n_d+1,n_b|s_t=\{n_d,n_b\},a=\mathit{draw})=(1-q)p_b+{\mathit{qp}}_g.$$

The temporal discounting task

Finding a group that discounts future rewards more does not explain why they discount future rewards. In other words, it does not provide a mechanistic description. There are several possible mechanistic descriptions. Here we adopt the hypothesis that a participant might consider any future reward to be unpredictable, even if the experiment suggests that the reward will be obtained with certainty (Keren & Roelofsma, 1995).

For the temporal discounting task we assume a state space in which a decision, a_i leads to a sequence of unrewarded states that terminate at the time of the (undiscounted) chosen dollar amount, which is a final, rewarded state. In addition, each unrewarded state on the way to the rewarded state can spontaneously transition to a terminal state in which no reward is collected. As this possibility occurs at each intermediate unrewarded state, the probability of transitioning to an unrewarded state increases with the delay to the reward. In other words, in this case, we assume that the discounting arises because of uncertainty about one’s ability to make it to the terminal state in which one can collect a reward. States are defined by whether one can progress beyond them s_t = s_b or not s_t = s_a and a final state in which one obtains a reward s_N = s_R. Thus, we have

$$r_n(s_N=s_R)=R$$

and

$$r_{t\ne N}(s_{t\ne N}\in \{s_a,s_b\})=0$$

The transition probabilities are given by

For t = 0

$$\begin{array}{l}{p}_0(s_1=s_a)=\mathit{\beta \delta }\\ p_0(s_1=s_b)=1-\mathit{\beta \delta }\end{array}$$

For t > 0

$$\begin{array}{l}{p}_t(s_{t+1}=s_a|s_t=s_a)=1\\ p_t(s_{t+1}=s_b|s_t=s_b)=1-\delta \\ p_t(s_{t+1}=s_a|s_t=s_b)=\delta \\ p_t(s_N=s_R|s_{N-1}=s_b)=1-\delta \\ p_t(s_N=s_a|s_{N-1}=s_b)=\delta \end{array}$$

This model implements quasi-hyperbolic discounting such that the value of delayed rewards is given by Q (a = choose R at delay N) = Rβδ^N.

The novelty task

For the novelty task the full state space is intractable and therefore we modeled it as a truncated-finite horizon problem. We examined action value estimates under increasing time horizons and found that they converged quickly. We present results for a horizon of t+3. The basic novelty task is a 3-armed bandit choice task. Thus, the state space is the number of times each option has been chosen and the number of times it has been rewarded, s_t = {n₁, R₁, n₂, R₂, n₃, R₃}. The immediate reward estimate is given by

$$r_t(s_t,a=i)=\frac{R_i+1}{n_i+2}.$$

The 1 in the numerator and the 2 in the denominator arise because of the assumption of a beta (1,1) prior (Gelman, Carlin, Stern, & Rubin, 2004). Thus, before an option has been chosen, it would have an assumed reward probability of 0.5. The set of possible next states, s_t+1, is given by the chosen target, whether or not it is rewarded, and whether one of the options is replaced with a novel option. Thus, each state leads to 21 unique subsequent states. We define q₁ = r_t (s_t, a = i), and ps_witch = 0.2, as the probability of a novel substitution. The transitions to a subsequent state without a novel choice substitution and no reward are given by:

$$p_t(\dots ,n_i+1,R_i,\dots |s_t=\{\dots ,n_i,R_i,\dots \},a=\mathit{\text{choose}}i)=(1-q_i)(1-p_{\mathit{switch}})$$

and for reward by

$$p_t(\dots ,n_i+1,R_i+1,\dots |s_t=\{\dots ,n_i,R_i,\dots \},a=\mathit{\text{choose}}i)=q_i(1-p_{\mathit{switch}}).$$

When a novel option was introduced, it could replace the chosen stimulus, or one of the other two stimuli. In this case if the chosen target, i, was not rewarded and a different target, j, was replaced, we have

$$p_t(\dots ,n_i+1,R_i,n_j=0,R_j=0|s_t=\{\dots ,n_i,R_i,\dots \},a=\mathit{\text{choose}}i)=(1-q_i)p_{\mathit{switch}}/3$$

and if the chosen target was not rewarded and was replaced

$$p_t(\dots ,n_i=0,R_i=0,\dots |s_t=\{\dots ,n_i,R_i,\dots \},a=\mathit{\text{choose}}i)=(1-q_i)p_{\mathit{switch}}/3.$$

And correspondingly, following a reward and replacement of a different target, j, we have

$$p_t(\dots ,n_i+1,R_i+1,n_j=0,R_j=0|s_t=\{\dots ,n_i,R_i,\dots \},a=\mathit{\text{choose}}i)=q_i{p}_{\mathit{switch}}/3$$

and

$$p_t(\dots ,n_i=0,R_i=0,\dots |s_t=\{\dots ,n_i,r_i,\dots \},a=\mathit{\text{choose}}i)=q_i{p}_{\mathit{switch}}/3.$$

Note that when a novel option is substituted for the chosen stimulus, the same subsequent state is reached with or without a reward.

Parameterization of group performance

The models given above are ideal models which describe optimal behavior. To characterize individual subject performance and compare performance among groups, we have parameterized uncertainty across the tasks. In each task we have introduced a single parameter. For the beads task, we have parameterized the transition probabilities as

$$p_t(n_d+1,n_b+1|s_t=\{n_d,n_b\},a=\mathit{draw})={\pi }_u{p}_b+(1-{\pi }_u)p_g$$

We fit π_u as a free parameter. We found that the algorithm converged most effectively when we parameterized this as π_u =qlogistic(−gamma) and fit gamma. Values plotted in Fig. 1A are logistic(gamma), as this represents the uncertainty. This parameter controls the belief that subsequent draws will lead to sequences of beads that are strongly predictive of the urn being drawn from. As can be seen, the belief that one will draw another blue bead is given by the belief that one is currently drawing from the blue urn p_b weighted by π_u. If π_u is small, it down-weights the belief that additional blue beads will be drawn when blue is more likely, and correspondingly for green. Thus, it favors sequences that are not strongly predictive of reward or an assumption that additional bead draws will not help inform future choices.

Fig. 1.

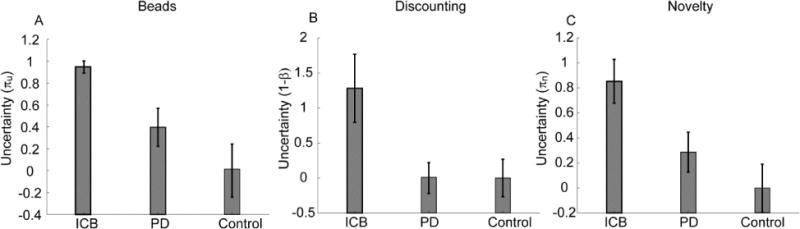
Parameter values in the 3 tasks. For comparison across tasks, all data was normalized by subtracting the mean and dividing by the standard deviation of the healthy control group, in each experiment. ICB indicates the PD group with behavioral addictions.

For the novelty task we parameterized the prior. Thus, we fit π_n as a free parameter in:

$$r_t(s_t,a=i)=\frac{r_i+{\pi }_n}{n_i+2}.$$

Finally, for the temporal discounting task we have parameterized the belief that the reward will be collected before a terminal, non-rewarding state is entered. To minimize the number of free parameters we fit a single β across participants from all groups (β =0.87) and allowed δ to vary for individual participants. Thus, in all 3 tasks we have modeled the participants’ beliefs about future transitions to rewarding states.

Parameter optimization

Parameters were optimized by maximizing the likelihood of the participants’ choices, given the data. Specifically, the MDP model generates value estimates for each action at each point in time. The utility is defined as the max over these actions (equation 1), but the subject can, for various reasons, choose not to maximize. These action values can be converted to choice probabilities using the soft max function:

$$d_{i,t}=\frac{e^{\alpha Q(s_t,a=i)}}{{\sum }_{a\mathit{\in }{A}_{s_t}}{e}^{\alpha Q(s_t,a)}}$$

The log likelihood is then give by

$$ll=-{\sum }_N{\sum }_{{a\prime }_i\mathit{\in }{A}_{s_t}}a{\prime }_i\mathit{log}(d_{i,t}),$$

Where $a{\prime }_i$ is an indicator variable which take the value $a_i\prime \mathit{=}\mathit{1}$ for the chosen action, and 0 for the actions which were not chosen. The log-likelihood can be minimized using fminsearch in Matlab.

ANOVAs for all three tasks were carried out using mixed-effects analysis with group as a fixed-effect and subject nested under group as a random effect. Paired comparisons were done using Fisher’s least significant difference test (Levin, Serlin, & Seaman, 1994). In this approach, a main effect of group in the ANOVA can be followed up by individual t-tests. Requiring a main effect in the ANOVA protects the t-tests, and does not lead to an increase in type-I errors when there are 3 groups. Statistical analyses were done using the anovan function in the Matlab toolbox.

Results

The behavior of the groups has been reported previously in separate studies (Djamshidian, O’Sullivan, Sanotsky, et al., 2012; Djamshidian, O’Sullivan, Wittmann, et al., 2011; Housden et al., 2010). We developed models which characterized group differences on the behavioral tasks with a single parameter which, in all cases, implies uncertainty about obtaining future rewards, based on information provided within the experiment (Fig. 1). In the beads task (Fig. 1A) there was a main effect of group (F(2,62) = 7.47, p = 0.001). Pair-wise comparisons showed that the PD patients with behavioral addictions differed from patients without behavioral addictions (F(1,46) = 7.95, p = 0.007). The group with addictions also differed from the healthy control group (F(1,37) = 18.25, p < 0.001). In the temporal discounting task (Fig. 1B) there was a main effect of group (F(2,42) = 4.25, p = 0.021). Pair-wise comparisons showed that PD patients with behavioral addictions differed from patients without addictions (F(1,31) = 5.01, p = 0.033) and the healthy control group (F(1,35) = 4.74, p = 0.038). In the novelty task (Fig. 1C) there was also a main effect of group (F(2,81) = 4.69, p = 0.012). Comparing the PD group with behavioral addictions to the PD group without behavioral addictions we found an effect of group (F(1, 46) = 4.11, p = 0.048) which was also found when comparing to healthy controls (F(1,39) = 10.06, p = 0.003). There were, however, no significant differences between PD patients without impulse control disorders and healthy control subjects in any of the tasks (p > 0.05).

Discussion

In this study we examined the behavior of Parkinson’s patients with and without behavioral addictions, and matched healthy volunteers, on three tasks which had previously been shown to elicit robust group differences between PD patients with and without behavioral addictions. Given that group effects had already been shown, our goal was to show that these tasks could be interpreted within a single theoretical framework, and to see whether this framework could suggest a common explanation for the behavioral differences in all tasks. To appropriately model these tasks we used the Markov Decision Process (MDP) framework, which takes into account how current decisions affect future rewards. Taken individually, the modeling results on the individual behaviors would not provide strong evidence to support the hypothesis that uncertainty over the future was fundamental to choices in the Parkinson patients with behavioral addictions. However, the consistent explanation across all 3 tasks strengthens this hypothesis.

Use of behavioral tasks and modeling to characterize impulsivity

Many of the tasks which have been used to study PD patients with behavioral addictions are thought to measure aspects of impulsivity. Impulsivity has often been studied with self-report questionnaires, and these have also been used in this patient group, showing group differences (Voon, Sohr, et al., 2011). Questionnaires have a long history and a deep literature. However, there are several disadvantages to using questionnaires that can be addressed using behavioral tasks, which is the approach we have adopted. First, questionnaires are not useable in animal models. Second, it is not clear how one would study the neural mechanism that gives rise to responses on questionnaires. Although one can correlate questionnaire responses with activations in behavioral tasks using functional MRI, this is done across subjects. Thus, this approach cannot identify a consistent neural mechanism that gives rise to patterns of choices within subjects. Third, self-report questionnaires often do not correlate well with behavioral tasks, such as those we have used, that putatively measure similar constructs (Barratt, Patton, Olsson, & Zuker, 1981; Meda et al., 2009; Reynolds, Penfold, & Patak, 2008) (Barratt et al. 1981; Meda et al. 2009; Reynolds et al. 2008). Finally, it is not clear to what extent self-reports represent true measures of behavioral dispositions (Wilson & Dunn, 2004) (Wilson and Dunn 2004). In other words, would the subject necessarily behave as they have indicated? Although behavioral tasks are simplified relative to real decision making situations, they can be directly used in animal models and in imaging experiments. Thus, the mechanisms that underlie them can be studied. In addition, they do not require subjects to indicate how they would hypothetically act in a particular situation. Rather, they create a scenario, often with real financial implications and then elicit a response. Progress in understanding pathological conditions like behavioral addictions will require identification of the neural circuits that are disrupted in these conditions (Robbins, Gillan, Smith, de Wit, & Ersche, 2012). Progress on this requires well-defined behavioral tasks that isolate particular computational operations that can be mapped to neural circuits.

Studies comparing PD groups with and without behavioral addictions can also help refine the concept of impulsivity, which is often noted as a correlate of addictive behavior (Verdejo-Garcia, Lawrence, & Clark, 2008). Specifically, impulsivity has historically been studied top-down, based on intuitive notions of what impulsivity is. This has led to the idea that impulsivity is multi-dimensional (Barratt, 1965; Eysenck & Eysenck, 1977). But this work has only shown that certain conceptions of impulsivity are multi-dimensional. The study of behavior in the group of PD patients with behavioral addictions, however, provides us with the opportunity to study behavioral correlates bottom up. We can start with a homogenous patient population that is clinically well-defined, and examine tasks which discriminate this population from PD patients that do not have behavioral addictions. In this way we can identify clusters of behaviors that do and do not discriminate these groups, and then use these behaviors to identify the neural circuits, and the pathology in these neural circuits, that differentiates these groups. Further, clusters of tasks that discriminate these groups, and map onto the same neural circuits would define homogeneous dimensions or aspects of impulsivity. In addition, in other patient groups where there is no evidence of striatal damage, dopamine agonists also cause behavioral addictions (Dang et al., 2011; Falhammar & Yarker, 2009; Holman, 2009). Whether these groups would behave similarly on these tasks, or whether differences in the underlying pathology between these patient groups would give rise to differences in their behavior would further support or refute the hypothesis that the dopamine agonists play a key role.

We have used the framework of sequential decision making or MDPs to model behavior in all 3 tasks (DeGroot, 1970; Puterman, 1994). Whereas temporal difference (TD) reinforcement learning (RL) models, particularly TD(0) models which are normally applied to behavioral data (Daw, O’Doherty, Dayan, Seymour, & Dolan, 2006; Djamshidian, O’Sullivan, Wittmann, et al., 2011; Voon, Pessiglione, et al., 2010), allow one to model the expected reward of an action based on past rewards, MDPs allow one to explicitly model the value of the information obtained when one takes an action or continues to accumulate evidence, over and above the expected immediate reward of the action. For standard choice learning paradigms, TD(0) RL models make predictions that are similar to an MDP. However, particularly for tasks like the beads task, the MDP framework is more appropriate as it can model the future value of information obtained with the current choice. The MDP framework can also deal with decision thresholds, which control the amount of information sampled before a decision is made, in a principled way (Drugowitsch, Moreno-Bote, Churchland, Shadlen, & Pouget, 2012; Moutoussis, Bentall, El-Deredy, & Dayan, 2011). Drift diffusion models, the sequential probability ratio test (Gold & Shadlen, 2001), and other related models, treat decision thresholds as a free and therefore arbitrary parameter (Averbeck, Evans, Chouhan, Bristow, & Shergill, 2011; Beck et al., 2008; Ditterich, 2006). It is in fact, possible to derive a threshold which is approximately optimal, if the sequential probability ratio test is analyzed within a sequential decision making framework (DeGroot, 1970).

Tasks which have been sensitive to group differences

We have modeled performance on an information sampling task, known as the beads task (Djamshidian, O’Sullivan, Sanotsky, et al., 2012). The beads task is related to the matching familiar figures task (Kagan, 1966). In the matching familiar figures task (MFFT), one is instructed to compare a target picture to a set of other pictures, and find the picture in the set that matches. The MFFT, however, does not make the dimension which should be compared explicit. Therefore an additional cognitive process, specifically identifying the features of the image which should be compared, must be employed. Another related task, the box opening task, is closely related to the beads task (Clark et al., 2006). This task has been shown to separate current and former substance abusers from control subjects (Clark et al., 2006). We have found that the beads task effectively discriminates PD patients with and without behavioral addictions (Djamshidian, O’Sullivan, Sanotsky, et al., 2012). However, we had not previously considered a specific behavioral mechanism that could account for these differences. In the present study, we found that we could model the effects of decreased information sampling, by assuming that subjects do not believe that they can accumulate information to improve reward related decisions by sampling additional beads.

Relatively increased discounting of delayed rewards has been observed in several patient groups, including the current group under study (Housden et al., 2010). Why humans and animals discount delayed rewards is, however, unknown (Frederick, Loewenstein, & O’Donoghue, 2004). There are rational reasons, for example inflation and interest rates, for exponentially discounting money. However, discounting is generally hyperbolic. In other words, rewards are generally discounted more over short delays than would be predicted by exponential discounting (Ainslie & Haslam, 1992), although the exact form of this function is still a matter of debate (Kable & Glimcher, 2010; Pine et al., 2009). Furthermore, rational explanations cannot account for group differences in delay discounting or for that matter the fact that temporal discounting is also observed in animals. One could argue that choices over immediate and delayed rewards could, in some instances, be accounted for by cue driven salience (Loewenstein, 2004), and that the decisions of some patients are driven more by immediately available cues than conceptual future rewards. In other words, the visual presence of a cue related to an immediately available reward increases its subjective value, and this effect is larger for some groups. This does not explain why the cues elicit increased subjective value; it only replaces one description (discounting) with another, psychological description (salience). Additionally, choices in temporal discounting tasks are often made over rewards presented as written statements, in which case there is no explicit monetary cue for either the delayed or the immediate reward, which is the case in the data used in the present study. Another possibility, and the assumption adopted here, is that any future reward is uncertain (Keren & Roelofsma, 1995). Further, the uncertainty increases with time. Uncertainty can arise for many reasons. One might not be able to collect a future reward, one might forget that a future reward will be available, one might die before obtaining a future reward, or the institution that promises the future reward may fail before the reward is delivered. In any case, delays increase the uncertainty that a reward will be collected, decreasing its value.

The final task we modeled was the novelty task (Wittmann et al., 2008). Novelty seeking behavior is often associated with addiction and impulsivity (Verdejo-Garcia et al., 2008; Weintraub et al., 2010). However, novelty seeking has been operationalized previously in human subjects using self-report questionnaires (McCourt, Gurrera, & Cutter, 1993; Voon, Sohr, et al., 2011). Here we operationalized novelty as a preference for new choice options, within an ongoing 3-armed bandit task. The model shows that the PD patients with behavioral addictions have reward priors which favor novel options, relative to the other groups, which correspondingly implies that they underweight evidence given in the form of reward feedback. This is different from not learning from feedback, which is explored in reinforcement learning tasks. In the novelty task it is specifically a trade-off between prior beliefs and updates to those prior beliefs on the basis of evidence.

Using the MDP framework we were able to account for group differences in all three tasks by assuming that they arose from increased uncertainty over the ability to map future actions into rewards in the PD group with behavioral addictions. In temporal discounting this can arise because the promised future reward may not actually be obtained. In the beads task, sampling additional information does not improve one’s ability to make reward related decisions. Finally, in the novelty task PD patients with behavioral addictions overestimate prior rewards, which implies that they rely more heavily on priors than accumulated evidence. This is also consistent with the finding in the beads task that PD patients with behavioral addictions often infer the wrong urn, given the evidence (Djamshidian, O’Sullivan, Sanotsky, et al., 2012). Anecdotally, many of these individuals report that they are making the inference because of an intuition, i.e. a prior belief.

Tasks which have not consistently been sensitive to group differences

There are a number of experiments which have not shown group differences between PD patients with and without behavioral addictions. For example, measures of motor impulsivity including the Stroop (Djamshidian, O’Sullivan, Lees, et al., 2011) and Eriksen flanker (Wylie et al., 2012) have failed to show differences between these patient groups. The studies on Stroop and Eriksen flanker did, however, show medication related effects, such that patients performed better on their regular dose of medication than off. Thus, these behaviors may be affected by acute changes in dopamine levels, but they are not affected by trait differences between the PD groups. Children with ADHD, who are also considered impulsive, have shown differences on tests of motor impulsivity, most specifically the stop-signal reaction time task (Winstanley, Eagle, & Robbins, 2006). It is likely, however, that ADHD and behavioral addiction are not closely related. Behavioral addictions are driven by compulsive cravings for intrinsically rewarding activities which are pursued to a detrimental extent. ADHD on the other hand is typified by inattention and/or hyperactivity that impairs normal function (Association. & DSM-IV., 1994). The hyperactive component of ADHD may in fact be driven by motor impulsivity, or an unfocused motor drive that cannot be constrained. This is not a core behavioral feature of PD patients with behavioral addictions.

In addition to measures of motor impulsivity, risky decisions, defined within a behavioral economics framework (Djamshidian et al., 2010; Rao et al., 2010; Voon, Gao, et al., 2011) have shown inconsistent differences between PD groups with and without addictions. While one often associates risk with impulsivity, this is driven by the use of self -report measurements to assess risk (Eysenck & Eysenck, 1977). Risk, as assessed by questionnaires, is often framed as activities which can lead to physical harm to oneself. This type of risk is not clearly related to risk as it is defined in behavioral economics, which defines risk as increased subjective value of larger rewards relative to smaller rewards. When larger rewards are valued more, gambles that offer low probabilities of obtaining large rewards will be preferred to gambles offering higher probabilities of smaller rewards, when matched for linear utility. These effects of nonlinear subjective values are also present in temporal discounting tasks, although being risk prone would actually make one favor delayed rewards, which have larger values (Pine, Shiner, Seymour, & Dolan, 2010). Separating these in temporal discounting tasks is difficult for technical reasons, although this has been pursued (Pine et al., 2010).

Standard 2-armed bandit reinforcement learning tasks have also yielded inconsistent results, often reporting no overall differences in PD groups (Djamshidian et al., 2010; Housden et al., 2010; Voon, Pessiglione, et al., 2010). These studies have, however, found medication (i.e. treated patients on vs. acutely off their medication) related changes in the way positive vs. negative reinforcement are integrated. The medication effects have been inconsistent across studies (Djamshidian et al., 2010; Djamshidian, O’Sullivan, Lees, et al., 2012; Voon, Pessiglione, et al., 2010) perhaps due to differences in reward schedules across experiments. For example, in the study of Voon et al., learning from positive feedback was related to the average learning rate across both positive and negative outcomes in a condition in which one stimulus was rewarded 80% of the time and one stimulus was rewarded 20% of the time. Learning from negative feedback in the same study was defined as the average learning rate across positive and negative outcomes when one stimulus led to a loss 80% of the time, and one stimulus led to a loss 20% of the time. In contrast to this in the study by Djamshidian et al. (2010), learning from positive feedback was defined as the learning rate from positive outcomes (i.e. you won with a gain of 10 pence) and the negative learning rate was defined as the learning rate from negative outcomes (which was a loss of 5 pence) for pairs of stimuli averaged across 65/35 and 75/25 reward schedules. These are likely important differences, and they may account for the discrepancies between these studies. In addition to this, recent work has also shown that medication (i.e. off vs. on medication) related changes in choice behavior which had originally been attributed to differences in learning (Frank, Seeberger, & O’Reilly R, 2004), are actually due to differences in choices over already learned values, with no actual effects on learning (Shiner et al., 2012). As our previous studies have focused on learning related effects (Djamshidian et al., 2010; Djamshidian, O’Sullivan, Lees, et al., 2012), our results are consistent with this. This suggests that relative reward estimates between a pair of stimuli are thought to be intact in PD patients with behavioral addictions. Furthermore, and consistent with our hypothesis, neither risk based decision making nor 2-armed bandit reinforcement learning tasks are structured such that current choices affect future choices. Thus, we would not predict that they would differentiate these groups.

Neural circuits that may underlie group differences

Although dopamine agonists appear to play an important causal role in behavioral addiction in PD, the neural circuits that are affected, and how they are affected, are not yet clear. Moving forward, it will be important to identify these in detail. There has been a long-standing hypothesis that frontal cortical areas exert an inhibitory influence on behavior (Milner, 1963; Mishkin, 1964) and current theories of behavioral control suggest that behavioral addictions arise from disrupted frontal inhibitory control of striatal or basal ganglia circuits (Cilia et al., 2011; Dalley, Everitt, & Robbins, 2011). Studies of temporal discounting consistently implicate a circuit composed of the ventral striatum, the ventral-medial prefrontal cortex and the posterior cingulate in representing the values of available options (Kable & Glimcher, 2007, 2010; McClure, Laibson, Loewenstein, & Cohen, 2004; Pine et al., 2009). While these studies show that values estimated under a discounted utility model correlate with activation in these structures, they do not provide insight into why some groups value immediate rewards more than others. Early work on this task suggested different networks for evaluation of immediate vs. delayed rewards (McClure et al., 2004). This would be consistent with a cortical representation of delayed rewards and a striatal representation of immediate rewards. This work has, however, not replicated (Kable & Glimcher, 2010). Thus, fMRI studies of temporal discounting tasks have not provided clear evidence that separate networks evaluate immediate vs. delayed rewards. One study has, however, suggested that inactivating lateral-prefrontal cortex with rTMS can increase temporal discounting, increasing choices for smaller immediate rewards (Figner et al., 2010). Imaging studies of the novelty task have similarly suggested that the ventral striatum is important for prediction error calculations in that task (Wittmann et al., 2008), suggesting that unfamiliar, novel choice options have increased value, and that prediction errors calculated under this assumption are represented in the ventral striatum.

Functional imaging of the beads task has shown that the decision to stop sampling information and guess an urn activates a reward anticipation network composed of the ventral striatum, anterior insula, anterior cingulate and parietal cortex (Furl & Averbeck, 2011). Further, a between subjects analysis in this study suggested that subjects that sampled more information before making a decision had stronger activation in lateral prefrontal and parietal cortex. Value estimates in this task correlated with activation in the insula, but not the ventral striatum. Thus, a parietal-frontal network appears to interact with a network which includes the ventral striatum, engaged at the time of the decision to stop sampling information.

Consistent with the work in healthy subjects implicating frontal-striatal networks in these tasks to various degrees, imaging studies in PD patients with and without behavioral addictions has also suggested that cortical-striatal interactions, specifically between the anterior-cingulate and the striatum, are disrupted (Cilia et al., 2011). Other studies have also shown effects of interactions between medication (off vs. on) and group on responses to feedback in learning tasks (Voon, Pessiglione, et al., 2010) and risk in gambling tasks (Rao et al., 2010; Voon, Gao, et al., 2011) that localized to the ventral striatum. Complementing the fMRI work, PET studies have also shown that PD patients with behavioral addictions have increased dopamine levels in the striatum relative to PD patients without behavioral addictions in response to reward related cues (O’Sullivan et al., 2011), gambling (Steeves et al., 2009), L-dopa administration (Evans et al., 2006) as well as decreased ventral striatal DAT levels (Cilia et al., 2010). Combined, these imaging results are consistent with a disruption in the interaction between a lateral, parietal-frontal cortical circuit that guides information accumulation that can be used to inform future decisions, and immediate value representations in ventral-medial PFC and the ventral striatum.

Conclusion

The present study provides a consistent interpretation of behavioral results across three studies. Previous work has shown that PD patients with behavioral addictions differ from PD patients without behavioral addictions on temporal discounting, information sampling and novelty preference. The modeling results suggest that PD patients with behavioral addictions may differ from other PD patients on a single behavioral dimension. Specifically, the group with behavioral addictions behaves as if they cannot use information to generate useful beliefs about actions that will result in future rewards. Additional experiments, effectively additional information sampling, will increase or decrease belief in this hypothesis.