Contour-Driven Regression for Label Inference in Atlas-Based Segmentation

Abstract

We present a novel method for inferring tissue labels in atlas-based image segmentation using Gaussian process regression. Atlas-based segmentation results in probabilistic label maps that serve as input to our method. We introduce a contour-driven prior distribution over label maps to incorporate image features of the input scan into the label inference problem. The mean function of the Gaussian process posterior distribution yields the MAP estimate of the label map and is used in the subsequent voting. We demonstrate improved segmentation accuracy when our approach is combined with two different patch-based segmentation techniques. We focus on the segmentation of parotid glands in CT scans of patients with head and neck cancer, which is important for radiation therapy planning.

1 Introduction

Atlas-based segmentation extracts information from image collections with manually labeled images to facilitate the automatic segmentation of new images. Methods that use atlas information can be broadly classified into two groups. The first group employs deformable registration to align atlas images to the novel scan [6,10]. The estimated deformation fields propagate labels from the atlas to the new image. The second group searches for image patches most similar to the voxel neighborhood [4,11]. Since similar patches tend to share the segmentation label, weighted voting based on patch similarity promises to produce accurate segmentation.

High anatomical variability presents a serious challenge for atlas-based segmentation. Registration approaches often fail to warp structures that vary significantly in shape due to regularization constraints. Such inaccuracies cause segmentation errors at the boundaries. Patch-based approaches also experience difficulties in correctly segmenting regions close to the boundaries. Fig. 1 illustrates this problem for a patch-based segmentation of the left parotid gland. To further investigate the source of errors, we examine patches in the atlas that are the most similar to the one example patch in the image. According to the manual labeling, the selected patch belongs to the left parotid gland. However, all of the closest patches vote for background, yielding a wrong result. Such errors are not surprising because it is possible that patches have a very similar appearance overall but vary slightly in the center. Such variations are especially problematic close to organ boundaries, where they can cause segmentation errors.

Fig. 1.

Left: CT image with segmentation of left parotid (yellow: manual, red: patch-based). Right: Magnification of the blue patch (top) with manual segmentation (bottom). The four most similar patches in the repository vote for background (black at the center location), although the patch belongs to the left parotid. Intensity values of patches are normalized for visualization.

We present a new probabilistic approach to atlas-based segmentation to incorporate image contour information into the decision on segmentation labels. We achieve this by defining an image-specific distribution over label maps based on Gaussian processes. We employ the concept of intervening contours [1] to construct contour-driven covariance functions. A robust contour estimation is obtained by calculating image and texture gradients on multiple scales. Conditioning the distribution over label maps on the atlas information results in label maps that are consistent with image contours while also accommodating the label maps proposed by the atlas. We experiment with two patch-based segmentation approaches to obtain the initial label maps that serve as input to our algorithm.

We evaluate our approach by segmenting parotid glands in CT scans of patients with head and neck cancer. Radiation therapy motivates our work. Radiation therapy planning aims to maximize the dose in the target region while minimizing the radiation dose in the surrounding tissue. Intensity modulated radiation therapy allows the more effective administration of the radiation dose to reduce the damage to healthy cells. During the planning phase, experts delineate most critical structures, also called organs at risk, to ensure low radiation in these regions. The parotid glands are organs at risk for head and neck cancer treatment because they are the most important salivary glands. Irradiation of the parotid glands can lead to xerostomia, resulting in difficulties for mastication, deglutition, and speech of the patients. Automatic segmentation is challenging due to low soft-tissue contrast in CT images and high anatomical variability.

1.1 Related Work

Our work builds on previously mentioned atlas-based segmentation methods and is related to algorithms for label refinement. Spectral label fusion [14] extracts superpixels from the image to perform region-based voting. It further relates to an approach for the refinement of atlas propagation with graph cuts [12]. Regression has been previously used to estimate correlations of errors for atlas-based segmentation [15]. Our probabilistic approach uses Gaussian processes, which arise in numerous fields of machine learning [9]. In [13], Gaussian processes were applied for image segmentation of natural images. In contrast to our work, the identity covariance function was used, samples from the process are thresholded, and no atlas information is available.

Atlas-based segmentation of parotid glands with deformable registration was demonstrated in [5,8]. In [3], the atlas images are used for training an active shape model of parotid glands. The refinement of head and neck segmentations based on classification with features was proposed in [7].

2 Method

Given a novel image I, we aim to infer segmentation S based on an atlas that contains images $\mathcal{I}=\{I_1,\dots ,I_n\}$ and segmentations $\mathcal{S}=\{S_1,\dots ,S_n\}$. A probabilistic label map L = {L¹, …, L^m} specifies the likelihood for each label l ∈ {1, …, m}, i.e., $L^l\left(x\right)=p\left(S\right(x)=l\mid I,\mathcal{I},\mathcal{S})$ and serves as an intermediate segmentation result. The estimated segmentation $\widehat{S}$ at voxel x is obtained by choosing the label with highest probability at voxel x. A perfect label map assigns probability one to the correct label for each location. Atlas-based methods produce label map L_o, which might be susceptible to errors, motivating the model $L_o^l=L^l+\epsilon$, where L^l is the underlying true label map for label l. Under the assumption of independent and identically distributed noise, we have $L_o^l\left(x\right)=L^l\left(x\right)+\epsilon \left(x\right)$ for all locations x in the image, with $\epsilon ~\mathcal{N}(0,{\sigma }^2)$. The assumption of independent Gaussian noise may interfere with the normalization requirements $\left({\Sigma }_l{L}_o^l\right(x)=1\text{and}0\le L_o^l(x)\le 1)$, which can be satisfied with a subsequent normalization step. In our application, this is not necessary because we decide on the segmentation based on the maximal value across label maps. We drop the label index l in the following discussion, to simplify notation.

2.1 Atlas-Based Segmentation

We briefly review two atlas-based segmentation methods we use to obtain the initial label map L_o. We focus on patch-based approaches because they are well suited to handle the high variability of parotid glands. Further, standardized intensity values of CT images make patches comparable across subjects. Prior to segmentation, we define regions of interest (ROI) that surround the parotid glands to restrict the search. Such regions could be obtained from a coarse registration. We exploit the knowledge that the parotid glands are adjacent to the mandible bone, which we detect with a simple template matching method.

The first baseline method is the non-local means (NLM) segmentation [4,11]. For each location x within the ROI, we create the surrounding patch P_x of size 7 × 7 × 3 and retrieve the N = 10 closest patches $\mathcal{P}$ with corresponding labels $\mathcal{L}$ from the repository. The label map is obtained as a weighted sum [4]:

$$L_o\left(x\right)=\frac{\sum _{i=1}^N{w}_{i,x}{\mathcal{L}}_i}{\sum _{i=1}^N{w}_{i,x}}\text{with}{w}_{i,x}=\exp \left(-\frac{\Vert {\mathcal{P}}_i-P_x{\Vert }_2^2}{{\min }_j\Vert {\mathcal{P}}_j-P_x{\Vert }_2}\right).$$ (1)

The second approach uses a random forest classifier [2] to predict the segmentation label L_o(x) for each location in the ROI. In contrast to NLM labeling, the classifier has to be trained first. In our experiments, we randomly select six patients for training. We train different classifiers for left and right parotid glands on patches selected from the ROI. We choose 500 trees per random forest with 12 predictors sampled for splitting at each node.

2.2 Gaussian Process Regression for Label Inference

Our approach to inferring the latent label map L from L_o employs a distribution over label maps p(L). In contrast to most atlas-based methods that make decisions at each voxel separately and do not consider contour information, we choose a label distribution that models the relationship between locations, exploiting the contour information in image I. Stochastic processes offer a versatile framework to model interactions between possibly infinite number of random variables. We view label maps as realizations from a Gaussian process, $L~\mathcal{G}\mathcal{P}(m,k)$, with mean m and covariance k. Gaussian processes are entirely characterized by mean and covariance functions and have the property that every finite subset is distributed according to a multivariate Gaussian distribution [9].

To obtain the posterior distribution over label maps, we condition the distribution of label maps L on the labels L_o implied by the atlas:

$$p(L\mid L_o)~\mathcal{N}(\mu ,\Sigma )$$ (2)

with mean and covariance

$$\mu =\mathbf{m}+K\cdot {[K+{\sigma }^2\mathbf{I}]}^{-1}\cdot (L_o-\mathbf{m}),$$ (3)

$$\Sigma =K-K\cdot {[K+{\sigma }^2\mathbf{I}]}^{-1}\cdot K,$$ (4)

where I is the identity matrix and σ² is the noise variance. The mean vector m and the kernel matrix K are constructed from the mean function m and kernel function k, respectively. We use the Cholesky factorization for the matrix inversion. The maximum a posteriori label map coincides with the mean label map for Gaussian distributions, $L^{\text{MAP}}=\arg {\max }_{L}p(L\mid L_o)=\arg {\max }_L\mathcal{N}(L;\mu ,\Sigma )=\mu$. Performing this estimation for all labels yields segmentation:

$$\widehat{S}\left(x\right)=\arg \underset{l}{\max }{\mu }^l\left(x\right).$$ (5)

The mean function m causes a constant additive shift of all label maps μl and therefore does not influence the segmentation result $\widehat{S}$, motivating the choice of m = 0. Fig. 2 illustrates the key steps of the segmentation process.

Fig. 2.

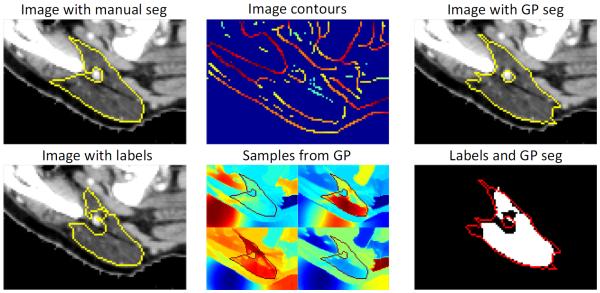
Gaussian process segmentation of parotid gland. The initial label from the atlas-based segmentation only partially agrees with the manual segmentation. We extract contours from the image and use them in the kernel function k that allows us to sample label maps $L~\mathcal{G}\mathcal{P}(0,k)$, supported by the image. Conditioning these on the atlas labels results in an improved segmentation.

2.3 Contour-Driven Distributions over Label Maps

The distribution over label maps p(L) is determined by the covariance or kernel function k. We seek label maps that are supported by intensity and texture features in the input image I. In the first step, we estimate image and texture gradients per slice with the oriented gradient signal, following closely the construction in [1]. This method calculates the χ² distance between the histograms of two half-discs at each location for various orientations and at multiple scales. Textons are calculated to quantify the texture by convolving the image with 17 Gaussian derivative and center-surround filters and subsequently clustering with K-means into 64 classes [1]. Image and texture gradients of multiple scales are added to yield the multi-scale contour Γ. We use the contour information to calculate weights between in-plane points x and x′, following the concept of intervening contours [1] by identifying the maximum response along the line $\overline{x{x}^{\prime }}$:

$$k(x,x^{\prime })=\exp \left(-\underset{y\in \overline{x{x}^{\prime }}}{\max }\left\{\Gamma \right(y\left)\right\}∕\rho \right).$$ (6)

We set the scale parameter to ρ = 0.1 and only consider locations within the ROI that are at most 20 pixels away from each other, giving rise to sparse kernel matrices. High weights are assigned to pairs of points that are not separated by a contour and these points are subsequently encouraged to share the same label.

Fig. 2 shows samples drawn from the prior distribution p(L), where we have overlaid the manual segmentation for reference. We observe that the prior promotes label maps that follow image structures. In this example, labels are propagated to the thin ends of the left parotid gland, which improves the segmentation in comparison to the initial labeling.

3 Experiments

We evaluate the method on 16 CT scans of patients with head and neck cancer. Each image was labeled by a trained anatomist for treatment planning. Images contain between 80 and 200 axial slices with a slice thickness of 2.5mm. The in-plane resolution is 0.9mm, slice size is 512 × 512 pixels. All 16 images have the left parotid gland labeled. The right parotid gland was consumed by a tumor in one patient. Experiments are performed on 10 datasets for left parotid gland and 9 datasets for right parotid gland that have not been selected for training the RF classifiers. We quantify the segmentation quality by calculating the Dice volume overlap score and modified Hausdorff distance between the automatic and manual segmentations. We compare our method to spectral label fusion (SLF) [14], which was previously demonstrated to refine segmentations based on image contours.

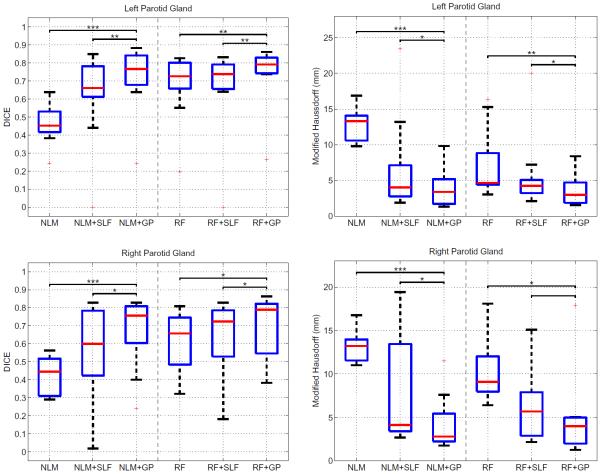
Fig. 3 presents the results for both parotid glands for different algorithms and σ² = 1. Non-local means (NLM) and random forests (RF) serve as initial label maps. The segmentation with NLM leads to many false positives, causing worse performance than RF. Applying spectral label fusion improves the segmentation results. The Gaussian process (GP) segmentation achieves the significantly best results in our experiments. A reason for the improvement of GP in comparison to SLF is that SLF votes on small image regions. If these regions are not well defined or if the baseline segmentation algorithm cannot gather enough votes in a region, this can cause large errors. The outlier of zero dice overlap for NLM+SLF of the left parotid illustrates this case. Fig. 4 shows example results for all methods.

Fig. 3.

Dice volume overlap and modified Hausdorff distance for left and right parotid glands. Red line indicates the median, the boxes extend to the 25^th and 75^th percentiles, and the whiskers reach to the most extreme values not considered outliers (red crosses). *, **, and *** indicate significance levels at 0.05, 0.01, and 0.001. For each baseline method (NLM, RF), the performance of the basic method, the variant that employs spectral label fusion (SLF) [14] and the variant based on Gaussian processes proposed here (GP) is reported.

Fig. 4.

Examples of automatic segmentation results for different methods are shown in yellow. Manual delineations are shown in red.

4 Conclusion

We proposed a novel probabilistic approach for improving atlas-based segmentation. The key contribution is a contour-driven distribution over label maps that is supported by features in the image. We employ Gaussian process regression to obtain MAP estimates of label maps, on which the voting is performed. The initial label map is estimated with two different patch-based segmentation approaches, non-local means segmentation and random forest classification. Our experiments in segmentation of the parotid glands show improved performance when the proposed method is used to refine the atlas-based label maps.