EVALUATING COSTS WITH UNMEASURED CONFOUNDING: A SENSITIVITY ANALYSIS FOR THE TREATMENT EFFECT

Abstract

Estimates of the effects of treatment on cost from observational studies are subject to bias if there are unmeasured confounders. It is therefore advisable in practice to assess the potential magnitude of such biases. We derive a general adjustment formula for loglinear models of mean cost and explore special cases under plausible assumptions about the distribution of the unmeasured confounder. We assess the performance of the adjustment by simulation, in particular, examining robustness to a key assumption of conditional independence between the unmeasured and measured covariates given the treatment indicator. We apply our method to SEER-Medicare cost data for a stage II/III muscle-invasive bladder cancer cohort. We evaluate the costs for radical cystectomy vs. combined radiation/chemotherapy, and find that the significance of the treatment effect is sensitive to plausible unmeasured Bernoulli, Poisson and Gamma confounders.

1. Introduction

Payers and health care providers, such as Medicare, private insurers and hospitals, routinely collect data on medical expenditures [Hornberger and Wrone (1997)]. Some of these data sources are readily available and have high external validity [Black (1996)] and therefore are widely used to compare treatment costs. Like all observational data, however, they are subject to confounding. That is, if all relevant confounders are measured and present in the data set, we can find a consistent estimate of the treatment effect by using a correctly specified statistical model for cost. If some confounders are unmeasured or unavailable, the model-based estimate is potentially biased. Here we develop a method to assess the sensitivity to potential unmeasured confounders when evaluating the effect of a medical intervention on mean cost.

Cost data are nonnegative and often highly skewed, features that can be readily described statistically in the generalized linear model framework. For example, a Gamma regression with a log link is often a suitable model for cost data [Dodd et al. (2006)]. The situation is more complex when some costs are censored. Costs accrue over time, and they may accrue at different rates among individuals. Therefore, cost at the time of censoring is generally correlated with cost at the time of ultimate failure, making censoring informative [Etzioni et al. (1999), Lin et al. (1997)]. One popular method which accounts for this is Inverse Probability Weighting (IPW), where observed costs are weighted by the inverse probability of censoring [Lin (2000, 2003), Bang and Tsiatis (2000, 2002), Tian and Huang (2007), Willan et al. (2002)]. In the context of observational cost data, the method of Lin (2003) is particularly useful. He applies IPW to generalized linear models, allowing adjustment for confounders in a Gamma regression. Other approaches which handle informative censoring are based on Bayesian methods or use multi-part models [Basu and Manning (2010), Heitjan, Kim and Li (2004), Liu (2009), Liu, Huang and O’Quigley (2008)].

The methods cited above do not address the potential bias due to unmeasured confounding. A natural approach to evaluate this bias is a sensitivity analysis, in which one posits models for the distribution of an unmeasured confounder and its effects on cost, then evaluates their effects on estimates of the treatment effect. Researchers have developed various methods implementing this idea [Axelson and Steenland (1988), Flanders and Khoury (1990), Gail, Wacholder and Lubin (1988), Hosman, Hansen and Holland (2010), McCandless, Gustafson and Levy (2007), Rosenbaum and Rubin (1983a), Schlesselman (1978), Yanagawa (1984)]. Further developments include the method of Lin, Psaty and Kronmal (1998), in which the authors present a formula to determine the magnitude of the bias due to an unmeasured Bernoulli or Normal covariate. Mitra and Heitjan (2007) extended this idea to assess the sensitivity of survival outcomes using a Weibull model.

As we have indicated, the method of Lin, Psaty and Kronmal (1998) assesses the sensitivity of the treatment effect to unknown binomial or normal confounders. Wang and Krieger (2006) have shown that in a matched pairs study, conclusions are most sensitive to a Bernoulli confounder and, thus, such an analysis is sufficient to describe maximal sensitivity. It is unclear whether an analogous result holds in cohort studies, however, or indeed whether the exploration of maximal sensitivity is most desirable in every context. Therefore, in this paper we generalize the Lin method to derive corrections for a broader range of distributions of unmeasured confounders. For example, applying our formula for a Gamma confounder, one can adjust for an unmeasured skewed continuous variable such as personal income. Or using our formula for a Poisson confounder, one can adjust for an unmeasured count variable such as pack-years smoked.

A major drawback of the Lin method and related sensitivity analyses for the effects of an unmeasured confounder is the assumption of independence between measured and unmeasured confounders given treatment status. Hernán and Robins (1999) demonstrated that such an assumption is implausible, as conditioning on treatment induces a correlation even between unrelated covariates. VanderWeele (2008) showed how one of Lin’s formulas can apply in certain circumstances with relaxed assumptions, and VanderWeele and Arah (2011) developed bias adjustment formulas that are valid more generally without requiring conditional independence. The implementation of these approaches can be complex, however, and a simpler alternative such as the Lin method would be invaluable in applications. In this paper, therefore, we both extend the basic Lin method to a range of loglin-ear models and use simulations to explore the limits of its validity under departures from conditional independence.

We demonstrate our method with a comparison of mean medical costs for two treatments for stage II/III muscle-invasive bladder cancer. As this is the ninth costliest cancer [National Cancer Institute (2011)], it is of substantial interest to determine cost-effective treatments for it. Here, we compare the lifetime costs for radical cystectomy, an aggressive surgical procedure that is the current standard of care, to combined radiotherapy and chemotherapy, an alternative organ-sparing curative treatment. The data are censored because many registry participants were still living when the database was closed. We base our cost comparisons on observational data from the linked SEER-Medicare registry, assessing the sensitivity of the treatment effect to potential Bernoulli, Poisson and Gamma unmeasured confounders.

The paper is organized as follows: in Section 2 we develop a general formula to quantify the magnitude of the bias of treatment effect due to an unknown confounder, and derive the correction for Poisson and Gamma confounders. We further show how these formulas and those of Lin et al. [Lin, Psaty and Kronmal (1998)] can be used to assess sensitivity with cost data, including censored costs. We specifically address criticisms that have been raised of the assumption of conditional independence of observed and unobserved covariates given treatment. In Section 3 we assess the performance of our method using Monte Carlo simulations, evaluating robustness to departures from conditional independence. In Section 4 we apply our method to the SEER bladder cancer data.

2. Bias with an unmeasured confounder

We first consider uncensored costs. Assuming a generalized linear model (GLM) with a log link, we define the true model as

$$\mathrm{E}(Y\mid X,Z,U)=exp(\alpha +{\beta }_{0}X+{\phi }_{0}U+{\psi }_{1}XU+{\theta }^{\prime }Z),$$

where Y is the total cost, X is the treatment of interest (X = 0 for control and X = 1 for treated), U is the unmeasured confounder and Z is a vector of measured covariates. The true regression parameters are α, β₀, θ, φ₀ and ψ₁. We allow the unmeasured confounder U to have different effects on cost in the treatment groups, so β₀ is the effect of X when U = 0, and β₀ + ψ₁ is the effect of X when U is nonzero. Likewise, φ₀ is the effect of U in the control group, and φ₀ + ψ₁ is the effect of U in the treated group. For convenience, we express the model as

$$\mathrm{E}(Y\mid X,Z,U)=exp(\alpha +{\beta }_{0}X+{\gamma }_{X}U+{\theta }^{\prime }Z).$$ (1)

This is equivalent to the model specified above, where γ₀ is the effect of U in the control group and γ₁ is the effect of U in the treated group. For simplicity, we henceforth suppress the subscript in β₀.

In practice, we cannot fit model (1) because we do not know the value of U. We define the reduced model, which we can fit, as

$$\mathrm{E}(Y\mid X,Z)=exp({\alpha }^{\ast }+{\beta }^{\ast }X+{{\theta }^{\ast }}^{\prime }Z).$$ (2)

Fitting model (2) yields an estimate of the apparent treatment effect β^*.

By conditional expectation,

$$\begin{array}{l}\mathrm{E}(Y\mid X,Z)={\int }_{-\infty }^{\infty }\mathrm{E}(Y\mid X,Z,U)dF(U\mid X,Z)\\ =exp(\alpha +\beta X+{\theta }^{\prime }Z){\int }_{-\infty }^{\infty }exp({\gamma }_{X}U)dF(U\mid X,Z)\\ =exp(\alpha +\beta X+{\theta }^{\prime }Z)M_{U\mid X,Z}({\gamma }_X),\end{array}$$

where M_{U |X,Z} (γ_X) is the moment generating function (m.g.f.) of U |X, Z. If we assume that U is conditionally independent of Z given X so that M_U|X,Z (γ_X) = M_U|X(γ_X), the following simplification is possible:

$$\mathrm{E}(Y\mid X,Z)=exp\left(\alpha +ln\left({\mathrm{M}}_{U\mid 0}({\gamma }_0)\right)+X\left[\beta +ln\left({\mathrm{M}}_{U\mid 1}({\gamma }_1)\right)-ln\left({\mathrm{M}}_{U\mid 0}({\gamma }_0)\right)\right]+{\theta }^{\prime }Z\right).$$ (3)

Setting (2) equal to (3) gives

$$\beta ={\beta }^{\ast }-ln\left({\mathrm{M}}_{U\mid X=1}({\gamma }_1)\right)+ln\left({\mathrm{M}}_{U\mid X=0}({\gamma }_0)\right).$$ (4)

Thus, we can conduct a sensitivity analysis by positing distributions for U |X and values for γ_X in the treated and control groups. Equation (4) holds for any distribution of U that one can characterize by a moment-generating function, a large class of distributions. In the following sections we show the solutions for β when U is distributed as Poisson or Gamma. We also present the formulas developed by Lin, Psaty and Kronmal (1998) for Bernoulli and Normal unmeasured confounders, and show how they are applicable in the cost setting.

2.1. Poisson unmeasured confounder

For U ~ Poisson(λ_X,Z), we have

$${\mathrm{M}}_{U\mid X,Z}({\gamma }_X)=exp\left({\lambda }_{X,Z}\left(e^{{\gamma }_X}-1\right)\right),$$

and under conditional independence (λ_X,Z = λ_X), (4) becomes

$$\beta ={\beta }^{\ast }-\left({\lambda }_1{e}^{{\gamma }_1}-{\lambda }_0{e}^{{\gamma }_0}+{\lambda }_0-{\lambda }_1\right),$$

where λ₀ is the mean of U in the control group and λ₁ is the mean in the treated group, β is the true treatment effect, β^* is the observed treatment effect, and γ₀ and γ₁ are the effects of U in the control and treated groups, respectively.

2.2. Gamma unmeasured confounder

An unobserved covariate

$$U~\text{Gamma}({\theta }_{X,Z},{\kappa }_{X,Z})$$

has m.g.f.

$${\mathrm{M}}_{U\mid X,Z}({\gamma }_X)={(1-{\theta }_{X,Z}{\gamma }_X)}^{-{\kappa }_{X,Z}}.$$

Under conditional independence (θ_X,Z = θ_X, κ_X,Z = κ_X), (4) implies

$$\beta ={\beta }^{\ast }-ln\frac{{(1-{\theta }_0{\gamma }_0)}^{{\kappa }_0}}{{(1-{\theta }_1{\gamma }_1)}^{{\kappa }_1}},$$

where the mean and variance of U are κ₀θ₀ and ${\kappa }_0{\theta }_0^2$ for the control group and κ₁θ₁ and ${\kappa }_1{\theta }_1^2$ for the treated group.

2.3. Bernoulli and Normal unmeasured confounders

Lin, Psaty and Kronmal (1998) derived the relationship between the true and apparent treatment effects for a binary outcome with a log link when unmeasured confounders are Bernoulli or Normal. Because the derivation also applies to a continuous outcome with a log link, their results are special cases of (4). Specifically, if U ~ Bernoulli(π_X,Z), and U is conditionally independent of Z (π_X,Z = π_X), then

$$\beta ={\beta }^{\ast }-ln\frac{e^{{\gamma }_1}{\pi }_1+(1-{\pi }_1)}{e^{{\gamma }_0}{\pi }_0+(1-{\pi }_0)},$$

where π₀ is the prevalence of U in the control group, π₁ is the prevalence of U in the treated group, and the other parameters are as above. Similarly, if U ~ Normal(μ_X,Z, 1) and again is conditionally independent of Z (μ_X,Z = μ_X), then

$$\beta ={\beta }^{\ast }+\left({\mu }_0{\gamma }_0-{\mu }_1{\gamma }_1+\left({\gamma }_0^2-{\gamma }_1^2\right)/2\right),$$

where μ_j is the mean of U in treatment group j, j = 0, 1, and β, β^*, γ₀ and γ₁ are as above.

2.4. Assumption of conditional independence

The conditional independence assumption (that U is conditionally independent of Z given X) cannot be tested in practice since U is not observed. However, it has been well-established that the assumption cannot actually hold in practice. Conditional independence would hold if the marginal correlation perfectly cancels the conditional correlation or if the covariates Z are not truly confounders, but either condition is highly improbable. Hernán and Robins (1999) observed that conditional independence cannot hold if Z and U are marginally independent and are both confounders. VanderWeele (2008) showed that closed-form solutions are available for normal unmeasured confounders and for a binary confounder with a normal outcome under a relaxed additivity assumption. VanderWeele and Arah (2011) developed general formulas for calculating an adjusted estimate of the treatment effect without assumptions about the relationship between the measured and unmeasured covariates. In the most general case one must specify E(Y) at each level of X, U and Z. When U or Z is continuous, this would be very difficult to implement in practice. For the case where the relationship between Y and U is constant across levels of Z, as would occur in a linear model, VanderWeele and Arah (2011) developed simplified formulas that require fewer sensitivity parameters. In our loglinear regression setting, however, an additional bootstrapping approach would be required to use these formulas.

Although we do not expect our corrections to hold exactly in practice due to weak tenability of the conditional independence assumption, if conditional dependence is modest, they may still be useful. In Section 3.2 we present simulations to investigate the effect of dependence within treatment strata.

2.5. Analysis with censored costs

We derived our adjustment formulas assuming uncensored data; nevertheless, because they are statements about parameters, they are valid also in the censored case provided that one estimates the parameters consistently. Lin (2003) developed a generalized regression method, appropriate for censored costs, that combines the generalized estimating equation approach with inverse probability of censoring weighting. This approach produces consistent estimates but forfeits efficiency because it uses only the uncensored data. Bang and Tsiatis (2002) developed a more efficient estimator for linear regression that uses all of the data, but an extension to the GLM has yet to be developed. We therefore recommend using the Lin (2003) approach, but note that our formulas are applicable with any method that gives consistent estimates for a loglinear mean model.

2.6. Sensitivity analysis for cost regression

The sensitivity analysis proceeds in four steps: first, estimate β^* in (2) by any consistent method. Second, specify the type of the unmeasured confounder: for example, Poisson for a count confounder; Gamma for skewed, positive continuous; Normal for symmetric continuous; and Bernoulli for binary. Third, hypothesize possible parameter values η for the distributions of the unmeasured confounder in the treated and control groups, and also the possible effect γ of the unmeasured confounder on cost. Finally, apply the correction via (4) to obtain β̂, the adjusted treatment effect.

The analysis assumes that the sensitivity parameters η are known. Because the adjustment is in every case additive, it follows that

$$\text{Var}(\widehat{\beta }\mid X,Z,\eta )=\text{Var}({\widehat{\beta }}^{\ast }\mid X,Z).$$

We use this relationship to calculate confidence intervals and determine the significance of the adjusted treatment effect, as was done by Lin, Psaty and Kronmal (1998), Mitra and Heitjan (2007) and VanderWeele and Arah (2011). Note that this does not imply that Var(β̂|X, Z, U) = Var(β̂^*|X, Z). If we were able to measure U, the variance of our estimate of β would be smaller, however, our correction does not reduce the uncertainty of our estimate, only the bias. Therefore, the appropriate variance estimate for the corrected β̂ is Var(β̂^*|X, Z). We confirm this via simulation in Section 3.1 where we show that coverage probabilities are close to the nominal level, indicating that Var(β̂^*|X, Z) is a reasonable estimate for the variance of the corrected treatment effect.

The investigator should repeat this procedure for a range of combinations of parameter values and effect sizes, assessing the plausibility of any combination of inputs that materially changes the conclusions. If the significance of the treatment effect changes due to unmeasured confounders with a small effect on cost and similar distributions in the treated and control groups, one can conclude that inferences are vulnerable to the effects of unmeasured confounding. We demonstrate the procedure in Section 4.

3. Simulations

The general plan of the simulations was to generate costs knowing the values of both measured and unmeasured covariates, then fit the reduced regression omitting the unmeasured covariate and compute the adjusted treatment effect. We evaluated performance by the bias of the adjusted estimate and the coverage probability of the resulting 95% confidence interval.

3.1. Method performance

Initial simulations evaluated the performance of the method under independence of the unmeasured confounder U and measured confounder Z given treatment status X. We constructed 1000 replications in each simulation, with 100, 200 and 500 subjects per treatment stratum. We drew U independently from its distribution f_U (U |X, η_X) using the parameter values η_X shown in Table 1. For example, a Poisson unmeasured confounder was Poisson(λ = 1) in the control group and Poisson(λ = 1.58) in the treated group. We next drew a scalar measured confounder Z, which can represent either a single confounder or a linear combination of a vector Z. Each Z was an independent draw from a Normal distribution with variance 1 and mean 0 in the control group and mean 1 in the treated group. We computed the mean cost according to (1), where α = 5, β = 1, θ = 1, and γ₀ = γ₁ = γ. We drew cost outcomes from f_Y (Y |X, Z, U), where f_Y was the Gamma with variance equal to the mean. We drew censoring indicators using a Bernoulli with varying probabilities as indicated in Table 1. We drew failure times from the Exponential with mean 5 and censoring times uniformly over [0, 10], independently of both treatment group and costs. It was only necessary to identify the subjects with censored costs, not generate their actual censored cost values, because the IPW method uses only noncensored observations [Lin (2003)]. In each replication, we calculated β̂^* from the apparent model and β̂ from the adjustment formula. For uncensored data, we used the Gamma GLM, and for censored data the IPW estimator.

Table 1.

Monte Carlo simulations of the adjusted treatment effect, n = 100 per treatment stratum

Distribution	γ	Mean of β̂† (coverage probability)
		Uncensored	25% censoring	50% censoring	75% censoring
Bernoulli⋄	0.25	0.999 (0.963)	1.001 (0.925)	1.001 (0.933)	0.997 (0.817)
	0.5	1.001 (0.958)	0.998 (0.936)	1.003 (0.885)	1.004 (0.790)
	0.75	1.000 (0.954)	1.004 (0.924)	0.999 (0.918)	1.005 (0.780)
	1	1.003 (0.946)	1.007 (0.935)	1.008 (0.909)	1.016 (0.744)
Normal*	0.25	1.001 (0.931)	0.996 (0.950)	1.000 (0.911)	1.000 (0.856)
	0.5	1.002 (0.949)	1.000 (0.950)	1.006 (0.910)	0.995 (0.841)
	0.75	1.010 (0.946)	0.994 (0.928)	1.003 (0.924)	0.983 (0.841)
	1	1.006 (0.941)	0.995 (0.923)	0.982 (0.892)	1.028 (0.815)
Poisson‡	0.25	1.002 (0.959)	1.003 (0.943)	1.001 (0.935)	0.998 (0.841)
	0.5	0.994 (0.939)	0.995 (0.936)	0.986 (0.899)	0.994 (0.804)
	0.75	0.981 (0.924)	0.979 (0.892)	0.965 (0.873)	0.895 (0.768)
	1	0.925 (0.894)	0.922 (0.850)	0.877 (0.828)	0.811 (0.758)
Gamma△	0.25	1.001 (0.957)	0.999 (0.948)	1.002 (0.924)	0.996 (0.855)
	0.5	0.999 (0.947)	0.997 (0.919)	0.996 (0.910)	0.997 (0.851)
	0.75	0.998 (0.951)	0.989 (0.913)	0.970 (0.893)	0.957 (0.840)
	1	0.931 (0.881)	0.908 (0.853)	0.915 (0.847)	0.882 (0.780)

^†For all models, the true value of β is 1.

^⋄Unmeasured Bernoulli covariate with π₀ = 0.3, π₁ = 0.866.

^*Unmeasured Normal covariate with μ₀ = 0, μ₁ = 1, σ₀ = σ₁ = 1.

^‡Unmeasured Poisson covariate with λ₀ = 1, λ₁ = 1.58.

^△Unmeasured Gamma covariate with κ₀ = κ₁ = 0.75, θ₀ = 0.5, θ₁ = 0.868.

Results of the simulation with 100 subjects per treatment stratum appear in Table 1. We observe that the correction worked well for Bernoulli and Normal confounders with modest censoring. As the proportion censored increased, coverage probability declined from the nominal level, although the bias remained small. For example, the treatment effect with a Bernoulli unmeasured confounder of effect size γ = 0.5 had a coverage probability of 0.96 with 0% censoring and 0.79 with 75% censoring, yet the mean of β̂ remained close to its true value of 1 regardless of censoring. The method worked well for Poisson and Gamma confounders with moderate effect sizes (γ ≤ 0.5), but as the effect of U drew close to the effect of X, the corrected β̂ incurred a bias and coverage probabilities fell below nominal levels. For example, with Gamma U and uncensored costs, if the effect of U was small (γ = 0.25), the bias of β̂ was 0% with a coverage probability of 0.96, but if the effect was large (γ = 1), the bias was −7% with a coverage probability of 0.88. Increased proportions of censoring further degraded the performance of the estimator. In the uncensored case, increasing the sample size to 2000 per treatment stratum resulted in negligible bias even for large effects (not shown). We conclude that with substantial confounding the adjusted estimates may incur bias in samples of moderate size.

With Gamma and Poisson confounders, 1%–4% of the reduced regression models failed to converge. This occurred only when U had a large effect on cost (γ ≥ 0.75). Analysis of the simulation data revealed that all true models converged, and reduced models failed only when there were single large outliers. Therefore, divergence of the reduced model may itself serve as an indicator of misspecification due to an unmeasured confounder.

3.2. Sensitivity to departures from conditional independence

A second set of simulations assessed robustness to violations of conditional independence. Following Hernán and Robins (1999) and VanderWeele (2008), we generated the treatment X conditional on the confounders. We first drew Z ~ Normal(1, 1), then U ~ f_U (U |Z = z) defined as follows: Bernoulli(π = expit(0.5 + 0.2z)); Normal(μ = 1 + 0.1z, σ = 1); Poisson(λ = 0.9 + 0.1z); or Gamma(κ = 0.5, θ = 0.65 + 0.2|z|). With these parameters the unconditional correlation between Z and U is approximately 0.1. Next, we generated X ~ Bernoulli(Pr(X = 1) = expit(φ₁ + φ₂z + φ₃u)), varying φ₁, φ₂, φ₃ to obtain different patterns of correlation. As before, we drew costs from a Gamma with mean function (1).

Figure 1 plots the bias in the corrected estimate vs. the maximum absolute within-stratum correlation (the larger of the correlations in the two treatment strata) for n = 500 under 25% censoring. We see that with correlations above 0.15, biases exceeded 5% even for moderate effect sizes, and the bias increased with the strength of U. Figure 2 plots the bias of the adjusted estimate vs. that of the unadjusted estimate, revealing that the adjustment was substantially more accurate in all cases. Figure 3 plots the coverage probability vs. the maximum absolute within-stratum correlation. We note that effects on coverage probability can be large for modest partial correlations, even when the confounder effect size is also modest.

Fig. 1.

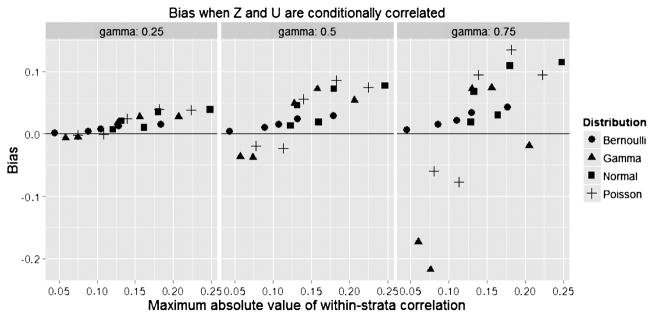
Bias of treatment effect.

Fig. 2.

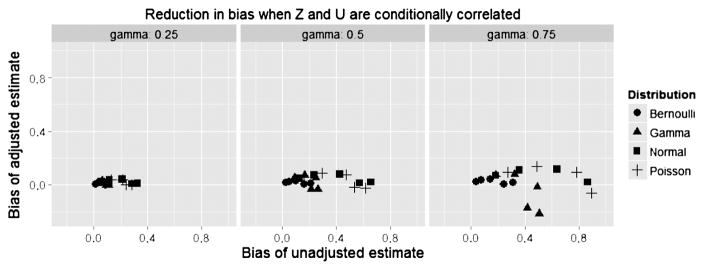
Reduction in bias from unadjusted estimate.

Fig. 3.

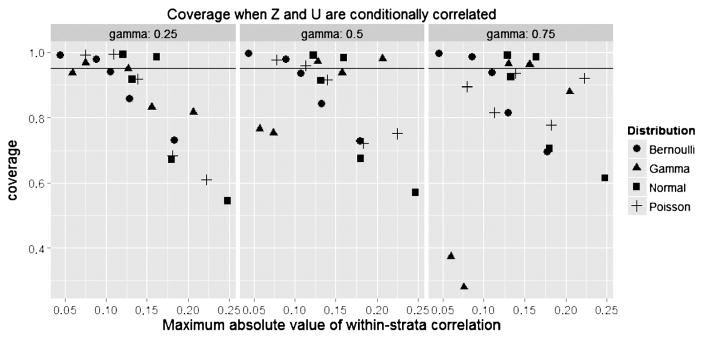
Coverage of treatment effect.

For example, consider a Bernoulli U where γ = 0.75 with φ₁ = −1, φ₂ = 1, and φ₃ = 2. For these parameters, the partial correlation of U and Z is −0.086 in the X = 1 stratum and −0.046 in the X = 0 stratum. Whereas the unadjusted estimate of β has a bias of 30.8% with 0% coverage, the adjusted treatment effect has a bias of only 1.6% and a coverage of 98.6%.

In further simulations, we explored the relative importance of correlations between U and individual elements of Z vs. the aggregate correlation of U with a summary of Z. We generated a fourvariate normal vector (U, Z) where U was a scalar unmeasured confounder and Z was a trivariate measured confounder, assuming two different correlation models: in model 1, the correlations between U and elements of Z were all set to 0.1; in model 2, the correlations were 0.3, −0.4 and 0. We then generated the treatment indicators and computed the propensity scores [estimated e = Pr(X = 1|Z)] [Rosenbaum and Rubin (1983b)] to summarize the effects of Z. Although individual partial correlations were larger in model 2 than model 1, within-stratum correlations between U and the propensity score were moderate under both models (e.g., −0.02 in the X = 1 stratum and −0.10 in the X = 0 stratum under model 2). Biases were 0% for model 1 and 2% for model 2. Thus, the simulation, although not exhaustive, suggested that the total correlation of U with the propensity score is more important than individual correlations between U and elements of Z. We also considered the effect of the unconditional correlation between U and Z on bias and coverage. Briefly, larger unconditional correlations of 0.2 and 0.3 led to larger within-stratum correlations, but the bias was largely driven by the within-stratum correlation.

Our simulations suggest that our correction is useful for moderately strong unmeasured confounders when the total within-stratum correlation between the unmeasured and measured confounders is less than 0.15. While the adjusted treatment effect may have some residual bias under conditional dependence, it can still give the investigator a sense of how strongly an unmeasured confounder might influence the treatment effect.

4. Bladder cancer study

We have applied our method to data from a cohort of stage II/III bladder cancer patients diagnosed between 1995 and 2005 and appearing in the linked SEER-Medicare data set [Schrag et al. (2005), Yabroff et al. (2008)]. We restrict analysis to the two main treatments: the standard therapy of radical cystectomy, and a bladder-sparing regimen consisting of radiotherapy and cisplatin-based chemotherapy (rad/chemo). We excluded patients who were diagnosed before age 65, for whom bladder cancer was not the first primary malignancy, who did not have continuous Medicare part A/B coverage or who had coverage from an HMO during the treatment period, or for whom key data such as histology were missing. Radiotherapy and chemotherapy could be given up to 3 months apart, so in order to avoid survivorship bias, we excluded patients who died before 90 days. The final cohort included 1860 patients, of whom 77.4% were treated with cystectomy.

We extracted payment data for Medicare parts A and B from the Carrier Claims file, the Outpatient file, and the Medicare Provider Analysis and Review Record. These files contained payment information for physicians, outpatient services from institutions such as hospitals and health clinics, and inpatient services from hospitals and long-term care facilities [National Cancer Institute (2010)]. All payments were adjusted to year 2000 dollars using the Medicare Economic Index [Centers for Medicare and Medicaid Service (2010), Yabroff et al. (2008)]. This method allowed us to compare total costs of care rather than costs due to treatment only. Two patients had zero costs, suggesting some incompleteness in the payment data; we corrected for this by adding half of the lowest nonzero cost to all observations [Mosteller and Tukey (1977)].

We modeled costs using a GLM with a log link and a gamma variance function. Because the observed total costs were subject to censoring, we estimated the model by the IPW method [Lin (2003)]. Our analysis considered all health care costs, for which the censoring rate was a moderate 39.0%.

Using a Gamma GLM accounting for censoring, we estimated the effect of rad/chemo on cost, adjusting for the available measured covariates tumor grade, sex, ethnicity, marital status, age, median income of the census tract, size of the metropolitan area, number of comorbidities, year of diagnosis and SEER site. We found that rad/chemo lowers the cost of treatment by a factor of 0.873 (95% CI: 0.793, 0.960).

4.1. Potential magnitude of conditional correlation

To determine the plausible extent of violations of the assumption Z ⊥ U |X, we calculated partial correlations between each of the measured confounders, Z_j, and the combined effect of the other covariates estimated by the propensity score excluding Z_j. Some individual pairwise correlations are substantial, for example, the correlation between sex and marital status among the treated is −0.405. When considering the aggregate correlation with all other confounders, however, we found that correlations were typically smaller, often less than 0.1 (see Table 2). The highest combined within-stratum correlations were with race, with the largest observed correlation being 0.148. Although we can never be sure of the magnitude of correlations between U and Z, if aggregate correlations with the unmeasured confounder are no more extreme than the highest observed value, our procedure will yield valid results.

Table 2.

Observed correlations in bladder cancer study

	Corr with propensity score			Largest individual corr
	Unconditional	Rad/chemo	Cystectomy	Rad/chemo	Cystectomy
Grade
1	0.004	−0.004	0.000	0.150	0.082
3	0.006	−0.085	0.024	0.153	0.124
4	−0.007	0.076	−0.013	0.183	0.136
5	−0.006	0.049	−0.051	0.153	0.061
Sex	−0.021	−0.035	−0.059	−0.405	0.373
Race
White	0.140	0.111	0.148	−0.189	−0.235
Black	−0.075	−0.070	−0.084	0.235	0.177
Other	−0.125	−0.099	−0.125	0.167	0.381
Hispanic	−0.074	−0.001	−0.071	0.264	0.202
Marital status
Married	−0.003	−0.001	0.012	0.384	0.373
Unmarried	0.014	0.007	0.003	0.405	0.351
Unknown	−0.032	−0.017	−0.044	0.153	0.322
Age	0.134	0.115	0.061	0.199	0.162
Urban Category
1	−0.053	−0.066	−0.043	−0.408	−0.311
2	0.013	0.009	0.005	0.328	0.297
3	0.048	0.067	0.045	0.490	0.359
Comorbidities
0	−0.043	−0.044	−0.019	0.097	−0.097
1	−0.071	−0.075	−0.051	0.128	0.066
2 or more	0.091	0.093	0.058	0.140	0.108

Because our unadjusted estimate was statistically significant, we were primarily interested in assessing potential unmeasured confounders that would displace the effect of treatment toward the null. To this end, we posited three potential confounders: access to health care, manifested as a Bernoulli variable; smoking history, manifested as Poisson; and personal income, manifested as Gamma.

4.2. Unmeasured Bernoulli confounder

Although this cohort had Medicare insurance that guaranteed coverage of their care, other factors that are unavailable in SEER-Medicare such as lack of transportation or low physician availability may have limited access [Penchansky and Thomas (1981)]. For example, if rad/chemo patients had poorer access, their overall medical costs may also have been lower. We performed a sensitivity analysis to determine how strong this unmeasured confounder would need to be to explain the treatment effect on costs. As access to health care is a difficult concept to quantify, we categorized it as binary, with U = 1 representing good access and U = 0 poor access.

Our sensitivity analysis (Table 3) varied both the effect of U on expected cost and the distributions of U in the treatment strata. We see that moderate imbalances in U produced tangibly different inferences from the original analysis, even when the effect of the unmeasured confounder was small. The adjusted treatment effect was nonsignificant when the prevalence of good access to care was 80% in the cystectomy group and 40% in the rad/chemo group and the confounder had an effect of 1.1 on the cost ratio. Alternatively, if the effect of access on cost was 1.25, prevalences of 70% in the cystectomy group and 50% in the rad/chemo group produced nonsignificant confidence intervals. We conclude that although the apparent treatment effect is significant, this could be easily explained by an unmeasured Bernoulli confounder.

Table 3.

Sensitivity of the estimated bladder cancer treatment cost ratio to an unmeasured Bernoulli confounder

π0	π1	Effect of confounder	Cost ratio	95% CI
0.7	0.5	1.1	0.89	(0.81, 0.98)
0.8	0.4	1.1	0.91	(0.82, 1.00)
0.8	0.3	1.1	0.92	(0.83, 1.01)
0.7	0.5	1.25	0.91	(0.83, 1.00)
0.8	0.4	1.25	0.95	(0.87, 1.05)
0.8	0.3	1.25	0.97	(0.89, 1.07)
0.7	0.5	1.5	0.94	(0.86, 1.04)
0.8	0.4	1.5	1.02	(0.93, 1.12)
0.8	0.3	1.5	1.06	(0.97, 1.17)

Unadjusted cost ratio = 0.87 (95% CI 0.79–0.96).

Boldface confidence intervals denote changes from the unadjusted inference.

π₀ = prevalence of unmeasured confounder in cystectomy group.

π₁ = prevalence of unmeasured confounder in rad/chemo group.

4.3. Unmeasured Poisson confounder

Smoking is a major risk factor for bladder cancer [Baris et al. (2009)] and for co-morbid conditions such as lung and artery disease [Freund et al. (1993)]. Treating these conditions is likely to increase costs. It is common to quantify smoking history in pack-years, defined as the number of packs smoked per day times the length of smoking in years; because this is a discrete count variable, it is natural to model it as Poisson [see Wang and Heitjan (2008)]. Smoking intensity is related to medical costs; a decrease of 20 pack-years has been associated with 10% lower costs [Leigh, Hubert and Romano (2005)]. This means that we could expect costs to increase by a factor of approximately 1.005 per additional pack-year smoked. We estimate the mean number of pack-years in our bladder cancer population to be between 15 and 30 [Baris et al. (2009)]. If exposure differs between treatment strata, the treatment effect may be subject to unmeasured confounding.

Table 4 presents the sensitivity analysis for smoking history. A single pack-year of smoking will not affect costs substantially, so moderate differences in smoking history between the groups are required to change the significance of the treatment effect. If the effect of a single pack-year on cost is 1.005, an average of 34 pack-years in the cystectomy group and 26 pack-years in the rad/chemo group would yield a nonsignificant confidence interval. Because a difference this large is plausible, we deem that the treatment effect is sensitive to smoking history manifested as a Poisson confounder.

Table 4.

Sensitivity of the estimated bladder cancer treatment cost ratio to an unmeasured Poisson confounder

λ0	λ1	Effect of confounder	Cost ratio	95% CI
15	13	1.005	0.88	(0.80, 0.97)
15	11	1.005	0.89	(0.81, 0.98)
17	11	1.005	0.90	(0.82, 0.99)
19	11	1.005	0.91	(0.83, 1.00)
19	9	1.005	0.92	(0.83, 1.01)
15	13	1.01	0.89	(0.81, 0.98)
15	11	1.01	0.91	(0.83, 1.00)
17	11	1.01	0.93	(0.84, 1.02)
30	28	1.005	0.88	(0.80, 0.97)
30	26	1.005	0.89	(0.81, 0.98)
32	26	1.005	0.90	(0.82, 0.99)
34	26	1.005	0.91	(0.83, 1.00)
34	24	1.005	0.92	(0.83, 1.01)
30	28	1.01	0.89	(0.81, 0.98)
30	26	1.01	0.91	(0.83, 1.00)
32	26	1.01	0.93	(0.84, 1.02)

Unadjusted cost ratio = 0.87 (95% CI 0.79–0.96).

Boldface confidence intervals denote changes from the unadjusted inference.

λ₀ = mean of unmeasured confounder in cystectomy group.

λ₁ = mean of unmeasured confounder in rad/chemo group.

4.4. Unmeasured Gamma confounder

Income is positively associated with health care spending at the population level [Centers for Medicare and Medicaid Service (2003), Di Matteo (2003)]. Median income for the census tract was available in SEER-Medicare data, and our analysis showed no evidence of imbalance on aggregate, but there was still a possibility of imbalance at the patient level. We therefore hypothesized that an effect of income on spending would be small, and a potential imbalance of income between the patient groups would also be small.

Income distributions are heavy-tailed. According to the U.S. census [US Census (2008)], the ratio of the variance to the mean (θ in the Gamma distribution) is approximately 3 for households with members 65 and older. We took income to be measured as a ratio of individual income to mean income. Therefore, if the true effect of income was 1.25, an increase from the mean to twice the mean would cause a 25% increase in medical spending. We further assumed equal θ across treatment strata. Our sensitivity analysis (Table 5) revealed that the treatment effect on cost became nonsignificant when income was 25% higher in the cystectomy group than the rad/chemo group if the effect of income on spending was only 1.05 and θ = 3. As such small differences and effect sizes are plausible, we conclude that the treatment effect is also sensitive to this Gamma confounder.

Table 5.

Sensitivity of the estimated bladder cancer treatment cost ratio to an unmeasured Gamma confounder

Mean0/Mean1	Var/Meanp	Effect of confounder	Cost ratio	95% CI
1.1	2	1.05	0.88	(0.80, 0.97)
1.25	2	1.05	0.89	(0.81, 0.98)
1.5	2	1.05	0.91	(0.83, 1.01)
1.1	3	1.05	0.89	(0.81, 0.98)
1.25	3	1.05	0.91	(0.82, 1.00)
1.5	3	1.05	0.94	(0.85, 1.03)
1.1	2	1.1	0.89	(0.81, 0.98)
1.25	2	1.1	0.92	(0.83, 1.01)
1.5	2	1.1	0.96	(0.87, 1.06)
1.1	3	1.1	0.90	(0.82, 0.99)
1.25	3	1.1	0.95	(0.86, 1.04)
1.5	3	1.1	1.02	(0.92, 1.12)

Unadjusted cost ratio = 0.87 (95% CI 0.79–0.96).

Boldface confidence intervals denote changes from the unadjusted inference.

Mean₀ = mean of unmeasured confounder in cystectomy group.

Mean₁ = mean of unmeasured confounder in rad/chemo group.

Mean_p = mean pooled across both groups.

5. Conclusion

We have developed a method to correct estimates of the treatment effect on mean cost for a range of potential unmeasured confounders. The method is simple to apply and readily accommodates potential binary, count and continuous confounders. Although it assumes independence of the measured and unmeasured confounders given treatment status, simulations reveal that the adjustments are robust to modest departures from this condition. Moreover, in all conditions we examined the adjustment reduced bias compared to an unadjusted analysis.

Conditional independence is a generally untestable assumption that is unlikely to hold exactly in applications. Investigators should therefore evaluate patterns of correlation within their data before applying the method. We recommend exploring the possible size of partial correlations by successively omitting individual observed confounders and estimating their partial correlations with the remaining measured confounders. Simulations show that the adjustment is robust to within-stratum correlations less than 0.15, a condition that appears to be satisfied in our bladder cancer example.

In some types of studies one expects to find substantial correlations among measured and unmeasured confounders. For example, in a study to examine cost of an intervention to improve student performance on a standardized exam, measured confounders related to socioeconomic status could be highly correlated with unmeasured confounders such as parental attitudes toward education. If most measured confounders are tightly interrelated with the unmeasured variable, this would render our adjustments inaccurate. Here the investigator should use the method of VanderWeele and Arah (2011), perhaps with simplifying assumptions about the confounder to render the procedure more tractable.

A second limitation of our method is that adjustments for strong Poisson and Gamma confounders can be biased in moderate sample sizes. The correction may also leave bias when there is a large proportion of censored data, as would occur in studies with short follow-up. This is likely due to the decreased efficiency of the Lin estimator when the proportion of censoring is high, a problem that could be ameliorated by splitting the time period into intervals [Lin (2003)] or the creation of a more efficient GLM for censored costs.

With our simple additive corrections, assuming fixed values of the sensitivity parameters leads us to use the unadjusted Var(β̂^*) to develop confidence intervals. A fully Bayesian approach would quantify uncertainty about the parameters using prior distributions and propagate the uncertainty using Bayes’s theorem. One could also conduct a probabilistic sensitivity analysis using Monte Carlo simulations as demonstrated in Arah, Chiba and Greenland (2008). Although it is appealing to incorporate uncertainty about the sensitivity parameters, both methods require sufficient knowledge about unmeasured parameters to fully characterize their distributions.

Despite its limitations, our method provides a practical approach to evaluate the sensitivity of costs to unmeasured confounding. The bladder cancer study provides an example where our method can be easily implemented to evaluate the effect of a wide range of confounders. Further research should develop extensions to allow sensitivity analysis for combined cost-effectiveness outcomes.