Abstract
Adjustment for an uncorrelated covariate in a logistic regression changes the true value of an odds ratio for a unit increase in a risk factor. Even when there is no variation due to covariates, the odds ratio for a unit increase in a risk factor also depends on the distribution of the risk factor. An instrumental variable can be used to consistently estimate a causal effect in the presence of arbitrary confounding. With a logistic outcome model, we show that the simple ratio or two-stage instrumental variable estimate is consistent for the odds ratio of an increase in the population distribution of the risk factor equal to the change due to a unit increase in the instrument divided by the average change in the risk factor due to the increase in the instrument. This odds ratio is conditional within strata of the instrumental variable, but marginal across all other covariates, and is averaged across the population distribution of the risk factor. Where the proportion of variance in the risk factor explained by the instrument is small, this is similar to the odds ratio from a randomized controlled trial without adjustment for any covariates, where the intervention corresponds to the effect of a change in the population distribution of the risk factor. This implies that the ratio or two-stage instrumental variable method is not biased, as has been suggested, but estimates a different quantity to the conditional odds ratio from an adjusted multiple regression; a quantity which has arguably more relevance to an epidemiologist or a policy-maker, especially in the context of Mendelian randomization.
1 Introduction
Of fundamental interest in scientific enquiry is the estimate of a change in outcome for a unit change in one variable keeping all other variables constant. In an epidemiological context, when individuals in a population are heterogeneous, the question can be posed in many different ways. For example: “what is the effect of a unit increase in the risk factor for an individual in a given substratum of the population?”; or “what is the effect of a unit increase in the risk factor for the population as a whole?”. More formally, we may consider the measure of difference between the potential outcomes for an individual at current and increased levels of the risk factor, or the averaged measure of difference between potential outcomes for a population integrated across the empirical distributions of the covariates and risk factor at current and increased levels of the risk factor.
1.1 Different estimates
If the outcome is continuous, the true outcome model is linear in the risk factor and there is no interaction between the risk factor and any other covariate, then, assuming the effect of interest is the mean change in outcome, the answer to these questions is the same. If the outcome is binary, the true outcome model for the probability of an event is log-linear in the risk factor and there is no interaction between the risk factor and any other covariate, then, assuming the effect of interest is a relative risk, the answer to each of these questions is the same [1]. However, if the outcome is binary, the true outcome model for the probability of an event is logistic-linear in the risk factor and there is no interaction between the risk factor and any other covariate, then, assuming the effect of interest is an odds ratio, the answer to each of these questions is, in general, different.
In logistic regression, the coefficient for the risk factor represents the odds ratio for a unit increase in the risk factor for an individual conditional on those covariates which are included in the model [2]. However, the true effect of interest for an epidemiologist is not usually an individual effect conditional on covariates, but an effect marginal across covariates which represents the effect of an intervention applied to a population [3]. Additionally, with a continuous risk factor, the odds ratio of interest is not usually for a unit increase from one specific level in the risk factor to an exposure of one unit greater (for example, the odds ratio for a risk factor of 4 units versus a risk factor of 3 units), but for a unit increase in the risk factor across the whole population. This marginal population-averaged odds ratio represents the increase in risk averaged across the whole population. Such population effects cannot generally be estimated without assuming complete knowledge of the risk model, except in a randomized controlled trial (RCT) where the intervention corresponds to a unit change in risk factor across the whole population.
1.2 Instrumental variables
An instrumental variable (IV) is a variable which acts like a randomization of the risk factor in an observational setting [4]. The IV divides the population into strata randomly with respect to all potential confounders, such that the strata differ systematically only with respect to the risk factor of interest [5]. As with treatment arms in a randomized trial, any difference in outcome between the strata above what would be expected by chance must be causally due to the risk factor.
This means that, assuming the IV satisfies certain conditions, the effect of the risk factor can be estimated in the absence of knowledge about confounders [6]. In the linear case with a continuous outcome, simple regression-based IV methods consistently estimate the true association [7]. However, in the logistic case, it is not clear what quantity an IV method is estimating, or even to what question an IV estimate should be the answer.
1.3 Mendelian randomization
The use of IVs in the epidemiological literature has expanded recently with the development of Mendelian randomization [8], the use of genetic variants as IVs in observational studies. While there are several conditions necessary to justify their use as an IV [9], genetic variants which are known to be associated with the risk factor of interest are ideal candidate instruments, as they are typically distributed in the population independently of social and environmental factors, and the specific function of many genes is well understood [10]. Although the general context of the examples in this paper will be that of Mendelian randomization, there is no restriction of the mathematical findings within the paper to the use of genetic IVs.
A difference between the estimate of an association using observational data from conventional regression methods with adjustment for known covariates and the estimate from IV analysis has been interpreted as evidence of, and may often be due to, unmeasured confounding or reverse causation [11]. But for the comparison of these quantities to be valid, it is important to know whether the estimates compared are targeting the same quantity or not.
1.4 Motivating example
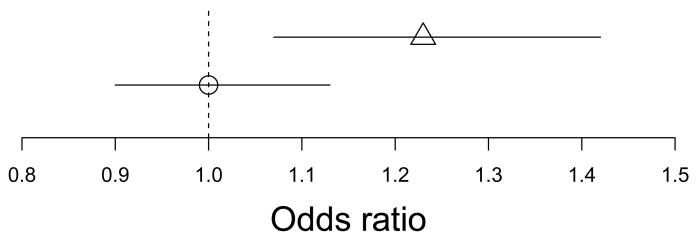
To illustrate this point, we consider the causal effect of C-reactive protein (CRP) on risk of coronary heart disease (CHD). From a meta-analysis of observational studies using a multivariable logistic regression model adjusting for several covariates, the odds ratio for a standard deviation increase in CRP was estimated as 1.23, with a 95% confidence interval (1.07, 1.42) excluding the null [12]. An instrumental variable analysis was also performed, giving an odds ratio estimate for a standard deviation increase in CRP of 1.00, with a 95% confidence interval (0.90, 1.13) [13]. These results are displayed in Figure 1. The question we seek to address is how to compare these estimates.
Figure 1.
Odds ratio estimates of one standard deviation increase in C-reactive protein on coronary heart disease risk from multivariable logistic regression model (triangle) and instrumental variable analysis (circle)
1.5 Structure of paper
In this paper, we define non-collapsibility, giving an example of how odds ratios differ whether viewed conditionally or marginally in a covariate, and whether considered for a subject-specific or population-averaged change in the risk factor (Section 2). We define the conditional odds ratio, which is the quantity estimated in logistic regression, and the population odds ratio, which is the quantity estimated in an idealized RCT, showing how these differ in real and simulated data for a range of scenarios (Section 3). We introduce instrumental variables and IV estimation, and define a further quantity, termed the IV estimand, which is the probability limit of the two-stage IV estimate as the sample size increases to infinity. We show by simulation that the IV estimand is close to the population odds ratio in a series of realistic scenarios (Section 4). We conclude by discussing the various estimates of odds ratios, and summarize the relevance of non-collapsibility to the estimation of odds ratios in practice, especially as related to Mendelian randomization (Section 5).
2 Collapsibility
A measure of association is collapsible over a covariate, as defined by Greenland et al. [14], if, when it is constant across the strata of the covariate, this constant value equals the value obtained from the overall (marginal) analysis. Non-collapsibility is the violation of this property. The relative risk and absolute risk difference are collapsible measures of association [15, 16]. Odds ratios are generally not collapsible unless both risk factor and outcome are independent of the strata, or risk factor and strata are conditionally independent given the outcome, or outcome and strata are conditionally independent given the risk factor [17].
2.1 Conditional and marginal effects
In a randomized controlled trial with a linear outcome model, adjustment for baseline covariates in a linear regression may be performed in order to correct for chance imbalance in the covariates, or to improve the precision of the effect estimate. But the true effect, thought of as the estimate one would obtain with an infinite sample size, remains the same, and the interpretation of the estimate is unchanged. With a binary outcome and a logistic outcome model where the target estimate is an odds ratio, conditioning on a covariate changes both the true effect and its interpretation [18]. Logistic regression gives an estimate of the log odds ratio for a unit increase in the risk factor of interest. In an unadjusted model, this is a marginal effect, averaged in the population across strata of the covariate. In an adjusted model, this is a conditional effect, conditional in being in a particular stratum of the population, with the stratum defined as those with a given value of the covariate.
2.2 Subject-specific and population-averaged effects
We also consider a second, less appreciated consequence of non-collapsibility. With a linear outcome model, the average effect for an increase in risk factor from x to x + 1 is the same as the average effect for the whole population increasing their risk factor distribution from X to X + 1. With a binary outcome and a logistic outcome model, the odds ratio for an increase from a given risk factor value is not the same as for the same increase averaged across the risk factor distribution.
We consider a situation where the probability of an event is entirely determined by a single continuous risk score. As illustrated in Table 1, if the true probability of event (π) is related to the risk score (X) by the risk model logit π = −2 + X log(2), then the odds ratio for a unit increase in X for any individual is 2. However, for a group of heterogeneous individuals with risk scores 0.2, 0.4, 1.4 and 1.8, the odds ratio when each individual increases their risk score by one unit is different to 2. As above, if the true risk model is log π = −2 + X log(2), then the subject-specific relative risk is 2 and the population-averaged relative risk is also 2.
Table 1.
Illustrative example of collapsing an effect across the risk factor distribution: non-equality of subject-specific and population-averaged odds ratios and equality of relative risks
| Logistic-linear model: logit π = −2 + X log(2) | |||
|---|---|---|---|
|
| |||
| Risk factor (x) | P (Y = 1|X = x) | P (Y = 1|X = x + 1) | Odds ratio |
| 0.2 | 0.135 | 0.237 | 2 |
| 0.4 | 0.152 | 0.263 | 2 |
| 1.4 | 0.263 | 0.417 | 2 |
| 1.8 | 0.320 | 0.485 | 2 |
|
| |||
| Average | 0.217 | 0.351 | 1.94 |
| Log-linear model: log π = −2 + X log(2) | |||
|---|---|---|---|
|
| |||
| Risk factor (x) | P (Y = 1|X = x) | P (Y = 1|X = x + 1) | Relative risk |
| 0.2 | 0.155 | 0.311 | 2 |
| 0.4 | 0.179 | 0.357 | 2 |
| 1.4 | 0.357 | 0.714 | 2 |
| 1.8 | 0.471 | 0.943 | 2 |
|
| |||
| Average | 0.291 | 0.581 | 2 |
The odds ratio attenuates when the probability of an event is averaged across a distribution. In the first case, where there is variation due to a covariate, different odds ratios represent the measure of association for a change conditional or marginal on the covariate. In the second case, even when the risk model is constructed so that there is no omitted covariate, simply individuals with different levels of the risk factor, different odds ratios represent the measure of association for a unit increase in the risk score for a subject-specific change in the level of the risk factor or for a population-averaged change across the distribution of the risk factor. In both cases, the odds ratio for an individual in the population is different to the odds ratio for the population as a whole.
In most previous work on non-collapsibility, the risk factor has been assumed to be dichotomous, as is usually the case in a clinical trial, where the risk factor is treatment which is either present or absent. Here, we consider the risk factor to be continuous, as is usually the case in Mendelian randomization.
3 Exploring differences in odds ratios
We consider the association between a risk factor (X) and an outcome (Y) and define various odds ratio parameters representing answers to the questions posed at the beginning of the paper. For convenience of notation, we assume the covariates (the competing risk factors) for the outcome can be summarized by a single random variable V [19].
3.1 Conditional and population odds ratios
A conditional effect is the change in outcome due to an intervention in the risk factor for an individual in the population, and a population effect is the change in outcome averaged across the population. For a binary outcome Y = 0, 1, the conditional odds ratio (COR) is defined as the odds ratio for unit increase in the risk factor from x to x + 1 for a given value of v:
| (1) |
where and Y|(σX = x, V = v) is the outcome random variable, conditional on covariate level v, where the risk factor level is set to x using the σX notation for intervention on X of Dawid [20]. This can also be written as Y|do(X = x), V = v using the do() notation of Pearl [21]. Under the assumptions that Y equals Y|(σX = x, V = v) if X = x and V = v (consistency) and that Y(x) ⫫ X|V (ignorability) [22], this can be expressed as:
| (2) |
In general, the COR may be a function of x and v, although in a logistic-linear model of association, where the logit of the probability of outcome (π) is a linear function in X and V with no interaction term:
| (3) |
the COR is exp(β1) independently of x and v. This is the odds ratio estimated by a logistic regression of Y on X and V.
The population odds ratio (POR) is defined as the odds ratio for unit increase in the distribution of the risk factor from the observed distribution X to X + 1. This is an increase marginalized over the risk factor distribution and the covariate V:
| (4) |
where Y|(σX = δt) is the outcome random variable, conditional on covariate level v, where the risk factor is distributed according to its distribution in the population, except translated by +t units, such that Y|(σX = δ0) is the average outcome in the population under the observational regime, and Y|(σX = δ1) is the average outcome if the risk factor for each individual is increased by one unit. Formally, we have X|(σX = δt) ≡ X + t|(σX = δ0), and X|(σX = δ0) ≡ X|(σX = ∅), which is the observational distribution of X.
The POR represents the ratio of the odds for a population with the whole distribution of the risk factor shifted up by one to the odds for a population with the original distribution of the risk factor. From here on, we assume that the model of association is logistic-linear, and drop the dependence of the COR on the values of x and v. The POR depends on the (usually unknown) distributions of the risk factor and covariate, and is generally attenuated compared to the exp(β1) due to the convexity of the logit function. In Model (3), we can write the population log odds ratio (PLOR = log POR) explicitly as:
| (5) |
where expit(x) = (1 − exp(−x))−1, the inverse of logit(x), and f(x, v) is the joint distribution of X and V.
3.2 Comparison with a randomized controlled trial
We can think of the PLOR as the estimate of association from a simulated RCT where the intervention is a unit increase in the risk factor. In the context of a randomized trial, the ratio between the odds of two randomized groups is known as an incident odds ratio [23]. In a simulated example, we can calculate the incident odds ratio. For each individual i = 1, …, N, we consider a counterfactual individual, identical to the first, except with risk factor xi increased by one. We separately draw two independent sets of outcomes y1i, y2i for the original and counterfactual populations.
| (6) |
The incident log odds ratio (ILOR) is calculated as the log odds ratio for a unit intervention on risk factor, which is the difference in log odds between the real and counterfactual populations.
| (7) |
| (8) |
This is a Monte Carlo approximation to the integrals in (5), meaning that ILOR → PLOR as N → ∞. In our simulations, we sum over the probabilities , rather than over the events y1i, y2i to reduce sampling variation in equation (8).
Both the conditional and population effects are ceteris paribus (Latin: “with all other things equal”) estimates; they estimate the effect on the outcome of an intervention on the risk factor with all other factors (such as covariates) kept equal [24]. For this reason, both can be thought of as causal effects [25].
3.3 Conditioning on covariates
If there are multiple covariates, then a causal effect can be conditional on some covariates and marginal across others, depending on which covariates are conditioned on. Although odds ratios typically differ depending on covariate adjustment, a null causal association of X on Y leads to an odds ratio of one no matter which covariates the odds ratio is considered to be marginal and conditional across. We here focus on the COR, as this represents a fully adjusted estimate for an individual, and the POR, as this is marginalized across all variation and so represents the effect for the population as a whole.
3.4 Conditional and population odds ratios in five studies
To illustrate the magnitude of difference between the population and the conditional odds ratios requires precise knowledge of the underlying data-generating model. Using real data, we construct simple logistic-linear models and calculate the COR and POR assuming that the model in question is correct. We consider five studies which investigate effect of C-reactive protein (CRP) on coronary heart disease (CHD), of which three are retrospective case-control studies: Precocious Coronary Artery Disease Study (PROCARDIS), Ludwigshafen Risk and Cardiovascular Health Study (LURIC), Stockholm Heart Epidemiology Program (SHEEP); and two are cohort studies: Cardiovascular Health Study (CHS) and Rotterdam Study (ROTTERDAM). We take cross-sectional data from 21 090 individuals including 6218 with a previous history of CHD. Logistic models of disease outcome on log-transformed CRP were constructed with various levels of adjustment for competing risk factors.
We compare the COR for a unit increase in log(CRP), as estimated by logistic regression, with the POR for a unit increase in log(CRP). The POR is estimated by increasing the predictor in the logistic model, which represents the probability of an event, by , the coefficient for a unit increase in log(CRP) from the logistic regression model, and summing over the new probabilities to obtain the mean number of cases for a counterfactual population with log(CRP) increased by one.
For individual i, if we have the linear predictor (ηi) for our regression model of probability of CHD event (πi) on log(CRP) (xi) and covariates (vij):
| (9) |
Then the PLOR is estimated as:
| (10) |
This is similar to the Monte Carlo approach of equation (8), except that summation of the event probabilities is across the empirical joint distribution of the risk factor and covariates from the data.
Each calculation assumes that the regression model in use is correct, and specifically that all covariates which represent competing risk factors have been accounted for. Although this is an unrealistic assumption, it is made here for purpose of illustration. This means that estimates based on adjustment for different covariates are incompatible. In case-control studies, as the probabilities of an event cannot be estimated directly, we have adjusted the model intercept to give a 7% incidence rate in the population from which the case-control sample was ascertained [26].
Table 2 shows how the conditional odds ratios represent an over-estimation of the population-averaged effect of a unit intervention in CRP levels on CHD risk. The estimates illustrate that, in real data, the conditional and population odds ratios can be somewhat different. The estimates of association in Table 2 should not be regarded as causal effects, due to the unrealistic assumption of no unmeasured confounders.
Table 2.
Conditional and population odds ratios (log odds ratios) for a unit increase in log-transformed C-reactive protein on coronary heart disease odds from logistic regression in five studies with different adjustment for covariates (N = number of participants, n = number of events)
| Model1 | Conditional (log) odds ratio |
Population (log) odds ratio |
|---|---|---|
|
| ||
| PROCARDIS (N = 6464, n = 3135) | ||
|
| ||
| No adjustment | 1.4408 (0.3652) | 1.4330 (0.3598) |
| Adjustment for sex, diabetes status and age |
1.4371 (0.3626) | 1.3911 (0.3301) |
| Further adjustment for tchol, hdl, log(tg) | 1.3048 (0.2661) | 1.2570 (0.2287) |
|
| ||
| LURIC (N = 3236, n = 1335) | ||
|
| ||
| No adjustment | 1.2801 (0.2470) | 1.2775 (0.2449) |
| Adjustment for sex, diabetes status and age |
1.2690 (0.2382) | 1.2633 (0.2337) |
| Further adjustment for sbp, tchol, hdl, bmi, log(tg) |
1.1927 (0.1762) | 1.1852 (0.1699) |
|
| ||
| SHEEP (N = 1994, n = 858) | ||
|
| ||
| No adjustment | 1.4312 (0.3585) | 1.4241 (0.3535) |
| Adjustment for sex, diabetes status and age |
1.4057 (0.3405) | 1.3881 (0.3280) |
| Further adjustment for tchol, hdl, bmi, log(tg) | 1.2872 (0.2525) | 1.2637 (0.2341) |
|
| ||
| CHS (N = 4506, n = 449) | ||
|
| ||
| No adjustment | 1.2554 (0.2275) | 1.2538 (0.2262) |
| Adjustment for sex, diabetes status and age |
1.2284 (0.2057) | 1.2186 (0.1977) |
| Further adjustment for sbp, tchol, hdl | 1.1854 (0.1701) | 1.1758 (0.1619) |
|
| ||
| ROTTERDAM (N = 5402, n = 647) | ||
|
| ||
| No adjustment | 1.3525 (0.3020) | 1.3476 (0.2983) |
| Adjustment for sex, diabetes status and age |
1.2327 (0.2092) | 1.2200 (0.1988) |
| Further adjustment for tchol, hdl | 1.1849 (0.1697) | 1.1732 (0.1597) |
tchol = total cholesterol, hdl = high-density lipid cholesterol, bmi = body mass index, sbp = systolic blood pressure, tg=triglycerides
The linear predictor, the logit of the probability of an event, has an approximate normal distribution. In PROCARDIS, with no adjustment, the standard deviation of the linear predictor for the cohort is 0.41, increasing to 0.92 on adjustment for sex, diabetes status and age, and to 1.38 on further adjustment for total cholesterol, high-density lipid cholesterol and log(triglycerides). This indicates that individuals in the population have heterogeneous levels of risk of CHD. In CHS, the standard deviation of the linear predictor for the fully adjusted model considered here is 0.89, and there is less attenuation of the conditional odds ratio compared with PROCARDIS. Even assuming the effect of CRP is no longer confounded, further adjustment for unmeasured covariates would lead to greater attenuation of the POR. This is because the logistic function is less well approximated by a linear function as the domain and range of the function considered widens. In the maximally-adjusted models considered here, there is a 5–14% attenuation of the POR compared to the COR. In practice, the attenuation of the population odds ratio is likely to be greater than observed here, due to further unmeasured covariates.
3.5 Conditional and population odds ratios in simulated data
In order to better estimate the magnitude of the potential attenuation of the POR compared to the COR, we consider a confounded model of association between a risk factor and outcome, simulating data for N participants indexed by i. The risk factor (X) is a linear combination of a covariate G which takes two values, a normally distributed covariate V and an error term. The outcome (Y) is a binary variable, taking value 1 with probability π1, which is a logistic function of the risk factor and covariate V. Although G will be thought of later as an IV, it could here be any covariate dividing the population independently of V into strata with different mean risk factor levels.
| (11) |
The conditional log odds ratio (CLOR) conditional on V is:
To illustrate the difference between the population and conditional log odds ratios, we set β0 = −2, α0 = 0 throughout and consider two different sizes of CLOR, β1 = 0.4, −0.8 (corresponding to CORs 1.49 and 0.45), varying the covariate effect β2 between −1 and +1. We assume that G divides the population into two strata of equal size (gi = 0, 1). We consider the PLOR in five scenarios:
X is constant (α1 = 0, α2 = 0, )
X varies independently of the covariate V (α1 = 0, α2 = 0, )
X is correlated with the covariate V (α1 = 0, α2 = 1, )
X has constant levels depending on G (α1 = 1, α2 = 0, )
X varies with V and G (α1 = 1, α2 = 1, )
Results were calculated using the Monte Carlo method (equation (8)) repeatedly for a large sample (N ≥ 1 000 000) and checked by numerical integration. Figure 2 shows that even in this simple model, the PLOR is only equal to the CLOR when X is constant and there is no other covariate which is a competing risk factor for Y (i.e. β2 = 0). A competing risk factor (even if it is not a confounder), variation in X, and stratification of X all result in an attenuation of the PLOR. The maximal attenuation in the examples considered here is 33% (−0.534 from −0.8). If we had instead considered a log-linear model of Y on X and examined the population log relative risk, Figure 2 would have consisted of five horizontal lines, as the population relative risk is equal to the conditional relative risk throughout.
Figure 2.
Population log odds ratio for unit increase in risk factor in five scenarios for varying for the covariate effect (β2) with conditional log odds ratio (β1) of 0.4 (left panel), −0.8 (right panel, y-axis is inverted)
This example illustrates the non-collapsibility of the odds ratio. The odds ratio for a risk factor does not average correctly, attenuating when averaged across a population with any variation or heterogeneity in the risk factor, or when there is an alternative risk factor. The relative risk does average correctly. This means that an odds ratio for a risk factor estimated from observational data by logistic regression conditional on covariates will be an overestimation of the expected average effect of the same intervention in the population, even in the absence of residual confounding.
4 Instrumental variables
Having defined various odds ratios, we turn our attention to instrumental variables (IV). We recall that the goal of this paper is the identification of the odds ratio estimated in an IV analysis. Having defined an IV and seen how if can be used to estimate a causal effect, we investigate the quantity estimated in a ratio or two-stage IV analysis with a logistic-linear outcome model, and see how it relates to a population odds ratio.
4.1 Definition
Given an outcome Y with potential outcomes Y (X, G), a risk factor X with potential outcomes X(G), and a covariate V which is a sufficient covariate for the association between X and Y (such a covariate contains all common causes of X and Y [27]), an instrumental variable G is a variable which satisfies the assumptions [28]:
G is not independent of X (that is, p(x|g) is a non-trivial function of g),
G is independent of the potential outcomes X(g) and Y (x, g),
The potential outcome Y (x, g) is the same for all values of g (exclusion restriction).
This means that the joint distribution of Y, X, V, G, p(y, x, v, g) factorizes as
| (12) |
which corresponds to the directed acyclic graph (DAG) Figure 3 [1, 27].
Figure 3.

Directed acyclic graph (DAG) of instrumental variable assumptions
In order to interpret the unconfounded estimates produced by IV analysis as causal estimates, we require the additional structural assumption:
| (13) |
where 1(.) is the indicator function. This ensures that intervening on X does not affect the distributions of any other variables except the conditional distribution of Y [29].
4.2 Causal estimation: ratio method
With a linear outcome model, the ratio of coefficients method, or the Wald method [30], is the simplest way of estimating the causal association β1 of X on Y. For a dichotomous IV G = 0, 1 and a continuous outcome, it is calculated as the ratio of the difference in the average outcomes to the difference in the average risk factor levels between the two IV groups [5, 31].
| (14) |
where is the average value of outcome for all individuals with IV G = j, and is defined similarly for the risk factor. This estimator is valid under the assumption of monotonicity of G on X and linearity of the causal association with no (X, V) interaction [29, 31, 32].
With a binary outcome, the estimator is defined similarly, with the log of the probability of an event in a log-linear model or the log-odds of an event in a logistic model. This is also commonly quoted in its exponentiated form as where R is the relative risk or odds-ratio and is the average difference in risk factor, between the two groups [33, 34]. This estimator is valid under the assumption of monotonicity of G on X and a log-linear model of outcome on risk factor with no (X, V) interaction [29], and has been widely explored using a logistic model [35].
For a polytomous or continuous IV, the estimator is calculated as the ratio of the regression coefficient of outcome on IV (G–Y regression) to the regression coefficient of risk factor on IV (G–X regression) [4, 36].
| (15) |
With a continuous outcome, the G–Y regression uses a linear model; with a binary outcome, a log-linear or logistic regression is preferred.
4.3 Causal estimation: two-stage method
Alternatively, a two-stage method may be used. A two-stage method comprises two regression stages: the first-stage regression of the risk factor on the IVs, and the second-stage regression of the outcome on the fitted values of the risk factor from the first stage [35].
With continuous outcomes and a linear model, the two-stage method is known as two-stage least squares (2SLS). It can be performed with multiple continuous or categorical IVs. The method is so called because it can be calculated using two regression stages [37]. The first stage (G-X regression) regresses X on G to give fitted values . The second stage (X-Y regression) regresses Y on the fitted values from the first stage regression. The causal estimate is this second-stage regression coefficient for the change in outcome caused by unit change in the risk factor. (Although estimation in two stages gives the correct point estimate, the standard error is not correct; the use of 2SLS software is recommended for estimation in practice [38].)
The analogue of 2SLS with binary outcomes is a two-stage estimator where the second-stage regression (X-Y regression) uses a log-linear or logistic regression model. This has been called the two-stage estimator [39], standard IV estimator [19], pseudo-2SLS [40], two-stage predictor substitution (2SPS) [41, 42] or Wald-type estimator [29]. However, such non-linear regression methods do not always yield consistent estimators for the structural parameter in the logistic equation and have been called “forbidden regressions” [38, 43].
An alternative estimate has been proposed, the adjusted two-stage estimate, which uses the residuals from the first-stage regression of the risk factor on the IV in the second-stage regression of the disease on the IV. This is known as the adjusted IV estimate [19], control function approach [35, 44], or two-stage residual inclusion (2SRI) [41]. If we have a first stage regression of X on G with fitted values and residuals , then the alternative IV estimator comes from a logistic regression additively on and (or equivalently on X and ). The residual incorporates information from confounders in the first stage regression.
With a single instrument, the ratio and two-stage estimates are equal [29], and so the two-stage method can be thought of as an extension to the ratio method. The ratio and two-stage methods are not the only methods for IV estimation with a binary outcome, but they are discussed here as they are the most widely used in the context of Mendelian randomization [45].
4.4 IV estimand
We consider the ratio expression for the IV estimator for a logistic-linear outcome model. We assume throughout that G is dichotomous, taking values 0 and 1, and that the outcome Y has a Bernouilli distribution with probability of event π and linear predictor η = logit(π):
| (16) |
where g(V), h(V) are arbitrary functions of V and EX is an error term. We consider the logistic regression of Y on G using the model:
| (17) |
As the sample size N tends to infinity, we have:
| (18) |
where X(0) is the distribution of the risk factor when G = 0 and σX = δt indicates a t unit increase across the distribution of X, as defined in Section 3.1. This uses the assumptions of consistency and ignorability, and equation 13, that manipulation of X does not affect the distribution of V.
The coefficient is the log odds ratio corresponding to an increase of α1 across the distribution of X with the IV (and all other confounding variables) kept constant. This log odds ratio is conditional in G but marginal in all other covariates. As the sample size increases, the denominator of the IV estimate converges in probability to the constant α1, so the IV estimator converges to the ratio by Slutsky’s theorem. We write this quantity as plim as we shall refer to it as the IV estimand. In Appendix A.1, we show that this quantity is close to the mean estimate from a two-stage analysis even in a finite sample setting.
4.5 Simulation 1: confounded association
To investigate how the IV estimator behaves in more realistic situations, we simulate data from logistic model (11) for confounded association with a single instrument similar to what would be expected in a Mendelian randomization analysis where the IV explained a small proportion of the variation in the risk factor.
We take a large sample size of 4000 divided equally into two groups (gi = 0, 1). The parameter α1 = 0.3 with corresponds to a strong instrument with mean F statistic in the regression of X on G of around 45. We set α0 = 0, α2 = 1, β0 = −2 and consider three values for β1 of 0.4, −0.8 and 1.2 and seven values for β2 of −1.0,−0.6, −0.2, 0, 0.2, 0.6, 1.0 corresponding to different levels and directions of confounding. We perform 2 500 000 simulations for each set of parameter values.
We estimate the observational log odds ratio by logistic regression of outcome on the risk factor with no adjustment for confounding. The PLOR and IV estimand are calculated using both numerical integration as per equation (5) and the Monte Carlo approach of equation (8); identical answers are produced by both approaches. Using IVs, we calculate the two-stage estimate and the adjusted two-stage estimate. The fitted residuals are unbiased scaled estimators of the covariate V, which is considered unknown, and so including these in the second stage regression is thought to give a better estimate of the CLOR (which is β1) [19].
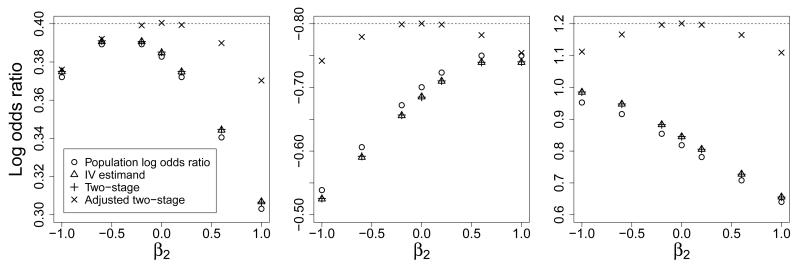
Table 3 shows the observational log odds ratio, PLOR and IV estimand, and median estimates across simulations of the two-stage and adjusted two-stage methods. These results are displayed graphically in Figure 4. We see that the observational estimate is biased in the direction of the confounded association (i.e. in the direction of the sign of β2). The two-stage method estimates are attenuated compared to the CLOR, but close to the IV estimand and PLOR throughout. The difference between the two-stage estimates and the PLOR is partially due to the conditioning on G; the IV estimand, which is marginal in V and conditional on G is closer to the median two-stage estimate. The difference between the PLOR and IV estimand is not large compared to that between the PLOR and CLOR. The adjusted two-stage method estimates are closer to the CLOR, with some attenuation when there is strong confounding. The Monte Carlo standard error due to the limited number of simulations is around 0.0001 in this and the subsequent simulation.
Table 3.
Observational log odds ratio, population log odds ratio (PLOR) and IV estimand compared to two-stage and adjusted two-stage estimates of log odds ratio for unit increase in risk factor from model of confounded association (Scenario 1). Median estimates across 2 500 000 simulations
| Confounded association | β2 = −1.0 | β2 = −0.6 | β2 = −0.2 | β2 = 0 | β2 = 0.2 | β2 = 0.6 | β2 = 1.0 | |
|---|---|---|---|---|---|---|---|---|
| β1 = 0.4 | Observational | −0.089 | 0.101 | 0.301 | 0.400 | 0.498 | 0.678 | 0.828 |
| PLOR | 0.372 | 0.389 | 0.389 | 0.383 | 0.372 | 0.341 | 0.303 | |
| IV estimand | 0.375 | 0.391 | 0.391 | 0.385 | 0.375 | 0.344 | 0.307 | |
| Two-stage method | 0.375 | 0.391 | 0.391 | 0.385 | 0.375 | 0.345 | 0.307 | |
| Adjusted two-stage | 0.376 | 0.392 | 0.399 | 0.401 | 0.399 | 0.390 | 0.370 | |
|
| ||||||||
| β1 = 0.8 | Observational | −1.198 | −1.066 | −0.897 | −0.800 | −0.700 | −0.492 | −0.288 |
| PLOR | −0.539 | −0.606 | −0.672 | −0.700 | −0.723 | −0.750 | −0.750 | |
| IV estimand | −0.525 | −0.590 | −0.656 | −0.685 | −0.710 | −0.739 | −0.739 | |
| Two-stage method | −0.526 | −0.592 | −0.657 | −0.685 | −0.710 | −0.740 | −0.740 | |
| Adjusted two-stage | −0.742 | −0.779 | −0.799 | −0.801 | −0.799 | −0.782 | −0.754 | |
|
| ||||||||
| β1 = 1.2 | Observational | 0.653 | 0.877 | 1.098 | 1.201 | 1.295 | 1.453 | 1.565 |
| PLOR | 0.953 | 0.916 | 0.854 | 0.819 | 0.781 | 0.708 | 0.640 | |
| IV estimand | 0.985 | 0.948 | 0.883 | 0.845 | 0.806 | 0.728 | 0.656 | |
| Two-stage method | 0.986 | 0.948 | 0.883 | 0.846 | 0.806 | 0.728 | 0.656 | |
| Adjusted two-stage | 1.112 | 1.166 | 1.197 | 1.201 | 1.197 | 1.165 | 1.109 | |
Figure 4.
Population log odds ratio and IV estimand compared to median two-stage and adjusted two-stage estimates of log odds ratio for unit increase in risk factor from model of confounded association (Scenario 1) for varying for the covariate effect (β2) with conditional log odds ratio (β1) of 0.4 (left panel), −0.8 (middle panel, y-axis is inverted), and 1.2 (right panel)
4.6 Simulation 2: unconfounded association
A further set of simulations was conducted with the same parameters using model (19) which is identical to the above model (11) except with independent covariates U and V for the risk factor and outcome. This means that the association between X and Y is no longer confounded. The residual R in the adjusted two-stage method is no longer related to the relevant covariate V in the second-stage logistic regression, but instead the variation in X not explained by G.
| (19) |
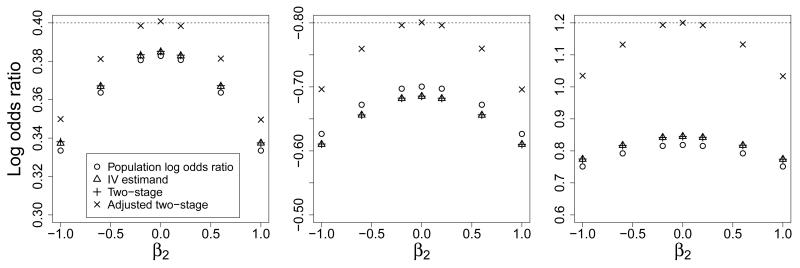
Results are given in Table 4 and displayed in Figure 5. We see that the PLOR and IV estimand are close throughout, and the median two-stage method is closest to the IV estimand as before. The median adjusted two-stage estimate is more attenuated than in the previous example [42], and is not different to the observational estimate. Although the observational estimate is a subject-specific odds ratio similar to the CLOR, the model is misspecified when β2 ≠ 0, and so compared the observational estimate is attenuated to the CLOR despite there being no confounding [46]. This is because adjustment is made in the adjusted two-stage method for the error term α2ui + εi, meaning that the odds ratio is conditional on all variation in X except that caused by G. Except for this variation in G, this is a subject-specific odds ratio marginal in V, which is the same as the observational estimate in this unconfounded example.
Table 4.
Observational log odds ratio, population log odds ratio (PLOR) and IV estimand compared to two-stage and adjusted two-stage estimates of log odds ratio for unit increase in risk factor from model of unconfounded association (Scenario 2). Median estimates across 2 500 000 simulations
| Unconfounded association | β2 = −1.0 | β2 = −0.6 | β2 = −0.2 | β2 = 0 | β2 = 0.2 | β2 = 0.6 | β2 = 1.0 | |
|---|---|---|---|---|---|---|---|---|
| β1 = 0.4 | Observational | 0.349 | 0.381 | 0.398 | 0.400 | 0.398 | 0.381 | 0.349 |
| PLOR | 0.334 | 0.364 | 0.381 | 0.383 | 0.381 | 0.364 | 0.333 | |
| IV estimand | 0.337 | 0.367 | 0.383 | 0.385 | 0.383 | 0.367 | 0.337 | |
| Two-stage method | 0.338 | 0.367 | 0.383 | 0.385 | 0.383 | 0.367 | 0.337 | |
| Adjusted two-stage | 0.350 | 0.381 | 0.398 | 0.401 | 0.398 | 0.381 | 0.350 | |
|
| ||||||||
| β1 = 0.8 | Observational | −0.696 | −0.759 | −0.796 | −0.801 | −0.796 | -0.759 | −0.696 |
| PLOR | −0.627 | −0.672 | −0.697 | −0.700 | −0.697 | −0.672 | −0.627 | |
| IV estimand | −0.610 | −0.656 | −0.682 | −0.685 | −0.682 | −0.656 | −0.610 | |
| Two-stage method | −0.611 | −0.656 | −0.682 | −0.686 | −0.682 | −0.656 | −0.610 | |
| Adjusted two-stage | −0.696 | −0.759 | −0.796 | −0.801 | −0.796 | −0.760 | −0.696 | |
|
| ||||||||
| β1 = 1.2 | Observational | 1.033 | 1.133 | 1.193 | 1.201 | 1.193 | 1.132 | 1.033 |
| PLOR | 0.751 | 0.792 | 0.816 | 0.818 | 0.815 | 0.792 | 0.751 | |
| IV estimand | 0.774 | 0.817 | 0.842 | 0.845 | 0.842 | 0.817 | 0.774 | |
| Two-stage method | 0.775 | 0.817 | 0.842 | 0.845 | 0.842 | 0.818 | 0.774 | |
| Adjusted two-stage | 1.035 | 1.132 | 1.193 | 1.200 | 1.193 | 1.133 | 1.033 | |
Figure 5.
Population log odds ratio and IV estimand compared to median two-stage and adjusted two-stage estimates of log odds ratio for unit increase in risk factor from model of unconfounded association (Scenario 2) for varying for the covariate effect (β2) with conditional log odds ratio (β1) of 0.4 (left panel), −0.8 (middle panel, y-axis is inverted), and 1.2 (right panel)
4.7 Further simulations
The theoretical result for the two-stage method relies on the assumption that the IV has an equal effect in all individuals. In Appendices A.2 and A.3, we perform a series of simulations as a sensitivity analysis for the impact of varying the IV effect in individuals, as well as allowing for skewness in the risk factor distribution, IV–covariate interaction in the risk factor model, and risk factor–covariate interaction in the outcome model. These are performed to investigate how similar a realistic IV estimate, such as one from a Mendelian randomization study, would be to the estimate from a RCT. The median two-stage estimate remains close to the PLOR and IV estimand when the IV effect in each individual is drawn randomly from a normal distribution. We observe that the median two-stage estimate, PLOR and IV estimand all vary as the sensitivity parameters from skewness and interactions are varied. When there is no IV–covariate interaction, the median two-stage estimate is fairly close to the PLOR and IV estimand despite moderate skew and risk factor–covariate interaction. When there is IV–covariate interaction, the median two-stage estimate is noticeably biased compared to the PLOR and IV estimand, although the bias is only around a third of the standard deviation of the causal estimate across simulations for the examples considered.
In Appendix A.4, we perform a simulation in a case-control setting for a rare outcome. In this setting, the PLOR is different in the overall population and in the case-control sample, as the distributions of the risk factor and covariate differ. The first-stage regression of the two-stage and adjusted two-stage methods in this setting can be undertaken by weighting the participants in inverse proportion to their probability of being selected into the case-control sample [47]. If the risk factor measurement was made after the outcome event, the risk factor is often discarded to guard against reverse causation, and the first-stage regression is performed in the control participants only. We found that the two-stage method using the whole sample in the first-stage regression gave estimates close to the PLOR. The adjusted two-stage method gave biased results in this case, even with no covariate effect, similar to the bias of the adjusted two-stage method observed by Vansteelandt et al. under the null [3].
4.8 Interpretation of the adjusted two-stage estimand
In an idealized setting, where the first-stage residual is precisely the correct term to adjust for in the second-stage regression, the adjusted two-stage estimate is a consistent estimator of the CLOR [3, 41]. In model (11), this would occur if . However, when this is not true, the adjusted two-stage estimate is attenuated [42]. In the situation where none of the covariates for Y are associated with variation in X (i.e. there is no confounding), the residual in the adjusted two-stage method adjusts for the variation in X independent of that explained by the IV, leading to an estimate close to a marginal subject-specific odds ratio. However, in such a scenario, the same estimate could be obtained by direct regression of Y on X. A more realistic situation is where some of the variation in X is due to covariates associated with Y, but not all. This corresponds to model (11) with . Here, the residual is a combination of the independent variation in X and the covariate V, meaning that the adjusted two-stage analysis is conditional on some unknown combination of variation in Y. If there are additional covariates in Y not associated with X, as in Model (19), the odds ratio is marginal in these covariates. When the covariates are unknown, as is usual in an IV analysis, it is not clear what odds ratio is being estimated by an adjusted two-stage approach; that is, to what question is the adjusted two-stage estimate the answer. We return to this question of interpretation of IV estimates in the discussion.
5 Discussion
In this paper, we have seen how odds ratios differ depending on their exact definition. The magnitude of an odds ratio corresponding to an intervention depends on the choice of adjustment for competing risk factors, even if these are not confounders (i.e. not associated with the risk factor), and on whether the estimate is for a subject-specific or population-averaged change in the risk factor. This is due to non-collapsibility of the odds ratio. This effect is especially severe when there is considerable between-individual heterogeneity for the risk of an event. When there is confounding, instrumental variable methods can be used to target a quantity close to the population odds ratio using a two-stage approach, assuming that the IV only has a small effect on the risk factor. The population odds ratio is the probability limit of the incident odds ratio from an idealized RCT with intervention corresponding to a unit population intervention on the risk factor. By including the residuals from the first-stage regression in the second-stage analysis, an adjusted two-stage approach targets an odds ratio which may be closer to the target parameter from a traditional multivariable regression analysis, the subject-specific odds ratio conditional on covariates. However there is attenuation in the adjusted two-stage estimator from the conditional odds ratio when there is variation in X not explained by covariates for Y or variation in the logistic model for Y not associated with variation in X.
5.1 Application to Mendelian randomization
This finding has specific application to Mendelian randomization studies, as the ratio or two-stage method is regularly used in applied practice [45]. The first conclusion from this work is that naive comparison of odds ratio estimates from multivariable regression and from two-stage IV analysis is not strictly valid, as the two odds ratios represent different quantities. Although it is difficult to reliably quantify the degree of attenuation of the IV estimate, realistic simulation studies showed a maximal attenuation of 33%. Epidemiological data has shown attenuation of 5–14%, although this is likely to be an underestimate of the true attenuation as not all covariates are known in practice. The second conclusion is that odds ratio estimates from Mendelian randomization studies using the two-stage method are best interpreted as population-averaged causal effects.
With respect to the motivating example of Section 1.4, we conclude that it is difficult to directly compare the observational and IV estimates of the effect of CRP on CHD in a qualitative way. In this example, even though the IV estimate is compatible with the null, it is also compatible with being both a risk factor and a protective factor with a small magnitude of effect. This statistical reason, alongside other qualitative reasons [48], implies that if an investigator wishes to demonstrate a null result, she should not rely on demonstrating a statistically significant difference between the estimates. Rather, she should define a minimal clinically relevant effect beyond which she is satisfied with concluding that the exposure is of negligible importance if the confidence interval excludes this value.
5.2 Spectrum of odds ratios
Different odds ratios can be thought of as a forming a spectrum from the conditional odds ratio representing the effect for an individual with a given risk factor level and risk profile, to the population odds ratio representing the average effect for the given population. The value of the odds ratio attenuates as more variation in the outcome model is averaged across. In an idealized fully adjusted logistic model, all explainable variation in the outcome is explained and a conditional odds ratio is estimated. If not all covariates are included, a partially adjusted logistic model is estimated. Assuming that there is no bias from confounding, the estimate is attenuated towards the population odds ratio. If there were confounding, the partially adjusted model may give an estimate which is not consistent for any causal odds ratio and may even be in the opposite direction to the true causal association. Assuming that the outcome model is logistic-linear with no interaction terms, the adjusted two-stage estimate also lies between the conditional and population odds ratios as some of the variation in the risk factor is explained by the inclusion of the first-stage residuals, but generally not all of the variation. The two-stage estimate is more attenuated than the adjusted two-stage estimate, and is generally close to the population odds ratio, especially if the proportion of variation explained by the IV is small. The population odds ratio can be thought of as the estimate from an idealized RCT, representing the average effect of an intervention in the risk factor, marginal on all variation of the risk factor in the population.
5.3 Connection to existing literature and novelty
The appropriateness of the two-stage and adjusted two-stage methods have been the subject of recent discussion. Terza et al. [41] advocated adjusted two-stage methods as unbiased (for the CLOR) under certain circumstances as discussed in Section 4.8, as opposed to unadjusted two-stage methods, which are biased under all circumstances. Cai et al. [42] question the unbiasedness of the adjusted two-stage method, and provide independently the same derivation of the two-stage estimate as presented here. Harbord et al. [49] recognize the issue of the non-collapsibility of the two-stage estimate across the distribution of the confounder, and provide interesting limiting results for the attenuation of the two-stage estimate from the conditional odds ratio. However, they do not address the non-collapsibility of the odds ratio across the distribution of the risk factor. This paper adds to the debate by interpreting the estimate from the two-stage method as a population effect, interpreting the estimate from the adjusted two-stage method as marginal in a certain combination of covariates, and by separating the effects of non-collapsibility into those due to unmeasured covariates and those due to averaging over an intervention in the entire risk factor distribution. The latter is an important issue in Mendelian randomization, where the exposure is usually a continuous risk factor, as opposed to in clinical trials, the context of the Terza and Cai papers, where the exposure tends to be dichotomous.
Similarly, the estimation of population (or marginal) odds ratios has also been the subject of recent discussion, with papers by Vansteelandt et al. [3] and Stampf et al. [50] introducing methods specifically aimed at the estimation of marginal odds ratios.
5.4 Choice of target effect estimate
Generally, a population-averaged causal effect marginal across all covariates is the estimate of interest for a policy-maker as it represents the effect of intervention on the risk factor at a population level [3]. This is the effect estimated by a RCT without adjustment for covariates [51]. However, the mathematical properties of the population odds ratio are not as nice as those of the conditional odds ratio, in that the attenuation from the structural coefficient β1 in the underlying model depends on the size of the intervention, the amount of variation in the risk factor and the distribution of the covariates for the outcome.
An adjusted two-stage approach targets an odds ratio conditional on some unknown combination of variables. For this reason, although there is mathematical interest in the adjusted method, an untestable and usually implausible assumption of a specific form of the error structure is required for interpretation of the adjusted two-stage estimator, and so its use should not be recommended in applied practice. A better alternative would be to use covariates in the first- and second-stage IV regressions, so that under the hypothesis of no unmeasured confounding, the same conditional odds ratio is estimated in the IV and observational analyses.
In a logistic regression, adjustment for covariates does not necessarily increase precision of the regression coefficients [52] and the decision of which covariates to adjust for should be guided by both understanding of the underlying model and desired interpretation of the effect estimate [46, 53]. If we desire to estimate a population-averaged effect marginal across covariates then the two-stage method would seem appropriate. If estimation of a conditional parameter is desired, adjustment can be made in the two-stage model for specific covariates. Estimation of a fully conditional parameter requires complete knowledge of the covariates, although a conditional odds ratio could be estimated by using mathematical formulations of the attenuation of the population to the conditional odds ratio under assumptions about the direction and strength of the unmeasured covariates [54].
The non-collapsibility of the odds ratio limits the interpretation of estimates from two-stage IV analyses with binary outcomes. The main motivating factor for the use of odds ratios is that the same odds ratio is estimated in a logistic regression analysis of the population and of a case-control sample from the same population. With population odds ratios or even subject-specific odds ratios marginalized across a covariate, this property is not retained. This also leads to between-study heterogeneity in a meta-analysis. However, this problem is not unique to IV estimation: the same objection could be made in a conventional logistic regression analysis for the misspecified odds ratio estimated if not all covariates were measured and adjusted for.
5.5 Relevance of the two-stage estimand
The parameter estimated by a two-stage approach, termed the IV estimand in this paper, is not of intrinsic interest as an odds ratio parameter. Its interest lies firstly in the widespread use of the two-stage method, and the need for the interpretation of the parameter estimated by the approach. Secondly, the two-stage and adjusted two-stage estimands are of interest as they are similar to the odds ratios estimated by other IV methods. For example, in the case that the risk factor is normally distributed, the logistic structural mean model estimate is equivalent to that from an adjusted two-stage approach [3]. Thirdly, the IV estimand is of interest when it is close to the population odds ratio, a parameter of intrinsic natural interest. We note that the simulations presented were performed in the context of an IV which only explains a small proportion of the variation in the risk factor, as in Mendelian randomization. If the IV explained a large proportion of the variation in the risk factor, such as treatment assignment as an IV for treatment received in a RCT, the finding that the IV estimand and the population odds ratio are similar may not be valid. An alternative approach in this case is to use an alternative method which specifically targets a specific marginal or a conditional odds ratio [3].
5.6 “Forbidden” regressions
Much of the criticism of two-stage methods for IV estimation with non-linear models in econometric circles centres around the question of consistency of the estimator [55]. Although consistency is a desirable property, it would seem to be a less important property in the context of Mendelian randomization than coverage under the null. This is because the main focus of Mendelian randomization is identifying causal risk factors, not precise estimation of causal effects. The work in this paper suggests that the problem of consistency is one of interpretation of the IV estimate, rather than one of intrinsic bias of the method. As the two-stage odds ratio gives a valid test of the same null hypothesis, while caution should be expressed in comparing the magnitude of odds ratios estimating different quantities, it seems that there is no justification in labelling all such regressions as “forbidden” for reasons of consistency. This is especially true as some non-linear functions are collapsible, and so do not suffer from the problems highlighted in this paper.
5.7 Relevance to epidemiological practice
The two-stage IV method with a logistic outcome model has been criticized in the past for a lack of theoretical basis and for giving inconsistent or biased estimates even under the true model [19, 29, 41]. We have shown that this inconsistency is a property not of the two-stage approach, but of logistic regression in general. Although the inconsistency compared to the estimate from logistic regression can be partially rectified under certain assumptions by use of an adjusted method, where the first-stage residuals are included in the second-stage regression model, it is better resolved by correct interpretation of the causal odds ratio from the two-stage analysis as a marginal population-averaged effect, approximately equal to the estimate from a randomized trial.
Acknowledgement
The author would like to thank Simon G. Thompson (Cambridge), Jack Bowden (MRC Biostatistics Unit) and Stijn Vansteelandt (Ghent) for helpful discussions in the drafting of this paper.
CRP CHD Genetics Collaboration (CCGC) Collaborating Investigators: Cardiovascular Health Study (CHS): L Lange, A Reiner, M Cushman, R Tracy (see http://www.chs-nhlbi.org for acknowledgements); The Ludwigshafen Risk and Cardiovascular Health Study (LURIC): W März, M E Kleber, B O Böhm, B R Winkelmann; Prococious Coronary Artery Disease Study (PROCARDIS): H Watkins, R Clarke, J Hopewell; Rotterdam Study (ROTT): O H Franco, A Hofman, F J A van Rooij, A Dehghan; Stockholm Heart Epidemiology Program (SHEEP): U de Faire, A Bennet, B Gigante, K Leander.
CCGC Coordinating Centre: F. Wensley, University of Cambridge; S. Anand, McMaster University; J. Bowden, MRC Biostatistics Unit; S. Burgess, University of Cambridge; J.P. Casas, London School of Hygiene and Tropical Medicine; E. Di Angelantonio, University of Cambridge; J. Engert, McGill University; P. Gao, University of Cambridge; S. Kaptoge, University of Cambridge; M.B. Pepys, University College London Medical School; T. Shah, University College London; L. Smeeth, London School of Hygiene and Tropical Medicine; S.G. Thompson, University of Cambridge; C. Verzilli, London School of Hygiene and Tropical Medicine; M. Walker, University of Cambridge; S. Watson, University of Cambridge; J. Whittaker, London School of Hygiene and Tropical Medicine; S. Yusuf, McMaster University; A. Hingorani (co-principal investigator), University College London; J. Danesh (co-principal investigator), University of Cambridge. The coordinating centre is supported by grant SP/08/007 from the British Heart Foundation.
Appendix
A.1 IV estimand in a finite sample
We note that , and so we cannot make any conclusion about the expected value of the IV estimator without considering the joint distribution of and . To consider the potential impact of ignoring this correlation, we simulate data from the model:
| (A.1) |
Running the model across 100 000 simulations with a sample size of 100, we obtained a mean two-stage estimate of 0.9488 (Monte Carlo error: 0.0012); with a sample size of 1000, mean estimate 0.9296 (0.0004); with a sample size of 10 000, mean estimate 0.9275 (0.0001). This compares with the true value of of 0.9273. As the sample size increases, the impact of the correlation between the numerator and denominator on the IV estimate reduces, and the IV estimate is closer to the ratio of probability limits of the two regression coefficients, the IV estimand.
A.2 Simulation 3: varying instrument effects
Following concerns that the simulations in the paper are too restrictive and unrealistic, simulation 1 was repeated with the IV parameter of association for each individual being randomly assigned. These parameters (α1i) were drawn from a normal distribution with mean 0.3, as in the fixed parameter case, and variance 0.12.
| (A.2) |
Parameters in the simulation model were taken as in simulation 1. Results are given in Table A.1 for β1 = 0.4 and −0.8. We see that similar results are obtained to the fixed IV parameter case, with the population log odds ratio (PLOR), IV estimand, and median two-stage estimate all approximately equal.
Table A.1.
Observational log odds ratio, population log odds ratio (PLOR) and IV estimand compared to two-stage and adjusted two-stage estimates of log odds ratio for unit increase in risk factor from model of confounded association with varying IV effects (Scenario 3). Median estimates across 2 500 000 simulations
| Confounded association | β2 = −1.0 | β2 = −0.6 | β2 = −0.2 | β2 =0 | β2 = 0.2 | β2 = 0.6 | β2 = 1.0 | |
|---|---|---|---|---|---|---|---|---|
| β1 = 0.4 | Observational | −0.088 | 0.102 | 0.301 | 0.400 | 0.498 | 0.677 | 0.826 |
| PLOR | 0.372 | 0.389 | 0.389 | 0.383 | 0.372 | 0.340 | 0.303 | |
| IV estimand | 0.375 | 0.391 | 0.391 | 0.385 | 0.375 | 0.344 | 0.307 | |
| Two-stage method | 0.376 | 0.393 | 0.393 | 0.387 | 0.377 | 0.346 | 0.308 | |
| Adjusted two-stage | 0.377 | 0.394 | 0.400 | 0.400 | 0.398 | 0.387 | 0.366 | |
| β1 = 0.8 | Observational | −1.197 | −1.066 | −0.896 | −0.801 | −0.700 | −0.492 | −0.289 |
| PLOR | −0.539 | −0.606 | −0.672 | −0.700 | −0.723 | −0.750 | −0.750 | |
| IV estimand | −0.525 | −0.590 | −0.656 | −0.685 | −0.710 | −0.739 | −0.739 | |
| Two-stage method | −0.523 | −0.587 | −0.652 | −0.680 | −0.705 | −0.733 | −0.733 | |
| Adjusted two-stage | −0.746 | −0.781 | −0.800 | −0.801 | −0.797 | −0.778 | −0.748 | |
A.3 Simulation 4: allowing skewed distributions and interactions
We continue to relax the simulation model, allowing for a skewed distribution in the risk factor, interaction between the IV and covariate, and between the risk factor and covariate:
| (A.3) |
As in simulation 3 above, we allow the parameters of IV association to vary between participants. We take three sets of values for each of our sensitivity parameters (α3, β3, ψ) ∈ ({0, ±0.1}, {0, ±0.2}, {1,1.5, 1.5−1}). We perform 250 000 simulations in each the 33 = 27 scenarios with β1 = 0.4 and β2 = −0.6, −0.2, 0, 0.2, 0.6. All other parameters are taken as in simulation 1.
Results are given in in Table A.2 for the PLOR, IV estimand and median two-stage estimate. The Monte Carlo standard error in the median two-stage estimate is approximately 0.0005 throughout. We observe that not only does the median two-stage estimate vary for different values of the sensitivity parameters, but the PLOR and IV estimand also vary. When there is no IV-covariate interaction (α3 = 0), the median two-stage estimate remains close to the PLOR and IV estimand, despite moderate skew and risk factor-covariate interaction. When there is IV-covariate interaction, the median two-stage estimate is not always close to the PLOR or IV estimand, although the difference is rarely greater than 0.1, compared to the standard deviation of the two-stage estimates across each set of simulations of around 0.3.
A.4 Simulation 5: case-control setting
To consider the performance of the estimator in a case-control setting, data were simulated using the generating model from simulation 1 with a much lower prevalence of disease. This was achieved by setting β0 = −4.
| (A.4) |
A case-control sample was ascertained by including cases with probability 1 and non-cases with a fixed probability determined to give an approximately equal number of cases and controls. As stated in Section 5.4, the PLOR is different in the case-control sample and in the population. This is because the distributions of the risk factor and covariate differ between the samples, meaning that the probabilities in the odds function are integrated across different distributions. In the two-stage method, results are given using the risk factor in the whole population with a weighted first-stage regression [47], and using the risk factor in the controls only. In practice, often the risk factor measurements are taken after the event of interest, and hence are discarded in the cases to prevent possible bias by reverse causation. For the adjusted two-stage method, this is not possible, as the risk factor is needed for both cases and controls in the second-stage regression to provide a residual value. The weights in the weighted regression are the reciprocals of the probabilities of selection into the study. These weights can be easily calculated in a simulation setting. In a practical setting, they can be estimated by using the prevalence of the disease, or calculated exactly in a nested case-control study. In Table A.3, we give the PLOR in both the sample and the population as well as the median two-stage (risk factor taken in the entire case-control sample and in the controls only) and adjusted two-stage estimates across 250 000 simulations for β1 = 0.4 and −0.8.
We see that the PLOR in the sample is typically more attenuated than the PLOR in the population, which may reflect increased heterogeneity of risk levels between individuals in the case-control ascertained sample. The two-stage estimates using the whole sample in the first-stage regression are close to the PLOR in the population. The two-stage estimates using the controls only in the first-stage regression are slightly less attenuated than the two-stage stage estimates using the whole sample or the PLOR. The adjusted two-stage estimates are biased even with β2 = 0, a finding which echoes the bias of the adjusted two-stage estimator under the null found by Vansteelandt et al. [3]. An unintended consequence of the case-control setting was that extreme estimates from the IV methods became more common, although this appeared to be a problem of theoretical rather than practical consequence, as it occured in around a dozen of the 250 000 simulations for each scenario.
Table A.2.
Population log odds ratio (PLOR) and IV estimand compared to two-stage estimate of log odds ratio for unit increase in risk factor from model of confounded association with IV–covariate interaction (α3), risk factor–covariate interaction (β3), and skewed distribution of risk factor (ψ) (Scenario 4). Median estimates across 250 000 simulations
| α3 = 0 | α3 = −0.1 | α3 = +0.1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| β3 = | 0 | −0.2 | +0.2 | 0 | −0.2 | +0.2 | 0 | −0.2 | +0.2 | ||
| No skew: ψ = 1 | β2 = −0.6 | PLOR | 0.393 | 0.421 | 0.364 | 0.412 | 0.497 | 0.300 | 0.377 | 0.350 | 0.432 |
| IV estimand | 0.392 | 0.420 | 0.364 | 0.412 | 0.496 | 0.298 | 0.376 | 0.349 | 0.431 | ||
| Two-stage method | 0.389 | 0.421 | 0.371 | 0.389 | 0.422 | 0.370 | 0.390 | 0.419 | 0.372 | ||
| β2 = −0.2 | PLOR | 0.392 | 0.380 | 0.399 | 0.378 | 0.424 | 0.311 | 0.412 | 0.338 | 0.491 | |
| IV estimand | 0.392 | 0.378 | 0.400 | 0.377 | 0.424 | 0.310 | 0.412 | 0.337 | 0.491 | ||
| Two-stage method | 0.389 | 0.385 | 0.395 | 0.390 | 0.387 | 0.396 | 0.389 | 0.383 | 0.393 | ||
| β2 = 0 | PLOR | 0.386 | 0.355 | 0.406 | 0.356 | 0.386 | 0.310 | 0.423 | 0.327 | 0.502 | |
| IV estimand | 0.387 | 0.354 | 0.406 | 0.354 | 0.385 | 0.310 | 0.422 | 0.326 | 0.502 | ||
| Two-stage method | 0.383 | 0.363 | 0.396 | 0.384 | 0.365 | 0.398 | 0.382 | 0.361 | 0.393 | ||
| β2 = 0.2 | PLOR | 0.376 | 0.329 | 0.404 | 0.330 | 0.349 | 0.305 | 0.424 | 0.313 | 0.501 | |
| IV estimand | 0.377 | 0.329 | 0.404 | 0.332 | 0.348 | 0.305 | 0.423 | 0.313 | 0.502 | ||
| Two-stage method | 0.372 | 0.339 | 0.389 | 0.373 | 0.341 | 0.392 | 0.371 | 0.337 | 0.386 | ||
| β2 = 0.6 | PLOR | 0.345 | 0.280 | 0.380 | 0.287 | 0.281 | 0.287 | 0.403 | 0.279 | 0.473 | |
| IV estimand | 0.346 | 0.280 | 0.382 | 0.288 | 0.281> | 0.286 | 0.403 | 0.280 | 0.472 | ||
| Two-stage method | 0.340 | 0.291 | 0.362 | 0.342 | 0.293 | 0.366 | 0.339 | 0.290 | 0.359 | ||
| Positive skew: ψ = 1.5 | β2 = −0.6 | PLOR | 0.390 | 0.417 | 0.362 | 0.411 | 0.492 | 0.299 | 0.377 | 0.347 | 0.429 |
| IV estimand | 0.393 | 0.421 | 0.364 | 0.412 | 0.496 | 0.298 | 0.377 | 0.349 | 0.431 | ||
| Two-stage method | 0.388 | 0.418 | 0.369 | 0.388 | 0.419 | 0.368 | 0.388 | 0.416 | 0.369 | ||
| β2 = −0.2 | PLOR | 0.391 | 0.377 | 0.397 | 0.374 | 0.422 | 0.309 | 0.411 | 0.336 | 0.488 | |
| IV estimand | 0.392 | 0.378 | 0.401 | 0.376 | 0.423 | 0.311 | 0.412 | 0.337 | 0.492 | ||
| Two-stage method | 0.388 | 0.383 | 0.393 | 0.388 | 0.385 | 0.394 | 0.388 | 0.381 | 0.392 | ||
| β2 = 0 | PLOR | 0.385 | 0.352 | 0.405 | 0.355 | 0.384 | 0.310 | 0.421 | 0.326 | 0.501 | |
| IV estimand | 0.387 | 0.354 | 0.407 | 0.354 | 0.385 | 0.311 | 0.421 | 0.327 | 0.502 | ||
| Two-stage method | 0.382 | 0.361 | 0.395 | 0.383 | 0.364 | 0.397 | 0.381 | 0.359 | 0.392 | ||
| β2 = 0.2 | PLOR | 0.376 | 0.329 | 0.404 | 0.332 | 0.348 | 0.306 | 0.422 | 0.312 | 0.500 | |
| IV estimand | 0.377 | 0.329 | 0.404 | 0.331 | 0.348 | 0.306 | 0.423 | 0.313 | 0.502 | ||
| Two-stage method | 0.371 | 0.338 | 0.389 | 0.372 | 0.340 | 0.392 | 0.370 | 0.336 | 0.386 | ||
| β2 = 0.6 | PLOR | 0.345 | 0.279 | 0.380 | 0.289 | 0.282 | 0.287 | 0.403 | 0.281 | 0.472 | |
| IV estimand | 0.345 | 0.279 | 0.381 | 0.287 | 0.281 | 0.288 | 0.402 | 0.280 | 0.473 | ||
| Two-stage method | 0.340 | 0.291 | 0.362 | 0.342 | 0.293 | 0.366 | 0.338 | 0.289 | 0.359 | ||
| Negative skew: ψ = 1.5−1 | β2 = −0.6 | PLOR | 0.394 | 0.422 | 0.366 | 0.413 | 0.499 | 0.298 | 0.377 | 0.350 | 0.434 |
| IV estimand | 0.392 | 0.420 | 0.364 | 0.412 | 0.496 | 0.299 | 0.376 | 0.349 | 0.432 | ||
| Two-stage method | 0.390 | 0.423 | 0.373 | 0.390 | 0.425 | 0.372 | 0.391 | 0.422 | 0.374 | ||
| β2 = −0.2 | PLOR | 0.394 | 0.380 | 0.403 | 0.377 | 0.425 | 0.312 | 0.415 | 0.338 | 0.493 | |
| IV estimand | 0.392 | 0.378 | 0.401 | 0.377 | 0.423 | 0.310 | 0.412 | 0.337 | 0.492 | ||
| Two-stage method | 0.390 | 0.387 | 0.397 | 0.391 | 0.389 | 0.398 | 0.390 | 0.385 | 0.395 | ||
| β2 = 0 | PLOR | 0.388 | 0.354 | 0.409 | 0.355 | 0.385 | 0.311 | 0.425 | 0.327 | 0.506 | |
| IV estimand | 0.386 | 0.354 | 0.405 | 0.355 | 0.385 | 0.309 | 0.422 | 0.326 | 0.504 | ||
| Two-stage method | 0.384 | 0.364 | 0.397 | 0.385 | 0.366 | 0.399 | 0.383 | 0.362 | 0.394 | ||
| β2 = 0.2 | PLOR | 0.378 | 0.328 | 0.406 | 0.332 | 0.350 | 0.304 | 0.426 | 0.315 | 0.503 | |
| IV estimand | 0.377 | 0.328 | 0.404 | 0.331 | 0.349 | 0.307 | 0.422 | 0.312 | 0.501 | ||
| Two-stage method | 0.373 | 0.340 | 0.390 | 0.374 | 0.342 | 0.393 | 0.371 | 0.338 | 0.387 | ||
| β2 = 0.6 | PLOR | 0.345 | 0.280 | 0.381 | 0.289 | 0.282 | 0.288 | 0.403 | 0.280 | 0.473 | |
| IV estimand | 0.346 | 0.280 | 0.381 | 0.289 | 0.281 | 0.288 | 0.403 | 0.280 | 0.472 | ||
| Two-stage method | 0.341 | 0.292 | 0.362 | 0.343 | 0.293 | 0.366 | 0.339 | 0.290 | 0.359 | ||
Table A.3.
Population log odds ratio (PLOR) in the overall population and in a case-control sample compared to two-stage (IV–risk factor association was taken both in the entire case-control sample using a weighted first-stage regression, and in the controls only) and adjusted two-stage estimates of log odds ratio for unit increase in risk factor from modelof confounded association in a case-control setting (Scenario 5). Median estimates across 250 000 simulations
| Confounded association | β2 = −1.0 | β2 = −0.6 | β2 = −0.2 | β2 =0 | β2 = 0.2 | β2 = 0.6 | β2 = 1.0 | |
|---|---|---|---|---|---|---|---|---|
| β1 = 0.4 | PLOR in population | 0.393 | 0.398 | 0.398 | 0.396 | 0.393 | 0.377 | 0.347 |
| PLOR in sample | 0.390 | 0.397 | 0.397 | 0.395 | 0.390 | 0.363 | 0.317 | |
| Two-stage – sample | 0.393 | 0.398 | 0.398 | 0.397 | 0.394 | 0.381 | 0.353 | |
| Two-stage – controls | 0.392 | 0.399 | 0.400 | 0.399 | 0.397 | 0.386 | 0.361 | |
| Adjusted two-stage | 0.395 | 0.400 | 0.417 | 0.428 | 0.443 | 0.468 | 0.474 | |
| β1 = 0.8 | PLOR in population | −0.629 | −0.700 | −0.753 | −0.769 | −0.779 | −0.789 | −0.789 |
| PLOR in sample | −0.556 | −0.635 | −0.713 | −0.743 | −0.764 | −0.783 | −0.783 | |
| Two-stage – sample | −0.611 | −0.683 | −0.741 | −0.760 | −0.773 | −0.783 | −0.784 | |
| Two-stage – controls | −0.651 | −0.718 | −0.769 | −0.783 | −0.792 | −0.795 | −0.792 | |
| Adjusted two-stage | −0.991 | −1.028 | −1.016 | −0.988 | −0.955 | −0.878 | −0.819 | |
Footnotes
This work was supported by the Wellcome Trust 100114.
References
- [1].Didelez V, Sheehan N. Mendelian randomization as an instrumental variable approach to causal inference. Statistical Methods in Medical Research. 2007;16(4):309–330. doi: 10.1177/0962280206077743. doi:10.1177/0962280206077743. [DOI] [PubMed] [Google Scholar]
- [2].Hosmer D, Lemeshow S. Applied logistic regression. Vol. 354. Wiley-Interscience; 2000. [Google Scholar]
- [3].Vansteelandt S, Bowden J, Babanezhad M, Goetghebeur E. On instrumental variables estimation of causal odds ratios. Statistical Science. 2011;26(3):403–422. doi:10.1214/11-sts360. [Google Scholar]
- [4].Greenland S. An introduction to instrumental variables for epidemiologists. International Journal of Epidemiology. 2000;29(4):722–729. doi: 10.1093/ije/29.4.722. doi:10.1093/ije/29.4.722. [DOI] [PubMed] [Google Scholar]
- [5].Martens E, Pestman W, de Boer A, Belitser S, Klungel O. Instrumental variables: application and limitations. Epidemiology. 2006;17(3):260–267. doi: 10.1097/01.ede.0000215160.88317.cb. doi: 10.1097/01.ede.0000215160.88317.cb. [DOI] [PubMed] [Google Scholar]
- [6].Zohoori N, Savitz D. Econometric approaches to epidemiologic data: Relating endogeneity and unobserved heterogeneity to confounding. Annals of Epidemiology. 1997;7(4):251–257. doi: 10.1016/s1047-2797(97)00023-9. doi:10.1016/s1047-2797(97)00023-9. [DOI] [PubMed] [Google Scholar]
- [7].Angrist J, Imbens G, Rubin D. Identification of causal effects using instrumental variables. Journal of the American Statistical Association. 1996;91(434):444–455. [Google Scholar]
- [8].Davey Smith G, Ebrahim S. ‘Mendelian randomization’: can genetic epidemiology contribute to understanding environmental determinants of disease? International Journal of Epidemiology. 2003;32(1):1–22. doi: 10.1093/ije/dyg070. doi:10.1093/ije/dyg070. [DOI] [PubMed] [Google Scholar]
- [9].Schatzkin A, Abnet C, Cross A, Gunter M, Pfeiffer R, Gail M, Lim U, Davey Smith G. Mendelian randomization: how it can – and cannot – help confirm causal relations between nutrition and cancer. Cancer Prevention Research. 2009;2(2):104–113. doi: 10.1158/1940-6207.CAPR-08-0070. doi:10.1158/1940-6207.capr-08-0070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Davey Smith G. Use of genetic markers and gene-diet interactions for interrogating population-level causal influences of diet on health. Genes & Nutrition. 2010;6(1):27–43. doi: 10.1007/s12263-010-0181-y. doi:10.1007/s12263-010-0181-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Nitsch D, Molokhia M, Smeeth L, DeStavola B, Whittaker J, Leon D. Limits to causal inference based on Mendelian randomization: a comparison with randomized controlled trials. American Journal of Epidemiology. 2006;163(5):397–403. doi: 10.1093/aje/kwj062. doi:10.1093/aje/kwj062. [DOI] [PubMed] [Google Scholar]
- [12].Emerging Risk Factors Collaboration C-reactive protein concentration and risk of coronary heart disease, stroke, and mortality: an individual participant meta-analysis. The Lancet. 2010;375(9709):132–140. doi: 10.1016/S0140-6736(09)61717-7. doi:10.1016/S0140-6736(09)61717-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].CRP CHD Genetics Collaboration Association between C reactive protein and coronary heart disease: Mendelian randomisation analysis based on individual participant data. British Medical Journal. 2011;342:d548. doi: 10.1136/bmj.d548. doi:10.1136/bmj.d548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Greenland S, Robins J, Pearl J. Confounding and collapsibility in causal inference. Statistical Science. 1999;14(1):29–46. doi:10.1214/ss/1009211805. [Google Scholar]
- [15].Whittemore A. Collapsibility of multidimensional contingency tables. Journal of the Royal Statistical Society: Series B (Methodological) 1978;40(3):328–340. [Google Scholar]
- [16].Geng Z. Collapsibility of relative risk in contingency tables with a response variable. Journal of the Royal Statistical Society: Series B (Methodological) 1992;54(2):585–593. [Google Scholar]
- [17].Ducharme G, LePage Y. Testing collapsibility in contingency tables. Journal of the Royal Statistical Society: Series B (Methodological) 1986;48(2):197–205. [Google Scholar]
- [18].Hauck W, Anderson S, Marcus S. Should we adjust for covariates in nonlinear regression analyses of randomized trials? Controlled Clinical Trials. 1998;19(3):249–256. doi: 10.1016/s0197-2456(97)00147-5. doi:10.1016/S0197-2456(97)00147-5. [DOI] [PubMed] [Google Scholar]
- [19].Palmer T, Thompson J, Tobin M, Sheehan N, Burton P. Adjusting for bias and unmeasured confounding in Mendelian randomization studies with binary responses. International Journal of Epidemiology. 2008;37(5):1161–1168. doi: 10.1093/ije/dyn080. doi: 10.1093/ije/dyn080. [DOI] [PubMed] [Google Scholar]
- [20].Dawid A. Influence diagrams for causal modelling and inference. International Statistical Review. 2007;70(2):161–189. doi:10.1111/j.1751-5823.2002.tb00354.x. [Google Scholar]
- [21].Pearl J. Causality: models, reasoning, and inference. Cambridge University Press; 2000. [Google Scholar]
- [22].Pearl J. Causal diagrams for empirical research. Biometrika. 1995;82(4):669–688. doi:10.1093/biomet/82.4.669. [Google Scholar]
- [23].Greenland S. Interpretation and choice of effect measures in epidemiologic analyses. American Journal of Epidemiology. 1987;125(5):761–768. doi: 10.1093/oxfordjournals.aje.a114593. [DOI] [PubMed] [Google Scholar]
- [24].Tan Z. Marginal and nested structural models using instrumental variables. Journal of the American Statistical Association. 2010;105(489):157–169. doi: 10.1198/jasa.2009.tm08299. [Google Scholar]
- [25].Zeger S, Liang K, Albert P. Models for longitudinal data: a generalized estimating equation approach. Biometrics. 1988;44(4):1049–1060. [PubMed] [Google Scholar]
- [26].Greenland S. Model-based estimation of relative risks and other epidemiologic measures in studies of common outcomes and in case-control studies. American Journal of Epidemiology. 2004;160(4):301–305. doi: 10.1093/aje/kwh221. doi:10.1093/aje/kwh221. [DOI] [PubMed] [Google Scholar]
- [27].Dawid A. Influence diagrams for causal modelling and inference. International Statistical Review. 2002;70(2):161–189. doi:10.1111/j.1751-5823.2002.tb00354.x. [Google Scholar]
- [28].Clarke P, Windmeijer F. Instrumental variable estimators for binary outcomes. Centre for Market and Public Organisation, University of Bristol; UK: 2010. (The Centre for Market and Public Organisation 10/239). [Google Scholar]
- [29].Didelez V, Meng S, Sheehan N. Assumptions of IV methods for observational epidemiology. Statistical Science. 2010;25(1):22–40. doi:10.1214/09-sts316. [Google Scholar]
- [30].Wald A. The fitting of straight lines if both variables are subject to error. Annals of Mathematical Statistics. 1940;11(3):284–300. [Google Scholar]
- [31].Angrist J, Graddy K, Imbens G. The interpretation of instrumental variables estimators in simultaneous equations models with an application to the demand for fish. Review of Economic Studies. 2000;67(3):499–527. doi:10.1111/1467-937x.00141. [Google Scholar]
- [32].von Hinke Kessler Scholder S, Davey Smith G, Lawlor D, Propper C, Windmeijer F. Genetic markers as instrumental variables: An application to child fat mass and academic achievement. Department of Economics, University of Bristol; UK: 2010. (The Centre for Market and Public Organisation 10/229). [Google Scholar]
- [33].Tobin M, Minelli C, Burton P, Thompson J. Commentary: Development of Mendelian randomization: from hypothesis test to ‘Mendelian deconfounding’. International Journal of Epidemiology. 2004;33(1):26–29. doi: 10.1093/ije/dyh016. doi: 10.1093/ije/dyh016. [DOI] [PubMed] [Google Scholar]
- [34].Thompson J, Minelli C, Abrams K, Tobin M, Riley R. Meta-analysis of genetic studies using Mendelian randomization – a multivariate approach. Statistics in Medicine. 2005;24(14):2241–2254. doi: 10.1002/sim.2100. doi:10.1002/sim.2100. [DOI] [PubMed] [Google Scholar]
- [35].Palmer T, Sterne J, Harbord R, Lawlor D, Sheehan N, Meng S, Granell R, Davey Smith G, Didelez V. Instrumental variable estimation of causal risk ratios and causal odds ratios in Mendelian randomization analyses. American Journal of Epidemiology. 2011;173(12):1392–1403. doi: 10.1093/aje/kwr026. doi:10.1093/aje/kwr026. [DOI] [PubMed] [Google Scholar]
- [36].Lawlor D, Harbord R, Sterne J, Timpson N, Davey Smith G. Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Statistics in Medicine. 2008;27(8):1133–1163. doi: 10.1002/sim.3034. doi:10.1002/sim.3034. [DOI] [PubMed] [Google Scholar]
- [37].Bowden R, Turkington D. Instrumental variables. Cambridge University Press; 1990. [Google Scholar]
- [38].Angrist J, Pischke J. Mostly harmless econometrics: an empiricist’s companion. Chapter 4: Instrumental variables in action: sometimes you get what you need. Princeton University Press; 2009. [Google Scholar]
- [39].Rassen J, Schneeweiss S, Glynn R, Mittleman M, Brookhart M. Instrumental variable analysis for estimation of treatment effects with dichotomous outcomes. American Journal of Epidemiology. 2009;169(3):273–284. doi: 10.1093/aje/kwn299. doi: 10.1093/aje/kwn299. [DOI] [PubMed] [Google Scholar]
- [40].Foster E. Instrumental variables for logistic regression: an illustration. Social Science Research. 1997;26(4):487–504. doi:10.1006/ssre.1997.0606. [Google Scholar]
- [41].Terza J, Basu A, Rathouz P. Two-stage residual inclusion estimation: addressing endogeneity in health econometric modeling. Journal of Health Economics. 2008;27(3):531–543. doi: 10.1016/j.jhealeco.2007.09.009. doi:10.1016/j.jhealeco.2007.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Cai B, Small D, Ten Have T. Two-stage instrumental variable methods for estimating the causal odds ratio: Analysis of bias. Statistics in Medicine. 2011;30(15):1809–1824. doi: 10.1002/sim.4241. doi:10.1002/sim.4241. [DOI] [PubMed] [Google Scholar]
- [43].Wooldridge J. Econometric analysis of cross section and panel data. MIT Press; 2002. [Google Scholar]
- [44].Nagelkerke N, Fidler V, Bernsen R, Borgdorff M. Estimating treatment effects in randomized clinical trials in the presence of non-compliance. Statistics in Medicine. 2000;19(14):1849–1864. doi: 10.1002/1097-0258(20000730)19:14<1849::aid-sim506>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- [45].Bochud M, Rousson V. Usefulness of Mendelian randomization in observational epidemiology. International Journal of Environmental Research and Public Health. 2010;7(3):711–728. doi: 10.3390/ijerph7030711. doi:10.3390/ijerph7030711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Ford I, Norrie J. The role of covariates in estimating treatment effects and risk in long-term clinical trials. Statistics in Medicine. 2002;21(19):2899–2908. doi: 10.1002/sim.1294. doi: 10.1002/sim.1294. [DOI] [PubMed] [Google Scholar]
- [47].Bowden J, Vansteelandt S. Mendelian randomisation analysis of case-control data using structural mean models. Statistics in Medicine. 2011;30(6):678–694. doi: 10.1002/sim.4138. doi: 10.1002/sim.4138. [DOI] [PubMed] [Google Scholar]
- [48].Burgess S, Butterworth A, Malarstig A, Thompson S. Use of Mendelian randomisation to assess potential benefit of clinical intervention. British Medical Journal. 2012;345:e7325. doi: 10.1136/bmj.e7325. doi:10.1136/bmj.e7325. [DOI] [PubMed] [Google Scholar]
- [49].Harbord R, Didelez V, Palmer T, Meng S, Sterne J, Sheehan N. Severity of bias of a simple estimator of the causal odds ratio in Mendelian randomization studies. Statistics in Medicine. 2012 doi: 10.1002/sim.5659. doi:10.1002/sim.5659. [DOI] [PubMed] [Google Scholar]
- [50].Stampf S, Graf E, Schmoor C, Schumacher M. Estimators and confidence intervals for the marginal odds ratio using logistic regression and propensity score stratification. Statistics in Medicine. 2010;29(7-8):760–769. doi: 10.1002/sim.3811. doi: 10.1002/sim.3811. [DOI] [PubMed] [Google Scholar]
- [51].Stukel T, Fisher E, Wennberg D, Alter D, Gottlieb D, Vermeulen M. Analysis of observational studies in the presence of treatment selection bias. Journal of the American Medical Association. 2007;297(3):278–285. doi: 10.1001/jama.297.3.278. doi: 10.1001/jama.297.3.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Robinson L, Jewell N. Some surprising results about covariate adjustment in logistic regression models. International Statistical Review. 1991;59(2):227–240. [Google Scholar]
- [53].Steyerberg E, Bossuyt P, Lee K. Clinical trials in acute myocardial infarction: Should we adjust for baseline characteristics? American Heart Journal. 2000;139(5):745–751. doi: 10.1016/s0002-8703(00)90001-2. [DOI] [PubMed] [Google Scholar]
- [54].Gail M, Wieand S, Piantadosi S. Biased estimates of treatment effect in randomized experiments with nonlinear regressions and omitted covariates. Biometrika. 1984;71(3):431–444. [Google Scholar]
- [55].Hausman J. Handbook of econometrics. Vol. 1. Elsevier; 1983. pp. 391–448. chap. Specification and estimation of simultaneous equation models. See footnote 60. [Google Scholar]