Thermodynamic basis of selectivity in guide-target-mismatched RNA interference

Abstract

Silencing in RNAi is strongly affected by guide-strand/target-mRNA mismatches. Target nucleation is thought to occur at positions 2–8 of the guide (“seed region”); successful hybridization in this region is the primary determinant of target binding affinity and hence target cleavage. To define a molecular basis for the target sequence selectivity in RNAi, we studied all possible distinct single mismatches in seven positions of the seed region — a total of 21 substitutions. We report results from soft-core thermodynamic integration simulations to determine changes in target binding free energies to Argonaute due to single mismatches in the guide strand, which arise during binding of an imperfectly matched target mRNA. In agreement with experiment, most mismatches impair target binding, consistent with a prominent role for binding affinity changes in RNAi sequence selectivity. Individual Argonaute residues located near the mismatched base pair are found to contribute significantly to binding affinity changes. We also employ this methodology to analyze the mismatch-dependent free energy changes for dissociation of a DNA·RNA hybrid from Argonaute, as a model for the escape of miRNAs from the silencing pathway. Several mismatched sequences of the miRNA have increased affinity to Argonaute, implying that some mismatches may reduce the probability for escape. Furthermore, calculations of base-substitution-dependent free energy changes for binding ssDNA reveal mild sequence sensitivity as expected for guide strand binding to Argonaute. Our findings give a thermodynamic basis for RNAi target sequence selectivity and suggest that miRNA mismatches may increase silencing effectiveness and thus could be evolutionarily advantageous.

1 Introduction

RNA interference (RNAi) is a fundamental mechanism for regulating the expression of genes in a variety of contexts. It is a process by which short RNAs can induce sequence-specific silencing of genes at the post-transcriptional stage, preventing their translation into proteins, mediated by a member of the Argonaute family of proteins ¹. In addition to its importance in gene regulation at homeostasis, RNAi is important in various other biological processes. For example, it has been implicated in the normal function of the immune system ² as well as in heterochromatin formation ³ and regulation of development ⁴. Additionally, it is important in various pathologies such as infectious tropical diseases and tumorigenesis ⁵. RNAi has found widespread application at the bench as the biochemical mechanism underlying gene knockdowns. The use of RNAi as a therapeutic vector for the suppression of specific genes (of the host or of a virus) to yield a positive clinical outcome is an active area of research ^6–8. The ability of RNAi to silence mRNAs that are not fully complementary to the guide strand is critical to RNAi function in any context. Mismatch tolerance enables a single guide strand to silence a variety of mRNAs ⁹. The specific set of genes silenced, and to what extent each gene is silenced, is dependent on how the function of the Argonaute complex is influenced by the mismatches between guide and target. This resulting ambiguity has profound sequelae: for example, if mismatches are tolerated a single guide could potentially inactivate multiple proteins involved in multiple pathways, yielding wide-ranging effects. In the context of therapeutics this may result in deleterious side effects — for example, a putative therapy for Huntington’s disease depends on the ability of siRNAs to discriminate mRNAs that differ by a single base ¹⁰. In this work, we examine the thermodynamic basis of sequence selectivity in RNAi, encompassing both mismatch tolerance and rejection of singly-mismatched targets, by studying target binding free energy change conferred by mismatches between guide and target strands.

Two of the earliest RNA interference processes to be discovered were the siRNA and miRNA target cleavage pathways ^11–15. In the siRNA pathway, cytoplasmic dsRNA, exogenous or genomic, is sliced into ~21 base pair siRNAs with 5′ overhangs by Dicer, an RNase-III-family enzyme ¹⁶. In contrast, miRNAs are encoded in the genome. The miRNA transcript, pri-miRNA, is processed in the nucleus by Drosha. The resulting pre-miRNA is exported into the cytoplasm and sliced by Dicer as in the siRNA pathway to yield a short dsRNA. At this point the separate pathways converge; the siRNA or miRNA may be used in three different ways. They may be either loaded into the Argonaute-containing RNA Induced Silencing Complex (RISC, described below), or they may bind to an Argonaute protein that cannot cleave RNA, or to a translation regulatory protein ¹⁷. In RISC, the strand with the less thermodynamically stable base pairing at the 5′ end is retained as the “guide strand” ^18,19. This strand serves as a template against which putative mRNA targets are matched and cleaved. The other strand, the “passenger strand”, is cleaved and jettisoned. However, if there are several mismatches between the passenger and the guide strands, the passenger strand may instead dissociate without being cleaved. This is common in the miRNA pathway ²⁰. The entire dsRNA may also dissociate without progressing further in the pathway, releasing the Argonaute.

The key mediator of RNAi in these pathways, RISC, is a multimeric protein complex ¹¹ that includes the nucleic acid guide strand. Successful hybridization of the guide strand and target mRNA positions the target such that RISC can silence the mRNA by cleaving it at a predefined position, between nucleotides 10 and 11, measured with respect to the 5′-end of the guide strand. The exact composition of RISC is not known. In many organisms it is likely to include GW182, a protein whose depletion attenuates silencing, though its mechanism is controversial ²¹. However, the catalytically active central component is known to be one of several members of the Argonaute family ²², depending on the organism and the particular RNAi pathway. This cleavage-competent Argonaute protein binds a guide strand and has RNAi activity (albeit reduced) even in the absence of the other RISC components ^23,24 and is the focus of this work.

Argonaute proteins, first identified in plants, are defined by the presence of PAZ (Piwi-Argonaute-Zwille) and PIWI domains, and they also contain a Mid domain that is critical for substrate binding ^{22,23,25–31}. Argonaute proteins are highly conserved and many species have more than one type. In humans, for example, there exist eight Argonautes, of which Argonaute2 is the RNAi-silencing-active protein ²⁷. Argonautes have been shown to have both transcriptional and post-transcriptional gene regulation activity. They bind short dsRNAs like siRNA and miRNA. Some Argonautes have ribonuclease H-like active sites in the PIWI domain, which allow them to cleave RNAs; this functionality has been called “slicer” activity and is prominent in RISC ²⁸. The structure of Pyrococcus furiosus Argonaute in the free form ²⁹ revealed the arrangement of the key domains in a catalytically-competent Argonaute. This arrangement suggested that a guide-target dsRNA could bind to Argonaute in a specific orientation: with the 3′-end of the guide strand complexed to the PAZ, and the catalytic motif of the PIWI domain positioned to cleave the target between nucleotides 10 and 11. The structure and the proposed binding of dsRNA were consistent with previous crystal structures of PAZ, PIWI and Argonaute proteins ^29,32,33, as well as experimental evidence demonstrating this cleavage position ^23,30,31.

For a target mRNA to be cleaved, it must form a ternary complex in which the mRNA hybridizes to a guide strand that is itself bound to Argonaute. In this complex, nucleotides 10 and 11 of the target (measured with respect to the 5′ end of the guide) are positioned close to the catalytic residues in the PIWI domain, allowing for target cleavage. The mechanism of formation of this complex has been a subject of several studies ^11,12,34 because it is an important determinant of the rate of target cleavage. In particular, a number of experiments have provided insight into the role of the seed region — nucleotides 2–10 of the guide strand — in the formation of the ternary complex. In the fully-matched Drosophila melanogaster RISC, mismatches in the 5′ region of the guide were shown to primarily affect K_M while mismatches in the 3′ region were shown to primarily affect k_cat, suggesting that the seed region is the primary determinant of substrate binding affinity ³⁴. Mismatches and bulges in the seed region were usually not well-tolerated ^23,35,36. Guide strands as short as 9 nucleotides, provided they included the seed region, were shown to be effective cleavage-enabling anchors for target RNAs in T. thermophilus Argonaute (TtAgo) ³⁵. The recent determination of several TtAgo-guide-target crystal structures at various extents of hybridization provides a model for this binding ³⁵, suggesting that the binding of a target RNA strand to the Ago-guide complex begins in the seed region and progresses in a 3′ direction ³⁷. These TtAgo structures clearly show base pairs 2–12 of guide DNA-target RNA hybrids, with position 1 unpaired. Once the seed region is hybridized, binding of the target must progress in the 3′ direction. These structures position the cleavage site of the target RNA close to the Argonaute catalytic region. This model of target RNA binding suggests that nucleation in the seed region is necessary for cleavage of the target to occur.

Several investigators have studied the cleavage activity of Argonaute complexes as a function of the presence, location, and type of guide-target mismatch. For example, a study of the effect of single mismatches on catalysis in the Drosophila RISC ³⁶ showed that the cleavage rate depended strongly on the position and type of the mismatch, though no kinetic analysis was conducted. Similar single-mismatch studies in A. aeolicus Argonaute ²³ (AaAgo) and TtAgo ²⁴ also showed that the degree of decrease in catalysis is dependent on the position and type of mismatch, in particular confirming the importance of the seed region, though also without analyzing the kinetics of the reaction. Mutation of a given RNA residue resulting in a specific mismatch in the guide-target hybrid may yield significantly different reductions in catalysis depending on the location and nature of the mismatch ^24,36. The mechanism underlying this observation is unclear. No study to date has described specifically the changes in substrate binding affinity, separately from catalysis, due to single mismatches in these prokaryotic Argonaute complexes. Furthermore, the selectivity of substitutions in each position of the guide strand has not been investigated. Since selectivity depends on the ensemble of all substitutions, such an undertaking requires an intense computational or experimental effort. Using the TtAgo complex crystal structure as a model, we investigated the changes in substrate binding affinity by evaluating, in a particular sequence, all possible guide strand single-base substitutions in seven consecutive positions in the seed region. Of note, this is a very large study providing new insights into structural and energetic elements influenced by the modified geometry of mismatched base pairs that contribute to the experimentally-determined decrease in silencing efficiency. For the first time it also gives the selectivity of each position within the limited sequences studied here. We show that there are two sources to the mismatch contribution to the reduction in binding energy and impaired activity. One originates from the mismatch alone while the other comes from the protein that exhibits an ability to discriminate between different mismatches in the same position as well as the same mismatches in different positions along the sequence.

2 Materials and Methods

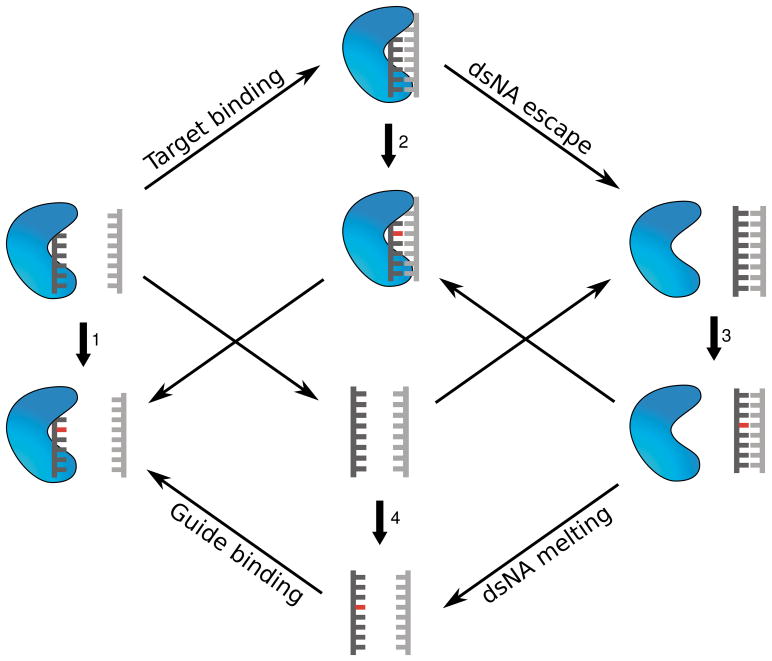
We wished to calculate the effect of a guide-target mismatch on the free energy changes due to various binding processes important in RNAi. Conceptually, the effect of a mismatch on the binding free energy (ΔΔG) can be estimated by calculating the ΔG of alchemical transformations using thermodynamic integration (TI) in a thermodynamic cycle depicted in Figure 1. Focusing on paths 1 and 2, the change of one base to another introduces a relatively small perturbation that is computable with TI. Using these results, the thermodynamic cycle allows us to calculate the binding energy of a mismatched sequence relative to that of a fully matched one, without simulating the binding event itself — which would involve a larger structural rearrangement that would require a vastly larger amount of configurational sampling. In this manner, TI has been successfully used to calculate relative binding free energies of RNA and protein ³⁸ as well as various ligands and proteins ³⁹.

Figure 1.

System of coupled thermodynamic cycles. Each endpoint is derived from ²⁴ (PDB accession number 3F73). TtAgo is represented as the blue structure, the guide strand in dark gray, and the target stand in light gray. The red-colored base represents a mutation from the sequence present in the crystal structure. Each set of diagonal arrows depicts a binding process. There is a ΔG value associated with each change, depicted by an arrow and numbered for convenience. Introducing a mutation in the endpoints (depicted by the vertical arrows) modulates the free energy change ΔG for that process by some value ΔΔG, which was calculated by thermodynamic integration. By construction, the sum of free energy changes around any closed loop is zero.

A brief summary of the TI method used here is provided. In TI, the molecular mechanics potential function V is interpolated between the endpoint states of interest ^2,40. V is dependent on the configuration of the system and non-physical coordinate λ that couples the two states V₀ and V₁ (a well-known approach, detailed in, e.g., ⁴¹):

$$V(\lambda )=f(\lambda )V_0+[1-f(\lambda )]V_1$$

At each point, an ensemble average of the derivative of the potential energy function with respect to the coupling parameter λ is taken. Integrating these averages yields the free energy change:

$$\mathrm{\Delta }G={\int }_0^1{\langle \frac{dV(\lambda )}{d\lambda }\rangle }_{\lambda }d\lambda$$

where the angled brackets denote an ensemble average at a given λ. In practice, λ is sampled at a small number of points and a numerical integration scheme is employed. In this study, Gaussian quadrature was used, sampling λ at 9 points. The potential function V is modified to include “soft-core” terms that modify the van der Waals and electrostatics terms to prevent simulation instabilities when a pair of particles is at close range ⁴². The interpolation function f is usually defined as linear when soft-core terms are used, though this is not strictly required. The van der Waals potential is calculated as the modified Lennard-Jones potential

$$V_{\text{vdW}}=4\epsilon \left({\left[\alpha \lambda +{(r/\rho )}^6\right]}^{-2}-{\left[\alpha \lambda +{(r/\rho )}^6\right]}^{-1}\right)$$

and the electrostatic interactions are calculated as the modified Coulomb’s Law

$$V_{\text{eel}}=\frac{q_i{q}_j}{4\pi \epsilon \sqrt{\beta \lambda +r^2}}$$

where ρ and ε are the standard Lennard-Jones parameters and α and β are parameters that must be tuned such that the resulting dV/dλ energy curve is smooth, in order to minimize numerical integration error. (For clarity, the complications introduced by interaction cutoffs and periodic boundary conditions are omitted here.) When α and β are set to zero, the original Lennard-Jones and Coulomb’s equations are recovered. In this study, α was set to 0.5 and β was set to 16 Ų. These parameters yielded smooth energy curves in preliminary testing.

The well-known molecular dynamics (MD) method was employed here to sample the potential energy function as required by TI. As we sought to reproduce effects due to perturbations at the atom level, in the ground state and without breaking or forming any bonds within a simulation, an all-atom force field parameterized for the simulation of large proteins and nucleic acids was used, as described below. Specifically with regard to Argonaute proteins, all-atom MD has been shown to accurately reproduce characteristics such as structural B-factors ⁴³ and domain flexibility ^25,26 as determined by x-ray crystallography. The ability of all-atom MD to produce results consistent with experiment for Argonaute-family proteins suggests that its use in the current context is appropriate, although it is important to work within the inherent limitations of the method. Since by the ergodic hypothesis time averages are considered equal to statistical ensemble averages, simulations should be of length sufficient to approximate the true ensemble average. In general, MD preferentially accesses low-energy states since these are the most probable; any high-energy states that may contribute significantly to the ensemble average might not be sampled at all given the practical limitations of conducting extensive MD simulations. For TI, sampling requirements are also increased when the two states V₀ and V₁ are dissimilar. We addressed these issues by limiting alchemical changes between states to relatively few atoms and carefully monitoring the convergence of our results. This is further described in the simulation and analysis protocol below.

Preparation of structures

The Argonaute-guide-target structure (ternary complex) from which all the simulated structures were derived was prepared from a crystal structure of Thermus thermophilus Argonaute (TtAgo) loaded with a guide-target DNA·RNA hybrid ²⁴ (PDB accession number 3F73). The 3F73 structure is one of several available TtAgo ternary complex structures; other primary candidates have PDB accession numbers 3HO1, 3HJF, 3HK2, 3HM9, 3HVR, and 3HXM ³⁵. These structures represent different stages in the RNAi guide-target binding process. The 3F73 structure was both without mutation in the active site (as in 3HO1, 3HJF, and 3HK2) and had considerably fewer unresolved amino acid residues than all other candidates, minimizing the requirement for de novo loop modeling to render the structure suitable for simulation.

In order to approximate a catalytically competent configuration, two Mg²⁺ ions were positioned in the active site by analogy with the active site configuration of an RNase H complex bound to a DNA·RNA hybrid ⁴⁴ (PDB accession number 1ZBI). Loops unresolved in the crystal structures, all distant from the catalytic region and binding groove, were predicted using MODELLER ⁴⁵. The nucleic-acid-only structure was constructed by removing the Argonaute and Mg²⁺ ions from the ternary complex. All structures were solvated with TIP3P waters in a truncated octahedral box and neutralized with Na⁺ ions. Mismatched structures were produced by manually substituting the base in question on the guide strand. The mismatched base pair conformation was constructed by analogy with similar base pairs in the Non-canonical Base Pair Database ⁴⁶, subject to the necessity of avoiding steric clashes with the surrounding structure.

The Argonaute-guide structure (binary complex) was constructed by removing the target strand and Mg²⁺ ions from the ternary complex rather than using the existing binary complex crystal structure 3DLH. This was done to minimize the number of structural perturbations in the thermodynamic cycle. The separation of the target strand from the ternary complex to form a binary complex involves (a) the separation itself and (b) relaxation of the resulting binary complex into a 3DLH-like form. Step (b) would be an energetically favorable process that is common to all guide sequences, so we can omit it in the current consideration. In addition, the 3DLH structure has considerably more unresolved protein residues that would require de novo loop modeling.

The force fields employed were the AMBER99SB all-atom force field with ParmBSC0 nucleic acid corrections ⁴⁷, TIP3P waters ⁴⁸, and the MD6 dummy-atom Mg²⁺ ion representation ⁴⁹. ParmBSC0 was developed to alleviate nucleic acid structural distortions that appear at long timescales when AMBER99-family force fields are used. The MD6 model was developed to improve the accuracy of simulations of DNA polymerases by alleviating active-site distortion caused by repulsive forces between two adjacent Mg²⁺ point charges. It was shown to accurately reproduce crystal structures for DNA polymerase β — an enzyme which, like RNase H and Argonaute, catalyzes a phosphoryl transfer reaction — while the point charge Mg²⁺ model introduced significant distortions ⁴⁹. The use of MD6 also produced calculated free energy of binding of dNTPs to DNA polymerase β that were in better agreement with experimental results compared to the same calculation with the point charge Mg²⁺ model. Since ParmBSC0 and MD6 address force field shortcomings that would affect key structural elements in our simulations, we expected that the use of these parameters should improve accuracy.

Molecular dynamics TI simulations were carried out for transformations in four types of systems: single base (as an approximation to an ssDNA), free double stranded nucleic acid, TtAgo-guide (binary complex), and TtAgo-guide-target (ternary complex). Six mutations were studied in the first and 21 mismatches were studied in each of the latter three systems, for a total of 69 TI transformations. Each transformation was sampled at nine points, at approximately 1 ns each, for a total TI simulation time on the order of 600 ns. Non-TI simulations were carried out using the same force fields and applicable methods.

Structural approximations

Only the first 12 base pairs of the guide-DNA/target-RNA hybrid bound to TtAgo were resolved in the TtAgo structure (PDB: 3F73). The “miRNA proxy” structure used in the loading process calculations was this DNA·RNA hybrid. Since it is believed that complementarity in the seed region (roughly positions 2–8) is the primary determinant of RNAi selectivity and that mutations in the seed region primarily affect the binding free energy ^11,24, we considered the use of a truncated nucleic acid hybrid substrate to be a reasonable approximation for the present study. The seed region and active site were included in all structures. Since the aim here was to calculate binding free energy changes due to substitutions in the seed region, omitting the 3′ region the proxy miRNA was a reasonable approximation. In addition, in the free energy calculations, we omitted from the simulated structures free-floating molecules that did not contribute to the free energy change. This was done to reduce simulation time and improve convergence. In legs 1 and 4, the target strand was omitted; and in leg 3, the TtAgo protein was omitted — see Figure 1.

Simulation and analysis protocol

A preliminary version of the AMBER 11 biomolecular simulation package ⁵⁰ implementing soft-core TI (T. Steinbrecher, personal communication) was used for all simulations. A separate minimization, heating (NVT), and equilibration (NVT followed by NPT) protocol was conducted for each λ value; the calculation at each λ was independent from all the others. This minimization-heating-equilibration protocol was designed for the simulation of nucleic acids ⁵¹. The solute was position-restrained with harmonic force constant 5 kcal/mol during minimization and heating. This restraint was gradually released during NVT equilibration. Periodic boundary conditions with the particle mesh Ewald method for evaluation of long-range electrostatics were used. C–H bonds were restrained using SHAKE⁵². For production simulations, NPT conditions were used, a 2 fs timestep was used and temperature was maintained at 300 K using a Langevin thermostat for minimums of 0.75 ns per λ for the binary and ternary complexes and 1 ns for the nucleic-acid-only structures. Since production simulations were run under the NPT ensemble, the free energies calculated were the Gibbs free energies.

In each case, a particular base in the guide strand was alchemically mutated to a different base. All single mutations in the guide strand in positions 2 through 8 were studied. Each of these transformations corresponded to one of vertical legs 1, 2 or 3 of the thermodynamic cycle shown in Figure 1. Each transformation was simulated independently at nine λ values — corresponding to the nine-point Gaussian quadrature rule for numerical integration — to produce a free energy curve. Integrating each curve with respect to λ yielded a corresponding ΔG value. Subtracting the ΔG of mutating the ternary complex from that of mutating the binary complex yielded the ΔΔG representing the change in target binding affinity due to the guide-target mismatch. Similarly, subtracting the ΔG of mutating the double-stranded nucleic acid from that of mutating the ternary complex yielded the ΔΔG representing the change in nucleic acid escape propensity due to the guide-target mismatch.

Convergence was assessed for a particular mismatch by comparing the ΔΔG value calculated from the first halves of the production trajectories to that calculated from the second halves. Statistical error due to serial correlations within the dV/dλ data was calculated by the method of block averages ⁵³ for each transformation. The statistical error (equivalently, the variance) of each ΔΔG value was estimated from the errors of the summed ΔG values by taking the root-mean-square average of their statistical errors. All statistical analysis was carried out using the R statistical analysis software (R Development Core Team, R Foundation for Statistical Computing, Vienna, Austria).

Non-TI MD simulations were run for the fully-matched TtAgo ternary complex as well as the all mismatched TtAgo ternary complexes for which TI calculations were done. The individual contributions of residue-residue interaction energies to the enthalpic component of dsNA binding to Argonaute and target binding to the Argonaute·guide-strand complex were calculated from the resulting trajectories using the MM/GBSA method as implemented by the MMPBSA.py script included with AMBER 11. This method calculates molecular mechanics (MM) energies as well as solvation energies using the generalized Born (GB) method ⁵⁴.

3 Results

Target strand binding

The target strand binding event represents the binding of a target RNA to the Argonaute·guide (binary) complex, resulting in a Argonaute·guide·target (ternary) complex. The bound target strand may then be cleaved and silenced with the resulting fragments jettisoned at the end of the process. We hypothesized that a guide-target mismatch would destabilize the bound form (ternary complex) relative to the unbound form (binary complex), thus impairing target binding. We tested this hypothesis by calculating the change in binding free energy ΔΔG due to each seed region mismatch relative to that of the fully matched sequence as

$$\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{binding},\text{mismatched}}^{\text{target}}-\mathrm{\Delta }{G}_{\text{binding},\text{matched}}^{\text{target}}=\mathrm{\Delta }{G}_2-\mathrm{\Delta }{G}_1$$

where the latter two terms are defined in the thermodynamic cycles shown in Figure 1. The ΔΔG value indicates the degree to which the presence of the mismatch stabilizes (ΔΔG < 0) or destabilizes (ΔΔG > 0) the bound state of the complex relative to its unbound state. The binary complex used here is derived from the ternary complex by removing the target strand without any further structural rearrangement. This approach allows us to study only the energetic changes arising from the mismatch without the complicating factor of the energetic cost of global structural rearrangement, which may vary according to the mismatch type and, in vivo, members of RISC. To explore whether the structural rearrangements associated with the formation of the ternary structure from the binary complex might significantly affect the results and their interpretation, we also studied target binding in two mismatch types using the 3DLH binary complex structure. This structure does not include the structural rearrangements found in the ternary complex (3F73). We found that the resulting ΔΔG values were congruent with the calculations involving the binary complex formed by removing the target strand from the ternary complex (see Table I). Thus, we limit our presentation to the results derived from 3F73.

Table I.

Binding Gibbs free energy changes (kcal/mol) due to single mismatches.

		Target binding			Nucleic acid escape
		ΔΔG	Convergence error c	Statistical error	ΔΔG	Convergence error	Statistical error
C2Ab	C·G→A·G	62.12	± 1.99	± 0.20	−50.64	± 1.79	± 0.21
C2T	C·G→T·G	2.77	± 0.90	± 0.18	5.94	± 1.04	± 0.17
C2G	C·G→G·G	13.83	± 1.81	± 0.17	−5.08	± 2.87	± 0.22
G3Ca	G·C→C·C	8.58	± 2.76	± 0.26	−11.77	± 1.54	± 0.16
G3A	G·C→A·C	2.93	± 0.92	± 0.15	3.00	± 1.80	± 0.15
G3T	G·C→T·C	1.62	± 0.31	± 0.11	7.23	± 0.50	± 0.13
A4C	A·U→C·U	0.72	± 0.88	± 0.19	2.75	± 0.42	± 0.18
A4G	A·U→G·U	−0.68	± 1.03	± 0.17	−0.16	± 0.26	± 0.17
A4T	A·U→T·U	2.89	± 0.07	± 0.22	2.66	± 1.22	± 0.16
A5C	A·U→C·U	1.06	± 1.84	± 0.17	−0.54	± 0.39	± 0.12
A5G	A·U→G·U	5.97	± 0.97	± 0.17	−1.55	± 0.04	± 0.11
A5T	A·U→T·U	3.27	± 0.07	± 0.14	−7.77	± 0.93	± 0.14
G6C	G·C→C·C	7.84	± 0.65	± 0.15	−6.38	± 2.26	± 0.29
G6C (3DLH)		3.79	±0.93	± 0.18
G6A	G·C→A·C	7.39	± 1.28	± 0.13	1.11	± 0.43	± 0.15
G6T	G·C→T·C	5.40	± 0.39	± 0.15	−3.70	± 0.40	± 0.14
T7G	T·A→G·A	−0.36	± 0.89	± 0.19	−4.84	± 0.05	± 0.16
T7G (3DLH)		0.24	± 0.74	± 0.22
T7A	T·A→A·A	2.75	± 0.61	± 0.09	2.99	± 1.02	± 0.16
T7C	T·A→C·A	0.94	± 1.48	± 0.13	0.19	± 4.06	± 0.22
A8C	A·U→C·U	4.33	± 3.96	± 0.33	−1.90	± 0.66	± 0.51
A8G	A·U→G·U	1.26	± 0.79	± 0.19	−1.51	± 0.37	± 0.20
A8T	A·U→T·U	3.76	± 1.86	± 0.15	−5.03	± 0.10	± 0.13

^aItalicized mismatches were studied in ³⁵. All mutations were in the guide strand.

^bThe mismatch type is read as original-position-mutated, e.g., A5T is a position 5 mutation from A to T.

^cConvergence error calculated as ΔΔG from the first half minus ΔΔG from the second half of the trajectory.

Statistical error arises from serial correlations in the data (see Methods).

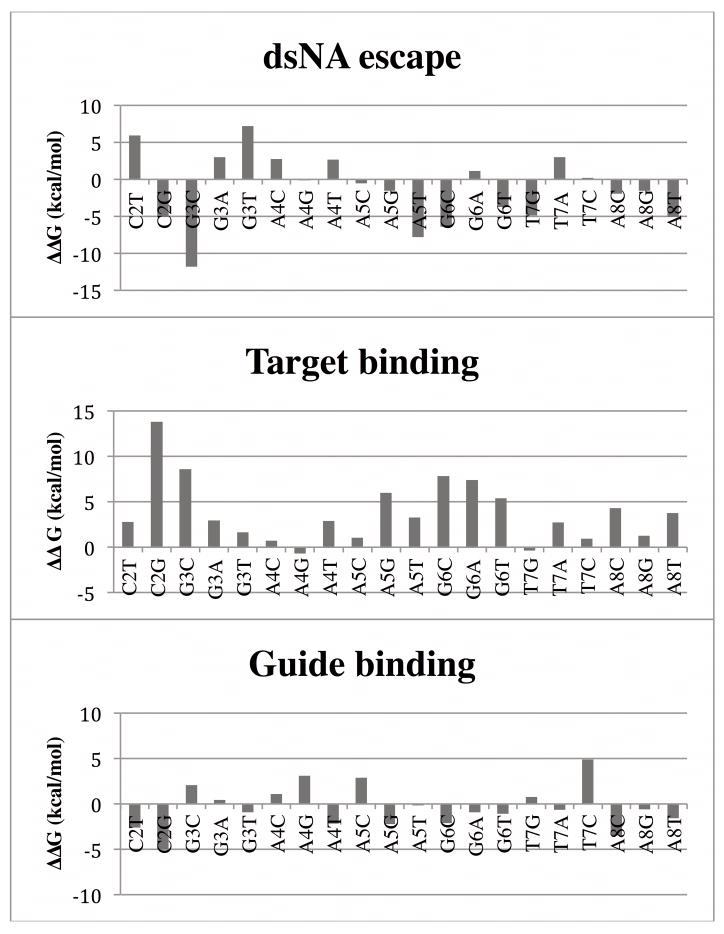
The ΔΔG values, listed in Table I and shown graphically in Figure 2, range in magnitude from fractions of a kcal/mol (e.g. T7G) to several kcal/mol (e.g. G6C). Most mismatches have ΔΔG values that are significantly positive, implying a destabilization of the ternary complex. This would impair the formation of the ternary complex via target binding and therefore, through a change in K_M, decrease the efficiency of silencing. Of the twenty-one mismatches tested, there are five whose ΔΔG values are not significantly different from zero in light of their convergence and statistical errors: A4C, A4G, A5C, T7G, and T7C. Our prediction is that these mismatches would not strongly impair target binding and consequently, if binding were the only mechanism to affect mRNA cleavage, they will not have an effect on RNAi activity. No ΔΔG values are clearly less than zero, suggesting that no tested mismatch enhances target binding.

Figure 2.

Guide binding, target binding, and dsNA escape ΔΔG values, by mismatch position. For clarity, C2A, which has comparatively very large ΔΔG values, is omitted. Note consistently positive values for target binding ΔΔG.

The guide·target sequence we studied contains three repetitions of the A·U base pair, two of G·C and a single T·A. Examining the data in Table I suggests that on the average the energetic cost of introducing a mismatch by substitution of the guide base is largest in a G·C base pair, less for A·U and the lowest cost is in T·A. In addition, of the substitutions of the G·C base pair, the worst in terms of energetics is G→C, followed by G→A and G→T. With respect to the A·U base pair, A→T is the most costly followed by A→C and A→G, which are nearly equal. For T·A, the A·A mismatch is the worst with A→G and A→C creating mismatches that are borderline deleterious. However, it is important to note that the mismatches also show position dependence. For example, G→A and G→T in position 6 have substantially greater energetic cost than the same substitutions in position 3. In contrast, A→T is weakly position dependent, although A→G is worst in position 5 and A→C in position 8.

The data in Table I allow a definition of position dependent selectivity and specificity. If the substitutions at a specific site produce a large change in binding affinity regardless of the specific substitution, the site is selective with high specificity; i.e., only the matched base will work properly. For example, both positions with a G·C are selective. Position 6 is clearly very selective with high specificity: the average ΔΔG_average = 6.9 ± 1.3 kcal/mol; the substitution of G is large for all other bases. Position 3 is less selective with a lower specificity: ΔΔG_average = 4.4 ± 3.7 kcal/mol; G→C and G→A are large while G→T may be tolerant. In the A·U base pairs, positions 5 and 8 show moderate selectivity and specificity: ΔΔG_average = 3.4 ± 2.5 kcal/mol and ΔΔG_average = 3.1 ± 1.6 kcal/mol, respectively, while position 4 is not selective: ΔΔG_average = 1.0 ± 1.8 kcal/mol. The T·A in position 7 is also non-selective: ΔΔG_average = 1.1 ± 1.6 kcal/mol.

This limited exploration illustrates the high selectivity and specificity associated with positions that contain G, especially in position 6 of the sequence. However, considerably more work would be required to establish a comprehensive table of position and sequence dependent selectivities in RNAi.

Relation to experimental results

The results described above suggest a biophysical basis for the experimental results of Wang et al. ³⁵, which showed decreased silencing activity for mismatches in positions 3–8; the same sequences used in that experiment were used here. In the Wang et al. experiment, the TtAgo-guide (binary) complex incorporating either a wild-type or a singly-mutated let-7 DNA guide strand was incubated with the wild-type let-7 target RNA. The relative concentration of cleaved target fragments was assayed after thirty minutes by gel band intensity for each mismatch, providing a measure of silencing activity as a function of a single mismatch at various positions. Notably, this experiment tested both target binding and cleavage, while our study only examined target binding but not the effect of local perturbations due to mismatches on catalytic rate constants as the latter was outside the scope of the present work. In general, mismatches in the seed region caused a decrease in cleavage, in line with the general trend of our data. Our results suggest that the observed decreased target cleavage in the setting of a seed region mismatch is indeed due to impaired target binding, as opposed to successful binding into a configuration that does not support catalysis. Free-energy-perturbation-type approaches, like the protocols used here, cannot address the allosteric effects of mismatch on catalytic rates.

With few exceptions, described below, our results are congruent with experiment. Considering all the mismatches that were studied computationally but were not included in the experiments, our results suggest that the target strands are less likely to bind to the binary complex that contains a mismatch, hence lowering the concentration of the productive ternary complex and leading to less efficient cleavage. Notably, the A5C and T7G mismatches had ΔΔG close to zero within error; this is consistent with the results of Wang et al. ³⁵, as these mismatches had a relatively small effect on cleavage activity. On the other hand, we found the A4C mismatch to have ΔΔG close to zero within a small error (see Table I) for target binding — but it exhibited significantly attenuated cleavage in the experiment. A possible explanation for this discrepancy is that binding affinity change in this particular positions is not the only factor in cleavage activity; possibly allosteric structural and dynamical factors affect the activation energy for the cleavage reaction.

The C2A homopurine mismatch (C·G → A·G) had very large calculated ΔΔG values, with magnitudes on the order of 50–60 kcal/mol, in both nucleic acid escape (described below) and target binding events. In addition, the C2G and C2T mismatches had substantially positive ΔΔG values in the target binding event. However, the presence of a C2A mismatch was shown by Wang et al. ³⁵ not to greatly impair silencing of this mismatched target in vitro. A potential explanation is that the target strand does not need to pair successfully in position 2 for successful silencing, especially since the adjacent position 1 is already unpaired. It is also possible that the formation of a ternary complex including these particular mismatches involves structural rearrangement that requires passing over a high-energy barrier. This type of barrier crossing would not have been sampled in our simulations since molecular dynamics and thermodynamic integration do not tend to explore high-energy regions of phase space. Thus, the results obtained for this mismatch may be less reliable.

Our data are also congruent with prior experiments by Schwarz et al., which tested the effect of a number of guide-target G·G mismatches on the efficiency of RNAi cleavage in Drosophila embryos ³⁶. Even though the sequences examined by Schwarz et al. were all different from the let-7 sequence we tested, their results are in general qualitative agreement with those from the present study: the majority of single mismatches impaired silencing, and no mismatches enhanced silencing. This suggests that the predominant molecular biophysical basis of silencing impairment in the presence of guide-target mismatches is that mismatches impair target binding to Argonaute, preventing formation of the cleavage-competent ternary complex.

In cases where ΔΔG was close to zero but experimental evidence showed a decrease in target cleavage, we speculate that a change in the global dynamics of the complex due to the presence of the mismatch could disturb the geometry of active site in the PIWI domain with respect to the scissile bond opposite guide bases 10–11, thus impairing cleavage. Since our studies were at the molecular mechanics level, this type of change in the chemistry of the reaction would not be captured. Regardless, our results show that the presence of a seed region mismatch tends to decrease target binding affinity, although this is dependent on the position and type of mismatch.

Escape of double-stranded nucleic acid

In order for the set of mRNAs silenced via RNAi to vary over time in a given cell, the lifetime of a given fully-assembled RISC must be finite. Since the assembly of the ternary complex involves binding of a dsNA, it is possible that a potential disassembly pathway would involve separation of the dsNA. This could occur at two points in the RNAi cycle: immediately after loading of the dsNA, and also upon binding of the target, when a similar structure is formed. Although this process has not been extensively experimentally studied, it may have an effect on overall RNAi efficiency, particularly since miRNAs, encoded in the genome, frequently contain mismatches. Hence, we sought to determine the influence of mismatches on the separation of the dsNA from Argonaute. It is possible that a mismatch may destabilize the Argonaute·dsNA ternary complex relative to the Argonaute free protein separated from the dsNA, favoring the dissociation of the double-stranded miRNA, leading to its “escape” from the ternary complex and the rest of the silencing pathway. We termed this the dsNA escape event.

Using the DNA:RNA hybrid (dsNA) in the TtAgo crystal structure as a model for an miRNA, we tested this hypothesis by calculating the change in ΔG of dsNA binding to TtAgo due to each seed region mismatch relative to the matched sequence. The thermodynamic cycle in Figure 1 defines this property as

$$\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{escape},\text{mismatched}}^{\text{dsNA}}-\mathrm{\Delta }{G}_{\text{escape},\text{matched}}^{\text{dsNA}}=\mathrm{\Delta }{G}_3-\mathrm{\Delta }{G}_2.$$

The ΔΔG values varied without relation to mismatch position or type (see Table I and Figure 1) with only 11 mismatches fulfilling the expectation that ΔΔG < 0. Interestingly, six of twenty-one mismatches had significantly positive ΔΔG values, indicating that the mismatched dsNA would be more tightly held relative to the fully-matched nucleic acid. Two had ΔΔG values close to zero, indicating that the mismatched dsNA was roughly equally tightly held as the fully-matched nucleic acid. Three of the four homopurine mismatches tested had negative ΔΔG for escape, suggesting that in the sequences tested, a bulky homopurine mismatch favors escape of the dsNA and prevention of the subsequent stages of the RNAi pathway. In all cases where ΔΔG > 0, it was true that ΔG₃ > ΔG₂ > 0, indicating that a mismatch destabilized both free and bound dsNA, but escape was disfavored because the free state had been more strongly destabilized than the bound state. This shows that a mismatched miRNA is unlikely to “fall off” the Argonaute before the passenger strand is jettisoned, promoting RNAi activity, and consistent with the existence of mismatches encoded in miRNAs.

Local energetic effects of mismatches in the ternary complex in dsNA binding and target binding events

In order to examine the structural and energetic basis for mismatch-dependent impaired binding with respect to interactions between the nucleic acid and the Argonaute protein, we performed conventional MD simulations of the mismatched ternary structures. None of these showed substantial structural rearrangement other than the mismatched base pair configuration, suggesting that the structural origin of the binding free energy change is localized to the mismatch itself and the proximal part of the protein. To further explore this idea, we examined specifically how the contribution of a given base pair to the binding energy was changed by substituting the base pair with a mismatch. We examined two types of binding: 1) that of a dsNA to Argonaute and 2) that of a target RNA to an Argonaute-guide complex. We calculated the time-averaged differences in interaction energies of matched and mismatched base pairs in guide positions 3–8 with the surrounding structure within 20 Å. Using the MM/GBSA (molecular mechanics/generalized Born surface area) method ⁵⁴, we calculated the changes in time-averaged interaction energies arising from a mismatch in each of these positions. Although this calculation ignores entropic changes, monitoring these residue-specific energy changes provides useful insight into which protein residues may be the primary determinants of nucleic acid binding selectivity in RNAi. These data are shown in Supplementary Tables S1 and S2.

We examined the distributions of these energy changes. The distribution of energy changes of the base pair interacting with the protein is bimodal with centers around 2 and -2 kcal/mol, whereas that involving the base pair and the nucleic acid is centered around 0 kcal/mol. All interaction energy changes of the target bases with respect to the protein only were shared between dsNA loading and target binding calculations. In target binding, the contributions of guide-protein interactions to the binding energy was largely unchanged by the presence of a mismatch. Rather, target-protein interactions were primarily affected. This suggests that the binding impairment conferred by substitution of the guide base in mismatched sequences is primarily transmitted through the unsubstituted target base. Since the interactions are position-and mismatch-dependent, we identified the main contributors to specific mismatches as well as their dependence on mismatch position. In general, the modified interactions contributing to the enthalpic component of the binding free energy changes are localized to the immediate region of the mismatched base pair, suggesting that a large part of RNAi sequence selectivity arises from the impairment of binding mediated by localized interactions with the Argonaute protein. The sterically and electrostatically important milieu for each base pair described below is diagrammed in Figure 4.

Figure 4.

Diagrams of each seed region position (except C2). White arrows point to the respective guide bases. Sterically important Argonaute residues in purple; electrostatically important Argonaute residues in cyan. For clarity, surrounding nucleotides are omitted.

For dsNA binding, introducing a mismatch at (G·C)₃ perturbs the interaction with the protein mostly in three residues: Y642, S645 and R661, each of which interact with G₃, while the unchanging base C₂₁ only has significantly changed interactions with R635. The interactions with Y642 and R661 track the changes in the stability of the mismatch but the interaction with S645 is constant. The latter interaction reflects the proximity of S645 to the sugar of G₃, suggesting than any change in this base increases the steric repulsion. On the other hand, R661 interacts both with the phosphate and the sugar of the position 3 guide nucleotide and as the mismatches progress from C·C → A·C → T·C, the interaction diminishes and becomes stabilizing. This suggests a competition between the repulsion with the sugar and the attraction with the phosphate. For target binding, only the target base C21 has significant modified interactions with the protein — only in R611.

The other G·C base pair in the sequence is in position 6, which has been shown to be much more sensitive to mismatches in A. aeolicus Argonaute ³⁵. Here the interactions with the protein are much more extensive; altogether, 14 residues participate in forming a pocket for the (G·C)₆ base pair and the mismatches perturb these interactions mostly through steric occlusions, both for dsNA binding and target binding. For example, L267 and E268 are part of a loop that defines a boundary for the C₁₈ in the target sequence; in the mismatched sequences it becomes a steric occlusion because it cannot adjust due to its interaction with the rest of the protein. On the guide strand side, the major residues are three arginines at sequence positions R608, R615 and R651, and P614. Only R651 forms an electrostatic interaction with the phosphate; this residue makes a large contribution to the energy difference upon introducing a mismatch. The other two arginines and the proline form a hydrophobic pocket that accommodates the sugar. Changes in this pocket due to the mismatches reflect steric perturbations. It seems that R661 plays a similar role in position 3 as R651 in position 6. However, the much more extensive set of steric/hydrophobic interactions with the sugars is the main source for the larger sensitivity of position 6 compared to position 3.

As expected, these results illustrate that the formation of a C·C mismatch is both unfavorable structurally and is expressed in a large energetic penalty. Furthermore, because the TI simulations are limited in sampling the configurational states during the conversion of G3 or G6 to C in their respective positions, we should consider their ΔΔG values as upper limits of the actual free energy difference. We would expect that under conditions of longer sampling the structure would distort to relieve the electrostatic and steric mismatches. Nevertheless, while the ΔΔG may be reduced, these mismatches would not create an acceptable configuration for RNAi processing.

The (A·U)₄ is a base pair that is held by several electrostatic interactions. The individual phosphate oxygens of A₄ interact with Y642 and R661. In dsNA binding, the effect of a mismatch on the interaction with Y642 is always costly, but it is relatively insensitive to the nature of the mismatch. In contrast, the interaction with R661 shows exquisite sensitivity to the substitution; A4C substitution stabilizes the interaction while A4G and A4T strongly destabilize the complex; this is also reflected in the respective ΔΔG values from the TI simulations (see Table I). R608 and R611 interact with the polar atoms N₃ of A₄ and O₂ of the complementary U₂₀ in the minor groove of the (A·U)₄ base pair. However, the ΔΔG of the A4C and A4T mismatches favor dsNA binding by ~ 3 kcal/mol, which is mostly due to the interaction with these arginines. This can be clearly seen in the A4C mismatch where the substitution is stabilized by the arginines, consistent with a small penalty in the free energy of target binding obtained in TI simulations and the stabilization of the ternary complex preventing escape of the dsNA. The A4G substitution, by contrast, destabilizes the interaction with R611 but stabilizes the interactions of U20 with F610 and G4 with R608, consistent with near-zero ΔΔG values for target binding and dsNA escape.

Like A4C, the A5C mismatch represents a substitution from A·U to C·U. Here, the most significant changes in interaction energies are actually stabilizing, in the case of A₅ with K575 and R611, and of U₁₉ with R611. The (A·U)₅ base pair shares with (A·U)₄ a common interaction with the two arginines — R608 and R611. The effects of introducing a mismatch in position 5 are somewhat similar as in position 4 since the mismatch A5C introduces a stabilizing effect consistent with the small ΔΔG for target binding from the TI simulations. In the A5G substitution, however, the mismatch leads to large target binding and significant dsNA escape free energy changes because it is a combination of perturbation of electrostatic and steric effects. The phosphate group of A₅ is held by three interactions: K575, H657 and the backbone N-H of R651. These interactions become unfavorable in the A5G mismatch. In addition, V606, P650 and the aliphatic side chain of R651 create a very tight hydrophobic pocket for the sugar of A₅, which cannot accommodate the mismatched G. In target binding, the position 5 base pair was the only one to exhibit significant changes in interaction energies of the guide base with the protein.

All mismatches in the (A·U)₈ base pair, the third A·U, disfavor target binding and favor dsNA escape. This base pair exhibits also a combination of electrostatic and steric interactions that are affected by the mismatches during both dsNA binding and target binding. For example, in both types of binding, the phosphate of the complementary U₁₆ interacts with K191, which shows a stabilization in the A8C mismatch but does not change in other mismatches. In dsNA binding, the phosphate of A₈ is held by R286, R615 and the backbone N–H of Y171. Only R615 shows a dependence on the mismatch: no effect in A8C but stabilizing effects in A8G and in particular in A8T. Three hydrophobic residues — I173, L267 and the methyl of T266 — create a very tightly packed environment that restricts the motion of the A₈ sugar. However, this restriction is relieved by introducing the mismatches, which reposition the sugar with respect to these residues, reducing the steric repulsion and stabilizing the electrostatic interactions, although this is not sufficient to render either type of binding event favorable.

The T7A mismatch is deleterious to the stability of the complex in both target binding and dsNA escape. T7G and T7C are equivocal for target binding, T7C is equivocal for dsNA escape, but T7G strongly favors dsNA escape. The (T·A)₇ base pair has a unique arrangement of electrostatic interactions that hold the T₇ in place. Three arginines — R286, R580, R615 — and one backbone N–H of T613 create an electrostatic cage that holds the phosphate of this nucleotide. The other residues G339, S280 and L279 form a continuous wall that confines the T₇ and L267 and T266 create a similar confinement for A₁₇. This steric boundary is sensitive to the mismatch; in T7A and T7C the effect is small and destabilizing whereas in T7G the effect is moderately stabilizing, consistent with the both T7A and T7C target binding and nucleic acid escape ΔΔG greater than and near zero and T7G’s corresponding ΔΔG values near to and less than zero.

Single guide strand binding

It has been experimentally shown that TtAgo can take up and release a ssDNA guide strand in the absence of its antisense strand; this is a mechanism for forming a functional binary complex, which can consist only of Ago bound only to a single-stranded guide ³⁵. We sought to determine whether the equilibrium between these bound and unbound states is sensitive to the sequence of the guide strand, since sequence specificity can be conferred by interactions of the binding region with the DNA bases ^55,56. To do so, we calculated the effect of single-base substitutions on the binding free energy of the guide strand with TtAgo.

The thermodynamic cycle in Figure 1 defines the free energy penalty for the binding of the mutated guide strand to TtAgo, relative to the binding of the wild-type guide strand, as

$$\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{binding},\text{mutated}}^{\text{ssDNA}}-\mathrm{\Delta }{G}_{\text{binding},\text{wild}-\text{type}}^{\text{ssDNA}}=\mathrm{\Delta }{G}_1-\mathrm{\Delta }{G}_4.$$

We studied the same set of single-base mutations as above, calculating ΔG₁ and ΔG₄ for each mutation via thermodynamic integration and then calculating ΔΔG. ΔG₄ was considered as the alchemical mutation of an isolated single DNA base in solution as a model for the same process in a ssDNA. We felt this approximation was reasonable because the distribution of conformations sampled by an unbound ssDNA should not depend on sequence of the ssDNA. Furthermore, base stacking changes introduced by a single base substitution contribute a small amount to the overall relative stability of ssDNA (ΔG < 1 kcal/mol) ⁵⁷.

The ΔΔG values for the binding of a single DNA strand to TtAgo ranged from about −5 to 5 kcal/mol, with a standard deviation of 2.4 kcal/mol (see Table II). Taking into account convergence and statistical error, seven of 21 substitutions could be said to have (absolute) ΔΔG values greater than 1 kcal/mol: C2A, C2T, C2G, A4G, A5C, T7C and A8C. Of these, ΔΔG for A4G, A5C, and T7C were positive, implying a destabilization, favoring dissociation, of the binary complex with altered sequence relative to the original guide strand. This suggests that the TtAgo protein is weakly sensitive to the sequence of the guide strand. Notably, all three position 2 mutations had negative ΔΔG values, suggesting that, in the binary complex, a cytosine in position 2 is disfavored. The guide base in position 2 interacts with several nearby protein residues (see Figure 3); different interaction modes for different bases in this position may be responsible for this pattern of ΔΔG values.

Table II.

Target ssDNA binding free energy changes (kcal/mol).

		ssDNA binding to TtAgo
		ΔΔG	Convergence error a	Statistical error a
C2A	C·G→A·G	−2.78	± 1.15	± 0.28
C2T	C·G→T·G	−2.62	± 0.88	± 0.26
C2G	C·G→G·G	−5.00	± 0.18	± 0.23
G3C	G·C→C·G	2.07	± 1.87	± 0.35
G3A	G·C→A·G	0.45	± 0.19	± 0.21
G3T	G·C→T·G	−0.93	± 1.15	± 0.16
A4C	A·U→C·U	1.10	± 0.11	± 0.25
A4G	A·U→G·U	3.13	± 0.97	± 0.24
A4T	A·U→T·U	−2.15	± 1.66	± 0.31
A5C	A·U→C·U	2.90	± 1.61	± 0.23
A5G	A·U→G·U	−2.20	± 1.61	± 0.22
A5T	A·U→T·U	−0.18	± 1.51	± 0.20
G6C	G·C→C·G	−2.09	± 0.40	± 0.21
G6A	G·C→A·G	−0.90	± 1.81	± 0.18
G6T	G·C→T·G	−1.07	± 0.47	± 0.21
T7G	T·A→G·A	0.77	± 1.59	± 0.27
T7A	T·A→A·A	−0.64	± 1.32	± 0.12
T7C	T·A→C·A	4.90	± 0.87	± 0.18
A8C	A·U→C·U	−3.49	± 1.62	± 0.46
A8G	A·U→G·U	−0.58	± 1.79	± 0.27
A8T	A·U→T·U	−1.57	± 0.43	± 0.21

^aThe convergence and statistical error includes only error from the TI simulations and not error from the ΔG values estimated from nearest-neighbor thermodynamic parameters.

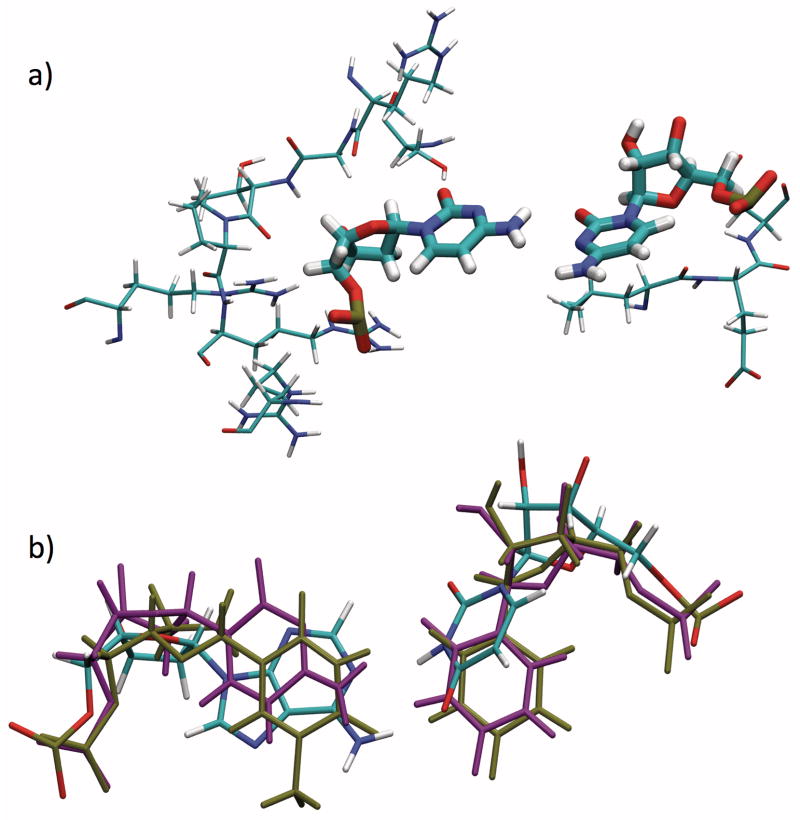
Figure 3.

a) Representative snapshot of position 6 C:C (G6C) mismatch and amino acid residues within 4 Å, from non-TI MD simulation. Note proximity of several amino acid residues with this base pair, which explains the sensitivity of binding affinity to a mismatch in this position.

b) Comparison of base pair geometries in position 4 of guide strand in TtAgo 3F73 ternary complex. T:U (A4T) in tan, C:U (A4C) in purple, fully-matched (A:U) colored by element. Representative snapshots are shown for the mismatches; for the fully-matched base pair the 3F73 crystal structure is shown. Note displacements of both guide and target bases in mismatches relative to fully-matched base pair.

4 Discussion

Overall, through the exhaustive evaluation of 21 seed region base substitutions, we propose a thermodynamic basis for varying degrees of target mRNA sequence selectivity in RNAi, encompassing both mismatch tolerance and strong selectivity. In agreement with experimental evidence ^23,34–36, the generally positive ΔΔG values for the binding of the target strand to a binary complex with a mismatched guide strand suggest that most single mismatches in the seed region of the guide strand reduce target binding affinity by destabilizing the mismatched ternary complex relative to the fully-matched version. The magnitudes of these values are consistent with the previously suggested hypothesis that a decrease in binding affinity is an important mechanism by which silencing activity is reduced due to a seed region mismatch between guide and target strands — experiments have shown that mismatches in the seed region tend to primarily affect, in Drosophila RISC, the Michaelis-Menten parameter K_M as opposed to k_cat ^11,34,58. For example, the change in ΔG of 5.4 kcal/mol for the formation of a G6T-mismatched ternary complex by target strand binding represents a roughly 10000-fold increase in K_M (a proxy for binding affinity) which leads to a decrease in catalytic efficiency. The enthalpic component of the binding affinity changes appears to be mediated largely through selective local effects on electrostatic interactions between the mismatched base pair and a select few Argonaute residues, although this is position- and sequence-dependent. In addition to electrostatic changes, the introduction of a mismatch can induce steric occlusion that can significantly change the binding free energies. This is congruent with the exquisite sequence dependence that has been experimentally observed in miRNA-target binding ⁵⁹.

As noted in the Introduction, not all guide-target mismatches strongly decrease silencing activity. Various investigators have profiled off-target effects of siRNAs ^9,60,61. That a particular siRNA may cause the silencing of a specific constellation of non-complementary genes can, in the context of the present data, be partly attributed to the lack of binding free energy penalties for certain mismatches. For example, in this study, target binding ΔΔG values for the A4C (A·U → C·U), A4G (A·U → G·U), T7G (T·A → G·A) and T7C (T·A → C·A) mismatches were found to be close to zero when convergence and statistical error are taken into account (see Table I), suggesting that guide strands with those mutations would still be able to bind and silence the target strands evaluated here with similar efficiency as the non-mutated versions. In the non-TI simulations of mismatched ternary complexes described above (including A4C and T7G), we found that significant structural distortion was limited to the mismatched base pair itself, suggesting that the Argonaute protein is generally well able to tolerate mismatches in its substrate without itself becoming distorted and destabilizing the ternary complex. Also, there were no cases of mismatched target binding that were more favorable than fully-matched target binding (in light of convergence and statistical error), suggesting that it is unlikely that a mismatch would actually enhance target binding, going beyond simply not impairing it.

We can also consider a given guide-target mismatch in the context of its effects on the relative stabilities of the binary, ternary, and free nucleic acid (see Figure 1). Each group of shifts in the various equilibria suggests a particular outcome of the RNAi cleavage pathway. The most common potential outcome is impaired target binding combined with enhanced dsNA escape. This is due to a destabilization of the mismatched ternary complex relative to the mismatched binary complex and destabilization relative to the free protein and mismatched dsNA. In this case, a mismatched miRNA would be less likely than a fully matched miRNA to remain bound to Argonaute long enough for the miRNA antisense strand to be cleaved and jettisoned to form a binary complex. If formed, this binary complex would silence the particular constellation of target mRNAs that most readily bind to it — which would primarily include the sequence fully complementary to the guide rather than the miRNA passenger strand. However, silencing activity would be reduced due to the reduced concentration of the binary complex, which would reduce the overall binding capacity for target RNAs. This is the intuitive result of a mismatch that we hypothesized.

Interestingly, another common case was of mismatches that impaired both target binding and dsNA escape. In this case, a mismatched miRNA would actually be more tightly held onto the Argonaute, increasing the likelihood that the antisense strand is cleaved and jettisoned to form a binary complex. This would increase the relative concentration of the binary complex containing that guide strand, enhancing the silencing of its constellation of targets, which, as above, primarily includes the fully complementary sequence rather than that of the passenger strand. Hence, this is a method to enhance the effectiveness of a particular miRNA/siRNA through the use of a selectively placed mismatch. These mismatches may be a source of evolutionarily selective pressure because they provide a mechanism to modulate the degree of silencing of particular targets. miRNAs are known to contain mismatches. A virus could introduce a mismatched siRNA that out-competes the host organism’s own short RNAs for uptake into Argonaute. Or else, RNAi therapy could make use of mismatched siRNAs to selectively silence a gene associated with a given pathological outcome.

The presence of mismatches in miRNA has been shown, in Drosophila, to determine the sorting of miRNAs into the correct Argonaute protein ⁶². A pre-RISC is assembled, containing the miRNA, Argonaute, and accessory proteins. This complex then matures into a functional RISC if the miRNA contains mismatches appropriate for the Argonaute to which it is bound. A mismatched miRNA with an increased propensity to escape its Argonaute would also escape this maturation process. Our results here show that the affinity of a mismatched miRNA for TtAgo is highly dependent on the position and type of the mismatch. Further, our results show that dependence arises largely from local modifications of interactions between the mismatched base pair and surrounding Argonaute protein residues. We speculate that given the exquisite dependence of ternary complex relative stability on small structural perturbations such as a mismatch, a particular mismatched miRNA would have different affinity for different Argonautes, and that this may be a significant contributor to miRNA sorting.

The binding affinity of a single guide strand to the free Argonaute protein appears to be both positively and negatively affected by single mutations in its sequence, depending on the particular mutation. With the exception of position 2, in which cytosine is disfavored, there does not appear to be a pattern to the relationship between mutation position and type and binding free energy change with respect to the formation of the binary complex from free Argonaute and guide strand. Also, the calculated errors for the free energy changes make it difficult to distinguish many of them from zero. Even so, certain guide strand mutations caused a significant destabilization of the binary complex relative to the original sequence (e.g. T7C). If the binary complex can be rendered significantly more likely to dissociate by certain guide sequences, how can RNAi reliably take place? In vivo, this binary complex does not mediate mRNA silencing by itself; rather, the binary complex is embedded in the RISC. We speculate that one function of the accessory RISC proteins may be to stabilize the binary complex for a wide variety of guide strand sequences, mitigating the destabilizing effect of such sequences on the bare binary complex.

While a binary complex can be formed in vitro by the binding of a single guide strand, the formation of a binary complex in vivo involves the loading of a double-stranded miRNA or siRNA in a particular orientation and the subsequent removal of the passenger strand. How is this orientation chosen? The strand with the less stable 5′ end is likely to be chosen as the guide ^63,64. Since all position 2 mismatches we examined decrease the stability of the dsNA, it is likely that the presence of a position 2 mismatch with respect to a given sense strand would favor its selection as the guide, and hence promote the silencing of the corresponding constellation of targets.

We have shown results for a specific nucleic acid sequence as well as all possible seed region substitutions for that sequence. Ultimately, we find that a large component of the mechanism behind target sequence selectivity is through binding affinity impairment related to local interactions of the mismatch and Argonaute; however, while this effect dominates, it is not universally the case that the local interactions will be modified by a mismatch in such a way as to result in binding impairment. We do observe that interactions of the nucleic acid with Argonaute play a crucial role in this selectivity. From a practical standpoint, the next steps would be to test more nucleic acid sequences along with the appropriate substitutions, so that all potential mismatches in a given guide sequence position could be studied. This would paint a more complete picture of the sensitivity of a given mismatch position to the type of substitution, and allow the elucidation in greater detail of the important nucleic acid-Argonaute interactions that govern binding affinity.

Our predictions about binding affinity modification could be tested experimentally by measuring how the relative equilibria of bound and unbound TtAgo species in solution change due to the presence of mismatches. This would require the use of a TtAgo protein that is made catalytically incompetent by residue substitution in the active site — else the equilibria would be distorted by target cleavage. We predicted that the equilibrium between the ternary and binary complexes, where the transition is made by the dissociation of the target strand, would be shifted toward the binary complex by most mismatches. In addition, for certain mismatches, the equilibrium between the ternary complex and the free protein dissociated from the dsNA is shifted toward the dissociated state. Finally, certain guide strands bind more strongly to the free protein than others. Hence there would be five species (ssDNA guide, ssRNA target, dsNA, binary and ternary complexes) all in equilibrium with each other. Showing that the relative concentrations of these species in solution are modified due to single mismatches, in agreement with our predictions, would serve as an in vitro validation of our theoretical approach.