SUMMARY
Moving is thought to take separate preparation and execution steps. While preparing, neural activity in primary motor and dorsal premotor cortices achieves a state specific to an upcoming action, but movements are not performed until the execution phase. We investigated whether this preparatory state (more precisely, prepare-and-hold state) is required for movement execution using two complementary experiments. We compared monkeys’ neural activity during delayed and non-delayed reaches, and in a delayed reaching task in which the target switched locations on a small percentage of trials. Neural population activity bypassed the prepare-and-hold state both in the absence of a delay and if the wrong reach was prepared. However, the initial neural response to the target was similar across behavioral conditions. This suggests that the prepare-and-hold state can be bypassed if needed, but there is a short-latency preparatory step which is performed prior to movement even without a delay.
INTRODUCTION
Movements are often prepared ahead of time. For example, when a soccer player makes a penalty kick, she takes time to set up the kick to improve her chances of scoring. At other times, movements may be performed without taking extra time to explicitly prepare. If an opposing defender appears just as the soccer player is about to kick, she may pass the ball to a teammate without taking time to carefully set up the pass. Because humans and other animals must contend with a variety of behavioral contexts, we are presumably capable of performing both prepared and relatively unprepared actions. However, how these behaviors relate to each other is not well understood. In this study, we examine this relationship to determine which aspects of motor control are consistent across different levels of preparation.
Motor control is often studied with a delayed-reach behavioral paradigm. In this paradigm, some or all aspects (e.g. direction, speed, extent) of an upcoming reach are revealed, but subjects must wait for a go cue before moving (Churchland, et al., 2006a; Messier and Kalaska, 2000; Riehle and Requin, 1989; Rosenbaum, 1980; Tanji and Evarts, 1976). This allows subjects to prepare their reaches ahead of time. The reaction time (RT) between the go cue and reach initiation decreases when the reach is pre-cued (Churchland et al., 2006c; Rosenbaum, 1980). Electrophysiological recordings have revealed that neurons in primary motor cortex (M1) and dorsal premotor cortex (PMd) change their firing rates (FR) in response to information about upcoming reaches (Tanji and Evarts, 1976; Weinrich et al., 1984; Cisek and Kalaska, 2002; Rickert et al., 2009). This activity is correlated with RT (Afshar et al., 2011; Churchland et al., 2006c) and other aspects of the reach, such as peak speed (Churchland et al., 2006b). Furthermore, electrically perturbing neural activity in PMd during the delay can largely erase the RT benefits of preparation (Churchland and Shenoy, 2007).
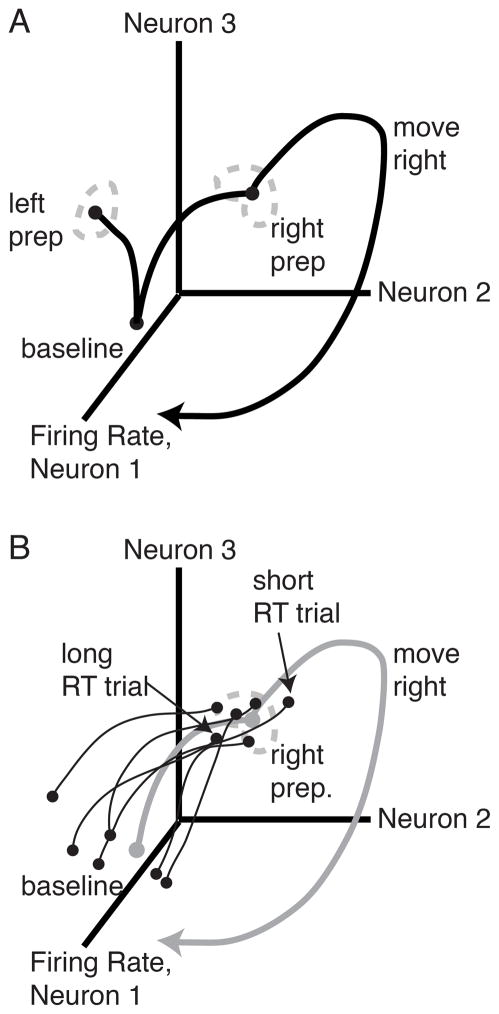
These observations have led to the idea that delay period neural activity reflects computations related to motor preparation (Crammond and Kalaska, 1994; Riehle and Requin, 1989). In particular, the model asserts that this preparation causes the observed decrease in RT. This model can be explained using a state-space framework, which has helped to understand neural population activity across a variety of paradigms in recent years (Broome et al., 2006; Churchland et al., 2012; Churchland et al, 2010; Harvey et al., 2012; Shenoy et al, 2011; Shenoy et al., 2013; Stokes et al., 2013). In this framework, neural population activity is projected into a neural state space, in which the FR of each neuron is a dimension in this space. The FRs across all neurons at a given time corresponds to a point in state space. The FRs over time form a trajectory through state space (Figure 1A). The optimal subspace hypothesis (Churchland et al., 2006c) states that when a reach is pre-cued, neural activity moves to a preparatory region (set of neural states) that is beneficial for the upcoming reach. The model states that, while there is almost certainly some drift and variability in the neural preparatory state, neural activity should pass through or near this preparatory region to generate a correct reach. Furthermore, slight variations in neural preparatory state also correlate with RT (Figure 1B) (Afshar et al., 2011). Trials in which the neural state happens to have progressed further in the direction that it will move after the go cue have a slightly shorter RT than trajectories which are further behind.
Figure 1.
State-space cartoons. (A) Optimal subspace hypothesis. For each reach, there is a corresponding neural preparatory state. After the go cue, the neural population activity takes a trajectory that begins in the preparatory state and generates the prepared reach. (B) Initial condition hypothesis cartoon. Gray trace, mean neural population trajectory; black traces, individual trial neural population trajectories. When a reach is pre-cued, neural population trajectories on individual trials move to the preparatory state. On a each trial, the degree to which the neural state has advanced by the time of the go cue correlates with RT.
While this framework has helped to elucidate some of the neural mechanisms of movement, it is limited by the use of just one task, the delayed reaching task. During the delay, subjects are not only preparing a reach, but are also holding the arm outstretched in front of them and withholding movement. The neural preparatory state observed during the delay is thus more precisely a prepare-and-hold state. It remains unclear to what degree neural activity in this prepare-and-hold paradigm can be generalized to reaches without an explicit delay. If reaching is dependent on the preparatory state (Churchland et al., 2012; Churchland et al., 2010), then initiating movement outside of the correct preparatory region ought to generate a different reach. If this were the case, we would expect either an incorrect reach or neural evidence of last-minute preparation in conditions where the monkey’s preparatory state is not correct.
We used two behavioral paradigms to investigate the neural correlates of reaching with different levels of neural preparation. First, we compared the neural activity of reaches performed with and without a delay, to examine what happens when monkeys are not given explicit time to prepare. Second, we compared the neural activity of delayed reaches and reaches where the target cue switched to a new location. We examined whether monkeys’ neural activity in the switch condition “re-prepared” by passing through or near the correct prepare-and-hold region.
In both cases, we determined that neural activity did not achieve the prepare-and-hold state for the performed movement and often passed quite far from this state. This suggests that achieving the prepare-and-hold state is not necessary for generating a reach. However, when examining the full time-course of neural trajectories, we found that the initial neural response to the target is similar between delayed and non-delayed reaches. These similar early neural target responses may allow conditions without a delay to engage some quantity of preparation before initiating movement.
RESULTS
The prepare-and-hold state is not achieved in the absence of a delay
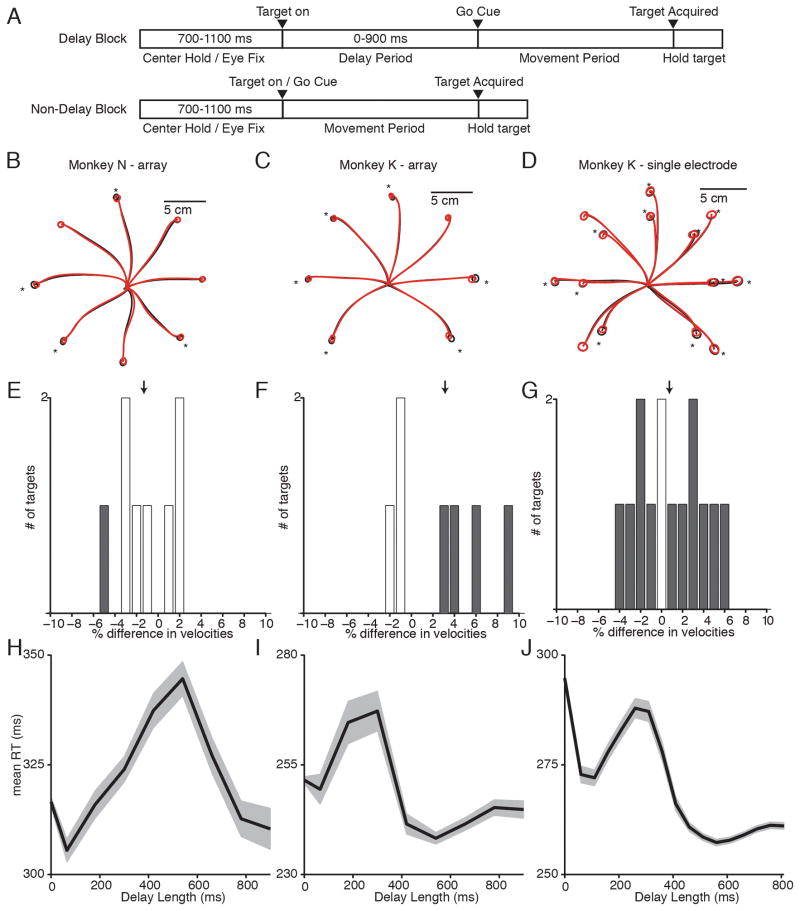
We first investigated the necessity of the prepare-and-hold state by comparing reaches with and without a delay. We trained monkeys N and K to perform a reaching task with blocks of delayed and non-delayed trials (Figure 2A). Mean reach trajectories were close (Figure 2B–D), with overlapping end point distributions. While several end point distributions had significant differences ( N: 4/8 reaches; K-array: 6/7 reaches; K-single electrode:12/14 reaches; p<.05 One-Way MANOVA), the magnitude of these differences was small, representing less than 15% of the target diameter. The peak velocities of the reaches were also similar (Figure 2E–G). For Monkey N-array, delayed and non-delayed reach velocities were not significantly different (p = 0.17, 2-sample unpaired t-test). For Monkey K, delayed and non-delayed reaches displayed a significant (but small magnitude) difference in reach velocity, with delayed reaches being an average of 3.1% faster than non-delayed reaches in the array dataset (p<.01, 2-sample unpaired t-test), and 0.75% faster in the single electrode dataset (p<.01, 2-sample unpaired t-test). Overall, reaches were quite similar across delayed and non-delayed reach conditions.
Figure 2.
Behavior for delayed and non-delayed reaches. (A) Task design. Monkeys performed trials broken into blocks of delayed and non-delayed reaches. In the delayed reach block, a delay of 0–900 ms separated target onset and go cue. In the non-delayed reach block, the target onset and go cue were simultaneous. (B–D) Mean reach trajectories for delayed reaches (black) and non-delayed reaches (red). Circles show 1 STD of end point positions. Starred reaches show significantly different endpoint distributions (p<.05) (E–G) Differences in maximum reach velocity for each reach direction. Positive values indicate delayed reaches were faster than non-delayed reaches. Gray bars show significantly different reach velocities (p<.05). (H–J) Mean +/− SEM RT vs. delay length in 100-ms sliding bins.
We observed some behavioral differences in RT, consistent with previous studies (Figure 2H–J). For Monkey K, long delay trials (>450 ms) had a significantly shorter RT than zero delay trials(p<.001, 2-sample t-test). The mean RT difference was 10.0 ms in K-array and 35.5 ms in K–single electrode. Both monkeys showed an irregularity in their RT curves, with an RT increase for intermediate-length delays. This effect lasts longer in Monkey N, resulting in long-delay trials not having a significantly shorter RT than zero delay trials (p>.05). This may be due to the monkeys learning the statistics of our task, which contained more long delays (450–900 ms) than intermediate (50–450 ms) delays. For our neural analyses, we used only trials with a zero delay or a long (450–900 ms) delay, excluding reaches with intermediate delays from our analyses.
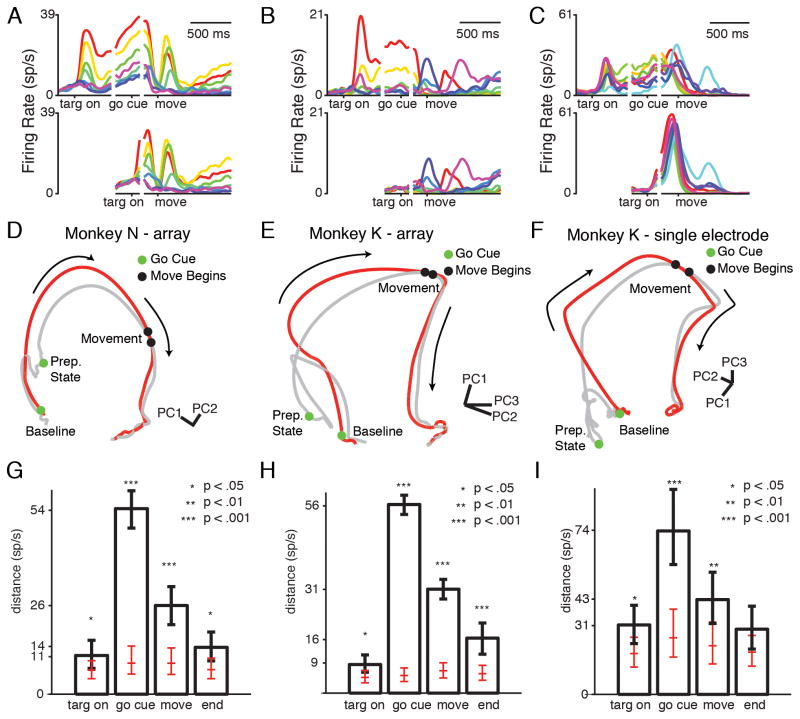
We recorded neural activity in M1 and PMd using tungsten microelectrodes in Monkey K, followed by two 96 electrode arrays (PMd, M1) in Monkeys N and K. We collected 125 units for N-array, 104 units for K-array, and 63 units for K-single electrode. We computed peri-stimulus time histograms (PSTHs) for each unit and target to estimate the mean neural activity for each reach direction (Figure 3A–C). To compare delayed and non-delayed reaches in the neural population as a whole, we examined the neural population states in these two conditions. To gain intuition about the neural population state as it evolves through time (i.e., the neural-population trajectory), we normalized the PSTHs (to avoid bias toward high-FR neurons), and performed principal component analysis (PCA) on the PSTHs for a given reach direction. Plotting the first three principal components (PCs) yields a low-dimensional neural trajectory which can be visualized easily and still represents much of the variance of the original neural data (>75% of the total variance for every reach direction).
Figure 3.
Neural data for delayed and non-delayed reaches. (A–C) Example individual neural PSTHs. Each color represents a different reach direction. Top: conditions with a delay. Bottom: conditions without a delay. (A) Unit where delay activity is quickly recapitulated in the non-delay condition. (B) Unit whose delay activity is skipped in the non-delay condition. (C) Unit whose delay and non-delay activity has similar tuning but different magnitude. (D–F) Example neural state-space diagrams. Gray trace: delayed reach. Red trace: non-delayed reach. Arrows show direction of time. (G–I) Median resampled distance between trajectories at different times, for the trajectories pictured in D–F. Error bars show 5th and 95th percentile of the distribution. Red ticks: median, 5th, and 95th percentile of the distance detected if neural trajectories were generated from the same underlying distribution. Stars show bootstrap significance. See also Figure S1, Movie S1, Table S1.
Tracing the neural trajectory for a delayed reach, we observe that the neural activity begins in a “baseline” state (Figure 3D–F, gray trace; Supplementary Movie 1). After the target cue, neural activity moves to a new part of the state space, representing the prepare-and-hold state for that reach. After the go cue, the trajectory follows a path into “peri-movement activity,” eventually slowing to a new hold state after reach completion.
We can compare this delayed reach neural-population trajectory to the non-delayed reach condition by plotting them in the same space (Figure 3D–F, red trace; Supplementary Movie 1). The neural-population trajectory in the non-delayed reach condition also begins at baseline. When the go cue (and target) turns on, the neural activity follows a path which resembles the peri-movement activity in the delayed reach condition. However, the two trajectories do not overlap for a large portion of their paths. In particular, the non-delayed reach neural trajectory does not appear to pass through the delayed reach’s prepare-and-hold state. Instead, it bypasses that state, moving along a path that resembles the peri-movement trajectory. The two conditions take parallel but separate paths through state space, converging around the time of movement onset. In this projection, it thus appears that neural activity only achieves the prepare-and-hold state if there is a delay.
Though looking at a low-dimensional plot can be useful for gaining intuition about neural processes, neural activity occupies more than three dimensions (Yu et al., 2009). Therefore, it is critical to examine neural activity in a higher-dimensional state. This helps to ensure that the intuition gained in the reduced-dimensional view is not an artifact of the projection and allows a more precise quantification of the trajectories’ differences and similarities.
We developed a distance quantification that could be computed in arbitrary (N) dimensions. We cannot simply compare the distance between trajectories at each time for two reasons. First, the delayed reach condition contains more time points than the non-delayed reach condition. Second, a misalignment in time could result in an overestimation of the distance between trajectories. Instead, we selected relevant times on the delayed reach neural trajectory (target onset, go cue, movement onset, and after the movement has finished), and then found the closest point on the non-delayed reach neural trajectory (across all times), to err statistically conservatively (on the side of estimating the trajectories to be as close as possible). The Euclidean distance between these two points represents the minimum possible distance between the trajectories at this time. A zero distance indicates that the non-delayed reach neural trajectory passes through the selected point on the delayed reach trajectory, while a large distance indicates that the non-delayed reach neural trajectory never comes near the selected point on the delayed reach neural trajectory. Because neural activity is variable across trials, our trajectories will never be exactly the same, so we will never see a true zero distance. To determine whether the distance is significantly higher than expected, we compared our estimated distance between delayed and non-delayed conditions to the distance between resamples pulled only from the delayed condition. This distance tells us how far apart we would expect the neural trajectories to be “by chance” if the data were truly pulled from the same underlying distribution. To determine the confidence interval of the distances at different times, we performed a bootstrap analysis by resampling our underlying trials for each condition, regenerating our neural trajectories from this resampled data set, and calculating neural distance as above. The distance distributions for the example trajectories plotted in Figure 3D–F are shown in Figure 3G–I (see also Figure S1).
Even at the time of target onset, many reach directions display significantly higher (p<.05) distances than expected if the trajectories were pulled from the same distribution (N-array: 8/8 targets; K-array: 4/7 targets; K-single electrode: 6/14 targets). This may reflect the “block structure” of the task, which allows the monkeys to predict whether the upcoming trial will contain a delay. This could lead to anticipatory differences in the baseline state. However, the magnitude of the baseline distance is still low. The mean +/− STD distance between trajectories, across targets, normalized by expected distance is: 2.1 +/− 0.4 for N-array, 1.6 +/− 0.2 for K-array, and 1.6 +/− 0.3 for K-single electrode. This reflects that neural activity is still similar at this time. At the time of the go cue, the distance between the trajectories is significantly larger than expected. The normalized mean +/− STD distance between trajectories across targets is: 6.4 +/− 1.1 for N-array, 6.7 +/− 2.4 for K-array, and 2.2 +/− 0.3 for K-single electrode (all targets, all datasets p<.01). This indicates that the neural population trajectory does not achieve the prepare-and-hold state during non-delayed reaches. At the time of movement onset, the distance between the neural trajectories is lower, reflecting that they have begun to re-converge. However, most reaches still have significantly higher than expected distances at this point. The normalized mean +/− STD distance between trajectories across targets is: 3.9 +/− 0.8 for N-array, 4.2 +/− 0.4 for K-array, and 1.8 +/− 0.3 for K-single electrode. By the end of the reach, the trajectories have largely re-converged. The normalized mean +/− STD distance between trajectories, across targets is: 2.0 +/− 0.4 for N-array, 2.1 +/− 0.7 for K-array, and 1.5 +/− 0.1 for K-single electrode. This distance analysis indicates that the prepare-and-hold state is not achieved in the absence of a delay.
Neural activity can move from one prepare-and-hold state to another during a delay
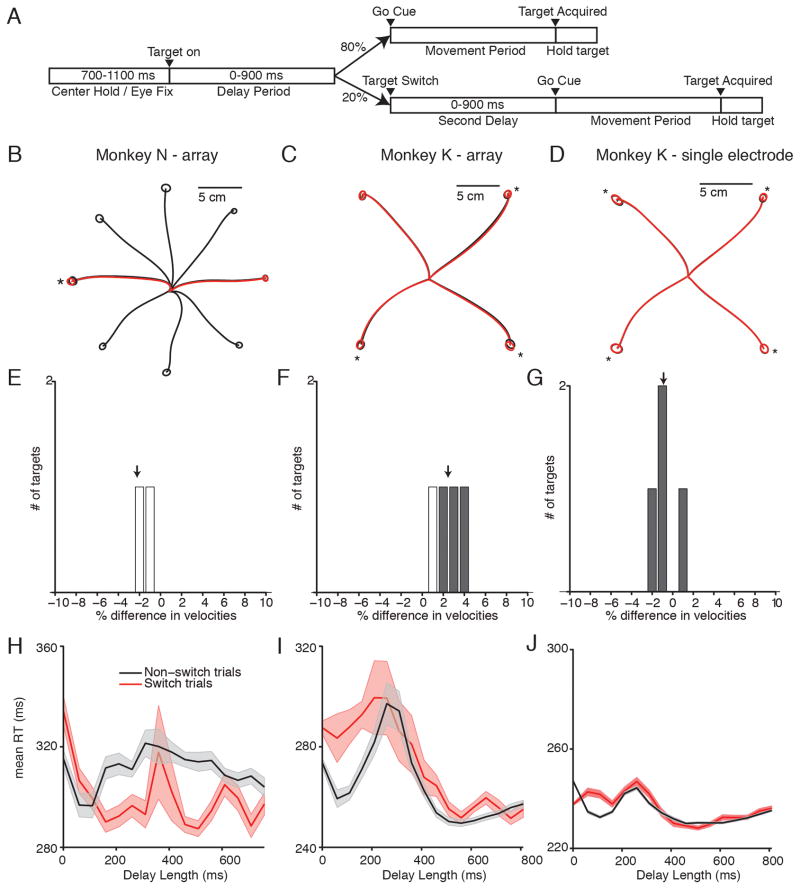
We next investigated whether monkeys must re-prepare if they have prepared the wrong reach. We trained monkeys N and K to perform a delayed-reaching task variant (Figure 4A). 80% of trials (non-switch trials), were delayed reach trials with the same parameters as the previous task. 20% of randomly interleaved trials were switch trials. Following a delay of 400 ms (N-array), 450 ms (K-single electrode) or 450–900 ms (K-array) after the initial target onset, the initial target turned off and a second target appeared 180 degrees separated from the initial target. There was then either a second delay (0–900 ms), or the monkey was allowed to reach immediately.
Figure 4.
Switch task behavior. (A) Task design. 80% of trials were delayed reaches. In 20% of trials, the initial target switched locations after 400 ms (N), 450 ms (K-single electrode) or 450–900 ms (K-array). The go cue either arrived immediately, or there was a second delay of 0–900 ms. (B–D) Mean reach trajectories for non-switch reaches (black) and switch reaches (red). Circles represent 1 STD of end point positions. Starred reaches show significantly different endpoint distributions (p<.05) (E–F) Difference in reach velocity between different reach directions. Positive indicates non-switch reaches were faster. Gray bars show significantly different reach velocities (p<.05). (G–H) Mean +/− SEM RT curves for non-switch (black) and switch (red) trials. In switch trials, delay length represents time from the target switch, rather than time from the initial target onset.
We compared the kinematics of the reaches between switch trials and non-switch trials. The mean reach trajectories were similar, with overlapping end point distributions (Figure 4B–D). The end point distributions were often significantly different (N-array: 1/ 2 targets; K-array: 3/ 4 targets; K-single electrode: 4/ 4 targets; p<.05 One-Way MANOVA), though the magnitudes of the differences were small (N-array: 8 +/− 8%; K-array: 7 +/− 4%; K-single electrode: 4 +/− 2 %; mean +/− STD Euclidean distance between mean reach endpoints, as percentage of target diameter) (Figure 4B–D). The peak reach speed was also similar between switch and non-switch trials (Figure 4E–G), with no target having a greater than 5% difference in velocity.
The target switch had a significant effect on RT when the switch and go cue were simultaneous. In this case, the monkeys had a longer RT for the switch condition. Moreover, the monkeys seemed to suffer an RT penalty for preparing to the wrong reach; the switch RT is even longer than the RT for zero-delay trials (Figure 4H–I) (19 ms, N-array, 14 ms, K-array, p<.01 2-sample unpaired t-test). When given sufficient time to re-prepare, however, this RT deficit is largely erased. In the Monkey K-single electrode data, however, the RT for zero-delay switch trials (red trace, Figure 4J) is lower than the RT for trials without a delay and without a switch (mean of 9.6 ms faster, p<.001 2-sample unpaired t-test). We believe that this is because, while collecting the single-electrode switching data, we held the switch time constant at 450 ms, which could have resulted in the monkey learning to “anticipate” that a switch was more likely at a particular time. To correct for this possibility, when later collecting the array data we instead switched the targets at a variable time between 450–900 ms. When we made this behavioral modification, the RT for zero-delay switch trials increased to longer than the RT for trials with no delay. While Monkey N also performed the task with a fixed 400-ms switch time, he did not appear to learn to anticipate the switch.
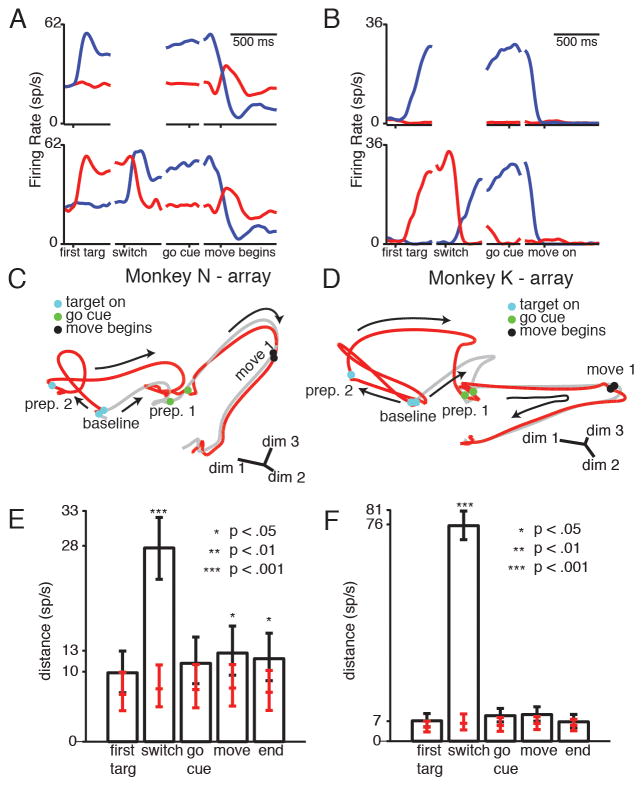
To determine the dynamics of re-preparation, we first examined conditions in which the target switch was followed by a second delay. We calculated PSTHs for the switching and non-switching conditions for each neuron and target (N-array: 119 units, 2 target; K-array: 114 units, 4 targets; K-single electrode: 83 units, 4 targets)(Figure 5A–B). In both example PSTH’s, neural activity first moves to the prepare-and-hold state of the cued target. After the switch, neural activity moves to the new target’s prepare-and-hold state. Movement-generation activity looks similar between switch and non-switch conditions.
Figure 5.
Neural activity for target switches followed by a second delay. (A–B) Example neural PSTHs. Traces are color coded by final reach direction. Top: conditions without a switch. Bottom: conditions with a switch. (C–D) Example state-space diagrams. Gray trace: non-switch condition. Red trace: switch condition. After the target switch, neural activity moves from prep state 2 to prep state 1, and then remains close to non-switch trajectory through the movement. (E–F) Median resampled distance between trajectories at different times, for the trajectories pictured in C–D. Error bars show 5th and 95th percentile of the distribution. Red ticks: median, 5th, and 95th percentile of the distance measured if neural trajectories were generated from the same underlying distribution. Stars show bootstrap significance. See also Figure S2, Movie S2, Table S2.
To observe the population neural state after the target switch, we again performed PCA on the normalized PSTHs to find an informative, low-dimensional projection of neural state (see methods for full details). We plotted the neural trajectories in this space, which still accounts for >45% of the variance of the original data (Figure 5C–D, Movie S2). When the initial target turns on, the switch condition (red trace) and non-switch condition (gray trace) move to different prepare-and-hold states, because different targets are cued. After the switch but before the go cue, the switch condition neural population trajectory moves from its initial prepare-and-hold state to the new prepare-and-hold state. After the go cue, movement generation activity appears quite similar between the switch and non-switch conditions.
Calculating the distance between the neural trajectories in the full-dimensional neural state space confirms the divergence and convergence of the neural trajectories observed in the low-dimensional projection (Figure 5E–F, Figure S2). The neural distance between conditions is initially low, rarely differing significantly from the expected distance distribution. The normalized mean +/− STD distance between switch and non-switch trajectories across targets is 1.4 +/− 0.09 for N-array, 1.4 +/− 0.2 for K-array, and 1.4 +/− 0.2 for K-single electrode (p>.01, all targets). The distance then increases after the appearance of the first target cue (when the two trajectories are preparing different reaches) and is significantly greater than expected if the trajectories were pulled from the same distribution. The normalized mean +/− STD distance between trajectories across targets is: 4.2 +/− 0.8 for N-array, 8.6 +/− 2.9 for K-array, and 3.0 +/− 0.5 for K-single electrode(p<.01, all targets). After the target switch, the distance between the two conditions returns to a level more comparable to the distance at baseline. The normalized mean +/− STD distance between trajectories is: 1.6 +/− 0.1 for N-array, 2.0 +/− 0.5 for K-array, and 1.7 +/− 0.1 for K-single electrode. The distance remains low through the remainder of the trial. The normalized mean +/− STD distance between trajectories at time of movement onset is: 1.6 +/− 0.10 for N-array, 1.5 +/− 0.08 for K-array, and 1.4 +/− 0.3 for K-single electrode.
If a target switch and go cue are simultaneous, neural activity does not pass through the prepare-and-hold state for the new target
We next examined whether reaches are also re-prepared in conditions with a simultaneous target switch and go cue. Observing the population neural state using PCA (Figure 6C–D, Movie S3), the neural trajectories initially look qualitatively similar to the previous switch-with-re-preparation case. When the first target turns on, the switch condition and non-switch condition move to opposing prepare-and-hold states. In this condition, the go cue and target switch are given at the same time. When this happens, the switching neural population trajectory does not divert to the new, correct prepare-and-hold state. Instead, it takes a path that appears to parallel the non-switching trajectory. The two trajectories gradually converge over the remainder of the trial.
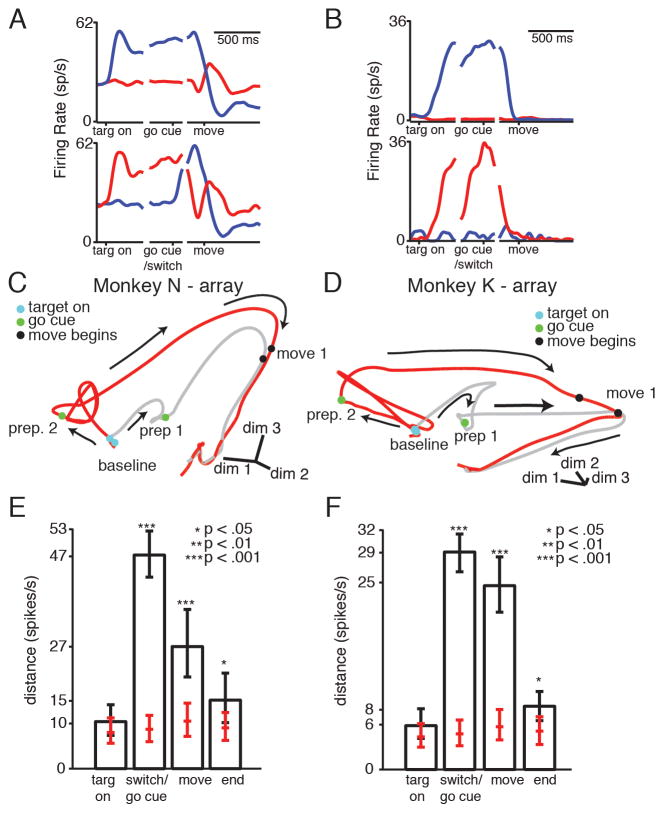
Figure 6.
Neural activity for target switches with a simultaneous go cue. (A–B) Example neural PSTHs. Traces are colored by final reach direction. Top: non-switch conditions. Bottom: switch conditions. (A) Delay period activity is recapitulated after the go cue in the switch condition. (B) The preparatory state is not achieved after the go cue in the switch condition. (C–D) Example state-space diagrams. Gray trace: non-switch condition; red trace, switch condition. After the target switch, neural activity does not divert through the correct prepare-and-hold state, instead converging gradually with the non-switch movement trajectory (E–F) Median distance between trajectories at different times, for the trajectories pictured in C–D. Error bars show 5th and 95th percentile of the distribution. Red ticks: median, 5th, and 95th percentile of the distance measured if neural trajectories were generated from the same underlying distribution. Stars show bootstrap significance. See also Figure S3, Movie S3, Table S3.
This low-dimensional impression is borne out in the high-dimensional distance analysis (Figure 6E–F, Figure S3). The distance between the trajectories starts out low. The mean +/− STD normalized distance between different trajectories is: 1.3 +/− 0.001 for N-array, 1.4 +/− 0.2 for K-array, and 1.2 +/− 0.08 for K-single electrode (p > .01, all targets). Once the target turns on, the trajectories diverge, and the distance at the time of the go cue is high. The normalized mean +/− STD distance between trajectories across targets is: 4.6 +/− 1.1 for N-array, 6.2 +/− 1.9 for K-array, and 2.9 +/− 0.4 for K-single electrode (p<.01, all targets). This implies that the state achieved by the correctly prepared trajectory during the delay is never achieved by the switch trajectory. The distance between the trajectories remains relatively high at the time of movement onset. The mean +/− STD normalized distance between trajectories, across targets is: 2.5 +/− 0.2 for N-array, 3.8 +/− 0.3 for K-array, and 2.4 +/− 0.07 for K-single electrode. This is despite the fact that the reaches themselves are kinematically similar (Figure 4). By the time the monkeys have finished reaching, the neural trajectories have largely re-converged. The mean +/− STD normalized distance between trajectories, across targets is: 1.7 +/− 0.06 for N-array, 1.6 +/− 0.08 for K-array, and 1.3 +/− 0.05 for K-single electrode. This analysis indicates that even if monkeys have prepared an incorrect reach at the time of the go cue, their neural activity still does not need to re-direct through the correct prepare-and-hold state to make a correct reach.
The initial target response is similar between delayed and non-delayed reaches
Given that the prepare-and-hold state is not achieved in the absence of a delay, we wanted investigate whether any neural response properties were similar between delayed and non-delayed reaches. To address this question, we compared the time course of neural responses under different behavioral conditions.
We first examined the timing of neural responses to command cues. For delayed reaches, we asked how long it takes for neural trajectories to respond to the target versus the go cue. We used a distance analysis to determine neural response time to different targets. We estimated neural FR’s on each trial as the number of spikes in a 40-ms bin preceding each time point. For delayed reaches to a given target, we estimated the distance over time between the average baseline activity and the average neural trajectory for that target (Figure 7A–B, green trace). Looking forward from the time of target onset, we defined the “neural response time” as the first time that the neural distance from baseline crosses a threshold of 20 spikes/s further than the neural distance at the time of target onset. 20 spikes/s is a threshold of approximately double the expected fluctuation in the distance metric, as measured during the baseline period. We repeated this analysis across all target directions to yield an across-target estimate of neural response time (Figure 7A–B, vertical green line). We repeated this analysis to generate a “go cue response time”, examining when the neural distance from the prepare-and-hold state starts increasing after the go cue (figure 7A–B, black trace and vertical black line).
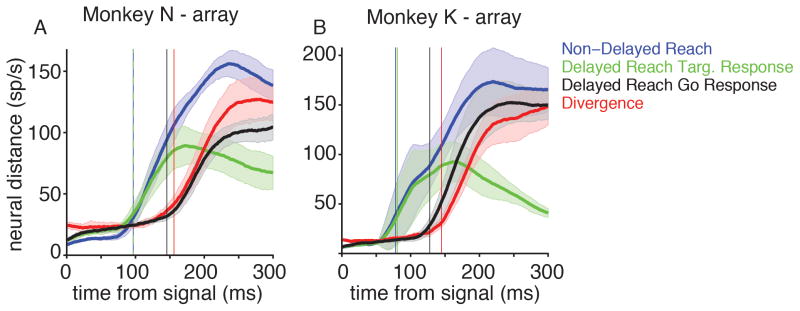
Figure 7.
Timing of neural responses to external cues. (A–B) Euclidean distance as a function of time from either the target or go cue (mean +/− STD across reach directions). Vertical lines show the time that the distance becomes greater than 20 sp/s (mean across reach directions). Green: Distance between delayed reach neural trajectories and baseline, as a function of time from target onset. Blue: Distance between non-delayed reach neural trajectories and baseline, as a function of time from target onset. Black: Distance between delayed reach neural trajectories and preparatory state, as a function of time from the go cue. Red: Distance between delayed reach neural trajectories and non-delayed reach neural trajectories, as a function of time from target onset. See also Figure S4.
In both N-array and K-array, the neural response to the target cue was faster than to the go cue (mean +/− STD difference in response times across reach directions: N: 49 +/− 13 ms, p<0.01; K: 47 +/− 13 ms, p<0.01; paired t-test) (Figure 7A–B, black vs. green trace). This suggests that target identity may reach the motor cortex faster than the putative “go” command. If this is true, then neural responses during a non-delayed reach should first resemble the initial target-cue response of a delayed reach, as target identity arrives first. Only after the go command reaches the motor cortices should delayed and non-delayed reaches diverge.
We therefore compared the neural responses of delayed and non-delayed reaches. Delayed and non-delayed reaches had a similar (though still significantly different in K) neural response latency to the target cue (mean +/− STD difference in response times across reach directions: N: 0 +/− 5 ms, p>0.05; K: 2 +/− 2 ms, p<0.05 ; paired t-test) (Figure 7A–B, blue vs. green trace), suggesting that the presence or absence of a delay does not strongly influence the arrival time of target information. Given the timing similarity, is the initial response itself also similar? To determine the similarity of responses, we calculated the neural “divergence time” between delayed and non-delayed trajectories. This was defined, for a given target, to be the first time the distance between delayed and non-delayed neural trajectories was >20 spikes/s greater than the distance at baseline. We found that this divergence time is later than the initial target response times (N: 59 +/− 17 ms later; K: 65 +/− 21 ms later, p<0.01, paired t-test, both monkeys) (Figure 7A–B, red trace). This means that the initial neural response to the target cue are highly similar across delayed and non-delayed reaches.
Delayed and non-delayed reach neural activity could remain similar until the “go cue” signal arrives. If this is true, then the divergence time should be close to the go cue response time of delayed reaches. And indeed, we see that for both monkeys, the divergence time is closer to the delayed reaches’ go cue response time, though still significantly different in K (mean +/− STD difference: N: divergence 10 +/− 17 ms longer, p >0.05; K: divergence 17 +/− 9 ms longer, p <0.01; paired t-test) (Figure 7A–B, red trace vs. black trace).
Even though the prepare-and-hold state is not achieved during non-delayed trials, the initial response is highly similar between delayed and non-delayed reaches. This suggests that the early neural target responses could be sufficient to distinguish where to reach and generate a correct movement.
DISCUSSION
We investigated whether neural activity always engages preparatory activity before generating movement. We first asked whether neural activity always achieves a specific prepare-and-hold state. First, we compared delayed and non-delayed reaches. These reaches were kinematically similar. However, non-delayed reaches did not achieve the same neural prepare-and-hold state as delayed reaching movements. Second, we asked whether reaches are re-prepared if the target switches locations. When the target switch was followed by a delay, the monkeys’ neural activity moved from the initial prepare-and-hold state to the new one. However, when the target switch and go cue were simultaneous, we did not observe the same effect. Instead, the switch condition neural population trajectories took a parallel but separate path through neural state space. The switch and non-switch neural population trajectories did not fully re-converge until the end of the trial. These results show that achieving a single, specific neural prepare-and-hold state is not necessary for generating a correct reach.
We then asked whether any neural preparatory activity was similar between delayed and non-delayed reaching conditions. Specifically, we examined the time course of the neural responses to different behavioral cues. We found that the neural target response has a similar latency in delayed and non-delayed reaches. These responses are similar to each other until about 50 ms after they begin. The time that the responses diverge is similar to the “go cue” response time in the delayed reach case. These findings suggest that there may be two separate inputs to motor cortex in this task. Target information arrives relatively quickly, while go cue information takes slightly longer, even if these cues are given simultaneously from an external perspective. If the go cue fails to arrive soon after the target cue, then neural activity moves to the prepare-and-hold state. When the go cue arrives, movement generation activity is engaged, regardless of whether the prepare-and-hold state was reached. This preserved neural target response, combined with the fact that reach kinematics are similar across delayed and non-delayed reaches, suggests that the early neural target response is sufficient to generate correct reaching dynamics.
Prepare and hold
It is worth noting that preparatory activity identified in this and previous studies (Cisek and Kalaska, 2002; Riehle and Requin, 1989; Tanji and Evarts, 1976; Wise and Mauritz, 1985) is observed when monkeys are simultaneously preparing a movement and holding a static posture. Our study indicates that fully attaining this state is potentially unique to this prepare-and-hold task, rather than a necessary step in all forms of voluntary motor generation. While there are certainly times when preparing for but withholding from movement may be warranted (particularly behaviors which require a short RT, such as swatting a fly, or dodging a dodge ball), it is likely that neural activity in this case is not universally representative of all movement generation activity. Previous studies have demonstrated that achieving this state decreases RT (Afshar et al., 2011; Churchland and Shenoy, 2007). However, if achieving this state is not necessary, it remains unclear why neural activity attains this particular state (instead of, for example, pausing at the state at which the delayed and non-delayed neural target responses diverge). It could be that this state allows motor preparation and avoids motor initiation, while other “preparatory” states would trigger a movement. It is also possible that this state is better optimized to generate a specific reach, having been given more time to prepare. Further work will be required to determine the significance of this particular state during prepare-and-hold paradigms.
Visual Effects
To make even simple movements, the brain must perform many computations. First, subjects must use sensory processing to identify potential targets and barriers. Subjects must then decide where and when to move, based on this sensory input and task goals. Finally the movement must be prepared and executed. Studies in the Frontal Eye Field (FEF), an area involved in the selection and execution of saccadic eye movements (Schall, 2002), have suggested that visual target selection has a fixed duration which does not co-vary with RT (Schall and Thompson, 1999; Thompson et al., 1996). In contrast, saccadic motor preparation takes a variable length of time and likely is the primary cause of RT variability in saccadic eye movements in a visual-search task. This observation of a two-step visuo-motor transform in the FEF agrees on a basic level with our findings that target-related neural responses are observed earlier than go-cue related neural responses. Indeed, target selection must certainly precede motor generation regardless of motor effector.
However, there are also many differences between FEF and PMd/M1. First, motor-related responses in FEF tend to display a “rise to threshold” form of motor generation – saccades are generated when neural activity has reached a specific threshold (Hanes and Schall, 1996). In contrast, neurons in PMd and M1 often display both increasing and decreasing FRs during movement preparation, which is not well predicted by a rise-to-threshold model. Furthermore, directional tuning during preparation is only loosely correlated with directional tuning during movement (Churchland et al., 2010; Churchland et al., 2006). Second, FEF contains separable populations of cells which primarily display visual-related activity or motor-related activity (Bruce and Goldberg, 1985; Sato and Schall, 2003), while these processes tend not to be separated on a neuron-by-neuron basis in the motor cortex (Churchland et al., 2010). Finally, the task used in the FEF studies described above was a visual search task in which when to move was not explicitly instructed. In our task, monkeys were instructed when to begin moving. It is thus presumably necessary that some form of trigger signal (or hold signal) be transmitted to the motor cortex, to allow the reach to be delayed until the go cue.
An updated model of motor cortical dynamics
The results in this paper offer an enhancement and expansion of previous models of motor cortical dynamics. The optimal subspace hypothesis (Churchland and Shenoy, 2007) suggested that there is an optimal preparatory region from which to generate a given movement. The initial condition hypothesis (Afshar et al., 2011; Churchland et al., 2010; 2012) further refined this model to suggest that the neural preparatory state serves as the initial condition for a dynamical system that generates the reach.
These previous models both concentrated on movement generation dynamics. These models acknowledge preparatory state as the initial condition for the movement-generation dynamical system but do not concentrate on the mechanism of how this state is achieved. It is clear, however, that neural activity behaves differently during different epochs (e.g., preparatory period vs. movement period). For example, neural activity approaches the prepare-and-hold state during the delay, but moves away from this state after the go cue. Therefore, motor cortical dynamics likely change as a function of task context and inputs, such as target information and the go cue (Shenoy et al., 2013).
We now describe a conceptual model of motor cortical activity that explicitly takes into account the distinct dynamics we observe during different task epochs. We propose that two principal dynamical systems are engaged during reaching: a “preparatory” system driven by target information, and a “movement generation” system driven by the go cue.
During a delayed reach, target information is transmitted to motor cortex first (Figure 8A, blue trace). This input sets the dynamics of the network, illustrated with a gray vector flow field. This preparatory dynamical system gives rise to the delay-period neural activity observed in this and previous studies. The preparatory dynamical system contains a putative attractor corresponding to the observed prepare-and-hold state. Given enough time, the neural state will converge to the prepare-and-hold attractor. When the go cue arrives, this changes the dynamics from preparatory dynamics to movement-generation dynamics. The neural state at the time of the change serves as the initial condition for this new dynamical system (Figure 8B, blue trace), consistent with the Initial Condition Hypothesis. Different initial conditions will yield slightly different motor-generation trajectories, as dictated by the dynamics. Given that RTs tend to be lower for fully prepared reaches, it seems reasonable to assume that the prepare-and-hold state represents a low RT initial condition. Being in this state could allow the subsequent movement-generation trajectory to initiate movement more quickly, consistent with the Optimal Subspace Hypothesis.
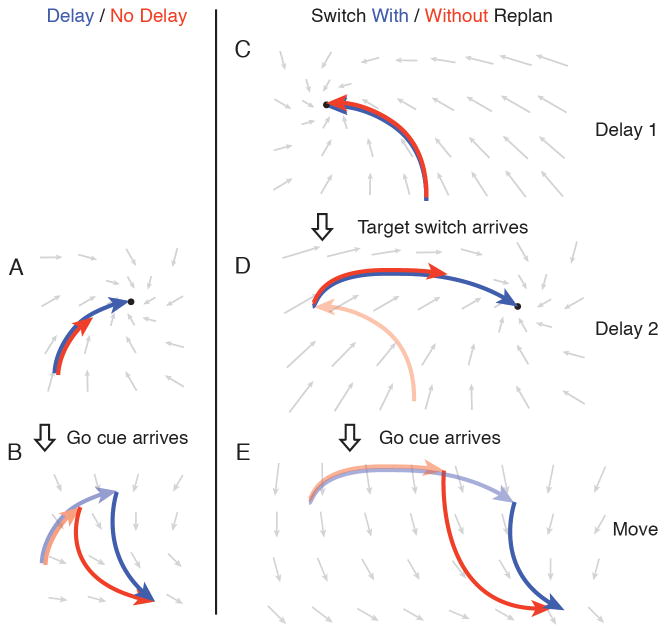
Figure 8.
Cartoon of preparation and movement dynamical systems. (A) When preparatory dynamics are engaged, neural activity approaches an attractor. Given a full delay (blue trace), neural activity reaches the attractor. Otherwise (red trace), neural activity approaches the attractor but may not converge. (B) The arrival of the go cue engages movement-generation dynamics. The neural state at the time of this transition (transparent red and blue traces) serves as the initial condition for the movement-generation neural trajectory (solid red and blue traces). (C) In target switch trials, neural activity moves to an attractor for the initially cued reach. (D) When the target switches, the attractor moves to a location corresponding to the preparatory state for the new target. If there is time, neural activity converges with this attractor (blue trace), otherwise approaches the attractor but may not converge (red trace). (E) The arrival of the go cue engages movement-generation dynamics. The neural state at the time of this transition serves as the initial condition for this new dynamical system.
In a non-delayed reach condition, one might initially think that either neural activity must go all the way to the prepare-and-hold state, or skip preparatory dynamics entirely and go directly into the movement-generation dynamical system. Our results indicate, however, that neither of these cases is true. Neural activity does not achieve the prepare-and-hold state during non-delayed reaching conditions. At the same time, the first portion of the neural response in the non-delayed reach condition looks much like the delayed-reach target response. We suggest that during non-delayed reaches, the preparatory dynamical system is engaged first, for a short period of time (Figure 8A, red trace). This could be caused by the target information reaching motor cortex more quickly than the go cue information. Preparatory dynamics are not engaged long enough to fully achieve the prepare-and-hold state. They are engaged long enough, however, to ensure that when the go cue arrives the subsequent trajectory can generate the correct reach (though usually with an RT penalty) (Figure 8B, red trace).
In behavioral conditions that involve a target switch, the progression from preparatory dynamics to movement dynamics is likely similar. When the first target turns on, this sets a preparatory dynamical system with a putative attractor corresponding to the prepare-and-hold state for this target (Figure 8C). When the target location changes, this moves the attractor to the prepare-and-hold state for the new target. Given sufficient time, neural activity will move to this new preparatory state (Figure 8D, blue trace). When the go cue comes, this engages the movement-generation dynamical system, and a movement is generated with neural activity that is similar to a standard delayed-reach (Figure 8E, blue trace).
If the go cue and target switch are given simultaneously from an external perspective, the target information is transmitted more quickly to the motor cortex. This allows a short period of time when the new target’s preparatory dynamics are engaged, similar to the non-delayed reach case. The neural state moves part of the way toward the new preparatory state (Figure 8D, red trace). When the go cue information arrives, the system changes into movement-generation dynamics. The neural population state at that time serves as the new initial condition, and the population state begins moving along a movement-generation trajectory (Figure 8E, red trace).
Several details of this two dynamical system model remain to be investigated in future work. For example, we cannot currently predict how neural dynamics will respond to perturbations while a reach is being executed. If the target goal changes mid-reach, or if the arm is perturbed unexpectedly, this will likely require on-line coordination of processes often ascribed separately to either motor preparation (e.g. determining and remembering task goal, setting up a reach), and motor generation (e.g. executing a reach to the correct target). We also cannot currently tell whether the transmission of the go cue is automatic. It could be that the go cue is always transmitted to motor cortex at a particular latency. Alternately, whatever system is sending the go cue could be monitoring the preparatory state of motor cortex, and only transmit the go cue when it detects that the neural state is sufficient to generate the correct reach, as hypothesized in early studies of the Optimal Subspace Hypothesis (Churchland and Shenoy, 2007).
Our results indicate that movement-generation neural trajectories can drive highly similar movements despite being initiated from different preparatory states. Many factors could relate to this effect. First, the preparatory region required for a given movement could be relatively broad, such that multiple states can result in the same movement. Neural trajectories are unlikely to achieve the same preparatory state from trial to trial, due to the variability of FRs. Therefore, some flexibility in required initial state could be beneficial, to allow a correct reach to be generated despite preparatory variability. Alternatively, target-specific information could be retained during the movement period, resulting in slightly different movement-generation dynamical systems for each reach. This could allow slight errors in initial state to be corrected by the movement-generation dynamical system itself. Further studies will be required to determine whether one or both of these possibilities is at work.
Previous work has uncovered neural features of movement generation which are preserved across reach directions (Churchland et al., 2012). This work has informed our investigation and interpretation, but also presents several methodological differences with our study. First, the prior work concentrated on across-target comparisons of delayed reaches. The present study, in contrast, compares delayed, non-delayed, and switch conditions for the same target. The previous work also uses a new method called jPCA, which accounts for a considerable percentage of the variance in the data (50–70% in the top 2–3 jPCA planes), but there still remains some neural variability to be accounted for. The previous study gives evidence for a single movement-generation dynamical system which depends only upon neural preparatory state (as opposed to unique dynamics for each reach). It is still possible, however, that there remain areas of variability which cannot be explained by this model. The evidence we present here cannot decisively distinguish whether or not movement dynamics are fully independent of target identity; additional investigation will be required to address this question.
This study represents one of the first substantial forays into examining not just motor preparation and execution, but the interaction between the two processes. We determined that fully achieving a specific prepare-and-hold state is not necessary, but that there are also aspects of delay-period activity that are preserved even without a delay. We propose that “motor preparation” may be more accurately defined as the engagement of a specific set of preparatory dynamics, rather than the achievement of a particular neural state. The set of states which are produced by these dynamics serve as initial conditions which are sufficient to generate a correct reach. This has helped advance our understanding of the nature of the dynamics of motor cortex, and how task constraints affect these dynamics.
EXPERIMENTAL PROCEDURES
Task Design
Two male rhesus macaques (Maccaca mulatta) (N and K) performed variants of a delayed reaching task. Animal protocols were approved by the Stanford Institutional Animal Care and Use Committee. Images were back-projected onto a vertical screen ~30 cm in front of the monkey. Timing of task events was confirmed using a photo box. Hand position was tracked optically by detecting a reflective bead taped between the first and second knuckle of the monkey’s middle two fingers (Polaris, Northern Digital Inc.). Eye position was monitored optically (Iscan).
In the delayed vs. non-delayed task variant, monkeys performed a reaching task composed of two block types. In the delayed reaching block, the monkeys either touched a central 9-mm radius square (K), or directed a cursor projected 10 cm above the monkey’s hand into the square (N) to initiate the trial. After 700–1100 ms, one of 8 (N), 14 (K-single electrode), or 7 (K-array) peripheral targets appeared (target cue). After a randomized delay (0–900 ms), the central target extinguished (go cue), and the monkeys were permitted to move their hand (K) or the cursor (N) into the cued target. After holding the target for 500–600 ms, they received a juice reward. In the non-delayed reaching block, the monkeys initiated trials in the same manner, but the target cue and go cue were always simultaneous.
In the switch task, two trial types were randomly interleaved. In 80% of trials, monkeys performed delayed reaches as in the previous task. In 20% of trials, the monkeys eye-fixated and either touched (K) or directed a cursor inside (N) a central, 9-mm radius square. After 700–1100 ms, a peripheral target appeared. After a delay, this target disappeared and a second, 180-degree separated target appeared (target switch). This switch occurred either at a fixed interval of 400 ms (N), 450 ms (K-single electrode), or a random interval of 450–900 ms (K-array). After an additional delay of 0–900 ms, the central target disappeared and the monkeys were required to touch and hold the second (new) target to receive a juice reward.
Behavioral Analysis
We generated mean reach trajectories for each reach direction and condition (delay, no-delay, switch) by averaging the x-y coordinates of each reach of a given type, aligned to movement onset. We defined the end of movement as the first time that reach velocity falls below 7% of maximum reach velocity. We used the hand position 30 ms after this as our end-point location, to ensure that the hand had fully stopped. We performed a one-way Multivariate Analysis of Variance (MANOVA) on the endpoint distributions. We examined the maximum reaching velocity for each reach direction and condition by performing a t-test on the distributions of maximum velocities for each condition pair. Velocity differences were normalized to the mean delayed-reach velocity.
Recording
Single electrode penetrations were guided by stereotactic coordinates, known response properties of PMd and M1, cortical microstimulation thresholds, and neural response to muscle palpation. Recordings were made anterior to the central sulcus, lateral to the spur of the arcuate sulcus, and posterior and medial to the precentral dimple, although some recordings were likely within the precentral dimple, based upon recording depth and stereotactic coordinates. Single electrode recordings were isolated online using the Plexon recording system. Only well-isolated single units were used. We recorded a total of 63 neurons over 42 days for the delayed / non-delayed task, and another 81 neurons over 67 days for the switch task.
Electrode arrays were implanted in PMd and surface M1 (Figure S5). Array recordings typically resulted in poorer isolation qualities than single electrodes, due to the static nature of the array, but allowed for a higher trial-count per neuron. We recorded waveforms on each channel which crossed a voltage threshold of −3.5 times the STD of the voltage, and spike sorted these waveforms offline using a custom spike sorter (Neurosort). In N, we performed a total of 13 days of recording for the pre-cue vs. non-pre-cue task and 18 days of recording for the switch task. In K, we performed a total of 7 days of recording for the pre-cue vs. non-pre-cue task and 3 days of recording for the switch task. Array data in this paper is from datasets recorded on November 5, 2010 and February 4, 2011 in N, and on July 18 and 19, 2012 in K. We selected datasets for analysis and publication based on maximizing recording quality and trial count. Results from a second set of recordings for each task and each monkey are in Supplemental Tables 1–3.
Peri-Stimulus Time Histograms
For each unit, we calculated PSTHs to estimate mean FR over time. We aligned trials to several times: target onset, switch (if relevant), go cue, and movement onset. We binned spike times in 1-ms bins and averaged over trials of the same reach direction and condition. We convolved these average FRs with a 25-ms Gaussian to smooth the FR estimate. We interpolated between the different aligned events to yield a trace which estimates the FR over time over the course of a trial.
Dimensionality Reduction
Prior to reducing the dimensionality of our data, we performed a softmax normalization of each PSTH, dividing FR for each neuron by the maximum variance across conditions for that neuron. This helps to avoid being biased by high FR neurons, by ensuring that each neuron has the same overall variability across conditions.
We elected to use Principal Component Analysis (PCA) to reduce the dimensions of our data. PCA imposes few assumptions on the underlying structure of the data, simply revealing dimensions which explain a large percentage of the variance. More complex methods, such as Factor Analysis (FA) or Gaussian Process Factor Analysis (GPFA) (Yu et al., 2009), often require additional assumptions on the data. For example, GPFA requires simultaneous recordings to accurately build a neural noise model, which we did not have in our single electrode datasets, and is optimized for predicting trial-by-trial neural activity, where here we concentrate on average neural activity. PCA has a strong precedent in the literature as a dimensionality reduction method for trial-averaged data (e.g. Churchland et al., 2012; Churchland et al., 2010; Harvey et al., 2012; Rivera-Alvidrez, et al., 2010). In addition, because we use enough dimensions to account for >90% of the neural variance in our distance quantification, the selection of dimensionality reduction method likely has little effect on the results. Indeed, we get very similar results without using any dimensionality reduction at all (see Figures S1–S3).
For a given target and condition (e.g., switching, non-switching, delayed, non-delayed), we generated a matrix of PSTH’s of dimension n × Σc,t c(t), where n is the number of recorded neurons, and c(t) denotes the selected conditions over time. We ran PCA on this space to reduce these dimensions to k × Σc,t c(t), where k represents the dimensions across which the most neural variance was explained. We then either plotted trajectories in the first three dimensions of this space (delay/no delay task), or performed a second calculation to find an informative rotation of this space (switch task).
Because the switching conditions featured reaches to more than one target, the top principal components often represent neural activity which is the same across multiple reaches. Therefore, the lowest principal components are often less informative about the differences between reach trajectories which we wish to observe. To find an informative projection, we reduced to a four dimensional space, using the first three principal component dimensions plus the dimension which best separates the prepare-and-hold states for the reaches we were comparing. Orthogonalizing this space gives us a rotation which allows us to visualize the neural difference between the different prepare-and-hold states. This allows us to observe re-preparation or the lack thereof in the switching conditions. This rotation is purely for visualization and is not used for subsequent distance analyses.
Distance Analysis
To estimate the minimum neural distance between different conditions over time, we performed a modified Euclidean distance analysis. We selected points on one of the two trajectories we were comparing (delay/no delay task: delayed reach trajectory; switch followed by a delay: switch trajectory; switch without a second delay: non-switch trajectory) (reference trajectory), and calculated the Euclidean distance between that point and every point on the second trajectory, in either the first 15 principal components (Figures 3–5) or the full-dimensional trajectory without dimensionality reduction (Figures S1–S3). We elected to use 15 principal components for the main manuscript to err on the high side of estimated dimensionality in this system (Yu et al. 2009). These 15 dimensions account for >90% of the variance of the data in all datasets. We selected the minimum Euclidean distance across all points on the second trajectory as our estimate of neural distance between the two trajectories at that time. This ensured that we would never overestimate the distance between the trajectories due to misalignment in time. A low distance indicates that the second trajectory achieves the selected state at some time, while a high distance indicates that the second trajectory never achieves the target state.
Bootstrap Procedure
To estimate the variability of the distance between traces, we performed a bootstrap analysis. For each reach direction and reach condition (delay, no delay, switch, non-switch), we resampled the trials recorded for that condition. We selected a new set of trials (randomly, with replacement) of the same size as our original set. We then calculated PSTHs from this resampled dataset, performed PCA on these resampled trajectories, and calculated the neural distance as described above. We collected 1000 resamples for each reach direction / condition set. This yields an estimate of the variability of the distance between neural trajectories.
It is possible that FR increases during the preparation and moving phases could artificially lead to an increase in average neural distance. To control for this possibility, we performed a second bootstrap analysis, where we resampled a single condition twice (reference trajectories: delay/no delay task: delayed reach trajectory; switch followed by a delay: switch trajectory; switch without a second delay: non-switch trajectory). We generated one set of the same size as the delayed reach set, and a second set of the same size as the non-delayed reach or the switch trials. By comparing the minimum neural distance between these resampled trial sets, we can estimate how far apart we would expect neural population trajectories to be if they truly were generated from the same underlying distribution. To determine the likelihood that the observed distance between trajectories was higher than expected by chance, we calculated the percentage of resamples in which the resampled distance was greater than this control resampled distance.
Response Timing Analysis
To determine when motor cortical neurons began responding to each unit, we first characterized the trial-by-trial FR of each neuron. To avoid timing confounds of convolving with an acausal Gaussian filter, we defined a neuron’s FR at a given time as the number of spikes in a 40-ms bin preceding that time. We then calculated the mean FR for each unit across all trials for each target and condition (delayed or non-delayed), aligned to different times in the trial (target onset, go cue, and movement onset).
To determine the neural response time to target onset, we estimated the baseline position as the mean FR in the 50 ms before target onset. We then calculated the neural distance at each time as the Euclidean distance between the full-dimensional neural position at that time and the baseline state. We considered the motor cortex to have begun responding to a target when it crossed a threshold of 20 spikes/s more distant than the distance at target onset. To determine this threshold, we observed the range of observed distances between neural trajectories and the mean baseline activity prior to target onset (when distance is expected to be as low as possible). This ranged from 7–11 spikes/s across targets in Monkey N, and 5–9 spikes/s in Monkey K. We selected a threshold of 20 spikes/s, which is approximately double that range. This minimizes the chances of a “false start” due to natural fluctuations in neural distance, while keeping the threshold relatively low.
We performed a similar analysis for the timing of response to the go cue, asking when neural activity became different from the mean position in the 50 ms before the go cue appeared (holding our 20 spikes/s threshold constant).
We next looked at the distance between the delayed and non-delayed neural trajectories at each time point after the target appeared. We set a threshold of 20 spikes/s greater than the distance at the time of target onset to serve as our “divergence time.” We performed all of these analysis for each target separately, using all units to generate our neural trajectories.
Supplementary Material
Acknowledgments
We thank J. Aguayo, M. Mazariegos, E. Morgan and C. Sherman for surgical assistance and veterinary care, B. Oskotsky for information technology support, and E. Castaneda, B. Davis, and S. Eisensee for administrative assistance. We thank M.M. Churchland and M.T. Kaufman for comments on the manuscript. We also thank our research group for helpful suggestions during manuscript preparation. This work was supported by a National Science Foundation Graduate Research Fellowship and a Stanford Graduate Fellowship (K.C.A), and the following awards to K.V.S.: Burroughs Welcome Fund Career Awards in the Biomedical Sciences, Defense Advanced Research Projects Agency (DARPA) Reorganization and Plasticity to Accelerate Injury Recovery (REPAIR) Program N66001-10-C-2010, and National Institutes of Health (NIH) Director’s Pioneer Award 1DP1OD006409.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFRENCES
- Afshar A, Santhanam G, Yu BM, Ryu SI, Sahani M, Shenoy KV. Single-Trial Neural Correlates of Arm Movement Preparation. Neuron. 2011;71(3):555–564. doi: 10.1016/j.neuron.2011.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broome BM, Jayaraman V, Laurent G. Encoding and Decoding of Overlapping Odor Sequences. Neuron. 2006;51(4):467–482. doi: 10.1016/j.neuron.2006.07.018. [DOI] [PubMed] [Google Scholar]
- Bruce CJ, Goldberg ME. Primate frontal eye fields. I Single neurons discharging before saccades. J Neurophysiol. 1985;53:603–635. doi: 10.1152/jn.1985.53.3.603. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Shenoy KV. Delay of movement caused by disruption of cortical preparatory activity. J Neurophysiol. 2007;97(1):348–359. doi: 10.1152/jn.00808.2006. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Afshar A, Shenoy KV. A central source of movement variability. Neuron. 2006a;52(6):1085–1096. doi: 10.1016/j.neuron.2006.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, Shenoy KV. Neural population dynamics during reaching. Nature. 2012:51–56. doi: 10.1038/nature11129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Ryu SI, Shenoy KV. Cortical preparatory activity: representation of movement or first cog in a dynamical machine? Neuron. 2010;68(3):387–400. doi: 10.1016/j.neuron.2010.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Santhanam G, Shenoy KV. Preparatory activity in premotor and motor cortex reflects the speed of the upcoming reach. J Neurophysiol. 2006b;96(6):3130–3146. doi: 10.1152/jn.00307.2006. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Ryu SI, Santhanam G, Shenoy KV. Neural variability in premotor cortex provides a signature of motor preparation. J Neurosci. 2006;26:3697–3712. doi: 10.1523/JNEUROSCI.3762-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, Kalaska JF. Simultaneous encoding of multiple potential reach directions in dorsal premotor cortex. J Neurophysiol. 2002;87(2):1149–1154. doi: 10.1152/jn.00443.2001. [DOI] [PubMed] [Google Scholar]
- Crammond DJ, Kalaska JF. Modulation of preparatory neuronal activity in dorsal premotor cortex due to stimulus-response compatibility. J Neurophysiol. 1994;71(3):1281–1284. doi: 10.1152/jn.1994.71.3.1281. [DOI] [PubMed] [Google Scholar]
- Crammond DJ, Kalaska JF. Prior information in motor and premotor cortex: activity during the delay period and effect on pre-movement activity. J Neurophysiol. 2000;84(2):986–1005. doi: 10.1152/jn.2000.84.2.986. [DOI] [PubMed] [Google Scholar]
- Diester I, Kaufman MT, Mogri M, Pashaie R, Goo W, Yizhar O, et al. An optogenetic toolbox designed for primates. Nature Neuroscience. 2011;14(3):387–397. doi: 10.1038/nn.2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goo W, O’Shea DJ, Kalanathi P, Diester I, Ramakrishnan C, Deisseroth K, Shenoy KV. Disruption of motor preparation by optogenetic stimulation of primate premotor cortex. Presented at the Society for Neuroscience; New Orleans, LA. 2012. [Google Scholar]
- Hanes DP, Schall JD. Neural Control of Voluntary Movement Initiation. Science. 1996;274(5286):427–430. doi: 10.1126/science.274.5286.427. [DOI] [PubMed] [Google Scholar]
- Harvey CD, Coen P, Tank DW. Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature. 2012;484(7392):62–68. doi: 10.1038/nature10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messier J, Kalaska JF. Covariation of primate dorsal premotor cell activity with direction and amplitude during a memorized-delay reaching task. J Neurophysiol. 2000;84(1):152–165. doi: 10.1152/jn.2000.84.1.152. [DOI] [PubMed] [Google Scholar]
- O’Shea DJ, Goo W, Kalanathi P, Diester I, Ramakrishnan C, Deisseroth K, Shenoy KV. Optogenetic perturbation of motor preparation in primate dorsal premotor cortex. Presented at the Society for Neuroscience; New Orleans, LA. 2012. [Google Scholar]
- Rickert J, Riehle A, Aertsen A, Rotter S, Nawrot MP. Dynamic encoding of movement direction in motor cortical neurons. J Neurosci. 2009;29:13870–13882. doi: 10.1523/JNEUROSCI.5441-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riehle A, Requin J. Monkey primary motor and premotor cortex: single-cell activity related to prior information about direction and extent of an intended movement. J Neurophysiol. 1989;61(3):534–549. doi: 10.1152/jn.1989.61.3.534. [DOI] [PubMed] [Google Scholar]
- Rivera-Alvidrez Z, Kalmar RS, Ryu SI, Shenoy KV. Low-dimensional neural features predict muscle EMG signals. Conference proceedings : .. Annual International Conference of the IEEE Engineering in Medicine and Biology Society IEEE Engineering in Medicine and Biology Society Conference. 2010;2010:6027–6033. doi: 10.1109/IEMBS.2010.5627604. [DOI] [PubMed] [Google Scholar]
- Rosenbaum DA. Human movement initiation: specification of arm, direction, and extent. J Exp Psychol Gen. 1980;109:444–474. doi: 10.1037//0096-3445.109.4.444. [DOI] [PubMed] [Google Scholar]
- Sato TR, Schall JD. Effects of Stimulus-Response Compatibility on Neural Selection in Frontal Eye Field. Neuron. 2003;38:637–648. doi: 10.1016/s0896-6273(03)00237-x. [DOI] [PubMed] [Google Scholar]
- Schall JD. The neural selection and control of saccades by the frontal eye field. Philos Trans R Soc Lond, B, Biol Sci. 2002;357:1073–1082. doi: 10.1098/rstb.2002.1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schall JD, Thompson KG. Neural selection and control of visually guided eye movements. Annu Rev Neurosci. 1999;22:241–259. doi: 10.1146/annurev.neuro.22.1.241. [DOI] [PubMed] [Google Scholar]
- Scott SH. Optimal feedback control and the neural basis of volitional motor control. Nat Rev Neurosci. 2004;5:532–546. doi: 10.1038/nrn1427. [DOI] [PubMed] [Google Scholar]
- Shen L, Alexander GE. Neural correlates of a spatial sensory-to-motor transformation in primary motor cortex. J Neurophysiol. 1997;77(3):1171–1194. doi: 10.1152/jn.1997.77.3.1171. [DOI] [PubMed] [Google Scholar]
- Shenoy KV, Kaufman MT, Sahani M, Churchland MM. A dynamical systems view of motor preparation: implications for neural prosthetic system design. Prog Brain Res. 2011;192:33–58. doi: 10.1016/B978-0-444-53355-5.00003-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shenoy KV, Sahani M, Churchland MM. Cortical Control of Arm Movements: A Dynamical Systems Perspective. Annu Rev Neurosci. 2013;36:337–359. doi: 10.1146/annurev-neuro-062111-150509. [DOI] [PubMed] [Google Scholar]
- Stokes MG, Kusunoki M, Sigala N, Nili H, Gaffan D, Duncan J. Dynamic Coding for Cognitive Control in Prefrontal Cortex. Neuron. 2013;78(2):364–375. doi: 10.1016/j.neuron.2013.01.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanji J, Evarts EV. Anticipatory activity of motor cortex neurons in relation to direction of an intended movement. J Neurophysiol. 1976;39(5):1062–1068. doi: 10.1152/jn.1976.39.5.1062. [DOI] [PubMed] [Google Scholar]
- Thompson KG, Hanes DP, Bichot NP, Schall JD. Perceptual and motor processing stages identified in the activity of macaque frontal eye field neurons during visual search. J Neurophysiol. 1996;76(6):4040–4055. doi: 10.1152/jn.1996.76.6.4040. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Weinrich M, Wise SP, Mauritz KH. A neurophysiological study of the premotor cortex in the rhesus monkey. Brain. 1984;107(Pt 2):385–414. doi: 10.1093/brain/107.2.385. [DOI] [PubMed] [Google Scholar]
- Wise SP, Mauritz KH. Set-related neuronal activity in the premotor cortex of rhesus monkeys: effects of changes in motor set. Proc R Soc Lond, B, Biol Sci. 1985;223:331–354. doi: 10.1098/rspb.1985.0005. [DOI] [PubMed] [Google Scholar]
- Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, Sahani M. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J Neurophysiol. 2009;102(1):614–635. doi: 10.1152/jn.90941.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.