Signal-dependent dynamics of transcription factor translocation controls gene expression

Summary

Information about environmental stimuli is often transmitted using common signalling molecules, but the mechanisms that ensure signalling specificity are not entirely known. Here we show that the identities and intensities of different stresses are transmitted by modulation of the amplitude, duration or frequency of nuclear translocation of the budding yeast general stress responsive transcription factor Msn2. Through artificial control of the dynamics of Msn2 translocation, we reveal how distinct dynamical schemes differentially affect reporter gene expression. Using a simple model, we predict stress-induced reporter gene expression from single-cell translocation dynamics. We then demonstrate that the response of natural target genes to dynamical modulation of Msn2 translocation is influenced by differences in the kinetics of promoter transitions and transcription factor binding properties. Thus, multiple environmental signals can trigger qualitatively different dynamics of a single transcription factor, and influence gene expression patterns.

Introduction

Living organisms respond to external cues and initiate appropriate physiological responses through signaling pathways that transmit signals to specific transcription factors, which regulate expression of target genes. In many cases, multiple inputs are transmitted by common signaling components or transcription factors ^1-3. However, the mechanisms that ensure specificity remain elusive. Information about environmental signals can be partially encoded in the dynamics of signaling molecule localization or activity, which in turn controls cellular responses ⁴. For example, in mammalian cells dynamical regulation of the nuclear localization of the transcription factor NFκB contributes to specificity in gene expression ^5-8. In budding yeast, external calcium concentration controls the activation frequency of the transcription factor Crz1 and leads to coordinated expression of multiple target genes ⁹. Here we study how information about diverse signals is transmitted in the activation dynamics of the Saccharomyces cerevisiae transcription factor Msn2, and then influence gene expression outputs.

Msn2 and its partially redundant homolog Msn4 are C₂H₂ zinc finger transcription factors that bind to stress responsive DNA elements (STREs) and regulate transcription of hundreds of genes in response to various stresses ^10,11. In normal growth conditions, Msn2 is phosphorylated and is localized to the cytoplasm. In the presence of stress stimuli, Msn2 is dephosphorylated, rapidly enters nucleus, and activates gene expression ^12,13. It is not fully understood how Msn2 is activated by unrelated stresses, nor is it known if information about stress identity and quantity is conveyed by Msn2 in the process of its activation.

Results

Dynamics of Msn2 translocation in response to stresses

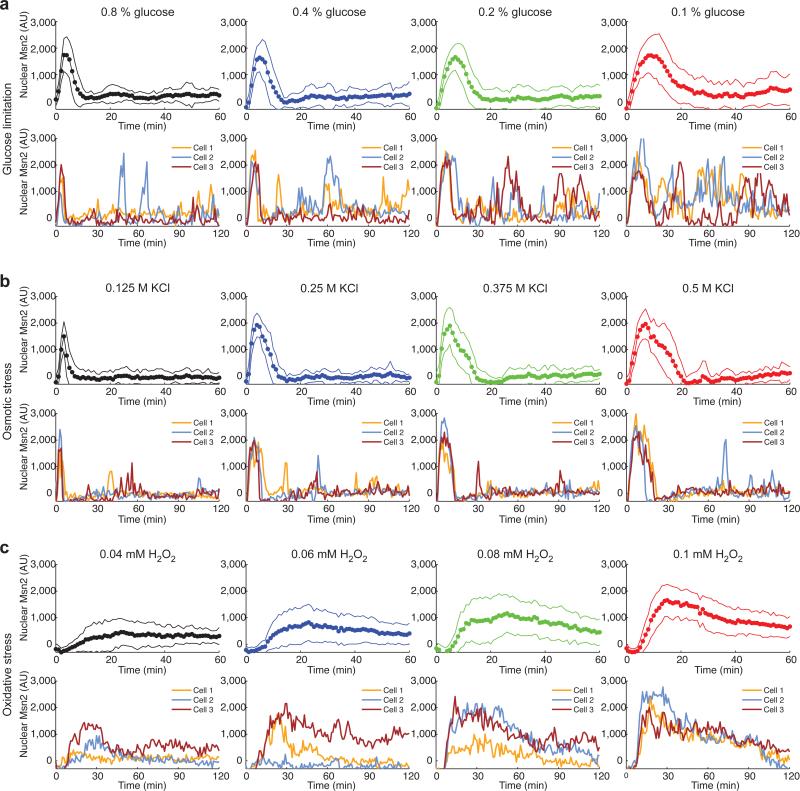
To determine how Msn2 responds to different stresses, we monitored nuclear translocation of Msn2-YFP in single cells cultured within a microfluidics platform ¹⁴ using time-lapse fluorescence microscopy. In response to each of the stresses tested, Msn2 rapidly translocates from the cytoplasm into the nucleus. However, different stresses elicit qualitatively different dynamics of Msn2 nuclear translocation (Fig. 1, Supplementary Fig. 1a-b and Supplementary Movies S1-3). In response to glucose limitation, single cells exhibit sporadic, heterogeneous translocation bursts following the initial relatively uniform nuclear burst of Msn2 (Fig. 1a) ^9,15,16. Osmotic stress induces a similar uniform initial nuclear burst of Msn2 in the population, but fewer subsequent sporadic bursts (Fig. 1b). In contrast, a prolonged nuclear enrichment of Msn2 was induced under oxidative stress conditions (Fig. 1c). In response to oxidative stress, single cells exhibit large variation in the time it takes to respond to stress and in the response amplitude. The single-cell variation in Msn2 translocation in response to natural stresses may come from variation in upstream signalling pathways and may be important for generating diversified cellular responses to stresses. We focused our study on stress intensity ranges that elicit detectable responses in gene expression at the population level; these ranges were determined with flow cytometry experiments, which monitored expression of an Msn2-dependent transcriptional reporter (Supplementary Fig. 1c). It is possible that lower signal strengths induce responses only in a small portion of cells while the majority of cells remain unresponsive ⁸.

Fig. 1.

Msn2 translocates to the nucleus with different dynamics in response to different stresses. Time traces of Msn2-YFP nuclear translocation are shown for (a) glucose limitation, (b) osmotic stress and (c) oxidative stress. In each panel, top row: averages of single-cell time traces of Msn2-YFP translocation in response to the indicated stresses (solid circles: averages of single-cell experimental data; solid lines: standard deviation of single cell responses of ~ 60 cells, from at least two independent experiments); bottom row: representative single-cell time traces of Msn2-YFP nuclear translocation. AU: arbitrary units of fluorescence. Additional single-cell traces are shown in Supplementary Fig. 1a-b.

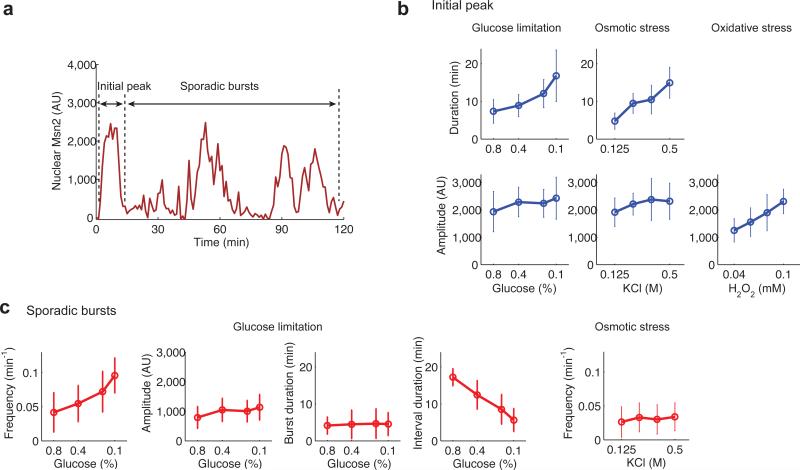
To determine how the intensities of different stresses affect the dynamics of Msn2 responses in single cells, we quantified the amplitude and duration of the initial Msn2 nuclear translocation peak and the amplitude, duration and frequency of the following sporadic bursts (Fig. 2 and Supplementary Fig. 2). For glucose limitation and osmotic stress, increasing stress intensities result in increases in the initial peak duration but no marked change in peak amplitude (Fig. 2b, top 2 rows, first 2 columns). In contrast, the amplitude of Msn2 nuclear localization increases with oxidative stress intensity (Fig. 2b, bottom row, right column). Increasing intensity of glucose limitation results in an increase in the frequency of the sporadic bursts following the initial peak, but no substantial changes in burst amplitude or duration (Fig. 2c). In contrast, the intensity of osmotic stress does not affect sporadic burst frequency (Fig. 2c, right panel). Therefore, cells modulate different dynamical parameters of Msn2 nuclear translocation in response to changes in intensity of different stresses: glucose limitation signals elicit a combination of duration modulation of the initial peak and frequency modulation of the following sporadic bursts; osmotic stress signals lead to duration modulation of the initial peak; and signals of oxidative stress induce primarily amplitude modulation of nuclear localization.

Fig. 2.

Quantification of single-cell Msn2-YFP translocation traces. (a) A schematic defines the initial peak of Msn2 nuclear translocation and subsequent sporadic bursts in a single-cell time trace. (b) Duration (top row) and amplitude (middle row) of the initial peak are quantified for the indicated stress conditions (open circles: mean value of single cells; error bars: standard deviation of single cell responses of ~60 cells, from at least two independent experiments). Duration is not quantified for the H₂O₂ treatment because a sustained translocation event was observed under this condition. (c), Frequency, amplitude, burst duration and interval durations of sporadic bursts in response to glucose limitation are quantified and shown as indicated. In addition, frequency of sporadic bursts under osmotic stress is quantified. The distributions of amplitude, duration, and frequency of sporadic nuclear burst in response to glucose limitation are shown in Supplementary Fig. 2a-c. Autocorrelation analysis of Msn2 localization traces upon glucose limitation has been performed and is presented in Supplementary Fig. 2d.

Influence of Msn2 dynamics on gene expression outputs

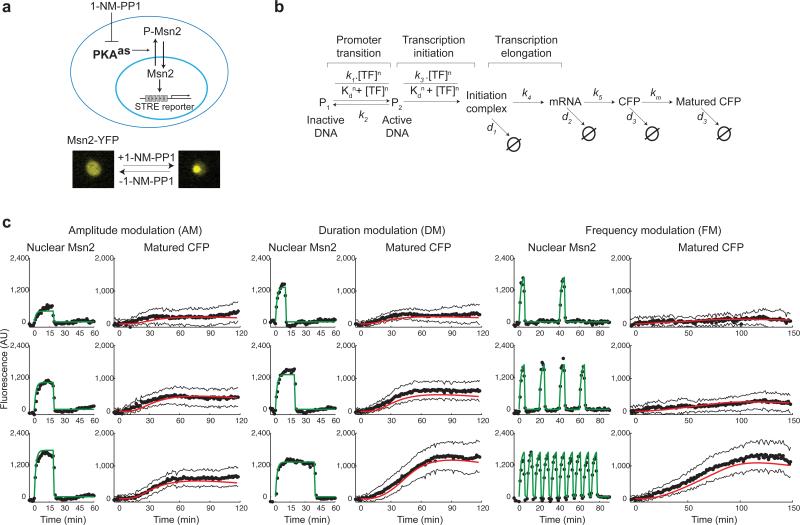
Having established that different stresses elicit distinct dynamics of Msn2 nuclear translocation, we then considered how dynamical modulation of Msn2 would affect gene expression. To enable systematic study of dynamical modulation schemes, we developed a method to artificially control the dynamics of Msn2 translocation. We introduced into the Msn2-YFP strain analog-sensitive mutations in all three protein kinase A (PKA) isoforms (Tpk1, Tpk2, Tpk3), which render them selectively inhibited by a small, cell-permeable inhibitor, 1-NM-PP1 ¹⁷. Phosphorylation and nuclear translocation of Msn2 are directly regulated by PKA ¹²; addition of inhibitor to the analog-sensitive strain leads to inhibition of PKA, dephosphorylation of Msn2, and subsequent nuclear localization (Fig. 3a). We also introduced a transcriptional reporter consisting of yECFP ¹⁸ under the control of a synthetic promoter containing 6 tandem STRE elements (CAAGGGG) to monitor Msn2-dependent gene expression in the same cells.

Fig. 3.

Experimental and computational analysis of gene expression in response to modulation of Msn2 nuclear translocation dynamics. (a) A diagram describes the analog-sensitive system used to control Msn2 nuclear translocation. (b) Gene expression model. A detailed description of the model construction and fitting procedure are included in Supplementary Results. (c) Averages of single-cell time traces of Msn2-YFP nuclear localization and reporter gene expression (CFP) measured in the same cells in response to inhibitor treatments (black solid circles: averages of time trace data; black solid lines: standard deviation of single-cell data of ~50 cells, from at least two independent experiments; green solid line: curve fitting of Msn2 translocation traces; red solid line: model simulation). The time traces of Msn2 nuclear localization were fit with a piecewise exponential function (Supplementary Fig. 3) to produce continuous time-dependent profiles, TF(t) , which served as input for the model. The model in b was fit to the averages of single-cell time traces of reporter gene expression (Supplementary Results). The complete dataset is included in Supplementary Fig. 3-5.

To provide a quantitative framework for understanding how gene expression is influenced by the dynamics of Msn2 activation, we developed a computational model of gene expression (Fig. 3b). The model considers the kinetics of the promoter transition from an inactive state (P₁) to active state (P₂). In the model, binding of the transcription factor to the gene promoter is approximated by a Hill equation, $\frac{TF{\left(t\right)}^n}{K_d^n+TF{\left(t\right)}^n}$ and is governed by parameters K_d and n. k₁ and k₂ are the rates of promoter activation and inactivation, respectively. These four parameters depend on the properties of target gene promoters and determine the behaviors of the model. A detailed description of the model equations is included in Supplementary Results.

We used a microfluidics device to dynamically and reversibly control the inhibitor treatment and artificially modulate the amplitude, duration, or frequency of Msn2 nuclear localization (Supplementary Fig. 3-5 and Supplementary Movie 4); for each of these treatments we collected single-cell time traces of Msn2 localization and gene expression (Supplementary Fig. 3-5). From these single cell measurements, we observed modest cell-to-cell variation in gene expression (Supplementary Figs. 4 and 5). Under all the conditions tested, the noise in gene expression was approximately proportional to the expression mean (Supplementary Fig. 6). Different input dynamics have no obvious influence on gene expression variance. Therefore, the single cell responses are well reflected by the averaged data. Using the measurements of Msn2 localization dynamics as input, we then fit the computational model to the gene expression data (Fig. 3c, and Supplementary Fig. 3-5; experimental data – solid black circles; model simulation – solid red line), and obtained an experimentally determined set of best-fit parameters (Supplementary Results).

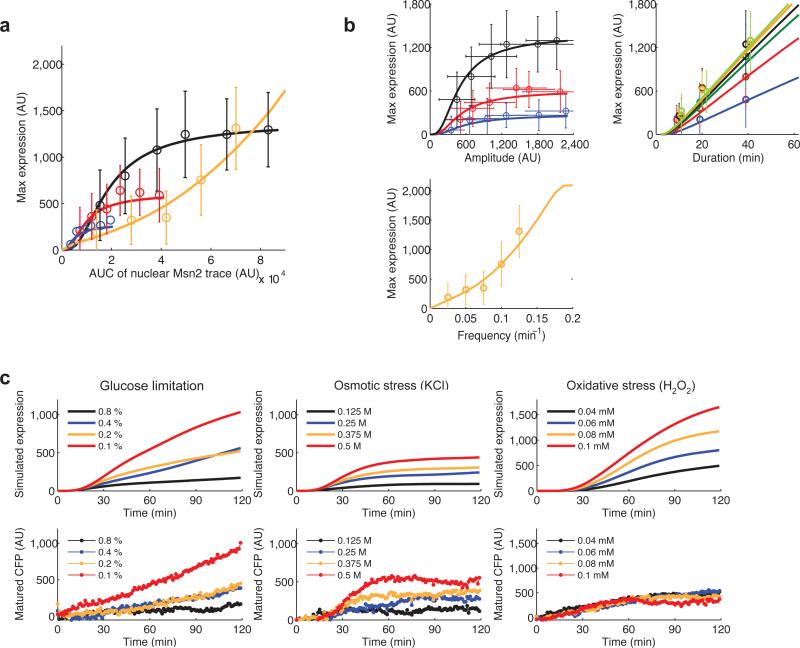
To determine whether the maximum gene expression level is simply a function of Msn2 nuclear localization level and time or is influenced by the dynamic profiles of Msn2 activation, we analyzed the relationship between gene expression and the area under the curve of Msn2 translocation traces. For single pulse stimulation (black, red and blue lines), gene expression shows a linear relationship with the area under the curve of Msn2 traces until saturation, which may be due to saturation in transcription factor binding (Fig. 4a). However, for oscillatory input (orange line) gene expression does not follow a linear relationship with the area under the curve of transcription factor nuclear localization (Fig. 4a). This analysis demonstrates that input dynamics indeed influences gene expression outputs and underscores the importance of studying translocation dynamics and its relationship to gene expression. We then used the model to systematically investigate how changes in the dynamics of Msn2 nuclear translocation affect expression of the reporter gene. We continuously changed each of the Msn2 translocation parameters – amplitude, duration or frequency – and simulated maximum gene expression output (Fig. 4b). The model simulations agree well with the experimental measurements (lines vs. data points in Fig. 4b). We observe that target gene expression is altered in different ways by different dynamics of Msn2 translocation. The relationship between gene expression and translocation amplitude follows a Hill function-like curve. In contrast, gene expression and translocation duration exhibits a linear relationship. Gene expression shows a nonlinear relationship with frequency of oscillatory transcription factor translocation, with a substantial increase over a threshold frequency.

Fig. 4.

The dynamics of Msn2 nuclear translocation influences target gene expression. (a) The relationship between gene expression and the area under the curve (AUC) of Msn2 inputs (open circles: experimental data; solid lines: model simulation; error bars: standard deviation of single cell data of ~50 cells, from at least two independent experiments). The integrals of Msn2 inputs were quantified from the data in Supplementary Fig. 3-5. Single Msn2 inputs with 10 min (blue), 20 min (red), or 40 min (black) durations were compared with oscillatory Msn2 inputs with 5 min pulse duration (orange). (b) Relationship between dynamic of Msn2 nuclear inputs and reporter gene expression. Top left panel: gene expression vs Msn2 input amplitude (input duration: black - 40 min; red - 20 min; blue - 10 min); top right panel: gene expression vs Msn2 input duration (input amplitude: yellow green - 2,190 AU; orange - 1,751 AU; black - 1,309 AU; green - 1,010 AU; red - 672 AU; blue - 406 AU); bottom panel: gene expression vs Msn2 input frequency (input amplitude: 1,751 AU; pulse duration: 5 min). (c) Model simulations reproduce the measured expression responses to natural stresses. For the indicated stress conditions, each single-cell traces of Msn2 translocation was used as input for the gene expression model. The simulated single-cell expression traces were averaged to generate the simulation curves (solid lines, top row) and compared with averages of measured single-cell expression (solid circles, bottom row).

To determine if consideration of the dynamics of Msn2 translocation is sufficient to predict gene expression for natural stresses, we used the time traces of Msn2 translocation in single cells induced by natural stresses as input for the model (e.g. Supplementary Fig. 1b), and simulated reporter gene expression (Fig. 4c). The simulated responses were averaged (Fig. 4c, top row) and compared with averaged experimental data for the same cells (Fig. 4c, bottom row); averaging was performed to eliminate stochastic effects on gene expression, which are not considered in the model or in this study. The gene expression responses to glucose limitation, osmotic stress, and H₂O₂ are distinct, reflecting the differences in Msn2 dynamical modulation induced by each stress. The model reproduces the responses to glucose limitation, osmotic stress and low intensity oxidative stress (0.04 mM H₂O₂). However, higher H₂O₂ concentrations resulted in experimental responses that were similar or even lower than that of 0.04 mM H₂O₂; this discrepancy is likely a complication of the global translational repression that occurs under severe oxidative stress conditions ¹⁹. Nonetheless, the computational model predicts the gene expression response for two of three stresses, suggesting that modulation of the dynamics of Msn2 translocation plays an important role in generating stress-specific gene expression outputs.

Model simulations of the responses of natural genes

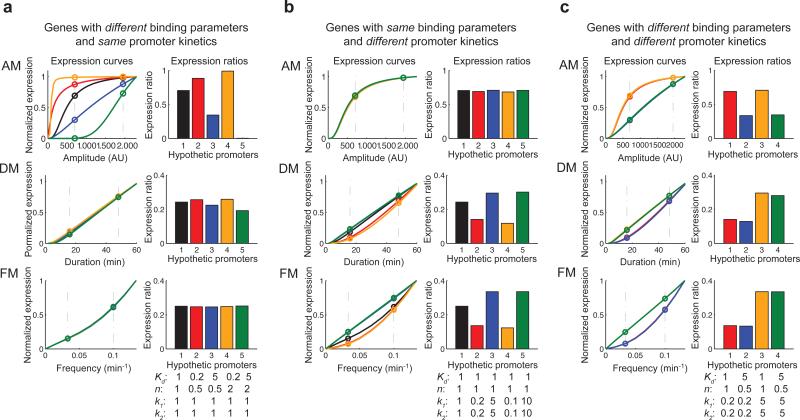
We next considered how natural target genes respond to modulation of transcription factor dynamics. We used the computational model to predict expression output in response to changes in two groups of promoter parameters: those that govern transcription factor binding, K_d and n; and k₁ and k₂ that govern the kinetics of promoter transition from an “inactive” state, to an “active”, transcription-competent state (see Fig. 3b for parameter definitions). We first simulated the expression responses for two sets of hypothetical genes: those with different transcription factor binding parameters but the same promoter kinetics (Fig. 5a); and those with the same binding parameters but different promoter kinetics (Fig. 5b). The responses of the genes to amplitude modulation of Msn2 translocation are sensitive to changes in the binding parameters (Fig. 5a, top panel), but the gene responses to duration and frequency modulation are insensitive (Fig. 5a, middle and bottom panels). In contrast, the gene responses to duration and frequency modulation are sensitive to the changes in promoter kinetics (Fig. 5b, middle and bottom panels), but less sensitive to responses to amplitude modulation (Fig. 5b, top panel).

Fig. 5.

The model predicts that target genes have distinct responses to different input regimes. Two sets of parameters were varied and alterations in gene expression output were predicted using the expression model: parameters that govern transcription factor binding, K_d and n; and parameters that govern kinetics of promoter transition, k₁ and k₂. The inputs are selected to be in physiological ranges of the natural stress responses (Fig. 2) (a) The expression curves upon amplitude modulation (AM), duration modulation (DM) and frequency modulation (FM) (left column) and the expression ratios (the ratio of gene expression level upon low stimulus to expression level upon high stimulus) calculated from the expression curves (right column, same genes use same colors for curves and ratios) are shown for hypothetical genes with different binding parameters (K_d, n) and the same promoter kinetics (k₁, k₂). The values below the bar graph represent the fold changes from the parameter values obtained from fitting the reporter response data (Fig. 3). (b) Model predictions are shown for hypothetical genes with same binding parameters and different promoter kinetics. (c) Natural target genes may differ in both binding parameters and promoter kinetics. Model predictions for four hypothetical genes with different binding parameters and different promoter kinetics. Genes 1 and 2 have the same slow promoter kinetics while Genes 3 and 4 have the same fast promoter kinetics. Genes 1 and 3 have the same high transcription factor binding while Genes 2 and 4 have the same low transcription factor binding.

Natural genes may differ in both transcription factor binding parameters and promoter kinetics. We therefore simulated the expression responses of four hypothetical genes with different transcription factor binding parameters and different promoter kinetics. Genes with the same high transcription factor binding parameters (Genes 1 and 3) respond similarly to AM, generating expression ratios that are higher than those with low transcription factor binding parameters (Genes 2 and 4) (Fig. 5c). In contrast, genes with the same fast promoter kinetics (Genes 3 and 4) respond similarly to duration and frequency modulation, generating expression ratios that are higher than those with slow promoter kinetics (Fig. 5c). Therefore, transcription factor binding parameters substantially influence the response of target genes to amplitude modulation, whereas the promoter kinetics have more influence on the response to duration and frequency modulation. A detailed discussion regarding model behaviors and parameter analysis is provided in the Supplementary Results (Supplementary Fig. 7-10).

Analysis of a simplified model

Previous modelling studies have analytically investigated gene expression responses to changes in the amount of active transcription factor (amplitude modulation) ^9,20. To further understand gene expression responses to duration or frequency modulation of transcription factor inputs, we constructed a simplified version of our gene expression model (Fig. 6a). The model includes three variables: P₁ and P₂ - inactive and active states of a promoter; and R – the gene product, such as mRNA. The parameters k₁ and k₂ govern the rates of promoter transition, and ω is the model input, representing the fraction of promoter-bound transcription factor. We use square pulses with constant height ω as inputs for duration modulation and pulse waves with constant height ω as inputs for frequency modulation – this allows us to solve the equations with a constant ω for the “on” part of input signals and with ω = 0 for the “off” part of the signals. Protein expression level correlates with the integral of mRNA (the gene product R in the simplified model) when the encoded protein is much longer-lived than its mRNA. In this regime, the degradation rate of mRNA does not affect the pattern of expression outputs. In contrast, when the target protein has a similar or shorter half-life than its mRNA, the protein expression level no longer correlates with the integral of the mRNA profile and the mRNA degradation rate affects the model outputs (see Supplementary Results and Supplementary Fig. 11). For simplicity, we use the integral of the gene product R (R_AUC), which is proportional to the integral of promoter activity P₂ (P_{2_AUC}) (Supplementary Fig. 11), as the gene expression output. Because P₂ cannot influence R when the input is off, we only consider the P₂ integral for the “on” part of the inputs (ω(t) = ω > 0).

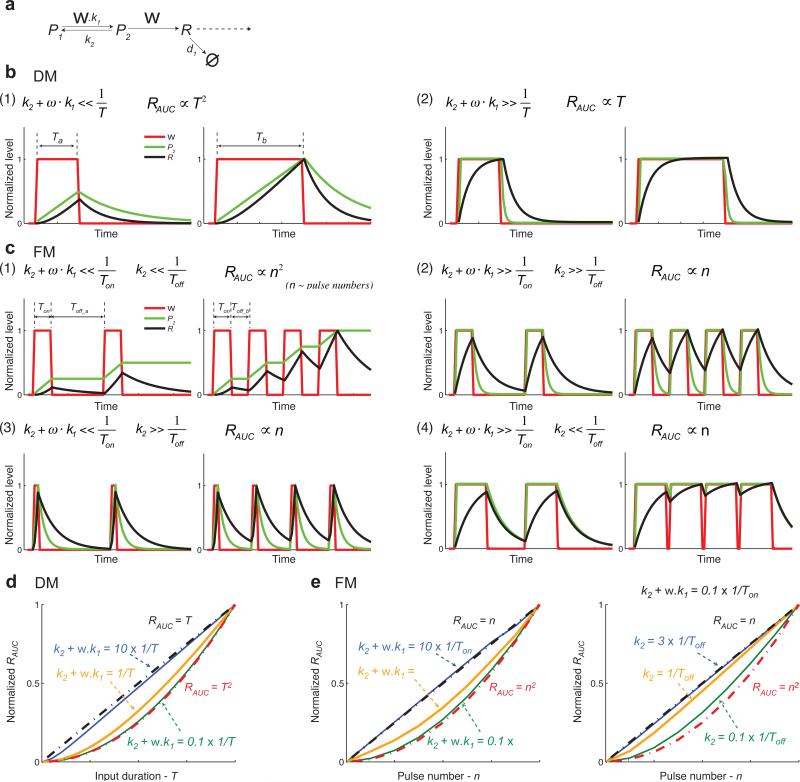
Fig. 6.

Analysis of a simplified model. (a) Schematic of the simplified model. (b) The model behaviors in response to duration modulation inputs. The input durations are T_a and T_b. Red lines: inputs (ω); Green lines: promoter activity (P₂); Black lines: gene product (R). (c) The model behaviors in response to frequency modulation inputs. Pulse duration is T_on; the interval durations are T_{off_a} and T_{off_b}. Red lines: inputs (ω); Green lines: promoter activity (P₂); Black lines: gene product (R). (d) The simulated relationship between gene expression output and input duration. Blue line: simulation with k₂ +ω · k₁ =10 ×1/T; orange line: simulation with k₂ +ω · k₁ =1/T; green line: simulation with k₂ +ω · k₁ = 0.1×1/T; these relationships are calculated with the median value of the input duration we used in the simulation. Black dashed lines: the curve of R_AUC = T; red dashed lines: the curve of R_AUC = T². (e) The simulated relationship between gene expression output and oscillatory input pulse number (n). Black dashed lines: the curve of R_AUC = n; red dashed lines: the curve of R_AUC = n². Left: we set k₂ =ω · k₁ and change k₂ +ω · k₁ to 10 × 1/T_on (blue line), 1/T_on (orange line), and 0.1 × 1/T_on (green line). With increasing frequency (pulse number), the interval duration changes from smaller than 1/T_on to larger than 1/T_on. Right: we set k₂ +ω · k₁ = 0.1×1/T_on and change T_off to 3 × 1/k₂ (blue line), 1/k₂ (orange line), and 0.1 × 1/k₂ (green line). k₂, ω, k₁, and T_on are fixed. In this case, pulse number does not correlate with pulse frequency.

We solve the equation of P₂ for constant ω (Supplementary Equations 1) and apply asymptotics to obtain simpler expression for P₂ integrals. A detailed mathematical presentation of this analysis is included in Supplementary Equations 1-3. For the response to duration modulation inputs, we consider two conditions (Fig. 6b): (1) when the time scale of the promoter transition is longer than the input duration ($k_2+\omega \cdot k_1<<\frac{1}{T}$), the promoter activity (P₂) increases linearly with time and does not saturate when the input is “on”. In this regime gene expression (correlates with the area under P₂) increases with the square of the input signal duration T (Supplementary Equations 2 (1) and Fig. 6b, panel (1)); (2) when the time scale of the promoter transition is short relative to the input duration ($k_2+\omega \cdot k_1>>\frac{1}{T}$), the promoter activity rapidly saturates and stays constant as the input signal duration increases. In this case, gene expression increases in a linear fashion with an increase in input signal duration (Supplementary Equations 2 (2) and Fig. 6b, panel (2)).

Similarly, for the responses to frequency modulation (Fig. 6c), we consider the condition in which the time scale of the promoter transition is long relative to the pulse duration ($k_2+\omega \cdot k_1<<\frac{1}{T_{on}}$) so that the promoter activity (P₂) increases linearly with time when the pulses are “on”, and at the same time, the time scale of promoter inactivation is longer than the interval between pulses ($k_2<<\frac{1}{T_{off}}$) so that the active promoter cannot return back to the inactive state during the intervals (Fig. 6c, panel (1)). In this situation the active promoter increases from a higher starting point when the next pulse occurs. As a result, the active promoter (P₂) increases linearly with pulse numbers or frequencies (pulse numbers per unit time). The gene expression correlates with the integral of the active promoter over the total “on” time of input pulses and therefore increases with the square of pulse numbers or frequencies (Supplementary Equations 3 (1)). In contrast, when the time scale of the promoter transition is shorter than the pulse duration ($k_2+\omega \cdot k_1>>\frac{1}{T_{on}}$) or when the time scale of promoter inactivation is shorter than the intervals between pulses ($k_2>>\frac{1}{T_{off}}$) (Fig. 6c, panels (2)-(4)), each input pulse generates an isolated promoter activation response; in this case, the gene expression output integrates the promoter activation response for all the pulses and is therefore proportional to pulse numbers or frequencies (Supplementary Equations 3 (2) - (4)).

To numerically explore how the relationship between input dynamics and promoter kinetics affects gene expression responses, we used the simple model to simulate the relationship between gene expression outputs (R_AUC) and input durations or frequencies. When the time scale of the promoter transition is 10 times shorter (blue lines) than the input pulse duration, the gene expression output responds linearly with increasing input signals (Fig. 6d). In contrast, when the time scale of the promoter transition is 10 times longer (green lines) than the input pulse duration, the gene expression output scales exponentially with increasing input signals (Fig. 6e, left panel). For oscillatory inputs, when the interval durations increase from 10 times shorter than the promoter inactivation time (green line) to 3 times longer (blue line), the expression curve changes from an exponential-like curve to a linear one (Fig. 6e, right panel). The genes whose expression response follows an exponential curve are less sensitive to weak input signals (inputs with short durations or low frequencies) than genes with a linear expression curve. Taken together, in response to duration or frequency modulation of input signals, the relationship between the input dynamics and time scale of the promoter transition determines how changes in input duration or frequency affects the expression of a target gene.

Our simple model can qualitatively reproduce the behaviors of the complex model (compare Fig. 6 and Supplementary Figs. 8 and 10). We then use our simple model to explain the experimental and modelling results in Fig. 3 and 4. In Fig. 3, we fit the reporter expression data with the complex model. The time scale of promoter transition ($\frac{1}{k_2+\omega \cdot k}$) inferred from the fit parameters (k₁ = 0.049 min⁻¹; k₂ = 0.194 min⁻¹) is ~5 minutes. For the duration modulation inputs, the durations we used are 10, 20 and 40 minutes, much longer than the time scale of promoter transition. According to the model analysis in Fig. 6b, panel (1), the expression outputs should be proportional to input durations. Consistent with the model prediction, we observe a linear relationship between the expression output and input duration (Fig. 4b). For the frequency modulation inputs, the pulse duration is 5 minutes, close to the time scale of promoter transition, and the pulse interval for the high frequency input is 3 minutes, shorter than the promoter inactivation time. Based on the model analysis in Fig. 6c, panel (1), the expression outputs should be proportional to the square of pulse numbers or frequencies. As predicted, the relationship between expression outputs and pulse frequencies follows a non-linear curve, close to an exponential curve (Fig. 4c).

Experimental validation of model predictions

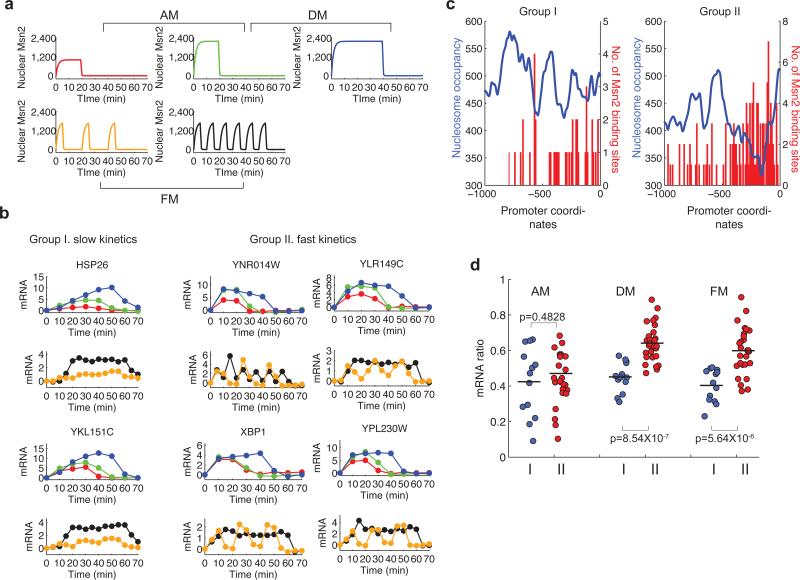
To test the model predictions experimentally, we performed microarray analysis on populations of cells that were exposed to different amplitudes (concentrations), durations, or frequencies of inhibitor treatment (Fig. 7a), and measured expression of 40 natural Msn2-dependent target genes (Supplementary Methods), which we expect to differ in promoter properties. The responses of these natural genes can be classified into two groups: (I) those with slow kinetics of induction; and (II) those with fast kinetics of induction (Fig. 7b and Supplementary Fig. 12-13). The two groups have similar mRNA stabilities (Supplementary Fig. 14). Therefore, the kinetic differences are not likely to be due to differences in mRNA degradation rates. Instead, these kinetic differences may be related to the rates of promoter transition, whose timescale may be set by chromatin remodelling. Chromatin remodeling may be influenced by the relative distributions of nucleosomes and transcription factor binding sites ²¹. Indeed, we observe that Msn2 binding sites in the promoters of target genes with fast kinetics (Group II) are typically enriched within the nucleosome-free region adjacent to the transcription start site (TSS) (Fig. 7c, right panel). In contrast, Msn2 binding sites in promoters of the genes with slow kinetics (Group I) exhibit no such pattern (Fig. 7c, left panel).

Fig. 7.

Microarray analysis to evaluate the model predictions. (a) Msn2 nuclear localization response to different 1-NM-PP1 treatments: red line - 120 nM 1-NM-PP1, 20 min; green line - 3 μM 1-NM-PP1, 20 min; blue line - 3 μM 1-NM-PP1, 40 min. orange line - 750 nM 1-NM-PP1, 5 min × 3; black line - 750 nM 1-NM-PP1, 5 min × 6. (b) Measured time courses of mRNA levels from representative target genes (solid circles: normalized fold change of mRNA level with baseline subtracted). The inputs in the panel a were used experimentally to produce the measured mRNA time traces (the input and the corresponding response use the same color). (c) Distributions of Msn2 binding sites (red) relative to the experimentally determined nucleosome profile (blue, unpublished data from the O'Shea lab) within promoters of target genes. The averaged nucleosome profiles were obtained by dividing the sum of nucleosome positioning signals of all genes in one group with the gene numbers. The distribution of Msn2 binding sites (AGGGG or CCCCT) is represented by bars corresponding to the sum of the numbers of Msn2 binding sites in each 10 bp window. (d) mRNA ratios of target genes in different encoding regimes (blue: Group I genes; red: Group II genes). The mRNA ratio of each gene is calculated from dividing the area under the curve of the mRNA time course (which correlates with gene expression level, Supplementary Fig. 7) at low transcription factor inputs by the area under the curve at high inputs.

To quantify the response of each gene we report the mRNA expression ratio – the ratio of the integral of mRNA abundance upon low stimulus (low amplitude, duration or frequency) to the integral of mRNA abundance upon high stimulus (see Fig. 7d legend). The distributions of the expression ratios for genes in the two groups were not markedly different in the amplitude modulation regime (Fig. 7d, AM). In contrast, the expression ratio distributions of the two groups exhibited substantial differences in the duration and frequency modulation regimes, with p-values of 8.54 × 10⁻⁷ and 5.64 × 10⁻⁶, respectively (Fig. 7d, DM and FM). The genes in Group II, which exhibited faster transcription kinetics, had higher expression ratios than those in Group I (Fig. 7d, red vs. blue circles). These observations are consistent with the model predictions for a scenario where Group I and II genes have different promoter kinetics (Fig. 5 and Supplementary Fig. 7); the expression ratios, or sensitivity, of genes are less affected by differences in the kinetics of transcriptional induction in the amplitude modulation regime, while in the duration and frequency modulation regimes genes show different sensitivity correlated with kinetics of transcriptional induction. Because the responses to distinct input regimes are controlled by different promoter properties, some genes from the two groups behave very differently in response to distinct input regimes. Two particularly dramatic examples are GRX1 from Group I and YLR312C from Group II. In response to amplitude modulation, the induction ratio of GRX1 is more than 3-fold higher than that of YLR312C; in contrast, in response to frequency modulation, YLR312C shows dramatically higher induction ratio (~3-fold) than GRX1 (Supplementary Fig. 15). Taken together, our experimental and computational analysis indicates that different promoter properties – the affinity of transcription factor binding and kinetics of promoter transition of a gene – influence its expression response to the dynamics of Msn2 localization.

Discussion

The findings presented here reveal how a single transcription factor can transmit quantitative information representing distinct environmental signals. Different stresses elicit qualitatively different dynamical patterns of transcription factor activation – these patterns are then interpreted by promoters with distinct properties to produce different patterns of target gene expression.

Using an analytical model in which different genes have different transcription factor binding affinity, Cai et al. showed that frequency modulation of the transcription factor Crz1 results in proportional gene expression ⁹. Using a kinetic model that includes a promoter transition step and considering genes that differ in the kinetics of this transition, we demonstrate that frequency or duration modulation of the transcription factor Msn2 can lead to differential gene expression. The different responses of Crz1 and Msn2 target genes may be due to differences in the kinetics of activation of the Crz1 and Msn2 target promoters. In response to oscillatory transcription factor inputs, slow promoters that are activated by an input pulse cannot fully return back to the inactive state when the next input pulse occurs, and thereby begin to increase expression from a higher starting point. This “head start” effect, which is more dramatic in response to high frequency input, results in a nonlinear relationship between response level and input frequency (Fig. 4b). In contrast, genes with fast promoter kinetics generate isolated expression responses to each transcription factor pulse; therefore the response is proportional to the input frequency. The different responses of Crz1 and Msn2 target genes suggests that most Crz1 genes have fast promoter kinetics but Msn2 targets include some promoters with fast kinetics and others that respond slowly (discussed in Supplementary Results and Supplementary Fig. 10). Interestingly, 6 of the 40 Crz1 genes tested by Cai et al. do not show proportional responses to frequency modulation, suggesting that some of the Crz1 genes may also have slower kinetics.

The properties of a promoter, which control the response of a gene to different dynamical modulation schemes, will depend on its architecture. Transcription factor binding affinity is likely most influenced by the number and nucleotide sequences of the binding sites; the kinetics of promoter transition is likely influenced by the position and stability of nucleosomes and the position and number of transcription factor binding sites ^20,22. Therefore, the response of a gene to a stress could be tuned individually through evolution by alterations in a certain property of its promoter, which will only affect the expression in response to a specific dynamical pattern of transcription factor activation. Further investigation is needed to elucidate how the promoter architecture influences the response of a gene to different dynamics of transcription factor activation.

Many signaling molecules transmit extracellular signals through time-dependent activity changes; the kinetics of these changes will influence signal transmission. In higher eukaryotes, dynamical patterns of some best-studied signalling molecules, such as mitogen-activated protein kinases ²³, or the transcription factors NFκB ^5-8,24 and p53 ^25,26, play important regulatory roles in physiological responses such as gene expression, cell growth, and differentiation. For example, the mammalian transcription factor NFκB exhibits distinct temporal profiles in response to different inflammatory stimuli. These temporal differences lead to selective gene activation and stimulus-specific physiological responses ²⁷. The mechanisms outlined here may represent a general strategy of information processing inside a cell.

Methods

Strain construction

Standard methods for the growth, maintenance and transformation of yeast and bacteria and for manipulation of DNA were used throughout. The yeast strains used in this study were generated from an ADE⁺ strain in the W303 strain background (MAT atrp1 leu2 ura3 his3 can1 GAL⁺ psi⁺). Details of strain construction are provided in Supplementary Methods.

Use of a microfluidics device

A microfluidics device ¹⁴ was constructed with polydimethylsiloxane using standard techniques of soft lithography and replica molding ²⁸.

Yeast cells were grown at 30°C to OD_600nm of 0.2. The cells were quickly concentrated, loaded into the microfluidic device and immobilized by incubation for 5 min in the device pre-treated with 2 mg ml⁻¹ concanavalin A solution. Two Falcon tubes filled with 40 mL of medium were connected with two inlets using soft polyethylene tubing (Intramedic, inner diameter: 0.86 mm, outer diameter: 1.27 mm). One Falcon tube with medium was connected with the outlet. The flow of medium in the device was maintained by gravity generated by a 15 cm height difference between Falcon tubes connected to the inlets and outlet. Exchange of medium in the device can be triggered in seconds by manually changing the connectivity of two inlets. The whole system was maintained at 30°C to avoid introduction of air bubbles by temperature changes.

Time-lapse microscopy

The microfluidics devices were mounted onto a Zeiss Axiovert 200M inverted microscope with Cascade 512 cooled charge-coupled (CCD) camera (Photometrics) and images were taken at 30°C with an oil-immersion 63 × objective. We used filter sets that are optimized for detection of CFP, YFP and RFP and acquired images in three different channels at 1-minute intervals, automated with Metamorph imaging software (Molecular Devices). Exposure times in each channel were setup as CFP: 300 ms, YFP: 300 ms and RFP: 200 ms. Details of image processing are provided in Supplementary Methods.

Use of 1-NM-PP1 to control Msn2 nuclear localization

Cells were initially grown in standard SD medium. At time point zero, we used the microfluidic device to change the medium to SD medium containing a given concentration of 1-NM-PP1 (#13330, Caymen Chemical). After a certain period of time, the medium was changed back to the initial medium without 1-NM-PP1. The image acquisition continued until the end of the experiments. Oscillatory Msn2 nuclear localization was generated by repetitive exchange between medium with and without the inhibitor.

The amplitude and duration of Msn2 nuclear localization was controlled by the inhibitor concentration and duration, respectively. Single-cell traces were collected in response to 18 inhibitor treatments (Fig. 3 and Supplementary Fig. 3-4). For the 6 different amplitudes, the concentrations of 1-NM-PP1 we used included 50 nM, 120 nM, 150 nM, 300 nM, 750 nM and 3 μM. The 3 durations are 10, 20 and 40 min.

We used 750 nM 1-NM-PP1 to generate oscillatory Msn2 nuclear localization. We produced two sets of data for oscillatory Msn2 localization. In the first set, we fixed the duration of each burst at 5 min and changed the burst frequency; this set of data mimics frequency modulation (Fig. 3-4, and Supplementary Fig. 5a). In the second set, the total time of Msn2 nuclear localization was 40 min and we changed the burst numbers; this data set evaluates the difference between one persistent signal and periodic signals (Supplementary Fig. 5b).

Quantification of single-cell traces

The quantification of duration, amplitude and frequency of Msn2 nuclear localization in single cells was performed as described previously ⁹. The frequency was quantified by dividing the total burst number by time for each Msn2 trace. Bursts were identified by thresholding each time trace at 2 × the standard deviation of the Msn2 traces under no stress condition. Similar quantification results were obtained using thresholds ranging from 1-3 times of the standard deviation (Supplementary Fig. 2c).

Computational modeling

Modeling analysis was conducted with MATLAB (The MathWorks). The experimental time traces of Msn2 localization were fit with a piecewise exponential function to produce continuous temporal profiles, TF(t), which served as input for the model. Binding of transcription factor to DNA is approximated by a Hill equation, $\frac{TF{\left(t\right)}^n}{K_d^n+TF{\left(t\right)}^n}$. An inactive promoter state (P₁) and an active promoter state (P₂) were considered. The rate of promoter activation depends on the rate constant k₁ and the binding of transcription factor to DNA. k₂ is the rate of promoter inactivation. k₃, k₄, and k₅ are transcription initiation, transcription elongation and protein production rates, respectively. d₁, d₂ and d₃ are initiation complex dissociation, mRNA degradation and protein degradation rates, respectively. k_m is the CFP maturation rate. The nonlinear least squares routine was used for the fitting. Details of computational modeling are provided in Supplementary Results.

Expression microarray analysis

For microarray analysis, mRNA was extracted and purified from the frozen cells with the RNeasy kit (Qiagen) and converted to cDNA using reverse transcription. The expression differences of the samples in a time course were determined with 2-color microarrays (Agilent) as described previously ^29,30. Details of experimental procedure are provided in Supplementary Methods.

The 40 Msn2-dependent genes were selected based on previous whole-genome analysis ^29,31. These genes are primarily dependent on Msn2/4 (significantly regulated by 1.5-fold, p<0.05) under various stresses, and have not shown to be regulated by other transcription factors. In our analysis, these genes exhibit dramatic expression changes (>5 fold) in response to PKA inhibition with 3 μM 1-NM-PP1. We observed striking kinetic differences in the transcription profiles of these genes. Some genes rapidly reach maximum induction 10-20 min after inhibitor addition; in contrast, some genes are induced slowly and reach maximum only 40 min after inhibitor treatment. To simplify the analysis, the genes were divided into two groups based on the time they take to reach half maximal induction. We set the cutoff time to be 15 min for responses to single pulse stimulation (t_1/2) and the cutoff to be 10 min for responses to oscillatory stimulations (t’_1/2). The genes in Group I are those with t_1/2 >15 min and t’_1/2>10 min; the genes in Group II are those with t_1/2 <= 15 min or t’_1/2 <=10 min.