Abstract
The characterization of the 3D structure of oligosaccharides, their conjugates and analogs is particularly challenging for traditional experimental methods. Molecular simulation methods provide a basis for interpreting sparse experimental data and for independently predicting conformational and dynamic properties of glycans. Here, we summarize and analyze the issues associated with modeling carbohydrates, with a detailed discussion of four of the most recently developed carbohydrate force fields, reviewed in terms of applicability to natural glycans, carbohydrate–protein complexes and the emerging area of glycomimetic drugs. In addition, we discuss prospectives and new applications of carbohydrate modeling in drug discovery.
Introduction
Oligo- and polysaccharides (glycans) have fundamental roles in the development and function of all living organisms. In vivo, they are most commonly found covalently bound to proteins or lipids, forming glycoproteins and glycolipids. These molecular aggregates, known collectively as `glycoconjugates', cover cell surfaces, often providing the first point of contact for host–pathogen interactions. Carbohydrate-binding proteins on the pathogen surface target specific host glycans, facilitating infection by both viruses and bacteria [1], perhaps the most well-known being the interaction between viral hemagglutinin and glycans on human respiratory epithelium [2]. Inhibition of the binding of adhesin proteins to host glycans forms the basis of anti-adhesion therapies [3]. Glycans are formed through the actions of various enzymes, which are responsible for both their assembly (transferases) and their degradation (glycosidases). Any alteration in the abundance or relative levels of such enzymes in an organism will be reflected in changes in the pattern of protein and cell-surface glycosylation, often disrupting normal cell development and leading to characteristic phenotypes, such as congenital diseases of glycosylation [4]. Moreover, aberrant glycosylation is a signature of many diseases, from rheumatoid arthritis [5] and IgA nephropathy [6] to a range of cancers [7–9]. Consequently, the development of treatments aimed at targeting glycan-processing enzymes represents a viable and innovative therapeutic approach [10,11]. In particular, the development of methods for characterizing the glycosylation state of serum proteins for disease diagnosis and surveillance is an active area of research [12,13]. On another front, polysaccharide chains present on the surface of many bacteria are the initial antigens presented to the host immune system. Bacterial surface polysaccharides, therefore, may be effectively employed in anti-bacterial vaccines [14,15].
Clearly, glycans and carbohydrate-binding proteins present numerous opportunities for therapeutic development [16].
Glycan chains can modulate the structure and function of the protein to which they are attached, both by partially occluding regions of the protein surface from direct interactions and by damping the protein dynamics by virtue of their large mass and inertial resistance [17]. Because of the intrinsic mobility of oligosaccharides, the use of X-ray crystallography (which has been very successful in the study of proteins) is not straightforward. NMR techniques are often applicable to glycans in solution, but the scarcity of data often limits the ability of NMR spectroscopy to determine uniquely the oligosaccharide 3D structure [18]. For these reasons, the full extent of the relationship between glycan 3D properties and biological function is still being elucidated [19]. Computational methods and, in particular, molecular dynamics (MD) simulations provide complementary tools to augment both X-ray and NMR data and are particularly well suited to the characterization of the structure and dynamics of glycans and glycoconjugates [20–22]. The two most important issues affecting the quality of MD simulations are conformational sampling and force field accuracy. In the early years of biomolecular simulations, MD simulations were limited to small biological systems – such as small proteins [23], short DNA helices [24] and mono- [25] or disaccharides [26] – and ran for very short timeframes. From the standpoint of today's technical achievements, the early computational experiments might seem rather basic and obsolete; however, by emphasizing the dynamical nature of biomolecules and the corresponding implication on biological function, the simulations opened the way for the development of computer modeling as a cornerstone of structural biology [27].
Advances in computer technology and software algorithms enable us today to sample the conformational space of biomolecular systems for on the order of hundreds of nanoseconds (ns). This timeframe is typically adequate for most internal motions in glycans [28,29]. It is also notable that exceptionally long timescales are not necessary for all simulations to be useful. For example, MD simulations can be very effectively employed in the refinement and rescoring of ligand–protein complexes generated from automated ligand docking [30–32]. In these scenarios, MD simulations are performed principally to provide some level of ensemble averaging to aid in generating robust affinity and specificity predictions.
This review is organized as follows: in the section `Protein–carbohydrate interactions', we summarize the characteristic structural features of carbohydrates and carbohydrate–protein interactions. In the section `Carbohydrate force fields', four recent parameterizations of popular biomolecular force fields are discussed in detail, namely, those for CHARMM [33–35], GLYCAM/AMBER [36], GROMOS [37] and OPLS-AA [38]. In the section `Discussion', several issues pertinent to the extension of carbohydrate modeling to other biomolecular systems and to glycomimetic drugs are discussed (Fig. 1).
FIGURE 1.
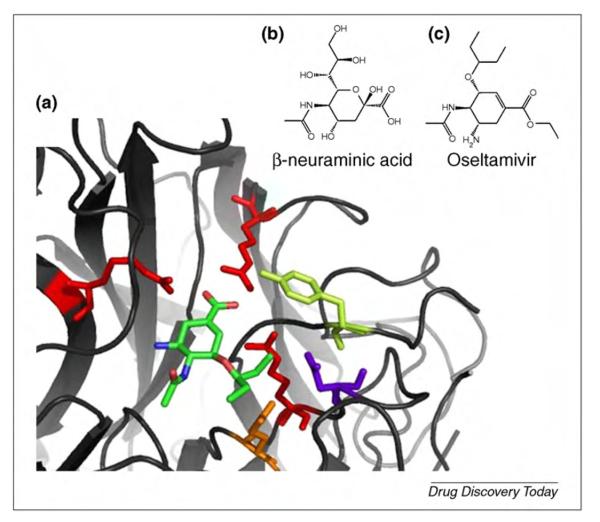
(a) Structure of the de-esterified form of the neuraminidase inhibitor oseltamivir in complex with the H274Y mutant of influenza virus N1 neuraminidase that displays resistance to treatment with oseltamivir (PDBID 3CL0 [134]). (b) Schematic representations of the natural substrate (neuraminic acid). (c) Schematic representations of the inhibitor.
Protein–carbohydrate interactions
Because of the crucial role of carbohydrate–protein interactions in human biology, there is considerable interest in employing computational simulations to help characterize these systems and aid in the rational design of new therapeutics [10,39–41] and vaccines [42–44].
Carbohydrate–protein interactions are often weak [45], facilitating the formation of transient states, which might aid in targeting the protein to its destination [46]. For example, dissociation constants for most lectin–monosaccharide interactions are in the mM range [47]. Binding affinity generally increases with increasing oligosaccharide size [48], but not always [49], and often does not yield greater than μm dissociation constants [50,51]. Although it has been technically possible to simulate the structure of a carbohydrate–protein complex for more than a decade, the accurate prediction of binding affinity remains a challenging task [44,52], which is highly dependent on the ability of the force field to reproduce both the solution and the bound properties of the carbohydrate and the protein.
A significant challenge comes from the fact that carbohydrate–protein interaction is intrinsically more dynamic than many other protein–ligand adducts and that their affinity arises from several relatively weak interactions. Indeed, carbohydrate-binding specificity results from the subtle balance of electrostatic, hydrogen bonding (H-bonding) and hydrophobic interactions between the protein, the solvent and the carbohydrate, which result in significant changes in both enthalpy and entropy upon binding.
Charged residues (such as Arg, Lys, Asp and Glu), as well as ions, are commonly found in the active sites of carbohydrate-binding proteins [53,54]. As an example of carbohydrate binding in lectins, we show in Fig. 2 the complex between concanavalin A and a trimannoside (PDBID 1CVN [55]). The key interactions between protein and carbohydrate in the binding site are highlighted, indicating direct H-bonds between the trimannoside and two Asp (D16 and D228) residues. One highly conserved water molecule is also directly H-bonded to the sugar and serves as a center for H-bonding networks with one Arg and one Asn. Such direct interactions are often cited as a major contribution to binding enthalpy. Clearly, there is an absolute requirement for a high level of compatibility between the force field treatments of carbohydrate and the protein electrostatics. For example, if the protein force field employs partial charges derived by fitting to quantum mechanical (QM)-derived molecular electrostatic potentials (ESPs), it would seem reasonable that the ligand should also. Notably, some computational approaches, such as some molecular docking protocols [56], often assign non-ESP-derived charges to the ligand to expedite the generalization of the method. Such mixed electrostatic models must resort to empirical adjustment of the interaction energy terms to compensate to some extent for the imbalance. The need in general to employ protein-consistent partial charges in the ligand and with the need for appropriate torsion terms, are significant bottlenecks with regard to applying biomolecular force fields to small molecule modeling. This is certainly an issue in the specific case of extending carbohydrate force fields to glycomimetic design [39].
FIGURE 2.
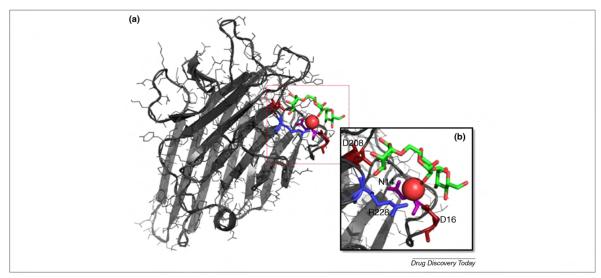
(a) A complex of concanavalin A (ConA) with trimannoside (PDBID 1CVN [55]). (b) A close-up of ConA binding site. Key residues for carbohydrate binding and recognition are highlighted: Asp 16 and Asp 208 in red, Arg 228 in blue, and Asn 14 in purple. The trimannoside is colored according to its atom types. The oxygen of a key water molecule is also represented as a red van der Waals (vdW) sphere.
Although many carbohydrates are neutral species, biologically relevant glycans often contain charged monosaccharides or charged derivatives, such as N-acetylneuraminic acid and sulfated glycosaminoglycans, respectively. Recognition of such species takes place through complementary electrostatic and H-bonding interactions with protein residues. In such cases, the accurate evaluation of electrostatic interactions is crucial for the correct description of carbohydrate protein recognition.
Recognition and binding of carbohydrates to proteins does not always involve charge–charge interactions, but most frequently it takes place through the formation of complex H-bonding networks. H-bonding schemes involving two or three hydroxyl groups are usually at the core of carbohydrate-binding specificity. For instance, lectin specificity is often explained in terms of orientation of the polar residues in the binding site that allow the formation of H-bonds only with specific monosaccharides [57]. The loss of a single specificity-defining H-bond - by chemical alteration of the ligand, for example – will, generally, drastically reduce affinity [58], and the use of deoxy sugars to map the carbohydrate-binding site specificities of proteins was a powerful technique [59] before the widespread availability of protein crystallography. Although carbohydrate–protein H-bonds are readily identifiable in crystal structures and clearly crucial for defining specificity [60], however, they do not necessarily contribute significantly to enhancing the affinity of these interactions [58]. This is not as surprising as it might at first seem, when it is recalled that the affinity arises from the difference in free energy between the free and bound states. In the free states, both the ligand and the protein are hydrated and, in fact, crystallography [61] and MD simulations [62] have demonstrated that the protein frequently will have discrete water molecules in the carbohydrate-binding site, located in positions approximately equivalent to the sites in which carbohydrate hydroxyl groups are to be found in the complex. Thus, qualitatively, there is little gain in enthalpy to be expected upon replacing these waters with the hydroxyl groups of the ligand.
By contrast, there might be significant changes in entropy associated with displacing bound waters from each interacting surface [63,64]. Indeed, entropic contributions have been implicated as a major factor in determining carbohydrate-binding affinity [65].
Computational simulations provide a unique tool to dissect these interactions into their component energies [44,52,61], which should greatly assist in the development of glycomimetics.
Carbohydrates are amphipathic molecules. They contain significant hydrophobic patches, arising from aliphatic hydrogen, which can be exploited in binding to proteins. The orientation of aromatic residues in the active sites of many carbohydrate-binding proteins plays a key part as in determining their affinity and to a lesser extent specificity. The amino acid side chains of Trp, Tyr or, less frequently, Phe residues are often seen stacked against the bottom face of pyranose rings [53] and can contribute approximately 0.5–1 kcal/mol to the binding free energy [66]. The heparin–AT3 complex is normally used as an example of carbohydrate recognition based on strong electrostatic interaction. Nonetheless, it has been reported that as much as ~60% of the total affinity comes from non-ionic interactions, with 43% of the total coming from interactions with only two Phe residues [67] (Fig. 3). To account correctly for the dispersive component of these interactions [68], the non-bonded van der Waals (vdW) interactions in both carbohydrate and protein parameter sets need to be consistent. It is noteworthy here that one of the advances likely to further enhance the accuracy of carbohydrate simulations will be the use of improved water models. Maximal benefit from the use of improved water models, however, will probably also depend on the development of carbohydrate force fields, tuned for use with the particular water model. For example, in the case of the GLYCAM for field, consistency with the TIP5P water model was achieved by introducing lone pairs into the oxygen atoms [69].
FIGURE 3.
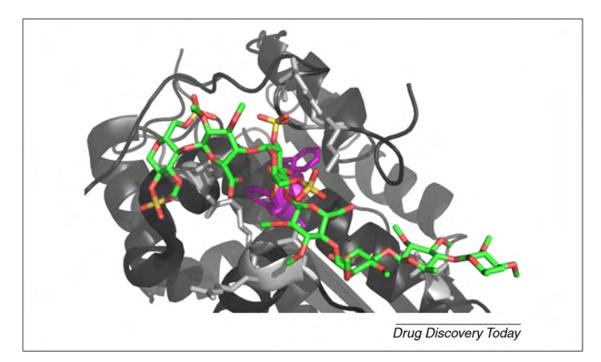
Detail of a complex between antithrombin (AT3) and heparin (PDBID 1SR5 [135]). Heparin is colored according to its atom types, and two Phe keys for heparin binding are highlighted in purple. The Arg and Lys residues in the binding site are shown in light gray.
Carbohydrate force fields
MD simulations are based on the deterministic propagation of forces acting on a molecular system [70,71]. Through MD simulations, it is possible to observe, at the atomic level, the progression of molecular motion. Given atomic positions and velocities, forces are calculated on the fly, as derivatives of the potential energy (V (r1, …, rN)), at specific time steps. The potential energy for a molecular system at a time ti can be expressed in classical mechanics as a function of the atomic positions using the familiar energy terms in Eqn (1):
| (1) |
where Vbonds, Vangles and Vdihedral refer to the potential energy associated with bond-stretching, angle-bending, and proper (and improper) dihedral angle rotations, respectively. VCoul. and VLJ refer to the pairwise electrostatic interaction and to the Lennard-Jones (LJ) repulsion–dispersion potential terms, respectively. Classical force fields are defined by the functional form of these components and by the set of parameters that each term requires.
Force field development is a challenging and necessarily meticulous task. It requires the determination of empirical parameters that when introduced in Eqn (1) lead to the correct potential energy landscape of the molecular system. Although early force field parameterizations employed principally experimental data, today their development is more often achieved with a mixture of high-resolution experimental data and QM data. Because of the coupling between many of the force field terms (e.g. torsions and electrostatics), approaches to parameterization inevitably require multiple sets of calculations, for development and testing; the more well-defined the force field refinement protocol, the more probably the resultant parameters will be broadly applicable [72]. The definition of valence interactions, modeled in most biomolecular force fields by bond-stretching, angle-bending and dihedral terms, requires the determination of force constants and equilibrium values for the distances and angles,
| (2) |
| (3) |
| (4) |
In Eqn (2), and indicate the bond-stretching constant and the equilibrium distance, respectively. In Eqn (3), and indicate the angle-bending constant and the equilibrium angle, respectively. It should be noted that the equilibrium values are not necessarily the values observed experimentally but are adjusted to achieve the best overall reproduction of the experimental (or theoretical) values for discrete molecules. Finally, in Eqn (4), kφ, n, and γ are the torsion constant, multiplicity and phase angle, respectively. It should be emphasized that torsion terms are corrections to the computed rotational energy profiles to ensure agreement with observed values (most often from QM calculations) and in a well-tuned force field represent principally contributions only from non-classical through H-bond interactions, such as hyperconjugation, electron delocalization and polarization. Improper potential energy terms may also be included in the force field to enforce structural requirements, such as chirality, or planarity of atoms in π-conjugated functional groups (such as peptide planes).
Non-bonded interactions are determined by the ESP and the repulsion-dispersion (i.e. vdW or LJ) potential. In classical force fields, charge polarization is in a general sense implicitly incorporated into torsions and vdW terms, which cannot be expected to reproduce effects arising from discrete atomic interactions. The explicit inclusion of charge polarizability is increasingly being considered [73]; however, it remains a challenge for parameterization [74] and leads to significant increases in computer demands. Eqn (5) shows the Coulomb ESP between point charges qi and qj located at a distance Rij in a medium with dielectric constant εr,
| (5) |
where ε0 is the dielectric permittivity in vacuo. In simulations performed with explicit solvent, the dielectric constant is generally set to unity; however, it has been argued that a value of between 3–4 Debye might be appropriate in environments where charge polarization would otherwise be expected to lead to further electrostatic shielding [75].
The LJ potential for non-bonded interactions is shown below in Eqn (6),
| (6) |
where ∈ij and σij are LJ repulsion–dispersion parameters, defined for each atom pair. The functional form of this term varies, but in all cases, it includes a steeply repulsive component (∝ – R−12). This dominates at short inter-atomic distances over the weakly attractive term (∝ – R−6), but at intermediate distances, they combine to approximate the weak attractions that arise from instantaneous dipole-induced dipole attractions. Both terms asymptotically approach zero at infinite separation.
The parameter development protocol is fundamentally a matter of philosophical conviction or developmental legacy requirements; thus, it is specific to each force field. Small differences in the parameter sets can lead to significant differences in the energy landscape, such as location and depth of minima [76,77]. Mixing parameters from different force fields, therefore, can result in a loss of internal consistency and, consequently, in erroneous simulations. This is profoundly important for flexible molecules such as oligosaccharides, the state populations of which are particularly sensitive.
The development of a robust carbohydrate force field is a particularly challenging task because of the need to consider the influence of the inherent flexibility of glycans on the approach to parameter development and validation. In addition, unlike proteins and oligonucleotides (which are built by linear assembly of residues), glycans are often branched structures. As shown in Fig. 4, the majority of carbon centers in a monosaccharide are chiral and bear a hydroxyl group. Each hydroxyl group can form a glycosidic link to another carbohydrate unit. Although only one dipeptide can be generated from the same two amino acids, 20 chemically distinct disaccharides can be formed from the same two hexopyranose monosaccharides. In analogy with proteins, however, glycan conformation is generally defined by the torsion angles between the residues (e.g. φ and ψ) (Fig. 4). Additional degrees of freedom are associated with hydroxyl group rotations and rotation around the C5–C6 ω-angle, when present (Fig. 4).
FIGURE 4.
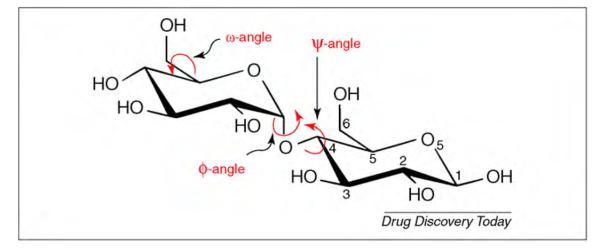
Illustration of the φ, ψ and ω dihedral angles for a representative 1–4 linked disaccharide (maltose).
The C–O–C–O atomic sequence (C5–O5–C1–O1 in pyranoses) is omnipresent in carbohydrates (Fig. 4), and its associated stereoelectronic effects radically differentiate the conformational properties of glycosides from those of structures based on cyclohexane or those in which the linking oxygen is replaced by a methylene group (C-glycosides) [78]. Ultimately, the degree to which a force field is able to correctly reproduce the stability and conformation of the carbohydrate ring and the interactions between the rings depend on a delicate balance between inter- and intramolecular forces [28]. The anomeric effect [79] identifies the preference of the electronegative substituent at the anomeric carbon (C1 in aldoses) for an axial configuration (α-anomer), rather than for the equatorial orientation (β-anomer). This preference has its basis in the electronic structure of the O5–C1–O1 atomic sequence. The widely accepted justification for the anomeric effect is that it originates from hyperconjugation between molecular orbitals (np) associated with the ring oxygen atom (O5) and the adjacent C1–O1 bond (σ*), although there are other interpretations [80]. For pyranoses, stabilizing hyperconjugation is maximized in the α-anomer [81–83]. The exo-anomeric effect arises again from hyperconjugation within the O5–C1–O1 sequence, but this time it is between O1 (np) and the O5–C1 bond (σ*) and manifests itself as a rotameric preference about the exocyclic C1–O1 bond (known as the φ-angle). Unexpected rotameric preferences are also seen for the exocyclic hydroxymethyl group (C5–C6 bond or ω-angle in hexopyranoses). In contrast to expectations based solely on steric effects, this single bond displays a strong preference for rotamers in which O6 and O5 are in a gauche orientation (Fig. 5). In contrast to the anomeric effect, the gauche effect is principally caused by solvation and electrostatic interactions [28], rather than steric or stereoelectronic effects. Rotamer preferences for this bond can profoundly impact the conformational properties of oligosaccharides containing 1–6 linkages, which are common in mammalian and bacterial cell-surface glycans [84–86]. The correct evaluation of the rotamer preferences for the ω-angle is a notoriously challenging task for carbohydrate force fields [87]. This is due to the need for delicately balanced inter- and intramolecular interactions and to the relatively long lifetimes of some states [28,29].
FIGURE 5.
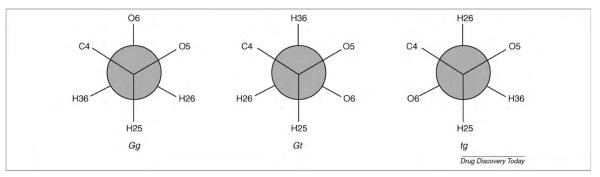
Newman projections of the gauche-gauche (gg), gauche-trans (gt) and trans-gauche (tg) rotameric conformers of the ω dihedral angle. The gg, gt and tg conformers are defined relative to the O5-C5-C6-O6 and C4-C5-C6-O6 torsions.
The choice of treatment of 1–4 non-bonded interactions in a carbohydrate force field is crucial for the correct reproduction of the rotational preference around the ω-angle [28]. In several biomolecular force fields, such as OPLS-AA [88] and AMBER [89], 1–4 non-bonded interactions are dampened, relative to longer range interactions, by the introduction of scaling factors. In carbohydrates 1–4 scaling hinders the correct parameterization of the exocyclic ω torsion (Fig. 4) in hexopyranoses. In fact, the weakening of 1–4 interactions (O6–O5), relative to 1–5 (O6–O4), prevents the accurate fitting of the rotational properties for this linkage [78,90]. Conversely, choosing not to use 1–4 scaling factors may cause a conflict with the treatment of non-bonded interactions in protein force fields. Thus, it might be necessary to employ separate treatments of 1–4 scaling in each class of molecule, particularly in the simulation of glycoproteins. It is worth noting, though, that when glycans bind to proteins, large internal rotations are generally reduced; thus, in the case of carbohydrate–protein complexes, the potential impact of choice of 1–4 scaling often becomes irrelevant and the default scaling appropriate for the protein may be employed.
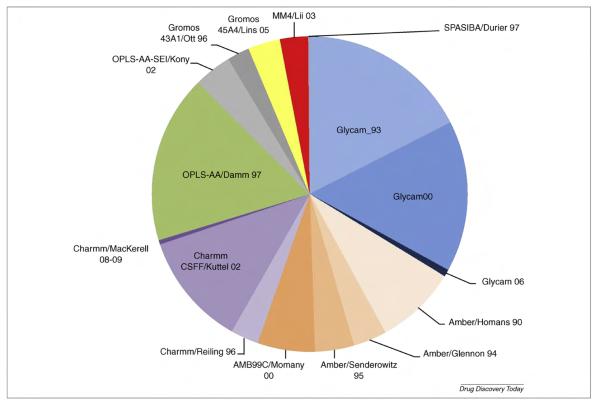
Various parameterization protocols have been developed to generate force field terms specific to carbohydrates [91]. Each of these protocols results in a unique parameter set, with characteristic strengths and weaknesses not only in terms of performance but also in terms of ease of implementation, transferability or generality for extension to glycans outside of the original parameterization scheme or to glycomimetics, as well as compatibility with other biomolecules and solvent models [29,69]. The pie chart in Fig. 6 attempts to quantify the usage of several popular carbohydrate force fields developed since 1990. Each slice is proportional to the number of citations that the original force field paper received during the past five years.3
FIGURE 6.
Approximate estimate of the usage of carbohydrate force fields developed after 1990; namely, GLYCAM, AMBER, CHARMM, OPLS-AA, GROMOS, MM4 [136–138] and SPASIBA [139]. Each slice is proportional to the number of citations of the seminal force field paper in the past five years, according to the ISI `Web of Science' (http://scientific.thomsonreuters.com/products/wos/).
Several reviews of earlier developments of carbohydrate force fields are available in the literature [76,90,92–95]. In the next sections, we discuss the most recent developments of widely used carbohydrate force fields (i.e. CHARMM, GLYCAM06, GROMOS-45A4 and OPLS-AA-SEI). A summary of the main characteristics of each of these force fields, with particular emphasis on the approaches to parameter derivation and validation, is presented in the following sections.
CHARMM
The CHARMM force field for carbohydrates [33–35] is the most recent addition to the CHARMM all-atom biomolecular force field [96,97]. The current parameterization allows for the simulation of monosaccharides (i.e. glucopyranoses and diastereoisomers [34] and aldo- and fructofuranoses [33]) and for unsubstituted oligosaccharides [35]. Consistent with the CHARMM all-atom force field development protocol [93], the carbohydrate parameterization is based on a hierarchical approach. The first parameter set was developed for glucopyranose monosaccharide [34]. Initial parameters were generated for six model compounds corresponding to fragments of a pyranose ring: methanol, ethanol, isopropanol, ethylene glycol, cyclohexane and tetrahydropyran. This preliminary set was applied directly to monosaccharides and then refined to reproduce QM data and experimental properties [34]. The QM data included vibrational frequencies4, conformational energies5, solute–water interaction energies6 and dipole moments. The reference experimental data set included thermodynamic quantities [i.e. heat of vaporization (ΔHvap), molecular volume (Vm) and free energies of solvation], IR vibrational frequencies, X-ray crystallographic intramolecular and unit-cell geometries, densities of concentrated water–glucose solutions, and thermodynamics and dynamics of exocyclic group rotation. Dihedral terms were obtained directly on monosaccharides by fitting over 1800 QM conformational energies.7 The final refinement step consisted of MD simulations of monosaccharides in different media, with the aim of obtaining parameters suitable for the simulations in condensed phase.
Non-bonded interaction parameters have been derived to reproduce carbohydrate–water interactions by fitting to scaled QM solute–water interaction energies and distances. Further refinement was done against experimental heats of vaporization and molecular volumes of neat liquids. Non-bonded interactions were evaluated in aqueous solution at different concentrations of glucopyranose in TIP3P water to assess the transferability to monosaccharides of the non-bonded parameters developed for small model compounds. The results for the solution densities showed less than 0.1% deviation relative to experiment, and based on these results, the non-bonded interaction parameters developed for the model compounds were transferred directly to the monosaccharides without further refinement. Different atom types were introduced for α- and β-anomers.
Validation tests confirm the ability of the force field to reproduce structure, dynamics and thermodynamic properties of glucose as a crystal and in aqueous solution. In conformity with the CHARMM biomolecular force field, no scaling factors were used to reduce 1–4 non-bonded interactions and the rotational preferences of the exocyclic group were analyzed for α- and β-d-glucoand galactopyranose [34].
The rotamer population analysis (Table 1) shows considerable variations in the experimentally derived populations. This reflects the limitations associated with the approximations employed in each case to convert the experimental NMR observables (typically J-values) to populations. Variations also arise from differences in the precision of the experimental measurements. To avoid some of these issues, it has been proposed that derivation of the experimental observable from the MD data is preferable to derivation of rotamer populations from NMR data [98]. Comparing experimental and theoretical J-couplings lacks the ease of physical interpretation of rotamer populations, and there are approximations associated with the computation of theoretical J-values [29]; nevertheless, such comparisons provide a more quantitative assessment of the level of agreement between experiment and theory. Most significantly, the data in Table 1 indicate that simulations with the CHARMM force field correctly reproduced the general rotamer preferences associated with the gauche effects in gluco- and galactosides.
TABLE 1.
Rotamer populations (%) for the ω-angle (gg:gt:tg) in methyl α-d- and β-d-gluco- and galactopyranosidesa
| α-d-Glcp-OMe | β-d-Glcp-OMe | α-d-Galp-OMe | β-d-Galp-OMe | |
|---|---|---|---|---|
| Simulation | ||||
| CHARMM [34] | 47:45:6 | 34:59:7 | 4:46:50 | 6:49:45 |
| GLYCAM06 [100] | 62:36:2 | – | 8:75:18 | – |
| GROMOS45A4 [37] | 54:46:0 | 55:45:0 | 31:38:31 | 34:41:25 |
| OPLS-AA-SEI [38] | 67:29:4 | – | 9:53:38 | – |
|
| ||||
| Experiment | ||||
| [111] | 57:38:5 | – | 16:75:9 | – |
| [109] | 53:47:0 | – | 14:47:39 | – |
| [110] | – | – | 21:61:18 | – |
| [112] | 40:53:7 | 31:61:8 | 3:74:23 | 3:72:25 |
See also Fig. 5.
The extension of the CHARMM force field to oligosaccharides required the addition of torsion parameters appropriate for glycosidic linkages [35]. All glycosidic torsional terms have been derived by fitting QM 2D-scans8 for tetrahydrofuran disaccharides and for tetrahydrofuran monosaccharide linked to cyclohexane. All glycosidic linkages have been scanned separately. The final parameter set was validated via MD simulations of disaccharides in aqueous and crystal phases and compared to X-ray geometries, experimental solution densities and NMR J-coupling data. Bond and angle parameters and point charges were initially transferred directly from the set developed for the monosaccharides, then adjusted to ensure good agreement with experimental geometries and conformational energies. The final optimized parameter set reproduces both conformations and relative energies of the α- and β-anomers relative to QM data.9
To extend the force field to five-membered sugar rings (furanoses), the bonded and non-bonded parameters were transferred directly from the set developed for pyranoses [34] and cyclic ethers [99]. Crystal phase simulation results showed that only slight modifications to bond and angle equilibrium values were necessary to accurately reproduce the crystal structure geometries [33]. New torsion parameters were derived to reproduce the unique ring puckering potential energy landscape associated with five-membered rings. The protocol involved the fitting to QM potential energy surfaces(see footnote 9) of arabinofuranose andribofuranose by means of a Monte Carlo simulated annealing method [100]. The optimized parameters were able to reproduce the QM torsional conformation energies within 1 kcal/mol. Ring pucker parameters and probability distributions were determined through MD simulation in water. The simulation results satisfactorily reproduced the experimental pseudorotation angles and amplitudes, as well as the qualitative trend of exocyclic rotamer population. The final optimized parameter set was validated against QM HF/6-31G(d) sugar–water interaction energies and distances, crystal lattice parameters, aqueous solution experimental densities and NMR conformational properties.
GLYCAM06
GLYCAM06 represents a complete, self-contained and transferable set of parameters for the simulation of carbohydrates and glycoconjugates [36]. GLYCAM06 parameters can be used for the simulation of carbohydrates of all ring sizes and conformations for both monosaccharides and oligosaccharides. Moreover, it includes parameters for many non-standard carbohydrate derivatives commonly found in complex biomolecular systems, such as N-acetylneuraminic acid (sialic acid), N-acetylglucosamine, N-acetylgalactosamine, N-acetylmannosamine, and glucuronic and galacturonic acids. As in the previous versions of GLYCAM [28,101], the parameterization protocol varies subtly from that employed for proteins within the AMBER all-atom force field, most notably in the fitting of partial charges, but maintains overall consistency [89,102]. Such consistency is particularly important for the simulation of glycoconjugates. GLYCAM06 is the only current carbohydrate force field that contains parameters for N-glycosidic linkages [36]. These parameters are suitable for combination with the param99sb version of the AMBER all-atom protein force field [103], allowing for the simulation of glycoproteins and glycopeptides. GLYCAM06 has been applied in combination with the AMBER protein force field to study a diverse range of interactions with proteins, including those of relevance to infection [104], cell development [105] and biomass conversion [106]. Because GLYCAM06 is self-contained, it can be employed in simulation packages other than AMBER; however, great caution should be taken before attempting to mix the GLYCAM parameters for carbohydrates with non-AMBER parameter sets. Although tools exist to convert the GLYCAM force field files to formats appropriate for use with other simulation packages [107], it is important to carefully check the results of any file conversions to ensure the reproduction of relevant benchmarks.
A distinctive feature of the GLYCAM06 force field, in contrast to earlier versions of GLYCAM [28,101] and in contrast to the other force fields reviewed here, is the use of the same carbon atom type (CG) for the anomeric centers in both α- and β-glycosides. This feature was achieved by fitting torsion terms to rotational data from small achiral molecular fragments, rather than to tetrahydropyran-based models of intact α- and β-pyranosides; thus, neither anomer-specific torsion terms nor torsion phase correction terms were employed. This feature facilitates the simulation of ring-flipping, which is known to exist in certain monosaccharides, leading to equilibrium between conformers with axial and equatorial substituents at the anomeric center. This equilibrium is akin to an interconversion between α- and β-anomers, which is not straightforward to simulate with force fields that employ unique torsion terms for α- and β-anomers. This may also be expected to be a significant issue when simulating oligosaccharides bound to carbohydrate-degrading enzymes, in which non-standard ring conformations are a hallmark of the transition state [108]. In point of fact, if the transition state is a half chair, where the anomeric center is neither axial (α-anomer in most pyranoses) nor equatorial (β-anomer in most pyranoses), it is not immediately clear which anomeric parameter set should be employed. For optimal reproduction of molecular ESPs, GLYCAM06 generally employs ensemble-averaged partial charge sets that are specific for each anomer; however, charge averaging can be employed to study variations in conformational energies that relate to ring interconversions [36].
In contrast to many biomolecular force fields, including carbohydrate force fields, the parameterization does not employ any generic torsion terms (e.g. of the type X–C–C–X). All torsion terms were derived in a hierarchical manner using fitting valence parameters to a series of more than 100 model compounds encompassing several molecular classes. These included hydrocarbons, alcohols, ethers, amides, esters, carboxylates and mixed functional groups, such as ether alcohols, ether amides, alcohol amides and ether carboxylates. To ensure consistency, QM data were employed to compute all torsion terms10, as well as for generating stretching and bending force constants.11 As in the case of torsion terms, the bond and angle force constants are fit to the difference between the classical (MM) and the QM data, although in practice – because the force field does not contain 1–3 interaction terms – the force constants are usually very similar to those derived by directly fitting to the QM data. Where NMR data are useful for evaluating the performance of parameters associated with bond rotations, crystallographic data provide insight into the precision of the valence bond lengths and angles. IR spectroscopic data can address the suitability of the stretching and bending force constants. When comparing to IR data, it is important to take into account effects arising from the crystal lattice, which are not reflected in an analysis of a single gas-phase geometry [58]. GLYCAM06 performs well in such comparisons, with the singular exception of the vibration frequencies of the hydroxyl hydrogen–oxygen bond. The QM data employed to fit a force constant to such a labile bond tend to overestimate its strength significantly. The length, however, is unaffected and well reproduced, relative to neutron-diffraction data.
In assessing the fits to the QM data for torsion terms, errors in the relative energies of the minima and in the overall rotational barriers were determined for the entire set of torsions by comparing the QM to the GLYCAM06 rotational curves. For most classes of model compounds, errors were less than 10% of the barrier height. Given that many glycan are highly flexible, it is important to characterize the fits to internal rotational curves. Carboxylates and ether carboxylates (as in N-acetylneuraminic acid) have significantly smaller rotational barrier heights; therefore, the relative errors seem to be larger (i.e. 38% and 29%, respectively). Tests performed on the axial and equatorial conformers of tetrahydro-2-methoxy-2H-pyran show that the use of common torsion parameters for α- and β-anomers in GLYCAM06 enable it to reproduce the QM rotational curves with quantitative accuracy [36]. This was a concern because previous versions of GLYCAM benefited from the simplicity and inherent precision of a single torsion term per rotatable bond, whereas in GLYCAM06 the rotational energy resulted from the sum of all contributing torsion terms. The advantage of this approach is that it makes the extension of the parameters to non-carbohydrates (such as lipids [109] or glycolipids [110]) or chemical analogs (such as glycomimetics) straightforward.
Results, shown in Table 1, for the ability of GLYCAM06 to reproduce the gauche effect, associated with 1–6 linkages, indicate that the force field correctly reproduces the preference for the gg conformer in d-glucopyranose and for the gt conformer in d-galactopyranose. The conformer population analysis is also in good agreement with the majority of the experimental data [36,111–114]. The importance and challenges of such comparisons were discussed in the preceding section.
To ensure consistency with the all-atom force field, non-bonded vdW parameters were taken directly from the PARM94 parameter set of AMBER [89] and atomic partial charges were derived from fitting to molecular ESPs.12 Consistent with the AMBER partial charge philosophy, the atomic charges are not generalized but are unique to each atom in each residue. To capture, in part, the effect of exocyclic group rotations (hydroxyl and hydroxymethyl, and so on) the charges in GLYCAM were computed from the average of the ESP-fit partial charges [115] determined for 100–200 conformations of each monosaccharide. A feature that is unique to GLYCAM is the use of solvated MD simulations to generate the ensemble of conformations employed in the charge averaging. Because of its iterative nature, this process is initiated with a single ESP-fit charge set and can be repeated until convergence in the charge values is achieved [116]. Such an approach leads to statistically robust partial charges, enabling an assessment of the extent to which each atomic center is electrostatically unique. On the basis of this ensemble averaging, it was concluded that aliphatic hydrogen atoms typically carried little if any significant charge. Similar conclusions have also been reached from earlier studies [116,117] and arise from the lack of a notable dipole moment for most C-H bonds. Moreover, fitting partial charges in molecules with many aliphatic hydrogen atoms leads to a degeneracy in the fit, which is reflected in the high sensitivity of the partial charges to ESP sampling protocols [118]. When eliminated from the fitting, robust partial charges emerge. For these reasons, in GLYCAM06 restraints were applied to ensure that the charge on aliphatic hydrogen atoms was zero (RESP). Because the C–H bond dipole is generally negligible, forcing the neutrality of aliphatic hydrogen atoms has no significant effect on the molecular dipole moments. For each monosaccharide, an MD trajectory of typically 50–100 ns was run. The final RESP charges were obtained by averaging the charges determined for the 100–200 snapshots selected from each MD simulation with an optimal RESP weighting derived from the simulation of carbohydrate crystal lattices [119]. Different sets of conformationally averaged partial charges were determined for α- and β-anomers. In all GLYCAM versions, unique partial charge sets are computed for each residue, and the charges are not transferable from monosaccharide to monosaccharide or atom to atom. Although this leads to the more accurate reproduction of ESPs for flexible molecules, it introduces an extra level of complexity over other parameterization approaches based on transferable charges (Table 3). The ensemble-averaged charge sets were able to reproduce the geometries of crystal lattices of monosaccharides, as well as IR spectral frequencies and the solution conformational properties of carbohydrates [36]. Although the use of unique charge sets for each anomer results in optimal representations of the external electrostatic properties, it may negatively impact the reproduction of internal energies – as, for example, the gas-phase relative energies of α- and β-anomers. Quantitative reproduction of internal energies can, however, be achieved when both anomeric charge sets are averaged, although with some reduction in the accuracy of external electrostatics [36].
TABLE 3.
Partial atomic chargesa for α- and β-d-glucopyranose in the force fields reviewed
| Atom name | CHARMM | GLYCAM06 (α/β) | GROMOS-45A4 | OPLS-AA-SEI |
|---|---|---|---|---|
| C1 | 0.340 | 0.509/0.384 | 0.232 | 0.365 |
| C2 | 0.140 | 0.246/0.310 | 0.232 | 0.205 |
| C3 | 0.140 | 0.286/0.284 | 0.232 | 0.205 |
| C4 | 0.140 | 0.254/0.276 | 0.232 | 0.205 |
| C5 | 0.110 | 0.283/0.225 | 0.376 | 0.170 |
| C6 | 0.050 | 0.276/0.282 | 0.232 | 0.145 |
| O1 | −0.650 | −0.639/−0.639 | −0.538 | −0.700 |
| O2 | −0.650 | −0.713/−0.718 | −0.642 | −0.700 |
| O3 | −0.650 | −0.699/−0.709 | −0.642 | −0.700 |
| O4 | −0.650 | −0.710/−0.714 | −0.642 | −0.700 |
| O5 | −0.400 | −0.574/−0.471 | −0.480 | −0.400 |
| O6 | −0.650 | −0.682/−0.688 | −0.642 | −0.683 |
| HO1 | 0.420 | 0.445/0.445 | 0.410 | 0.435 |
| HO2 | 0.420 | 0.427/0.437 | 0.410 | 0.435 |
| HO3 | 0.420 | 0.427/0.432 | 0.410 | 0.435 |
| HO4 | 0.420 | 0.436/0.440 | 0.410 | 0.435 |
| HO6 | 0.420 | 0.418/0.424 | 0.410 | 0.418 |
| H1 | 0.090 | 0.000b | – c | 0.100 |
| H2 | 0.090 | 0.000 | – | 0.060 |
| H3 | 0.090 | 0.000 | – | 0.060 |
| H4 | 0.090 | 0.000 | – | 0.060 |
| H5 | 0.090 | 0.000 | – | 0.030 |
| H6R, H6s | 0.090 | 0.000 | – | 0.060 |
Charges obtained from the following sources: CHARMM (http://mackerell.umaryland.edu/CHARMM_ff_params.html); GLYCAM (http://www.glycam.org); GROMOS-45A4 [136]; OPLS-AA-SEI [123].
Aliphatic hydrogen atoms constrained to zero charge.
Aliphatic carbon atoms are represented as united atoms.
GROMOS 45A4
The 45A4 version of the GROMOS force field [37] contains the latest carbohydrate parameter set developed consistently with the GROMOS96 parameter set [120,121] for biomolecules. The 45A4 version includes parameters for mono- and oligosaccharides based on pyranosides. It was developed as a refinement of the previous 45A3 parameter set [122,123] with the aim to correct for underestimation of the anomeric effect and for the incorrect dihedral angle distribution in di- and oligosaccharides, which sometimes lead to ring deformation [37]. The refinement consists of a re-parameterization of atomic point charges and torsional terms. Non-torsional covalent interactions and vdW terms have been transferred directly from the previous version. As in GLYCAM06, the torsion parameters were derived exclusively from fitting to QM data. Atomic point charges were developed by a restrained fit of the ESP [115] of cellotriose [i.e. β(1 → 4)-linked d-glucopyranose trisaccharide].13 By employing a trisaccharide for charge development, the charges on the central residue should be directly transferable to larger polysaccharides containing the same residue in the same sequence. The extent to which such a model is transferable without loss of accuracy to other oligosaccharide sequences remains to be determined. Restraints in the charge fitting protocol included neutrality of the aliphatic hydrogen atoms, with the molecular dipole moment restrained to the QM value, and neutrality of the carbon–hydroxyl building blocks (e.g. CH–OH and CH2–OH). Charges of topologically similar atoms within the central unit of cellotriose were averaged (Table 3). Charges for terminal C1–OH and C1–OMe groups were obtained through a RESP fit on β-d-glucopyranose, where all charges on other atoms constrained to the value determined for the central unit of cellotriose. After GROMOS96 convention, 1–4 non-bonded interactions are not scaled; however, first and second covalent neighbors are excluded from the vdW pair-list [37].
Dihedral parameters were determined by fit of the MM to the QM rotational energy profiles14 calculated for methyl α-d-glucopyranoside and for methyl β-d-galactopyranoside. Specific parameters were assigned to φ, ψ and ω dihedral angles. α- and β- anomers have been assigned different parameter sets.
The force field was validated through a series of 5 ns and 20 ns MD simulations of monosaccharides, α- and β-d-gluco- and galactopyranose, and the disaccharides trehalose, maltose and cellobiose in SPC water [124]. Unlike the other force fields analyzed here, which are consistent with the TIP3P water model, GROMOS 45A4 was developed to be consistent with the SPC water model. Analysis of the ring conformational energies showed that the 4C1 chair is predicted to be the most stable among the other four conformations studied (i.e. 1C4, B1,4, B2,5 and B3,O). However, the boat B3,O conformation was incorrectly placed at lower energy than the 1C4. The conformational space of the ω torsion for α- and β-d-glucopyranose was sampled by performing a 20 ns MD simulation in SPC water. Population analysis (Table 1) shows that the force field correctly predicts the rotameric preference with a 46:0:54 ratio for the gt:tg:gg rotamers (Fig. 5). Furthermore, inter-conversion between gt and gg was observed in the ns timescale, in good agreement with experiment [37]. Conformational maps calculated for φ and ψ torsions for the disaccharides were also in good agreement with experimental data [37].
OPLS-AA-SEI
The OPLS-AA-SEI parameter set [38] is a refinement of the carbohydrate parameter set included in the OPLS-AA biomolecular force field [88]. New parameters were developed to improve the prediction of conformational energies associated with the φ and ψ angles of the exocyclic hydroxymethyl rotameric distribution in solution [38]. The large discrepancies observed in reproducing gas-phase relative energies were attributed not to the parameterization protocol of OPLS-AA but, mainly, to an imbalance of 1–5 and 1–6 non-bonded interactions caused by the scaling of 1–4 interactions. Rather than remove such scaling as in the other three force fields, the new OPLS-AA carbohydrate force field, namely OPLS-AA Scaling of Electrostatic Interactions (SEI), included additional scale factors for 1–5 and 1–6 non-bonded interactions. This scaling scheme corrected for the shortcomings of the old parameter set for carbohydrates, while maintaining compatibility with the functional form of the biomolecular OPLS force field. 1–5 interactions in 1,2 ethandiol and hexopyranoses were scaled by a factor of 1.25 and 1.26, respectively. For hexopyranoses, 1–6 interactions involving the hydroxymethyl group and the proximal hydroxyl groups were scaled by a factor of 1.22. Such adjustments forced the re-parameterization of the associated dihedral terms.15 All non-torsional valence and non-bonded parameters were imported directly from the parent force field OPLS-AA [125]. Point charges in OPLSAA were derived for standard alcohols and acetals to reproduce properties of neat liquids and thermodynamic properties, such as heats of vaporization [88,125], and transferred to carbohydrates. Validation of the final parameter set OPLS-AA-SEI was done through comparison against experimental 3JH,H NMR data [38].
The performance of OPLS-AA-SEI in solution phase was evaluated by MD simulation of α-d-gluco- and galactopyranose in TIP3P [126] water. Rotational preferences around the ψ dihedral angles were determined over 10 ns MD simulations and are shown in Table 1. The new parameter set correctly predicts the stability of the gg conformer in glucopyranose, whereas the old OPLS-AA carbohydrate parameter set greatly underestimated the stability of the gg relative to the gt conformer. For α-d-galactose, the results between OPLS-AA and OPLS-AA-SEI are very similar, indicating a modest preference for the gt conformer. Moreover, compared to OPLS-AA, OPLS-AA-SEI is able to more accurately reproduce the QM relative energies of gluco-, manno- and galactopyranose [38].
Discussion
A complete parameter set for carbohydrates, directly transferable to a biomolecular force field, allows for the simulation of complex hybrid biological systems (such as glycoproteins and glycolipids) but might not be readily extendible to non-natural carbohydrate-based ligands. Here, we discuss some of the broader similarities and differences between each current force field.
Summarized in Table 2 are some of the key characteristics of the developmental protocols for the four carbohydrate force fields described in detail in the previous sections. All parameter sets are built based on training sets of molecules and have been developed with an eye to maintaining consistency with a larger biomolecular force field, which commonly includes parameters for proteins, nucleic acids and lipids. The training sets might include molecular fragments or monosaccharides and oligosaccharides, or a combination of both. Each force field also varies in the metrics used for validation and parameter refinement. Equilibrium bond lengths and angles are transferred directly from earlier parameterizations in GROMOS-45A4 and OPLS-AA-SEI, whereas both CHARMM and GLYCAM06 introduce carbohydrate-specific QM-derived force constants and equilibrium bond and angle properties. All four force fields present carbohydrate-specific torsion parameters and point charges, although in GLYCAM06, by virtue of the fragment-based development, many of the torsion terms are transferable to other classes of molecule. Obtaining the correct balance of electrostatic interaction energy and torsion energy is one of the key aspects in the development of an accurate force field [127]. As these properties are coupled, however, a robust and diverse validation protocol needs to be employed. The partial charges provide a convenient parameter to compare to illustrate the extent of the differences between each of the force fields. Variations in the numerical values of the charges for α-d- and β-d-glucopyranose between each force field (Table 3) reflect the differences in the manner of their derivation and illustrate the effects to which transferable partial charges differ from residue-specific atomic charges. These and other differences make each parameter set unique and generally incompatible with each other.
TABLE 2.
A summary of the parameterization protocol used for the development of four carbohydrate force fields reviewed
| CHARMM | GLYCAM06 | GROMOS-45A4 | OPLS-AA-SEI | |
|---|---|---|---|---|
| Valence terms | ||||
| Equilibrium bond lengths (r) and angles (θ) | Chosen to reproduce crystal internal and unit-cell geometries | Chosen to reproduce neutron-diffraction geometries | GROMOS-45A3 | OPLS-AA |
| Force constants kb/kθ | Fit to QM data | Fit to QM data | GROMOS-45A3 | OPLS-AA |
|
| ||||
| Torsion terms | Fit to QM rotational energy curves | Fit to QM rotational energy curves | Fit to QM rotational energy curves | Fit to QM rotational energy curves |
|
| ||||
| Partial charges | Empirically fit for carbohydrate fragments, and refined to reproduce: QM solute–water Eint, and experimental Vm of carbohydrate solutions | QM RESP fit and ensemble averaged over multiple conformations. RESP scaling to reproduce crystal unit-cell geometries | QM RESP fit with averaging over atom types | OPLS-AA (empirically fit to reproduce heat of vaporization and densities of pure liquids) |
|
| ||||
| vdW terms | CHARMM22 | AMBER PARM94 | GROMOS-45A3 | OPLS-AA |
|
| ||||
| 1,4 scaling (Elec/vdW) | No/no | No/no | No/no | Yes/yes |
|
| ||||
| Unique charge sets for α- and β-anomers | No | Yes | No | No |
|
| ||||
| Unique charges on each atom | No | Yes | No | No |
|
| ||||
| Unique atom types for α- and β-anomers | Yes | No | Yes | Yes |
Summary and prospectives
The ubiquity of carbohydrates in cell biology and the diversity of their biological functions make them a fascinating yet complex research subject. The potential of this field has promoted in the past five years the development of several high-level parameter sets specific for carbohydrates, enabling accurate computer simulations. In particular, the compatibility of these parameter sets with large biomolecular force fields enables us to study complex bio-molecular systems, such as glycolipids and glycoproteins. Large-scale computational studies of carbohydrate interactions at the cell surface are now feasible. Modern sampling techniques together with accurate force fields could give us an atomistic level of detail on processes such as cell–cell recognition and cell–matrix aggregation. Indeed, the molecular basis underlying these events is extremely difficult to characterize with experimental techniques [128].
Various other areas of carbohydrate research would benefit from the use of computational simulations. Carbohydrate-based drug design is one of the new frontiers of pharmacology and medicinal chemistry [129]. The development of synthetic carbohydrates and carbohydrate derivatives (or glycomimetics) with better pharmaco-kinetic properties is a technical challenge. In fact, the lack of chemical diversity and complex stereochemistry of carbohydrates greatly challenges synthetic approaches to all but the simplest structures. Conversely, several chiral atomic centers make carbohydrates a very useful scaffold for the creation of libraries of high functional and structural diversity [130]. Given a sufficiently accurate force field, computational methods could greatly assist in both carbohydrate-based lead discovery and optimization, thus avoiding the synthesis and screening of large numbers of compounds. Interesting examples of automated docking in combination with carbohydrate–specific parameters, and with free-energy functions designed specifically for carbohydrate–protein interactions, are emerging [131–133].
There have long been two bottlenecks in the application of MD simulations to practical problems in biomolecular design. The first is the need for lengthy simulation times to adequately sample molecular motion, on a timescale of biological relevance. Advances in code algorithms and computer architecture now allow simulations of systems containing on the order of 100K particles to reach the μs timescale in reasonable real time. This system size and timescale enable many biologically relevant systems, such as protein–carbohydrate complexes, oligosaccharides, membrane-bound glycolipids and glycoproteins to be simulated for long enough to provide data that can be employed as a basis to interpret otherwise sparse experimental data or to predict the molecular properties a priori. The second long-standing issue is inaccuracies in force fields, which can often only be identified through careful critical assessment of data from converged simulations. Although the performance of carbohydrate force fields rivals or surpasses that of other biomolecular classes, as simulation times extend, weaknesses in the force fields will continue to be identified. Thus, longer simulations provide an additional basis for evaluating force field performance, and it may be anticipated that features such as charge polarization, lone pair directionality, and choice of water and ion models are likely to be seen as increasingly important. The more consistent and general-izable the parameterization scheme, the more readily the sources of any such weaknesses may be found and corrected and the easier it will be to extend them to the study of less-common glycans or to the design of glycomimetics. Nevertheless, the current performance of carbohydrate force fields on problems of real-world significance is sufficiently accurate that it can be concluded that carbohydrate modeling has come of age.
Acknowledgements
The authors gratefully acknowledge the Science Foundation of Ireland (SFI) for funding (07/RP1/B1321).
Biographies

Elisa Fadda obtained her Ph.D. in theoretical and computational chemistry at the Université de Montréal (Canada) in 2004. After her Ph.D. she worked as a postdoctoral fellow in Molecular Structure and Function at the Hospital for Sick Children (Sickkids) Research Institute in Toronto (Canada), where she specialized in biophysics and statistical mechanics-based methods. In 2008 she joined Rob Woods' group in the School of Chemistry, at the National University of Ireland, Galway, as a senior research scientist in the Computational Glycobiology Laboratory. Her current research focuses on the study of carbohydrate-protein interactions, aimed at the development of glycoprotein-based disease diagnostics and therapeutics.

Professor Robert J. Woods received his Ph.D. from Queen's University at Kingston (Canada) and completed his post-doctoral studies at the Glycobiology Institute at Oxford (UK), where he developed the GLYCAM force field for carbohydrate modeling. He is currently a full professor at the Complex Carbohydrate Research Center and the Department of Biochemistry and Molecular Biology at the University of Georgia (USA). In 2008 he accepted an additional position as Chair of Computational Glycoscience at the National University of Ireland at Galway. His research focuses on the application of computational methods in the characterization of carbohydrate-protein interactions and in their application to the optimization of these interactions.
Footnotes
Web of Science (http://scientific.thomsonreuters.com/products/wos/).
QM vibrational frequencies calculated at the MP2/6-31G(d) level of theory.
QM conformational energies for the model compounds were calculated at the MP2/cc-pVTZ level of theory.
QM solute-water interaction energies were calculated at the HF/6-31G(d) level of theory.
QM conformational scans for the monosaccharides were performed at the MP2/6-31G(d) level of theory.
QM 2D-scans calculated at the MP2/6-31G(d) level with conformational single point energies at the MP2/6-31G(d) level of theory.
QM unrestrained potential energy surfaces obtained at the MP2/cc-pVTZ//MP2/6-31G(d) level of theory.
QM rotational curves were built by increments of 30° from 0° to 360° at the B3LYP/6-311++G(2d,2p) level of theory.
QM distortion curve calculated at the B3LYP/6-311++G(2d,2p) level of theory.
Molecular electrostatic potential determined at the HF/cc-pVTZ/HF/6-31G* level of theory.
Geometry optimization and electrostatic potential calculated at the HF/6- 31G* level of theory.
Rotational profiles calculated at the HF/6-31G* level of theory.
QM geometry optimizations and rotational curves were determined at the B3LYP/6-31G** and at the RHF/6-31G** levels of theory, respectively, for 1,2-ethandiol and hexopyranoses.
References
- 1.Karlsson KA. Bacterium–host protein–carbohydrate interactions and pathogenicity. Biochem. Soc. Trans. 1999;27:471–474. doi: 10.1042/bst0270471. [DOI] [PubMed] [Google Scholar]
- 2.Rogers GN, Paulson J. Receptor determinants of human and animal influenza virus isolates: differences in receptor specificity of the H3 hemagglutinin based on species of origin. Virology. 1983;127:361–373. doi: 10.1016/0042-6822(83)90150-2. [DOI] [PubMed] [Google Scholar]
- 3.Sharon N. Carbohydrates as future anti-adhesion drugs for infectious diseases. Biochim. Biophys. Acta. 2006;1760:527–537. doi: 10.1016/j.bbagen.2005.12.008. [DOI] [PubMed] [Google Scholar]
- 4.Freeze HH. Update and perspectives on congenital disorders of glycosylation. Glycobiology. 2001;11:129r–143r. [PubMed] [Google Scholar]
- 5.Arnold JN, et al. The impact of glycosylation on the biological function and structure of human immunoglobulins. Annu. Rev. Immunol. 2007;25:21–50. doi: 10.1146/annurev.immunol.25.022106.141702. [DOI] [PubMed] [Google Scholar]
- 6.Coppo R, Amore A. Aberrant glycosylation in IgA nephropathy (IgAN) Kidney Int. 2004;65:1544–1547. doi: 10.1111/j.1523-1755.2004.05407.x. [DOI] [PubMed] [Google Scholar]
- 7.Brooks SA, et al. Altered glycosylation of proteins in cancer: what is the potential for new anti-tumour strategies. Anticancer Agents Med. Chem. 2008;8:2–21. doi: 10.2174/187152008783330860. [DOI] [PubMed] [Google Scholar]
- 8.Xu Y, et al. Tumor-associated carbohydrate antigens: a possible avenue for cancer prevention. Immunol. Cell Biol. 2005;83:440–448. doi: 10.1111/j.1440-1711.2005.01347.x. [DOI] [PubMed] [Google Scholar]
- 9.Hakomori S. Aberrant glycosylation in tumors and tumor-associated carbohydrate antigens. Adv. Cancer Res. 1989;52:257–331. doi: 10.1016/s0065-230x(08)60215-8. [DOI] [PubMed] [Google Scholar]
- 10.Kawatkar SP, et al. Structural basis of the inhibition of Golgi alpha-mannosidase ii by mannostatin a and the role of the thiomethyl moiety in ligand–protein interactions. J. Am. Chem. Soc. 2006;128:8310–8319. doi: 10.1021/ja061216p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sly WS, Vogler C. Brain-directed gene therapy for lysosomal storage disease: going well beyond the blood-brain barrier. Proc. Natl. Acad. Sci. U. S. A. 2002;99:5760–5762. doi: 10.1073/pnas.102175599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Abbott KL, et al. Targeted glycoproteomic identification of biomarkers for human breast carcinoma. J. Proteome Res. 2008;7:1470–1480. doi: 10.1021/pr700792g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Block TM, et al. Use of targeted glycoproteomics to identify serum glycoproteins that correlate with liver cancer in woodchucks and humans. Proc. Natl. Acad. Sci. U. S. A. 2005;102:779–784. doi: 10.1073/pnas.0408928102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lucas AH, et al. Carbohydrate moieties as vaccine candidates. Clin. Infect. Dis. 2005;41:705–712. doi: 10.1086/432582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Roy R. New trends in carbohydrate-based vaccines. Drug Discov. Today: Tech. 2004;1:327–336. doi: 10.1016/j.ddtec.2004.10.005. [DOI] [PubMed] [Google Scholar]
- 16.Fuster MM, Esko JD. The sweet and sour of cancer: glycans as novel therapeutic targets. Nat. Rev. Cancer. 2005;5:526–542. doi: 10.1038/nrc1649. [DOI] [PubMed] [Google Scholar]
- 17.Dwek RA. Glycobiology: toward understanding the function of sugars. Chem. Rev. 1996;96:683–720. doi: 10.1021/cr940283b. [DOI] [PubMed] [Google Scholar]
- 18.DeMarco ML, Woods RJ. Structural glycobiology: a game of snakes and ladders. Glycobiology. 2008;18:426–440. doi: 10.1093/glycob/cwn026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Varki A. Biological roles of oligosaccharides – all of the theories are correct. Glycobiology. 1993;3:97–130. doi: 10.1093/glycob/3.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brady JW. Molecular dynamics simulations of carbohydrate molecules. In: Bush CA, editor. Advances in Biophysical Chemistry. Vol. 1. JAI Press Inc.; 1990. pp. 155–202. [Google Scholar]
- 21.Woods RJ. The application of molecular modeling techniques to the determination of oligosaccharide solution conformations. In: Lipkowitz KB, Boyd DB, editors. Reviews in Computational Chemistry. Vol. 9. VCH Publishers, Inc.; 1996. Ch. 3. [Google Scholar]
- 22.Weimar T, Woods RJ. Combining NMR and simulation methods in oligosaccharide conformational analysis. In: Jiménez-Barbero J, editor. NMR of Glycoconjugates. Wiley–VCH; 2002. pp. 111–144. [Google Scholar]
- 23.McCammon JA, et al. Dynamics of folded proteins. Nature. 1977;267:585–590. doi: 10.1038/267585a0. [DOI] [PubMed] [Google Scholar]
- 24.Beveridge CJ, Ravishanker G. Molecular dynamics studies of DNA. Curr. Opin. Struct. Biol. 1994;4:246–255. [Google Scholar]
- 25.Brady JW. Molecular dynamics simulations of α-d-glucose. J. Am. Chem. Soc. 1986;108:8153–8160. [Google Scholar]
- 26.French AD, Brady JW. Computer Modeling of Carbohydrate Molecules. American Chemical Society; 1990. [Google Scholar]
- 27.Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002;9:646–652. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 28.Kirschner KN, Woods RJ. Solvent interactions determine carbohydrate conformation. Proc. Natl. Acad. Sci. U. S. A. 2001;98:10541–10545. doi: 10.1073/pnas.191362798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gonzalez-Outeiriño J, et al. Reconciling solvent effects on rotamer populations in carbohydrates: a joint MD and NMR analysis. Can. J. Chem. 2006;84:569–579. doi: 10.1139/v06-036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Alonso H, et al. Combining docking and molecular dynamic simulations in drug design. Med. Res. Rev. 2006;26:531–568. doi: 10.1002/med.20067. [DOI] [PubMed] [Google Scholar]
- 31.Taft CA, et al. Current topics in computer-aided drug design. J. Pharm. Sci. 2008;97:1089–1098. doi: 10.1002/jps.21293. [DOI] [PubMed] [Google Scholar]
- 32.Jorgensen WL. The many roles of computation in drug discovery. Science. 2004;303:1813–1818. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- 33.Hatcher E, et al. CHARMM additive all-atom force field for aldopentofuranose, methyl-aldopentofuranosides, and fructofuranose. J. Phys. Chem. B. 2009;113:12466–12476. doi: 10.1021/jp905496e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Guvench O, et al. Additive empirical force field for hexopyranose monosaccharides. J. Comput. Chem. 2008;29:2543–2564. doi: 10.1002/jcc.21004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Guvench O, et al. CHARMM additive all-atom force field for glycosidic linkages between hexopyranoses. J. Chem. Theory Comput. 2009;5:2353–2370. doi: 10.1021/ct900242e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kirschner KN, et al. GLYCAM06: a generalizable biomolecular force field. Carbohydrates. J. Comput. Chem. 2008;29:622–655. doi: 10.1002/jcc.20820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lins RD, Hunenberger PH. A new GROMOS force field for hexopyranose-based carbohydrates. J. Comput. Chem. 2005;26:1400–1412. doi: 10.1002/jcc.20275. [DOI] [PubMed] [Google Scholar]
- 38.Kony D, et al. An improved OPLS-AA force field for carbohydrates. J. Comput. Chem. 2002;23:1416–1429. doi: 10.1002/jcc.10139. [DOI] [PubMed] [Google Scholar]
- 39.Pedatella S, et al. New sialyl lewisx mimic containing an α-substituted β3-amino acid spacer. Carbohydr. Res. 2008;343:31–38. doi: 10.1016/j.carres.2007.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wen X, et al. A combined STD-NMR/molecular modeling protocol for predicting the binding modes of the glycosidase inhibitors kifunensine and salacinol to Golgi alpha-mannosidase II. Biochemistry. 2005;44:6729–6737. doi: 10.1021/bi0500426. [DOI] [PubMed] [Google Scholar]
- 41.Germer A, et al. Solution-state conformational study of the hevamine inhibitor allosamidin and six potential inhibitor analogues by NMR spectroscopy and molecular modeling. J. Org. Chem. 2002;67:6328–6338. doi: 10.1021/jo0163703. [DOI] [PubMed] [Google Scholar]
- 42.Shreif Z, et al. Enveloped viruses understood via multiscale simulation: computer-aided vaccine design. Sci. Mod. Sim. 2008;15:363–380. [Google Scholar]
- 43.McGaughey GB, et al. Progress towards the development of a HIV-1 gp41-directed vaccine. Curr. HIV Res. 2004;2:193–204. doi: 10.2174/1570162043484933. [DOI] [PubMed] [Google Scholar]
- 44.Kadirvelraj R, et al. Understanding the bacterial polysaccharide antigenicity of Streptococcus agalactiae versus Streptococcus pneumoniae. Proc. Natl. Acad. Sci. U. S. A. 2006;103:8149–8154. doi: 10.1073/pnas.0602815103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Laederach A, Reilly PJ. Modeling protein recognition of carbohydrates. Proteins. 2005;60:591–597. doi: 10.1002/prot.20545. [DOI] [PubMed] [Google Scholar]
- 46.Somers WS, et al. Insights into the molecular basis of leukocyte tethering and rolling revealed by structures of P- and E-selectin bound to SLex and PSGL-1. Cell. 2000;103:467–479. doi: 10.1016/s0092-8674(00)00138-0. [DOI] [PubMed] [Google Scholar]
- 47.Schwarz FP, et al. Thermodynamics of monosaccharide binding to concavalin, pea (Pisum sativum) lectin, and lentil (Lens culinaris) lectin. J. Biol. Chem. 1993;268:7668–7677. [PubMed] [Google Scholar]
- 48.Zou W, et al. Conformational epitope of the type III group B Streptococcus capsular polysaccharide. J. Immunol. 1999;163:820–825. [PubMed] [Google Scholar]
- 49.Kanbe T, Cutler JE. Minimum chemical requirements for adhesin activity of the acid-stable part of Candida albicans cell wall phosphomannoprotein complex. Infect. Immun. 1998;66:5812–5818. doi: 10.1128/iai.66.12.5812-5818.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ramkumar R, Podder SK. Elucidation of the mechanism of interaction of sheep spleen galectin-1 with splenocytes and its role in cell-matrix adhesion. J. Mol. Recognit. 2000;13:299–309. doi: 10.1002/1099-1352(200009/10)13:5<299::AID-JMR504>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 51.Ramkumar R, et al. Energetics of carbohydrate binding by 14 kDa S-type mammalian lectin. Biochem. J. 1995;308:237–241. doi: 10.1042/bj3080237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bryce RA, et al. Carbohydrate–protein recognition: molecular dynamics simulations and free energy analysis of oligosaccharide binding to concanavalin A. Biophys. J. 2001;81:1373–1388. doi: 10.1016/S0006-3495(01)75793-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Boraston AB, et al. Carbohydrate-binding modules: fine-tuning polysaccharide recognition. Biochem. J. 2004;382:769–781. doi: 10.1042/BJ20040892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Quiocho FA. Carbohydrate-binding proteins: tertiary structures and protein–sugar interactions. Annu. Rev. Biochem. 1986;55:287–315. doi: 10.1146/annurev.bi.55.070186.001443. [DOI] [PubMed] [Google Scholar]
- 55.Naismith JH, Field RA. Structural basis of trimannoside recognition by concanavalin A. J. Biol. Chem. 1996;271:972–976. doi: 10.1074/jbc.271.2.972. [DOI] [PubMed] [Google Scholar]
- 56.Morris GM, et al. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998;19:1639–1662. [Google Scholar]
- 57.Rini JM. Lectin structure. Annu. Rev. Biophys. Biomol. Struct. 1995;24:551–577. doi: 10.1146/annurev.bb.24.060195.003003. [DOI] [PubMed] [Google Scholar]
- 58.Sigurskjold BW, Bundle DR. Thermodynamics of oligosaccharide binding to a monoclonal-antibody specific for a salmonella O-antigen point to hydrophobic interactions in the binding site. J. Biol. Chem. 1992;267:8371–8376. [PubMed] [Google Scholar]
- 59.Lemieux RU. The origin of the specificity in the recognition of oligosaccharides by proteins. Chem. Soc. Rev. 1989;18:347–374. [Google Scholar]
- 60.Drickamer K. Engineering galactose-binding activity into a C-type mannose-binding protein. Nature. 1992;360:183–186. doi: 10.1038/360183a0. [DOI] [PubMed] [Google Scholar]
- 61.Kadirvelraj R, et al. Involvement of water in carbohydrate-protein binding: concanavalin A revisited. J. Am. Chem. Soc. 2008;130:16933–16942. doi: 10.1021/ja8039663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mishra NK, et al. Molecular dynamics study of Pseudomonas aeruginosa lectin-II complexed with monosaccharides. Proteins. 2008;72:382–392. doi: 10.1002/prot.21935. [DOI] [PubMed] [Google Scholar]
- 63.Shimokhina N, et al. Contribution of ligand desolvation to binding thermodynamics in a ligand–protein interaction. Angew. Chem. Int. Ed. Engl. 2006;45:6374–6376. doi: 10.1002/anie.200602227. [DOI] [PubMed] [Google Scholar]
- 64.Williams BA, et al. Energetics of lectin–carbohydrate binding. J. Biol. Chem. 1992;267:22907–22911. [PubMed] [Google Scholar]
- 65.Lammerts van Bueren A, Boraston AB. Binding sub-site dissection of a carbohydrate-binding module reveals the contribution of entropy to oligosaccharide recognition at “non-primary” binding subsites. J. Mol. Biol. 2004;340:869–879. doi: 10.1016/j.jmb.2004.05.038. [DOI] [PubMed] [Google Scholar]
- 66.Laughrey ZR, et al. Carbohydrate–π interactions: what are they worth? J. Am. Chem. Soc. 2008;130:14625–14633. doi: 10.1021/ja803960x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Jairajpuri MA, et al. Antithrombin III phenylalanines 122 and 121 contribute to its high affinity for heparin and its conformational activation. J. Biol. Chem. 2003;278:15941–15950. doi: 10.1074/jbc.M212319200. [DOI] [PubMed] [Google Scholar]
- 68.Spiwok V, et al. Modeling of carbohydrate-aromatic interactions: ab initio energetics and force field performance. J. Comput. Aid. Mol. Des. 2005;19:887–901. doi: 10.1007/s10822-005-9033-z. [DOI] [PubMed] [Google Scholar]
- 69.Tschampel SM, et al. A TIP5P-consistent treatment of electrostatics for biomolecular simulations. J. Chem. Theory Comput. 2007;3:1721–1733. doi: 10.1021/ct700046j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Oxford University Press; 1987. [Google Scholar]
- 71.Rapaport DC. The Art of Molecular Dynamics Simulation. Cambridge University Press; 2004. [Google Scholar]
- 72.Halgren TA. Potential energy function. Curr. Opin. Struct. Biol. 1995;5:205–210. doi: 10.1016/0959-440x(95)80077-8. [DOI] [PubMed] [Google Scholar]
- 73.Warshel A, et al. Polarizable force fields: history, test cases, and prospects. J. Chem. Theory Comput. 2007;3:2034–2045. doi: 10.1021/ct700127w. [DOI] [PubMed] [Google Scholar]
- 74.Elking D, et al. Gaussian induced dipole polarization model. J. Comput. Chem. 2007;28:1261–1274. doi: 10.1002/jcc.20574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.French AD, et al. A QM/Mm analysis of the conformations of crystalline sucrose moieties. Carbohydr. Res. 2000;326:305–322. doi: 10.1016/s0008-6215(00)00051-3. [DOI] [PubMed] [Google Scholar]
- 76.Pérez S, et al. A comparison and chemometric analysis of several molecular mechanics force fields and parameter sets applied to carbohydrates. Carbohydr. Res. 1998;314:141–155. [Google Scholar]
- 77.Yoda T, et al. Comparisons of force fields for proteins by generalized-ensemble simulations. Chem. Phys. Lett. 2004;386:460–467. [Google Scholar]
- 78.Vidal P, et al. Conformational behaviour of glycomimetics: NMR and molecular modelling studies of the C-glycoside analogue of the disaccharide methyl β-d-galactopyranosyl-(1→3)-β-d-glucopyranoside. Carbohydr. Res. 2007;342:1910–1917. doi: 10.1016/j.carres.2007.04.017. [DOI] [PubMed] [Google Scholar]
- 79.Raghavendra Rao VS, et al. Conformation of Carbohydrates. CRC Press; 1998. [Google Scholar]
- 80.Vila A, Mosquera RA. Atoms in molecules interpretation of the anomeric effect in the O–C–O unit. J. Comput. Chem. 2007;28:1516–1530. doi: 10.1002/jcc.20585. [DOI] [PubMed] [Google Scholar]
- 81.Jeffrey GA, et al. Application of ab initio molecular-orbital theory to anomeric effect – comparison of theoretical predictions and experimental-data on conformations and bond lengths in some pyranoses and methyl pyranosides. Carbohydr. Res. 1972;25:117–131. [Google Scholar]
- 82.Jeffrey GA, et al. Application of ab initio molecular-orbital theory to structural moieties of carbohydrates. Carbohydr. Res. 1974;38:81–95. [Google Scholar]
- 83.Jeffrey GA, et al. Application of ab initio molecular-orbital calculations to structural moieties of carbohydrates. 3. J. Am. Chem. Soc. 1978;100:373–379. [Google Scholar]
- 84.González-Outeriño J, et al. Structural elucidation of type III group B Streptococcus capsular polysaccharide using molecular dynamics simulations: the role of sialic acid. Carbohydr. Res. 2005;340:1007–1018. doi: 10.1016/j.carres.2004.12.034. [DOI] [PubMed] [Google Scholar]
- 85.Homans SW, et al. Solution conformation of biantennary complex type oligosaccharides. FEBS Lett. 1983;164:231–235. [Google Scholar]
- 86.Brisson J-R, Carver JP. Solution conformation of αD(1–3)- and αD(1–6)-linked oligomannosides using proton nuclear magnetic resonance. Biochemistry. 1983;22:1362–1368. doi: 10.1021/bi00275a007. [DOI] [PubMed] [Google Scholar]
- 87.Kuttel M, et al. Carbohydrate solution simulations: producing a force field with experimentally consistent primary alcohol rotational frequencies and populations. J. Comput. Chem. 2002;23:1236–1243. doi: 10.1002/jcc.10119. [DOI] [PubMed] [Google Scholar]
- 88.Jorgensen WL, et al. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 89.Cornell WD, et al. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 90.Tschampel SM, et al. Incorporation of carbohydrates into macromolecular force fields. In: Vliegenhart JFG, Woods RJ, editors. NMR Spectroscopy and Computer Modeling of Carbohydrates, Recent Advances. American Chemical Society; 2006. [Google Scholar]
- 91.Tschampel S, et al. Incorporation of carbohydrates into macromolecular force fields. In: Vliegenhart JFG, Woods RJ, editors. NMR Spectroscopy and Computer Modeling of Carbohydrates. Recent Advances. Vol. 930. American Chemical Society; 2006. [Google Scholar]
- 92.Imberty A, Pérez S. Structure, conformation, and dynamics of bioactive oligosaccharides: theoretical approaches and experimental validations. Chem. Rev. 2000;100:4567–4588. doi: 10.1021/cr990343j. [DOI] [PubMed] [Google Scholar]
- 93.Mackerell AD., Jr Empirical force fields for biological macromolecules: overview and issues. J. Comput. Chem. 2004;25:1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 94.Woods RJ. Three-dimensional structures of oligosaccharides. Curr. Biol. 1995;5:591–598. doi: 10.1016/0959-440x(95)80049-2. [DOI] [PubMed] [Google Scholar]
- 95.Woods RJ. Carbohydrate force fields. In: Kollman PA, et al., editors. Encyclopedia of Computational Chemistry. Vol. 1. John Wiley and Sons; 1998. pp. 220–233. [Google Scholar]
- 96.MacKerell AD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 97.MacKerell AD, Jr, et al. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 98.Yongye AB, et al. On achieving experimental accuracy from molecular dynamics simulations of flexible molecules: aqueous glycerol. J. Phys. Chem. A. 2008;112:2634–2639. doi: 10.1021/jp710544s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Vorobyov IV, et al. Additive and classical drude polarizable force fields for linear and cyclic ethers. J. Chem. Theory Comput. 2007;3:1120–1133. doi: 10.1021/ct600350s. [DOI] [PubMed] [Google Scholar]
- 100.Guvench O, MacKerell AD., Jr Automated conformational energy fitting for force-field development. J. Mol. Model. 2008;14:667–679. doi: 10.1007/s00894-008-0305-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Woods RJ, et al. Molecular mechanical and molecular dynamical simulations of glycoproteins and oligosaccharides. 1. GLYCAM-93 parameter development. J. Phys. Chem. 1995;99:3832–3846. [Google Scholar]
- 102.Case DA, et al. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Hornak V, et al. Comparison of multiple AMBER force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Newhouse EI, et al. Mechanism of glycan receptor recognition and specificity switch for avian, swine, and human adapted influenza virus hemagglutinins: a molecular dynamics perspective. J. Am. Chem. Soc. 2009;131:17430–17442. doi: 10.1021/ja904052q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Diehl C, et al. Conformational entropy changes upon lactose binding to the carbohydrate recognition domain of galectin-3. J. Biomol. NMR. 2009;45:157–169. doi: 10.1007/s10858-009-9356-5. [DOI] [PubMed] [Google Scholar]
- 106.Petersen L, et al. Mechanism of cellulose hydrolysis by inverting gh8 endoglucanases: a QM/MM metadynamics study. J. Phys. Chem. B. 2009;113:7331–7339. doi: 10.1021/jp811470d. [DOI] [PubMed] [Google Scholar]
- 107.Dejoux A, et al. AmberFFC, a flexible program to convert AMBER and GLYCAM force fields for use with commercial molecular modeling packages. J. Mol. Model. 2001;7:422–432. [Google Scholar]
- 108.Biarnés X, et al. Substrate distortion in the Michaelis complex of bacillus 1,3–1,4-beta-glucanase. J. Biol. Chem. 2006;281:1432–1441. doi: 10.1074/jbc.M507643200. [DOI] [PubMed] [Google Scholar]
- 109.Tessier MB, et al. Extension of the GLYCAM06 biomolecular force field to lipids, lipid bilayers and glycolipids. Mol. Simul. 2008;34:349–364. doi: 10.1080/08927020701710890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.DeMarco ML, Woods RJ. Atomic-resolution conformational analysis of a ganglioside in a lipid bilayer and its implications for ganglioside-protein interactions at the plasma membrane surface. Glycobiology. 2009;19:344–355. doi: 10.1093/glycob/cwn137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Bock K, Duus JO. A conformational study of hydroxymethyl groups in carbohydrates investigated by H-1-NMR spectroscopy. J. Carbohydr. Chem. 1994;13:513–543. [Google Scholar]
- 112.Nishida Y, et al. H-1-NMR analyses of rotameric distribution of C5–C6 bonds of d-glucopyranoses in solution. J. Carbohydr. Chem. 1988;7:239–250. [Google Scholar]
- 113.Nishida Y, et al. H-1-NMR studies of (6R)-deuterated and (6S)-deuterated d-hexoses – assignment of the preferred rotamers about C5–C6 bond of d-glucose and d-galactose derivatives in solutions. Tetrahedron Lett. 1984;25:1575–1578. [Google Scholar]
- 114.Thibaudeau C, et al. Correlated C–C and C–O bond conformations in saccharide hydroxymethyl groups: parametrization and application of redundant H-1–H-1, C-13–H-1, and C-13–C-13 NMR J-couplings. J. Am. Chem. Soc. 2004;126:15668–15685. doi: 10.1021/ja0306718. [DOI] [PubMed] [Google Scholar]
- 115.Bayly CI, et al. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges – the RESP model. J. Phys. Chem. 1993;93:10269–10280. [Google Scholar]
- 116.Basma M, et al. Solvated ensemble averaging in the calculation of partial atomic charges. J. Comput. Chem. 2001;22:1125–1137. doi: 10.1002/jcc.1072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Woods RJ, et al. Derivation of net atomic charges from molecular electrostatic potentials. J. Comput. Chem. 1990;11:297–310. [Google Scholar]
- 118.Carey C, et al. Charges fit to electrostatic potentials II: can atomic charges be unambiguously fit to electrostatic potentials? J. Comput. Chem. 1996;17:367–383. [Google Scholar]
- 119.Woods RJ, Chappelle R. Restrained electrostatic potential atomic partial charges for condensed phase simulations of carbohydrates. J. Mol. Struct. THEOCHEM. 2000;527:149–156. doi: 10.1016/S0166-1280(00)00487-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Scott WRP, et al. The GROMOS biomolecular simulation program package. J. Phys. Chem. A. 1999;103:3596–3607. [Google Scholar]
- 121.van Gunsteren WF, et al. Biomolecular Simulations: The GROMOS96 Manual and User Guide. 1996. [Google Scholar]
- 122.Schuler LD, et al. An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 2001;22:1205–1218. [Google Scholar]
- 123.Schuler LD, van Gunsteren WF. On the choice of dihedral angle potential energy functions for n-alkanes. Mol. Simul. 2000;25:301–319. [Google Scholar]
- 124.Berendsen HJC, et al. In: Intermolecular Forces. Pullman B, editor. Reidel; 1981. p. 331. [Google Scholar]
- 125.Damm W, et al. OPLS all-atom force field for carbohydrates. J. Comput. Chem. 1997;18:1955–1970. doi: 10.1002/jcc.10139. [DOI] [PubMed] [Google Scholar]
- 126.Jorgensen WL, et al. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 127.Sorin EJ, Pande VS. Empirical force-field assessment: the interplay between backbone torsions and noncovalent term scaling. J. Comput. Chem. 2005;26:682–690. doi: 10.1002/jcc.20208. [DOI] [PubMed] [Google Scholar]
- 128.Bucior I, Burger MM. Carbohydrate-carbohydrate interaction in cell recognition. Curr. Opin. Struct. Biol. 2004;14:631–637. doi: 10.1016/j.sbi.2004.08.006. [DOI] [PubMed] [Google Scholar]
- 129.Wong C-H. Carbohydrate-based Drug Discovery. Wiley-VCH; 2003. [Google Scholar]
- 130.Le GT, et al. Molecular diversity through sugar scaffolds. Drug Discov. Today. 2003;8:701–709. doi: 10.1016/s1359-6446(03)02751-x. [DOI] [PubMed] [Google Scholar]
- 131.Hill AD, Reilly PJ. A Gibbs free-energy correlation for automated docking for carbohydrates. J. Comput. Chem. 2007;29:1131–1141. doi: 10.1002/jcc.20873. [DOI] [PubMed] [Google Scholar]
- 132.Laederach A, Reilly PJ. Specific empirical free energy function for automated docking of carbohydrates to proteins. J. Comput. Chem. 2003;24:1748–1757. doi: 10.1002/jcc.10288. [DOI] [PubMed] [Google Scholar]
- 133.Kerzmann A, et al. BALLDock/SLICK: a new method for protein-carbohydrate docking. J. Chem. Inf. Model. 2008;48:1616–1625. doi: 10.1021/ci800103u. [DOI] [PubMed] [Google Scholar]
- 134.Collins PJ, et al. Crystal structures of oseltamivir-resistant influenza virus neuraminidase mutants. Nature. 2008;453:1258–1262. doi: 10.1038/nature06956. [DOI] [PubMed] [Google Scholar]
- 135.Dementiev A, et al. The ternary complex of antithrombin-anhydrothrombin-heparin reveals the basis of inhibitor specificity. Nat. Struct. Mol. Biol. 2004;11:863–867. doi: 10.1038/nsmb810. [DOI] [PubMed] [Google Scholar]
- 136.Lii JH, et al. Alcohols, ethers, carbohydrates, and related compounds. IV. Carbohydrates. J. Comput. Chem. 2003;24:1504–1513. doi: 10.1002/jcc.10271. [DOI] [PubMed] [Google Scholar]
- 137.Lii JH, et al. Alcohols, ethers, carbohydrates, and related compounds. II. The anomeric effect. J. Comput. Chem. 2003;24:1473–1489. doi: 10.1002/jcc.10269. [DOI] [PubMed] [Google Scholar]
- 138.Lii JH, et al. Alcohols, ethers, carbohydrates, and related compounds. III. The 1,2-dimethoxyethane system. J. Comput. Chem. 2003;24:1490–1503. doi: 10.1002/jcc.10270. [DOI] [PubMed] [Google Scholar]
- 139.Durier V, et al. Molecular force field development for saccharides using the SPASIBA spectroscopic potential. Force field parameters for alpha-d-glucose. J. Mol. Struct. THEOCHEM. 1997;395:81–90. [Google Scholar]