Abstract
The present study examined delay discounting of hypothetical monetary rewards over a wide range of amounts (from $20 to $10 million) in order to determine how reward amount affects the parameters of the hyperboloid discounting function and to compare fits of the hyperboloid model with fits of two discounting models used in neuroeconomics: the quasi-hyperbolic and the double-exponential. Of the three models assessed, the hyperboloid provided the best fit to the delay discounting data. The present delay discounting results may be compared to those of a previous study on probability discounting (Myerson, Green, & Morris, 2011) that used the same extended range of amounts. The hyperboloid function accurately described both types of discounting, but reward amount had opposite effects on the degree of discounting. Importantly, the amount of delayed reward affected the rate parameter of the hyperboloid discounting function but not its exponent, whereas the opposite was true for the amount of probabilistic reward. The finding that the exponent of the hyperboloid discounting function remains relatively constant across a wide range of delayed amounts provides strong support for a psychophysical scaling interpretation, and stands in stark contrast to the finding that the exponent of the hyperboloid function increases with the amount of probabilistic reward. Taken together, these findings argue that delay and probability discounting involve fundamentally different decision-making mechanisms.
Keywords: discounting, delay, amount, hyperboloid, quasi-hyperbolic, double-exponential, magnitude effect, humans
In making everyday decisions, choice is governed by some basic principles. For example, when offered two monetary rewards that differ in amount but not in the time until their receipt, one typically would choose the larger amount, whereas when offered two rewards of the same amount that would be received at different times, one typically would choose the one that is available sooner. Similarly, when offered two monetary rewards of the same amount that differ in the probability that they will actually be received, one typically would choose the more probable. Clearly, individuals typically prefer to have more and to have it sooner and with greater certainty. Although predicting choice may be straightforward when, as in the preceding examples, rewards differ only along one dimension (e.g., amount, delay, or likelihood), predicting choice is more complicated when the options differ on more than one dimension.
For example, what would an individual choose if the options were a smaller amount available immediately and a larger amount available later? To understand why individuals often choose the smaller, sooner reward, economists and psychologists have introduced the concept of delay discounting, according to which the value of a future reward is a decreasing function of how long one would have to wait to receive it (for reviews, see Frederick, Loewenstein, & O’Donoghue, 2002; Green & Myerson, 2004). In fact, if the delay to its receipt is long enough, the subjective (i.e., present) value of the larger reward actually may be less than that of the smaller, immediate reward. The concept of probability discounting is analogous to that of delay discounting (Rachlin, Raineri, & Cross, 1991): If the likelihood that a large reward will be received is low enough, then the subjective (i.e., certain) value of that reward may be less than the subjective value of a smaller, certain reward.
One of the more robust findings in the human discounting literature is that the degree of discounting changes as the amount of reward changes. Such changes have been termed the magnitude effect. Interestingly, however, reward amount affects the degree of discounting in different ways depending on whether the reward is delayed or probabilistic. In the case of delay discounting, larger rewards are discounted less steeply than smaller ones (e.g., Green, Myerson, & McFadden, 1997; Kirby, 1997; Thaler, 1981), whereas in the case of probability discounting, the opposite is true: Larger rewards are discounted more steeply than smaller ones (e.g., Green, Myerson, & Ostaszewski, 1999; Mitchell & Wilson, 2010).
In previous studies, the decrease in the degree to which delayed rewards were discounted appeared to level off at a reward size of around $20,000 (Estle, Green, Myerson, & Holt, 2006, Green et al., 1997, Green et al., 1999). Estle et al. and Green et al. (1999) examined probability as well as delay discounting, and the degree to which probabilistic rewards were discounted also appeared to level off as reward amount increased in the Estle et al. study but not in the study by Green et al. However, the maximum reward in these studies was $100,000. When probability discounting recently was examined over a wider range of amounts ($20 to $10 million), it was clear that the degree to which probabilistic rewards were discounted did not level off, but rather increased as reward amount was increased all the way to $10 million (Myerson, Green, & Morris, 2011). This finding by Myerson et al. raises the question of whether discounting of delayed rewards also would continue to change as amount increased if amount of reward were studied over a similarly wide range.
Both delay and probability discounting are well described by a hyperboloid function:
| (1) |
where V is the subjective value of a delayed or probabilistic reward, A is the amount of that reward, X is the delay until or odds against its receipt, and b is a rate parameter that describes how rapidly the reward loses its value as the delay or odds against increase (Green et al., 1999). It has been proposed (e.g., Green & Myerson, 2004) that the exponent, s, reflects the psychophysical scaling of amount, delay, and probability, but more recent findings raise questions regarding this interpretation, at least in the case of probability discounting (Myerson et al., 2011). In light of these findings, a major purpose of the present study is to re-examine the psychophysical scaling interpretation of the exponent in Equation 1 as it applies to delay discounting.
If the exponent of the discounting function (Eq. 1) reflects the psychophysical scaling of amount, delay, and probability, then the exponent should remain constant across changes in the amount of delayed or probabilistic reward. This is because a psychophysical scale is a quantitative rule that describes the way changes in an objective quantity affect perceived quantity, and such scales are often well described by a power function (Stevens, 1957). Although the perceived quantity will change with the objective quantity, of course, the rule that describes that change, and thus the exponent that characterizes the rule, remains constant.
As a consequence, the psychophysical scaling interpretation predicts that the exponent in the discounting function will remain constant regardless of changes in reward amount. In the case of probability discounting, however, Myerson et al. (2011) found that the value of the exponent (s) increased continuously as the amount of probabilistic reward was increased from $20 to $10,000,000. In contrast, the value of the b parameter showed no systematic change as a function of amount, suggesting that the increasingly steep discounting of probabilistic rewards was entirely attributable to changes in the exponent of the probability-discounting function. Based on these findings, Myerson et al. argued that the exponent of the probability-discounting function does not reflect the psychophysical scaling of reward likelihood, but rather that s provides an index of how probabilities are weighted and that this weighting changes with the amount of reward.
With respect to delay discounting, previous studies have suggested that the exponent of the discounting function does not depend on reward amount, consistent with the psychophysical scaling interpretation and unlike what has been found with probability discounting (Estle et al., 2006; McKerchar, Green, & Myerson, 2010; Myerson & Green, 1995; Myerson et al., 2011). In the case of delay discounting, however, the relation between amount and the parameters of the discounting function has not been examined over anywhere near the five orders-of-magnitude range examined in the probability-discounting study by Myerson et al.. Thus, it is possible that the exponent in the delay-discounting function is only stable over a relatively narrow range of amounts.
If it were to be demonstrated that increases in reward amount have opposite effects on the parameters of the discounting function, decreasing b while s remains constant in the case of delayed rewards and increasing s while b remains constant in the case of probabilistic rewards, then it could be argued strongly that different processes are involved in delay and probability discounting despite the fact that both types of discounting are well described by mathematical functions of the same form (Eq. 1). So, too, if the degree of delay discounting levels off as amount increases but the degree of probability discounting continues to change, it could be argued that the two types of discounting involve different processes. Accordingly, in the present study we varied reward amount over the same wide range examined by Myerson et al. (2011) in their study of probability discounting, and we examined the effects of amount on the degree of discounting and on the parameters of the hyperboloid delay-discounting function.
We also examined the effects of reward amount on the parameters of two other current models of delay discounting: the quasi-hyperbolic model proposed by Laibson (1997) and a double-exponential model recently proposed by van den Bos and McClure (2013). Both of these models are used in neuroeconomics and assume that choice involving delayed rewards reflects the competing activation of separate neural systems (e.g., Kable & Glimcher, 2007; Peters & Büchel, 2011).
The quasi-hyperbolic discounting function (also referred to as the beta-delta model; e.g., McClure, Laibson, Loewenstein, & Cohen, 2004) is a prominent model widely used in economics. According to this model, the subjective value of a monetary reward is equal to its actual amount, A, if it is available immediately, and it maintains this value so long as the reward is delayed by less than one time period. If the delay to the reward is one time period or more, however, then the subjective value of the reward declines exponentially as a function of the delay:
| (2) |
where βA is the subjective value of the reward at the end of the first time period, b is the rate constant for the exponential decay, and X is the total delay (including the first period, which is c time units in duration).1
We write Equation 2 in the form shown above, rather than in the form often used in economics and neuroeconomics (e.g., McClure et al., 2004), in order to highlight one problem with the quasi-hyperbolic model, specifically, the definition of the time period. In some economic situations, the definition of a time period is relatively obvious (e.g., one pay period or the period over which compound interest is calculated). In other situations, however, the definition of a time period is arbitrary, but the selection of units (e.g., days vs. weeks) determines the point at which the subjective value of a reward begins to decline (i.e., when c = 1), as well as the value of the b parameter (e.g., b values for time periods of 1 day are one-seventh of those for time periods of 1 week). In Equation 2, it is clear that the choice of time period is a free parameter, revealing that the model in effect has three free parameters rather than just two (i.e., β and b) parameters, where the third parameter, c, defines the duration of “now.”
Although the quasi-hyperbolic model can be thought of in terms of two neural systems (e.g., McClure et al., 2004), one for the valuation of immediate rewards and one for the valuation of delayed rewards, more recently, van den Bos and McClure (2013) have proposed a double-exponential model that they claim better represents activation in the brain systems involved in decision making. According to this model (which, again, we write using the standard scientific form for the exponential rather than the one favored by economists),
| (3) |
where w reflects the relative involvement of a valuation system and a control system in neuroeconomic decision making, and activation in each of these systems is characterized by its own decay rate (b1 and b2, respectively).2 van den Bos and McClure argue that the systematic variations in discount rates observed across contexts (e.g., types of reward, deprivation levels) reflect differences in neural activity in the brain’s valuation and control systems, and in the examples they provide, this variation in discount rates is effectively captured by changes in the w parameter with the other two parameters fixed. We would assume that the systematic variation in degree of discounting produced by changes in amount of delayed reward constitutes a context effect of the kind covered by the double-exponential model, and therefore that changes in w should capture the effect of amount manipulations.
Indeed, for each of the various discounting models (Eqs. 1, 2, and 3), it is potentially of interest how the parameters are affected by amount of delayed reward. Which parameters (if any) remain stable across amounts and which change systematically? More specifically, do the parameters behave in the ways predicted by the assumptions underlying the models? With respect to the hyperboloid model, because the model assumes that the s parameter in Equation 1 represents psychophysical scaling, it follows that this parameter will not change with amount and, thus, variations in the degree of discounting represent systematic changes only in the b parameter of Equation 1. In contrast, the predictions of the quasi-hyperbolic model are unclear. If the model were to provide a good fit, however, then changes in the value of the parameter c in Equation 2, which indicates the duration of one time period and which may be interpreted as the psychological duration of “now”, might shed light on the underlying hypothetical mechanisms. Finally, the question with respect to the double-exponential model is whether the variation in degree of discounting across amounts will be captured by changes in a single parameter, w in Equation 3, that reflects the relative involvement of the two underlying neural systems.
Method
Participants
Sixty-four undergraduate students (35 males and 29 females, mean age = 19.6 years) were recruited from the Washington University Department of Psychology’s human subject pool and received course credit for their participation. Data from five participants were excluded because it could not be adequately fit by a hyperboloid function, and therefore the analyses here are based on data from 59 participants.
Procedure
Participants were tested individually in a small, quiet room. The experimenter read the participants the following instructions that also were displayed on a computer monitor:
Two amounts of money will appear on the screen. One amount can be received right now. The other amount can be received later. The screen will show you how long you will have to wait to receive that amount. The amount of the "right now" reward will change after each of your decisions. The "later" reward will stay the same for a group of choices. Indicate the option you would prefer by clicking the appropriate button. There are no correct or incorrect choices. If you change your mind about a choice, you can return to the start of that group by clicking the "Reset" button on the screen. You will get to practice before you begin, so don't worry if you might not understand everything yet. Many people say the task makes more sense once they begin. During practice, ask as many questions as you like. Once the actual study begins, we cannot answer any further questions, so please be sure you understand the decision-making task before the end of the practice choices.
The participants then performed six practice trials on the computer-administered discounting task in which they made choices between two hypothetical rewards, a smaller amount of money that could be received immediately and a larger amount that could be received after a delay. These practice trials were similar to those in the experiment, but with different amounts and delays. After answering any questions, the experimenter left the room, and the experiment proper began.
The experiment consisted of 54 conditions: 9 amounts of delayed reward ($20, $250, $3,000, $20,000, $50,000, $100,000, $500,000, $2,000,000, and $10,000,000) crossed with 6 delays (1 month, 3 months, 6 months, 1 year, 6 years, and 12 years). In each condition, an adjusting-amount procedure was used to obtain an estimate of the amount of the smaller, immediate reward that was equivalent in value to the larger, delayed amount (Du, Green, & Myerson, 2002).
The computer program randomly selected a delayed reward amount (without replacement) and then administered all six delay conditions for that amount in a random order, before selecting another delayed reward amount. The side of the computer screen on which the delayed reward was presented alternated randomly across conditions. Each condition consisted of a series of six choice trials. On the first trial, the participant chose between receiving either the delayed amount or half of that amount “right now.” On each subsequent trial, the amount of the immediate reward was adjusted based on the participant’s choice on the preceding trial. Specifically, if the participant chose the immediate reward on the previous trial, the amount of immediate reward was decreased; if the participant chose the delayed reward, the amount of immediate reward was increased.
In each condition, the size of the adjustment (i.e., the decrease or increase in immediate reward amount) decreased with successive choices. The first adjustment was half of the difference between the amounts of the immediate and delayed rewards presented on the first trial, and the size of each subsequent adjustment was half that of the preceding adjustment, rounded to the nearest dollar. For example, in the condition with $100,000 received in 1 year, the choice on the first trial would be between “$100,000 in 1 year” and “$50,000 right now.” If the participant chose the “$100,000 in 1 year,” the choice on the second trial would be between “$100,000 in 1 year” and “$75,000 right now.” If the participant then chose the “$75,000 right now,” the choice on the third trial would be between “$100,000 in 1 year” and “$62,500 right now.” Following the sixth and last trial of each condition, the subjective value of the delayed reward was estimated as the amount of immediate reward that would have been presented on the seventh trial.
Curve fitting
Nonlinear curve-fitting analyses were performed using the Regression Wizard in SigmaPlot for Windows Version 11.0 (Systat Software, Inc.). The Regression Wizard finds the minimum sum of the squares of the errors between data points and a nonlinear function using the Levenberg-Marquardt algorithm (Levenberg,1944; Marquardt, 1963), a standard iterative technique for solving least squares problems.
Results
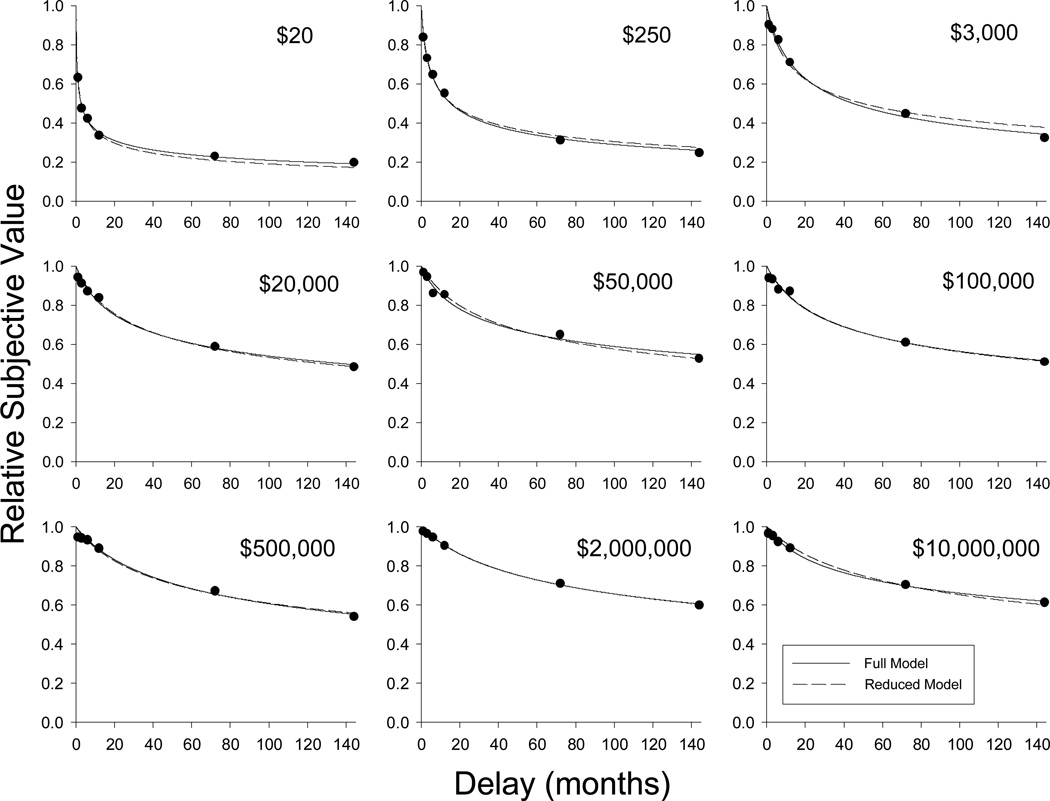
Figure 1 shows group mean relative subjective value plotted as a function of time to receipt of the delayed reward for each of the nine amounts studied. Relative subjective value (i.e., subjective value as a proportion of the actual amount of the delayed reward) is used as the dependent variable in order to facilitate comparisons across different reward amounts. In each panel, the solid curve represents the hyperboloid function (Eq. 1) that best fit the data for that amount condition. As may be seen, the hyperboloid function provided excellent fits (all R2s > .97) to the group data for each of the nine amount conditions. (The dashed curves, to be discussed later, represent a hyperboloid function with separate b parameters for the different amounts, but a single s parameter fit simultaneously to the data for all nine amounts.) The hyperboloid function also provided reasonably good fits to the data at the individual level. For each participant, the hyperboloid function was fit simultaneously to the data from all nine amount conditions in order to obtain separate estimates of the b and s parameters for each condition along with a single overall fit measure (R2) for all nine amount conditions combined. Across the 59 participants, the mean and median R2s were .849 and .893, respectively.
Figure 1.
Relative subjective value as a function of the delay in months to receiving a reward. Each graph depicts the group mean subjective values for a different amount of delayed reward. Solid curves represent Equation 1 fitted to the data from each of the nine amount conditions separately (i.e., the full model); dashed curves represent a reduced model (Equation 1 with a single s parameter but a separate b parameter for each amount) fit to the data from all nine amount conditions simultaneously.
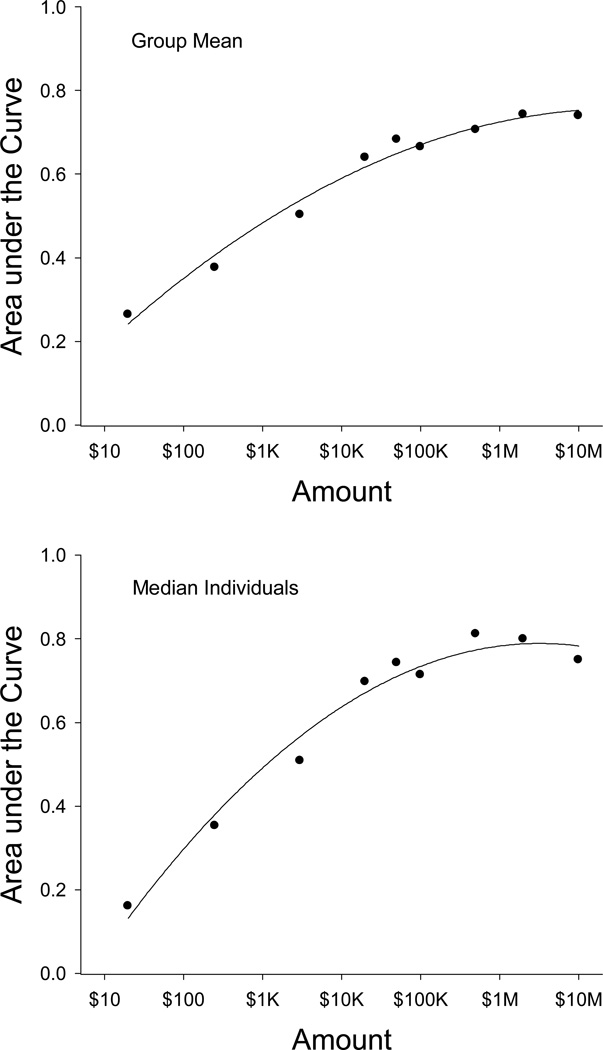
A clear magnitude effect was observed, in that larger delayed amounts were discounted less steeply than smaller delayed amounts. The relation between steepness of discounting and amount of delayed reward may be seen clearly in Figure 2, which plots the area under the (discounting) curves (AuC) as a function of the logarithm of amount. The top panel shows the AuCs based on the group means presented in Figure 1, and the bottom panel shows the median individual AuC at each delayed amount. The AuC measure (Myerson, Green, & Warusawitharana, 2001) represents the area under the observed subjective values and provides a single, theoretically neutral measure of the degree of discounting. The AuC values are normalized so as to range from 0.0 (maximal discounting) to 1.0 (no discounting: the subjective value of the reward at each delay is judged to be equal to that of the same amount received immediately). As may be seen in Figure 2, AuC was a negatively accelerated increasing function of reward amount, reflecting the fact that the degree of discounting decreased with amount, but tended to level off as the amount of delayed reward got very large.
Figure 2.
Area-under-the-curve (AuC) as a function of amount of delayed reward. The AuCs in the top graph were calculated based on the group mean data at each amount (shown in Figure 1), and the bottom graph depicts the median individual AuC at each amount.
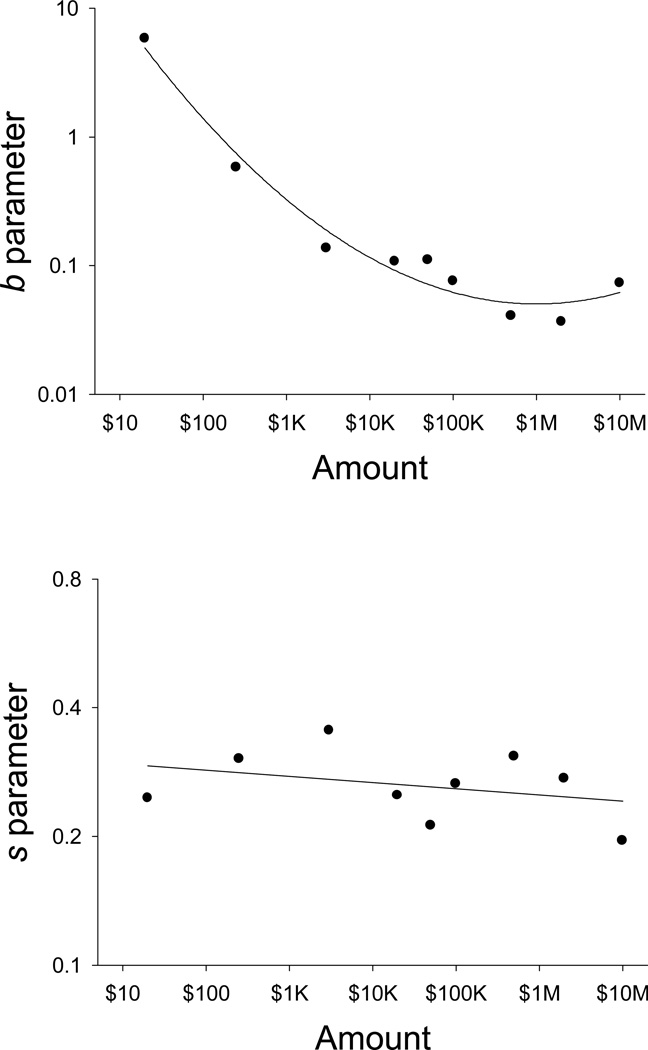
Next, we sought to determine what changes in the parameters of the hyperboloid discounting function (Eq. 1) underlie this magnitude effect (i.e., the decrease in discounting as amount of delayed reward increases). Figure 3 shows the parameter estimates from the fits of the hyperboloid discounting function to the group mean data depicted in Figure 1. The value of the b parameter decreased in a negatively accelerated manner as a function of amount of delayed reward (top panel), whereas the s parameter showed no systematic change (bottom panel).
Figure 3.
Values of the b (top graph) and s (bottom graph) parameters of Equation 1 as a function of amount of delayed reward. Values are based on fits of Equation 1 to the group mean data (shown in Figure 1).
A similar pattern of relations between amount of reward and the parameters was observed at the individual level, although there was considerable variation among participants. The distribution of correlations between log amount and log b tended to be positively skewed with a median r of −.414, whereas the correlations between log amount and log s tended to show a relatively flat distribution with a median r of .120. With respect to the negative correlation between amount and the b parameter, the 95% confidence interval about the mean Fisher z (−.436 ± .144) did not include zero, indicating that the correlation was significant. In contrast, the correlation between amount and the s parameter was not significant, as indicated by the fact that in this case, zero was within the 95% confidence interval about the mean Fisher z (.101 ± .137). Thus, at the individual level as at the group level, there were significant changes in the b parameter, but no systematic changes in the s parameter, as a function of the amount of reward.
Note that the change in b with reward amount depicted in the top panel of Figure 3 is the inverse of the pattern observed in the AuC measure in Figure 2. This, taken together with the lack of change in s, suggests that changes in b underlie the magnitude effect for delay discounting. Notably, the relative stability of s across amount conditions is consistent with the psychophysical scaling interpretation of the s parameter and suggests further that a more parsimonious hyperboloid model, one with only a single s parameter and multiple amount-dependent b parameters, can describe the effect of reward amount on delay discounting. Accordingly, we fit a reduced model (Eq. 1 with a single exponent and a separate discount rate parameter for each amount) to the group mean data from all nine amount conditions simultaneously. The fit of this reduced model to the group mean data is represented by the dashed curves in Figure 1. As may be seen, this model provides an excellent fit (R2 = .991), virtually as good as the fit of the full model (which has many more free parameters because a separate s parameter is estimated for each amount) when it, too, is fit to the data from all of the amounts simultaneously (R2 = .994). Indeed, an incremental-F test revealed that the fits of the two models did not differ significantly; F(8,36) = 1.73, p > .10.
For each participant, we also fit the reduced model to the data from the nine amount conditions simultaneously, and we found that the reduced model provided relatively good fits at the individual level (mean R2 = .816, median = .863), which may be compared to the fits provided by the full model (.849 and .893, respectively). Finally, we evaluated whether the additional parameters of the full model significantly improved the fit to the data from the individual participants, and the incremental-F reached significance in only 5 out of the 59 individual cases, and the median incremental-F was less than 1.0.
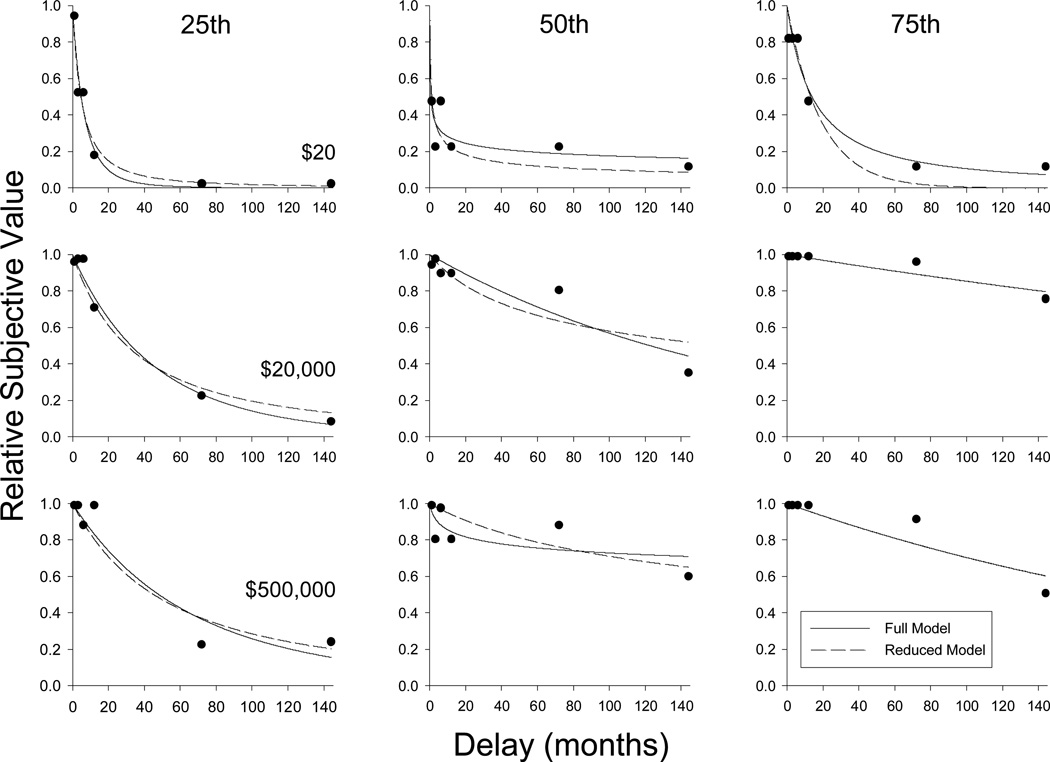
For purposes of illustration, we selected six representative individual participants: Three were selected based on how well their data from all nine amount conditions were fit by the full hyperboloid model, and three were selected based on how steeply they discounted delayed rewards in all the amount conditions. Figure 4 shows data from the individuals whose R2s for the full hyperboloid model were at the 25th, 50th, and 75th percentiles, so as to illustrate how the reduced model fit data that were relatively poorly, moderately, and very well fit, respectively, by the full model. Figure 5 shows data from the individuals whose mean AuCs were at the 25th, 50th, and 75th percentiles, so as to illustrate steep, moderate, and shallow discounters, respectively. The solid and dashed curves in Figures 4 and 5 represent the fit of the full and reduced model to the data, respectively, from each individual’s nine amount conditions, although for purposes of illustration, only data from three amount conditions are presented. As may be seen, there was a magnitude effect in all six cases depicted (i.e., the degree of discounting was steeper when the delayed amount was smaller). In none of the six cases depicted did the full hyperboloid model provide a significantly better fit than the reduced model (median incremental-F(8, 36) = 1.36, p = .25).
Figure 4.
Relative subjective value as a function of delay in months for representative participants selected on the basis of fits of Equation 1. The left, middle, and right columns show data from participants whose R2s for the full hyperboloid model were at the 25th, 50th, and 75th percentiles (R2s of .83, .89, and .92, respectively). For simplicity, only three amount conditions are shown: $20 (top row of panels), $20,000 (middle row), and $500,000 (bottom row). In each panel, the solid curve represents the fit of the full model; the dashed curve represents the fit of the reduced model.
Figure 5.
Relative subjective value as a function of delay in months for representative participants selected on the basis of their mean area under the curve (AuC). The left, middle, and right columns show data from participants whose AuCs were at the 25th, 50th, and 75th percentiles (AuCs of .39, .64, and .74, respectively). For simplicity, only three amount conditions are shown: $20 (top row of panels), $20,000 (middle row), and $500,000 (bottom row). In each panel, the solid curve represents the fit of the full model; the dashed curve represents the fit of the reduced model.
Finally, we fit the quasi-hyperbolic and double-exponential models to the group mean data from each amount condition. In principle, comparisons with the hyperboloid model are complicated by the fact that the quasi-hyperbolic and double-exponential models have more parameters than the hyperboloid – when applied to the data from a single amount condition, both the quasi-hyperbolic and double-exponential models have three free parameters whereas the hyperboloid has two (compare Eqs. 1, 2 and 3). As a result, if the quasi-hyperbolic or double-exponential model were to fit better than the hyperboloid, one might question whether this was simply due to the additional free parameter, and because the models are not nested, one could not use standard statistical tests to resolve the question. As it turns out, however, the hyperboloid turned out to provide a better fit than either of the other models – a result that obviously cannot be attributed to the difference in the number of free parameters.
It may be recalled that the full hyperboloid model with its 18 free parameters (one rate parameter and one exponent for each amount condition) did not provide a significantly better fit than the reduced hyperboloid model with its 10 free parameters (nine free rate parameters but only one free exponent parameter). Therefore, we compared the fits of the reduced hyperboloid model with the fits of correspondingly reduced quasi-hyperbolic and double-exponential models.
The reduced quasi-hyperbolic model had 11 free parameters: nine rate parameters (one for each amount), one parameter (c) capturing the duration of the initial (“now”) time period that precedes the exponential decay, and one parameter (β) that captures the subjective value right after the end of that initial time period. The reduced double-exponential model also had 11 free parameters: one rate parameter (b1) describing the effect of delay on activity in the hypothesized neural valuation system, one rate parameter (b2) describing the effect of delay on activity in the hypothesized neural control system, and nine free (w) parameters, one for each amount condition, describing the relative involvement of activity in the two systems in the decision-making process.
Fit simultaneously to the data from all nine amount conditions, the reduced quasi-hyperbolic model accounted for 87.6% of the variance in subjective values, whereas the reduced double-exponential model accounted for 96.4%. In contrast, the reduced hyperboloid accounted for 99.1% of the variance, despite having one fewer free parameter than either of the other two models.
Finally, we examined the relation between the parameters of the double-exponential model and both amount of delayed reward and the degree of discounting. (We did not do further analyses of the quasi-hyperbolic model because it accounted for so much less of the variance than the other two models.) In multiple applications of the double-exponential model, van den Bos and McClure (2013) held the decay rates (b1 and b2) that characterize the two underlying neural systems constant across situations– only the weighting (w) of the activation in the two systems was free to change (as in the reduced double-exponential model just reported). When all three parameters are free to vary, however, the estimated values of all three varied systematically as a function of amount of delayed reward. That is, each parameter was strongly correlated with the logarithm of the amount of the delayed reward: For b1, r = −.909, for b2, r = −.815, and for w, r = .901 (all ps < .01). Moreover, each parameter was strongly correlated with the degree of discounting as measured by the AuC: For b1, r = −.928, for b2, r = −.876, and for w, r = .966 (all ps < .01). These results are inconsistent with van den Bos and McClure’s assumption that changes in w alone capture the effects of manipulations on the degree of discounting, at least in the case of reward amount.
Discussion
The overarching goal of the present study was to examine the basis for the effects of reward amount on delay discounting (in which larger delayed rewards are discounted less steeply than smaller ones) and to compare these effects with those observed with probability discounting (in which larger rewards are discounted more steeply than smaller ones). The degree to which probabilistic rewards are discounted changes continuously as reward amount is increased from $20 to $10 million (Myerson et al., 2011), and we sought to determine whether that is true also for discounting of delayed rewards, or whether, as some previous reports suggest, the degree of delay discounting levels off at some amount (e.g., $20,000; Green et al., 1997). Finally, we sought to determine whether reward amount differentially and selectively affects the parameters of the delay- and probability-discounting functions, affecting only the rate parameter in the case of delayed rewards and only the exponent in the case of probabilistic rewards. Such a finding would provide strong evidence that different processes are involved in delay and probability discounting.
In the present study, the degree of discounting decreased markedly as the amount of a delayed reward increased, with almost all of this effect occurring before the amount of delayed reward reached $50,000. Indeed, the AuC for the median individual at each amount increased more than 400% between $20 and $50,000 and showed relatively little subsequent increase as reward amount was increased from $50,000 to $10 million. A similar pattern was observed for the group mean AuCs. These results are consistent with those of previous studies in showing that larger delayed rewards are discounted less steeply than smaller ones (e.g., Estle et al., 2006; Green et al., 1997; Kirby, 1997; Thaler, 1981). However, this is the first study to examine the effect of amount on individuals’ choices between immediate and delayed rewards over a range extending up to millions of dollars, thereby revealing that the effect of amount on delay discounting tends to level off as reward amount increases. This pattern of results stands in stark contrast to that observed with probability discounting across the same range of amounts (Myerson et al., 2011). In the latter case, degree of discounting increased markedly as reward amount increased, as indicated by a continuous decrease in the AuC for the median individual at each amount with no sign of leveling off like that observed with delayed rewards.
Given that the degree of delay discounting varies as a function of the amount of the delayed reward, what is responsible for this variation? To address this question, we sought to determine what changes in the parameters of the hyperboloid discounting function underlie the effects of reward amount on the extent to which people discount delayed rewards. As predicted by the psychophysical scaling interpretation of the exponent in the hyperboloid function, and consistent with previous studies (e.g., Estle et al., 2006; Myerson, Green, Hanson, Holt, & Estle, 2003) that examined the effects of amount over a much smaller range than that studied here, the value of the s parameter did not vary systematically as a function of the amount of delayed reward. In contrast, the b parameter decreased markedly with the initial increases in reward amount, leveling off as the amount of the delayed reward got very large.
Again, the present results stand in stark contrast to those for probability discounting studied over the same wide range of reward amounts. In the case of delay discounting, the exponent, s, of the hyperboloid discounting function showed no systematic change with increases in the amount of the delayed reward, whereas the rate parameter, b, decreased as reward amount increased (see Figure 3). In the case of probability discounting, however, the exponent of the discounting function increased as reward amount increased, whereas the rate parameter showed no systematic change (see Figure 4 in Myerson et al., 2011). Consistent with these results for the parameter estimates at different reward amounts, a model with one s and a different rate parameter for each amount provided an excellent fit to the present delay discounting data, whereas a model with a single rate parameter and a different exponent for each amount provided an excellent fit to the probability discounting data.
The present study and that of Myerson et al. (2011) use the effect of reward amount on degree of discounting as a lens through which to examine the processes underlying delay and probability discounting. Our overarching goal in these studies was to highlight the ways in which these two types of discounting, and the mechanisms underlying them, differ. What remains to be addressed, however, is the difficult theoretical question of why reward amount affects discounting in the first place. A number of hypotheses have been proposed, but there is no consensus as to which is correct.
Thaler (1985) argued that people have different “mental accounts” and may consider small rewards as “spending money” whereas large rewards are thought of as “savings”. In the context of delay discounting, Loewenstein and Thaler (1989) suggested that because they keep separate mental accounts, people may be less willing to wait for a small reward because waiting represents foregoing consumption, whereas they are more willing to wait for a large reward because in that case, waiting represents foregoing interest on savings. Raineri and Rachlin (1993) suggested that the degree of discounting depends on the rate at which a reward would be consumed and, in order to account for the magnitude effect with delayed rewards, suggested further that larger amounts are consumed or spent more slowly. Prelec and Loewenstein (1991) proposed that the magnitude effect arises from a property of the shape of the value function that they termed “increasing proportional sensitivity,” according to which the ratio of a pair of small amounts appears to be less than the ratio of a larger pair even if the actual ratio is the same for both pairs. Finally, Myerson and Green (1995) proposed that there is some minimum delay to even “immediate” rewards, and that the shallower discounting of larger reward amounts reflects larger minimum times to their consumption, a result consistent with data from choices between two delayed rewards (Green, Myerson, & Macaux, 2005).
It is to be noted, however, that regardless of whether these hypotheses can account for the magnitude effect with respect to delay discounting, their application to probability discounting is not at all straightforward. Indeed, in their attempt to formulate a common approach to decision making involving delayed and probabilistic outcomes, Prelec and Loewenstein (1991) were forced to propose separate mechanisms for the magnitude effects observed in the two domains. So, too, Green and Myerson (2004) suggested localizing the source of magnitude effects in the separate weighting functions associated with delay and probability discounting, rather than in the shared value function, in order to accommodate the differing effects of reward amount.3
It is possible, of course, that other models that reconceptualize the mechanism underlying the discounting of delayed rewards might facilitate an integrated account of delay and probability discounting. Accordingly, a secondary goal of the current effort was to compare the ability of alternative models of delay discounting, one a leading economic model and the other a model from the emerging field of neuroeconomics, to describe data across a wide range of amounts. However, neither the quasi-hyperbolic model (Laibson, 1997) nor the double-exponential model (van den Bos & McClure, 2013) provided as good a fit of the current data as the hyperboloid model, despite the fact that the hyperboloid model was the most parsimonious of the three (i.e., it incorporated fewer free parameters, and thus on purely statistical grounds, one might have expected the other models to have provided better fits).
Moreover, in presenting the double-exponential model and demonstrating its application to various kinds of context effects, van den Bos and McClure (2013) assumed that changes in discounting reflect changes in a single parameter (i.e., w in Eq. 3), and fixed the values of the other two parameters. However, our analyses showed that even though the model provided a good fit to the present data, this assumption is incorrect, at least for amount effects. Rather, the values of all three parameters of their model changed systematically both as a function of the amount of delayed reward and as a function of degree of discounting. It is not improbable, of course, that changes in reward amount affect multiple neural systems, including both of the systems modeled by the double-exponential, and that this is why all three model parameters change systematically. In the examples provided by van den Bos and McClure, however, changes in the relative involvement of what are hypothesized to be the two relevant neural systems are captured by changes in the w parameter alone. Because van den Bos and McClure said little about the factors affecting the two parameters that characterize the valuation and control systems, whether the current results actually represent evidence against the double-exponential model awaits specification of the model’s predictions in this regard.
Conclusion
The present results for delayed monetary rewards together with those of Myerson et al. (2011) for probabilistic monetary rewards clearly illustrate the difficulty of finding a common theoretical approach to the effect of reward amount on delay and probability discounting. Not only would such an account have to explain the opposite direction of the magnitude effects, it also would have to explain why the effect of amount on delay discounting levels off but the effect on probability discounting does not. Moreover, a common approach also would have to deal with the fact that amount of reward influences the rate parameter of the hyperboloid delay-discounting function whereas in the case of the probability-discounting function, it is the exponent that is affected. In short, it appears that there is no magnitude effect – rather, there are magnitude effects. Future theoretical efforts may need to focus on the effects of amount on specific kinds of discounting (e.g., delay vs. probability) and perhaps even on specific types of outcomes (e.g., money vs. directly consumable rewards, or gains vs. losses). Despite the fact that delay and probability discounting are described by the same mathematical form, the present findings contribute to the emerging evidence that underlying this similarity in form are fundamentally different decision-making mechanisms.
Acknowledgments
The research was supported by NIH Grant RO1 MH055308. Luís Oliveira was supported by a graduate fellowship (SFRH/BD/61164/2009) from the Foundation for Science and Technology (FCT, Portugal).
Footnotes
In economics, an exponential function is typically written as δτ, where δ (delta) is the degree to which the value of the reward is discounted when it is to be presented τ time units later, hence the term β-δ or beta-delta model.
In typical economic notation, the double-exponential model may be written as V = A[w δ1τ + (1-w)δ2τ].
Prelec and Loewenstein (1991) proposed that the magnitude effect with delayed rewards was due to a property of the value function, although they did not offer a mathematical form for that function. Instead, they proposed that the critical property was what they termed increasing proportional sensitivity: v(a) / v(b) < v(αa) / v(αb), where v(x) is the value function, b > a > 0, and α > 1. They acknowledged that this property resulted in implausible predictions for probabilistic rewards, however, and proposed that the magnitude effect in this case was due to anticipation of greater disappointment resulting from not obtaining a larger probabilistic reward than from not obtaining a smaller probabilistic reward.
Green and Myerson (2004) suggested that the different effects of amount on delay and probability discounting could be better accommodated if both of these effects were assumed to involve the weighting component of the discounting function rather than the valuation component. After all, the valuation component is common to both delay and probability discounting. Thus, if the valuation component were the source of the magnitude effects, then such effects would be the same for delay and probability discounting.
In formalizing Green and Myerson’s (2004) proposal, we describe discounting in terms of the economic construct of utility, rather than value, to avoid confusion from different uses of the term value. The discounted utility of a delayed or probabilistic reward may be defined as the product of its psychophysically scaled value and the weight given to that value: U = V * W. Following the usual practice (e.g., Tversky & Kahneman, 1992), we assume that V is a power function of amount (A). For a delayed reward, Wd = [1/(1 + f(A)*D)] s, where f(A) and D are equivalent to b and X, respectively, in Equation 1; for a probabilistic reward, Wp = [1/(1 + h*Θ)] g(A), where h and Θ are equivalent to b and X, and g(A) is equivalent to s in Equation 1. This formalism provides for parallel descriptions of the discounted utility of delayed and probabilistic rewards, using the same valuation function for both, and localizes the source of magnitude effects in either the rate parameter (delay discounting) or the exponent (probability discounting) of the appropriate weighting function, consistent with the present results and those of Myerson et al. (2011).
References
- Du W, Green L, Myerson J. Cross-cultural comparisons of discounting delayed and probabilistic rewards. Psychological Record. 2002;52:479–492. [Google Scholar]
- Estle SJ, Green L, Myerson J, Holt DD. Differential effects of amount on temporal and probability discounting of gains and losses. Memory & Cognition. 2006;34:914–928. doi: 10.3758/bf03193437. [DOI] [PubMed] [Google Scholar]
- Frederick S, Loewenstein G, O’Donoghue T. Time discounting and time preference: A critical review. Journal of Economic Literature. 2002;40:351–401. [Google Scholar]
- Green L, Myerson J. A discounting framework for choice with delayed and probabilistic rewards. Psychological Bulletin. 2004;130:769–792. doi: 10.1037/0033-2909.130.5.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green L, Myerson J, Macaux EW. Temporal discounting when the choice is between two delayed rewards. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2005;31:1121–1133. doi: 10.1037/0278-7393.31.5.1121. [DOI] [PubMed] [Google Scholar]
- Green L, Myerson J, McFadden E. Rate of temporal discounting decreases with amount of reward. Memory & Cognition. 1997;25:715–723. doi: 10.3758/bf03211314. [DOI] [PubMed] [Google Scholar]
- Green L, Myerson J, Ostaszewski P. Amount of reward has opposite effects on the discounting of delayed and probabilistic outcomes. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:418–427. doi: 10.1037//0278-7393.25.2.418. [DOI] [PubMed] [Google Scholar]
- Kable JW, Glimcher PW. The neural correlates of subjective value during intertemporal choice. Nature Neuroscience. 2007;10:1625–1633. doi: 10.1038/nn2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirby KN. Bidding on the future: Evidence against normative discounting of delayed rewards. Journal of Experimental Psychology: General. 1997;126:54–70. [Google Scholar]
- Laibson D. Golden eggs and hyperbolic discounting. The Quarterly Journal of Economics. 1997;112:443–478. [Google Scholar]
- Levenberg K. A method for the solution of certain non-linear problems in least squares. Quarterly of Applied Mathematics. 1944;2:164–168. [Google Scholar]
- Loewenstein G, Thaler RH. Anomalies: Intertemporal choice. Journal of Economic Perspectives. 1989;3:181–193. [Google Scholar]
- Marquardt D. An algorithm for least-squares estimation of nonlinear parameters. SIAM Journal on Applied Mathematics. 1963;11:431–441. [Google Scholar]
- McClure SM, Laibson DI, Loewenstein G, Cohen JD. Separate neural systems value immediate and delayed monetary rewards. Science. 2004 Oct 15;306:503–507. doi: 10.1126/science.1100907. [DOI] [PubMed] [Google Scholar]
- McKerchar TL, Green L, Myerson J. On the scaling interpretation of exponents in hyperboloid models of delay and probability discounting. Behavioural Processes. 2010;84:440–444. doi: 10.1016/j.beproc.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell SH, Wilson VB. The subjective value of delayed and probabilistic outcomes: Outcome size matters for gains but not for losses. Behavioural Processes. 2010;83:36–40. doi: 10.1016/j.beproc.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myerson J, Green L. Discounting of delayed rewards: Models of individual choice. Journal of the Experimental Analysis of Behavior. 1995;64:263–276. doi: 10.1901/jeab.1995.64-263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myerson J, Green L, Hanson JS, Holt DD, Estle SJ. Discounting of delayed and probabilistic rewards: Processes and traits. Journal of Economic Psychology. 2003;24:619–635. [Google Scholar]
- Myerson J, Green L, Morris J. Modeling the effect of reward amount on probability discounting. Journal of the Experimental Analysis of Behavior. 2011;95:175–187. doi: 10.1901/jeab.2011.95-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myerson J, Green L, Warusawitharana M. Area under the curve as a measure of discounting. Journal of the Experimental Analysis of Behavior. 2001;76:235–243. doi: 10.1901/jeab.2001.76-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters J, Büchel C. Overlapping and distinct neural systems code for subjective value during intertemporal and risky decision making. Journal of Neuroscience. 2011;29:15727–15734. doi: 10.1523/JNEUROSCI.3489-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prelec D, Loewenstein G. Decision making over time and under uncertainty: A common approach. Management Science. 1991;37:770–786. [Google Scholar]
- Rachlin H, Raineri A, Cross D. Subjective probability and delay. Journal of the Experimental Analysis of Behavior. 1991;55:233–244. doi: 10.1901/jeab.1991.55-233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raineri A, Rachlin H. The effect of temporal constraints on the value of money and other commodities. Journal of Behavioral Decision Making. 1993;6:77–94. [Google Scholar]
- Stevens SS. On the psychophysical law. Psychological Review. 1957;64:153–181. doi: 10.1037/h0046162. [DOI] [PubMed] [Google Scholar]
- Thaler R. Some empirical evidence on dynamic inconsistency. Economics Letters. 1981;8:201–207. [Google Scholar]
- Thaler R. Mental accounting and consumer choice. Marketing Science. 1985;4:199–214. [Google Scholar]
- Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty. 1992;5:297–323. [Google Scholar]
- van den Bos W, McClure SM. Towards a general model of temporal discounting. Journal of the Experimental Analysis of Behavior. 2013;99:58–73. doi: 10.1002/jeab.6. [DOI] [PMC free article] [PubMed] [Google Scholar]