High-harmonic generation and parametric amplification in the soft X-rays from extended electron trajectories

Abstract

We report, for the first time, the generation of high-order harmonics in a spectral range between 200 eV and 1 keV with an unusual spectral property: only every 4^th (4i + 1, i∈ℵ) harmonic line appears, whereas the usual high-harmonic spectra consist of every odd (2i + 1) harmonic. We attribute this unique property to the quantum path interference of two extended electron trajectories that experience multiple re-scattering. In the well-established theory, electrons emitted via tunnel ionisation are accelerated by a laser field, return to the ion and recombine. The acceleration typically lasts for less than one optical cycle, and the electrons radiate in the extreme ultraviolet range at recombination. In contrast, for extended trajectories, electrons are accelerated over two or more optical cycles. Here, we demonstrate that two sets of trajectories dominate and provide substantial contributions to the generated soft X-ray radiation because they fulfil the resonance condition for X-ray parametric amplification.

In the past several years, high-harmonic generation (HHG) has become a promising method of generating coherent radiation in the extreme ultraviolet (XUV) and soft X-ray (SXR) spectral ranges. HHG converts the frequency of intense laser pulses from the visible or near-infrared region into its harmonics whilst maintaining the spatial and temporal coherence of the driving laser pulses. The generated short-wavelength pulses have durations that range from femtoseconds down to a few tens of attoseconds¹, and the spectra can span the wavelength range from 100 nm to far below 1 nm²,³,⁴. This type of radiation paves the way for high-resolution time-resolved spectroscopy in the keV spectral range³,⁵,⁶.

Shortly after the experimental discovery of HHG⁷, a theoretical model was developed⁸ that is able to describe the experimental findings very accurately. According to this model, a strong but non-relativistic laser field generates the harmonic field from single atoms or molecules in the gas phase. The observed harmonic field is the coherent superposition of independently generated fields, and the macroscopic build-up is affected by the phase-matching conditions⁹,¹⁰. The model described in Ref. 8 separates the HHG process into three distinct steps. First, in a strong laser field, an electron is released from an atom via tunnel ionisation. Next, the electron is accelerated in the laser field and gains energy within a time frame of approximately ¾ optical cycles. Finally, the electron returns to the atom and recombines, and the excess kinetic energy is radiated as an XUV photon. This model relies on the strong-field approximation, i.e., the Coulomb field of the ion is neglected during the electron acceleration. Furthermore, because of the non-relativistic intensity, the magnetic field of the laser beam is also neglected. If the magnetic field is not neglected, one must consider a small, but non-negligible (even for non-relativistic intensities), acceleration of the electron in the direction of the laser propagation. The resulting longitudinal displacement of the re-colliding electron compared to the ion is referred to as the impact parameter b.

The generated high-harmonic spectrum contains only the odd harmonics (q = 2i + 1, i∈ℵ) of the generating laser frequency with a well-defined cut-off (highest) energy. The preferred method of extending the cut-off into the soft X-ray region is to increase the intensity (I) or the wavelength (λ) of the driving laser pulses, as the cut-off is proportional to λ²I. However, for longer driving wavelengths, the electron wave packet spreads out farther, resulting in a rapid decrease in the recombination probability and a reduction in the high-harmonic generation efficiency¹¹,¹²,¹³. On the other hand, an increase in the intensity or wavelength of the driving laser increases the impact parameter b (b ∝ λ³I)¹⁴. Again, the higher the impact parameter, the lower is the recombination probability and, hence, the HHG conversion efficiency. However, it has been theoretically proposed¹⁴ that for higher laser intensities, up to the relativistic regime, extended electron trajectories can overcome the limitation imposed by the impact parameter, and hence, harmonics can be generated up to the hard X-ray range; furthermore, the interference of the multiple re-scattered electrons originating from different optical cycles determines the temporal build-up of HHG¹⁵. An electron moving along an extended trajectory returns to the ion much more than ¾ optical cycles after emission, which is the latest possible return time for conventional HHG.

In this study, we present, for the first time, experimental evidence of HHG radiation from extended electron trajectories. The measured spectra, which extend to 1 keV, can be explained only by the presence of X-ray parametric amplification¹⁶,¹⁷ (XPA) combined with HHG from electrons returning to the ion two or more optical cycles after ionisation. In our recent experiments, high-order harmonic radiation was generated using 30-fs-long laser pulses with peak intensities of up to 1 × 10¹⁶ W/cm² and a centre wavelength of 800 nm. For this parameter range, many possible electron trajectories exist. However, the resonance condition for XPA is best matched by two distinct sets of electron trajectories that produce two X-ray pulses in every optical half-cycle. The quantum path interference between the two extended electron trajectories results in harmonic spectra that contain only every 4^th harmonic (q = 4i + 1) in the spectral range of a few hundred eV to keV.

Results

In this section, we present experimental results that demonstrate the unusual behaviour of the generated high-order harmonic spectra, and we then propose an explanation for this unexpected behaviour by invoking the combined action of two processes: (i) the quantum paths of two electron trajectories interfere during the generation process, and (ii) the two trajectories fulfil the conditions for X-ray parametric amplification.

Measured uncommon HHG spectra

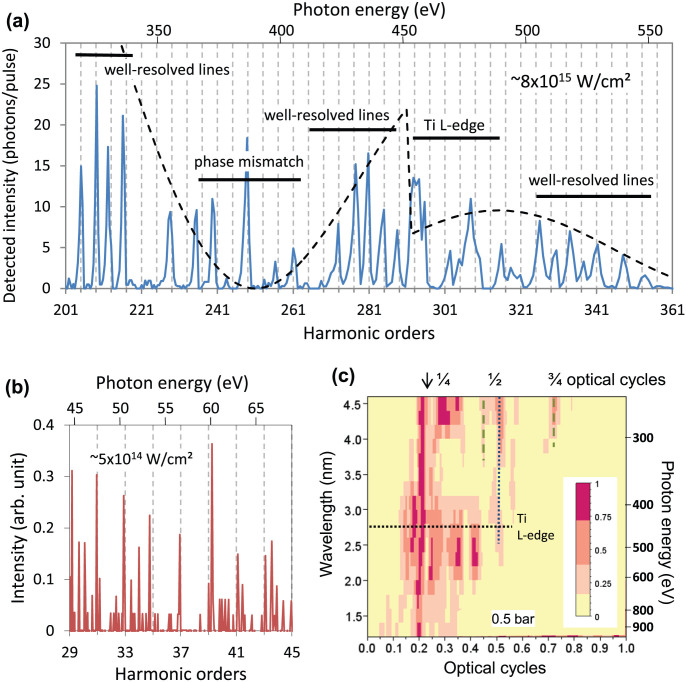
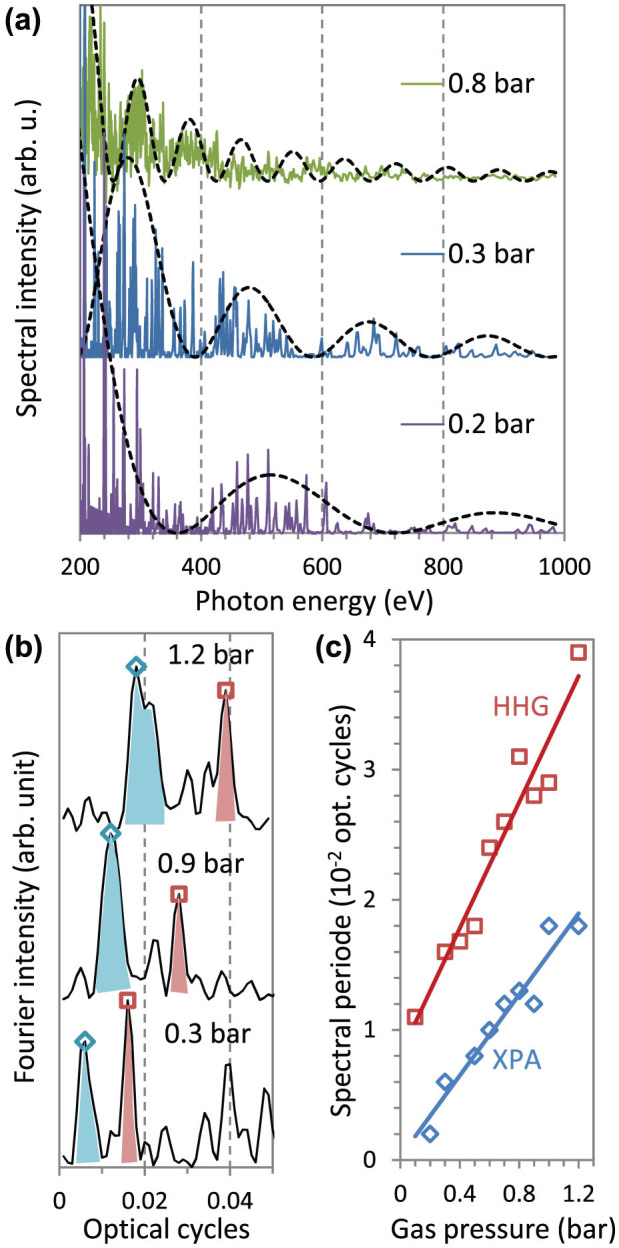
A series of spectral measurements was performed using the JETI Ti:sapphire laser system of the university in Jena, Germany. It delivers 30-fs-long pulses with energies of up to 1 J at a central wavelength of 800 nm and a repetition rate of 10 Hz. The high laser-pulse energy permitted a loose focusing geometry (f/100), and a peak intensity of up to 1 × 10¹⁶ W/cm² in a helium gas target was achieved. The HHG spectra were measured in the spectral range of 0.2–1 keV using an X-ray spectrograph (details can be found in the Methods section). A recorded X-ray spectrum is presented in Fig. 1(a) to permit the detailed examination of the spectrum in the range between the 200^th and 360^th harmonic, corresponding to an energy range of approximately 300 to 600 eV, respectively. In this range, we observed primarily harmonic lines corresponding to the harmonic orders of q = 4i + 1 (where i is an integer). The harmonic lines are very pronounced in the range of the 201^st to 221^st orders and between the 269^th and 289^th. In the range between harmonic orders 221 and 261 and near the high-energy cut-off, the signal is much weaker because of the lack of phase matching; this phenomenon will be discussed later. Above harmonic order 321, the visibility of the harmonic lines is weaker as a consequence of the decreasing spectral resolution of the spectrograph and the limited sampling rate. The small anomaly near harmonic order 293 is attributed to the L-edge absorption of the thin Ti-filter in the beam path.

Figure 1. Measured spectra with unusual spectral lines.

(a) Only harmonic lines of order q = 4i + 1 appear in the measured HHG spectra in the spectral range of 300–600 eV for a laser peak intensity of 8 × 10¹⁵ W/cm². (b) At a peak intensity of approximately 5 × 10¹⁴ W/cm², the harmonic lines appear at every odd harmonic position. (c) The harmonic lines and their quarter-optical-cycle periodicity can be resolved up to ~1 keV (1.2 nm) at 0.5 bar and 8 × 10¹⁵ W/cm². High-order Fourier components (highlighted with green dashed lines) also appear. Standard harmonics of half-optical-cycle periodicity (highlighted by blue dashed lines) are generated in regions with a lower intensity in space and/or time.

The full spectra of the generated high-order harmonic lines were further examined by calculating their Fourier transforms. The results of the transformation clearly reveal a quarter-optical-cycle periodicity for signals in the spectral range of up to 1 keV (1.2 nm) for a gas backing pressure of 0.5 bar, as shown in Fig. 1(c). The small deviation from the expected exact ¼-cycle periodicity originates from the blue shift of the harmonic lines, which is a consequence of the blue shift of the driving laser wavelength caused by the fast ionisation in the gas jet¹⁸ and the atomic phase contribution¹⁹. The additional frequency components in the wavelength range below 3 nm (~267^th harmonic) can be well explained as numerical artefacts caused by the low signal-to-noise ratio of the measurement in this spectral range. Furthermore, additional spectral modulation arises from the Ti foil in the beam path. The spectral range of interest extends well above the Ti L-absorption edge, so we expect a strong spectral modulation in the near-edge region (XANES) and the extended range above the edge (EXAFS)²⁰. In the results summarised in Fig. 1(c), we can also identify weaker modulations that correspond to periodicities of ½ and ¾ optical cycles (green dashed lines), which can be explained as higher-order Fourier components attributable to the non-sinusoidal shape of the harmonic lines, especially at longer wavelengths. Further components originate from conventional harmonics with a half-optical-cycle periodicity (blue dotted line) generated in the low-intensity leading pedestal of the laser pulse. This conclusion is supported by the measurement presented in Fig. 1(b). Here, the peak intensity was reduced by more than one order of magnitude to approximately 5 × 10¹⁴ W/cm², and we observed every odd harmonic in the low-photon-energy range, as expected for conventional HHG. The additional lines that deviate from the predicted positions and the line at the position of the 249^th harmonic in Fig. 1(a) are attributed to atomic/plasma emission lines.

X-ray parametric amplification

Here, we briefly summarise the important features of the X-ray parametric amplification (XPA) process that contribute to the present experimental findings.

In our model (described in detail in Ref. 16 and 17) based on the conventional three-step model of high-order harmonic generation¹,⁸, the Coulomb field of the ion plays an important role in the third step, i.e., at the instant when the electron re-collides (re-scatters) and the X-ray photon is generated. In the equation that describes the interaction between the electron and the ion, the Coulomb force is expanded into a Taylor series, and the contributions of the different orders can be discussed separately. The 0^th-order term defines a resonance frequency 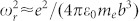, where b is the impact parameter, i.e., the distance of the scattering electron from the ion. The first-order term describes a parametric interaction, i.e., a high-order difference-frequency generation, namely, ω_q = 2qω₁ − ω_q, where ω₁ and ω_q are the angular frequencies of the first-order E₁ (the driving laser) and the q^th-order harmonic E_q field. This parametric coupling between the laser and X-ray fields appears in the form of 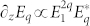, giving a contribution to the signal only if an X-ray field E_q is already present, e.g., from conventional HHG. The impact parameter also plays a very important role in the X-ray parametric amplification process; if it is of the correct order of magnitude, the conditions for parametric resonance are fulfilled, resulting in a substantial amplification of the short-wavelength signal generated via conventional HHG. This amplification process has been experimentally observed and theoretically described in Ref. 16 and 17, respectively, and is known as X-ray parametric amplification (XPA).

Extended electron trajectories

In this section, we describe how extended electron trajectories can be created, how they behave and how they can support XPA in the few-100-eV range by examining the distance of the released and accelerated electron from the ion.

In a strong laser field, atoms are ionised via tunnel or above-barrier ionisation. Subsequently, the freed electrons are accelerated in the laser field. The probability of tunnelling ionisation depends on the electric field, so most electrons are released near the maximum of the electric field. The motion of the freed electrons in the laser field has been calculated by considering the electric and magnetic fields of the laser beam and the Coulomb potential of the ion¹⁶,¹⁷ (for details, see the Methods section). Note that in the context of XPA, it is not necessary to consider a softened Coulomb potential to correctly predict the experimental results. In our model, the electron trajectories are calculated classically, as in many high-harmonic generation theories¹⁴. At re-collision, when the electron is described quantum mechanically, the impact parameter represents the distance to the centre of gravity of the electron wave packet and can be easily included in the calculation for the atomic polarisation¹⁴.

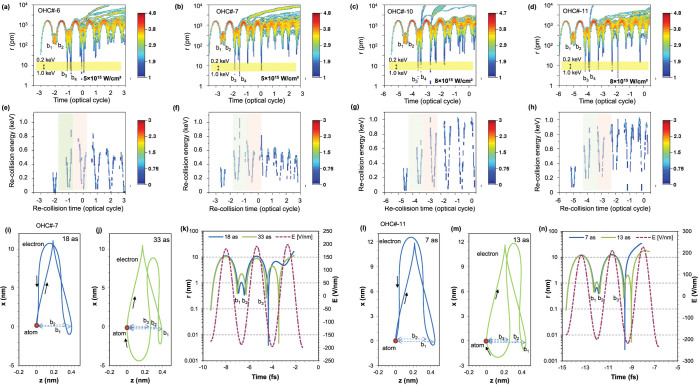
To match our experimental conditions, we considered a 30-fs-long laser pulse with a central wavelength of 800 nm and a peak intensity of 5 × 10¹⁵ W/cm² or 8 × 10¹⁵ W/cm². Furthermore, the calculations were performed at the leading edge of the laser pulse, where atoms are usually ionised and harmonics are generated. In Fig. 2(a)–2(d), we show the distance of the electron from the ion during acceleration in the electric and magnetic fields of the laser pulse. The details of the model used and the manner in which the initial distance and speed of the electron were determined are described in the Methods section. For a laser intensity of 5 × 10¹⁵ W/cm² (Fig. 2(a) and 2(b)), we show the trajectories for electrons emitted 6 or 7 optical half cycles (OHC) before the intensity maximum, whereas for a peak intensity of 8 × 10¹⁵ W/cm², we considered electron trajectories originating 10 and 11 OHC before the intensity maximum. These trajectories have been confirmed to support XPA. Furthermore, these electron trajectories were followed throughout several optical cycles, including several re-scattering events on the ion, where the re-scatterings were considered to be elastic. These electron trajectories must begin within a 20-as time window (beginning 10 as, 15 as, 10 as and 5 as after the electric-field maxima of 6, 7, 10 and 11 OHC, respectively); otherwise, the electrons will not undergo multiple re-scattering, or, even worse, may not re-scatter at all, implying that neither HHG or XPA can take place.

Figure 2. Extended electron trajectories.

For He gas interacting with a 30-fs-long laser pulse with a central wavelength of 800 nm, extended electron trajectories were calculated for two intensities: (a), (b) 5 × 10¹⁵ W/cm² and (c), (d) 8 × 10¹⁵ W/cm². (a)–(d) The distance of the electron from the ion was calculated throughout several re-scattering events and plotted as a function of time, assuming that ionisation occurred a few optical half-cycles (OHC) before the intensity maximum. The scale of the colour bars is proportional to the probability of finding the electron at a certain distance from the atom. (e)–(h) At every re-scattering, the moment of re-scattering (re-collision) and the kinetic energy of the electron were also calculated and exhibit strong correlation. In every OHC, two re-collisions occur, and two soft X-ray pulses are generated. The scale of the colour bars is proportional to the probability of the electron having a certain kinetic energy at the time of collision. (i), (j), (l), (m) For both intensities, two corresponding electron trajectories with a re-collision time of approximately 2 optical cycle are presented; they fulfil the condition of X-ray parametric amplification in the corresponding X-ray energy range because they collide with suitably small impact parameters. (k), (n) The temporal evolution of the distance of the electron from the ion is also plotted separately for both chosen trajectories.

For all trajectories originating in the stated time window, the impact parameters at the first (b₁) and second (b₂) returns are too large for a high recombination probability. However, the electrons will interact with the ion via elastic scattering. So, with a high probability, the electrons are further accelerated in the laser field, travel along extended trajectories, and return to the ion several more times. The impact parameter after the third (b₃) or fourth (b₄) return can be suitably small, not only enabling recombination but also fulfilling the condition for X-ray parametric resonance in the few-100-eV range. The resonance frequency ω_r for XPA is a function of the impact parameter and can be calculated¹⁶,¹⁷ as 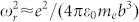, where e and m_e are the charge and mass of the electron, respectively. The impact-parameter range for resonance is highlighted in yellow in Fig. 2(a)–2(d). When the electron trajectories pass through this range, then the condition for XPA resonance is fulfilled. This can occur two, three or possibly more optical cycles after ionisation. Furthermore, the electron must have gained sufficient kinetic energy at the instant of re-collision. The acquired electron energies are plotted in Fig. 2(e)–2(h), where the time windows for re-collision after 2 and 3 optical cycles after ionisation are indicated. The re-collision energies have characteristic V shapes, implying one collision in every optical half cycle at low X-ray energies and two collisions at higher X-ray energies: two collisions in the second half of the ranges (Fig. 2(e) and 2(g), highlighted by grey and pink backgrounds) and another two collisions in the first half of the ranges (Fig. 2(f) and 2(h), highlighted by grey and pink backgrounds). In summary, there are up to four collisions in every optical cycle. Within a certain energy range, between 200 and 400 eV in Fig. 2(e) and 2(f) and between 300 and 500 eV in Fig. 2(g) and 2(h), these collisions are essentially uniformly distributed, leading to the full destructive interference of every second harmonic line, thereby yielding spectra in which only every 4^th harmonic line is present and explaining the measurement results.

The shapes of the two corresponding electron trajectories, with re-collision times of approximately 15/8 and 17/8 optical cycles, are shown in more detail in Fig. 2(i) and 2(j), respectively, for a laser intensity of 5 × 10¹⁵ W/cm² and in Fig. 2(l) and 2(m), respectively, for a laser intensity of 8 × 10¹⁵ W/cm². The corresponding distances of the electron from the ion are summarised in Fig. 2(k) and 2(n) for the two different intensities. For both laser intensities, the corresponding trajectories appear very similar; only the instants of ionisation (18 as and 7 as or 33 as and 13 as, respectively, after the local electric-field maximum) are somewhat different. As a consequence of the quantum path interference between these two electron trajectories, the generated harmonic spectrum will consist only of harmonics of the order q = 4i + 1, where q is the harmonic number, in contrast to the conventional high-harmonic spectrum.

At lower laser intensities, e.g., 5 × 10¹⁴ W/cm², the kinetic energies of the electrons are sufficient for generating HHG radiation in the spectral range below 150 eV. Furthermore, at such a moderate laser intensity, the impact parameters at the first returns (b₁) are very small. Therefore, if the electrons do not recombine, then their trajectories will be strongly perturbed by the Coulomb potential of the ion, circumventing further returns; consequently, extended electron trajectories with multiple re-scattering do not exist. Nevertheless, in this low-intensity regime, high-order harmonics are generated for electrons that return ~7/8 optical cycles after ionisation, which are commonly known long trajectories, and the corresponding impact parameters are in a range that fulfils the condition for XPA in the spectral range below 150 eV. Here, ionisation and recombination can occur only once in every optical half-cycle, and the observed high-harmonic spectrum consists of odd harmonics (q = 2i + 1), in full agreement with the conventional high-harmonic spectrum (see Fig. 1(b)).

Phase matching and XPA

In Fig. 1(c), the low-frequency Fourier components were filtered out so that they would not overwhelm the important high-frequency components. However, the lower components carry important information regarding the phase-matching condition in HHG. The phase mismatch modulates the amplitude of the harmonics following a sinc²(φ(p)/2) function, where 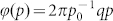; q is the harmonic order, p is the gas pressure and 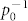is a phase-matching parameter. Corresponding sinc² envelopes are plotted in Fig. 1(a) (dotted black line) along with the transmission of the thin-film Ti filter used in this study, and the sin² envelopes are also plotted in Fig. 3(a), which presents several spectra from the series recorded at various pressures. The Fourier transforms of the spectra contain two distinct peaks at very small fractions of an optical cycle (see three examples in Fig. 3(b)). The peak positions from every evaluated spectrum are plotted in Fig. 3(c), and this figure exhibits a linear dependence for both spectral contributions, as expected from theory. The blue line crosses the axis near zero, as can be expected for XPA (see Eq. (32) in Ref. 17). The red peaks should originate from the conventional HHG contribution in the generated spectra. The slope of the fitted line for the XPA contribution is smaller, which indicates a better phase-matching condition; and a phase-matching parameter of p₀ = 64 ± 6 bar was determined from this slope. Using this parameter, the calculated pressure dependence of the XUV signal in the presence of XPA was fitted to the measured data (see Fig. 4) in various spectral ranges. For the fitting, the electric field of the q^th harmonic as a function of the pressure was estimated to be¹⁷ 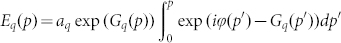, with the pressure-dependent gain 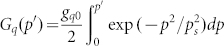, and a_q denotes the signal amplitude of the phase-matched high harmonics without XPA. The measured and fitted curves in three different photon energy ranges exhibit perfect agreement between the measurement and the prediction of our XPA model, as shown in Fig. 4. After estimating a saturation pressure of p_s = 0.7 bar from our measurement, only two free fitting parameters remain in our model, namely, the phase-matched HHG intensity (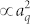) and the XPA gain (g_q0). The parameters obtained for the best fits in various photon-energy ranges are summarised in the inset of Fig. 4. The measured gain parameter is nearly independent of the photon energy; this result is consistent with our model, assuming a uniform electron distribution at the position of re-collision¹⁷.

Figure 3. Phase matching.

(a) In the measured spectra, long-period intensity modulations can be observed (black dashed lines) with pressure-dependent periods. This modulation is identified as a consequence of the non-phase-matched generation of the high harmonics. (b) The long-period modulations produce two distinct peaks in the Fourier transforms of the spectra at positions that depend on the gas pressure. (c) In accordance with the pressure dependence of the peak positions, an XPA contribution and a non-phase matched HHG contribution can be recognised in the generated spectra.

Figure 4. XPA-assisted HHG.

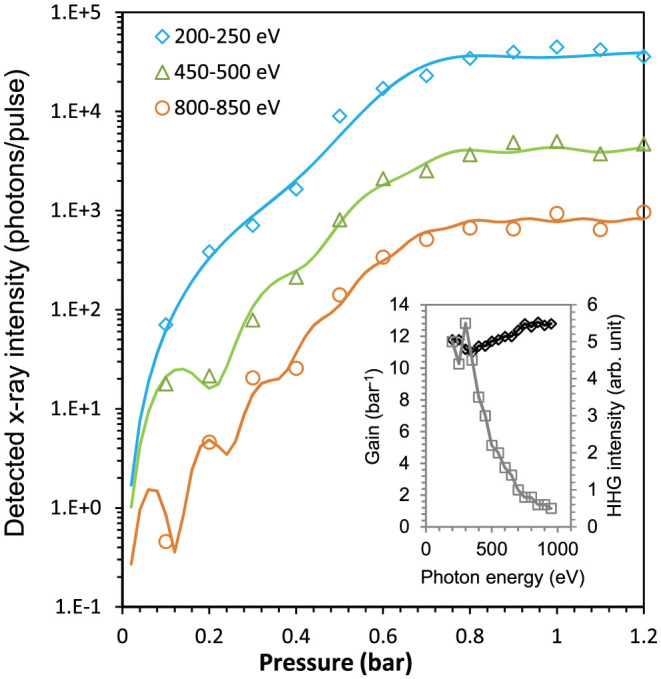
Using the measured phase-matching parameter of XPA-assisted HHG, the pressure dependence of the generated harmonic intensity can be perfectly modelled using the XPA theory. The only free parameters in the model are the XPA gain (black diamonds) and the phase-matched HHG intensities (grey squares), which are summarised in the inset for the best fits obtained for various spectral ranges.

Discussion

From the presented measurements, we can draw the following major conclusions. For laser intensities in the range of 10¹⁵–10¹⁶ W/cm², high-order harmonics can be generated, and the X-ray yield is enhanced via parametric amplification from extended electron trajectories. For these extended trajectories, the time between ionisation and recombination is approximately two or more optical cycles, and in every optical cycle, four X-ray pulses are generated. The prolonged time spent as a free electron results in a more pronounced spreading of the electron wave packet¹³, thus lowering the recombination probability. However, the spreading of electron wave packet can be compensated by Coulomb focusing²¹.

The findings presented in this study provide an improved understanding of high-order harmonic generation and X-ray parametric amplification at higher laser intensities and will allow the establishment of guidelines for extending the XUV signal to higher photon energies with increased efficiency. It is therefore worth mentioning that our X-ray source, at approximately 1 keV, provides a photon flux comparable to those of other recently published approaches using driving lasers with longer wavelengths⁴. Such an efficient source paves the way for attosecond science far beyond 100-eV photon energies and/or using shorter laser wavelengths for improved efficiency and photon yield¹¹,²².

Methods

Electron-trajectory calculation

In a strong laser field, atoms are ionised, and the released electrons are accelerated in the laser field. The motion of the electron can be described by the classical equations of motion in the static Coulomb field of the ion and the E₁ electric and B₁ magnetic fields of the driving laser as follows:

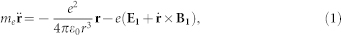where r is the distance of the electron from the ion. For the calculation, we consider a linearly polarised laser beam propagating in the z direction and polarised in the x direction. Thus, the electric field has only an x component, E₁ = (E₁, 0, 0), and the magnetic field has only a y component, B₁ = (0, B₁, 0); therefore, the motion of the electron remains in the x-z plane. The trajectory is defined by the initial conditions {t_i,x_i,v_i}, where t_i is the moment of ionisation and x_i and v_i are the position and velocity, respectively, of the electron at t_i. In the calculation, we consider laser pulses with a central wavelength of λ₁ = 800 nm, a Gaussian temporal shape with a duration of ΔT = 30 fs (FWHM) and a peak intensity of 5 × 10¹⁵ W/cm² or 8 × 10¹⁵ W/cm², in accordance with the experimental conditions. Driven by the strong electric field, the atom can be either tunnel ionised at lower intensities (see Fig. (5a)) or can be ionised above the barrier (see Fig. 5(b)). Because of the field dependence of the ionisation probability¹, most electrons are released near the field maximum in every optical half-cycle (OHC). At such high intensities, the ionisation rate is very high, so almost all atoms are ionised by the leading edge of the laser pulse within a few optical cycles prior to the intensity maximum. The time of ionisation is defined as

where t₀ is measured from the maximum/minimum of the electric field, and at this time, the electric field is

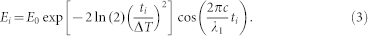For our estimation, we consider helium atoms. The energy required to remove the first electron from the He atom is 24.6 eV, and the energy required to ionise the He⁺ ion is 51.4 eV, i.e., therefore 76 eV is required to fully ionise a He atom. This means that the two electrons in the He atom in the 1 s² ground state are at the −38 eV level (see Fig. 5(a) and 5(b)). For tunnel ionisation (Fig. 5(a)), one of the electron moves down to the −51.4 eV ground state of the He⁺ ion, whilst the other moves up to the −24.6 eV binding energy (−W_b) and is released via tunnelling through the potential barrier at the level of the binding energy. This can be written as

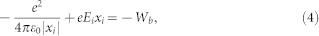and provides a solution for the location x_i, outside the barrier, where the electron appears after tunnelling:

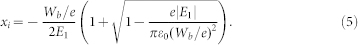According to the principle of energy conservation, the electron released at x_i must have zero velocity, v_i = 0. The electron can tunnel at a lower energy level (thin arrows in Fig. 5(a)), and the remaining energy will be the kinetic energy of the electron with non-zero initial velocity v_i′ > 0. However, the probability of ionisation through a broader barrier is much smaller, so ionisation at the binding-energy level should dominate.

Figure 5. Tunnel and above-barrier ionisation of He atoms.

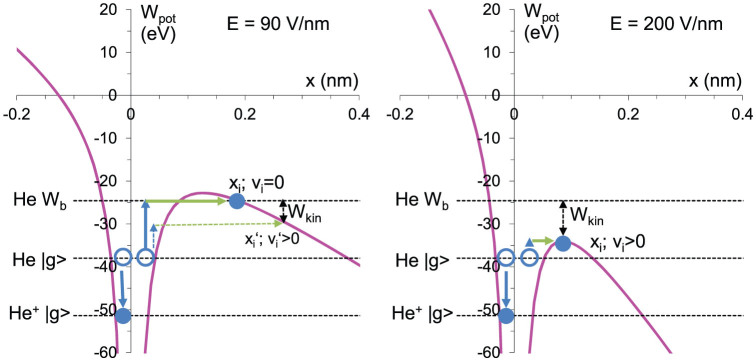
(a) For an electric-field strength of lower than 104.9 V/nm, electrons (blue circles) from the ground state can leave the He atom via tunnel ionisation through the potential barrier (pink). The remaining electron of the He⁺ ion will then be much more tightly bound. (b) For higher electric-field strengths, the electrons will be freed above the barrier. After ionisation, the electrons will initially have the position x_i and the velocity v_i.

When the electric field satisfies the condition

which is 104.9 V/nm for He, the atoms are ionised over the barrier, and x_i is defined at the maximum of the barrier (see Fig. 5(b)):

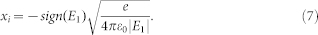Furthermore, the remaining energy is released as kinetic energy and defines the initial velocity:

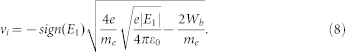For our experimental conditions, the atoms were primarily ionised via above-barrier ionisation, so Eq. (7) and (8) define the initial distance and velocity. After ionisation, the electron is accelerated by the laser field and passes by the atom at a certain distance one or two times during every optical cycle. This distance is called the impact parameter b, which is relatively small, so the bypass is referred to as re-collision. In the calculations, we followed the trajectory of the electron throughout several optical cycles and re-collisions. A set of trajectories was calculated for various ionisation times, with a resolution of 20 trajectories per attosecond. In Fig. 2, the distance of the electron at every time of ionisation (t₀) and the kinetic energy of the electron at every re-collision are plotted.

HHG source

The gas target consisted of a Ni tube with an interaction length of 1 mm backed with helium in a pressure range of 0.1 to 1.2 bar. To reduce the gas load and the reabsorption, the target was operated with a pulsed valve at 10 Hz. The experimental conditions — He as the target material, the high ionisation rate that corresponds to a laser intensity of 8 × 10¹⁵ W/cm² and a gas-jet position that ensured that the atomic phase and the Gouy phase would compensate each other — were carefully chosen and fully ruled out the possibility of pressure-induced phase matching. In certain spectral ranges, this phase-matching scheme exhibited a similar scaling as XPA (Ref. ²³), suggesting the possibility of a different explanation of the experimental observations.

HHG detection

After the fundamental laser light was blocked with thin Al (200 nm) and Ti (100 nm) foils, the HHG spectra were measured using an X-ray scanning monochromator (McPherson 248/310 G) equipped with a 1200-groove/mm grating and a photomultiplier (Channeltron 4751 G). The photomultiplier was operated at a supply voltage of −2.5 kV (SRS PS350) and read out by a lock-in amplifier (Signal Recovery 5209) with an integration time of 0.1 ms. Using this equipment, we were able to record harmonic spectra in the spectral range of 0.2–2 keV with a resolution sufficient for the detection of single harmonic lines below 1 keV.

Number of detected photons

The efficiency or sensitivity is not very precisely known for all components involved in the detection of the X-ray photons. Therefore, we opted for a device-independent method of estimating the detected number of X-ray photons. For our evaluation, we need only assume that Poisson statistics correctly describe the incoming photons. Then, we can estimate the number of photons N from the mean value (mean) and the standard deviation (sdev) using the following equation: N = (mean/sdev)². For the estimation of N, we selected four well-resolved harmonic lines between 300 and 350 eV (see the spectrum in Fig. 1(a)) for a backing pressure of 0.3 bar. The signals within the harmonic lines were integrated, and the mean and sdev were calculated. Taking into account that every measurement point was produced by two laser shots, we obtained a value of 43 photons per harmonic line per pulse, and this value was used to correct the scales of Fig. 1(a) and Fig. 4. In the saturated regime, for a backing pressure above 0.8 bar (see Fig. 4), the number of photons was approximately 50 times higher, i.e., we detected approximately 2000 photons per harmonic line per pulse. It should be noted that this method tends to underestimate the true number of detected photons because it assumes a driving laser with no fluctuations.

Number of generated photons

To estimate the number of X-ray photons generated in the 300–350 eV range, we corrected the number of detected photons using the specifications of the elements in the beam path. According to the manufacturer, the photomultiplier used in this study has a quantum efficiency of approximately 10% in a spectral range of up to 1 keV. In the literature, we found the diffraction efficiency of the grating, which is on the order of 10⁻² to 10⁻³. The transmission of the thin-foil X-ray filters (200 nm Al + 100 nm Ti) is approximately 10%, assuming no additional contamination on the filters. The size of the X-ray beam at the entrance of the X-ray spectrograph is unknown, making it impossible to correctly determine the fraction of photons transmitted through the input slit; therefore, we assumed a ratio between 0.1 and 1. The reabsorption of the generated X-rays in the gas jet and gas background was neglected, as it is relatively small in this spectral rage. All these contributions amount to an attenuation factor of between 10⁴ and 10⁶. Therefore, in the 300–350 eV range, approximately 10⁷–10⁹ photons per line per pulse were generated. At 1 keV, the signal was approximately 2 orders of magnitude smaller, but the transmission of the filters is also higher, so we estimate that 10⁴–10⁶ X-ray photons per line per pulse were generated.

Author Contributions

J.S., E.S., T.K. and C.S. designed the experiments and wrote the manuscript; J.S., E.S., B.L., B.E. and B.A. conducted the X-ray experiments; J.S. developed the theory. All authors analysed the data and contributed to the completion of the manuscript.