Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Feb 28;4:4109. doi: 10.1038/srep04109

Superconductivity in an electron band just above the Fermi level: possible route to BCS-BEC superconductivity

K Okazaki 1,9,a, Y Ito 1, Y Ota 1, Y Kotani 1,10, T Shimojima 1,11, T Kiss 1,12, S Watanabe 2, C-T Chen 3, S Niitaka 4,5, T Hanaguri 4,5, H Takagi 4,5, A Chainani 6,7, S Shin 1,5,6,8,a
PMCID: PMC3937798  PMID: 24576851

Abstract

Conventional superconductivity follows Bardeen-Cooper-Schrieffer(BCS) theory of electrons-pairing in momentum-space, while superfluidity is the Bose-Einstein condensation(BEC) of atoms paired in real-space. These properties of solid metals and ultra-cold gases, respectively, are connected by the BCS-BEC crossover. Here we investigate the band dispersions in FeTe0.6Se0.4(Tc = 14.5 K ~ 1.2 meV) in an accessible range below and above the Fermi level(EF) using ultra-high resolution laser angle-resolved photoemission spectroscopy. We uncover an electron band lying just 0.7 meV (~8 K) above EF at the Γ-point, which shows a sharp superconducting coherence peak with gap formation below Tc. The estimated superconducting gap Δ and Fermi energy 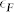Inline graphic indicate composite superconductivity in an iron-based superconductor, consisting of strong-coupling BEC in the electron band and weak-coupling BCS-like superconductivity in the hole band. The study identifies the possible route to BCS-BEC superconductivity.

The iron-based high-temperature superconductors1 possess multi-band hole and electron Fermi surfaces (FSs) which have motivated the role of FS nesting, spin- and orbital-fluctuations, or a combination of these mechanisms for understanding their properties2,3,4. Electronic structure studies have concentrated on band dispersions in the occupied states lying below the Fermi level (EF)5,6,7, which open up a superconducting gap (Δ) below Tc. However, the observation of a pseudogap in the normal phase of the high-Tc copper oxide superconductors8,9 identified a remarkable challenge in our understanding of superconductivity and its origin is still extensively debated. In particular, does the pseudogap represent preformed Cooper pairs, or does it reflect another ground state competing with superconductivity10,11,12? More recently, a pseudogap was also found in the strongly interacting ultracold Fermi gas above the superfluid condensation temperature13. These fascinating results suggest the important role of pairing in the normal phase, above the onset of superfluidity/superconductivity in strongly interacting systems. The existence of a pseudogap state has been discussed in the scheme of BCS-BEC crossover14. Very interestingly, the study on ultracold Fermi gases reported a pseudogap for a system with 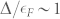Inline graphic13 while the optimally doped copper oxide Bi2212 shows a 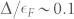Inline graphic7. In a recent study on the Fe(Te,Se) superconductor, it was concluded that the system was in the BCS-BEC crossover regime with a 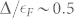Inline graphic associated with a hole band centered at the Γ-point7. The obtained band dispersions were similar to prior studies of the normal phase15,16, while Δ was much smaller than an earlier report which claimed strong coupling superconductivity17. Although a pseudogap is expected based on theories of the BCS-BEC crossover18,19,20,21, no study to date has identified a pseudogap in the momentum resolved electronic structure of Fe(Te,Se). Further, a tuning of the BCS to BEC regimes across the Feshbach resonance using a magnetic field which eventually leads to a change in sign of the chemical potential for fermions21, is well-known in ultracold atomic gases22,23. However, a similar control of the chemical potential in a solid is not possible, and consequently, the BEC superconductivity in a solid has eluded experiments. In the following, we report experiments indicative of composite superconductivity in an iron-based superconductor: Cooper pairing in a hole band coexisting with Bose-Einstein condensation in an electron band.

Results

Electron band lying just above EF

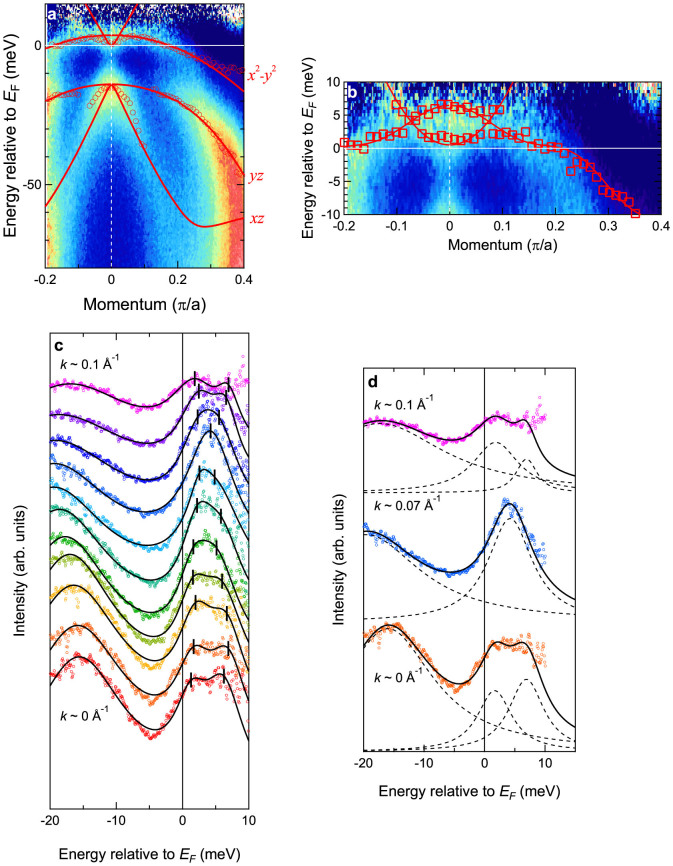
Figure 1(a) shows an intensity plot of E vs. k (energy vs. momentum) measured at 25 K (>Tc = 14.5 K) along Γ-X line in the Brillouin zone of FeTe0.6Se0.4 after dividing by the Fermi-Dirac (FD) function broadened with the Gaussian corresponding to the experimental energy resolution. We employed three different methods to determine the band dispersions: a second derivative map with respect to energy, fitting to the energy distribution curves (EDCs), and fitting to the momentum distribution curves (MDCs) (see Supplementary Information). Three hole bands can be clearly recognized in the second derivative map. Band-structure calculations based on density functional theory (DFT) were carried out for the parent FeTe and are overlaid as solid lines in Fig. 1(a) after a suitable energy shift and rescaling which are ascribed to renormalization effects, as is known from earlier work7,15,16,17. The calculation details and complete band structure are discussed in the Supplementary Information and the energy shifts and rescaling are listed in Table 1. The calculated band structure and orbital characters are also consistent with known results24,25 and were confirmed by measuring the linear polarization dependence of spectral intensities (see Supplementary Information). However, in contrast to the DFT calculations which predict existence of three hole FSs around the Γ point, we find that the band top of the two dominantly xz/yz-orbital derived bands are located around 15 meV below EF, i.e., these bands sink below EF, and only one hole band originating in the x2 − y2 orbital crosses EF. From the degeneracy of the two xz/yz bands, we conclude that kz ~ 0 in the reduced Brillouin zone for the present laser ARPES measurements.

Figure 1. Band dispersions of FeTe0.6Se0.4 along Γ-X line measured at 25 K.

Figure 1

Open in a new tab

(a) Intensity plot of E vs. k measured at 25 K along Γ-X line. The shifted and rescaled DFT result is overlaid as solid lines. The open circles indicate band dispersions deduced from the peak positions of the second derivative spectra. (b) Intensity plot near EF. The open rectangles indicate band dispersions deduced from the fitting to the EDCs. The solid lines are dispersions by fitting to the rectangles with a polynomial function. (c) Fitting to several cuts of EDCs after dividing by the FD function. The solid lines indicate the fitting results. The fitting functions were obtained using three Lorentzians convoluted with the Gaussian corresponding to the experimental energy resolution. (d) Fitting results with the component Lorentzians for three cases, around the Γ point, k ~ 0.07 Å, and k ~ 0.1 Å.

Table 1. Energy shifts and rescaling values required for matching the calculated dispersions with the experimental dispersions.

  shift scale
31 st −130 meV 1/15
30 th −278 meV 1/10
29 th −110 meV 1/4.5
28 th −110 meV 1/12
Open in a new tab

The open circles in Fig. 1(a) show band dispersions deduced from the peak positions of the second derivative spectra shown in Fig. S3. The second derivative map after dividing by the FD function shown in Fig. S3(b) clearly shows that the dispersion around the Γ point is electron-like. The origin of this electronic dispersion is presumably another dominantly xz/yz-orbital derived band, which is located just above EF for the DFT results for the parent FeTe (According to the reported DFT results for FeSe, the electronic disperion is located at ~0.5 eV above EF at the Γ point. Hence, we can expect that the electron band in the DFT regime is located at ~0.2 eV above EF for FeTe0.6Se0.4. This is small enough to be shifted just above EF by a renormalization effect, because the two hole bands which are predicted to make Fermi surfaces by the DFT calculations get shifted below EF). For checking the dispersions above EF, Fig. 1(b) shows the band dispersions in a narrow energy window near EF, and band dispersions deduced from fits to the EDCs are overlaid. The fits to the EDCs, obtained after dividing by the FD function, are shown in Fig. 1(c). It is clear that there are two bands above EF at the Γ-point, which get merged around k ~ 0.07 Å and then again separate out into two bands around k ~ 0.1 Å. Figure 1(d) shows the fits with the component Lorentzian functions for these three cases. We also performed measurements with another sample at higher temperatures of 35 K and 50 K in addition to 25 K as shown in Fig. S7. The peak positions are consistent with those shown in Fig. 1.

In the occupied states below EF, the degenerate band top of the xz/yz hole bands are positioned at ~15 meV below EF. The band top of the EF-crossing x2 − y2 band is located at least above ~6.5 meV from EF at the Γ-point. Most interestingly, we do find the expected electron band existing just above EF at the Γ-point, with the band bottom located at ~0.7 ± 0.2 meV above EF (Fig. 1(b)). This electron band has been missed in all earlier studies of the momentum resolved electronic structure of Fe(Te,Se)7,15,16,17. We note that the x2 − y2 hole band and the electron-like band just above EF may be hybridized due to spin-orbit interactions (However, the spin-orbit interaction of Fe 3d states is ~70 meV, for Se 4p states is ~400 meV, and for Te 5p is ~1 eV32, and all these values are significantly larger than the hole and electron-like dispersions being discussed here), for example, and result in a wing-shaped dispersion. However, even if these two bands are hybridized and merge to a single band, this does not affect our conclusions. Since the nature of the conducting carriers being electron-like or hole-like is determined by the gradient of the band dispersion (∂E/∂k), the carriers at kF and the thermally-excited carriers at the Γ point will be hole-like and electron-like, respectively. Also, the details of electron band at the higher energy region above EF are not relevant to superconductivity. Only the positions of the top of hole band and the bottom of the electron band are important, and they can be evaluated rather clearly from the MDCs, of which line shape is not affect by dividing by the FD function (see Supplementary Information).

Sharp superconducting coherence peak in the electron band just above EF

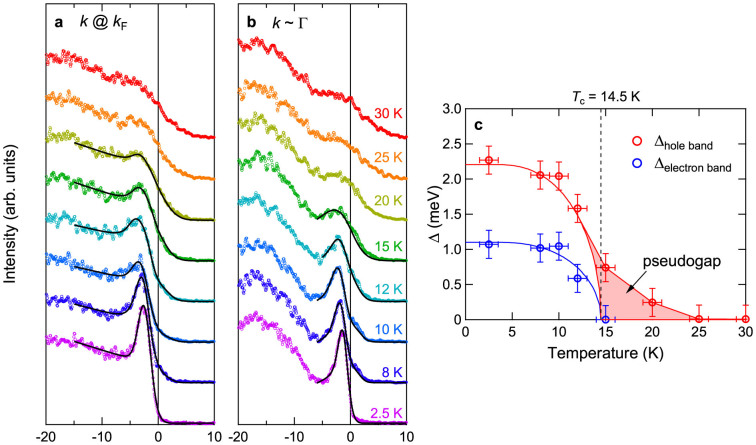
Figures 2(a) and 2(b) show the energy distribution curves (EDCs) after dividing by the FD functions corresponding to each temperature along Γ-X line at T = 25 K (above Tc) and at T = 2.5 K (below Tc), respectively. The open circles in Fig. 2(a) mark the normal-state band dispersions obtained from the second derivative spectra shown in Fig. S3. In Fig. 2(b), we can clearly see that the superconducting coherence peaks emerge below Tc for the hole band. The small circles in Fig. 2(b) mark the positions of the coherence peaks, and they are plotted in the enlarged scale in Fig. S10. Figures 2(c) and 2(d) show the EDCs above Tc (25 K) and below Tc (2.5 K) at k = kF and k ~ Γ, respectively. We can see that the electron band just above EF at the Γ point also shows a sharp superconducting coherence peak, although this band does not cross the EF in the normal state. The solid lines are fits to the BCS spectral function ABCS(k, ω)26,27,28, which can be expressed as

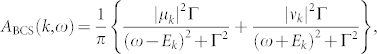graphic file with name srep04109-m5.jpg

where Ek and |uk|2, |vk|2 are the quasiparticle energy and the coherence factors of Bogoliubov quasiparticles (BQPs), respectively. Using the normal-state dispersion 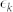Inline graphic with respect to the chemical potential μ and the SC gap Δ(k), Ek can be expressed

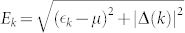graphic file with name srep04109-m7.jpg

and

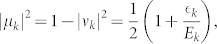graphic file with name srep04109-m8.jpg

respectively. From the fits to the data, we estimate the Bogoliubov quasiparticle energy 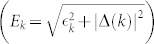Inline graphic of the hole band to be 2.3 meV (= Δ(k), because 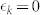Inline graphic at k = kF of this band) and of the electron band to be 1.3 meV, respectively. From the value of 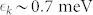Inline graphic, Δ(k) is estimated to be ~1.1 meV for the electron band. This indicates different pairing strengths and reduced gap values 2Δ/kBTc for the electron and hole bands. In addition, 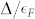Inline graphic for the hole band is estimated to be ~0.3, corresponding to a relatively weak coupling. On the other hand, since the energy position of the electron band is just 0.7 meV (~8 K) above EF, it means that its occupancy in the normal state will strongly depend on temperature. Accordingly, the exact value of 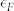Inline graphic of the electron band cannot be described in the usual way. If we regard Tc as a measure of 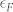Inline graphic, based on the fact that Tc is the lowest temperature representing the normal state (Tc = 14.5 K ~ 1.2 meV), we obtain 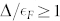Inline graphic, indicative of the strong coupling limit. This estimation may seem to be fairly rough. However, if 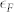Inline graphic equals to Δ, the bottom of the electron band should be located at E = −Δ below EF. Hence, we can say at least 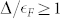Inline graphic. Thus, the electron band with a smaller Δ is actually in the strong-coupling regime. This represents the condition of an electron band with only a small number of carriers, but with a strong pairing interaction and a finite Δ exists for this band. On the otherhand, the hole band with a larger Δ lies in the relatively weaker-coupling regime. It is suggestive of Cooper pairing for the hole band and Boson condensation for the electron band. We note that even for the strong-coupling electron band, we have used a BCS spectral function to estimate the value of Δ. This is not a problem as the obtained value of Δ represent the lower bound of Δ, because a smaller value of 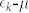Inline graphic for the BEC regime will give a larger value of Δ7,13.

Figure 2. Laser-ARPES spectra of FeTe0.6Se0.4 above and below Tc.

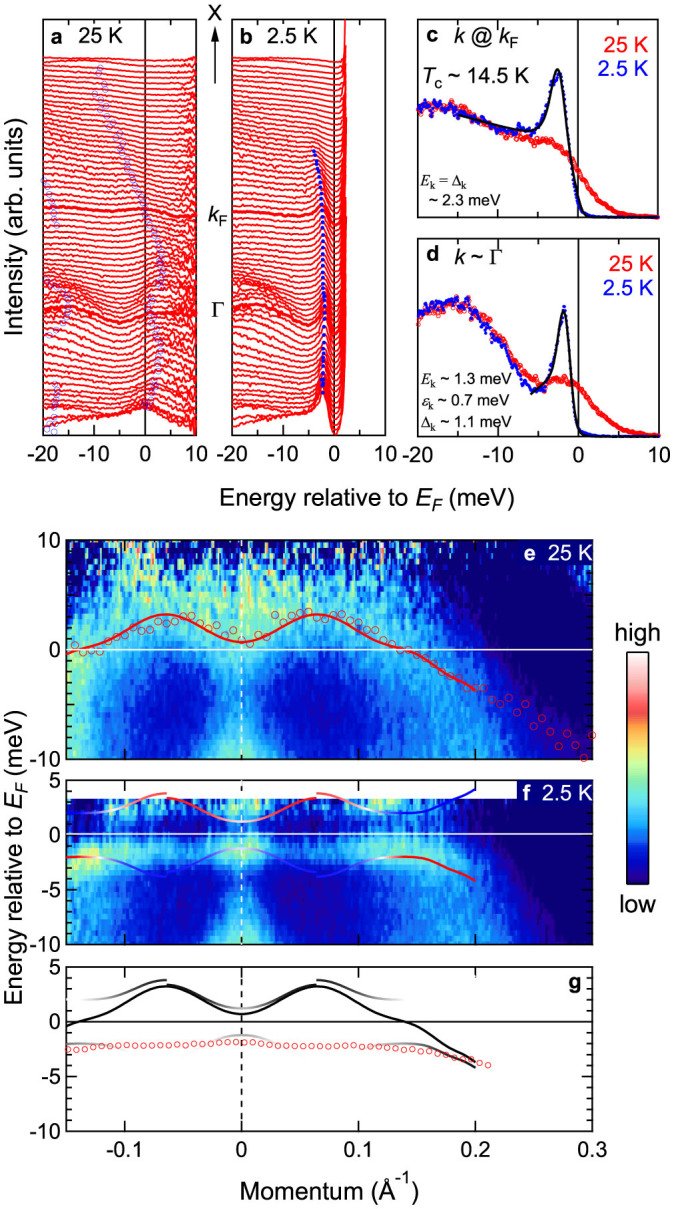
Figure 2

Open in a new tab

FD-divided EDCs along Γ-X direction above Tc (a) and below Tc (b), respectively. EDCs above and below Tc at k = kF (c) and k ~ Γ (d), respectively. The solid lines are the fitting results using the BCS spectral function. Intensity plots of the spectra above Tc (e) and below Tc (f), respectively. The solid line in panel (e) is a fitting result using a polynomial function for the dispersion indicated by the open circles. The solid lines in panel (f) are Bogoliubov quasiparticle (BQP) dispersions using the normal-state dispersion in panel (e) and the SC gap Δ(k) = 2 meV for the hole band and Δ(k) = 1 meV for the electron band, respectively. Colors of the lines correspond to the amplitude of coherence factors |uk|2 and |vk|2. The red and blue regions have larger and smaller coherence factors, respectively. (g) The normal-state and BQP dispersions have been plotted in the same panel. The open circles in panel (g) correspond to the dispersion of the coherence peaks at T = 2.5 K in panel (b). The BQP dispersions merge for the electron and hole bands, indicative of a composite type of BCS-BEC superconductivity.

Figures 2(e) and 2(f) show the intensity maps of the spectra above and below Tc, respectively, after dividing by the corresponding FD functions. The open circles are the same as in Fig. 2(a) and the solid line is a fitting result to the open circles using a polynomial function, representing the normal-state dispersion Inline graphic (Here, the normal state dispersions of the hole and electron bands merge to a single band. This means that these two bands are assumed to be hybridized at the band crossing). The solid lines in Fig. 2(f) are the BQP dispersions using Inline graphic in Fig. 2(e) and the Δk values obtained above for the electron and hole bands. Colors of the lines corresponds to the amplitude of the coherence factors |uk|2 above EF and |vk|2 below EF. The red and blue regions correspond to the higher and lower values, respectively. It is noted that the BQP dispersion does not cross the brightest intensity around the Γ point above EF. This is attributed to the tail of the hole-band top, which is also positioned at the Γ-point. The normal-state and BQP dispersions have been plotted in the same panel of Fig. 2(g). The open circles plotted in Fig. 2(g) correspond to the dispersion of the coherence peaks at T = 2.5 K shown in Fig. 2(b). The gray-scale density of the BQP dispersion corresponds to the amplitude of coherence factors. It is interesting to note that the BQP dispersions merge for the electron and hole bands, indicative of a composite BCS-BEC superconductivity. The results indicate that irrespective of weak or strong coupling, both the hole and electron bands in the superconducting state exhibit Bogoliubov quasiparticle dispersions due to particle-hole mixing29. However, the superconductivity in the electron band can be expected to be very sensitive to the occupancy of the electron band with Se substitution for Te, as well as pressure/strain. This possibly explains the reported large variation in Tc with pressure for FeSe (Tc = 8.5–36.7 K)30.

Discussion

Another difference can be recognized between the weak-coupling hole band and the strong-coupling electron band. Figures 3(a) and 3(b) show the temperature dependence of EDCs at kF for the hole band and k ~ Γ for the electron band, respectively. The black solid lines indicate the fitting results using the BCS spectral function. The estimated SC-gap sizes are shown in Fig. 3(c). The existence of the pseudogap only for the hole band is clearer from the symmetrized EDCs (Fig. S11) or the FD-divided EDCs (Fig. S12). The temperature dependence of the gap opening indicates another important difference for the weaker-coupling hole band compared to the strong-coupling electron band. A pseudogap behavior can be recognized for the weaker coupling hole band in the spectra above Tc (The exsitence of the pseudogap for the hole band can be clearly recognized also from the temperature-dependent symmetrized EDC (see Fig. S9)). However, in strong contrast to the currently available BCS-BEC crossover theory21 which predict existence of a pseudogap in the BEC strong coupling regime, the electron band does not show a pseudogap above Tc (This observation might lead to suspect that the superconducting gap near the Γ point is not originated from the electron band, but just a continuation from the BQP near kF. However, as shown in Fig. S5, the observation of the superconducting coherence peaks well separately at k = kF and the Γ point evidently indicate that the superconducting gap at the Γ point is originated from the electron band just above EF). Thus, we find a coexistence of the weak coupling and strong coupling superconductivity in the same material but with attributes not fully consistent with our present understanding of weak and strong coupling superconductivity. Our study identifies the required band structure for composite superconductivity, which is closely related to Dirac point dispersions, coexisting with a simple electron or hole band as schematically shown in Fig. 4.

Figure 3. Temperature dependence of EDCs at k = kF and k ~ Γ.

Figure 3

Open in a new tab

Temperature dependence of raw EDCs at (a) k = kF of x2 − y2 hole-like band and (b) k ~ Γ (bottom of the electron-like band), respectively. Fitting results with the BCS spectral function are indicated by black solid lines. (c), Temperature dependence of the obtained SC-gap sizes from the fitting to the BCS spectral function. Shaded area indicates pseudogap for the hole-like band.

Figure 4. Schematic band structure showing: a typical electron band, a typical hole band, an electron band lying just above EF, the band structure in the absence of hybridization, and with hybridization showing composite BCS-BEC superconductivity.

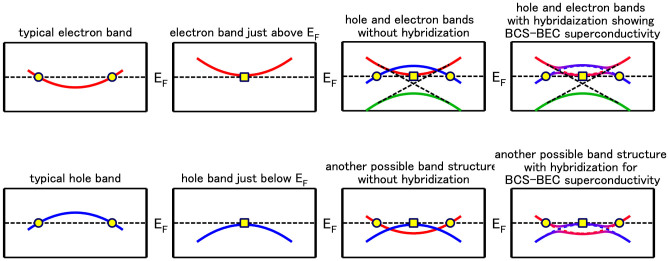
Figure 4

Open in a new tab

Similarly, a hole band lying just below EF and another possible route to BCS-BEC superconductivity. The black dashed lines show similarity to Dirac point dispersion (see also Fig. S1 for relation with band-structure calculations).

Methods

Single crystals of FeTe0.6Se0.4 were prepared by a melt-growth technique. Chemical composition of the grown crystals was determined by electron probe microanalysis (EPMA) and inductively coupled plasma (ICP) atomic emission spectrometry. Details have been described in Ref. 36. ARPES data were collected using the laser ARPES apparatus developed at ISSP with the 6.994 eV, 6th harmonic of Nd:YVO4 quasi continuous wave (q-CW, repetition rate = 120 MHz) laser and VG-Scienta HR8000 electron analyzer28. While this apparatus achieves the maximum energy resolution of 70 μeV, the overall energy resolution was set to ~1.2 meV for the measurements of EDCs and MDCs near EF and 5 meV for E-k map measurements, The angular resolution was 0.1 deg, corresponding to the momentum resolution of 0.0015 Å−1. Polarization of incident excitation laser was adjusted using a half-wave (λ/2) plate and a quarter-wave (λ/4) plate. The EF positions were calibrated by measuring the Fermi edge of a gold film evaporated onto the sample substrate.

Author Contributions

K.O., Y.O., Y.K., T.S. and T.K. developed the laser-ARPES apparatus; S.W. and C.T.C. developed the 7-eV laser system using the nonlinear optical crystal; S.N., T.H. and H.T. grew high-quality single crystals and characterized them; K.O., Y.I. and Y.O. performed the experiments and data analysis; K.O. and A.C. wrote the manuscript; S.S. designed the project; All authors discussed the results and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep04109-s1.pdf (3.9MB, pdf)

Acknowledgments

We would like to thank K. Kuroki and R. Arita for valuable discussions and comments. This research is supported by JSPS through its FIRST Program.

References

  1. Kamihara Y., Watanabe T., Hirano M. & Hosono H. Iron-Based Layered Superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc 130, 3296–3297 (2008). [DOI] [PubMed] [Google Scholar]
  2. Mazin I. I., Singh D. J., Johannes M. D. & Du M. H. Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO1−xFx. Phys. Rev. Lett. 101, 057003 (2008). [DOI] [PubMed] [Google Scholar]
  3. Kuroki K. et al. Unconventional Pairing Originating from the Disconnected Fermi Surfaces of Superconducting LaFeAsO1−xFx. Phys. Rev. Lett. 101, 087004 (2008). [DOI] [PubMed] [Google Scholar]
  4. Kontani H. & Onari S. Orbital-Fluctuation-Mediated Superconductivity in Iron Pnictides: Analysis of the Five-Orbital Hubbard-Holstein Model. Phys. Rev. Lett. 104, 157001 (2010). [DOI] [PubMed] [Google Scholar]
  5. Lu D. H. et al. Electronic structure of the iron-based superconductor LaOFeP. Nature 455, 81–84 (2008). [DOI] [PubMed] [Google Scholar]
  6. Zabolotnyy V. B. et al. (π, π) electronic order in iron arsenide superconductors. Nature 457, 569–572 (2009). [DOI] [PubMed] [Google Scholar]
  7. Lubashevsky Y., Lahoud E., Chashka K., Podolsky D. & Kanigel A. Shallow pockets and very strong coupling superconductivity in FeSexTe1−x. Nat. Phys. 8, 309–312 (2012). [Google Scholar]
  8. Ding H. et al. Spectroscopic evidence for a pseudogap in the normal state of underdoped high-Tc superconductors. Nature 382, 51–54 (1996). [Google Scholar]
  9. Loeser A. G. o. Excitation Gap in the Normal State of Underdoped Bi2Sr2CaCu2O8+Δ. Science 273, 325–329 (1996). [DOI] [PubMed] [Google Scholar]
  10. Lee W. S. et al. Abrupt onset of a second energy gap at the superconducting transition of underdoped Bi2212. Nature 450, 81–84 (2007). [DOI] [PubMed] [Google Scholar]
  11. Yang H.-B. et al. Emergence of preformed Cooper pairs from the doped Mott insulating state in Bi2Sr2CaCu2O8+Δ. Nature 456, 77–80 (2008). [DOI] [PubMed] [Google Scholar]
  12. Kondo T., Khasanov R., Takeuchi T., Schmalian J. & Kaminski A. Competition between the pseudogap and super-conductivity in the high-Tc copper oxides. Nature 457, 296–300 (2009). [DOI] [PubMed] [Google Scholar]
  13. Gaebler J. P. et al. Observation of pseudogap behaviour in a strongly interacting Fermi gas. Nat Phys 6, 569–573 (2010). [Google Scholar]
  14. Chen Q., Stajic J., Tan S. & Levin K. BCS-BEC crossover: From high temperature superconductors to ultracold superfluids. Physics Reports 412, 1–88 (2005). [Google Scholar]
  15. Chen F. et al. Electronic structure of Fe1.04Te0.66Se0.34. Phys. Rev. B 81, 014526 (2010). [Google Scholar]
  16. Tamai A. et al. Strong Electron Correlations in the Normal State of the Iron-Based FeSe0.42Te0.58 Superconductor Observed by Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 104, 097002 (2010). [DOI] [PubMed] [Google Scholar]
  17. Nakayama K. et al. Angle-Resolved Photoemission Spectroscopy of the Iron-Chalcogenide Superconductor Fe1.03Te0.7Se0.3: Strong Coupling Behavior and the Universality of Interband Scattering. Phys. Rev. Lett. 105, 197001 (2010). [DOI] [PubMed] [Google Scholar]
  18. Eagles D. M. Possible Pairing without Superconductivity at Low Carrier Concentrations in Bulk and Thin-Film Superconducting Semiconductors. Phys. Rev. 186, 456–463 (1969). [Google Scholar]
  19. Leggett A. Modern trends in the theory of condensed matter. Springer-Verlag, Berlin, (1980). [Google Scholar]
  20. Randeria M., Duan J.-M. & Shieh L.-Y. Bound states, Cooper pairing, and Bose condensation in two dimensions. Phys. Rev. Lett. 62, 981–984 (1989). [DOI] [PubMed] [Google Scholar]
  21. Sá de Melo C. A. R., Randeria M. & Engelbrecht J. R. Crossover from BCS to Bose superconductivity: Transition temperature and time-dependent Ginzburg-Landau theory. Phys. Rev. Lett. 71, 3202–3205 (1993). [DOI] [PubMed] [Google Scholar]
  22. Timmermans E., Furuya K., Milonni P. W. & Kerman A. K. Prospect of creating a composite Fermi-Bose superfluid. Physics Letters A 285, 228–233 (2001). [Google Scholar]
  23. Regal C. A., Greiner M. & Jin D. S. Observation of Resonance Condensation of Fermionic Atom Pairs. Phys. Rev. Lett. 92, 040403 (2004). [DOI] [PubMed] [Google Scholar]
  24. Subedi A., Zhang L., Singh D. J. & Du M. H. Density functional study of FeS, FeSe, and FeTe: Electronic structure, magnetism, phonons, and superconductivity. Phys. Rev. B 78, 134514 (2008). [Google Scholar]
  25. Miyake T., Nakamura K., Arita R. & Imada M. Comparison of Ab initio Low-Energy Models for LaFePO, LaFeAsO, BaFe2As2, LiFeAs, FeSe, and FeTe: Electron Correlation and Covalency. J. Phys. Soc. Jpn 79, 044705 (2010). [Google Scholar]
  26. Matsui H. et al. BCS-Like Bogoliubov Quasiparticles in High-Tc Superconductors Observed by Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 90, 217002 (2003). [DOI] [PubMed] [Google Scholar]
  27. Shimojima T. et al. Orbital-Independent Superconducting Gaps in Iron-Pnictides. Science 332, 564 (2011). [DOI] [PubMed] [Google Scholar]
  28. Okazaki K. et al. Octet-Line Node Structure of Superconducting Order Parameter in KFe2As2. Science 337, 1314–1317 (2012). [DOI] [PubMed] [Google Scholar]
  29. Campuzano J. C. et al. Direct observation of particle-hole mixing in the superconducting state by angle-resolved photoemission. Phys. Rev. B 53, R14737–R14740 (1996). [DOI] [PubMed] [Google Scholar]
  30. Medvedev S. et al. Electronic and magnetic phase diagram of β-Fe1.01Se with superconductivity at 36.7 K under pressure. Nature Mater 8, 630–633 (2009). [DOI] [PubMed] [Google Scholar]
  31. Hanaguri T., Niitaka S., Kuroki K. & Takagi H. Unconventional s-Wave Superconductivity in Fe(Se, Te). Science 328, 474–476 (2010). [DOI] [PubMed] [Google Scholar]
  32. Herman F. & Skillman S. Atomic structure calculations. Prentice-Hall, New Jersey, (1963). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep04109-s1.pdf (3.9MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES