Abstract
A force-velocity relationship in overarm throwing was determined using ball weights varying from 0.2 to 0.8 kg. Seven experienced handball players were filmed at 240 frames per second. Velocity of joints of the upper extremity and ball together with the force on the ball were derived from the data. A statistically significant negative relationship between force and maximal ball velocity, as well as between ball weight and maximal ball velocity was observed. Also, with increase of ball weight the total throwing movement time increased. No significant change in relative timing of the different joints was demonstrated, suggesting that the subjects did not change their “global ”coordination pattern (kinematics) within the tested range of ball weights. A simple model revealed that 67% of ball velocity at ball release was explained by the summation of effects from the velocity of elbow extension and internal rotation of the shoulder. With regard to the upper extremity the internal rotation of the shoulder and elbow extension are two important contributors to the total ball velocity at release.
Key Points.
An inverse relationship between load and velocity and a linear force-velocity exists in overarm throwing with ball weights varying from 0.2 to 0.8 kg.
Qualitatively, no changes in coordination pattern (relative timing) occur with increasing ball weight within the tested range of ball weights.
The absolute throwing movement time increased with ball weight.
Quantitatively, with regard to the upper extremity, the internal rotation of the shoulder and elbow extension are two important contributors to the total ball velocity at release.
Key Words: Kinematics, handball, ball weight, proximal distal sequence
Introduction
In many movements, resistance (load) and velocity are inversely related to each other. This relationship is often ascribed to skeletal muscle properties. Hill (1938) described an hyperbolic relationship between force and velocity for isolated muscles (often referred to as the Hill curve). Many other researchers in muscle physiology as well as researchers in the more applied sciences used this relationship to describe and explain phenomena of muscle contraction. In sport science, many training experiments, set up to enhance the performance of the athlete, are based on Hill’s force-velocity relationship (e.g. Kaneko et al., 1983; Komi and Häkkinen, 1988). By prescribing a particular speed or resistance, specific effects along the force-velocity description of movement is expected.
For overarm throwing, several studies showed that by increasing ball weight ball velocity at release decreases (Toyoshima and Miyashita, 1973; Kunz, 1974; Toyoshima et al., 1976; Cross, 2004). Toyoshima and Miyashita (1973) and Toyoshima et al. (1976) determined the relationship between maximal ball velocity and ball weight using ball weights varying from 0.1 to 0.5 kg. Kunz (1974) and Cross (2004) used a larger domain of ball weights varying from respectively 0.08 to 0.8 kg and 0.057 to 3.4 kg, but with a low resolution (0.08, 0.4 and 0.8 kg; Kunz, 1974) or with a different shape and weight intervals between the different balls (0.057, 0.16, 0.20, 0.73, 1.42, 2.10 and 3.4 kg; Cross, 2004).
Several researchers studied the contribution of the body segments to the throwing performance. Toyoshima and Miyashita (1973) showed that by constraining more body segments during the throwing task, the maximal ball velocity decreases in the whole range of ball weights that were used. To our knowledge no data are available regarding changes in coordination due to ball weights with the same shape. Fleisig et al. (1996) compared the kinematics and kinetic of baseball pitching with football passing. No relationship between force production and movement velocity was described in these studies (Toyoshima and Miyashita, 1973; Kunz, 1974; Toyoshima et al., 1976). Thus, the aim of this study was to investigate the force-velocity relationship in overarm throwing of experienced throwers with different ball weights of the same shape. The description was to be expressed as ball velocity and force applied to the ball, not merely ball weight. In this form, a description would reveal more information regarding neuromuscular characteristics. It was hypothesized that the force-velocity relationship was linear over the range of ball weights tested in this study. Furthermore, it was the aim to examine if coordination of the throwing technique changes due to these different ball weights. It was hypothesized that the experienced subjects would demonstrate differences in key upper body kinematic variables such as maximal velocity of the different joints of the upper extremity. A possible lack of coordinative changes would indicate the importance of muscular force-velocity properties for such explosive movements as the overarm throw.
Methods
Subjects
Seven subjects participated in this experiment. The subjects were experienced male handball players, playing in the second division of the Norwegian national competition (mean age 25 ± 2.5 years, weight: 84.4 ± 9.9 kg., height: 1.84 ± 0.08 m.). All the subjects in this study were right-handed. Experienced team handball players were chosen in order to avoid the possible effect of inadequate coordination patterns on the findings, i.e. a coordination pattern that is not categorized as a fully developed coordination pattern (Roberton, 1977).
The study complied with the requirements of the local Committee for Medical Research Ethics and current Norwegian law and regulations.
Procedure
After a general warm-up of 15 minutes, throwing performance was tested in an overarm throw towards a target at four meters distance. The subjects performed a standing throw with holding the front foot on the floor during throwing (Figure 1). The instruction was to throw as fast as possible aiming at a 0.5 by 0.5 m square target at 1.65 m height. The subjects threw 5 times randomly with each of 7 different weight adjusted javelin balls (circumference 0.3 m; weights 0.206, 0.305, 0.409, 0.503, 0.616, 0.706 and 0.818 kg). They were not informed about the ball weight during the test.
Figure 1.
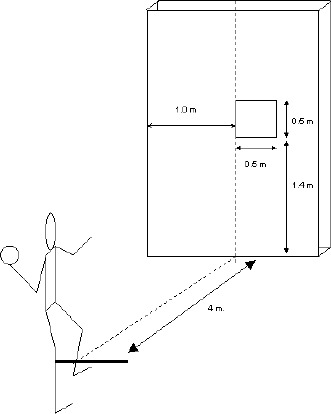
Experimental set-up. Subject at a 4-meter distance from the target drawn on a large mattress that avoids the balls bouncing back toward the subject.
Measurements
The displacements in time of the different segments of the body were recorded at a sample rate 240 Hz using a 3D digital video movement analysis system positioned in half circle around the throwing position (Qualysis, Sävedalen, Sweden,). The positions of the 5 cameras were placed in a matter that it could cover an area of 4 by 2 by 3m. Reflective markers (2.6 cm diameter) were used to identify the following anatomical landmarks:
Hip: trochanter major on the side of the throwing arm
Shoulder: lateral tip of the acromion on the side of the throwing arm
Elbow: lateral epicondyle of the throwing arm
Wrist: styloid process of the ulna of the throwing arm
Ball: the ball was taped with reflective tape, which made is possible to identify the centre of the ball during the attempts.
It was not possible to identify a marker on a finger, as the ball and finger marker were to close to each other. Computation of velocity of the different joints and the ball was done using a five point differential filter (van den Tillaar and Ettema, 2003a; 2003b). The force on the ball was calculated by differentiating velocity which was then multiplied by the ball mass. The velocity at ball release and the moment of release were derived from the change in distance between the wrist and the ball. At the moment the ball leaves the hand the distance between the wrist marker and the ball marker increases abruptly and dramatically.
The total movement time of the throw was defined by the time at which the hip reached the maximal linear velocity (begin of the throw) and the time at which the ball released the hand. Maximal hip velocity was taken as an early and clearly identifiable moment in the goal directed movement. This was done because the actual onset of goal directed movement was hard to identify. Furthermore, at about this moment, the ball velocity started to increase dramatically (Figure 4; van den Tillaar and Ettema, 2000; 2002). Timing of events was presented as time before ball release.
Figure 4.
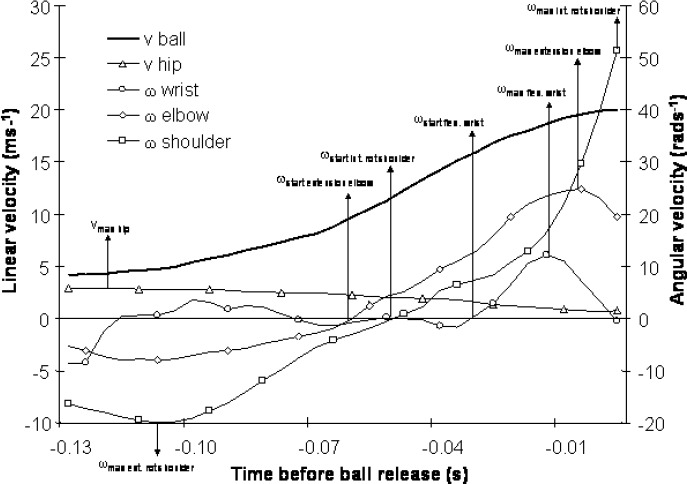
A typical example of development of linear of the hip segment, ball, and angular velocity of the wrist (○), the elbow (◊) and ext/int rotation of the shoulder (□) in time before ball release (the symbols indicate different signals and not points of measurements).
The angular movement of elbow extension and flexion of wrist were derived from relative positions between shoulder, elbow, and wrist marker and between elbow, wrist, and ball marker, respectively. External and internal rotation of the shoulder were derived from positions of shoulder, elbow and wrist marker: the orthogonal coordinate system was first translated to centre the system in the shoulder (origin); subsequently, it was rotated to align the shoulder-elbow line with the x-axis; the shoulder rotation angle was calculated as the angle between the shoulder-elbow-wrist plane and the horizontal plane.
Statistics
To assess effects of ball weight on velocity of the ball and joints, as well as timing, a one-way ANOVA for repeated measures was used. Polynomial contrasts analysis was used to identify trend characteristics. For the force-velocity relationship a linear regression procedure was employed.
Results
The total movement time increased and ball velocity decreased significantly with increased ball weight (F(6,36) = 2.95; p = 0.017 Figure 2A; (F(6,36) = 134; p < 0.001 Figure 2B, respectively). Each subject showed a significant negative linear relationship for ball velocity against both ball weight (F(1,5) ≥ 103; p < 0.001, r ≥ 0.98) and applied force (F(1,5) < 14; p < 0.012, r ≥ 0.87). When all observations were used in a pooled manner, i.e. irrespective of subject, still a linear relationship for ball velocity against both ball weight (F(1,236) = 510; p < 0.001, r = 0.83) and applied force (F(1,226) = 156; p < 0.001, r = 0.64) (Figure 3 inset) was found.
Figure 2.
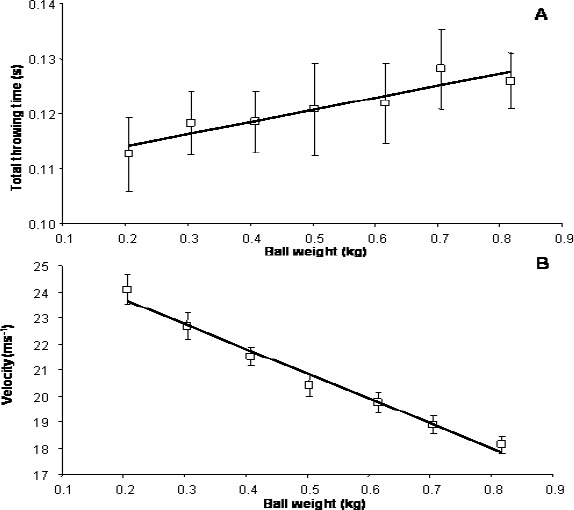
Relationship between ball weight and total throwing time (A) and release velocity (B) averaged over all subjects. Vertical bars indicate standard error of the mean (SEM).
Figure 3.
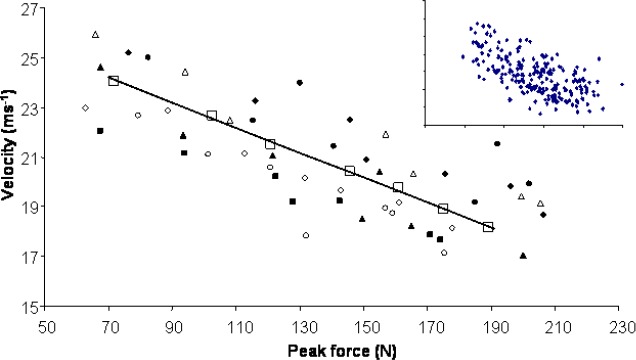
Relation between peak forces on the ball and release velocity of the ball Symbols indicate subjects; mean data are indicated by (□). Inset: all observations.
Joint velocity
Figure 4 shows the development of angular velocity of the different joints and linear velocity of the hip and ball over time. The vertical lines indicate the time at which the hip segment (start of movement) and different joints reached the maximal linear velocity and angular velocity during the throw.
Maximal velocity of wrist flexion (F(6,30) = 3.73; p = 0.007), elbow extension (F(6,36) = 17.28; p < 0.001), and internal rotation of the shoulder (F(6,18) = 6.33; p = 0.001), as well as the angle of the elbow joint at ball release (F(6,24) = 2.84; p = 0.031) were affected by the increase of ball weight. Tests for polynomial contrasts revealed that all joints aspects showed a significant negative linear trend (Figure 5; p < 0.04).
Figure 5.
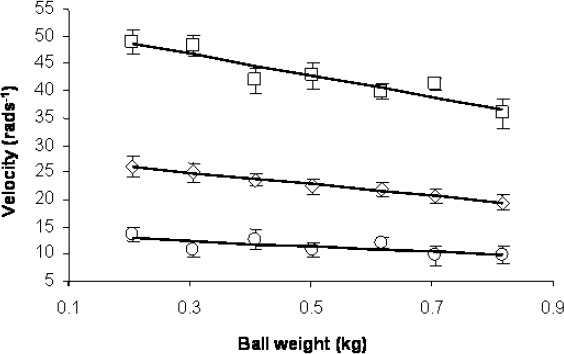
Relation between ball weight and maximal angular velocity of the flexion of the wrist (○), extension of the elbow (◊), and internal rotation of the shoulder (□), averaged over all subjects with SEM.
Timing
As already mentioned before, the total time of the throwing movement increased with ball weight (Figure 2A). Also the time before ball release increased for the occurrence of initiation of the internal rotation of the shoulder (F(1,5) = 23.17; p < 0.005) and elbow extension (F(1,6) = 11.37; p = 0.015). However, initiation of the wrist flexion (F(1,6) = 1.91; p = 0.216), time of maximal extension elbow (F(1,6) = 0.328; p = 0.59) and time of maximal flexion wrist (F(1,6) = 1.65; p = 0.247), did not show a significant relationship with ball weight (Figure 6A).
Figure 6.
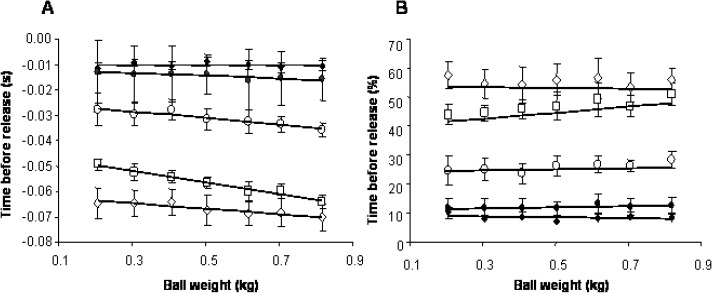
Mean values and sem (n=7) of (A) absolute time before ball release and (B) relative time of the initiation of the internal rotation of the shoulder (□), elbow extension (◊) and wrist flexion (○) together with occurrence of the maximal angular velocity of the elbow extension (♦) and wrist flexion (●).
Whereas time before ball release increased for maximal angular velocities (Figure 6A), in accordance with total movement time (Figure 2A), no ball weight effects were apparent for relative timing, i.e. time of event over total movement time within the tested range of ball weights (Figure 6B).
Discussion
The objective of this study was to investigate the relationship between load and velocity in overarm throwing, as well as the effect of ball weight on coordination patterns of the overarm throw. The results confirm earlier studies (Toyoshima and Miyashita, 1973; Kunz, 1974; Toyoshima et al., 1976) and indicate that an inverse relationship between load and velocity exists for the range of ball weights tested in this study. In other words, high ball velocities are obtained with low load (ball weight) requiring less force exertion. The maximal angular velocities of the different joints decreased with increasing ball weight. The absolute throwing movement time increased with ball weight. No significant trends or changes in relative timing were notified in this study.
Force-velocity
A significant linear force-velocity relationship per subject was found for the range of ball weights (Figure 3). Kaneko et al. (1983) found a curvi-linear relationship. The discrepancy may be explained by the small range of ball weight, which results in a small range of force production. In anyway, the force-velocity relationship, demonstrated in this study has strong resemblance with the classic force-velocity curve for isolated muscle as described by Hill in 1938. It should be noted that this curve does not represent the relationship between force and velocity during a movement in one joint. Rather, for several movements in several joints in which one parameter was systematically altered (ball weight), standard points in the time traces of two variables (maximal force and velocity) were determined and plotted against each other. Although the force-velocity curves for throwing and isolated muscle contraction may be similar, the systems and actions from which these performance curves arise are quite different (e.g., complexity of the movement, the number of factors [e.g. motivation, muscle activity levels, muscle synergies and coordination] and system elements [e.g. nervous system, various muscles and joints] that are involved). One should therefore take extreme care by interpreting the current force-velocity curve as being mainly determined by muscle properties. Still the overall coordination pattern (relative timing) seems independent of load. For example, no changes in the relative timing of the different joints were found in ball weights ranged from 0.2 to 0.8 kg. The observed power of this relative timing of the different joints varied from 0.22 to 0.49. This was rather low as was expected with only 7 subjects. However, correlations per subject over all throws between relative timing of the different joints and ball weight did not show any significant relationship. Some subjects showed a positive relationship while others showed a negative one. This possibly explains the low power together with the low number of subjects. No changes in the relative timing of the different joints were also found in an earlier study (van den Tillaar and Ettema 2000, 2003a, b) regarding effects of instructions, which emphasise on accuracy velocity or both. Thus, with reservation, one may suggest that a force-velocity curve was obtained for a single synergistic musculoskeletal system in overarm throwing with an unaltered neural input. It should be noted that, although the effort was maximal, the muscular effort might not have been maximal. As the time to build up a maximal contractile state may have exceeded the total time available to do so in all muscles in a rapid movement as an overarm throw (Bobbert and van Ingen Schenau, 1990). Future studies, including for example electromyography, may elucidate if with varying ball weight the neural input and muscular coordination pattern is unaltered and if maximal contractile state is affected by the short duration of muscular activation.
The maximal velocity at ball release with the different balls were comparable with the release velocity in football passing (Fleisig et al, 1996) and 3 to 5 ms-1 faster than throws of novices with ball weights varying from 0.2 to 0.73 kg (Cross, 2004). In the study of Fleisig et al (1996) the subjects were college and high school quarterbacks with the same weight and height as the subjects in this study. Both throw balls of the amount of 0.409 (this study) and 0.43 kg (Fleisig et al., 1996) with respectively 21.5 and 21 ms-1. However, when the kinematics between the two studies was compared it is shown that the football players were allowed to take a preliminary stride. The football players also performed the throws with a higher maximal elbow extension (30.72 rads-1 vs. 23.53 rads-1) and a higher maximal internal rotation of the shoulder (86.4 rads-1 vs. 42.8 rads-1). The difference in maximal internal rotation of the shoulder is explainable by the time at which this was measured. In this study the point of maximal internal rotation of the shoulder was taken at ball release even when the maximal velocity increased after ball release. This was done, because all movements after ball release do not contribute to an increase of ball velocity. In the study of Fleisig et al (1996) the maximal internal rotation was 6 % after ball release. The timing of the maximal elbow extension of the two studies was on exactly the same time 0.010 before ball release.
In Figure 4 it was shown that the maximal internal rotation of the shoulder occurred at ball release and that the maximal extension of the elbow occurred on average only 0.010 seconds before ball release. The angular velocity of these two joints (mean: 42.5 rads-1: internal rotation shoulder, 22.7 rads-1: extension elbow) was also much higher than the angular velocity of the wrist joint (11.3 rads-1). These findings indicate the importance of these different joints to the total contribution of the ball velocity. Ball velocity can, in principle, be calculated from the joint velocities at ball release. However, the different joint velocities lead to ball velocity in a complex interactive manner. For example, elbow extension and internal rotation independently create ball velocity in perpendicular directions. Therefore, these two joint movements (along with others) must be coordinated well to optimise ball velocity.
Still, in a first approximation, one can estimate the potential contribution of elbow extension, and internal shoulder rotation according to:
D being distance from elbow to ball (approx. forearm length), α joint velocity and ω joint angle. The angular velocity of the wrist is not included as it approaches zero at ball release (see Figure 4).
Equation (1) is the resultant vector of the two vectors obtained from elbow extension and the internal shoulder rotation. Equation (1) can be transformed to obtain relative contribution of elbow extension and shoulder rotation together by taking the ratio of the components over total ball velocity and the ball velocity relative to the shoulder marker. This last analysis was performed to obtain only the contribution of the upper extremity and not of the trunk rotation.
On average, the model explains that about 67% (± 9%) of total ball velocity at ball release was contributed by the internal rotation of the shoulder and extension of the elbow. The contribution increased significantly to 73% (± 11%) when the modelled velocity was compared with the ball velocity relative to the shoulder marker. It should be noted that the model assumed a perfect transfer of joint velocity to ball velocity. As mentioned above, this is not likely. Thus, the 67% contribution of the internal rotation of the shoulder and extension of the elbow to the total ball velocity at release is likely overestimated, but still remains extremely high. Other significant contributions could come from maximal angular velocity of shoulder horizontal adduction, shoulder abduction, forearm supination, upper torso rotation, forward trunk tilt and pelvis rotation (Matsuo, et. al. 2001). However, in this study the torso rotation, forward trunk tilt and pelvis rotation only contribute very little (6%) since the ratio of the modelled velocity and the ball velocity relative to the shoulder marker only increases 6 % compared with the total ball velocity at ball release. This was to be expected as the subjects had to throw from the spot without lifting their front foot, which is normal for handball players when they have to take a penalty throw. Thus, the other 27 % of could come from maximal angular velocity of shoulder horizontal adduction, shoulder abduction, forearm supination and wrist flexion. However, wrist flexion can only contribute to minor extend (given the leverage of the hand and maximal wrist flexion speed as found in this study). It should be noted that these data do not indicate that maximal ball speed can be obtained by merely using internal rotation and elbow extension. It is not unlikely that these joints obtain these high speeds by making use of slower movements in other joints in a chain of segments earlier in the throwing movement.
Proximal distal sequence
In earlier studies on overarm throwing in handball, a proximal-distal sequence was found (Jöris et. al., 1985; Tuma and Zahalka, 1997). The proximal-distal sequence is the phenomenon of a time lag between movements of proximal and distal joints and segments, where the distal movements are delayed with regard to the proximal movements. Herring and Chapman (1992) showed that the proximal-distal sequence in timing of the segments may be due to anatomical-mechanical principles and appeared to be the most effective strategy in reaching high throwing speeds. In the present findings not all movement characteristics were conform this principle. For example, the onset of the elbow extension preceded the onset of the internal shoulder rotation, (Figure 4 and Figure 6A). Hong et al. (2001) also stated that the onset of torques was not strictly in a successive proximal-distal order. Hong et al. (2001) found that the forearm extensors and the internal rotators were recruited at almost the same time and kept acting until shortly before release. Another characteristic found here (Figure 4 and Figure 6A) and by Hong et al. (2001) that are not in line with the proximo-distal sequence is the earlier occurrence of maximal angular velocity of the wrist than that of elbow extension. This early wrist flexion may be explained by the bi-articular function of the wrist flexors. The flexor carpi ulnaris and - radialis have a flexor moment on the elbow and a flexor moment in the wrist (Ettema, Styles, and Kippers, 1998). Thus, wrist flexion may be enhanced by the strong elbow extension if these wrist flexors are active and by doing so counteract the original elbow extension movement. Also the role of the wrist flexion can explain the timing. As already mentioned earlier, wrist flexion contributes only for a very small amount to the total throwing velocity, but may be more important for throwing accuracy (e.g. Hore et al., 1995).
Conclusions
In conclusion it can be stated that there is a linear force-velocity relationship in overarm throwing with ball weights varying from 0.2 to 0.8 kg. Qualitatively, no changes in coordination pattern (relative timing) occur with increasing ball weight within the tested range of ball weights Quantitatively, with regard to the upper extremity, the internal rotation of the shoulder and elbow extension are two important contributors to the total ball velocity at release.
Biographies

Roland van den TILLAAR
Employment
Associated researcher, Human Movement Science Section, Norwegian University of Science and Technology, Trondheim, Norway
Degree
PhD
Research interests
Coordination and mechanics of fast discrete complex movements (throwing), sprint training, biomechanics and physiology of strength training, whole-body vibration training.
E-mail: rolandv@svt.ntnu.no

Gertjan ETTEMA
Employment
Senior lecturer in Human Movement Science Section, Norwegian University of Science and Technology, Trondheim, Norway.
Degree
PhD
Research interests
Biomechanics and motor control in ski-jumping, neuromuscular constraints in human motor skills, biomechanics and physiology of strength training, modeling muscle contraction.
E-mail: gertjane@svt.ntnu.no
References
- Bobbert M., van Ingen Schenau G.J. (1990) Isokinetic plantar flexion: experimental results and model calculations. Journal of Biomechanics 23, 105-119 [DOI] [PubMed] [Google Scholar]
- Cross R. (2004) Physics of overarm throwing. American Journal of Physics, 72, 305-312 [Google Scholar]
- Ettema G.J.C., Styles G., Kippers V. (1998) The moment arms of 23 muscle segments of the upper limb with varying elbow and forearm positions: Implications for motor control. Human Movement Science 17, 201-220 [Google Scholar]
- Fleisig G.S., Escamilla R.F., Andrews J.R., Matsuo T., Satterwhite Y., Barentine S.W. (1996) Kinematic and kinetic comparison between baseball pitching and football passing. Journal of Applied Biomechanics, 12, 207-224 [Google Scholar]
- Herring R.M., Chapman A.E. (1992) Effects of changes in segmental values and timing of both torque and torque reversal in simulated throws. Journal of Biomechanics 25, 1173-1184 [DOI] [PubMed] [Google Scholar]
- Hill A.V. (1938) The heat of shortening and dynamic constants of muscle. Proceedings of the Rohal Society Series B 126, 136-195 [Google Scholar]
- Hong D., Cheung T.K., Roberts E.M. (2001) A three-dimensional, six-segment chain analysis of forceful overarm throwing. Journal of Electromyography and Kinesiology 11, 95-112 [DOI] [PubMed] [Google Scholar]
- Hore J., Watts S., Martin J., Miller B. (1995) Timing of finger opening and ball release in fast and accurate overarm throws. Experimental Brain Research 103, 277-286 [DOI] [PubMed] [Google Scholar]
- Jöris H.J.J., Edwards, van Muijen A.J., van Ingen Schenau G.J., Kemper H.C.G. (1985) Force velocity and energy flow during the overarm throw in female handball players. Journal of Biomechanics 18, 409-414 [DOI] [PubMed] [Google Scholar]
- Kaneko M., Fuchimoto T., Toji H., Suei K. (1983) Training effect of different loads on the force-velocity relationship and mechanical power output in human muscle. Scandinavian Journal of Sports Sciences 5, 50-55 [Google Scholar]
- Komi P.V., Häkkinen K. (1988) Strength and power. The Olympic book of sports medicine; volume I of the encyclopaedia of sport medicine. Dirix A., Knuttgen H.G., Tittel K.Oxford: Blackwell Scientific Publications; 181-193 [Google Scholar]
- Kunz H. (1974) Effects of ball mass and movement pattern on release velocity in throwing. Biomechanics IV. Nelson R.C., Morehouse C.A.Baltimore, MD: University Park Press; 163-168 [Google Scholar]
- Matsuo T., Escmilla R.F., Fleisig G.S., Barrentine S.W., Andrews J.R. (2001) Comparison of kinematic and temporal parameters between different pitch velocity groups. Journal of Applied Biomechanics, 17, 1-13 [Google Scholar]
- Roberton M. A. (1977) Stability of stage categorizations across trails: implications for the ‘stage theory’ of overarm throw development. Journal of Human Movement Studies 1, 49-59 [Google Scholar]
- Toyoshima S., Hoshikawa T., Miyashita M., Oguri T. (1976) Contribution of the body parts to throwing performance. Biomechanics V-B. Komi P.V.Baltimore, MD: University Park Press; 169-174 [Google Scholar]
- Toyoshima S., Miyashita M. (1973) Force-velocity relation in throwing. Research Quarterly 44, 86-95 [PubMed] [Google Scholar]
- Tuma M., Zahalka F. (1997) Three dimensional analysis of jump shot in handball. Acta Universitatis Carolinae Kinanthropologica 33, 81-86 [Google Scholar]
- Van den Tillaar R., Ettema G. (2000) Influence of instruction on velocity and coordination of overarm throwing in handball. Current research in motor control. Raczek J., Wakiewicz Z., Juras G.Katowice: Interaktiv SC; 210-214 [Google Scholar]
- Van den Tillaar R., Ettema G. (2002) The proximal-distal sequence in overarm throwing and the effect of ball weight. proceedings CD of the IV World congress of biomechanics, Calgary, 4-9 August 2002. Calgary: Omnipress [Google Scholar]
- Van den Tillaar R., Ettema G. (2003a) Influence of instruction on velocity and accuracy of overarm throwing. Perceptual and Motor Skills 96, 423-434 [DOI] [PubMed] [Google Scholar]
- Van den Tillaar R., Ettema E. (2003b) Instructions emphasizing velocity, accuracy, or both in performance and kinematics of overarm throwing by experienced team handball players. Perceptual and Motor Skills 97, 731-742 [DOI] [PubMed] [Google Scholar]


