Abstract
Objectives
To show the effects of chance on meta-analyses, and the potential dangers of being prompted to do a meta-analysis by one favourable trial.
Design
In total, 100,000 trials were simulated and combined into 10,000 meta-analyses, using data from the control group of a cancer trial. Each participant record was randomly coded to simulate allocation to ‘treatment’ or ‘control’.
Setting
Simulated study.
Participants
De-identified records for 578 patients from the control group of a cancer trial, of whom 147 had died.
Main outcome measure
Time to death from any cause.
Results
Of the 100,000 trials, 4897 (4.9%) were statistically significant at 2p < 0.05 and 123 (1.2%) of the 10,000 meta-analyses were significant at 2p < 0.01. The most extreme result was a 20% reduction (99% CI: 0.70–0.91; 2p = 0.00002) in the annual odds of dying in the ‘treatment’ group. If a meta-analysis contained at least one trial with a statistically significant result (at 2p < 0.05), the likelihood of the meta-analysis being significant (at 2p < 0.01) increased strikingly. For example, among the 473 meta-analyses in which the first trial in a batch of 10 was statistically significant (at 2p < 0.05), 18 (3.8%) favoured treatment at 2p < 0.01.
Conclusions
Chance can influence the results of meta-analyses regardless of how well they are conducted. Researchers should not ignore this when they plan a meta-analysis and when they report their results. People reading their reports should also be wary. Caution is particularly important when the results of one or more included studies influenced the decision to do the meta-analysis.
Keywords: Systematic reviews, meta-analysis, randomized trials, statistical analysis, chance
Introduction
In the two previous D.I.C.E. papers,1,2 attention was drawn to how chance might influence the results of randomised trials and to the need for chance effects to be kept in mind by people doing trials and using their findings, using the expanded acronym ‘Don’t Ignore Chance Effects’. In the research reported here, we turn our attention to systematic reviews and meta-analyses, to illustrate the potential effects of chance on their findings and the need for caution in their interpretation. We have used simulation, rather than mathematical calculations, to demonstrate the power of chance, in the hope that will increase the impact of our findings.
To begin with a not uncommon dilemma given the large, and growing, number of systematic reviews that now exist,3,4 what should one think of a well-conducted meta-analysis of the results of 10 fairly large randomised trials of a new treatment for patients with colorectal cancer which includes a meta-analysis of individual participant data showing an odds ratio for mortality of 0.80 (99% CI 0.70–0.91, 2p = 0.00002)? Would your opinion be strengthened or weakened if you knew that five of these 10 trials were statistically significantly in favour of treatment on their own? Do you think such a treatment should be recommended for everyone with colorectal cancer? This paper shows how such a finding could, and did, arise by chance alone.
Background
The first D.I.C.E. paper discussed the effect of chance on whether patients in one treatment group of a randomised trial were more likely to die during the trial, and the subsequent influence of subgroup analysis and publication bias.1 It highlighted how extreme results (such as 6 deaths out of 10 patients in the control group but none out of 10 in the treated group) could happen by chance and showed how a series of simulated trials when combined in a meta-analysis using typical methods could produce a false, but strong, positive result. The second D.I.C.E. paper showed how important it is to give consideration to the effects of chance in the analysis of fairly large randomised trials using time-to-event data, especially when subgroup analyses are done.2
The present study, D.I.C.E. 3, investigates how the effects of chance might influence the results of systematic reviews and meta-analyses when a set of well-conducted, large randomised trials are brought together, and the need for caution if the statistically significant results of some of these trials influenced the decision to conduct the systematic review and meta-analysis. It is important to understand the power of chance to produce false positives and false hopes, particularly in light of the growth in the number of systematic review,3,4 which is not least due to the influence of The Cochrane Collaboration.5–7
Methods
Data on the time between randomisation and death or most recent follow-up were extracted for 578 patients allocated to the control group of a colorectal cancer trial, 147 of whom had died. The data contained insufficient information to identify any of the participants in the data-set. A computerised random number generator was used to assign each patient in a trial to a predefined ‘treatment’ or ‘control’ group to simulate a randomised trial. This was repeated 100,000 times, and each trial was analysed using logrank methods.8 To simulate the effect of chance in any subsequent meta-analysis, the 100,000 trials were combined into 10,000 meta-analyses by taking consecutive runs of 10 trials. The results of the trials were combined in each of these meta-analyses, using regular methods for individual participant data.9 The statistical significance threshold for a trial was set at 2p = 0.05, since this might be taken as indicative of a promising intervention, worthy of further investigation, perhaps in a systematic review. To demonstrate the power of chance in a meta-analyses, we focused on a threshold of 2p = 0.01 for the combined analyses.
Results
Not surprisingly, most of the trials and most of the meta-analyses gave results that were not statistically significant. However, all trials and meta-analyses are, regardless of size, subject to the effects of chance. By definition, there will be approximately five statistically significant results in every 100 studies by chance alone using the 2p = 0.05 threshold for significance and approximately one per 100 using the 2p = 0.01 threshold, even if there is truly no difference between the treatments being compared. In D.I.C.E. 3, we found that 4897 (4.9%) of the 100,000 trials were statistically significant at 2p < 0.05 and 123 (1.2%) of the 10,000 meta-analyses were significant at 2p < 0.01. A total of 46 (37.4%) of these 123 meta-analyses favoured treatment, while 77 (62.6%) favoured control.
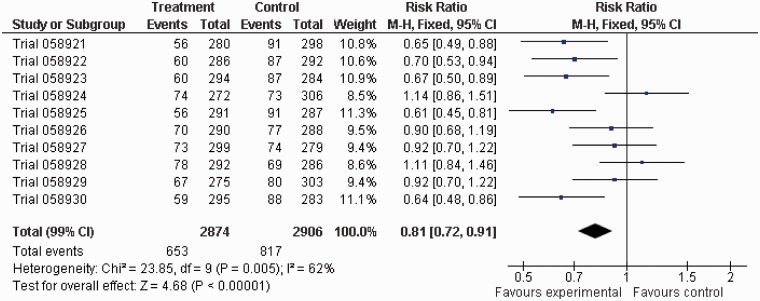
The most statistically significant meta-analysis had a 2p value of 0.00002 (Figure 1), arising from a 20% reduction (99% CI: 9–30%) in the annual odds of dying in the treatment group. This meta-analysis contained five trials with statistically significant results, all in favour of treatment. None of the 10,000 meta-analyses had exactly four trials statistically significantly in favour of treatment, but 12 meta-analyses had three trials statistically significantly in favour of treatment, with no trials statistically significantly in favour of control. Five meta-analyses had no trials statistically significantly in favour of treatment but four trials statistically significantly in favour of control, and there were eight meta-analyses with no trials statistically significantly in favour of treatment but three statistically significantly in favour of control.
Figure 1.
Forest plot for the meta-analysis with the most statistically significant result.
Table 1 shows how the number of statistically significant trials in favour of treatment in each batch of 10 was related to the statistical significance of their meta-analysis. As would be expected, this shows that as the number of trials with results that strongly favour the treatments increased, so did the likelihood of a highly significant, false-positive result in the meta-analysis.
Table 1.
Distribution of meta-analyses by numbers of trials with statistically significant results favouring treatment.
| Trials with 2p < 0.05 favouring treatment (n) | Meta-analyses (n) | Meta-analyses with 2p < 0.01 favouring treatment (n, %) |
|---|---|---|
| 0 | 7787 | 11 (0.1) |
| 1 | 1952 | 14 (0.7) |
| 2 | 246 | 15 (6.1) |
| 3 | 14 | 5 (35.7) |
| 4 | 0 | 0 (–) |
| 5 | 1 | 1 (100) |
We also examined the distribution of the results of the meta-analyses on the basis of a statistically significant (at 2p < 0.05) result for the first trial in each batch of 10, to simulate what might happen if a systematic reviewer is prompted to do their review by their knowledge of a single, favourable trial. This was the case for 473 (4.7%) of the 10,000 meta-analyses. In 18 (3.8%) of these 473 meta-analyses, the meta-analysis itself was statistically significant at 2p < 0.01. In contrast, when the first trial in a batch was not statistically significant, its meta-analysis was statistically significant at 2p < 0.01 only 105 times (1.1%) in 9527.
Discussion
This report concentrates on a large number of simulated meta-analyses, each containing 10 simulated randomised trials based on data from the control group in a colorectal cancer trial, with 147 deaths among 578 patients. Given that each of the 10,000 meta-analysis results in our study was generated purely by chance and remembering that there are already thousands of systematic reviews containing tens of thousands of meta-analyses in the literature,4 our findings should instil caution in the researchers who do reviews and in users of these reviews. Although, by their nature, systematic reviews and meta-analysis of randomised trials will minimise bias in the estimates of the effects of the interventions being investigated, the effects of chance can only be reduced by including more data. The amount of data needs to be sufficient so that any statistically significant effect estimates generated by chance will be small.
Anyone trying to interpret the results of a meta-analysis should remember that the standard test of statistical significance (based on a p value < 0.05) is almost as achievable by chance as rolling two sixes with a pair of dice, which has a probability of just under 0.03. Thus, as with scientific studies generally, those considering the findings of a meta-analysis should ideally look for stronger evidence than is provided by relying on this level of statistical significance. This may require even larger scale randomised evidence than is available for most systematic reviews, but it will reduce the likelihood of being misled by a false-positive finding. In addition, if the threshold for rejecting chance was reduced from 0.05 to 0.01, this would greatly reduce the number of false-positive results. However, results at or below a p value of 0.01 would still occur in 1% of meta-analyses when there is truly no difference between the interventions being compared.
Of particular concern, though, are those circumstances in which a statistically significant result in one study prompts the conduct of a meta-analysis. As has been shown in these simulations, this increases the probability of a statistically significant result for the meta-analyses. For example, imagine the circumstance where researchers become aware of a single study and this study is statistically significant. Our series of simulations found that adding nine further studies to this – where all 10 studies had results that are purely due to chance – produced a statistically significant result at 2p < 0.01 in 3.8% of the meta-analyses.
Focusing solely on the results favouring treatment, since these are the ones that might encourage the conduct of a meta-analyses more than those favouring control, and remembering that in all our simulated trials the post-hoc allocation of a patient to treatment or control was done purely by chance, only 11 (0.1%) of the 7787 meta-analyses with no statistically significant trials favouring treatment had a statistically significant overall result at 2p < 0.01. However, in the 2213 meta-analyses in which there was at least one trial favouring treatment at 2p < 0.05, 35 (1.6%) favoured treatment at 2p < 0.01 (see Table 1). This increased likelihood of a false-positive result should be remembered whenever the existence of a positive study leads to the conduct or prioritisation of a meta-analysis.
Our study used a large-scale simulation approach to highlight the importance of careful consideration of the effects of chance, especially if an early, statistically significant trial leads to the decision to do a systematic review. Other researchers have explored the impact of early trials on real meta-analyses in healthcare using a cumulative meta-analysis approach and a systematic review of these is underway.10 These studies show how early results might over-estimate11 or under-estimate12 the eventual results of the review. In another example, Herbison et al. examined data from 65 meta-analyses in 18 Cochrane Reviews to compare the eventual results with estimates after three and five trials were included. They found that it took a median of four studies to get within 10% of the final point estimate of the meta-analysis and that although ‘many of the conclusions drawn from systematic reviews with small numbers of included studies will be correct in the long run, but it is not possible to predict which ones’.13
Conclusion
Chance can influence the overall results of randomised trials and systematic reviews regardless of how well they are conducted. The premise to keep in mind continues to be Don’t Ignore Chance Effects.1,2 We would add a further caution: if the result of a study stimulates the conduct of a meta-analysis, which then includes that study’s result, the likelihood that the meta-analysis will also produce a false-positive result will be higher than the unadjusted statistical significance threshold.
Declarations
Competing interests
None declared
Funding
None declared
Ethical approval
Not required because the study used simulation on existing non-identifiable data.
Guarantor
MC
Contributorship
Both authors developed the idea. Jim Halsey ran the simulations. Mike Clarke drafted the manuscript. Both authors approved the manuscript.
Acknowledgements
We thank the peer reviewers, and our host organisations for the opportunity to pursue this research.
Provenance
Not commisioned; peer-reviewed by Jan Van der Meulen and Zbys Fedorowicz
References
- 1.Counsell CE, Clarke MJ, Slattery J, Sandercock PAG. The miracle of DICE therapy for acute stroke: fact or fictional product of subgroup analysis? BMJ 1994; 309: 1677–81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Clarke M, Halsey J. D.I.C.E. 2: a further investigation of the effects of chance in life, death and subgroup analyses. Int J Clin Pract 2001; 55: 240–2 [PubMed] [Google Scholar]
- 3.Moher D, Tetzlaff J, Tricco AC, Sampson M, Altman DG. Epidemiology and reporting characteristics of systematic reviews. PLoS Med 2007; 4: e78–e78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bastian H, Glasziou P, Chalmers I. Seventy-five trials and eleven systematic reviews a day: how will we ever keep up? PLoS Med 2010; 7: e1000326–e1000326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Clarke M, Li Y. Editorial for Issue 2 2012. J Evidence Based Med 2012; 5: 47–47 [Google Scholar]
- 6.Mallett S, Clarke M. How many Cochrane reviews are needed to cover existing evidence on the effects of health care interventions? ACP J Club 2003; 139: A11–2 [PubMed] [Google Scholar]
- 7.Starr M, Chalmers I, Clarke M, Oxman AD. The origins, evolution, and future of The Cochrane Database of Systematic Reviews. Int J Technol Assess Health Care 2009; 25(Suppl. 1): 182–95 [DOI] [PubMed] [Google Scholar]
- 8.Peto R, Pike M, Armitage P, Breslow NE, Cox DR, Howard SV, et al. Design and analysis of randomised clinical trials requiring prolonged observation of each patient. II: analysis and examples. Br J Cancer 1977; 35: 1–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Early Breast Cancer Trialists’ Collaborative Group. Systemic treatment of early breast cancer by hormonal, cytotoxic or immune therapy: 133 randomised trials involving 31,000 recurrences and 24,000 deaths among 75,000 women. Lancet 1992; 339: 1–15, 71–85 [PubMed] [Google Scholar]
- 10. Clarke M, Brice A and Chalmers I. A systematic review of cumulative meta-analyses of clinical intervention studies (in preparation)
- 11.Klein JB, Jacobs RH, Reinecke MA. Cognitive-behavioral therapy for adolescent depression: a meta-analytic investigation of changes in effect-size estimates. J Am Acad Child Adolesc Psychiatry 2007; 46: 1403–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li LH, Sun TS, Liu Z, Guo YZ, Li SG, Qin CC. Plating versus intramedullary nailing of humeral shaft fractures in adults: a systematic review. Chin J Evidence-Based Med 2008; 8: 662–7 [Google Scholar]
- 13.Herbison P, Hay-Smith J, Gillespie WJ. Meta-analyses of small numbers of trials often agree with longer-term results. J Clin Epidemiol 2011; 64: 145–53 [DOI] [PubMed] [Google Scholar]