Targeting of White Matter Tracts With Transcranial Magnetic Stimulation

Abstract

Background

TMS activations of white matter depend not only on the distance from the coil, but also on the orientation of the axons relative to the TMS-induced electric field, and especially on axonal bends that create strong local field gradient maxima. Therefore, tractography contains potentially useful information for TMS targeting.

Objective/methods

Here, we utilized 1-mm resolution diffusion and structural T1-weighted MRI to construct large-scale tractography models, and localized TMS white matter activations in motor cortex using electromagnetic forward modeling in a boundary element model (BEM).

Results

As expected, in sulcal walls, pyramidal cell axonal bends created preferred sites of activation that were not found in gyral crowns. The model agreed with the well-known coil orientation sensitivity of motor cortex, and also suggested unexpected activation distributions emerging from the E-field and tract configurations. We further propose a novel method for computing the optimal coil location and orientation to maximally stimulate a pre-determined axonal bundle.

Conclusions

Diffusion MRI tractography with electromagnetic modeling may improve spatial specificity and efficacy of TMS.

Introduction

A figure-of-eight TMS coil placed at the exact same location over the motor cortex has vastly different physiological and behavioral effects depending on coil orientation. Depending on the relative orientation between the TMS-induced E-field and the neuronal elements, pyramidal axons are activated directly (D-mechanism) in white (or gray) matter, or indirectly (I-mechanism) via interneurons in gray matter [1,2]. In addition to the optimal orientations, also the thresholds for the D- and I-mechanisms differ, which makes it possible to adjust the relative contributions between the two mechanisms. These ideas derive from (i) physiological studies showing that axons are maximally activated when they are at least partially parallel to the E-fields and that axonal bends form particularly sensitive “hot spots” [3–10] and (ii) corresponding modeling studies [4,11–25].

Here, our goal was to quantify the effect of TMS on white matter, focusing exclusively on the D-mechanism activating pyramidal axon bends (for gray matter pyramidal structures potentially activated through the D-mechanism, see ‘Discussion’ section). We were particularly interested in large-scale spatial patterns of activations and therefore included a substantially larger white matter volume (block of a gyrus) and number of tracts (~750) than previous studies [19–21]. To estimate tract activation likelihoods it is necessary to (a) model the geometry of the axonal bundles and (b) compute the TMS-induced E-field. We extracted the required anatomical detail from in vivo 1 mm-resolution T1 and diffusion tensor imaging (DTI) data. E-field computations require a volume conductor model, for which we used a computationally efficient yet reasonably accurate realistically shaped 1-layer boundary element model (BEM) [26]. As a novel application, we examined the possibility of computing the optimal position and orientation of the TMS coil that will maximally activate a pre-determined white matter bundle at the individual level. This could be useful especially for activating tracts that go to therapeutically relevant deep brain areas that cannot be stimulated directly [27,28].

Methods

Subject and MRI recordings

The protocol was approved by the Massachusetts General Hospital institutional review board. MRI and DTI data were acquired from one healthy subject with a 3T Siemens Tim Trio scanner and a 32-channel coil (Siemens Medical Solutions, Erlangen, Germany). The whole-head T1-weighted MEMPRAGE data were collected at 1 mm resolution. The DTI data were collected from 34 spatially continuous 1-mm coronal slices covering the motor and somatosensory cortices using a 2D single-shot DW-SE EPI sequence with 1 mm in-plane resolution (data previously used in [29]). For details see Supplementary methods online.

MRI and tractography analyses

The MEMPRAGE data were segmented and reconstructed with the FreeSurfer software [30,31]. To produce tractography results of sufficient quality for TMS modeling, we developed a custom algorithm implemented in MATLAB (2012a, The Mathworks, Inc. Natick, MA, USA) described in detail in Supplementary methods. Since the dominant diffusion direction of gray matter may vary [29], inside gray matter we utilized the a priori knowledge that pyramidal neurons and cortical columns are oriented perpendicular to the cortex [32,33]. Inside white matter, DTI data were used for tract estimation (Supplementary Fig. 1).

TMS forward modeling

The volume conductor was a realistically-shaped single-compartment Boundary Element Model (BEM) with the inner skull surface as the boundary [26], and the TMS coil model followed a 60-mm figure-of-eight TMS coil design (MagPro C-B60, MagVenture, Falun, Denmark); for details see Supplementary methods.

To estimate the tract activation likelihood we computed the gradient of the E-field along the tracts. We used the natural parameterization by arc length s for the tract curves and thus calculated the derivative of the E-field component parallel to the tract as $\frac{\mathrm{d}(\mathbf{E}(s)·\mathbf{t}(s))}{\mathrm{d}s}$, where t(s) is the tract unit tangent vector [34]. Hence, the likelihood that any tract segment was activated depended on the (i) distance from the coil (that largely determines the E-field amplitude) and the (ii) orientation and (iii) bending of the tract with respect to the E-field.

Simulations

Simulation 1: the effect of coil rotation

We selected a coil center position over lateral hand motor cortex where the thumb representation is typically located. Tractography was done using the entire hand knob as seed ROI (Supplementary Fig. 2). The TMS coil was tangential to the local curvature of the scalp, and its orientationwas varied from 0° (anterior-posterior) to 170° in steps of 10°.

Simulation 2: computation of the best coil position and orientation to activate a pre-determined tract bundle

We pre-selected a smaller seed ROI (approximately 5mm radius in the middle of the hand knob) and calculated the maximum E-field gradient that can be induced to this bundle of tracts (averaged across all tracts originating from the seed ROI), when both the position and orientation of the coil were varied. The coil location was varied within a radius of 5 cm over the motor cortex, and in each coil position the coil orientation was varied between 0° and 170° in steps of 10° (Supplementary Fig. 3). This allowed us to find the maximally efficient coil location/orientation to stimulate the particular tract bundle.

Results

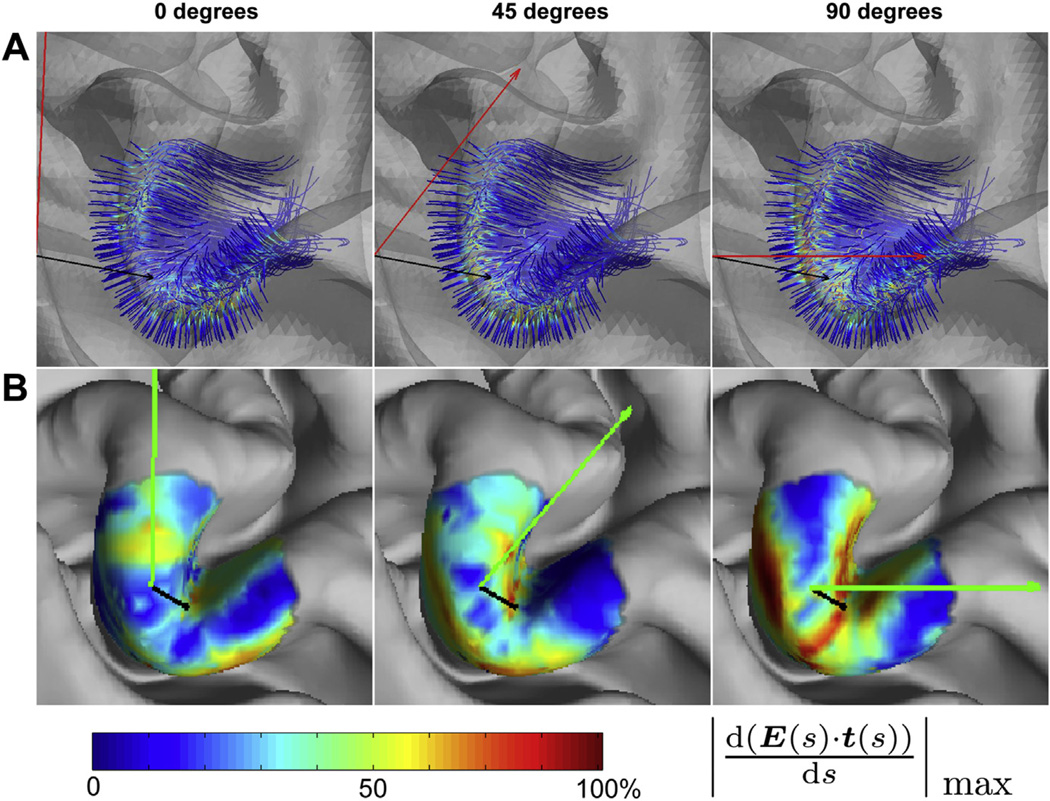
Figure 1A (simulation 1) shows the effect of coil rotation over the left hemisphere hand motor area for three different coil orientations. As expected, the gradients were largest close to the gray–white matter border where tract bending was maximal. Largest gradients were generally observed directly under the coil at sulcal walls at locations where the E-fields (and coil orientations) were best aligned with the initial part of the tract (and cortical normal). Figure 1B shows the corresponding results projected on the cortical surface (maximal absolute value of the E-field gradient along the tract plotted on the intermediate cortical surface). The patterns reveal details that would not have been obvious without modeling large numbers of tracts. At 0° (anterior–posterior direction), the E-field gradient maximum was displaced medially from the point directly under the coil. At 45°, a relatively large and uniform area of highly effective stimulation was observed in the posterior bank of the precentral gyrus. On the opposite side of the gyrus (precentral sulcus), where the cortex curves more tightly, the hot spot was spatially more compact. At 90°, the E-field gradients were overall stronger than in the other two conditions, and again showed a different distribution. For enhanced visualizations with smaller angle steps see Supplementary Movies 1A and 1B.

Figure 1.

Effect of coil orientation. (A) E-field gradients along the tracts for coil orientations of 0 (A-P), 45°, and 90°, in the hand knob of the motor cortex (precentral gyrus) viewed from above. The color-scale is normalized to the maximum of the E-field gradient across tracts. (B) Maximal E-field gradients for white matter tracts projected on the intermediate cortical surface for three different coil orientations (green arrow) for the same three coil orientations. The maximum of the color-scale corresponds to the maximum across the three coil orientations. For corresponding movies that show finer grading of coil orientations, see Supplementary material.

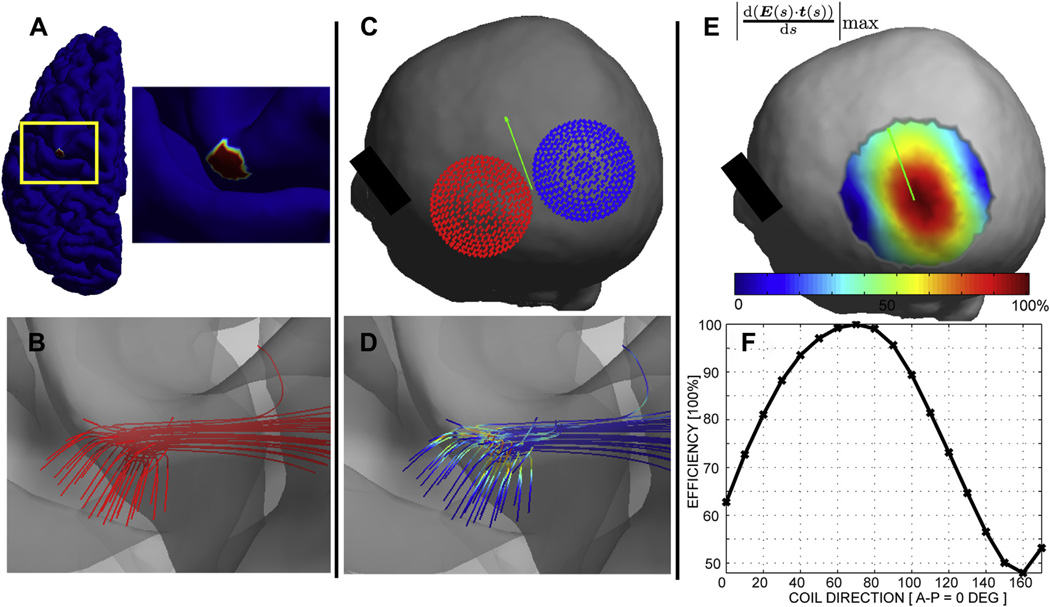
Figure 2 (simulation 2) shows the result of determining the best coil location and orientation to activate a pre-determined axonal bundle. Using a fixed optimal orientation of about 70° the area where the coil was producing strongest responses was quite small, with relative stimulation efficiency decreasing rapidly when moving away from the center, and more quickly in the direction orthogonal to the coil orientation. To investigate the relative contributions between coil orientation and location, Supplementary Fig. 4 shows the corresponding relative efficiency distributions for non-optimal coil orientations. When the coil was turned 90° from the optimal orientation, even ideal coil centering resulted in only weak stimulation (<50% of maximum).

Figure 2.

Optimizing coil location and orientation to stimulate an axonal bundle. (A) The target ROI used as tractography seed shown on the intermediate cortical surface. (B) Tractography results in the ROI. (C) The computed optimal coil location for stimulating the axonal bundle (see text). (D) Spatial pattern of E-field gradients for the optimal coil location/orientation. (E) Spatial map of relative axonal stimulation efficiency as a function of the coil position when the orientation is fixed to the optimal one (green arrow). (F) The relative efficiency of stimulation as a function of TMS coil orientation when the coil center is fixed to the optimal spot.

Discussion

The present simulations suggest that the figure-of-eight coil orientation has a major effect on if and where white matter axons are activated, which agrees with the well-known effect of coil rotation on motor cortex activation. The model is supported by physiological studies showing that TMS-induced E-field gradient strength correlates with axonal activation [4–6]. In accord with previous simulations and simultaneous TMS-PET recordings [19–21,35], the model also suggests that pyramidal axons in sulcal walls may be more strongly activated than those in crests of gyri, even though the pyramidal axons in gyri are closer to the coil. In addition, the model predicted unforeseen features of TMS activation distributions (Fig. 1B). Previous TMS simulation studies examining the effect of tract curvature in gyri vs. sulci have shown up to 3 example pyramidal fibers with synthesized tracts in a schematic gyrus [20,21] or tens of tracts derived from real diffusion MRI data in a realistically shaped gyrus [19]. The present study included ~750 geometrically detailed tracts, which offered new insight. Finally, as a novel application, we show how the developed methods could be utilized for individual level planned stimulation of any pre-determined axonal bundle (Fig. 2). The results likely apply to all cortical areas, given that the general gyral/sulcal architecture with fanning axonal patterns is preserved throughout the cortex [33].

Inherent to any macroscopic biophysical model of realistic anatomy, the present simulations contained approximations which may have influenced the results. For example, while the present study focused on white matter, inside gray matter magnetic stimulation may initiate action potentials in pyramidal neurons via the D-mechanism close to the soma and/or axon initial segment [36,37] due to, e.g., increased density of voltage-sensitive channels [11,38–41] (for the I-mechanism in gray matter, see, e.g., [42]). Further, we used a BEM [26,43] rather than the more complex and potentially more accurate finite element model (FEM) [19,21]. Both BEM and FEM approaches have their relative merits in terms of assumed accuracy, number of parameters and their uncertainties, imaging requirements (MRI/CT), quality of brain segmentations, computational speed, and practical applicability. BEMs also cannot incorporate tissue anisotropy, albeit anisotropy has been suggested to have only a modest effect on the spatial distribution in MEG/EEG [44] and TMS [19,45] electromagnetic modeling. Here we chose a BEM because BEMs are widely used, validated, and give consistent results; for further discussion see [26]. While simplified models such as those employed in the present study may contain some inaccuracies, they have proven highly successful in clinical and research applications of magneto- and electroencephalography (MEG/EEG) [46–49], and it is possible that they may offer practical benefits for (especially large-scale) TMS studies as well.

In conclusion, diffusion MRI tractography and TMS modeling have reached a stage where relatively large brain volumes and quantities of tracts can be analyzed in terms of their TMS activation likelihood. Further developments in tractography may be expected with improvements is diffusion MRI hardware, such as the Connectome scanner at Massachusetts General Hospital [50,51] and novel pulse sequences and image reconstruction algorithms [52]. Incorporating such data in future navigation and stimulation planning systems has potential for improving spatial efficacy and specificity of TMS in various research and clinical applications.

Abbreviations

DTI

diffusion tensor imaging

MRI

magnetic resonance imaging

TMS

transcranial magnetic stimulation