Variable selection in semi-parametric models

Abstract

We propose Bayesian variable selection methods in semi-parametric models in the framework of partially linear Gaussian and problit regressions. Reproducing kernels are utilized to evaluate possibly non-linear joint effect of a set of variables. Indicator variables are introduced into the reproducing kernels for the inclusion or exclusion of a variable. Different scenarios based on posterior probabilities of including a variable are proposed to select important variables. Simulations are used to demonstrate and evaluate the methods. It was found that the proposed methods can efficiently select the correct variables regardless of the feature of the effects, linear or non-linear in an unknown form. The proposed methods are applied to two real data sets to identify cytosine phosphate guanine methylation sites associated with maternal smoking and cytosine phosphate guanine sites associated with cotinine levels with creatinine levels adjusted. The selected methylation sites have the potential to advance our understanding of the underlying mechanism for the impact of smoking exposure on health outcomes, and consequently benefit medical research in disease intervention.

1 Introduction

The work proposed in this article was motivated by an epidemiological project aimed to choose important epigenetic variants (predictor variables) potentially associated with smoking exposures (outcome) including exposure to maternal smoking and posnatal smoking exposure. The epigenetic variants are represented by deoxyribonucleic acid (DNA) methylation sets of cytosine phosphate guanine (CpG) sites. DNA cytosine methylation plays a critical role in modulating the transcriptional potential of the genome and may influence the development of complex human diseases.¹ Maternal smoking during pregnancy and postnatal smoking exposure are important risk factors for adverse health outcomes in children including cancer and respiratory illnesses such as asthma.^2–5 The underlying mechanisms for the diverse impacts of smoking exposure may involve epigenetic modifications such as DNA methylation.⁶ Identifying important methylation sites from a pool of candidates possibly associated with smoking exposure will advance our understanding of the underlying mechanisms and consequently benefit medical research in disease intervention.

Existing variable selection methods in general are not applicable to select variables such as genetic or epigenetic variants (GEVs). Most methods in the Frequentist framework were proposed for parametric linear models by use of penalty functions.^7–9 Recently, some methods for feature selections in non-linear models were developed.^10,11 These methods generally built on splines or Taylor series expansions and may have difficulty in accommodating a large number of predictors and describing complex interaction effects. However, in genetic or epigenetic studies, very often, the number of possible predictors in the candidate pool is not small due to biological uncertainty. It is also considered that the effects of variants on the outcome are not linear and can be in any unknown form. Genes or epigenes (genes associated with epigenetic variants) do not necessarily function individually; rather, they work in concert with others to manifest a disease condition. Furthermore, these approaches are not appropriate for discrete variables such as single nucleotide polymorphism (SNP) genotypes. In the area of machine learning, methods of variable selection in semi-parametric models constructed by reproducing kernels have been discussed,¹² although it is also limited to continuous variables and requires intensive computing. Similarly, in the Bayesian framework, most variable selection methods are built upon model selections in parametric linear models. These methods utilize indicator variables for variable inclusion,^13–16 Zellner’s g-prior controlling the importance of variables,^17–19 or Bayes factors comparing posterior probabilities between models.²⁰ Bayesian variable selection methods in semi-parametric models are rather limited. In the area of genetic or epigenetic studies, this type of methods is particularly appealing simply because researchers can embed prior knowledge of genetic or epigenetic factors into the selection process in order to obtain more meaningful selection results.

In this article, under a Bayesian framework, we propose a variable selection method built into reproducing kernels to evaluate the effect of a set of variables (e.g. GEVs). These variables can be continuous such as measurements of DNA methylation or gene expression. They can also be discrete such as SNP genotypes. The evaluation of a set effect is built upon the method of set analysis²¹ to capture the significance of a group of variants allowing (for possible) unknown non-linear effects. The set analysis has the ability to capture the overall contribution from a whole group of variants, which may involve convoluted unknown interactions between the variants. The result from this type of analysis, however, is influenced by the choice of candidate variants, and it can be misleading if variants included in the kernel lack proper justification.²²

In our method, two types of statistical models with reproducing kernels included are considered, partially linear regressions and probit regressions. To select important variables, we introduce an indicator variable into the reproducing kernel for the inclusion of a variable in the kernel. Compared to the existing methods, the proposed method has the ability to choose important variables regardless of the effect forms, e.g. linear or non-linear with unknown complex interactions. It thus has strong potential for application in gene and epigenetic studies to detect potentially important genetic and/or epigenetic variants associated with health outcomes, but the general association trend is unknown. There are many other possible applications of this method including, for example, studies examining the effects of nutrition or physical activity on health outcomes.

The structure of the article is as follows. The modeling and the Bayesian framework are presented in Section 2 including the selection of prior distributions and a discussion on posterior distributions and sampling. Simulations are presented in Section 3, where different structures of variable effects are considered. We apply the methods to select important CpG sites of which DNA methylation is potentially associated with maternal smoking and cotinine levels. This is discussed in Section 4. Finally, we summarize our findings and propose future work in Section 5.

2 The statistical models

Suppose we observe a vector of responses Y_n×1, a matrix of variables g_n×p whose joint effect is of interest (e.g. DNA methylation in a pathway), and a covariate matrix X_n×p0. Here n is the sample size, p is the number of variables of interest such as genetic or epigenetic variants, and p₀ is the number of covariates. Note that it is possible p + p₀ > n. We assume that the mean of the response is modeled as E(Y_i|X_i, g_i) = f⁻¹{X_iβ + h(g_i)}, where h(·) is an unknown function, and β_p0×1 describes the additive linear effects of p₀ covariates X. Define h(g)_n×1 to be a vector of unknown functions evaluating the joint effect of p variables g that is possibly non-linear and may involve complex interactions between g; h(g) can be modeled parametrically or non-parametrically. Function f (·) is a known link function. For instance, f (·) being the identity function results in a partially linear model and the inverse of a probit function gives a probit regression model. Our goal is to select a set of important variables from g that have legitimate contributions to the joint effect and exclude variables with no contributions.

As noted above, we allow the p variables g to have a complex (interaction) effect on the response variable. In practice, this is particularly true among genes or epigenes functioning in the same pathway. To this end, we incorporate reproducing kernels into the modeling process in appreciation of their ability to describe any underlying unknown patterns and the ability of handling high-dimensional data with p + p₀ > n.^21,23 Specifically, we represent h(·) using a kernel function K(·, ·). By the Mercer’s theorem,^24,25 under some regularity conditions, the kernel function K(·, ·) specifies a unique function space spanned by a particular set of orthogonal basis functions. The orthogonality is defined with respect to L₂ norm. Following the Mercer’s theorem, any function h(·) in the function space 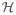can be represented as a linear combination of reproducing kernels,^25,26 $h({\mathit{g}}_i)={\sum }_{k=1}^{n}K({\mathit{g}}_i,{\mathit{g}}_k){\alpha }_k={{\mathit{K}}^{\prime }}_i\mathit{\alpha }$, where α = (α_k, k = 1, …, n)′ is a vector of unknown parameters and ${\mathit{K}}_i^{\prime }$ is the ith row of kernel matrix K. Defining h(·) non-parametrically as above has two major advantages in that it can handle large number of covariates and can capture potentially complex interaction between variables g via the specified kernel function.

The kernel function K(·, ·) determines the space of functions used to approximate the function h(·). For instance, $K({\mathit{g}}_{\mathit{i}},{\mathit{g}}_{\mathit{j}})={(1+{\mathit{g}}_{\mathit{i}}^{\prime }{\mathit{g}}_{\mathit{j}})}^d$ generates a space of functions 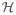spanned by all possible dth order monomials of g. It corresponds to models with dth-order polynomials including the cross product terms. Another example is the Gaussian kernel, which is a function of smoothness parameter ρ and we denote by K(ρ). The (i, j) th entry of the kernel matrix K(ρ) is defined as k_ij(ρ) = exp{−Σ_m || g_im − g_jm||²/ρ}, with i, j = 1, …, n, m = 1, …, p, where g_im is the measure of variable m of subject i. This kernel acts as a correlation matrix. The functionality of Gaussian kernels is similar to that of exponential and Laplacian kernels.^27,28 All these kernels are constructed for continuous variables. For discrete variables, a commonly used kernel is the IBS (identity by state) kernel, which is constructed based on the agreement between variables and usually used for genetic variants such as SNPs.²³ In this article, to ensure a clear presentation of the proposed methods, we take g to be continuous and adopt a Gaussian kernel because of its flexibility and its ability in modeling complex functions.²¹ However, other kernels can be used as well. In addition, we emphasize that the methods can be easily extended to fit discrete variables.

Turning back to the Gaussian kernel, we note that different values of ρ with different sets of selected variables can result in the same K(ρ) and consequently the same likelihood. In the context of variable selection, we fix ρ at ρ = ρ₀ with ρ₀ being the value at the full model with all variable included, considering that unimportant variables do not significantly contribute to the joint effect of g. We also examine the sensitivity of variable selection results with respect to the choice of ρ₀. In the following sections, we particularly discuss variable selections in the setting of two models, partially linear regressions and probit regressions, in that these are used most often in practice.

2.1 Partially linear regression model

Consider the following setting to evaluate the effect of a set of variables:

$$\mathit{Y}=\mathit{X}\mathit{\beta }+\mathit{h}(\mathit{g})+\mathit{\epsilon }$$ (1)

where Y, X, β, and h(·) are defined as before. Random error ε is with dimension n × 1 and we assume ε ~ N(0, σ²I), where I is an identity matrix. Hereinafter, to simplify the notation, we use h instead of h(g) without ambiguity that h evaluates the joint effect of g. To select variables from g, we introduce an indicator variable δ = {δ_m|m = 1 ···, p} into the kernel matrix with δ_m = 1 denoting the inclusion of variable m and 0 otherwise. For instance, with p = 3, δ = {1, 1, 0} means that the first two variables are selected. Accordingly, we update the notation of kernel matrix as K(ρ₀, δ) with its th entry defined as (i, j)-th entry defined as

$$k_{ij}({\rho }_0,\mathit{\delta })=exp\left\{-\sum _m{\Vert (g_{im}-g_{jm}){\delta }_m\Vert }^2/{\rho }_0\right\}$$

If variable m is excluded, then it will not appear in any entry of the kernel matrix. The idea of using indicator variables for the inclusion or exclusion of a variable has been applied in previous studies.¹³ Selecting covariates X in linear models is not the focus of our work and interested readers are referred to the Bayesian or Frequentist methods discussed in the literature.^{13,16,19,20,29,30} Assuming K(ρ₀, δ) is positive definite, as shown in an earlier study,²¹ parameter estimation in the semi-parametric model (1) based on penalized least squares is equivalent to the estimates from a linear mixed model with random effects h ~ N(0, τK(ρ₀, δ)), where τ is an unknown variance component.

Denote by Θ = {β, σ², τ, δ} a collection of parameters to be inferred. In the following sections, we discuss a fully Bayesian method to infer these parameters.

2.1.1 The prior distributions

The prior distribution of β will be selected as normal distributions with vague hyper-parameters $\mathit{\beta }~N(\mathbf{0},{\sigma }_{\beta }^2\mathit{I})$, with ${\sigma }_{\beta }^2$ selected to be large to ensure a vague prior for β.

The prior distributions for σ² and τ are chosen as inverse gamma distributions with vague hyper-parameters, σ² ~ Inv − Gam(a_σ², b_σ²), and τ ~ Inv − Gam(a_τ, b_τ), where the shape and scale parameters a_σ², b_σ², a_τ, b_τ are chosen to be small. As noted in an earlier study,³¹ cautions should be taken on the choice of these hyper-parameters. Note that our goal is to remove non-important variables, which are expected not to be associated with the response variable. Thus, τ measures the effect of a collection of important variables, if there are any.

The prior distribution of δ_m is assumed to be Bernoulli with parameter q_m. We can take q_m = 0.5 or assign a hyper-prior distribution to q_m such as Beta (η, 1) with η known. Our simulations indicate that adopting a hyper-prior distribution for q_m does not necessarily improve our results. So far, all the prior distributions are chosen to be vague, which is aimed to draw inferences fully based on data. In some situations, prior knowledge may guide us to select more rigorous and informative prior distributions. For instance, if it is known that some variables are potentially important, then we can set q_m > 0.5 for those variables to indicate their importance a priori.

2.1.2 Posterior distributions and their calculations

The joint posterior density is

$$p(\mathbf{\Theta }\mid \mathit{Y})\propto p(\mathit{Y}\mid \mathit{\beta },{\mathit{\sigma }}^2,\mathit{\delta })p(\mathit{\beta })p(\mathit{\tau })p({\mathit{\sigma }}^2)Pr(\mathit{\delta }\mid \mathit{q})p(\mathit{q})$$ (2)

where Θ = {β, σ², τ, δ, q} denotes an expanded set of parameters and q = {q₁, …, q_p}. To differentiate between continuous and discrete random variables, “Pr(·)” is used to denote probability mass functions for discrete random variables. We use the Gibbs sampler to sample from this joint posterior distribution.

In the following presentation, (·) denotes the parameters and data to be conditioned on. The full conditional posterior of β is β|(·) ~ N(Σ_β/σ²(Y − h), Σ_β), where ${\mathrm{\sum }}_{\beta }={\{{\mathit{X}}^{\prime }\mathit{X}/{\sigma }^2+\mathit{I}{({\sigma }_{\beta }^2)}^{-1}\}}^{-1}$, and that of h is h|(·) ~ N(Σ_h(Y − Xβ)/σ², Σ_h) with Σ;_h = {τ⁻¹K⁻¹ + σ²I}⁻¹. The full conditional posterior distributions of σ² and τ are inverse gamma,

$$\begin{array}{l}{\sigma }^2\mid (·)~\text{Inv}-\text{Gam}(n/2+a_{{\sigma }^2},\{{(\mathit{Y}-\mathit{X}\mathit{\beta }-\mathit{h})}^{\prime }(\mathit{Y}-\mathit{X}\mathit{\beta }-\mathit{h})+2b_{{\sigma }^2}\}/2)\\ \tau \mid (·)~\text{Inv}-\text{Gam}(n/2+a_{\tau },({\mathit{h}}^{\prime }{\{\mathit{K}({\rho }_0,\mathit{\delta })\}}^{-1}\mathit{h}+2b_{\tau })/2)\end{array}$$

The full conditional posterior distribution of q_m is Beta (δ_m + η, 2 − δ_m), where η is the prior distribution of q_m such that the prior mean of q_m is η/(1 + η). The full conditional posterior distribution of δ_m is

$$Pr({\delta }_m\mid (·))\propto exp\{-{(\mathit{Y}-\mathit{X}\mathit{\beta }-\mathit{h})}^{\prime }(\mathit{Y}-\mathit{X}\mathit{\beta }-\mathit{h})/(2{\sigma }^2)-[{\mathit{h}}^{\prime }{\{\mathit{K}({\rho }_0,\mathit{\delta })\}}^{-1}h]/(2\tau )\}\times {\mid \mathit{K}({\rho }_0,\mathit{\delta })\mid }^{-1/2}{q}_m^{{\delta }_m}{(1-q_m)}^{1-{\delta }_m}$$ (3)

The possible values of δ_m are 1 and 0. Denote the right side of equation (3) by cPr(δ_m), with c being the proportion. Let a be cPr(δ_m = 0|(·)), proportional to the conditional posterior probability of δ_m = 0 and b denote cPr(δ_m = 1|(·)), proportional to the conditional posterior probability of δ_m = 1. Then the full conditional posterior distribution of δ_m is Bernoulli with parameter b/(b + a) measuring the conditional posterior probability of including variable m in the kernel. Clearly, all the conditional posterior distributions are standard. It is worthy of note that this feature holds regardless of the choice of kernels or the continuity of g. Extension to discrete g is thus expected to be straightforward, so is in the probit regression model to be discussed in the next section. To obtain posterior samples of Θ, we sequentially draw from the standard full conditional posterior distributions, which are expected to converge quickly. For the situation that K is singular, the conditional posterior of h and τ do not exist. This can be solved by bypassing direct posterior sampling of h; instead, we infer the parameters in the prior distribution of h. By doing so, valid but non-standard posterior distributions of τ and σ² will be obtained and the Metropolis-Hastings algorithm has to be used to draw the posterior samples.

Determination of important variables

To conclude the importance of each variable, we summarize the posterior probabilities (posterior mean of q) of including each variable in the model. To determine which variable should be kept, we apply the concept in scree plot to the posterior probabilities, calculated as the percentage of times that a variable is selected among a certain number of uncorrelated MCMC samples. Scree plots are often used in principal component analysis to determine the number of components, where a sharp decrease in eigenvalues indicates less importance for the rest of the components. Analogously, in our application of scree plots, a sharp decrease in probabilities indicates less importance of the remaining variables. Variables identified by this rule are treated as the most important variables. In addition, a reference probability 0.50 will be used to identify a group of possibly important variables. This reference probability represents the expected frequency if a variable is chosen randomly.

2.2 Probit regression model

In this section, we consider probit regression models for binary outcomes. Like logistic regressions, probit regressions are commonly used in case–control studies to infer factor effects on the risk of disease. Denote by Z_i a binary 0/1 response on the ith observation and let Z = {Z₁, …, Z_n} be the collection of response on n subjects. A generalized linear model with probit link function that links Z to the g variables and X covariates can be conveniently formulated through data augmentation via Gaussian latent variables. Define a latent variable Y_i with Y = (Y₁, …, Y_n)^T such that

$$Z_i=1_{\{Y_i>0\}},\mathit{Y}=\mathit{X}\mathit{\beta }+\mathit{h}+\mathit{\epsilon }$$ (4)

where 1_A denotes the indicator function of the event A, and h and ε are defined as in partially linear regression models. Note that the second part of equation (4) is a partially linear model. To be consistent with the partially linear model discussed earlier, we keep using Y to denote response although Y is latent in this framework. The probability of Z = z satisfies

$$Pr(\mathit{Z}=z\mid \beta ,\tau ,{\sigma }^2)={\int }_{A(Z)}{\left(\frac{1}{{\sigma }^2+\tau }\right)}^{n/2}{\mid {\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })\mid }^{-1/2}exp\left\{-\frac{{(\mathit{Y}-\mathit{X}\mathit{\beta })}^{\prime }{\mathrm{\sum }}_0{({\rho }_0,\mathit{\delta })}^{-1}(\mathit{Y}-\mathit{X}\mathit{\beta })}{2({\sigma }^2+\tau )}\right\}\mathrm{d}Y$$ (5)

where A(Z) = {A(Z₁), …, A(Z_n)} with

$$\mathit{A}(Z_i)=\{\begin{array}{ll}(-\infty ,0],\hfill & \text{if}{Z}_{\mathrm{i}}=0\hfill \\ (0,\infty ),\hfill & \text{if}{Z}_{\mathrm{i}}=1\hfill \end{array}$$

and Σ₀(ρ₀, δ) is an n × n matrix with (i, j)-th entry being τ/(τ + σ²)k_ij(ρ₀, δ) when i ≠ j, and 1 when i = j. Note that under the model given in equation (5), the parameters (β, σ², τ) are not identifiable. It can be shown that for any positive constant a₀, the parameter vectors (a₀β, $a_0^2{\sigma }^2,a_0^2\tau$) will give the same likelihood. To avoid this problem, we fix σ² and τ at known values ${\sigma }_0^2$ and τ₀.³² In this article, we take σ₀ = 1 and τ₀ = 0.8. The selection of ${\sigma }_0^2$ and τ₀ in principle is arbitrary, but their ratios will influence the estimates of β. Furthermore, since τ measures the contribution of a set of variables, e.g. expression of genes or DNA methylation of different CpG sites, setting τ₀ = 0.8 a priori assumes that the variable set has some effect. Our simulations indicate that choosing τ₀ small compared to σ₀ can possibly lead to under selection, which is likely due to the pre-assumed large random error (large σ₀) in Y.

As in partially linear regressions, we define δ as a vector of 1 or 0 indicating the inclusion/exclusion of a variable. The likelihood of β, δ is given as

$$\begin{array}{l}L(\mathit{\beta },\mathit{\delta }\mid \mathit{Z})\propto p(\mathit{Z}\mid \mathit{\beta },\mathit{\delta })=\int p(\mathit{Z},\mathit{Y}\mid \mathit{\beta },\mathit{\delta })\mathrm{d}Y\\ \propto {\int }_{\mathit{A}(\mathit{Z})}{\mid {\mathrm{\sum }}_0\mid }^{-1/2}exp\{-{(\mathit{Y}-\mathit{X}\mathit{\beta })}^{\prime }{\{{\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })\}}^{-1}(\mathit{Y}-\mathit{X}\mathit{\beta })/4\}\mathrm{d}Y\end{array}$$ (6)

We assign the same prior distribution as in partially linear regressions to β and δ, and to the hyper parameter q in the probability mass function of δ. The collection of parameters is denoted as Θ = {β, δ, q}.

2.2.1 The joint posterior distribution

To derive the joint posterior distribution of Θ, we start from equation (6). However, the set of integrations in equation (6) can slow down the whole estimating process and may bring in computing difficulty. To avoid this, instead of integrating out Y, we formulate the posterior distribution as the joint distribution of Θ and the latent variable Y,^33,34

$$\begin{array}{l}p(\mathit{\beta },\mathit{\delta },\mathit{q},\mathit{Y}\mid \mathit{Z})\propto Pr(\mathit{Z}\mid \mathit{Y},\mathit{\beta },\mathit{\delta })p(\mathit{Y}\mid \mathit{\beta },\mathit{\delta })p(\mathit{\beta })Pr(\mathit{\delta }\mid \mathit{q})p(\mathit{q})\\ =I\{\mathit{Y}\in \mathit{A}(\mathit{Z})\}p(\mathit{Y}\mid \mathit{\beta },\mathit{\delta })p(\mathit{\beta })Pr(\mathit{\delta }\mid \mathit{q})p(\mathit{q})\\ p(\mathit{Y}\mid \mathit{\beta },\mathit{\delta })\propto {\mid {\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })\mid }^{-1/2}exp\{-{(\mathit{Y}-\mathit{X}\mathit{\beta })}^{\prime }{\{{\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })\}}^{-1}(\mathit{Y}-\mathit{X}\mathit{\beta })/4\}\end{array}$$ (7)

The second line in equation (7) is a result of equation (4).

2.2.2 Full conditional posterior distributions and their calculations

We apply the Gibbs sampler to the full conditional posterior distributions to draw posterior samples. From equation (7), the full conditional posterior distribution of β is

$$p(\mathit{\beta }\mid \mathit{\delta },\mathit{Y},\mathit{Z})=p(\mathit{\beta }\mid \mathit{\delta },\mathit{Y})\propto exp\left\{-{(\mathit{Y}-\mathit{X}\mathit{\beta })}^{\prime }{\{{\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })\}}^{-1}(\mathit{Y}-\mathit{X}\mathit{\beta })/4-{\beta }^{\prime }/{\sigma }_{\beta }^2\right\}$$

which is $N(\frac{1}{2}{\mathit{V}}_0^{-1}{\mathit{X}}^{\prime }{[{\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })]}^{-1}\mathit{Y},{\sigma }_{\beta }^{2}I+\frac{1}{2}{\mathit{X}}^{\prime }{[{\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })]}^{-1}\mathit{X})$. The full conditional posterior distribution of Y_i is a truncated normal, given as

$$Y_i\mid Y_{(i)},\mathit{\beta },\mathit{\delta }~1_{\{Y_i\in A(Z_i)\}}N({\beta }^{\prime }{\mathit{X}}_i+V_i^{\prime }{\mathrm{\sum }}_0{(i)}^{-1}(Y_{(i)}-{\mathit{X}}_{(i)}\mathit{\beta }),2(1-V_i^{\prime }{\mathrm{\sum }}_0{(i)}^{-1}{V}_i))$$

where Y_(i) is with ith observation removed, Σ₀(i)⁻¹ is [Σ₀(ρ₀, δ)]⁻¹ with elements in the ith row and ith column removed, X_(i) is the matrix of X with the ith row removed, and $V_i^{\prime }$ is the ith row of Σ₀(ρ₀, δ) with its ith element removed.

The full conditional posterior distribution of q is only related to δ and is the same as that in partially linear regressions. The derivation of the full conditional posterior of δ also follows the same path as in Section 2.1.2. From equation (7), we have

$$\begin{array}{l}Pr({\delta }_m\mid (·))\propto p(\mathit{Y}\mid \mathit{\beta },\mathit{\delta })Pr({\delta }_m\mid q_m)\\ ={\mid {\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })\mid }^{-1/2}exp\{-{(\mathit{Y}-\mathit{X}\mathit{\beta })}^{\prime }{\{{\mathrm{\sum }}_0({\rho }_0,\mathit{\delta })\}}^{-1}(\mathit{Y}-\mathit{X}\mathit{\beta })/4\}{q}_m^{{\delta }_m}{(1-q_m)}^{1-{\delta }_m}\end{array}$$

Then following the same procedure as in Section 2.1.2, we draw posterior samples of δ_m from a Bernoulli distribution. All the full conditional posterior distributions are in the family of standard distributions, which ensures an efficient sampling process. To obtain posterior samples of Θ, we apply the Gibbs sampler to sequentially draw from the full conditional posterior distributions.

3 Simulation studies

3.1 Simulation scenarios

We consider 500 Monte Carlo (MC) replicates each with sample size n. Each MC replicate includes 12 predictors (e.g. DNA methylation of different CpG sites), generated from uniform distributions with lower bound 0.0001 and upper bound 12/(2m), m = 1, …, 12, plus one covariate X, generated from N(0, 2²). The random errors are assumed to be independently and identically distributed with N(0, σ²). We consider the following three types of models:

1. Model 1 (linear): E(Y_i|X_i, g_i) = f⁻¹{X_i + 3g_i1 − 2.5g_i2 + 3.5g_i4}.

2. Model 2 (quadratic): E(Y_i|X_i, g_i) = f⁻¹{X_i + 3(g_i1 − g_i2)² + 2g_i3}.

3. Model 3 (non-linear): E(Y_i|X_i, g_i) = f⁻¹{X_i + 3 cos(g_i1 × g_i2) + 2g_i3}.

In the above, g_i = {g_i1, …, g_ip} are the measures of the predictors and p = 12. For partially linear regressions, we consider n = 100 and take σ² = 0.5². Recall that by using reproducing kernels, we are able to evaluate the joint effect of a set of predictors, which may result from main effects plus any unknown interactions between the predictors. Even if it was known that only additive main effects and two-way interactions were possibly present, with 12 predictors plus one covariate X, in a standard linear regression model, we will have 80 effect terms (one for X, 12 main effects, 66 interactions, and one intercept) plus one variance parameter in the model. For probit regressions, because of the use of binary data, we consider a relatively large sample size n = 300 and assume σ² = 1.9².

The literature of variable selection in semi-parametric models is rather limited. To demonstrate the performance of the method, we compare our method with a recently developed variable selection approach, the adaptive least absolute shrinkage and selection operator (ALASSO).⁹ ALASSO is applied to linear additive models and with the feature of enjoying the oracle property,⁹ that is, the method will correctly select the model as if the correct submodel were known. ALASSO thus serves as a benchmark for models 1 and 2. The early developed variable selection method LASSO,⁷ on which ALASSO is built, is also included in our comparison. To compare between different methods, the variables selected using the proposed methods are the most important variables identified using the rule given in Section 2.1.2. Our focus is on variable selection, and thus percentages of correct selection (all important variables and no inclusion of unimportant ones), under selection (a subset of important variables and no unimportant ones), and over selection (all important variables plus at least one unimportant variables), along with model size (the number of variables selected) are recorded. The method is coded in statistical computing package R and the programs along with instructions and sample data are available on the first author’s website (http://www.sph.sc.edu/epid_bios/facultystaffdetails.php?ID=574).

3.2 Results

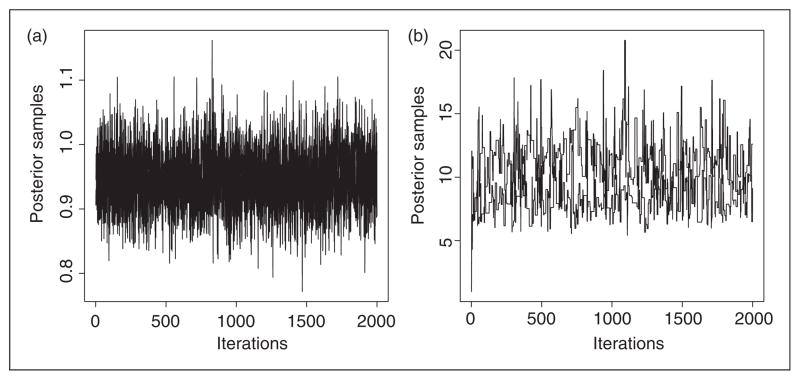
We run two chains with overdispersed starting values for each data set and the convergence is evaluated by comparing the between and within sequence variations as proposed by Gelman et al.³⁵ This diagnostic step is included in our R programs. Converged MCMC simulations are usually represented by well-mixed MCMC sequences from different chains. As an illustration, Figure 1 shows the time series for the two key parameters (β, τ) in the partially linear regression setting for model 3 for the first 2000 iterations. The sequences converge quickly within about 1200 iterations. The inference discussed below is based on MCMC samples from one chain after burn in. To ensure true convergence, we in total run 10,000 iterations and use the last 5000 to draw the inferences. Table 1 lists the selection results in partially linear regression models. For each data set, the parameter ρ₀ is estimated based on the full model and the posterior mean is used in the subsequent variable selection steps. Also listed in the table are the results from LASSO and ALASSO.

Figure 1.

Plot of posterior samples for the coefficient β (left) and set effect τ (right).

Table 1.

Summary of variable selection for partially linear regressions.

Method	% Correctness	% Under selection	% Over selection	Model size
Model 1
RKB	94.0	0.0	6.0	3.06
LASSO	100.0	0.0	0.0	3.00
ALASSO	82.2	0.0	17.8	3.25
Model 2
RKB	88.0	0.0	12.0	3.12
LASSO	81.0	0.0	19.0	3.20
ALASSO	100.0	0.0	0.0	3.00
Model 3
RKB	98.0	0.0	2.0	3.02
LASSO	0.0	33.0	67.0	4.90
ALASSO	0.0	100.0	0.0	1.00

For linear additive effect models (Model 1), the three methods all perform reasonably well (Table 1). Since LASSO and adaptive LASSO are both for linear additive effect models, this result is expected. This observation also indicates that the selection method built into reproducing kernels has the ability to capture additive linear effects and select the truly important variables. Although the LASSO and adaptive LASSO also do well for Model 2 (Table 1), essentially still a linear model with additive effect, these two methods lose their power in Model 3. The proposed method performs much better. In Model 3, the adaptive LASSO severely under-selects variables, while the LASSO tends to over-select, which is consistent with previous findings.³⁶ These findings are not surprising. LASSO and adaptive LASSO were designed specifically for linear regression models, which fits nicely the linearity property in the first two models. In Model 3, the main effects of g₁ and g₂ are absent and the effect of their interaction is non-linear. Both LASSO and adaptive LASSO do poorly in Model 3, while the proposed method does roughly equally well in all the three models.

Table 2 lists the results of variable selection under probit regression models. Following the same direction for variable selection in partially linear regressions, we compare the results with those from LASSO and adaptive LASSO in the framework of logistic regressions. It is clear that the proposed method has a better model selection results compared to those two methods. LASSO tends to select more variables, while adaptive LASSO severely under select important variables, consistent with the findings in the setting of partially linear models.

Table 2.

Summary of variable selection for probit regressions.

Method	% Correctness	% Under selection	% Over selection	Model size
Model 1
RKB	74.0	6.0	20.0	2.86
LASSO	15.0	0.0	85.0	5.65
ALASSO	10.0	90.0	0.0	0.45
Model 2
RKB	56.0	44.0	0.0	2.59
LASSO	1.6	60.8	37.6	4.50
ALASSO	0.4	99.6	0.0	1.63
Model 3
RKB	77.0	14.0	9.0	3.02
LASSO	2.4	37.0	60.6	4.3
ALASSO	0.0	100.0	0.0	1.01

We also compared our approach with the traditional AIC- and BIC-based forward, backward, and step-wise selection methods, and our approach always performed better than these standard approaches (results not shown). In summary, the new method overall out-performs both LASSO-related methods and other standard approaches, and chooses variables effectively regardless of linear or non-linear complex variable effects. In terms of computing time, however, the proposed method is relatively slower compared to the competing methods, which is due to the nature of almost all simulation-based Bayesian methods.

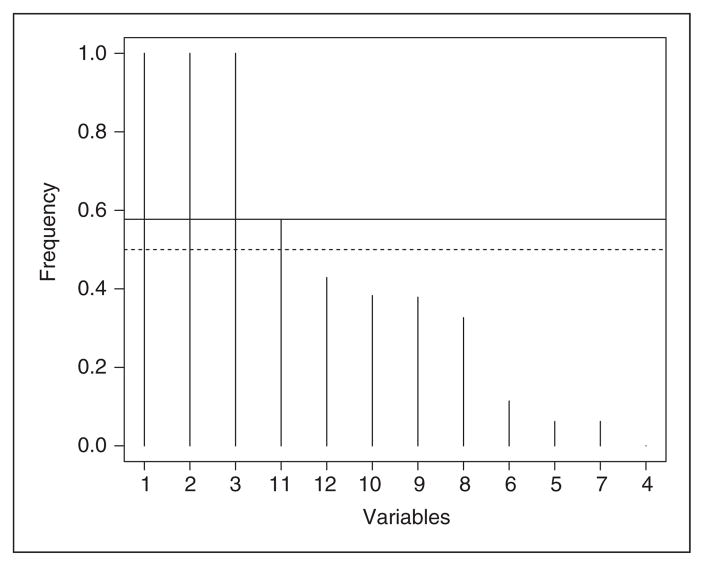
The results in Tables 1 and 2 are drawn using the rule utilized in scree plots, which aims to identify the most important variables. It is possible that some variables are still of interest but not selected by using this approach. An alternative way is to utilize the reference probability of 0.5 to identify a pool of potentially important variables such that their posterior probabilities of being included in the reproducing kernel are greater than the reference probability. Figure 2 illustrates this approach using model 3 in the probit regression setting, which clearly shows that the first three variables are the most important ones by use of scree plot. However, the posterior probability of including variable 11 in the model is higher than 0.5, which indicates that we might want to treat variable 11 as a potentially important variable. We did not identify any strong correlation between variable 11 and the other three most important variables. Its selection could be due to complex interactions with the most important ones. Thus, this potentiality in practice is likely to be data specific, but in our simulations, it is random because this variable is not chosen often among all the 500 data replicates. If we want to use the reference probability of 0.5 to identify whether variable 11 is a truly important variable, permutations on the variables can be considered to empirically test its significance of being an important variable, although this approach may impose strong computing burden.

Figure 2.

Plot of posterior probability of each variable to be included in the model in the probit regression setting. The horizontal axis is for variable indices. The solid horizontal line indicates where the sharp decrease occurs in posterior probabilities. The dotted line is the 0.5 line representing the probability of selecting a variable randomly.

3.3 The influence of ρ₀

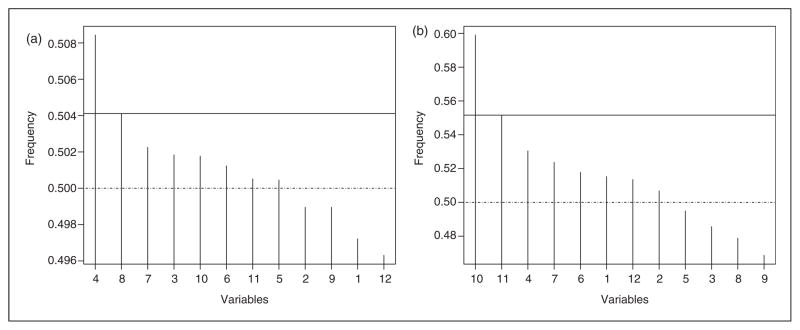
The value of ρ₀ in the above section is taken as the posterior mean of ρ based on the full model, that is, all variables are included in the reproducing kernel. In the following, we numerically evaluate the sensitivity of selection results to different choices of ρ₀. We consider additional three values of ρ₀. One choice is to set ρ₀ = 1, and the other two are either 10% smaller (ρ_s) or larger (ρ_l) than the estimated ρ₀ from the full model. We choose the first 100 data sets used in the above section from each scenario under each model setting (partially linear regressions and probit regressions) to examine the sensitivity to ρ₀. Empirical intervals at the level of 95% are derived based on estimates of ρ₀ from the 100 data sets.

Overall, the variable selection results are not substantially influenced by the choice of ρ₀ (Table 3). Except for model 1 in the setting of probit regressions, all the correctness percentages based on ρ₀ = 1 are higher than 63% and close to the percentages from the other two choices of ρ₀ (ρ_l and ρ_s), indicating the robustness of the approach with respect to the value of ρ₀. Furthermore, for the three choices of ρ₀, the model sizes are all comparable and close to the truth.

Table 3.

Variable selection results for different choices of ρ₀.

Model	Choice of ρ0	95% EI of ρ0	% CS	% US	% OS	Model size
Partially linear regression setting
1		(6.64, 2095.09)
	1		67.0	33.0	0.0	2.60
	ρl		93.8	0	6.2	3.08
	ρs		100.0	0.0	0.0	3.00
2		(2.49, 451.10)
	1		100.0	0.0	0.0	3.00
	ρl		94.0	0.0	6.0	3.06
	ρs		92.4	0.0	7.6	3.08
3		(2.34, 21.86)
	1		85.0	0.6	14.4	3.10
	ρl		98.2	0	1.8	3.04
	ρs		100.0	0.0	0.0	3
Probit regression setting
1		(0.99, 14.92)
	1		34.8	60.6	4.61	2.41
	ρl		76.0	23.0	1.0	2.79
	ρs		74.6	25.4	0.0	2.74
2		(1.06, 2.70)
	1		63.8	36.0	0.2	2.68
	ρl		55.0	44.4	0.6	2.61
	ρs		62.0	38.0	0.0	2.64
3		(0.91, 5.18)
	1		85.6	9.0	5.4	2.98
	ρl		77.0	12.2	10.8	3.02
	ρs		80.4	13.0	6.6	3.07

ρ_s is 10% lower and ρ_l is 10% higher than the posterior mean based on the full model.

EI: empirical interval of ρ₀ inferred from the full model; CS: correct selection; US: under selection; OS: over selection.

We shall point out that for a given model, the value of ρ₀ affects the fit of the reproducing kernel. For instance, model 1 in the setting of linear regressions is a regular linear regression model. In this case, a reproducing kernel built upon first order polynomial kernels shall provide the best fit. Since a Gaussian kernel approaches to a first order polynomial kernel when ρ₀ goes to infinity, taking large values of ρ₀ in Gaussian kernels will provide a reasonable approximation. Our overall large estimates of ρ₀, shown by the 95% empirical intervals (third column of Table 3), reflect the effort of approximation. Furthermore, the choice of ρ₀ will influence the estimate of a variable set effect. Given that unimportant variables provide negligible effects on the outcome, we expect ρ₀ under the true model to be comparable to that under the full model. It is thus recommended that, if estimating the effect of the whole group of variables is also desired besides selecting the variables, we should use the estimate of ρ₀ under the full model to provide simultaneous results on variable selection and group effect estimate.

3.4 Handling high-dimensional data

Earlier simulations indicated the feasibility of the method in dealing with complicated interaction effects. By design, the method has the ability to handle high-dimensional data, in particular, data with large p and small n. To illustrate this, we use model 3 in the setting of partially linear regression. Model 3 is chosen because it represents a more realistic association common in many high-dimensional data, e.g. microarray gene expression data or DNA methylation data. Instead of 12 predictors as noted in Section 3.1, we simulate 100 data sets with each including 120 predictors and of sample size n=100. These 120 predictors are generated from uniform distributions with lower bound 0.0001 and upper bound 120/(2m), a range the same as that in Section 3.1.

We use the same sampling methods noted in earlier sections to infer the parameters and select the variables. Based on the 100 data sets, the percentages of correct selections and over selections are 96% and 4%, respectively, and there is no under selection. The average model size is 3.04, which is consistent with the high percentage of correctness. These findings are similar to those listed in Table 1. We also considered the probit regression model and observed a similar pattern as in Table 2 (results not shown). On the other hand, the competing methods, LASSO and adaptive LASSO, missed almost all the correct models. These findings demonstrate that the new methods not only have the potential to deal with complicated interaction effects but also have the ability to handle high-dimensional data with the number of variables larger than sample size.

4 Real data application

We apply the proposed methods to identify epigenetic factors potentially associated with environmental tobacco smoke exposure. The epigenetic factors considered in this application are DNA methylation of 12 CpG sites (columns 1 to 3 in Table 4). These 12 CpG sites are chosen based on their potential association with asthma and maternal smoking drawn from our preliminary study and other studies.^37,38 There is evidence that DNA methylation is associated with maternal smoking,³⁸ a strong risk factor of asthma.³⁹ Furthermore, maternal smoking might be linked to early onset of offspring smoking.⁴⁰ Assuming a CpG site is stable once it is methylated as indicated in some recent studies,^38,41 it will be of interest to identify CpG sites whose methylation level is associated with maternal smoking during pregnancy and those whose methylation level is associated with tobacco smoke exposure in postnatal life. For the first case, we use the method designed for continuous outcomes, i.e. the setting of partially linear regressions, and use cotinine level as the outcome variable. Cotinine is an alkaloid detected in tobacco and has been used as a biomarker of smoke exposure.⁴² In this model, we further include creatinine as an adjusting factor to adjust the effect of fluid intake on the urinary concentration of cotinine.⁴³ The sample size for the first application is 114. For the second application, we select the CpG sites in the setting of probit regressions and use maternal smoking status as the response. In total, 245 observations are available for this application.

Table 4.

Information of the 12 CpG sites, ordered by gene names and CpG ID, and the selection results (selected CpG sites are marked with “✓”).

CpG ID	Reference gene name	Chromosome	Partially linear models			Probit models
			RKB	LASSO	ALASSO	RKB	LASSO	ALASSO
cg05575921	AHRR	5	✓	✓	✓	✓	✓	–
cg17924476	AHRR	5	✓	–	–	–	✓	–
cg21161138	AHRR	5	✓	–	–	✓	✓	✓
cg23067299	AHRR	5	–	–	–	–	✓	–
cg05549655	CYP1A1	15	✓	✓	✓	–	✓	–
cg11924019	CYP1A1	15	✓	–	–	✓	✓	–
cg17852385	CYP1A1	15	✓	–	–	✓	✓	✓
cg18092474	CYP1A1	15	✓	–	–	✓	–	–
cg25949550	CNTNAP2	7	–	–	–	✓	–	–
cg07989490	GATA3	10	–	–	–	✓	✓	–
cg11679455	GATA3	10	✓	–	–	–	✓	✓
cg09791102	IL4R	16	–	–	–	✓	✓	–

RKB: the reproducing kernel based method.

For the selection of CpG sites based on cotinine levels, the estimate of ρ₀ is 745.245, implying a possible linear association of methylation with cotinine level. We run two chains with 10,000 iterations each to estimate the number of iterations needed for convergence. The sequences converged within about 800 iterations for β and τ, similar as those observed in the simulations. The inference given below is based on one chain of 10,000 iterations with 5000 iterations used as burn in to ensure true convergence. By using the rule in scree plots, we identified the most important CpG site, cg11924019, which is in the CYP1A1 gene. Additional seven CpG sites are identified with posterior probabilities larger than 0.5 and should be treated as important sites as well (Figure 3(a), column 4 in Table 4). We further apply the LASSO and ALASSO methods to select the CpG sites. Both methods give the same selection results with two CpG sites (cg05549655 and cg05575921) selected (columns 5 and 6 in Table 4). These two sites are selected by the proposed method as well. A further calculation on the correlations in methylation indicates that methylation of these two sites are highly correlated with the methylation of CpG sites selected using the reproducing kernel based method. Except for site cg11679455 showing a weak correlation with cg05549655 and cg05575921 (|r|<0.2), most other correlations are higher than 0.91 indicating strong collinearity. This possibly explains the under-selection from the LASSO and the ALASSO methods.

Figure 3.

Plot of posterior probability of each variable to be included in the model. (a) Cotinine level-based (partially linear regression setting). (b) Maternal smoking-based (probit regression setting). The horizontal axis is for variable indices. The solid horizontal line indicates where the sharp decrease occurs in posterior probabilities. The dotted line is the 0.5 line representing the probability of selecting a variable randomly.

When selecting CpG sites based on maternal smoking status, ρ₀ in the probit model is estimated as 0.675. As expected, the convergence of the two Markov chains is observed around 1700 iterations, slower than that under the partial linear regression models. The results are from 5000 iterations after 5000 iterations for burn in. One most important CpG site is identified by the scree plot rule (cg05575921) and seven additional CpG sites are identified after comparing with the reference probability of 0.5 (Figure 3(b), column 7 in Table 4). The methods of LASSO and ALASSO are also applied and identified 10 and three CpG sites (last two columns in Table 4), respectively. Based on previous studies³⁶ and from the findings in our simulation studies in terms of overselection and underselection patterns of these two methods, we conclude that the selection results from the proposed method are closer to the truth.

Overall, the proposed methods seem to conclude a more accurate selection of CpG sites in both situations, continine level-based and maternal smoking-based. In addition, among the selected CpG sites using the proposed methods, three sites are unique to the selection process based on maternal smoking, three are unique based on cotinine levels, and five are in common. This indicates that exposure to maternal smoking and postnatal smoking (reflected by cotinine levels) may affect DNA methylation differently to some extent.

5 Summary

We present Bayesian methods for variable selection in semi-parametric models assuming possibly non-linear in an unknown form of associations between candidate variables and a response variable. The association is described using reproducing kernels, which allow linear or non-linear effects in any form. An indicator variable is introduced to the reproducing kernels to indicate the inclusion or exclusion of a variable. Two model settings are considered: partially linear regressions and probit regressions.

The method is demonstrated and evaluated through simulations. The simulation results show that the proposed method can efficiently identify the correct variables regardless of association patterns. We compare the methods with the LASSO and adaptive LASSO methods. In the simulations, we assumed the variables are not correlated. Thus, for regular linear regression models (models 1 and 2), the LASSO and adaptive LASSO give similar results to those from the proposed methods, but they become inferior when the variable effects are non-linear (model 3). When applying the methods to real data sets, the selection results from the proposed methods seem to be more reliable.

The proposed methods are easy to implement and expected to have quick convergence because all the full conditionals are standard distributions. On the other hand, as for all Bayesian methods, the inferences generally are drawn from MCMC simulations. Thus, in terms of computing speed, when the number of predictors is large, the Bayesian methods are relatively slower than the Frequentist approaches considered in this article (LASSO and ALASSO), especially under the probit regression models due to the computing time used to infer the latent variables Z. However, the results from the proposed Bayesian methods are much improved compared to those from the Frequentist approaches. In addition, extending the two methods to discrete g variables is straightforward. We believe these advantages will benefit medical researchers to efficiently identify important risk factors that may have convoluted effects on a certain type of health outcome. Finally, our methods can be easily modified to fit other types of statistical models including log-linear models and models applied to survival data analysis. On the other hand, the methods have some limitations that warrant a discussion. Recall that the variable selection approaches are built upon the evaluation of an overall set effect measured through reproducing kernels. The selection of each important predictor is based on the evaluation of its contribution to the overall set effect on an outcome variable instead of each individual variable’s direct effect on the outcome. In some situations, it may be desired to evaluate the direct effect of each selected variable, besides their overall contribution as a group. Furthermore, it is possible that the candidate variables are a mixture of categorical and continuous variables. The kernels normally applied are either suitable for categorical variables or continuous variables. Developing an approach that has the ability to handle the mixture of two types of variables is our on-going work.