Quantifying cell-generated mechanical forces within living embryonic tissues

Abstract

Cell-generated mechanical forces play a critical role during tissue morphogenesis and organ formation in the embryo. However, little is known about how these forces shape embryonic organs, mainly because it has not been possible to measure cellular forces within developing three-dimensional (3D) tissues in vivo. Here we present a method to quantify cell-generated mechanical stresses that are exerted locally within living embryonic tissues using fluorescent, cell-sized, oil microdroplets with defined mechanical properties and coated with surface integrin or cadherin receptor ligands. After introducing a droplet between cells in a tissue, local stresses are determined from the droplet shape deformations, which are obtained via fluorescence microscopy and computerized image analysis. Using this method, we quantify the anisotropic stresses generated by mammary epithelial cells cultured within 3D aggregates and confirm that these stresses (3.4 nN/µm²) are dependent on myosin II activity and more than two-fold larger than the stresses generated by cells of embryonic tooth mesenchyme when analyzed within similar cultured aggregates or in developing whole mouse mandibles.

Mechanical forces have been known to sculpt embryonic structures for over a century¹ and their influence on cell behavior is now well established^2–10. In vitro studies with cultured cells have shown that cellular forces affect their directionality, intensity and coherence of movement^11–13, orientation of division^14,15, rate of proliferation^16–19 and even differentiation^18,20. Furthermore, the application of external forces to living embryonic tissues has proved that mechanical forces can induce the expression of key developmental genes^21,22. Despite abundant evidence that cell behavior depends critically on mechanical forces, the precise mechanisms by which these forces influence cell behavior in vivo and drive developmental processes that shape whole embryonic tissues and organs remain unknown.

Most of our current knowledge on how mechanical forces alter cell behavior was enabled by the development of techniques that permit either the measurement of cellular forces or the application of controlled mechanical force on cultured cells. Atomic Force Microscopy^23,24, Micropipette Aspiration^25,26 and Magnetic Cytometry²⁷ have been applied to measure cell mechanics and adhesion forces, and, more recently, FRET-based molecular force sensors have been developed to measure molecular tension in cultured cells^28,29. These approaches have been complemented by in vitro experiments using soft gel substrates (Traction force microscopy^11,30,31), elastic micro-pillars^32,33 and gel matrices^34,35 to quantify traction forces generated by cultured cells, individually and collectively in 2D and 3D geometries. However, none of these techniques can be used to measure mechanical forces generated by individual cells within the physiological context of living tissues and organs in vivo.

Measuring cellular forces in vivo has proven very challenging. To date, the only available technique to probe cellular tension is Laser Ablation³⁶. Using a femtosecond pulsed laser to ablate cell-cell junctions in the living embryo and quantifying the retraction speed of the cut cell junction, this technique allows to qualitatively infer relative differences in cell tension in different tissue contexts. While useful to qualitatively estimate the tension state at a cell junction^36,37 and even in portions of a tissue^38,39, it does not provide a quantitative measure of cellular forces. This is because the material properties of the cells and tissue surrounding the ablation site are unknown, which makes it impossible to determine the quantitative relation between cell tension and retraction speed at the ablated site.

Here we describe a new technique that permits direct quantification of endogenous cellular forces in situ within living tissues and developing organs. The technique consists of using oil microdroplets, similar in size to individual cells, with defined mechanical properties and displaying ligands for cell surface adhesion receptors, as force transducers in living embryonic tissues (Fig. 1a). When a fluorescently-labeled microdroplet is injected in the intercellular space of a living embryonic tissue, adjacent cells adhere to the surface receptor ligands on the microdroplet and exert forces on it, causing its deformation from the equilibrium spherical shape. By reconstructing the shape of the deformed droplet in 3D using confocal microscopy and computerized image analysis, and knowing its precise mechanical properties, we can obtain the stresses (force per unit surface) that cells apply at every point on the droplet surface. In situations where droplets are fully embedded within tissues (as in most studies described below), this method only permits measurement of spatial variations of cellular stresses around the droplet (anisotropic stresses). However, total (both anisotropic and isotropic) cellular stresses can be measured in certain tissues (e.g., epithelial tissues, cultured cell layers, etc.) at scales comparable to cell size using this technique if droplets are only partially embedded in the tissue.

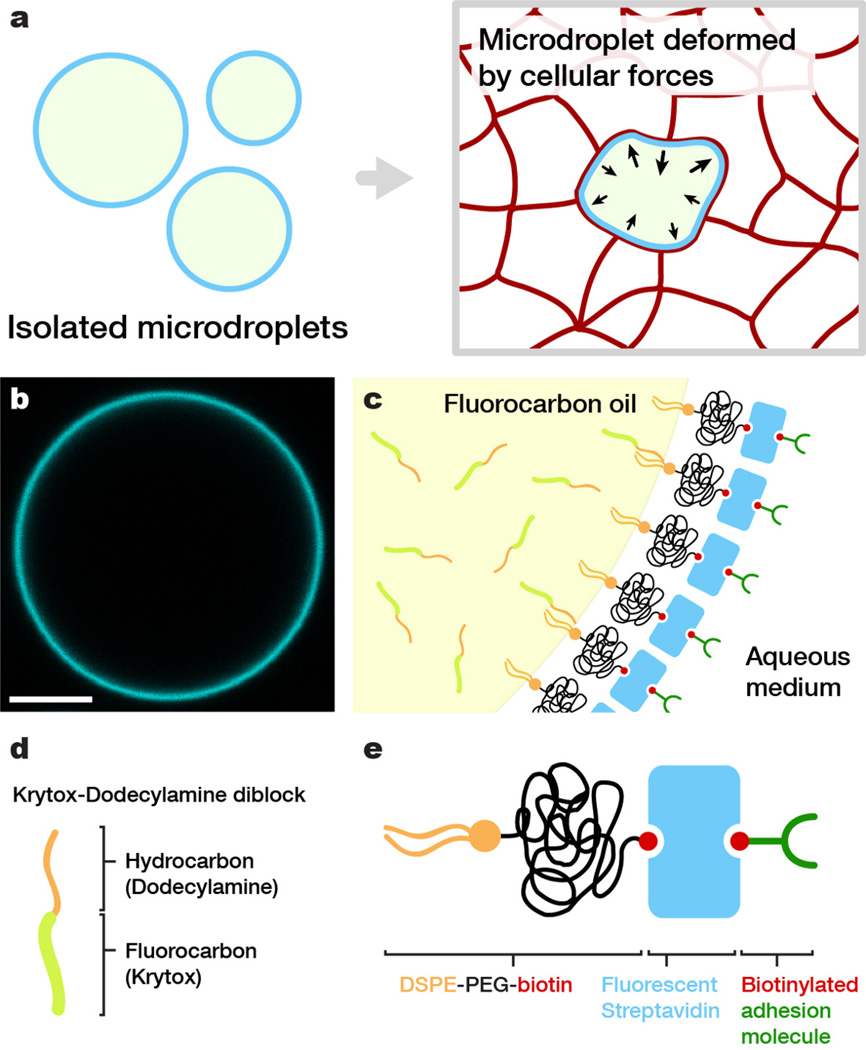
Figure 1. Oil microdroplets as force transducers.

(a) Sketch of isolated spherical oil droplets in solution (left) and a droplet embedded in-between the cells forming an embryonic tissue (right); the deformation of the droplet is a consequence of local cellular forces. (b) Confocal section of an isolated fluorocarbon oil droplet coated as described in the main text. Droplet surface is fluorescently labeled with Cy5-streptavidin. Bar, 10 µm. (c) Sketch of the interface between fluorocarbon oil and surrounding medium, indicating the different molecules involved in the coating (functionalization) of the droplets. (d) Sketch of fluorocarbon-hydrocarbon (Krytox-Dodecylamine) diblocks used to vary the interfacial tension and (e) surfactant molecules (DSPE-PEG-biotin) used to stabilize and control the surface properties of the droplet.

Results

Oil microdroplets as force transducers

Vegetable oil droplets with defined mechanical properties have been previously employed to successfully measure forces generated by growing actin networks in vitro, using the droplet deformations as a local force gauge^40,41. Unlike experiments with isolated molecules, force measurements involving living cells or tissues cannot be performed with vegetable oils as the lipids composing the droplets easily transfer to cell membranes, potentially causing toxicity or complicated side effects. To overcome this problem, we used biocompatible fluorocarbon oils^42,43 that are immiscible in vegetable oils. In order to use fluorocarbon oil droplets as force transducers, it is necessary to: (1) stabilize them and control their interfacial tension (which determines the droplet’s resistance to deformation), (2) modify their surface chemistry to promote specific adhesion of adjacent living cells, and (3) fluorescently label the droplet (or its surface) to visualize its deformation in situ in real-time.

We achieved these goals by stabilizing droplets (ranging from about 2 to 40 µm in radius) composed of Fluoroinert FC-70 fluorocarbon oil (Perfluorotripentylamine) using a biocompatible surfactant consisting of an amphiphilic molecule, 1,2-Distearoyl-sn-glycero-3-phosphoethanolamine (DSPE), with a polyethylene glycol spacer linked to biotin (PEG-biotin) attached to its head group (Fig. 1c,e and Online Methods). The PEG spacer of the DSPE-PEG-biotin surfactant prevents non-specific interactions at the droplet surface, while the biotin group enables specific coating of the droplet with biotinylated ligands for integrins (RGD peptide) or cadherins (anti-E-cadherin antibody) using intervening bifunctional fluorescent streptavidin molecules, which also enable microscopic visualization of the droplets (Fig. 1b,c). The interfacial tension of the fluorocarbon droplets needs to be adjusted to allow the measurement of stresses applied by different types of cells. We accomplished this by using fluorocarbon-hydrocarbon co-surfactants (Krytox-Dodecylamine or Krytox-DDA; see Online Methods and⁴⁴), that are soluble in fluorinated solvents (Fig. 1c,d) and allowed us to lower the interfacial tension 6-fold.

To quantify the mechanical forces that cells apply on the surface of an oil droplet, it is necessary to relate the geometry of the droplet to the local cellular forces responsible for its deformation. Such a relation is provided by Laplace’s Law⁴⁵, which accounts for the local normal force balance at every point of the droplet interface. The internal pressure, p_i, of an oil droplet with radius R suspended in aqueous medium is given by p_i = p_e + 2γ/R, where p_e is the external pressure and γ the interfacial tension of the droplet and the surrounding medium. In absence of external forces other than the isotropic hydrostatic pressure, the equilibrium droplet shape is a sphere (Fig. 1b). However, when large enough anisotropic forces are applied on the droplet, its shape deviates from the sphere. Specifically, when placed in spaces between cells within living tissues (Fig. 1a), droplets will be deformed if the stresses generated by the cells are greater than the resisting stresses (2γ/R) of the droplet interfacial tension. Consider the forces per unit area, or stresses σ_nn, applied by cells in the outward normal direction at each point on the droplet surface (positive values of σ_nn indicate cells pulling on the droplet and vice versa). In general, as the cells surrounding a droplet apply different forces at different points, the normal stresses σ_nn vary across the droplet surface. Accounting for the normal stresses σ_nn that cells apply on the droplet, local normal force balance (Laplace’s Law) on the droplet surface reads⁴⁰

$$p_i^{\prime }=p_e^{\prime }+2\gamma H(\theta ,\varphi )-{\sigma }_{nn}(\theta ,\varphi ),$$ (1)

where H is the local mean curvature of the droplet surface⁴⁶, parameterized using angular spherical coordinates θ and ϕ, and $p_i^{\prime }$ and $p_e^{\prime }$ are, respectively, the droplet internal and external hydrostatic pressures, which are in general different from the initial values (p_i and p_e) of the spherical droplet in solution. It is convenient to decompose the isotropic and anisotropic contributions to H and σ_nn by defining H = H_i + δH and σ_nn = −P_i + δσ_nn, where H_i and −P_i are the isotropic contributions to the droplet mean curvature and normal stress respectively, and δH(θ, ϕ) and δσ_nn(θ, ϕ) are their anisotropic components (hence the explicit dependence on the position on the droplet surface). The isotropic component of the stress, −P_i, is independent of the fluid hydrostatic pressure and is generated by cells in the tissue^17,47; it corresponds to an effective tissue pressure P_i due to cellular crowding. Given that oil is essentially incompressible, the isotropic component of the mean curvature H_i is given by H_i = 1/R, with R being the radius of the initial undeformed spherical droplet, while the tissue pressure reads $P_i=(p_i^{\prime }-p_i)-(p_e^{\prime }-p_e)$. This implies that a measure of the local tissue pressure P_i requires monitoring of the droplet internal hydrostatic pressure. In cases where the droplet is only partially covered by cells, it is possible to measure the total tissue pressure P_i (isotropic stress) from the droplet shape (see Supporting Note 3). However, if the droplet is fully embedded in the tissue, as in the experiments presented below, it is not possible to determine the isotropic component of the stresses using this approach. While a measure of the isotropic stresses is required to obtain the value of the local normal stresses at the droplet surface, many morphogenetic events during embryonic development are driven by local cell rearrangements caused by local spatial inhomogeneities in cellular stresses^7,37, which correspond to the anisotropic component of the normal stresses on the droplet surface δσ_nn(θ, ϕ). Writing Eq. 1 for the anisotropic components leads to

$$\delta {\sigma }_{nn}(\theta ,\varphi )=2\gamma \delta H(\theta ,\varphi )=2\gamma \left(H(\theta ,\varphi )-\frac{1}{R}\right),$$ (2)

which provides a direct relation between the droplet shape in 3D and the anisotropic stresses responsible for inducing that deformation. We note that Eq. 2 is the 3D analog of the force-extension relation for a linear spring, with the droplet interfacial tension and the local mean curvature playing the roles of the spring constant and the spring extension, respectively.

Cellular stresses in cultured 3D aggregates

To explore the utility of this method, fluorocarbon droplets (ranging from about 2 to 40 µm in radius) lacking Krytox-DDA co-surfactant, but functionalized with ligands for either integrin or E-cadherin receptors, were respectively combined with suspensions of mesenchymal cells (isolated from day 10 embryonic tooth rudiments) or premalignant mammary epithelial cells (isolated from mammary glands of 8 week-old transgenic mice), compacted into 3D cell aggregates via centrifugation, and maintained in culture for 2–5 days depending on cell type (Fig. 2a and Online Methods). Cell-droplet attachment was confirmed using confocal microscopy in sparse mixtures of cells and droplets (Online Methods). Confocal imaging of the compact 3D cellular aggregates confirmed that both epithelial and mesenchymal cells were able to apply large enough forces to induce moderate droplet deformations (Fig. 2b,d). The 3D shape of a given droplet was obtained through computerized reconstruction using confocal stacks through the sample (Fig. 2a), allowing the calculation of the local mean curvature H(θ, ϕ) at the droplet surface (Online Methods). The interfacial tension of the droplets in contact with cell culture medium was determined to be γ = 26 ± 2 mN/m under cell aggregate culture conditions (Online Methods). Using Eq. 2 and the measured local mean curvature and interfacial tension, we mapped the anisotropic stresses applied by cells on the droplet surface (Fig. 2c,e). Regions on the droplet surface with positive anisotropic stresses (δσ_nn > 0) are associated with cells either pushing the droplet less strongly than the isotropic pressure P_i or directly pulling on the droplet (tensional stresses), whereas regions with δσ_nn < 0 (compressive stresses) are associated with cells pushing stronger on the droplet than the isotropic tissue pressure P_i, either directly or indirectly by pulling on surrounding regions. The values of the anisotropic stresses measured in situ within cell aggregates are in the range of several nN/µm² for both cell types, in agreement with previous in vitro measurements^34,48.

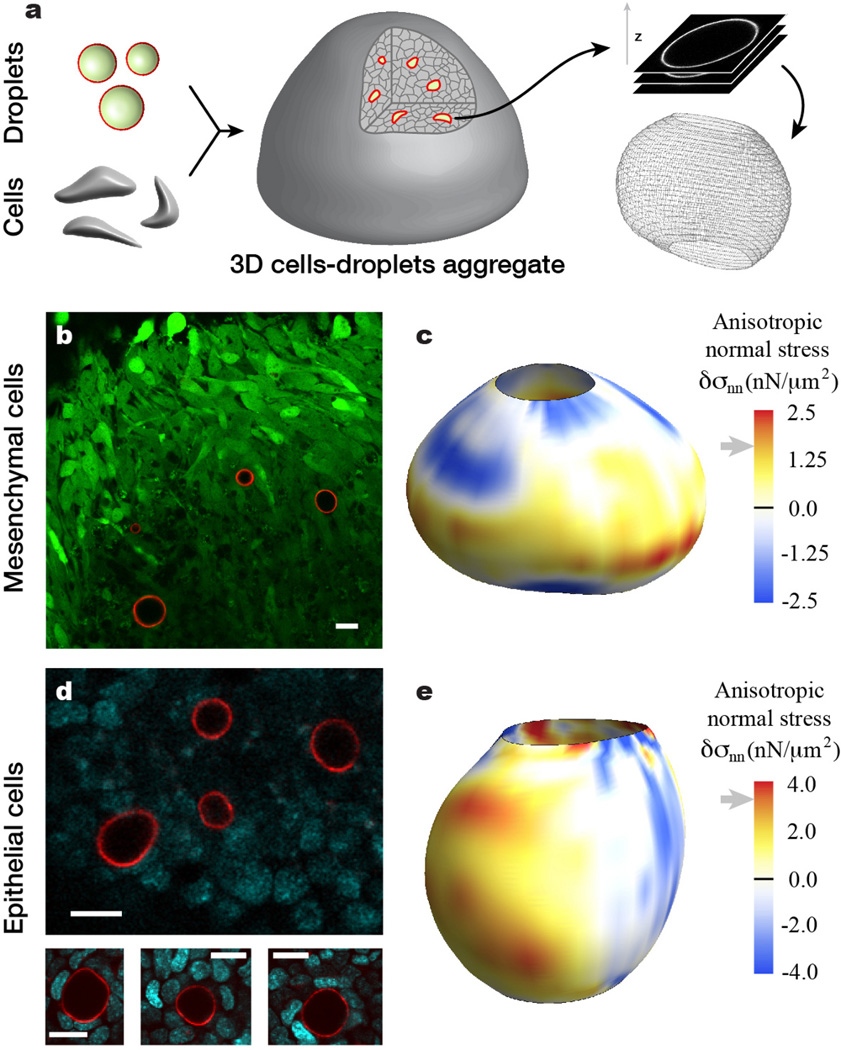
Figure 2. Measure of cell-generated mechanical stresses in epithelial and mesenchymal cell aggregates.

(a) Sketch of cells-droplets aggregate formation. Functionalized droplets and cells are mixed, compacted and cultured to form aggregates. Oil droplet shapes are obtained via high-resolution 3D confocal imaging and their surface coordinates are obtained from image analysis of the data (Online Methods). (b) Confocal section through an aggregate of GFP-positive tooth mesenchymal cells (green) containing fluorocarbon droplets (droplet surface labeled fluorescently; red) coated externally with ligands for integrin receptors. (c) Example of 3D reconstruction of a droplet in a tooth mesenchymal cell aggregate with the values of the anisotropic stresses mapped on the droplet surface. (d) Confocal section through an aggregate of mammary epithelial cells (DNA is visible; cyan) and fluorocarbon droplets coated externally with ligands for E-cadherin receptors. (e) Example of 3D reconstruction of a droplet in a mammary epithelial cell aggregate with the values of the anisotropic stresses mapped on the droplet surface. Gray arrows next to stress scales indicate the average values of the maximal anisotropic stresses obtained from statistics on 2D confocal sections of multiple droplets (see main text). Scale bars, 20 µm.

While in situ measurements of the stresses acting on a droplet require 3D reconstruction of its shape, statistical values of cellular stresses within a tissue can be obtained from ensemble statistics on 2D confocal sections of different droplets in the cellular aggregate or whole tissue. Specifically, the average value of the maximal anisotropic stresses, $\overline{\delta {\sigma }_{nn}^M}$, can be obtained from the average value of the maximal curvature difference, $\overline{\mathrm{\Delta }\kappa }$, along the contour of droplet sections (Fig. 2b,d and Fig. 3a–d; see Online Methods), namely

$$\overline{\delta {\sigma }_{nn}^M}=\gamma \overline{\mathrm{\Delta }\kappa }$$ (3)

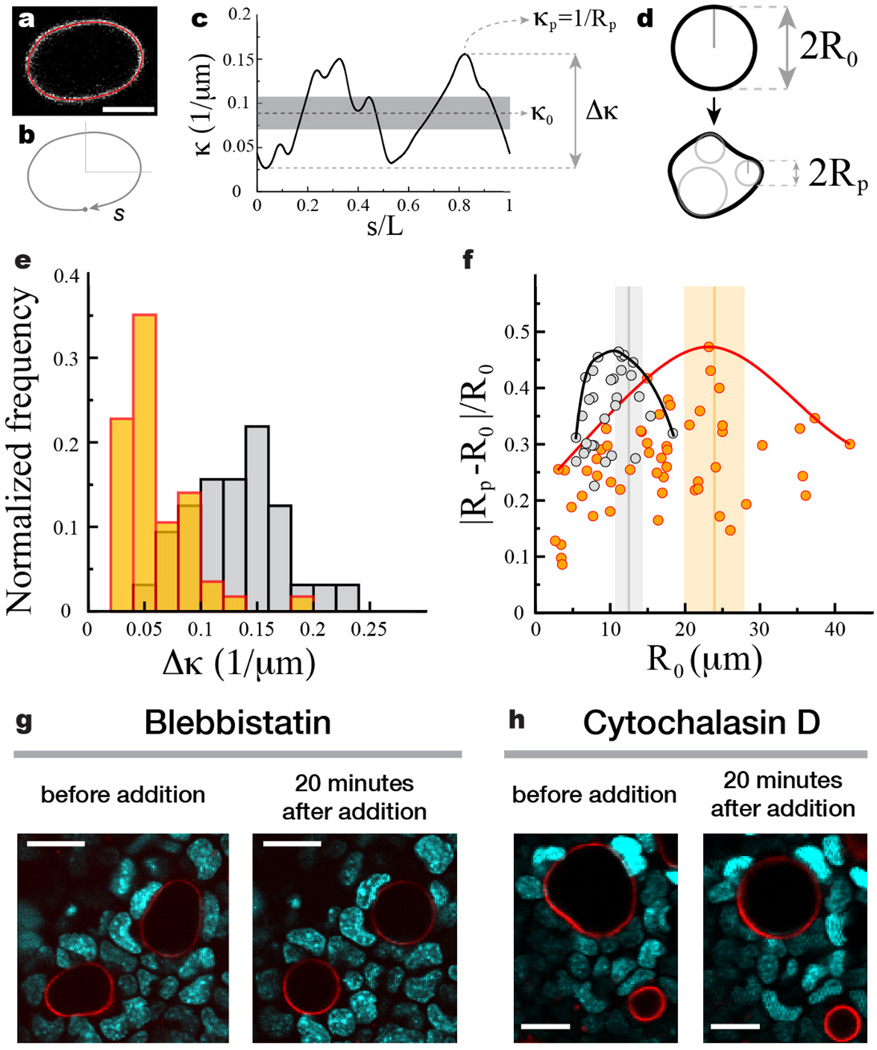
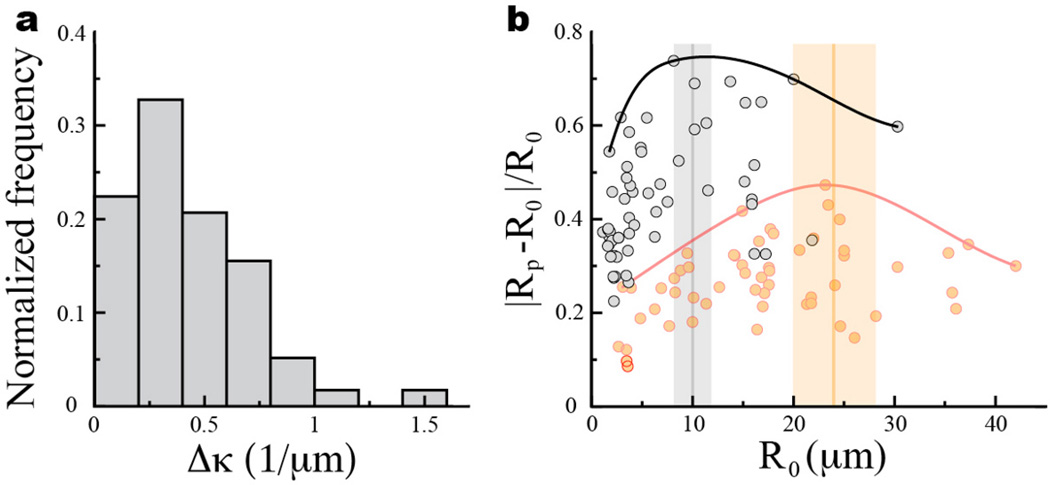
Figure 3. Ensemble statistics of droplet deformations in cell aggregates using 2D droplet confocal sections.

(a) Confocal section of a droplet with the detected droplet contour overlaid (red). (b) The contour is parameterized by its contour length s normalized by the total contour length L. (c) Calculated curvature along the contour. The average curvature, maximal curvature and the difference between the maximal and minimal values of the curvature are defined as κ₀, κ_p and Δκ, respectively. (d) Sketch of undeformed and deformed confocal sections of a droplet with definitions of the droplet average radius of curvature R₀ = 1/κ₀ and the minimal radius of curvature along the contour R_p = 1/κ_p. (e) Normalized frequency of Δκ for droplets in aggregates of mammary epithelial cells (gray; N = 32) and tooth mesenchymal cells (orange; N=56). (f) Relative droplet deformation |R_p − R₀|/R₀ as a function of the radius R₀ of the undeformed droplet section. Solid lines depict the envelope of maximal values of relative droplet deformation (black - epithelial cells; red - tooth mesenchymal cells). The vertical bars indicate the measured values (mean (vertical line) ± standard deviation of the mean (vertical bar)) of cell size in the aggregates (see Supplementary Note 1). (g–h) Effects of inhibition of myosin II and actin polymerization on cellular forces, using (g) Blebbistatin and (h) Cytochalasin D, respectively. Confocal sections through mammary epithelial cell aggregates (DNA is visible; cyan) showing deformed droplets (droplet surface labeled fluorescently; red) before addition of the drugs and 20 minutes after drug addition. Droplets round up as a consequence on myosin II and actin polymerization inhibition. For a time-lapse of the inhibition process see Supplementary Videos 1 and 2.

Measuring the curvature along 2D confocal sections (Fig. 3a–c) on multiple droplets embedded in cell aggregates allowed us to build the distribution of maximal curvature differences Δκ for both mammary epithelial cells and tooth mesenchymal cells (Fig. 3e). The average value of the maximal curvature differences, $\overline{\mathrm{\Delta }\kappa }$, is obtained directly from their distribution and measured to be 0.132 ± 0.007 µm⁻¹ (mean ± standard deviation of the mean) and 0.059 ± 0.006 µm⁻¹ for droplets in aggregates of mammary epithelial cells and tooth mesenchymal cells, respectively. Using Eq. 3, the measured average values of maximal curvature differences and the value of the interfacial tension, we obtained the average value of maximal anisotropic stresses to be 3.4 ± 0.4 nN/µm² and 1.5 ± 0.2 nN/µm² for mammary epithelial cells and tooth mesenchymal cells, respectively. These values are in good agreement with our in situ 3D measurements of anisotropic stresses (Fig. 2c,e) and also with recent 3D traction force microscopy measurements³⁴ which reported that fibroblasts generate maximal stresses of about 2 nN/µm². Analysis of the relative droplet deformations with varying droplet sizes shows the existence of a characteristic length scale, different for epithelial and mesenchymal cells, for which relative droplet deformations are maximal (Fig. 3f). Measuring the average cell size in the aggregates (see Supplementary Note 1) shows that the observed length scale of largest relative droplet deformations corresponds to the average cell size in each aggregate (Fig. 3f), indicating that the largest departures from the isotropic mechanical state occur at cellular scales.

Importantly, inhibition of myosin II activity and actin polymerization in mammary epithelial cell aggregates (see Online Methods), using blebbistatin (Fig. 3g) and cytochalasin D (Fig. 3h) respectively, led, in both cases, to complete rounding of the droplets, confirming that the measured stresses are actively generated by cells via an actomyosin-based contraction mechanism (see also Supplementary Videos 1 and 2). Moreover, disruption of cells with the detergent sodium dodecyl sulfate led to the disassembly of cell aggregates and complete rounding of the droplets (Supplementary Video 3).

Cellular stresses in living embryonic tissue

Based on our successful measurements of stresses in cultured cell aggregates, we set out to determine whether this new method can be used to directly quantify cell-generated forces within living embryonic tissues (Fig. 4). To do this, we measured the cellular stresses exerted by tooth mesenchymal cells in living tooth mandible explants (Fig. 4b–f), which contain the same tooth mesenchymal cells as in the 3D cell aggregates we studied in vitro. Between 10 to 30 microdroplets coated with ligands for integrin receptors (RGD peptide) were microinjected into the dental mesenchyme of living dissected mouse mandibles at either stage E11 or E13.5 (Fig. 4g and Online Methods). The droplets were placed as close as possible to the thickened epithelium that overlies the tooth buds during these early developmental stages. Interestingly, negligible droplet deformations were observed when droplets identical to those used previously in the 3D cell aggregate experiments were utilized. We hypothesized that the stresses generated by cells within these developing tissues were not large enough to deform the droplets, and took advantage of the Krytox-DDA co-surfactant we developed (Fig. 1c–d) to lower the interfacial tension to 4 ± 3 mN/m (see Online Methods), thereby making the droplets more easily deformable.

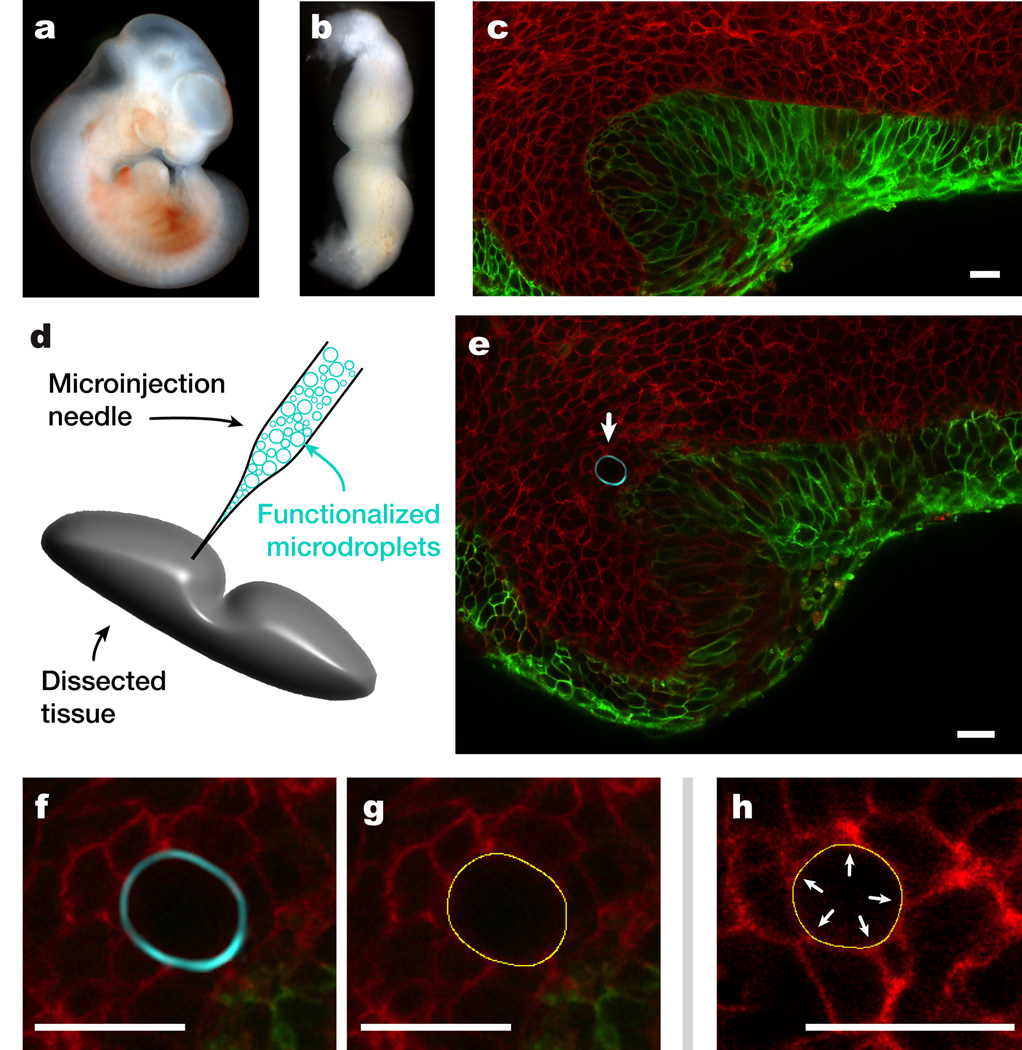
Figure 4. Measure of cell-generated mechanical stresses in living tooth mandibles.

(a) Mouse embryo at 11 days post fertilization (E11). (b) Dissected, living tooth mandible (mandibular arch) at stage E11. (c) Maximal intensity projection of a 3D reconstruction of a fluorescent reporter E13.5 embryonic mouse mandible. Epithelial cells express N-terminal membrane tagged version of EGFP and all other cells express an N-terminal membrane tagged version of tdTomato (Online Methods). (d) Same as in c but showing only the epithelium. The thickening of the epithelium characteristic of tooth bud formation at E13.5 appears as localized increase in the EGFP signal (arrows indicate the location of epithelial thickening). (e) Confocal section of an incisor tooth bud at E13.5. (f) Enlarged region of e showing the boundary between epithelial and mesenchymal cells. (g) Sketch of functionalized droplet micro-injection in a dissected living mandible. (h) Confocal section of an incisor tooth bud with a fluorocarbon droplet (droplet surface labeled fluorescently; cyan) embedded in between cells of the dental mesenchyme. White arrow indicates the location of the droplet. (i) Enlarged region in h showing a close-up of the embedded droplet. (j) Detected pixel-resolution contour (yellow) of droplet in i. (k) Detected pixel-resolution contour (yellow) of a droplet embedded in living tooth mesenchymal tissue showing correspondence between higher curvature regions (arrows) on the droplet surface and cell-cell junctions contacting the droplet. Scale bars, 20 µm, except in c–d, which are 200 µm.

Microdroplets similar in size as those used previously but with this lower interfacial tension showed substantial deformations when embedded between cells of the dense dental mesenchymal tissue (Fig. 4h–k). Statistical analysis of confocal sections of multiple droplets in the tissue allowed us to obtain the distribution of maximal curvature differences Δκ (Fig. 5a), as well as its average value $\overline{\mathrm{\Delta }\kappa }=0.41\pm 0.04\mathrm{\mu }{\mathrm{m}}^{-1}$. Using Eq. 3, the measured average value of the maximal curvature differences and the interfacial tension, we obtained the average value of the maximal anisotropic stresses generated by mesenchymal cells in living dental mesenchyme at embryonic stage E11 to be 1.6 ± 0.8 nN/µm². This value corresponds, within the experimental error, to the value measured for tooth mesenchymal cells in cultured aggregates. Analysis of relative droplet deformations shows that these are maximal at a length scale of about 10 µm (Fig. 5b), which corresponds to the average size (10 ± 2 µm) of tooth mesenchymal cells that we measured in the dental mesenchyme (Fig. 5b and Supplementary Note 1). As the stresses necessary to deform a droplet with interfacial tension γ at cellular size ℓ are of order γ/ℓ (for droplets larger than cell size), the smaller size that tooth mesenchymal cells exhibit within living tooth mandibles prevents them from deforming the original droplets with higher interfacial tension, despite the fact that they are able to generate the same stresses in vivo and in vitro. Indeed, knowing the average size of tooth mesenchymal cells in living mandibles, the minimal cell-generated stresses necessary to deform the original droplets (with γ = 26 ± 2 mN/m) at the cell scale would be γ/ℓ ≃ 2.6 nN/µm², which are larger than our measured average values of maximal stresses for tooth mesenchymal cells, explaining why negligible deformations were observed on the original droplets with higher interfacial tension.

Figure 5. Statistics of droplet deformations in living tooth mandibles.

(a) Normalized Δκ frequency for confocal sections of multiple droplets in the dental mesenchyme of living mandibles at E11 (N = 58). Droplet interfacial tension is 4 mN/m. (b) Relative droplet deformation |R_p − R₀|/R₀ as a function of the radius R₀ of the undeformed droplet section (R₀ = 1/κ₀). Solid line (black) depicts the envelope for maximal values of relative droplet deformation in E11 living mandibles. The data for droplets in tooth mesenchymal cell aggregates (orange/red; same as in Fig. 3f; droplet interfacial tension is 26 mN/m) is shown for comparison. The vertical bar indicates the measured value (mean (vertical line) ± standard deviation of the mean (vertical bar)) of mesenchymal cell size in living mandibles.

Discussion

Our results show that fluorescent oil microdroplets coated with specific ligands for cellular adhesion receptors allow quantitative measurements of cellular stresses within the local 3D microenvironment of both cultured dense cell aggregates and whole living embryonic tissues. Using surface-functionalized oil microdroplets as force transducers, we measured the cell-generated anisotropic stresses in cultured 3D aggregates of epithelial and tooth mesenchymal cells as well as in the dental mesenchyme of living mouse mandibles. We confirmed that the stresses generated by mammary epithelial cells are myosin II-dependent and more than 2-fold larger than those generated by tooth mesenchymal cells, whether these are measured in cultured aggregates or in their native tissue environment. This finding suggests that epithelial tissues require stronger mechanical contacts between cells than mesenchymal tissues, which is consistent with the typical cell packing densities observed in these tissues (i.e., higher in epithelium than mesenchyme), as well as the presence of a loose interstitial extracellular matrix only within the mesenchyme.

Importantly, the measured average values of maximal anisotropic stresses generated by tooth mesenchymal cells in cultured aggregates and in living tissue (dental mesenchyme) were very similar to each other, and to values measured in vitro for cultured fibroblasts in 2D⁴⁸ and 3D³⁴ geometries. However, cell shape and size varied strongly between cultured 3D cell aggregates and living 3D embryonic tissues, suggesting an important role of cell shape in directing cell-generated stresses during tissue growth and remodeling.

Several morphogenetic movements are driven by local cellular rearrangements (e.g., cell intercalation) caused by local spatial inhomogeneities in cellular stresses that can readily be measured with the technique presented here. However, one of the challenges of this technique in its current form is the inability to measure the isotropic component of the stresses (tissue pressure), as large scale tissue flows may also be driven by tissue-scale spatial variations in the tissue pressure. Therefore, in order to fully understand morphogenetic movements in the embryo it will be important to measure both the local value of the tissue pressure, as well as the local spatial inhomogeneities in cellular stresses that we are able to quantify with this microdroplet method. This limitation in our ability to measure the isotropic component of the stresses disappears, however, if droplets are only partially embedded in tissues or in contact with cells in culture and a region of their surface remains free of cell contact. For example, we were able to measure the isotropic component of the normal stresses on a droplet partially embedded in dental epithelium in a E11 stage embryo (see Supporting Note 3). In cases where droplets are fully embedded in an embryonic tissue, it may be possible to measure the local tissue pressure by monitoring the internal hydrostatic pressure of the droplet using pressure-controlled oil microinjection techniques⁴⁹.

The results presented here focus on the quantification of normal cellular stresses because the fluid nature of a droplet interface limits considerably its resistance to local shear stresses. Cells can apply and also resist shear stresses during morphogenetic events and may even change their behavior depending on the resistance of their substrate to shear. For example, the formation of tight junctions and focal adhesions may depend on the local resistance to both normal and shear forces. It is unclear whether the resistance to normal stresses that droplets provide is sufficient to support formation of junctional complexes in cells contacting droplets, or if resistance to shear is also required for their formation. Importantly, while the lack of resistance to shear at the droplet surface might potentially affect the formation of junctional complexes and the forces developed by these cells, the average values of the maximal anisotropic stresses measured here for tooth mesenchymal cells are in good agreement with the stresses developed by similar cells (fibroblasts) in 3D gel matrices³⁴, which can resist shear as well as normal stresses.

Finally, measurements of spatial patterns of cellular forces in vivo require the injection of multiple droplets in the embryonic tissue of interest. To be sure not to interfere with normal tissue development, the droplets need to be administered sparsely between the cells forming the tissue, separated by several cell lengths. Although a single measurement of this type can only provide a low spatial resolution map of cellular forces in a tissue, stereotypical patterns of cellular forces (force fields) with cellular resolution may be obtained from statistics over several samples at the same developmental stage.

Although we focused here on demonstrating the value of this technique to quantify cellular stresses in situ within dense 3D cell aggregates and whole living tissues, the technique can also be applied to quantify stresses generated by single cells or cells grown in standard monolayer cultures. The combination of 3D droplet reconstruction and time-lapse fluorescence microscopy allows quantitative measurements of both tensional and compressional cellular stresses surrounding the droplet as well as their temporal changes. In addition, the ability to control the type and concentration of ligands on the surface of the droplet, as well as its interfacial tension, allows these force transducers to be adapted to a wide variety of experimental conditions. Therefore, the characteristics of this technique are well suited for any study that requires quantification of stresses generated by individual living cells or groups of cells in culture, embryonic tissues or adult organs. This technique should therefore enable quantitative analysis of the role of cellular forces in embryonic development, and potentially, in disease processes as well.

Online Methods

Formation and functionalization of oil droplets

All oil droplets used in these experiments consist of Fluoroinert FC70 fluorocarbon oil (a kind gift from 3M Co.). Purified, deionized water for droplet preparation and functionalization was obtained by reverse osmosis (Milli-Q Purification System, Millipore) and autoclaved thereafter. FC70 oil was filtered using a syringe filter (Pall Life Sciences) with a 0.2 µm pore size before preparing the droplets. A stable emulsion of polydispersed droplets was obtained by mixing 150 µl of filtered FC70 with 1 ml of purified water solution containing biocompatible surfactants, namely 1,2-distearoyl-sn-glycero-3 phosphoethanolamine-N-[biotinyl(polyethylene glycol)-2000] (DSPE-PEG-biotin; Avanti Polar Lipids, Inc.), at a concentration of 0.2 mM. The surfactant concentration used is above the critical micelle concentration of DSPE-PEG[2000] (about 1µM⁵⁰), ensuring an excess of surfactant in solution. The mix was shaken vigorously to achieve droplets with radii ranging from about 1 µm to 40 µm. The resultant stable emulsion was positioned on a polycarbonate membrane (Transwell, Corning Inc.) with 3 µm size holes and a water flow was imposed through the membrane to eliminate droplets smaller or about 3 µm in diameter. The droplet emulsion remaining on the porous membrane was rinsed three times with purified water, where it remains stable for several days. The resulting stabilized droplets were further coated with fluorescent streptavidin (Cy5-Streptavidin, Alexa488-Streptavidin, Alexa555-Streptavidin from Invitrogen were used depending on the experiment) by slowly pouring 50 µl of highly concentrated DSPE-PEG-biotin coated FC70 droplets into a 30 ml solution of fluorescent streptavidin at a concentration of 1 µM while constantly stirring. A large excess of fluorescent streptavidin molecules in solution allowed fast and high density coating of the droplets via biotin-streptavidin linkages. The resulting droplets were rinsed three times with purified water. Lastly, 25 µl of high density emulsion of the droplets obtained in the previous step were poured into 0.5 ml of purified water solution of a biotinylated adhesion molecule of choice at a 10 µM concentration. Droplets used to measure mechanical stresses in mammary epithelial cell aggregates were coated with biotinylated mE-cadherin Antibodies (R&D systems). Droplets used to measure mechanical stresses in tooth mesenchymal cell aggregates and in the dental mesenchyme of mouse mandibles were coated with RGD peptide, the integrin-binding domain of fibronectin. Specifically, we used cyclo [Arg-Gly-Asp-d-Phe-Lys(Biotin-PEG-PEG)] (Peptides International), which is composed of a biotinylated PEG group bound to the RGD peptide. The resulting droplets were then rinsed three times in purified water and stored in 1 ml of purified water in a glass vial. Functionalized droplets were always used within a week from their preparation.

Synthesis of fluorocarbon-hydrocarbon diblocks

In order to obtain fluorocarbon-hydrocarbon diblocks, we coupled a Krytox fluorinated molecule to a hydrocarbon dodecylamine (DDA) molecule. For the coupling reaction, we diluted 32 g of perflouro-polyether Krytox 157 FSH (DuPont) with an equal volume of HFE-7100 (3M Co.) in a round flask and activated the carboxylic groups with a 10× molar excess of oxalyl chloride (4.2 ml; Sigma-Aldrich). The mixture became hazy and slightly yellow and was stirred overnight. Then, the solvent and unreacted oxalyl chloride were distilled off and neutralized by bubbling the vapors through 2M KOH. To remove all possible oxalyl chloride, we continued on a rotation evaporator under vacuum and heating the flask to 70 °C. The activated Krytox was allowed to cool down before diluting it in 50 ml HFE-7100, and a 5× molar excess of DDA (4.6 g, Sigma-Aldrich), dissolved in 50 ml anhydrous dichloromethane, was added to the flask. The sample was briefly placed in a heating bath (65 °C) under stirring, until strong evaporation was observed. The flask was then left stirring at room temperature overnight to avoid complete evaporation of the solvents. A milky-white sample was obtained, and the mixture of HFE-7100 and dichloromethane was removed on a rotation evaporator. The sample was re-diluted in a small quantity of HFE-7100 and equally distributed into 50 ml plastic centrifuge tube. After centrifugation at 15000g for 1 hour, the sample separated into a clear bottom phase and a white top layer consisting of the excess of unreacted DDA. With a sharp razor, we cut into the bottom of the plastic tube and collected the clear fluorinated bottom fraction into a new tube. After evaporation of the solvent at 65 °C over two days, the sample was viscous and still turbid. We extracted the product with 3 × 40 ml hexane to remove all residual DDA that was not coupled to Krytox. After drying the sample, we obtained a clear product. After several weeks of storage in a closed tube, the sample became opaque again. We attribute this to the molecules re-organizing into large micellar structures that cause strong scattering of light. The obtained Krytox-DDA diblocks were functional, as shown by their ability to lower the interfacial tension of the droplets (see below).

Measure of droplet interfacial tension

Interfacial tension was measured using the Du Noüy ring technique (Sigma 700, Biolin Scientific). An interface of FC70 and purified water was prepared and the interfacial tension was measured at every step of the coating procedure explained above (see Supplementary Note 2 for details). After the final coating step, purified water was substituted by the culture media used to grow the cells and tissue in our experiments. Interfacial tension between the coated interface and the culture media was measured at 37 °C (incubation conditions) to be 26 ± 2 mN/m. The value of the interfacial tension was further checked by measuring it with the pendant drop method (homemade experimental set-up and Matlab analysis software), obtaining a value of 28 ± 3 mN/m. The interfacial tension of FC70 oil, containing 1% w/w Krytox-DDA diblocks and coated with the previously described protocol, with culture media at 37 °C was measured to be 4 ± 3 mN/m.

Formation of mammary epithelial cell aggregates

Premalignant mammary epithelial cells, M28, isolated from 8 week-old FVB/C3(1)/SV40 T-antigen transgenic mice (kindly provided by Cheryl Jorcyk) were cultured in Dulbeccos Modified Eagles Medium (DMEM), supplemented with 10% Fetal Bovine Serum (FBS), and 1% penicillin and streptomycin (PenStrep), and maintained at 37 °C and 5% CO₂. Mammary epithelial cell aggregates containing functionalized droplets were prepared as follows: mammary epithelial cells, M28, from two T75 flasks at 80% confluence were centrifuged (720g for 5 min) and the obtained cell pellet was resuspended in 0.25 ml of cell culture media. Between 4 – 10 µl of concentrated functionalized droplet emulsion (prepared as described above) were added to this high density cell suspension and carefully stirred for 5 minutes. The suspension was then centrifuged again (720g for 7 min) to obtain a high density cells-droplets pellet. Portions of this pellet containing microdroplets in-between cells were added to a glass-bottom dish (MatTek Co.) containing 3 ml of cell culture media. Cell pellets containing droplets were cultured for 48h–72h, until cells formed a compact cell aggregate. Culture media was replaced every 24h. About 1 hour before imaging the aggregates, we supplemented the culture media with the DNA dye Hoechst 33342 (Invitrogen) at a final concentration of 3 µM, to be able to visualize the location of cells nuclei.

Formation of tooth mesenchymal cell aggregates

Tooth mesenchymal cells were obtained from the dental mesenchyme of mouse embryos. Specifically, the first pharyngeal arch was dissected from E10–11 embryos using a sterile technique. For isolation of tooth mesenchymal cells, the tissues were treated with Dispase II (2.4 U/ml; Roche) and DNase I (QIAGEN) at 37 °C for 23 min. After separating epithelium and mesenchyme using fine forceps, the presumptive dental mesenchyme (DM) was dissected out and physically triturated several times using a fire-polished Pasteur pipette before being cultured on fibronectin (Becton Dickinson) coated glass-bottom dishes (MatTek Co.) in DMEM supplemented with 10% FBS. We confirmed the purity of the isolated dental epithelium (DE) for cell culture and DM overlay studies using GFP-labeled DE cells isolated from keratin (K)-14/GFP transgenic mice from The Jackson Laboratory. The DM cells were passaged using fibronectin-coated microcarrier beads for the first several passages (Thermo Scientific). Tooth mesenchymal cells were GFP labeled with retroviral transduction. All cell aggregates used in our experiments were prepared with these GFP-positive tooth mesenchymal cells and all studies utilized cells at passage less than eight. Cell aggregates of GFP-positive tooth mesenchymal cells were prepared as follows: high-density pellets of tooth mesenchymal cells containing functionalized droplets (prepared in the same way as those of mammary epithelial cells described above) were carefully positioned on a porous polycarbonate membrane (Whatman Nucleopore track-etched membrane; 0.2 µm pore size) lying on top of a sterile metal mesh (mesh size of 1 mm) inside a well of a 6-well plate (Trowel’s method). Sterile metal supports 3 – 4 mm tall were used to keep the metal mesh elevated from the bottom of the well. The gap between the bottom of the well and the porous polycarbonate membrane was filled with cell culture media (DMEM supplemented with 10% FBS and 1% PenStrep). The pellets lying on the top of the polycarbonate membrane were covered with a very thin film of culture media. Surface tension sustained the pellets on the membrane. Cell culture media was kept in contact with the porous polycarbonate membrane at its lower side, allowing the transfer of nutrients from the culture media reservoir under the membrane to the pellets, which can be cultured in these conditions for over 7 days at 37 °C and 5% CO₂. Pellets were cultured for 3 – 4 days, changing cell culture media every 24h, until they became compact cell aggregates. The cell aggregates were transferred to glass-bottom dishes (MatTek Co.) for imaging.

Adhesion of cells on functionalized droplets

Microdroplets used to measure forces in mammary epithelial cell aggregates and GFP-positive tooth mesenchymal cell aggregates were respectively coated with mE-Cadherin antibodies and RGD peptide to allow cells to adhere on the droplet surface. Cells from a single T25 flask at 80% confluence were resuspended in 0.25 ml of culture media (DMEM supplemented with 10% FBS and 1% PenStrep) and 10 µl of functionalized droplets were added to the suspension. Cells and droplets were carefully stirred for 5 min and placed on a 35 mm diameter glass-bottom dish containing 2 ml of culture media (both cells and droplets sedimented on the glass coverslip; FC70 oil density is 1940 kg/m³), incubated for 1 h (37 °C and 5% CO₂) and imaged using confocal microscopy. By imaging the droplets 20 – 30 µm away from the coverslip, we could see if cells were attached at the droplet surface (Supplementary Fig. 1a). Tooth mesenchymal cells localized at the surface of RGD-coated droplets even far away from the coverslip (Supplementary Fig. 1b), indicating attachment of cells on the droplets. 3-dimensional reconstruction of the sample shows cells localized on the droplet surface. If cells were not adhered to the droplets, they would have been found on the coverslip surface instead. In order to be able to observe localization of mammary epithelial cells with respect to E-cadherin antibody coated droplets, we supplemented their culture media with the DNA dye Hoechst 33342 (Invitrogen) at a concentration of 3 µM, 30 min before imaging. Nuclei of mammary epithelial cells were observed to surround E-cadherin antibody coated droplets even far away from the coverslip (Supplementary Fig. 1c), suggesting their adhesion to the droplets. However, as contacts could not be observed directly, we decided to test adhesion further using a different method. A large excess of E-cadherin antibody coated droplets were deposited on mammary epithelial cells at 50% confluence cultured on a glass-bottom dish, making a thin layer of droplets covering the cells as well as cell-free surface at the bottom of the dish (Supplementary Fig. 1d, left panel). The entire dish was then filled with culture media (approx. 5 ml) and the top was sealed with a thin plastic plate. We then turned the glass-bottom dish upside-down and imaged the cells using an upright fluorescence microscope (Supplementary Fig. 1d, right panel). Droplets not attached to cells fell to the plastic cover because of gravity (a FC70 oil droplet of 30 µm in diameter weights approx. 100 pN in culture media). E-cadherin antibody coated droplets were observed to localize perfectly with regions of the coverslip containing cells (Supplementary Fig. 1e), indicating that droplets were attached to cells, which were preventing the droplets from falling by their own weight.

Perturbation of cellular forces with drugs

In all cases, drug addition was done directly to the glass-bottom culture dish containing mammary epithelial cell aggregates while imaging the samples, and the culture media was mixed using a pipette to achieve a homogeneous distribution of the drug in the culture dish. Myosin II inhibition was achieved by addition of Blebbistatin at a 50 µM final concentration. Inhibition of actin polymerization was achieved by addition of Cytochalasin D at a 4 µM final concentration. Disruption of cell membranes was achieved with detergent (sodium dodecyl sulfate) at 1% v/v final concentration.

Mouse mandible dissection

Keratin14-Cre recombinase mice, STOCK Tg(KRT14-cre)1Amc/J (#004782), were purchased from Jackson laboratories (http://jaxmice.jax.org/strain/004782.html). Double-Fluorescent Cre reporter mice, STOCK Gt(ROSA)26Sortm4(ACTB-tdTomato,-EGFP)Luo/J (#007576), were purchased from Jackson Laboratories (http://jaxmice.jax.org/strain/007576.html). We mated male mice containing a Cre recombinase transgene under the regulation of an epithelial keratin enhancer element, Keratin 14, with a double-fluorescent Cre reporter mouse that expresses membrane-targeted tandem dimer Tomato prior to Cre-mediated excision and membrane-targeted GFP after excision. This mating combination allowed us to generate embryos in which we could distinguish the plasma membranes of mesenchymal cells (red) and epithelial cells (green) (Fig. 4e–f). Wild type CD1 mouse embryos (Charles River) were used in some cases. Embryos were harvested from pregnant females 11 or 13 days post detection of a copulation plug and were kept at room temperature in phosphate buffered saline. Embryonic heads were immediately decapitated. Embryonic mandibles were dissected using Dumont #5 forceps and the associated tongue was removed for optimal imaging. Dissected mandibles were kept on ice, in a petri dish containing tissue culture media (DMEM supplemented with 10% FBS and 1% PenStrep), and immediately prepared for droplet micro-injections.

Microinjection of functionalized oil droplets in living tooth mandibles

Tissue microinjection of previously functionalized oil microdroplets was accomplished by positioning freshly dissected mouse mandibles (E11 and E13.5 depending on experiment) dorsal surface up in a drop of tissue culture media (DMEM supplemented with 10% FBS and 1% PenStrep) stabilized against a PDMS (SYLGARD 184 silicone elastomer; Dow Corning) block located on a petri dish surface. Surface tension of the tissue culture media drop with air was sufficient to immobilize both the PDMS block and tissue on the surface during injections. Between 5 – 10 µl of functionalized oil microdroplets emulsion were back-filled into microinjection needles pulled from glass capillaries with 0.75/1 mm inner/outer diameters (World Precision Instruments). Microdroplets were injected using a pressure-controlled PLI-100 Pico-Injector (Harvard Apparatus). Six to eight injections, each releasing from 1 to 5 droplets, were done along the mandible and into the dental mesenchyme, as close as possible to the boundary with the epithelium. All injections were performed on a standard epifluorescence stereo dissection microscope (Nikon SMZ1500) to visualize injection sites and the fluorescent microdroplets upon injection. After injections, mandibles containing oil droplets were transferred to glass-bottom dishes with tissue culture media and maintained at 37 °C and 5% CO₂ for 7 – 10 hours before imaging.

Imaging of microdroplets in cell aggregates and living mouse mandibles

Glass-bottom dishes containing the samples were imaged with a laser scanning confocal microscope (Zeiss LSM 710) equipped with incubation chamber (XL1 heating chamber, PeCon GmbH) and environmental control. Both cell aggregates and living mandible tissue were imaged under the same incubation conditions (37 °C and 5% CO₂). Samples were mostly imaged using a (LD) C-Apochromat 40× water-immersion objective with 1.1 NA. Confocal imaging parameters were optimized for maximal resolution and minimal noise in each experiment.

Image analysis

When visualized using confocal microscopy, a 2D confocal section of a surface-labeled droplet appears as a closed curve (Supplementary Fig. 2a). In order to detect the 2D contour of the droplet, we first filtered the image using Steerable filters. While these filters can be implemented in Matlab or other programming languages, we used the SteerableJ plugin for ImageJ. Steerable filters convolve a kernel optimized to detect specific image patterns with the original image to obtain an image where patterns similar to the kernel pattern are enhanced. Using a specific kernel for edge detection (kernel shown in Supplementary Fig. 2b, left panel) we were able to obtain enhanced images of the droplet confocal section with substantially reduced noise (Supplementary Fig. 2b, right panel). The filtered image was then processed in Matlab (Mathworks) to obtain the coordinates of the droplet contour. To do so, we defined a linear path from a point close to the droplet center to the outside of the droplet (Supplementary Fig. 2c, left panel) and measured the intensity profile along that path (Supplementary Fig. 2c, right panel). By fitting a gaussian profile to the measured intensity profile along the linear path, we obtained the coordinates of the location along the droplet contour intersecting the defined linear path. These coordinates are given by the maximum (mean) of the gaussian fit. To obtain the coordinates of the entire contour, we rotated the defined linear path around the starting point (Supplementary Fig. 2c, left panel) and repeat the procedure described above to determine the contour coordinates at each angle. Using this method, the contour of the confocal section of the droplet can be detected at pixel resolution (Supplementary Fig. 2d). Once the coordinates of the contour were known, we obtained a closed BSpline curve (using Wolfram Mathematica 8) from the droplet contour coordinates. The BSpline curve specifies a continuous curve for the droplet contour (Supplementary Fig. 2e and Supplementary Fig. 2f) and eliminates high frequency noise at the pixel level that would otherwise make the calculation of the curvature very complicated. The curvature along the droplet contour was obtained from the continuous droplet contour (BSpline) using standard differential geometry of curves⁴⁶. To reconstruct the 3D shape of a droplet, we obtained, using the procedure just described for confocal sections, the droplet contour coordinates for each of the confocal sections of the droplet in a 3D confocal stack (Supplementary Fig. 2G). The obtained contour coordinates for each confocal section were combined to obtain the coordinates of the droplet surface in 3D (Supplementary Fig. 2h). Once the coordinates of the droplet surface were known, we obtained a 2D BSpline of the entire droplet surface (using Wolfram Mathematica 8). In this case, the BSpline specifies a continuous surface for the droplet shape (Supplementary Fig. 2i) and eliminates high frequency noise at the pixel level. The mean curvature at each point of the droplet surface (Supplementary Fig. 2j) was obtained from the continuous droplet shape (BSpline) using standard differential geometry of surfaces⁴⁶.

Measuring average values of maximal stresses from 2D confocal sections of multiple droplets

Given two principal directions on the surface of a droplet, with principal curvatures κ₁ and κ₂ and mean curvature H = (κ₁ + κ₂)/2, the anisotropic stress on the droplet surface (Eq. 2) can be written as δσ_nn = γ((κ₁ − /1R) + (κ₂ − 1/R)). The maximal and minimal possible values of the anisotropic stresses are given by $\delta {\sigma }_{nn}^{\mathit{\text{max}}}=\gamma (({\kappa }_1^{\mathit{\text{max}}}-1/R)+({\kappa }_2^{\mathit{\text{max}}}-1/R))$ and $\delta {\sigma }_{nn}^{\mathit{\text{min}}}=\gamma (({\kappa }_1^{\mathit{\text{min}}}-1/R)+({\kappa }_2^{\mathit{\text{min}}}-1/R))$, respectively. The maximal amplitude of anisotropic stresses is given by $\delta {\sigma }_{nn}^{\mathit{\text{max}}}-\delta {\sigma }_{nn}^{\mathit{\text{min}}}$, which reads $\delta {\sigma }_{nn}^{\mathit{\text{max}}}-\delta {\sigma }_{nn}^{\mathit{\text{min}}}=\gamma (({\kappa }_1^{\mathit{\text{max}}}-{\kappa }_1^{\mathit{\text{min}}})+({\kappa }_2^{\mathit{\text{max}}}-{\kappa }_2^{\mathit{\text{min}}}))$. Defining the curvature amplitude along a principal direction as Δκ ≡ κ^max − κ^min, the maximal anisotropic stress amplitude reads $\delta {\sigma }_{nn}^{\mathit{\text{max}}}-\delta {\sigma }_{nn}^{\mathit{\text{min}}}=\gamma (\mathrm{\Delta }{\kappa }_1+\mathrm{\Delta }{\kappa }_2)$. The average value of the anisotropic stress amplitude over many different droplets reads $\overline{\delta {\sigma }_{nn}^{\mathit{\text{max}}}-\delta {\sigma }_{nn}^{\mathit{\text{min}}}}=\gamma (\overline{\mathrm{\Delta }{\kappa }_1}+\overline{\mathrm{\Delta }{\kappa }_2})$. While the specific values of Δκ₁ and Δκ₂ are different for different droplets, their average values are equal, i.e., $\overline{\mathrm{\Delta }{\kappa }_1}=\overline{\mathrm{\Delta }{\kappa }_2}=\overline{\mathrm{\Delta }\kappa }$, if no major anisotropies are present at the tissue scale (long range anisotropies). In this case, the average value of the maximal anisotropic stresses, $\overline{\delta {\sigma }_{nn}^M}$, is given by $\overline{\delta {\sigma }_{nn}^M}=\overline{\delta {\sigma }_{nn}^{\mathit{\text{max}}}-\delta {\sigma }_{nn}^{\mathit{\text{min}}}}$, and reads $\overline{\delta {\sigma }_{nn}^M}=\gamma \overline{\mathrm{\Delta }\kappa }$, which corresponds to Eq. 3.