Rostral Cingulate Zone and correct response monitoring: ICA and source localization evidences for the unicity of correct- and error-negativities

Abstract

Falkenstein et al. (1991) first described a negative wave occurring just after an erroneous response in choice Reaction time tasks (“Error Negativity”—Ne or “Error Related Negativity”—ERN). Thanks to Laplacian transform of the data, Vidal et al. (2000, 2003a) described a wave on correct trials with similar topography and latency, although of smaller amplitude compared to the errors. A critical question is whether the Ne observed on errors and the negativity reported on correct trials reflect the same (modulated) activity, or whether they reflect completely different mechanisms. These two alternative possibilities were tested thanks to Independent Component Analysis (ICA) and source localization. ICA results showed that the waves recorded on errors and correct trials can be accounted for by the same independent component, corresponding to a dipolar source located within the Rostral Cingulate Zone. Source localization on the raw data also confirmed a common generator for correct and error trials. These data suggest that the waves on errors and correct trials reflect the same brain activity, whose amplitude varies as a function of the correctness of the response. The implications of this result for cognitive control are discussed.

Introduction

Keeping our behavior adapted to ever changing environments requires a constant evaluation of one’s own performance. In this respect, errors play an essential role in this evaluation, since they strongly signal the need for adaptation. In the early 1990s, Falkenstein et al. (1991) described an EEG component peaking just after error commission in reaction time (RT) tasks (see also Gehring et al., 1993): This fronto-central negative wave starts just before the mechanical response, and peaks between 50 and 100 ms later. With conventional monopolar recordings, this activity has originally been observed only on errors and was hence interpreted as reflecting an “Error Detection” mechanism. Accordingly, it was named “Error Negativity” (Ne, Falkenstein et al., 1991) or “Error-Related Negativity” (ERN, Gehring et al., 1993). Source localization approaches (Dehaene et al., 1994; Herrmann et al., 2004; van Veen and Carter, 2002) and fMRI data (Debener et al., 2005; Ullsperger and von Cramon, 2001) have pointed to a Rostral Cingulate Zone (RCZ, Ridderinkhof et al., 2004) generator of this activity. This generator would be more likely located within the anterior cingulate cortex (ACC) and/or the supplementary motor area (SMA) (Dehaene et al., 1994; Ullsperger and von Cramon, 2001). The Ne was later included in more general models of response monitoring, like the conflict monitoring model (Botvinick et al., 2001; Yeung et al., 2004, see however Burle et al., 2008), or reinforcement learning theories (Holroyd and Coles, 2002; Frank et al., 2005).

The specificity of the Ne to errors was disputed by Vidal et al. (2000). These authors computed the Current Source Density (by applying the Laplacian operator), which has been shown to dramatically improve the spatial resolution of monopolar recordings (Babiloni et al., 2001). Thanks to this methodological improvement, Vidal et al. (2000) evidenced that a similar activity could also be observed on correct trials, albeit with smaller amplitude. They first analyzed some particular correct trials in which partial errors occurred: on such trials, although the correct response was given, electromyographic (EMG) recordings allowed to reveal a small EMG burst on the muscles involved in the incorrect response (Burle et al., 2002; Coles et al., 1985; Eriksen et al., 1985). Vidal and colleagues observed a negative wave just after the onset of such partial errors with comparable latency and topography as the wave reported on errors (see Scheffers et al., 1996 for similar data in a go/nogo task). More importantly, they also reported a similar negativity, of smaller amplitude though, just after the EMG leading to the correct response on pure correct trials (i.e. trials without any sign of incorrect EMG activation). Ford (1999) also observed a similar wave on correct trials in schizophrenic patients, even with conventional (monopolar) recordings. Actually, on those patients, this wave on correct trials was as large as the one on errors, which was interpreted as reflecting a perturbed error detection in these patients.

The negative activities obtained on errors, partial errors and pure correct trials had similar topographies, comparable time-courses (after Laplacian transform), and their amplitude was shown to decrease from errors to pure correct, with partial errors in between. Based on these similarities, Vidal et al. (2000) argued that the Ne-like was of same nature as the Ne on errors.

Coles et al. (2001) disputed this view and argued that the negativity reported by Vidal et al. (2000) on correct trials was due to an artifact caused by the temporal overlap between stimulus-locked and response-locked activities. To address this point, Vidal et al. (2003a) visualized the single-trial dynamics of the stimulus and response evoked potentials as a function of the reaction time, and showed that the Ne-like was clearly response-locked and independent from stimulus-locked activities. Several other studies have reported a negative wave on correct trials, and there is now a consensus on its existence (Falkenstein et al., 2000; Luu et al., 2000; Mathalon et al., 2002).

It remains to be deciphered, however, whether the negativities recorded on correct and error trials reflect the same functional and physiological mechanisms modulated in amplitude or whether they result from completely different processes.

While the hypothesis that the negativities observed on pure correct, partial errors and errors reflect the same modulated mechanism (Vidal et al., 2000, 2003a) is supported by the fact that the negativity on correct trials is also sensitive to the subject’s performance (Luu et al., 2000; Ridderinkhof et al., 2003; Allain et al., 2004; Hajcak et al., 2005), this view was disputed by Yordanova et al. (2004). These authors reported that on correct trials the negativity tended to be lateralized toward the hemisphere controlateral to the responding hand whereas the topography was more central for errors. Based on the difference in topography and in the time-frequency pattern of negativities on correct and erroneous trials, they concluded that the two negativities reflected different processes. The lateralization reported by Yordanova et al. (2004) might well be due, however, to an independent source. Indeed, following the motor lateralization induced by response execution processes (Vidal et al., 2003b, see Burle et al., 2004 for a review), the lateralization of the Ne-like observed by Yordanova et al. (2004) could be due to the propagation of the primary motor cortex activity towards premotor areas (see Tandonnet et al., 2005, Fig. 1, p. 21): If this pre-motor activity is of same amplitude for correct and errors trials, it may contribute more to the topography when the amplitude of the medial activity is lower, that is for correct trials. This may give the false impression of a lateralization limited to correct trials, although the same lateralized activity could also be present on errors, but less visible. In line with this view, a critical look at Figs. 1 and 6 of Yordanova et al. (2004, p. 593 and 598) shows that, even on errors, the iso-contour lines present a lateralization.

Clarifying this debate is theoretically important since, if the negativity on correct trials is of same nature as that on errors, this would challenge all the current models of cognitive control as none of them can easily account for the presence of a “Ne-like” on correct trials. Furthermore, this would indicate that control processes operate gradually from correctness to errors, therefore opening new perspectives on cognitive control modeling.

One difficulty is that concluding that the three waves are the same incurs the risk of accepting the null hypothesis. One can, however, try to establish conditions that, although maybe not sufficient, are necessary for this unicity. One such necessary condition is that the three negativities have common relevant structural properties.

In the present report, we assessed the unicity of those negativities with Independent Component Analysis (ICA, Onton et al., 2006) and source localization techniques (sLORETA, Pascual-Marqui, 2002).

Applied to EEG, ICA posits that the scalp activity is a linear combination of a limited set of elementary brain signals (the independent components). Based on the assumption of temporal independence, ICA allows to recover the mixture of components and hence to estimate the time course and the topography of each component. Of special interest in the present context, ICA blindly recovers the components, that is, it does so without any a priori assumptions about the components (except that they must be maximally independent from each other). We reasoned that if the three negativities recorded on errors, partial errors and correct trials reflect the same modulated elementary brain activity, they should be captured by ICA in the same component. On the contrary, if they reflect different mechanisms, it should not be possible to find a single component accounting for these three waves. Recently, a similar logic has been followed by Gentsch et al. (2009) to evaluate whether the Ne (on errors) and the FRN (a brain activity occurring after incorrect feedback) were of same nature. These authors could show that the same component(s) could account for both the Ne and for the FRN, and argued that the two activities reflect different manifestations of the same evaluation process (Holroyd et al., 2004). Our aim was to test, with the same methodology, whether the Ne on errors, on partial errors and on correct trials could be captured by the same component.

In addition to the ICA argument, we also applied source localization techniques to recover the generator(s) of the three activities. Indeed, although there are now strong arguments for an RCZ origin of the Ne on errors (Dehaene et al., 1994; Debener et al., 2005), no explicit localization of the negativities recorded on both partial errors and correct trials has been reported so far¹. Obtaining similar localizations for these three activities would provide a further argument in favor of the unicity of the phenomenon.

Materials and methods

The data relative to partial errors have been reported in a previous study for different purposes (see Burle et al., 2008 where a detailed description of the experiment is available). The method will thus be briefly summarized, with emphasis on the aspects relevant for our current goals.

Subjects

Ten subjects aged 20 to 31 years (mean: 25 years) volunteered for the experiment. All of them were right-handed and had normal or corrected-to-normal vision. According to the declaration of Helsinki, written informed consent before the start of the experiment was obtained from each subject.

Task, recordings and EEG data preprocessing

The subjects performed an Eriksen’s flanker task (Eriksen and Eriksen, 1974). On each trial, three letters were presented to subjects who had to respond to the central one (target) while ignoring the others (distractors). They ran 20 experimental blocks of 128 trials each.

Electroencephalographic activity (EEG) was recorded with 64 Ag/AgCl scalp electrodes (10-20 system positions, BIOSEMI Active-two electrodes, Amsterdam) and electromyographic activity (EMG) from the flexor pollicis brevis of each hand was recorded by paired surface Ag/AgCl electrodes. The sampling rate was 1024 Hz (filters: DC to 268 Hz, 3 dB/octave). The data were off line referenced to the left mastoid.

The vertical and horizontal EOG was recorded in order to correct eye movement artifacts by the statistical method of Gratton et al. (1983)². All other artifacts were rejected after visual inspection of individual traces. The onset of the EMG activity was marked manually after visual inspection (for further details, see Burle et al., 2008).

The retained EEG data were then downsampled to 256 Hz (with BrainAnalyzer^©, Munich), since the original sampling rate was too high for running ICA.

EEG data analysis

The trials were sorted into three categories based on responses and on EMG patterns: pure-correct, error and partial error trials (see Burle et al., 2002, 2008 for more details). Partial error trials are characterized by the presence of a small EMG burst on the incorrect response side preceding the EMG burst leading to the correct response. The EEG data were epoched, time-locked to the EMG activity that led to the overt response, namely the correct EMG burst for pure correct trials and partial errors, and the supraliminal incorrect EMG for errors.

Since previous reports have shown that the negativity on correct trials is much easier to observe after Laplacian computation, we also applied this transformation to the monopolar data, for the sake of comparison. The signal was interpolated with spherical spline interpolation, and hence the second derivatives in two dimensions of space were computed. We choose 3 for the degree of the spline since this value minimizes errors, and the interpolation was computed with a maximum of 15 degrees for the Legendre polynomial (Perrin et al., 1989). We assumed a radius of 10 cm for the sphere representing the head, rather than the unrealistic default radius of 1 m assumed by BrainAnalyzer^©. With such a realistic radius, the most suitable unit is μV/cm².

Blind Source Separation (BSS): general principle

ICA algorithm performs a “Blind Source Separation” (BSS) of the signal. Applied to EEG, BSS posits that the activities x_i(t) recorded on each sensor i (among I) at time t can be decomposed as a sum of elementary components defined as the product of a topography (α_ij∈R^I, representing the contribution of the component j to each of the i electrodes) and a time course s_j(t)∈R^T (with I the number of sensors, J the number of components with J≤I, and T the number of time samples):

$${\mathit{x}}_i\left(t\right)=\sum _{j=1}^J{\alpha }_{\mathit{ij}}{s}_j\left(t\right)$$ (1)

Generally speaking, the goal of BSS is to recover both the α_ij and the s_j(t) knowing only the realization across time of the signal x_i(t). This problem can also be formalized in matrix terms and becomes:

$$\mathbf{X}=\mathbf{A}\cdot \mathbf{S}$$ (2)

where X∈R^I×T is the observation matrix, A∈R^I×J is the mixing matrix and S∈R^J×T is the matrix of the components time course (i.e. the “sources” in the BSS terminology³).

Thus, BSS decomposes the input matrix X into the product of two matrices A and S. The decomposition of X is not unique, however, and additional constraints are needed.

One widely used constraint is that the sources must be statistically maximally independent. Such an approach is usually called “Independent Component Analysis”. One way to quantify the independence between time series is to compute their mutual information (Bell and Sejnowski, 1995) and the infomax algorithm (used in the current study, see below) searches for the S matrix whose mutual information across components is minimal.

Applied to EEG, ICA aims at recovering elementary brain activities that are mixed at the sensors level because of volume conduction and diffusion effects, without any modeling of such conduction and diffusion effects (Jung et al., 2001).

ICA in the present study

Since, by demixing the observation matrix, ICA aims at recovering the elementary brain activities, we used ICA to address the unicity of the Ne and Ne-like observed on errors, partial errors and correct trials. A necessary, although maybe not sufficient, condition for unicity is that the same ICA component can account for the waves observed on the three categories of trials. In other words, will ICA blindly attribute a single brain origin to the three waves? Addressing this question was performed in four steps, as detailed below.

Step 1: construction of the matrices

We first selected all the trials that were identified as correct, partial error or error. Partial errors were identified based on the EMG data. We removed trials contaminated by artifacts (see Burle et al., 2008 for more details on artifact rejection). The selected trials were then segmented into epochs from −400 to +400 ms, centered on the EMG onset that triggered the overt response, either correct (correct and partial error trials) or incorrect (errors). Trials were then concatenated to form the X matrix of size 64×T (where 64 is the number of electrodes, and T is equal to Number_of_trials×Time_sample_per_trials). One single X matrix containing all the trials was built for each of the 10 subjects with the monopolar data. The individual matrices were of slightly different sizes since T depends on the number of trials included. Note that these data matrices are mainly composed of correct trials (76.8% on average) compared to errors and partial errors trials (5.2% and 18% on average, respectively).

Step 2: ICA on individual matrices

ICA was applied to each of the X matrices. ICA computations were performed with the runica() function (as implemented in the EEGLAB software, Delorme and Makeig, 2004) which is derived from the Infomax ICA algorithm (Bell and Sejnowski, 1995). This returned 64 components per subject.

Step 3: searching for the component accounting for errors

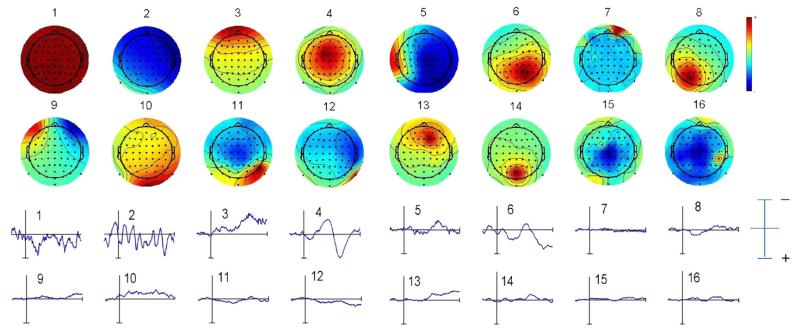
We searched for the component that could account for the Ne on errors (see Debener et al., 2005). As already indicated, a component is defined by a topography and a time course. A component was thus selected if its averaged time-course on errors presented a clear phasic activity whose projection on the scalp was of negative polarity at fronto-central sites (see Fig. 2 for an example). The selected component accounting for the Ne will be termed Ne_IC_s for each subject S. Note that components were selected without any reference to correct trials.

Fig. 2.

Example of decomposition and component selection for one representative subject. This figure presents the 16 first components (among 64). The first two rows present the topographies of the components, and the last two rows present the corresponding averaged time courses for the same components for error trials, time locked to incorrect EMG onset. In this example, the fourth component clearly presents a fronto-central distribution and a clear increase in activity just after the incorrect EMG. This component was thus selected for this particular subject. The same procedure was applied to all the subjects.

Step 4: averaging of the selected component for partial error and correct trials

Once the Ne_IC_s, accounting for the Ne on errors, had been identified, we averaged the time course of Ne_IC_s for partial errors and correct trials. Based on these averages, we sought whether the Ne_IC_s could also account for the negativities observed on partial errors and on correct trials. To do so, we compared the component averages to both monopolar and Laplacian averages on the same trials.

Source localization

To further probe similarities and differences between the negativities observed in the three categories of trials, we searched for the brain regions responsible for the genesis of those activities. Although source localization on errors has already been performed in several studies, to the best of our knowledge, the generator of the negativities on partial errors and on correct trials have never been localized so far. We thus sought for the generator of these three waves thanks to the standardized Low Resolution Electromagnetic Tomography (sLORETA) method, which implements a normalized form of the minimum norm constraint (see Pascual-Marqui, 2002 for technical details).

Results

Behavioral data

Behavioral and EMG results replicate previous data: The number of errors was higher in the incompatible condition (7.5%) than in the compatible one (2.9%, t(9)=6.55, p<0.001). The same pattern was obtained for partial errors (21.7% and 14.3% for incompatible and compatible trials, respectively, t(9)=5.78, p<0.001). For all correct trials (including partial errors) RTs were longer in the incompatible condition (416 ms) than in the compatible one (386 ms, t(9)=15.39, p<0.001). The RTs associated with these three types of trials were significantly different (F(2,18)=84.6, p<0.001), with the shortest RTs obtained for errors (342 ms), followed by pure-correct trials (382 ms) and partial errors (445 ms).

EEG data

This section will be organized as follows: we will first present the monopolar data for comparison with the literature. We will then present the Laplacian data, since this transformation permits to reveal the negativity on correct trials. We will then present the ICA data, and finally the source localization results.

Monopolar data

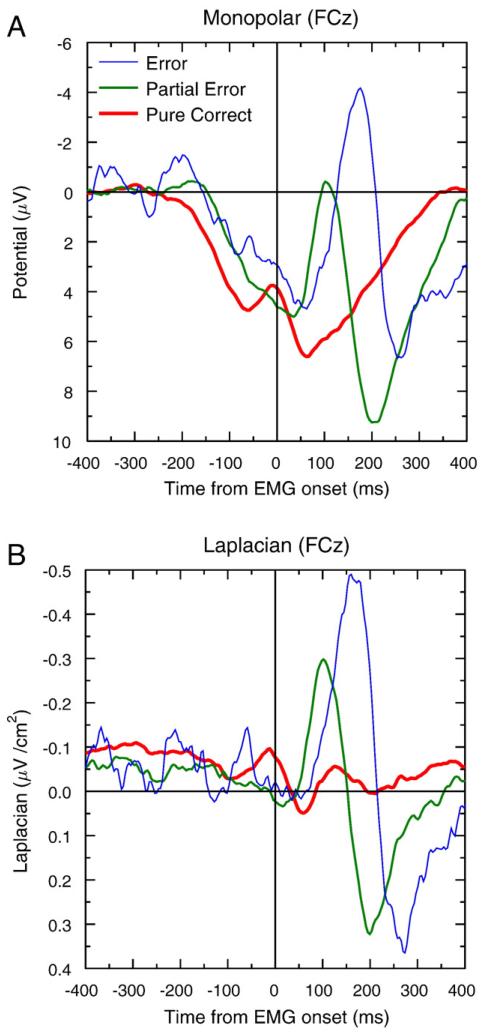
Fig. 1A presents the monopolar grand averages obtained over FCz for errors (blue line), partial errors (green) and correct trials (red), time-locked to the relevant EMG activity onset (see above). The presented data replicate already published results, showing a clear negative wave for errors (Falkenstein et al., 1991; Gehring et al., 1993) and partial errors (Scheffers et al., 1996; Vidal et al., 2000) shortly after EMG onset. The amplitude of this wave was higher for errors (14.4 μV) than for partial errors (7.05 μV, F(1,9)=13.26; p<0.01). As usually reported, no such phasic negativity could be observed on correct trials (Fig. 1A, red line).

Fig. 1.

Grand averages (FCz) of the three categories of trials (Error: blue, partial error: green and pure correct: red, for the monopolar data (panel A), and for the Laplacian transformed data (panel B). The zero of time indicates the relevant EMG onset: for correct trials, this corresponds to the EMG burst that triggered the correct mechanical response. For errors, it corresponds to the EMG burst that triggered the error. For partial errors, the relevant EMG is the small, subliminal, EMG burst occurring on the incorrect hand before the EMG burst triggering the correct response. On the monopolar data (panel A), one can clearly see the Ne for errors and partial errors, but no negativity is visible on correct trials just after EMG onset. As already reported, a large positivity is observable, instead. On the contrary, after Laplacian transform, a clear negativity, although of smaller amplitude, appears also for correct trials. The large positivity, likely generated by remote sources, has disappeared, hence allowing to reveal the small negative wave, much more focal, present on correct trials.

Laplacian data

The Laplacian data provide a different picture: although negative waves are still clearly observable on errors and partial errors (Fig. 1B, lines blue and green, respectively) over FCz, a small negative activity now becomes visible on correct trials over the same electrode (red line on Fig. 1B), with a latency comparable to that observed for errors and partial errors. Statistical analysis of the slope in a window from 65 to 118 ms (which correspond to the peak on the grand average) after EMG onset confirms that the slope is significantly different from 0 even for correct trials (F(1,9)=7.3, P<0.05). The amplitude of those negativities significantly differs across trial types (F(2,18)=34.9, P<0.001). A latency effect of the peak also shows up (F(2,18)=24.5, P<0.001), with a peak occurring earlier for partial error (mean latency: 109 ms) than for correct trials (mean latency: 123 ms⁴) and errors (mean latency: 162 ms). The latency difference between partial and full errors replicates results already reported by Carbonnell and Falkenstein (2006) and extend them, by showing that the latency for correct trials lies in between partial and overt errors.

We also analyzed possible compatibility effects on the amplitude of the Ne. No compatibility effect was obtained on errors and partial errors (F(1,9)=1.82; P=0.21 and F<1, for errors and partial errors, respectively). In contrast, a compatibility effect was obtained on pure-correct trials (F(1,9)=8.21; P<0.05), with compatible trials inducing smaller Ne than incompatible ones.

ICA data

To select the component accounting for the Ne on errors, we followed the procedure previously used by Debener et al. (2005) and Gentsch et al. (2009). Fig. 2 illustrates how this was done for a representative subject (no. 02). This figure presents the 16 first components, with their topography (top) and their temporal dynamics on error trials (bottom, the vertical bar indicates EMG onset). As one can easily see, the component no. 4 presents a topography and a temporal dynamic compatible with the Ne, with a large activity occurring shortly after EMG onset. This component was thus chosen as representing the Ne on errors, and will be called Ne_IC₀₂, where “02” stands for subject 02. The same procedure was applied to all the subjects, allowing to identify the Ne_IC_S, S ∈ {1,10}. Note that, during this selection stage, the time course of the components for correct and partial error trials was unknown.

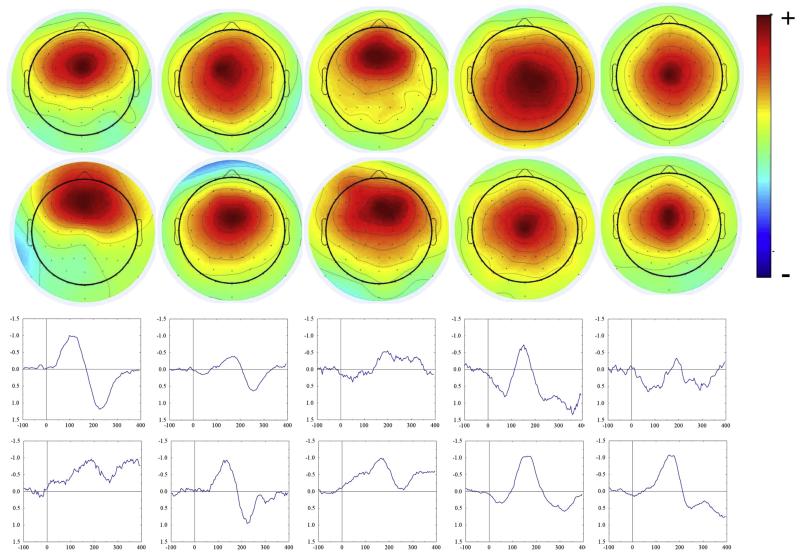
Based on those criteria, we could find a component Ne_IC_S whose topography and time course could account for the Ne on errors (first step described above) for each subject. Fig. 3 shows the topography and the time course of all the selected Ne_IC_S for each subject S and Table 1 gives the rank of the selected Ne_IC_S for each subject S. It is to be noted that the Ne_IC_S are always among the first components, for all the subjects (lowest rank=9). As components are ranked according to their energy, this indicates that they account for a large part of the original signal.

Fig. 3.

Topographies (upper panels) and averaged time course (lower panels) of the Ne_IC_S for each of the 10 subjects. All of them present a fronto-central topography. Note that, although all the maps present a positive polarity, this polarity is somehow arbitrary. Indeed, the projected signal on the sensors space is the product of the topography and the time-course. Hence inverting the polarity of both the topography and the time course produces exactly the same results. For the sake of simplicity, all the topographies have thus been plotted as positive, and the time course as negative in the period of interest. Importantly, for all the Ne_IC_S, the projected activity in the sensors space was always of negative polarity at the time of the Ne. The lower panels present the averaged time courses obtained for errors, ordered in the same way as the topographies. The corresponding topographies and time courses thus correspond to the same subject.

Table 1.

Summary of the equivalent dipole fitting for all the subjects. For each subject, this table indicates the rank of the Ne_IC_S, the residual variance (R. V.), and the dipole coordinates, in both Talairach and MNI coordinates.

Subject	Rank	R. V.	Talairach coordinates			MNI coordinates
			x	y	z	x	y	z
01	3	4.73	0.7	5.7	36.7	46.4	66.0	57.1
02	4	2.67	0.6	−15.6	20.1	46.3	55.4	47.5
03	5	5.51	0.9	25.3	35.7	46.5	76.1	57.0
04	1	2.56	0.6	−17.4	2.5	46.3	55.0	37.9
05	2	1.99	0.6	−13.9	37.6	46.3	55.9	57.1
06	4	2.95	−15.1	5.9	36.7	38.4	66.1	57.1
07	9	4.53	0.9	23.9	18.1	46.5	75.7	47.5
08	4	5.25	0.7	2.2	1.5	46.4	65.1	37.9
09	2	3.66	0.7	5.7	36.7	46.4	66.0	57.1
10	4	5.40	0.7	−13.9	37.6	46.3	55.9	57.1
Median	–	–	0.6	4.0	36.2	46.3	65.6	57.1

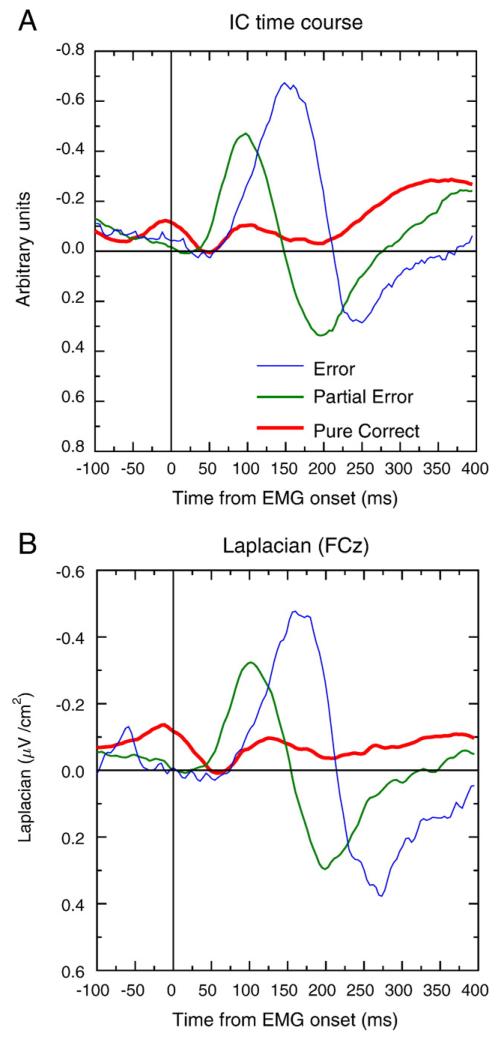
Once each of Ne_IC_S had been identified, we averaged, for each subject S, the time courses of these Ne_IC_S for correct trials and partial errors. The grand average is presented in Fig. 4A. One can clearly see a negative activity for both partial errors and, more importantly, for correct trials, albeit of smaller amplitude⁵. Statistical analysis revealed that the amplitudes of the peaks depend on trial types (F(2,18)=24.0, P<0.001). A latency peak effect also showed-up (F(2,18)=34.5, P<0.001, mean latencies: 116, 111 and 162 ms for correct, partial errors and errors, respectively). For the sake of comparison, Fig. 4B also presents the Laplacian data plotted with the same baseline and focus. The similar statistical results, along with the comparison between panels A and B indicate a close similarity between the Laplacian data and the components isolated by ICA. We will come back on this similarity in the discussion.

Fig. 4.

Grand average of the Ne_IC_S time course (panel A) and of the Laplacian transformed data (panel B, electrode FCz), for the three categories of trials. The zero of time corresponds to EMG onset (see Fig. 1 for details). The ICA data present a clear negative activity just after EMG onset, for both the partial errors and the correct trials.

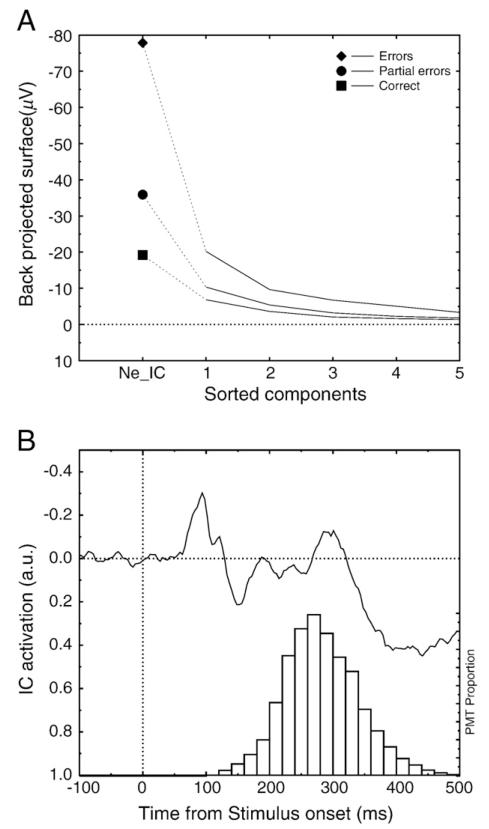
Although the selected components undoubtedly contribute to the “Ne” on correct trials, it might be possible that other components could also contribute to this activity. We evaluated this possibility in the following way: for each components, we back-projected the component onto the electrodes, and we measured the surface of the reconstructed signal at FCz, in a time window from −30 to +30 centered on the peak of the Ne. We then compared this reconstructed surface for all the non-retained components to the one computed for the retained one. Fig. 5A presents the mean reconstructed surface for the retained component (first point on the left), and for the 5 components showing the highest negative surfaces in the analysis windows, sorted in decreasing order. For the three types of trials, one can clearly see that the surface at FCz is always higher for the selected component than for the highest non-selected one. We also checked the time-course of the non-retained components with a negative surface in the analysis windows. None of them had a time course compatible with Ne (i.e. a phasic change shortly after EMG). This clearly supports the notion that the selected component account for, at minimum, the largest part of the Ne on correct trials.

Fig. 5.

(A) Mean back-projected surface measured at FCz for the retained component (first time point), and for the non-retained components, sorted as a function of the measured amplitude at FCz during the window of the Ne. Thus, component 1 correspond to the mean surface obtained for the non-retained component showing the most negative surface at FCz. One can see that even the most negative non-retained components present a surface at FCz that is lower than the retained components. (B) Grand-Average of the retained component time-locked to stimulus onset (upper panel) and distribution of PMT (lower panel). The retained components present two main activities: an early one, peaking around 100 ms, and a later one peaking around 250–300 ms, which largely occurs after EMG onset (see PMT distribution). Although visible time-locked to the stimulus, this negativity likely reflects the EMG-locked Ne.

The above analysis indicates that the selected ICs are the main contributors to the Ne and Ne-like on all trial types. One symmetrical question is whether the selected ICs also contribute to other EEG activities unrelated to the Ne. We thus averaged the components time-locked to stimulus onset. Fig. 5B shows the grand average of the selected ICs. This figure reveals two main negative activities: one peaking around 100 (N1) and another peaking around 300 ms (N2), followed by a positivity around 400 ms. The lower panel shows the distribution of the pre-motor times for all the subjects. This distribution reveals that the N2 mainly occurs around or after the response. This “N2” can hence be accounted for, to a large extent, by the post-response Ne (see figure S1 on supplementary material for a raster-plot representation of the data obtained for two representative subjects). More unexpectedly, a short latency wave shows up around 100 ms. Such a fronto-central, stimulus-locked, activity might be surprising, since one does not expect medial–prefrontal responses triggered by sensory events. However, such a medio-frontal activity was already visible in the data reported by Vidal et al. (2003a, Figs. 2 and 4) and sensory related activities have often been reported in both Supplementary Motor Area and Cingulate Cortex (see e.g. Russo et al., 2002) which have been interpreted as reflecting an “alerting” signal indicating to the motor structures that a response is likely to be required (Isomura et al., 2003). The early phasic wave observed in our data might well be the EEG correlate of such an alerting processes. The link between such an alerting signal and response monitoring may deserve further investigations, but is beyond the scope of this paper.

Although the above presented data provide argument for the presence of a negativity on correct trials similar to the one on errors and partial errors, we searched whether such a negativity could be also recovered by ICA when applied on correct trials only⁶. For nine subjects among the ten, we could find a component with a topography and time course compatible with the negativity observed on correct trials. To check whether those components were similar to the one obtained on the global ICA (with the three categories of trials), we computed the correlation coefficient between the grand averages obtained with the two ICA in the windows around the Ne (from −100 to +140 ms). The correlation was highly significant (r(62)=0.83; p<0.001), indicating that even on the correct trials only, one could extract the same component as in the global analysis.

Source localization

Localization of the selected component

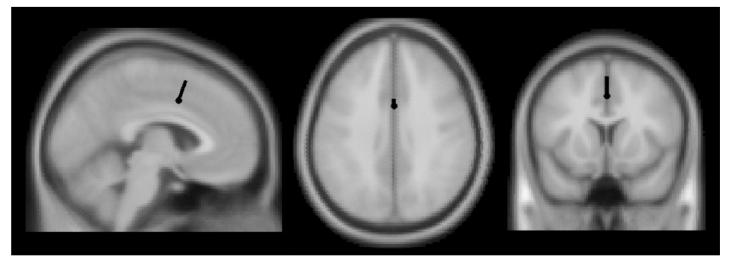
Assuming that each Ne_IC_S reflects a single neural source, one can attempt to localize the generator of the component with a single equivalent dipole. This was done for each Ne_IC_S (i.e. for each subject) with the “dipfit” module of EEGLAB. The median position of the individual dipoles was computed, and plotted in Fig. 6. The median position (x=0.6, y=4 and z=36.2, Talairach coordinates) clearly points to a source in the Rostral Cingulate Zone (Ridderinkhof et al., 2004) which is very likely the generator of the Ne (Dehaene et al., 1994; van Veen and Carter, 2002; Debener et al., 2005; Herrmann et al., 2004).

Fig. 6.

Source localization of the Ne_IC_S. A localization of all the Ne_IC_S was performed with the dipfit plugin of EEGLAB. The median position of all those dipoles coordinates and orientation was taken, and the equivalent median dipole is plotted in the MNI averaged brain. The equivalent dipole accounting for the Ne_IC_S is located within the RCZ.

Distributed sources localization on the original data

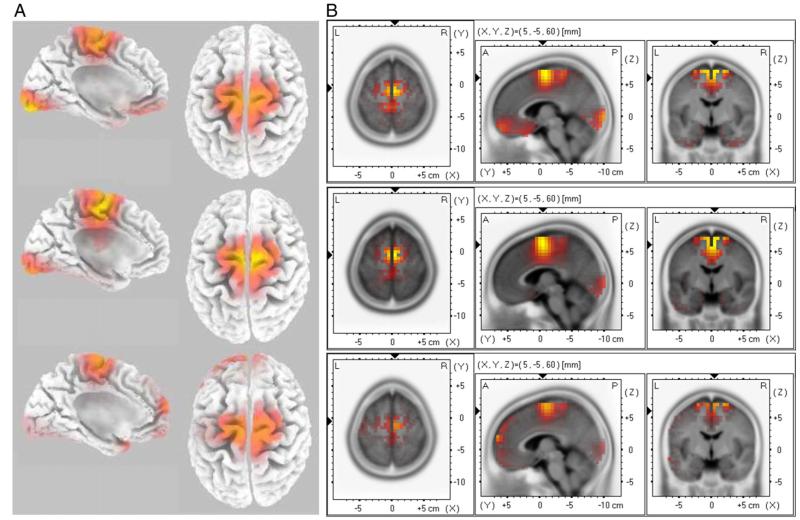
The ICA data support a unicity view of the negativities observed on errors, partial errors and correct trials. To further establish this point, we searched for the source(s) of those negativities with a distributed source algorithm (standardized Low Resolution Electromagnetic Tomography-sLORETA method, Pascual-Marqui, 2002). The Ne on errors has already been localized, both with single dipole modeling (Dehaene et al., 1994; van Veen and Carter, 2002) and with distributed sources (Herrmann et al., 2004). The results converge toward a source in the RCZ, although the precise structure might still be debated.

In the present study, source localization was performed on both the grand average and on individual averages by sLORETA (Pascual-Marqui, 2002), which implements a particular normalization of the minimum norm algorithm. Sources were estimated between 105 and 115 ms after EMG onset. Fig. 7A presents the sLORETA solution obtained for the grand average (from top to bottom, correct, partial errors and errors). The solution for errors (bottom) points to a source of the Ne on errors within the RCZ, in the ACC and/or in the SMA, which replicates previous results. Importantly very similar sources were found for the two other types of trials. Indeed, for both the partial errors and the correct trials, sLORETA solutions are also clearly localized in the RCZ region. To statistically establish these observations, source localization was performed for each individual subjects, and for each voxel a t-test (comparison to zero) was computed. Statistical significance level were estimated through randomized Statistical non-Parametric Mapping (number of permutations=5000, smoothed variance) that allows to correct for multiple comparisons (Nichols and Holmes, 2001). The statistically significant voxels (p<0.05, corrected) are plotted in Fig. 7B. As for the solution based on the grand average, one can see that the significant voxels cover the ACC/SMA regions. Note that, although largely overlapping, the solution is less significant for errors than for partial errors and correct trials. This is due to the low number of errors, leading to more noisy data. Besides the RCZ sources, some other sources (mainly occipital and, much weaker, orbito-frontal) emerge. As shown in supplementary material (see section 2 and Figure S2), the occipital source is due to an ongoing visual processing still present at the time of the response.

Fig. 7.

Source localization results obtained with sLORETA. (A) Solutions based on the grand averages for (from top to bottom), correct trials, partial errors and errors. (B) Statistical maps (p<0.05, corrected) for the three trials types (same ordering as in A). For the three trial types, a clear source within the RCZ was obtained.

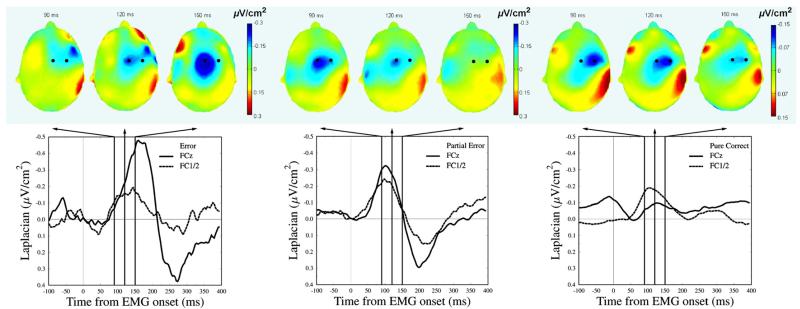
Lateralization of the Ne-like on correct trials?

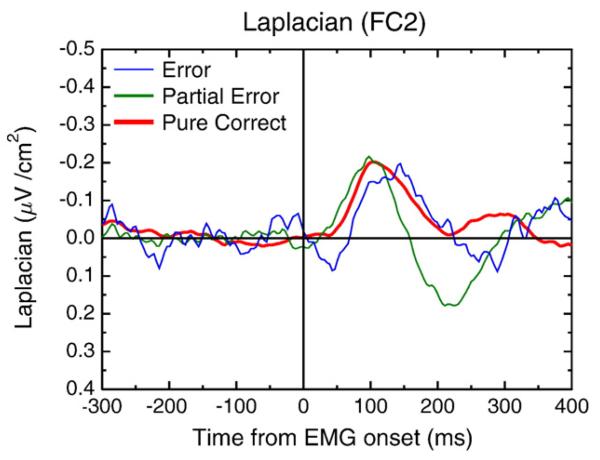
Yordanova et al. (2004) observed that on correct trials the Laplacian topography had a fronto central dominance with “[…] an additional tendency for a greater involvement of controlateral regions […]” (p. 594), whereas it was central on errors. This led them to conclude that the generators of the negativities in correct and error trials differ, at least partially. The finding that a single component could account for the negativities in the three categories of trials clearly speaks against different generators. Here, we explored another hypothesis, namely that the observed lateralization is due to another, lateralized, generator. If one assumes that the strength of this second generator is independent of correctness, it will largely impact the observed topography on correct trials (where the central activity is small), whereas its effect will be limited when the central activity is large (i.e. for errors). In order to evaluate this hypothesis we measured the activity over the FC1 and FC2 electrodes (depending on response side, FC1 for right hand responses, FC2 for left hand responses). Confirming the Yordanova et al. (2004) report, a clear negativity was observed over these electrodes for the three categories of trials (Fig. 8). Its surface (between 90 and 110 ms, around the peaks) did not vary as a function of correctness (−0.195, −0.201 and −0.144 μV/cm² for correct, partial errors and errors, respectively, F (2,18)=0.93, P=0.41). Although the medio-central negativities present a latency shift (see above), the latency of the lateral negativities did not (103 ms, 98 ms and 104 for correct, partial errors and errors, respectively, F(2,18)=0.49, P=0.62). This analysis confirms the presence of a negativity controlateral to the produced EMG activity for all three types of trials. Its amplitude being the same for the three categories, the lateralization is more visible for correct trials. This impression is further amplified by latency effects (see Fig. 9). Indeed, the FC1/FC2 activity peaking earlier than the Ne on errors, the topography at the peak of the Ne is less influenced by the lateralized activity. On the contrary, partial errors, and even more, correct trials present a greater lateralization since the time-course of the medial component is similar to the lateralized one. A further argument for a dissociation of the medial and the lateral activity comes from the influence of stimulus-response compatibility on the activities of interest. Indeed, although a significant compatibility effect was observed on the medial activity on correct trials (see above), no such effect is observed on the lateral part (F(1,9)=3.03; P=0.11).

Fig. 8.

Grand average of the fronto-lateral negativity observed over FC1/FC2 (depending on response side) after Laplacian computation, for errors (blue), partial errors (green) and correct (red) trials. This lateral activity is present for the three categories of trials, and neither its amplitude nor its latency differs across the three trial types. This activity is likely a follow-up of the negativity observed above the primary motor cortices contralateral to the response, just before EMG onset (see, Burle et al., 2004 for an overview).

Fig. 9.

Topographies and time courses of the medial and lateral activities, for the three types of trials (error, partial errors and correct trials, from left to right, respectively). The enhanced lateralization on correct comes from two interacting factors: first, on correct, the amplitude of the lateralized activity being closer (actually even larger) than the medial one, it largely contributes to the topography. The larger amplitudes for the medial activity on partial errors and errors, while the lateralized one does not change, reduces the impression of lateralization, although the lateralized component is of same amplitude. The second factor is timing. Indeed, the latencies of the medial activity differ across trial types, but it is not the case for the lateralized one. The peaks of the medial and lateralized activity are very similar for correct, but less so for errors, which further emphasizes the impact of the lateralized activity on correct trials.

Discussion

The discovery of the Ne by Falkenstein et al. (1991) has attracted a lot of interest in the cognitive control literature. Since this initial description, several other EEG activities have been observed and tentatively linked to the Ne. Miltner et al. (1997) reported that a negative feedback elicits a frontal–central negativity (the Feedback Related Negativity—FRN), that the authors interpreted as the equivalent of the Ne for externally signaled errors. Vidal et al. (2000) also reported a fronto-central negativity on correct trials, with similar topography and latency. These authors argued that this negativity on correct trials was of same nature as the one on errors, and hence that the functional interpretation of the Ne needs to be reevaluated. The question as to whether all those activities belong to the same family is essential for our understanding of cognitive control.

Both EEG and fMRI data already suggest that the Ne on errors and the Feedback Related Negativity (Miltner et al., 1997) reflect the same process: recently Gentsch et al. (2009) addressed the unicity of the Ne on errors and of the FRN by applying ICA to their data. They observed that the independent component(s) accounting for the Ne also accounted for the FRN. They concluded that the two phenomena represent the same functional process. Similarly, Holroyd et al. (2004) reported that the same ACC region responds to both internally and externally signaled errors.

In the present study, following Gentsch et al. (2009), we addressed this point by using the property of ICA to blindly identify the elementary components of the EEG signal. We reasoned that if the Ne on errors and on correct trials reflect the same brain activity modulated in amplitude, it should be captured in the same component by ICA. On the contrary, these negativities should be scattered into different components if they reflect different brain processes.

For all subjects, ICA could isolate a single component that was in a further step localized in the RCZ (Fig. 6), whose time course accounts for the negativities in the three categories of trials (correct, partial errors and errors). This result indicates that the scalp topographies of the negativities observed on the three trial types are identical, or at least that they are so close that ICA could not separate them, despite the large number of trials used in the decomposition. Taken alone, one may argue that the topographic argument might not be very strong, since different sources configurations can create very similar topographies. In particular, sources with different depth may produce very close topographies, if they also have the same orientation. However, besides topography, the isolated component also presents a clear evoked potential compatible with the Ne on the three categories of trials. Importantly, although ICA constraints the time course to be as independent as possible, it does not impose any constraint on the shape of the evoked potential. Therefore the similarity of evoked potential is not a mandatory consequence of the similar topography, which further supports the unicity conclusion. Interestingly, although not discussed at length, the ICA component extracted by Gentsch et al. (2009) to account for both the Ne and the FRN, also presented a clear negativity following the response on correct trials, also suggesting a same activity for correct trials and errors and FRN.

Besides the ICA argument, the source localization results also point towards a unique, modulated, brain activity. Confirming earlier reports (Dehaene et al., 1994; van Veen and Carter, 2002; Herrmann et al., 2004), the generator of the Ne on errors was located within the RCZ. The present data extend this result by localizing, for the first time, the Ne-like within the RCZ, for both partial error and correct trials. A common generator (at the level of precision achievable with the present methodology), although not a definitive argument, provides strong support for the unicity of the underlying process. One may also note that the Ne-like being generated within the RCZ, known to be largely involved in cognitive control (Ridderinkhof et al., 2004), this further supports the interpretation of the Ne-like in terms of cognitive control, even on correct trials. This is in line with previous data showing that the Ne-like amplitude is sensitive to performance (Luu et al., 2000; Allain et al., 2004). For example, Allain et al. (2004), capitalizing on previous results (Ridderinkhof et al., 2003), have shown that the Ne-like amplitude was reduced on correct trials preceding an error, hence foreshadowing the forthcoming error.

Yordanova et al. (2004) disputed the unicity in reporting that the topography on correct trials was lateralized contralaterally to the produced response while the Ne on error trials was not. The present data confirm this lateralized topography. However, they also show that this lateralization is due to an independent, lateralized, activity also present on errors and partial errors trials (Fig. 8). The amplitude of this lateralized activity is the same for the three type of error, showing that it is unrelated to the Ne. As a consequence of this equivalent amplitude, the impact of this lateralized activity appears stronger on correct trials, since the medial and frontal activities have approximately the same amplitude. The much larger amplitude for the medial activity on partial errors and errors dramatically reduces the lateralization. These results thus confirm that the Ne-like is really medial.

Altogether, these results clearly point to a single process whose amplitude is modulated by performance. We shall now discuss the functional consequences of this unicity for current models of cognitive control, and then provide some possible theoretical directions.

None of the current neurocomputational models of cognitive control can easily account for the presence of the negativity on correct trials. Obviously, the error detection view (Coles et al., 2001) of the Ne is de facto invalidated by the presence of this activity on correct trials. The conflict-monitoring model can, under some circumstances, predict the presence of negativity on correct trials. However, this negativity should occur before the response, not after (Yeung et al., 2004). A last class of models is based on reinforcement learning theory and the role of dopaminergic (DA) neurons (Holroyd and Coles, 2002; Frank et al., 2005). Although those models differ in several respects, they share one common assumption which is critical for the current purpose: negative outcome will induce a burst of DA-neurons discharge, while a positive outcome will reduce the frequency discharge of DA-neurons. The phasic increase in DA-neurons discharge is thought to be at the origin of both the Ne on errors, and the FRN. However, since positive outcomes, among which correct responses likely are, induce a suppression of DA-neurons discharge, those models cannot easily predict a similar negativity on correct trials and on errors. One may argue that for some trials, for example the long RT trials, subjects judged their performance as suboptimal. However, Vidal et al. (2003a) splitted the correct RT distribution and showed that the Ne amplitude was the same for long and short RTs, rendering this interpretation unlikely.

Instead of considering the Ne as an all-or-none process occurring for erroneous responses (or negative feedback), it may be necessary to change our view on this activity. This activity might well be a default process, present after every (behaviorally relevant) response. However, its amplitude could be modulated, both positively (increase) or negatively (decrease). The critical question is then to find what modulates it. Hints may come from pathologies: several patients studies have shown an increased Ne on correct trials compared to controls (schizophrenia—Mathalon et al., 2002; pre-frontal lesions—Gehring and Knight, 2000; OCD—Endrass et al., 2008, etc.). Instead of considering this increase as a degraded error detection, which is not supported by the fact that in those pathologies patients present a normal post-error slowing, it may reflect a disruption of the modulatory process. A reinterpretation of Gehring and Knight (2000) data may provide interesting clues: since lesion of the PFC leads to equivalent amplitudes for correct and error trials, it might be that PFC plays an essential role in the modulation process. Another obvious candidate, not necessarily exclusive, for such modulation is DA activity. Instead of being at the core of the genesis (Holroyd and Coles, 2002), it may well act as a modulator (Frank et al., 2005). A recent study in de novo Parkinson disease (PD) patients may go into that direction (Willemssen et al., 2009). Indeed, the authors reported that de novo PD patients present a reduced negativity on errors, but a larger one on correct trials, the two being of same amplitude. Since PD patients, especially de novo, have a large deficit in DA, these data clearly indicate that the amplitude of the Ne is not directly related to DA release. But, if one assumes that the amount of DA triggered by positive and negative outcomes modulate the Ne amplitude, the reduced level of DA may prevent the modulation to occur, hence leading to negativities of similar amplitude. Although speculative, this view may be testable in future research.

Finally, our results call for a more methodological comment. The results obtained with ICA and Laplacian transform are remarkably similar. Although both techniques aim at separating the contribution of the underlying sources, they are, however, extremely different from a mathematical point of view. Indeed, ICA decomposition is mainly based on the temporal statistical dependence between signals recorded across sensors, while Laplacian is the second spatial derivative of the recorded signal. The high convergence between these two different methods cross-validates their results and strengthens the above results. It also exemplifies the hazard of deriving conclusions on monopolar, mixed data, and strongly speaks for the use of deblurring methods in EEG.