Abstract
We provide a method for estimating brain metabolic state based on a reduced-order model of EEG burst suppression. The model, derived from previously suggested biophysical mechanisms of burst suppression, describes important electrophysiological features and provides a direct link to cerebral metabolic rate. We design and fit the estimation method from EEG recordings of burst suppression from a neurological intensive care unit and test it on real and synthetic data.
I. INTRODUCTION
Burst suppression is an electroencephalographic (EEG) pattern in which periods of high voltage activity (bursts) alternate with periods of isoelectric quiescence (suppression) (see Figure 1). It is characteristic of a profoundly inactivated brain and occurs in conditions such as deep general anesthesia [1], hypothermia [2] and coma [3]. That these different conditions lead to seemingly similar brain activity suggests that burst suppression is the result of a fundamental, low-order process that is prominent when higher-level brain activity is depressed.
Fig. 1.

Example of burst suppression. (A) Continuous EEG activity, (B) Burst suppression
The main features of burst suppression have been well described [4], [5], [6]. Classically, burst suppression is thought to be a global state where bursts begin and end nearly simultaneously across the entire scalp. It is different from typical faster EEG oscillatory patterns, in that suppression epochs can be very irregular and may last several seconds. Importantly, burst suppression is not a homogeneous state but, instead, varies continuously as a function of brain inactivation. As the brain becomes progressively more inactivated, the amount of suppression, relative to the amount of burst, increases. This variation has been traditionally quantified with the burst suppression ratio [6], which measures the amount of suppression in a sliding window of EEG data. Recent research on the burst suppression probability [7] (BSP) has provided a statistically rigorous, and window-free, approach to estimating the burst suppression state.
Here, we introduce a method for estimating not simply burst suppression, but the underlying brain metabolic state. Our method is based on a recent nonlinear, biophysical model [5], which attributes the parametric increase in suppression duration with brain inactivation to decreases in brain metabolism.
We begin by characterizing the relationship between brain metabolic state and observable EEG features, namely the lengths and variability of bursts and suppressions. We then introduce and fit a reduced state-space model of burst suppression to recordings from neurological intensive care unit (ICU) patients. From this model, we demonstrate the inference of the underlying metabolic state.
The remainder of this paper is organized as follows. Section II provides a brief background on the biophysical mechanisms of burst suppression and the resulting models. Section III introduces the reduced state-space model and methods for metabolic state inference. Brief conclusions are formulated in Section IV.
II. BACKGROUND
A. Neurophysiology of Burst Suppression
Although many features of burst suppression have been described, the neurophysiological mechanisms that are responsible for creating it are less well understood. In the context of general anesthesia, the early work by Steriade [8] helped establish certain neural correlates of burst suppression, describing the participation of different cell types in bursts and suppressions, though an underlying mechanism was not suggested. Other studies [9] have suggested that burst suppression involves enhanced excitability in cortical networks, and have implicated fluctuations in calcium as related to the alternations between bursts and suppressions.
B. Existing Models of Burst Suppression
A unifying biophysical model for burst suppression – one that accounts for its characteristics, and also its range of etiologies – was recently proposed [5]. The key insight of the model is that each of the conditions associated with burst suppression (general anesthesia, hypoxic/ischemic coma, hypothermia) is associated with decreased cerebral metabolic rate of oxygen (CMRO). The model links this decrease in CMRO to deficiencies in ATP (adenosine triphosphate, the energetic substrate for neuronal activity) production in cortical networks (see Figure 2). The termination of each burst is a reflection of ATP consumption due to the neuronal activity underlying fast EEG oscillations, whereas suppressions are governed by the slow dynamics of ATP regeneration.
Fig. 2.
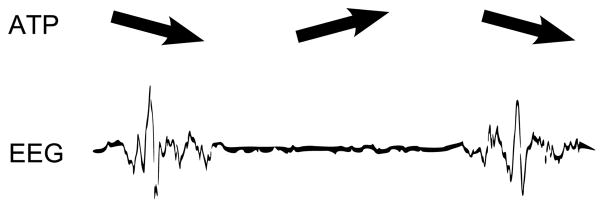
ATP-based mechanism for burst suppression. ATP is depleted through the course of each burst, leading to suppression. During suppression ATP gradually recovers until, eventually, activity begins again
This model provided an explanation for why three cardinal features of burst suppression – the spatial synchrony of bursts onsets across the scalp, the increase in suppression durations with increasing brain inactivation, and the long timescales of suppressions – can arise across its disparate etiologies. The present paper is intended to provide a simplification of the model in [5], and simultaneously, to describe a fourth cardinal feature that was not previously explored, namely the variability of burst lengths at different burst suppression levels. This, in turn, enables the estimation of brain metabolism (CMRO) from EEG recordings.
III. PROBABILISTIC MODELING AND ESTIMATION OF BURST SUPPRESSION
A. Simplified Burst Suppression Model
Based on [5], we present a reduced order state-space model for burst suppression governed by the following:
| (1) |
Here, a(t) is the concentration of local ATP in a cortical region, kc is the rate of ATP consumption during each burst, kr is the rate of ATP regeneration during each suppression, and u(a) indicates whether burst activity can or cannot be sustained. We select
| (2) |
meaning that burst activity can only be initiated when ATP levels increase beyond the threshold α.
By fixing the parameter kc = 1, (1) can be rewritten as
| (3) |
where x, a value from 0 to 1, is the brain metabolic state. A value of x = 0 corresponds to full CMRO (when ATP regeneration equals consumption), while x = 1 is complete metabolic depression.
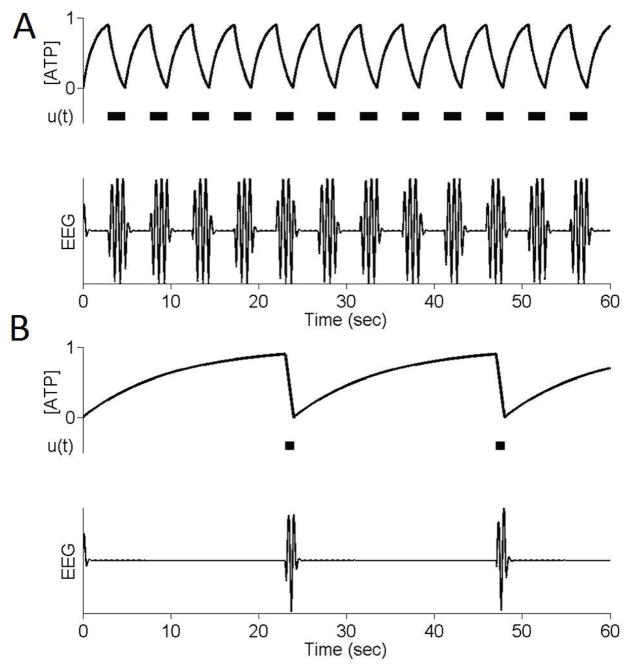
Figure 3 illustrates the output of the model for two different values of x. When x is moderate, the model produces epochs of burst and suppression that are commensurate in length. When x is reduced to a low value, the bursts are much shorter (due to more rapid consumption) and the suppressions are longer (due to slower regeneration).
Fig. 3.
Example of model output for different values of metabolic state. (A) x = 0.8, (B) x = 0.1. Simulated EEG signal shown for schematic purposes only.
The model (1) offers increased analytical tractability as compared to the full nonlinear model in [5]. In particular, we can derive explicit expressions for burst and suppression lengths (LS and LB) at different metabolic state levels as:
| (4) |
where
| (5) |
The burst suppression state itself can then be quantified in terms of the suppression lengths, relative to the total length of a burst-suppression cycle, specifically:
| (6) |
Note that in practice, (6) can be estimated using the burst suppression probability (BSP) [7] algorithm. Through (4) and (6), we can estimate x based on measurement of burst suppression and calculation of burst and suppression lengths from the EEG.
B. Automatic EEG Segmentation
In order to infer the metabolic state in our model, we must first establish a method to segment EEG recordings into bursts and suppressions. That is, if xt, t = 0, 1, 2, … is the sampled EEG signal, then we must obtain a corresponding binary series nt where nt = 1 if xt is in a suppression and 0 if it is in a burst.
While several algorithms have been developed for this purpose [10], [11], we choose to use adaptive variance thresholding as follows:
| (7) |
| (8) |
| (9) |
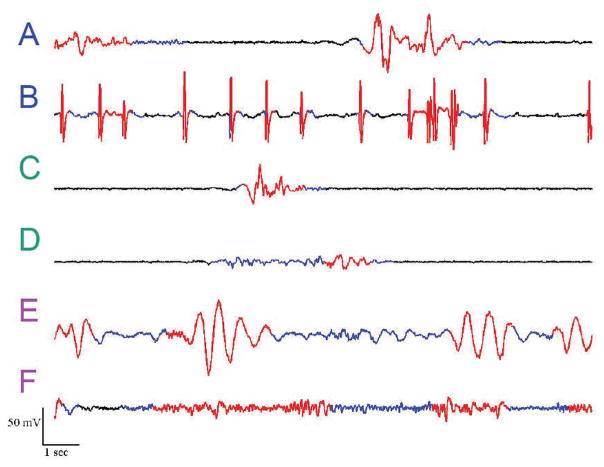
where γ is a tunable filter parameter and is an amplitude threshold. We have applied this method to a variety of EEG recordings of burst suppression from the neurological ICU [12] and, as illustrated in Figure 4, it can reliably segment the EEG into bursts and suppressions.
Fig. 4.
Examples of ICU burst suppression with automatic segmentation. Segmented bursts (i.e., nt = 0) are shown in red, while suppressions (i.e., nt = 1) are blue. (A,B) Patterns containing epileptiform spikes, (C,D) Patterns with distinct bursts and suppressions, (E,F) Patterns with less distinct bursts
From the binary signal nt it is straightforward to obtain empirical lengths of bursts and suppression (simply, the lengths of consecutive 0s or 1s), facilitating estimation of metabolic state.
C. Inference of Metabolic State
In order to estimate the metabolic state x as a function of time, and to account for anticipated stochastic effects in burst and suppression lengths, we introduce a probabilistic model as follows:
| (10) |
This model is a rectified Gaussian random walk and, if σ is suitably small, implies that x does not exhibit large and sudden temporal changes.
We will, furthermore, make a Markovian assumption that
| (11) |
and, in particular, that
| (12) |
where Li denotes the length of the ith event (either a burst or suppression) and H(·) denotes the entire history.
What remains is to define the probabilities for continuation:
| (13) |
and switching:
| (14) |
Based on the characterization from (4) and (6), we choose to model these probabilities using the Weibull hazard function
| (15) |
and its cumulative distribution function (CDF)
| (16) |
Note that (15) and (16) are common in medical survival analysis and reliability engineering.
We proceed to fit (16) to the burst suppression level, which can be well-estimated from the segmented EEG using the burst suppression probability (BSP) algorithm [7]. In particular, we compute an empirical CDF for (13) and (14) by finding, for each suppression and burst, the corresponding BSP level. We then fit (16) to these CDFs using the constraints
| (17) |
for bursts and
| (18) |
for suppressions. For this, we use a nonlinear least squares numerical method over the free parameters ai, bi, ci. Figure 5 illustrates the empirical CDF for switching from the EEGs of 20 ICU patients1 and the resulting fit for two BSP levels. In both cases, the functions (17)–(18), together with (16), are able to closely match the empirical CDFs. Figure 6 illustrates these fits, as compared to the empirical CDFs for switching, across the entire range of BSP values. As shown, the resulting model characterization is close to what we find from our data.
Fig. 5.
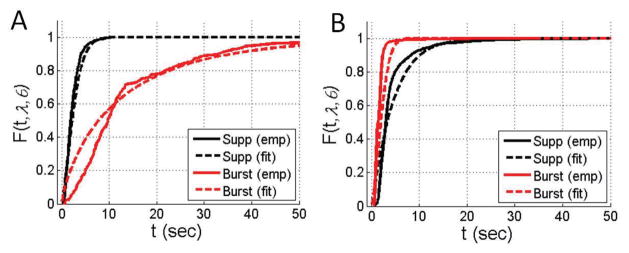
Example of CDF for switching and resulting fits for two BSP levels. (A) BSP of 0.2, (B) BSP of 0.7
Fig. 6.
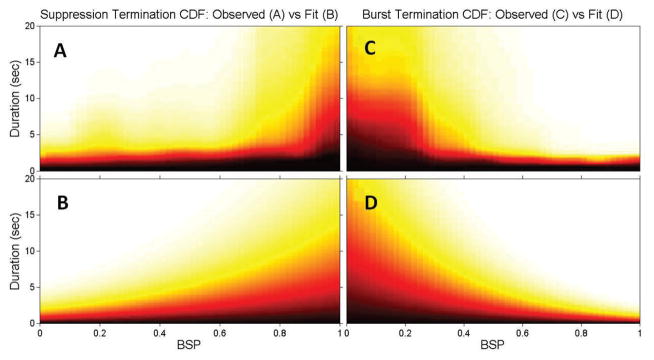
Empirical1 and fit switching probability functions vs. BSP for suppressions (A,B) and bursts (C,D). The fitted functions (B,D) closely match the empirical CDFs (A,C). White indicates values close to 1 (high probability of switching) whereas black indicates values close to 0 (low probability of switching).
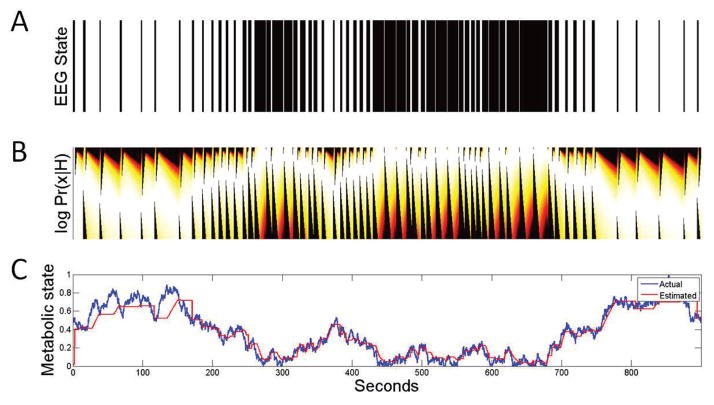
The one-to-one relationship (6) relates our continuation and switching functions (for BSP) directly to metabolic state. We can thus proceed to perform inference of the metabolic state through a direct application of Bayes formula to (12). We illustrate the estimation using synthetic data generated from the model (1). Figure 7A illustrates the burst and suppression output (nt) from the model when x(t) is a realization of the random walk (10). Through (12)–(16), and the fits of (17)–(18) obtained empirically from our ICU data (i.e., Figure 6), we obtain the posterior probability density function of metabolic state x at each point in time. The mean of each distribution is the metabolic state estimate, which is plotted in Figure 7C and compared with the true value. Clearly, the estimate closely tracks the true value. One feature of note is that the estimate does not immediately change at each switch from burst to suppression. Instead, and consistent with our model, it remains stable during each burst and suppression until such time as its length is improbable given the current BSP estimate.
Fig. 7.
Example of inference of metabolic state from simulated burst suppression. (A) Simulated bursts and suppressions from (1), (B) Probability density function of metabolic state x estimated from (12)–(18) (and corresponding fits). (C) Inferred x (red trace) as compared to the true value used to generate (A) (blue trace).
IV. CONCLUSIONS
We have provided a reduced-order model for burst suppression that links the EEG directly to reductions in cerebral metabolic rate. From this model, we developed a probabilistic inference scheme to estimate brain metabolic state from measured EEG activity. The resulting method was fit and tested on EEG data gathered from patients in the neurological ICU. We then tested the method on synthetic burst suppression data, showing correct inference of metabolic state.
Further testing is, of course, necessary to validate the use of this method in the clinical setting. Nevertheless, the model provides justification for the practice of pharmacologically inducing burst suppression as a therapeutic target for brain protection in neurological intensive care settings such as unrelenting seizures (refractory status epilepticus), severe traumatic brain injury, and in cardiac surgery during circulatory arrest [13]. The model and estimation scheme may also help inform strategies for optimizing burst suppression when using anesthetic drugs. An eventual goal is to provide a neurophysiologically-principled basis for inferring and tracking brain metabolism in the ICU or surgical settings.
Supplementary Material
Acknowledgments
This work has been supported by NIH DP1-OD003646 (to ENB). SC holds a Career Award at the Scientific Interface from the Burroughs-Wellcome Fund
Footnotes
These data were collected at the Massachusetts General Hospital as part of routine clinical monitoring and with institutional review board approval.
References
- 1.Clark DL, Rosner BS. Neurophysiologic effects of general anesthetics. i. the electroencephalogram and sensory evoked responses in man. Anesthesiology. 1973 Jun;38(6):564–582. [PubMed] [Google Scholar]
- 2.Stecker MM, Cheung AT, Pochettino A, Kent GP, Patterson T, Weiss SJ, Bavaria JE. Deep hypothermic circulatory arrest: Ii. changes in electroencephalogram and evoked potentials during rewarming. Ann Thorac Surg. 2001 Jan;71(1):22–28. doi: 10.1016/s0003-4975(00)02021-x. [DOI] [PubMed] [Google Scholar]
- 3.Young GB. The eeg in coma. J Clin Neurophysiol. 2000 Sep;17(5):473–485. doi: 10.1097/00004691-200009000-00006. [DOI] [PubMed] [Google Scholar]
- 4.Amzica F. Basic physiology of burst-suppression. Epilepsia. 2009 Dec;50(Suppl 12):38–39. doi: 10.1111/j.1528-1167.2009.02345.x. [DOI] [PubMed] [Google Scholar]
- 5.Ching S, Purdon PL, Vijayan S, Kopell NJ, Brown EN. A neurophysiological-metabolic model for burst suppression. Proc Natl Acad Sci U S A. 2012 Feb;109(8):3095–3100. doi: 10.1073/pnas.1121461109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Akrawi WP, Drummond JC, Kalkman CJ, Patel PM. A comparison of the electrophysiologic characteristics of eeg burst-suppression as produced by isoflurane, thiopental, etomidate, and propofol. J Neurosurg Anesthesiol. 1996 Jan;8(1):40–46. doi: 10.1097/00008506-199601000-00010. [DOI] [PubMed] [Google Scholar]
- 7.Chemali JJ, Wong KFK, Solt K, Brown EN. IEEE EMBC. Boston, MA: 2011. A state-space model of the burst suppression ratio. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Steriade M, Amzica F, Contreras D. Cortical and thalamic cellular correlates of electroencephalographic burst-suppression. Electroencephalogr Clin Neurophysiol. 1994 Jan;90(1):1–16. doi: 10.1016/0013-4694(94)90108-2. [DOI] [PubMed] [Google Scholar]
- 9.Kroeger D, Amzica F. Hypersensitivity of the anesthesia-induced comatose brain. J Neurosci. 2007 Sep;27(39):10 597–10 607. doi: 10.1523/JNEUROSCI.3440-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lofhede J, Lfgren N, Thordstein M, Flisberg A, Kjellmer I, Lindecrantz K. Classification of burst and suppression in the neonatal electroencephalogram. J Neural Eng. 2008 Dec;5(4):402–410. doi: 10.1088/1741-2560/5/4/005. [DOI] [PubMed] [Google Scholar]
- 11.Sarkela M, Mustola S, Seppnen T, Koskinen M, Lepola P, Suominen K, Juvonen T, Tolvanen-Laakso H, Jntti V. Automatic analysis and monitoring of burst suppression in anesthesia. J Clin Monit Comput. 2002 Feb;17(2):125–134. doi: 10.1023/a:1016393904439. [DOI] [PubMed] [Google Scholar]
- 12.Westover MB, Ching S, Shafi M, Cash S, Brown EN. Real-time segmentation of burst suppression patterns in critical care eeg monitoring. 2012 doi: 10.1016/j.jneumeth.2013.07.003. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hall R, Murdoch J. Brain protection: physiological and pharmacological considerations. part ii: The pharmacology of brain protection. Can J Anaesth. 1990 Oct;37(7):762–777. doi: 10.1007/BF03006535. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.