Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Apr 1.
Published in final edited form as: Magn Reson Imaging. 2013 Dec 14;32(3):245–249. doi: 10.1016/j.mri.2013.10.013

Assessing reproducibility of diffusion-weighted magnetic resonance imaging studies in a murine model of HER2+ breast cancer

Jennifer G Whisenant a,g, Gregory D Ayers b, Mary E Loveless a, Stephanie L Barnes a,c, Daniel C Colvin a,c, Thomas E Yankeelov a,c,d,e,f,g,h,*
PMCID: PMC3939718  NIHMSID: NIHMS549803  PMID: 24433723

Abstract

Background and purpose

The use of diffusion-weighted magnetic resonance imaging (DW-MRI) as a surrogate biomarker of response in preclinical studies is increasing. However, before a biomarker can be reliably employed to assess treatment response, the reproducibility of the technique must be established. There is a paucity of literature that quantifies the reproducibility of DW-MRI in preclinical studies; thus, the purpose of this study was to investigate DW-MRI reproducibility in a murine model of HER2+ breast cancer.

Materials and methods

Test–Retest DW-MRI scans separated by approximately six hours were acquired from eleven athymic female mice with HER2+ xenografts using a pulsed gradient spin echo diffusion-weighted sequence with three b values [150, 500, and 800 s/mm2]. Reproducibility was assessed for the mean apparent diffusion coefficient (ADC) from tumor and muscle tissue regions.

Results

The threshold to reflect a change in tumor physiology in a cohort of mice is defined by the 95% confidence interval (CI), which was ± 0.0972 × 10−3 mm2/s (±11.8%) for mean tumor ADC. The repeatability coefficient defines this threshold for an individual mouse, which was ± 0.273 × 10−3 mm2/s. The 95% CI and repeatability coefficient for mean ADC of muscle tissue were ± 0.0949 × 10−3 mm2/s (±8.30%) and ± 0.266 × 10−3 mm2/s, respectively.

Conclusions

Mean ADC of tumors is reproducible and appropriate for detecting treatment-induced changes on both an individual and mouse cohort basis.

Keywords: Reproducibility, Diffusion-weighted MRI, Apparent diffusion coefficient, Mouse

1. Introduction

Current radiographic analysis of treatment response is based on the Response Evaluation Criteria in Solid Tumors (RECIST), which uses one-dimensional changes in tumor size to determine response [1]. However, it is well recognized that RECIST may not provide the most sensitive response assessment to novel and emerging therapies that target the molecular or cellular aspects of the tumor itself or, for example, its microenvironment [2, 3]. Development of imaging methods that can provide an earlier assessment of disease response is an active area of research, as it would allow for the initiation of alternative, potentially more effective, treatments while avoiding unnecessary toxicities associated with ineffective therapy. Diffusion-weighted magnetic resonance imaging (DW-MRI) has the potential to offer earlier assessments of disease response, as parameters derived from quantitative analyses of such data can be used to characterize treatment-induced alterations in tumor cell density [4–7].

The microscopic, thermally-induced behavior of molecules moving in a random pattern is referred to as self-diffusion or Brownian motion. The rate of diffusion in cellular tissues is described by an apparent diffusion coefficient (ADC), which is influenced by the number and separation of barriers that a diffusing water molecule encounters. DW-MRI maps the ADC, and in well-controlled situations the variations in ADC have been shown to correlate inversely with tissue cellularity [8]. It has been shown, in preclinical [9–12] and clinical [13–15] settings, that exposure of tumors to both chemotherapy and radiotherapy consistently leads to measurable increases in water diffusion in cases of favorable treatment response.

In their 2009 DW-MRI review, Padhani et al. recommended that each imaging center determine the reproducibility of DW-MRI data at their institution to allow for proper study design and to assess the significance of treatment-induced changes [16]. Reproducibility of clinical DW-MRI data have been previously assessed in normal and diseased tissues with a variety of image acquisition methods and data analyses including differences in the number and strength of diffusion-weighted images, as well as the reproducibility statistics themselves [17–20]. However, there is a paucity of such data in the preclinical setting. With the increasing use of DW-MRI as a surrogate biomarker of response in preclinical studies [9, 10, 12], investigating reproducibility is imperative to interpret whether parameter changes during therapeutic interventions reflect tumor cell-ularity instead of measurement error in mouse models of disease. Thus, the objective of this study was to quantify DW-MRI reproducibility in a murine model of HER2+ breast cancer in order to assist in the interpretation of results collected from future longitudinal treatment response studies.

2. Materials and methods

2.1. Animal and tumor xenograft model

Trastuzumab-resistant breast cancer cells, HR6, were generously gifted from Dr. Carlos Arteaga, M.D. at Vanderbilt University. This cell line was developed by harvesting cells from BT474 xenografts that initially responded but recurred in the presence of maintained trastuzumab [details are provided in Ref. 21]. (This cell line was selected as it is part of an ongoing investigation of trastuzumab-resistance in breast tumors.) Female athymic nude mice (n = 11, 4–6 weeks, Harlan, Indianapolis, IN) were implanted with 0.72 mg, 60-day release, 17β-estradiol pellets (Innovative Research of America, Sarasota, FL). Twenty-four hours later, approximately 107 HR6 cells were injected subcutaneously into the right flank. Mice were anesthetized with 2% isoflurane in pure oxygen for both procedures. Tumor volumes were measured weekly after cell injection via calipers, and the mean tumor volume at the start of imaging was 298 mm3 (range: 136 mm3–526 mm3). All animal procedures were approved by our Institution's Animal Care and Use Committee.

2.2. Image acquisition

Test–retest DW-MRI sessions were performed on 11 mice using a 7 T MRI scanner (Agilent Technologies (formally Varian), Palo Alto, CA) equipped with a 38-mm quadrature RF coil (Doty Scientific, Columbia, SC). Anesthesia was induced and maintained for each imaging session via 2% isoflurane in pure oxygen. Animal respiration rate was monitored, and animal body temperature was maintained at an external temperature of 32°C by means of a flow of warm air directly into the bore of the magnet. Each animal was placed in a custom built restraint, and the tumor region was first localized via 3D gradient echo scout images. Fifteen 1 mm thick slices with a 1 mm gap were acquired in order to cover the entire tumor region. A standard pulsed gradient spin echo sequence was used to acquire diffusion-weighted images with three b values (150, 500, and 800 s/ mm2) and gradients applied simultaneously along the three orthogonal directions (x, y, and z). Scan acquisition parameters were: TR/TE = 2000/30 ms, gradient duration δ = 3 ms, gradient interval Δ = 20 ms, two signal excitations, and an acquisition matrix of 128 × 128 over a 28 × 28 mm2 field of view. Image acquisition was triggered with respiration and navigator corrected [22] to reduce image artifacts due to bulk motion. Animals were removed from the scanner, allowed to recover completely from anesthesia, and given free access to food and water between test–retest imaging sessions. Repeat DW-MRI scan acquisitions were separated by a median of 5.88 hours (range: 1.50–7.82).

2.3. Image analysis

To construct an ADC parametric map, signal intensities from images acquired at three b values were fit for each image voxel using a nonlinear least squares optimization method to Eq. (1):

S(b)=S0·exp(−ADC·b), (1)

where S0 and S(b) are the signal intensities before and after application of diffusion gradients, respectively. As we did not acquire images without application of diffusion gradients (i.e., b = 0), S0 was a free parameter in our optimization routine. Both image volumes were viewed simultaneously to ensure that a similar tissue section was analyzed, and the b = 150 s/mm2 image was utilized to define tumor boundaries. Care was taken during setup so that animal position and orientation in the magnet were similar between repeat acquisitions; however, image co-registration was not performed and thus separate regions of interest (ROIs) were manually drawn around the tumor for each scan. ROIs were also drawn within the skeletal muscle on the same slice as the tumor ROIs. Mean ADC values from each ROI were calculated and compared between repeated measurements. To ensure data integrity, a water phantom was imaged simultaneously with the animal in each imaging session. Additionally, the reproducibility of the mean ADC from the water phantom was computed. All data analysis methods were performed in MATLAB® (The MathWorks, Natick, MA).

2.4. Reproducibility statistics

Reproducibility statistics employed in this study follow the methods previously described by Bland and Altman [23], and are similar to what was previously implemented with imaging data by Galbraith et al. [24]. For each data set, the difference between repeat measurements, dwas calculated. The distribution of the differences d was tested for normality using a two-sided Shapiro–Wilk test. A Kendall's tau test was used to estimate the correlation between the magnitude of the difference values and overall mean parameter value for the repeated measurements. A Wilcoxon signed-rank test was performed with the original data to test the null hypothesis of no bias (i.e., average difference is zero) between repeated measurements. The statistical measurements of reproducibility were then calculated as follows:

  1. The root-mean-square deviation (rMSD) is computed using the differences between repeat measurements d:
    rMSD=Σd2n (2)
  2. The 95% confidence interval (CI) for change which might occur in a group of n subjects:
    CI=±1.96·std(d)n, (3)
    where std(d) is the standard deviation of the difference between repeated measurements. Any change in a group of size n greater than this value would be significant at the 5% level.
  3. The within-subject standard deviation (wSD) is:
    wSD=rMSD2. (4)
  4. The repeatability coefficient (r) is:
    r=2.77.wSD, (5)
    or, equivalently:
    r=1.96.rMSD. (6)

The repeatability coefficient defines the magnitude of the maximum difference expected in 95% of paired observations; i.e., an observed difference greater than this value between scans for an individual would be significant at the 5% level.

Due to our moderate sample sizes, we replaced 1.96 in Eq. (3) with the appropriate t-statistic for our sample size, which for 11 data sets is 2.228. Statistical analyses were performed using the statistical toolbox in MATLAB®. A significance value of p < 0.05 was used for all statistical tests.

In addition to the above reproducibility statistics, we also quantified the intraclass correlation coefficient (ICC). As defined by Landis and Koch for interpreting the strength of agreement of categorical data, an ICC greater than 0.61 is considered substantial agreement between repeated measurements [25].

3. Results

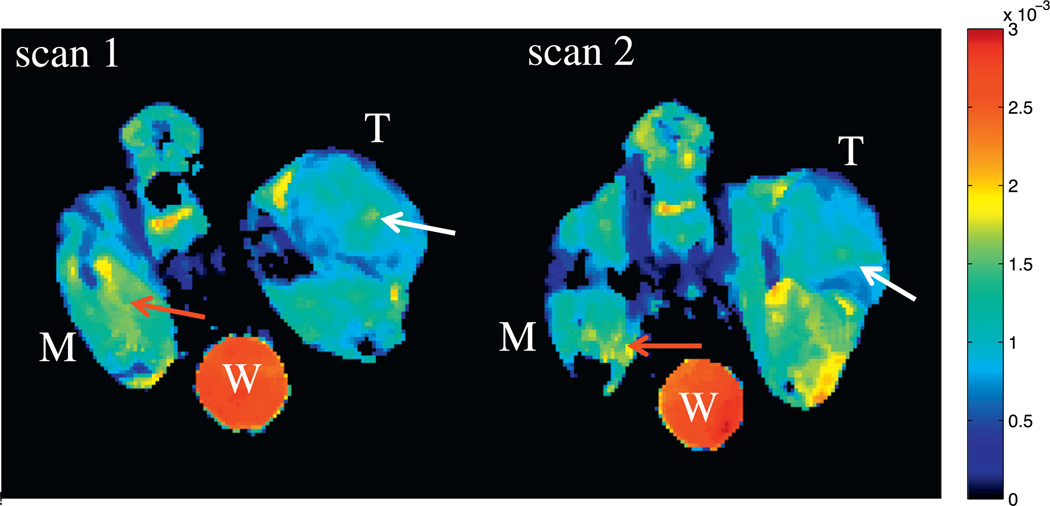
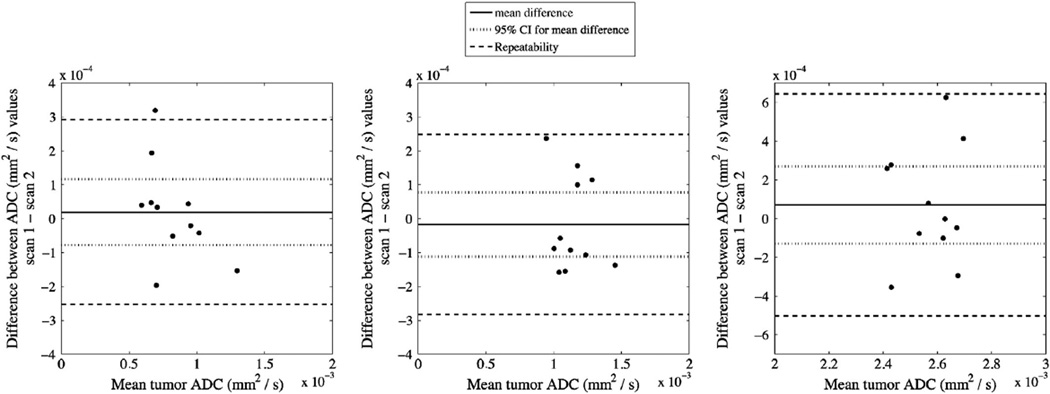
Examples of ADC parametric maps from repeated scans are depicted in Fig. 1annotated with labels for tumor (‘T’), muscle (‘M’), and water phantom (‘W’). It can be noted from the figure that the animal orientation is slightly different between repeated scans, thus showing the need for drawing separate ROIs for each imaging session. The average volume (±standard error) of the tumor ROIs was 46.02 mm3 (±5.2004) and 44.5 mm3 (±4.86) from scan 1 and 2, respectively. Statistically, there is no difference in tumor volume ROIs between repeated scans (Wilcoxon, p > 0.05). The reproducibility statistics for the tumor, muscle, and water phantom are listed in Table 1. Neither ROI had an average difference significantly different from normal as determined from the Wilcoxon signed-rank test. Additionally, the difference between repeat measurements d was independent of the mean for each ROI (thus, a logarithmic (or other) transformation was not required). Fig. 2 displays Bland– Altman plots for all ROIs, with each panel plotting the differences in ADC values between the repeated scans against the mean ADC value. The mean difference and 95% CIs are displayed as solid and dotted lines, respectively. The 95% CIs, which define the required change to surpass the expected measurement variability for a group of mice, are ± 0.0972 × 10−3 mm2/s (±11.8%), ± 0.0949 × 10−3 mm2/s (±8.30%), and ± 0.200 × 10−3 mm2/s (± 7.78%) for mean tumor, muscle, and water phantom ADC, respectively. Repeatability ranges (dashed lines), which provide thresholds of significance for individuals, are ± 0.273 × 10−3 mm2/ s, ±0.266 × 10−3 mm2/s, and ± 0.574 × 10−3 mm2/s for mean tumor, muscle, and water phantom ADC, respectively.

Fig. 1.

Fig. 1

Open in a new tab

Test–retest example of ADC parametric maps. Three regions of interest are indicated: tumor (denoted with a ‘T’), skeletal muscle (denoted with ‘M’), and a water phantom (denoted with a ‘W’). Take note of how the animal orientation is slightly different between repeat scans, which might affect ADC reproducibility as the same tissue sections from each scan might not be analyzed. This variation in positioning is somewhat noticeable in the tumor, as the location and size of higher ADC regions (white arrows) are different; however, the variability of regions with higher ADC values (red arrows) is much larger in the muscle. Units of ADC are in mm2/s.

Table 1.

ADC (mm2/s) reproducibility analysis for the tumor, muscle, and water phantom.

ROI Mean (×10−3) Mean difference (×10−3) 95% CI for mean difference (×10−3) wSD (×10−3) Repeatability (×10−3) ICC
Tumor 0.822 0.0193 ±0.0972 (11.8%) 0.0985 0.273 0.80
Muscle 1.14 −0.0173 ±0.0949 (8.30%) 0.0960 0.266 0.63
Water phantom 2.57 0.0707 ±0.200 (7.78%) 0.207 0.574 0.00
Open in a new tab

ADC, apparent diffusion coefficient; ROI, region of interest; CI, confidence interval; wSD, within-subject standard deviation; ICC, intraclass correlation coefficient.

Fig. 2.

Fig. 2

Open in a new tab

Bland–Altman plots displaying the difference in ADC between scans plotted against mean ADC for both tumor (left panel) and muscle (right panel) ROIs. The mean difference (solid line) is shown with 95% confidence intervals (dotted lines), which defines the significant threshold for the population. Repeatability is also shown (dashed lines), and represents the threshold required to guarantee a statistically significant change in an individual mouse.

We calculated the ICC for each ROI (please see Table 1). The ICCs for the tumor and muscle ROIs were greater than 0.61; thus, mean ADC for each ROI had substantial agreement between repeated measurements [25]. The ICC of the water phantom is zero, suggesting that the measurement system is producing 100% of the variability because the variability between subjects is (essentially) zero.

4. Discussion

We chose to quantify reproducibility for individuals and groups in a manner similar to Galbraith et al. [24], which is based on the limits of agreement methods described by Bland and Altman [23]. This analysis provides objective statistical thresholds that define the range of repeatability by quantifying the maximum difference expected to be observed between two repeat observations for an individual. Additionally, the 95% CI for the mean difference provides a measure of spontaneous change that is expected in groups of similar size to our cohort. Both the 95% CI and repeatability coefficient are useful in, for example, a longitudinal treatment response study where the objective is to quantify changes in parameters after a specific intervention. For example, mean tumor ADC would need to increase or decrease by 0.0972 × 10−3 mm2/s to reflect a treatment-induced change in a group analysis, or change by ± 0.273 × 10−3 mm2/s for an individual animal. The 95% CI when expressed as a percentage of the mean is ± 11.8%, which is not unreasonable as treatment-induced changes greater than ± 20% have been reported when evaluating DW-MRI as a biomarker of response in several preclinical mouse models of cancer [12, 26], including a mouse model of HER2+ human breast cancer [9]. The reproducibility for muscle ADC was also expressed as a 95% CI and repeatability coefficient, which were ± 0.0949 × 10−3 mm2/s and ± 0.266 × 10−3 mm2/s, respectively. The 95% CI expressed as a percentage of the mean is ± 8.30%, so that changes greater than this value would reflect a significant change in muscle for a cohort of mice of similar size as in our study.

Reproducibility in terms of agreement between repeat measurements (defined by the ICC) was worse for muscle (ICC = 0.63) compared to tumor (ICC = 0.80). This result is not surprising, considering that muscle ADC values in this study are calculated from a diffusion-weighted pulse sequence that encodes along a single diffusion direction, instead of the trace, for each b value. Since diffusion in muscle tissue is anisotropic [27–29], ADC values measured along only one direction, acquired by applying diffusion gradients simultaneously on all three axes, would be dependent on animal orientation in the scanner. Although the orientation was kept as consistent as possible, one might expect that slight differences between scans would have a greater impact on reproducibility in muscle tissue compared to most tumor models where water diffusion is nearly isotropic [16].

The ICC for tumor and muscle from our study were slightly lower than a previous reproducibility study by O’Flynn et al. who observed an ICC of 0.91 for mean ADC of normal human breast tissue [20]. It is worth noting that, while we observed lower ICCs than O’Flynn et al., our main objective was to quantify a threshold by which changes greater than that value would represent therapeutic interventions. The 95% CI and repeatability coefficient define these thresholds in a population or an individual, respectively, and thus are more appropriate than the ICC when interpreting results from a longitudinal treatment response study [19, 30].

The reproducibility data provided in this manuscript can also be used to assist in prospectively powering, for example, a study designed to test the therapeutic response of a given drug regimen. If a quality estimate of the error in an individual ADC measurement is known, then a quality estimate on the number of animals required in each cohort to achieve a desired power can be determined. We take the standard deviation of the difference between the repeated measurements to be a reasonable estimate of the standard deviation of the difference in the response of matched pairs (i.e., two measurements on the same animal separated by time). If we set the type 1 error (i.e., α) to be 0.05 and assume a (reasonable) difference in ADC between the experimental and control groups of 20%, then 10 animals per group is sufficient to reject the null hypothesis that the population means of the two groups are equal with a probability (power) of 0.90.

In our study, we attempted to be as consistent as possible when determining the imaging FOVs between repeated acquisitions. However, differences in the measured ADC values from the ROIs exist. A possible explanation for this is that we are not comparing the exact sections of tissue from each scan. We chose to remove the animal from the scanner between repeat acquisitions to more closely mimic a study in which an animal is scanned multiple times over multiple days, thereby allowing us to quantify the variability that we might expect during a treatment study. Additionally, allowing the animal to recover between repeat scans minimized any physiological stress that may occur during long periods (> ~2.5 hours) of anesthesia. Removing the animal and allowing for recovery would mean that there might be slight differences in ROIs (both tumor and muscle), and thus possible repositioning errors between acquisitions. We expect that errors associated with differences in animal position would negatively impact reproducibility, thus resulting in larger 95% CIs and repeatability coefficients.

5. Conclusion

The development of imaging biomarkers with the sensitivity to detect treatment-induced changes in tumor physiology before tumor volume change is an active area of interest. Before an imaging biomarker can be reliably employed in a treatment response study, the reproducibility must be assessed. In this study, we assessed reproducibility of DW-MRI data in conjunction with an ADC measurement. These test–retest analyses of mean tumor ADC measurements were very reproducible, and thus DW-MRI can be used in serial studies to measure treatment-induced changes of tumor physiology in our mouse model of HER2+ human breast cancer.

Acknowledgments

We thank the National Institutes of Health for funding through R01 CA138599, P50 CA98131, P30 CA68485, 1R21CA169387, and 1 S10 RR17858. We also thank Dr. Henry Ong, Ph.D. and Dr. Jack Skinner, Ph.D. for image acquisition/analysis advice, as well as Dr. Zoe Yu, M.D. and Ms. Cammie Rinehart Sutton for cell culture and animal assistance.

Footnotes

Conflicts of interest: T.E.Y. is a consultant for Eli Lilly and Company. No other authors declare any conflicts of interest.

References

  • 1.Wahl RL, Jacene H, Kasamon Y, Lodge MA. From RECIST to PERCIST: evolving considerations for PET response criteria in solid tumors. J Nucl Med. 2009;50(Suppl 1):122S–150S. doi: 10.2967/jnumed.108.057307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Guarneri V, Barbieri E, Dieci MV, Piacentini F, Conte P. Anti-HER2 neoadjuvant and adjuvant therapies in HER2 positive breast cancer. Cancer Treat Rev. 2010;36(Suppl 3):S62–S66. doi: 10.1016/S0305-7372(10)70022-0. [DOI] [PubMed] [Google Scholar]
  • 3.Jackson JR, Patrick DR, Dar MM, Huang PS. Targeted anti-mitotic therapies: can we improve on tubulin agents? Nat Rev Cancer. 2007;7(2):107–117. doi: 10.1038/nrc2049. [DOI] [PubMed] [Google Scholar]
  • 4.Galons JP, Altbach MI, Paine-Murrieta GD, Taylor CW, Gillies RJ. Early increases in breast tumor xenograft water mobility in response to paclitaxel therapy detected by non-invasive diffusion magnetic resonance imaging. Neoplasia. 1999;1(2):113–117. doi: 10.1038/sj.neo.7900009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Jensen LR, Garzon B, Heldahl MG, Bathen TF, Lundgren S, Gribbestad IS. Diffusion-weighted and dynamic contrast-enhanced MRI in evaluation of early treatment effects during neoadjuvant chemotherapy in breast cancer patients. J Magn Reson Imaging. 2011;34(5):1099–1109. doi: 10.1002/jmri.22726. [DOI] [PubMed] [Google Scholar]
  • 6.Jordan BF, Runquist M, Raghunand N, Baker A, Williams R, Kirkpatrick L, et al. Dynamic contrast-enhanced and diffusion MRI show rapid and dramatic changes in tumor microenvironment in response to inhibition of HIF-1alpha using PX- 478. Neoplasia. 2005;7(5):475–485. doi: 10.1593/neo.04628. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Karroum O, Mignion L, Kengen J, Karmani L, Leveque P, Danhier P, et al. Multimodal imaging of tumor response to sorafenib combined with radiation therapy: comparison between diffusion-weighted MRI, choline spectroscopy and (18) F-FLT PET imaging. Contrast Media Mol Imaging. 2013;8(3):274–280. doi: 10.1002/cmmi.1525. [DOI] [PubMed] [Google Scholar]
  • 8.Anderson AW, Xie J, Pizzonia J, Bronen RA, Spencer DD, Gore JC. Effects of cell volume fraction changes on apparent diffusion in human cells. Magn Reson Imaging. 2000;18(6):689–695. doi: 10.1016/s0730-725x(00)00147-8. [DOI] [PubMed] [Google Scholar]
  • 9.Aliu SO, Wilmes LJ, Moasser MM, Hann BC, Li KL, Wang D, et al. MRI methods for evaluating the effects of tyrosine kinase inhibitor administration used to enhance chemotherapy efficiency in a breast tumor xenograft model. J Magn Reson Imaging. 2009;29(5):1071–1079. doi: 10.1002/jmri.21737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Larocque MP, Syme A, Allalunis-Turner J, Fallone BG. ADC response to radiation therapy correlates with induced changes in radiosensitivity. Med Phys. 2010;37(7):3855–3861. doi: 10.1118/1.3456442. [DOI] [PubMed] [Google Scholar]
  • 11.Lee SC, Poptani H, Pickup S, Jenkins WT, Kim S, Koch CJ, et al. Early detection of radiation therapy response in non-Hodgkin's lymphoma xenografts by in vivo 1H magnetic resonance spectroscopy and imaging. NMR Biomed. 2010;23(6):624–632. doi: 10.1002/nbm.1505. [DOI] [PubMed] [Google Scholar]
  • 12.Loveless ME, Lawson D, Collins M, Nadella MV, Reimer C, Huszar D, et al. Comparisons of the efficacy of a Jak1/2 inhibitor (AZD1480) with a VEGF signaling inhibitor (cediranib) and sham treatments in mouse tumors using DCE-MRI, DW-MRI, and histology. Neoplasia. 2012;14(1):54–64. doi: 10.1593/neo.111478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Thoeny HC, Ross BD. Predicting and monitoring cancer treatment response with diffusion-weighted MRI. J Magn Reson Imaging. 2010;32(1):2–16. doi: 10.1002/jmri.22167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Galban CJ, Chenevert TL, Meyer CR, Tsien C, Lawrence TS, Hamstra DA, et al. Prospective analysis of parametric response map-derived MRI biomarkers: identification of early and distinct glioma response patterns not predicted by standard radiographic assessment. Clin Cancer Res. 2011;17(14):4751–4760. doi: 10.1158/1078-0432.CCR-10-2098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Sun YS, Zhang XP, Tang L, Ji JF, Gu J, Cai Y, et al. Locally advanced rectal carcinoma treated with preoperative chemotherapy and radiation therapy: preliminary analysis of diffusion-weighted MR imaging for early detection of tumor histopathologic downstaging. Radiology. 2010;254(1):170–178. doi: 10.1148/radiol.2541082230. [DOI] [PubMed] [Google Scholar]
  • 16.Padhani AR, Liu G, Koh DM, Chenevert TL, Thoeny HC, Takahara T, et al. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: consensus and recommendations. Neoplasia. 2009;11(2):102–125. doi: 10.1593/neo.81328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Gibbs P, Pickles MD, Turnbull LW. Repeatability of echo-planar-based diffusion measurements of the human prostate at 3 T. Magn Reson Imaging. 2007;25(10):1423–1429. doi: 10.1016/j.mri.2007.03.030. [DOI] [PubMed] [Google Scholar]
  • 18.Kim SY, Lee SS, Park B, Kim N, Kim JK, Park SH, et al. Reproducibility of measurement of apparent diffusion coefficients of malignant hepatic tumors: effect of DWI techniques and calculation methods. J Magn Reson Imaging. 2012;36(5):1131–1138. doi: 10.1002/jmri.23744. [DOI] [PubMed] [Google Scholar]
  • 19.Koh DM, Blackledge M, Collins DJ, Padhani AR, Wallace T, Wilton B, et al. Reproducibility and changes in the apparent diffusion coefficients of solid tumours treated with combretastatin A4 phosphate and bevacizumab in a two-centre phase I clinical trial. Eur Radiol. 2009;19(11):2728–2738. doi: 10.1007/s00330-009-1469-4. [DOI] [PubMed] [Google Scholar]
  • 20.O'Flynn EA, Morgan VA, Giles SL, deSouza NM. Diffusion weighted imaging of the normal breast: reproducibility of apparent diffusion coefficient measurements and variation with menstrual cycle and menopausal status. Eur Radiol. 2012;22(7):1512–1518. doi: 10.1007/s00330-012-2399-0. [DOI] [PubMed] [Google Scholar]
  • 21.Ritter CA, Perez-Torres M, Rinehart C, Guix M, Dugger T, Engelman JA, et al. Human breast cancer cells selected for resistance to trastuzumab in vivo overexpress epidermal growth factor receptor and ErbB ligands and remain dependent on the ErbB receptor network. Clin Cancer Res. 2007;13(16):4909–4919. doi: 10.1158/1078-0432.CCR-07-0701. [DOI] [PubMed] [Google Scholar]
  • 22.Anderson AW, Gore JC. Analysis and correction of motion artifacts in diffusion weighted imaging. Magn Reson Med. 1994;32(3):379–387. doi: 10.1002/mrm.1910320313. [DOI] [PubMed] [Google Scholar]
  • 23.Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8(2):135–160. doi: 10.1177/096228029900800204. [DOI] [PubMed] [Google Scholar]
  • 24.Galbraith SM, Lodge MA, Taylor NJ, Rustin GJ, Bentzen S, Stirling JJ, et al. Reproducibility of dynamic contrast-enhanced MRI in human muscle and tumours: comparison of quantitative and semi-quantitative analysis. NMR Biomed. 2002;15(2):132–142. doi: 10.1002/nbm.731. [DOI] [PubMed] [Google Scholar]
  • 25.Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33(1):159–174. [PubMed] [Google Scholar]
  • 26.Suh JY, Cho G, Song Y, Lee CK, Kang JS, Kang MR, et al. Is apparent diffusion coefficient reliable and accurate for monitoring effects of anti-angiogenic treatment in a longitudinal study? J Magn Reson Imaging. 2012;35(6):1430–1436. doi: 10.1002/jmri.23574. [DOI] [PubMed] [Google Scholar]
  • 27.Westin CF, Maier SE, Mamata H, Nabavi A, Jolesz FA, Kikinis R. Processing and visualization for diffusion tensor MRI. Med Image Anal. 2002;6(2):93–108. doi: 10.1016/s1361-8415(02)00053-1. [DOI] [PubMed] [Google Scholar]
  • 28.Galban CJ, Maderwald S, Uffmann K, de Greiff A, Ladd ME. Diffusive sensitivity to muscle architecture: a magnetic resonance diffusion tensor imaging study of the human calf. Eur J Appl Physiol. 2004;93(3):253–262. doi: 10.1007/s00421-004-1186-2. [DOI] [PubMed] [Google Scholar]
  • 29.Williams SE, Heemskerk AM, Welch EB, Li K, Damon BM, Park JH. Quantitative effects of inclusion of fat on muscle diffusion tensor MRI measurements. J Magn Reson Imaging. 2013;38(5):1292–1297. doi: 10.1002/jmri.24045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Galbraith SM, Rustin GJ, Lodge MA, Taylor NJ, Stirling JJ, Jameson M, et al. Effects of 5,6-dimethylxanthenone-4-acetic acid on human tumor microcirculation assessed by dynamic contrast-enhanced magnetic resonance imaging. J Clin Oncol. 2002;20(18):3826–3840. doi: 10.1200/JCO.2002.09.144. [DOI] [PubMed] [Google Scholar]

RESOURCES