Significance
The data rate of modern optical fiber communication channels is increasingly constrained by the noise inherent in its principal light source: the semiconductor laser (SCL). Here, we examine the phase noise of SCLs due to the spontaneous recombination of excited carriers radiating into the lasing mode as mandated by quantum mechanics. By incorporating a very high-Q optical resonator as an integral part of a hybrid Si/III-V laser cavity, we can remove most of the modal energy from the optically lossy III-V active region, thereby reducing the spontaneous emission rate while increasing the number of phase-stabilizing stored photons. Our fabricated SCLs boast more than a 10× linewidth improvement compared with commercial SCLs, with the possibility of a further major coherence increase.
Keywords: narrow linewidth, silicon photonics, phase noise, coherent optical communications
Abstract
The semiconductor laser (SCL) is the principal light source powering the worldwide optical fiber network. The ever-increasing demand for data is causing the network to migrate to phase-coherent modulation formats, which place strict requirements on the temporal coherence of the light source that no longer can be met by current SCLs. This failure can be traced directly to the canonical laser design, in which photons are both generated and stored in the same, optically lossy, III-V material. This leads to an excessive and large amount of noisy spontaneous emission commingling with the laser mode, thereby degrading its coherence. High losses also decrease the amount of stored optical energy in the laser cavity, magnifying the effect of each individual spontaneous emission event on the phase of the laser field. Here, we propose a new design paradigm for the SCL. The keys to this paradigm are the deliberate removal of stored optical energy from the lossy III-V material by concentrating it in a passive, low-loss material and the incorporation of a very high-Q resonator as an integral (i.e., not externally coupled) part of the laser cavity. We demonstrate an SCL with a spectral linewidth of 18 kHz in the telecom band around 1.55 μm, achieved using a single-mode silicon resonator with Q of 106.
Almost from the inception of the semiconductor distributed feedback (DFB) laser, there has been a continuous effort to improve its coherence. The methods used to this end include long cavities (1), longitudinal mode engineering via multiple phase-shifts (2, 3), optimization of the active medium [e.g., strained quantum well (QW)] (4), and wavelength detuning (5, 6). Progress has been hindered by the inevitable penalty paid for the coherence-limiting optical absorption, the result of spatially colocalizing both photons and electrons in a highly absorbing active medium.
The finite coherence of laser light is of fundamentally quantum-mechanical origin, the result of spontaneously generated photons entering the lasing mode from the active region of the laser medium. Under the effect of many independent spontaneous emission events, the laser field phasor performs a random walk in the complex plane, which results in a phase excursion given by (7)
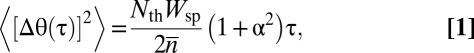 |
where 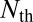 is the number of excited carriers at threshold,
is the number of excited carriers at threshold,  is the spontaneous emission rate
is the spontaneous emission rate  into the lasing mode,
into the lasing mode, 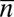 is the average number of coherent photons in the lasing mode, α is the linewidth enhancement factor due to coupling of amplitude and phase fluctuations, and τ is the symbol duration (s). The numerator and denominator of Eq. 1 conceptually represent spontaneous photon generation and photon storage, respectively. Increasing the quality factor, Q, of the laser cavity provides a double benefit to phase noise by reducing the number of excited carriers needed to reach threshold, thus decreasing spontaneous photon generation while increasing photon storage.
is the average number of coherent photons in the lasing mode, α is the linewidth enhancement factor due to coupling of amplitude and phase fluctuations, and τ is the symbol duration (s). The numerator and denominator of Eq. 1 conceptually represent spontaneous photon generation and photon storage, respectively. Increasing the quality factor, Q, of the laser cavity provides a double benefit to phase noise by reducing the number of excited carriers needed to reach threshold, thus decreasing spontaneous photon generation while increasing photon storage.
The quality factor of conventional III-V semiconductor lasers (SCLs) is limited by free carrier absorption in the heavily doped p- and n-type cladding regions, as well as in the active region, where photons, both spontaneous and induced, are generated. There is an inevitable compromise resulting from carrying out both photon generation and photon storage in the same III-V material. Although III-V is needed for gain, its high absorption makes it unsuitable for photon storage. Heterogeneous Si/III-V integration (8–11) allows lossy III-V material to be replaced with low-loss silicon without significantly changing the properties of the optical mode. The total Q of a hybrid Si/III-V resonator may then be expressed as
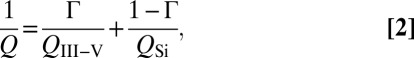 |
where Γ is the mode confinement factor in III-V, 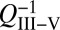 is the absorption-dominated loss in III-V, and
is the absorption-dominated loss in III-V, and 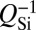 is the loaded Q of a passive silicon-only resonator (Fig. 1C). Absorption losses in high-resistivity silicon typically are three orders of magnitude lower than in III-V, so replacing excess III-V material with silicon creates a large potential improvement in laser coherence. This potential may be realized only by maximizing the total Q of the resonator (i.e., making
is the loaded Q of a passive silicon-only resonator (Fig. 1C). Absorption losses in high-resistivity silicon typically are three orders of magnitude lower than in III-V, so replacing excess III-V material with silicon creates a large potential improvement in laser coherence. This potential may be realized only by maximizing the total Q of the resonator (i.e., making 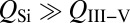 ). Hybrid Si/III-V thus opens a new regime in which absorption losses no longer are necessarily dominant and other components of loss, previously only relevant in high-Q passive resonator design, must be addressed to maximize the coherence of an SCL.
). Hybrid Si/III-V thus opens a new regime in which absorption losses no longer are necessarily dominant and other components of loss, previously only relevant in high-Q passive resonator design, must be addressed to maximize the coherence of an SCL.
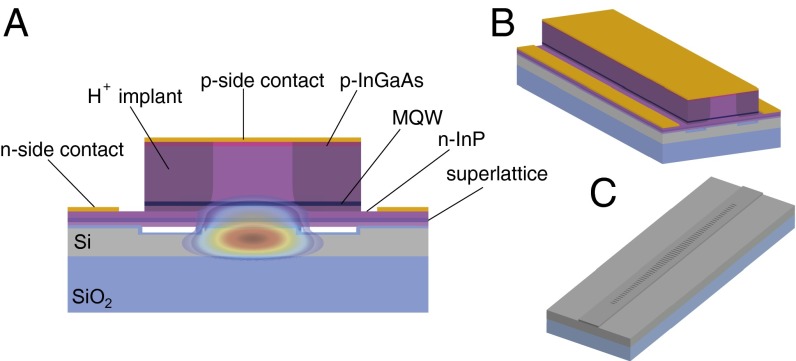
Fig. 1.
High-Q hybrid laser device schematics (not to scale). (A) Two-dimensional cross-section of the hybrid platform, with superimposed optical transverse mode profile. (B) Perspective view of a high-Q hybrid laser. (C) Perspective view of the high-Q silicon resonator.
Additionally, manipulating the transverse geometry of the hybrid Si/III-V waveguide alters the modal confinement between the lossy III-V and the low-loss silicon (12). Engineering the waveguide mode to decrease Γ has two effects on laser coherence: (i) the cavity Q increases according to Eq. 2, thus improving photon storage,  , and (ii) the intensity of the laser mode in the active region decreases, decreasing the spontaneous emission rate into this mode,
, and (ii) the intensity of the laser mode in the active region decreases, decreasing the spontaneous emission rate into this mode, 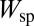 . Removing light from III-V appears counterintuitive because it reduces the modal gain available to the laser; however, in the limit that the
. Removing light from III-V appears counterintuitive because it reduces the modal gain available to the laser; however, in the limit that the 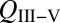 term of Eq. 2 dominates the total Q, the reduction in modal gain is exactly balanced by a reduction in total modal loss, and thus the threshold carrier density remains constant.
term of Eq. 2 dominates the total Q, the reduction in modal gain is exactly balanced by a reduction in total modal loss, and thus the threshold carrier density remains constant.
It thus emerges that 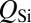 is the factor limiting how much light can be removed from III-V and is the focus of the work presented here. The design paradigm following from Eq. 2 shifts the focus of laser design from optimization of the active material to optimization of a high-Q passive resonator, independent of the gain medium used.
is the factor limiting how much light can be removed from III-V and is the focus of the work presented here. The design paradigm following from Eq. 2 shifts the focus of laser design from optimization of the active material to optimization of a high-Q passive resonator, independent of the gain medium used.
High-Q Cavity Design
Designing the laser’s high-Q integral resonator is constrained by its role in determining the oscillation frequency and the longitudinal mode profile. To maximize the resonator Q, subject to these constraints, it is instructive to separate 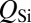 conceptually into its constituent optical loss mechanisms (13):
conceptually into its constituent optical loss mechanisms (13):
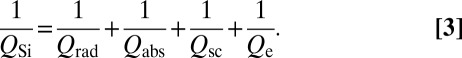 |
Losses due to radiation  , absorption
, absorption 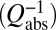 , and scattering
, and scattering 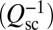 comprise the intrinsic component of losses in silicon. Added to it is the resonator loading,
comprise the intrinsic component of losses in silicon. Added to it is the resonator loading, 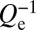 (i.e., external coupling), which determines the fraction of stored energy tapped as useful output through the laser mirrors. There inevitably is a tradeoff in laser design between large stored energies, necessary for narrow linewidths, and useful output.
(i.e., external coupling), which determines the fraction of stored energy tapped as useful output through the laser mirrors. There inevitably is a tradeoff in laser design between large stored energies, necessary for narrow linewidths, and useful output.
The high-Q silicon resonator is fashioned from a silicon waveguide patterned with a 1D grating (Fig. 1C). Coupling to radiation modes 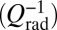 is minimized via a bandgap-modulated defect section in the middle of an otherwise uniform grating (14–17), as shown in Fig. 2A. The defect is designed directly in the frequency domain by parabolically modulating the lower-frequency band edge of the grating as a function of position along the resonator (Fig. 2B). This quadratic modulation acts as a potential well, localizing a resonant mode with a Gaussian-like profile in both real and reciprocal space (Fig. 2 D and E), similar to the ground-state electron wave function in a quantum harmonic oscillator. By appropriately choosing the well depth V, defined as an offset frequency from the uniform grating band edge, and its spatial width
is minimized via a bandgap-modulated defect section in the middle of an otherwise uniform grating (14–17), as shown in Fig. 2A. The defect is designed directly in the frequency domain by parabolically modulating the lower-frequency band edge of the grating as a function of position along the resonator (Fig. 2B). This quadratic modulation acts as a potential well, localizing a resonant mode with a Gaussian-like profile in both real and reciprocal space (Fig. 2 D and E), similar to the ground-state electron wave function in a quantum harmonic oscillator. By appropriately choosing the well depth V, defined as an offset frequency from the uniform grating band edge, and its spatial width 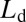 , the mode can be localized tightly in k-space, thereby greatly reducing coupling to the continuum of radiation modes (Fig. 2E). To fabricate a device, the frequency band edge profile is translated to a grating structure modulation by varying the transverse width
, the mode can be localized tightly in k-space, thereby greatly reducing coupling to the continuum of radiation modes (Fig. 2E). To fabricate a device, the frequency band edge profile is translated to a grating structure modulation by varying the transverse width  of etched holes along the length of the resonator (Fig. 2A).
of etched holes along the length of the resonator (Fig. 2A).
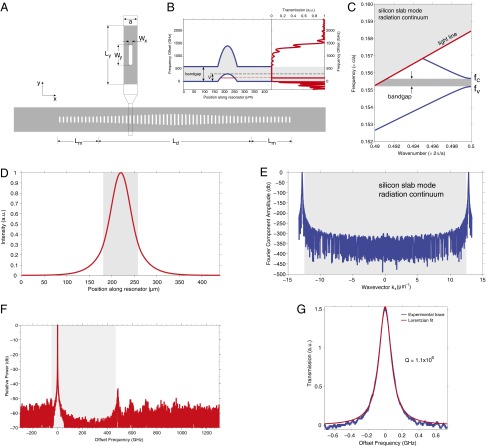
Fig. 2.
Design features of the high-Q hybrid resonator. (A) Top view of the geometry of the grating in silicon. (B) Spatial band structure of a high-Q hybrid resonator plotted against the simulated transmission spectrum. Example shown for design parameters  ,
,  ,
, 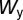 from
from 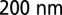 to
to  . (C) Dispersion diagram of a local unit cell. Eigenfrequencies
. (C) Dispersion diagram of a local unit cell. Eigenfrequencies 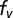 ,
, 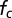 correspond to modulated frequency distribution
correspond to modulated frequency distribution  ,
,  of the resonator spatial band structure. (D) Simulated profile of the longitudinal field intensity of a high-Q hybrid resonator. The gray-shaded area denotes the defect section of the resonator. (E) Fourier component amplitude distribution of the longitudinal field of a high-Q hybrid resonator. The gray-shaded area denotes the continuum of radiation modes. (F) Simulated emission spectrum of a high-Q hybrid laser. The gray-shaded area denotes the resonator bandgap. (G) Experimental trace and Lorentzian fit of the transmission resonance of a high-Q silicon resonator. (Structure design parameters used in all the above simulations:
of the resonator spatial band structure. (D) Simulated profile of the longitudinal field intensity of a high-Q hybrid resonator. The gray-shaded area denotes the defect section of the resonator. (E) Fourier component amplitude distribution of the longitudinal field of a high-Q hybrid resonator. The gray-shaded area denotes the continuum of radiation modes. (F) Simulated emission spectrum of a high-Q hybrid laser. The gray-shaded area denotes the resonator bandgap. (G) Experimental trace and Lorentzian fit of the transmission resonance of a high-Q silicon resonator. (Structure design parameters used in all the above simulations:  ,
,  ,
, 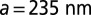 .)
.)
To minimize scattering loss  , we choose a shallow rib geometry for the waveguide to “bury” the mode in the silicon slab and thus isolate it from the roughness of the etched sidewalls (Fig. 1). Absorption losses in silicon are small compared with the other sources of loss in silicon and therefore may be neglected.
, we choose a shallow rib geometry for the waveguide to “bury” the mode in the silicon slab and thus isolate it from the roughness of the etched sidewalls (Fig. 1). Absorption losses in silicon are small compared with the other sources of loss in silicon and therefore may be neglected.
Uniform grating reflectors of length  on either side of the defect determine the fraction of the total power generated in the active region that is coupled as useful output and, therefore, the external loading of the resonator
on either side of the defect determine the fraction of the total power generated in the active region that is coupled as useful output and, therefore, the external loading of the resonator  . Because we seek to maximize the total loaded Q to reduce phase noise, high-Q hybrid resonators are designed to be significantly undercoupled (i.e., in the limit of high
. Because we seek to maximize the total loaded Q to reduce phase noise, high-Q hybrid resonators are designed to be significantly undercoupled (i.e., in the limit of high 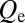 ). Conventional DFB lasers in this loading regime become susceptible to spatial hole burning-induced mode instability and linewidth rebroadening due to their sharply peaked spatial mode profile (18, 19). In the high-Q hybrid laser, spatial hole burning is mitigated by the broad Gaussian longitudinal mode profile, thus allowing considerable undercoupling and, therefore, large stored energies in the cavity.
). Conventional DFB lasers in this loading regime become susceptible to spatial hole burning-induced mode instability and linewidth rebroadening due to their sharply peaked spatial mode profile (18, 19). In the high-Q hybrid laser, spatial hole burning is mitigated by the broad Gaussian longitudinal mode profile, thus allowing considerable undercoupling and, therefore, large stored energies in the cavity.
Results
To determine the 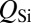 metric for the resonators used in this work, we fabricated and tested passive silicon resonators of the same type and scale as the hybrid, only without the III-V attached. We measured loaded quality factors for these resonators exceeding 106 (Fig. 2G), which represent record high Q for 1D photonic crystal waveguide resonators on silicon-on-insulator. In the hybrid lasers, the confinement factor in III-V is fixed at
metric for the resonators used in this work, we fabricated and tested passive silicon resonators of the same type and scale as the hybrid, only without the III-V attached. We measured loaded quality factors for these resonators exceeding 106 (Fig. 2G), which represent record high Q for 1D photonic crystal waveguide resonators on silicon-on-insulator. In the hybrid lasers, the confinement factor in III-V is fixed at 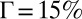 and realized with a silicon device layer
and realized with a silicon device layer 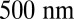 thick.
thick.
We fabricated high-Q hybrid lasers using standard e-beam lithography and plasma etching to create low-loss gratings on silicon, followed by die-scale direct bonding to the III-V material. Details of the fabrication process may be found in Materials and Methods. The hybrid Si/III-V resonators are based on photonic wells with a design parameter set of (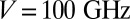 ,
, 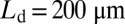 ), which results in a single localized defect mode. Fourier analysis for the selected design parameter set yields an estimate of
), which results in a single localized defect mode. Fourier analysis for the selected design parameter set yields an estimate of  . The length of the distributed Bragg reflectors on either side of the defect is set to significantly undercouple the resonator, with calculated
. The length of the distributed Bragg reflectors on either side of the defect is set to significantly undercouple the resonator, with calculated 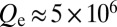 , based on the assumption of a predominantly III-V absorption-limited intrinsic Q for the resonator. Typical cavity lengths, including the reflectors, are in the range of
, based on the assumption of a predominantly III-V absorption-limited intrinsic Q for the resonator. Typical cavity lengths, including the reflectors, are in the range of 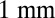 .
.
High-Q hybrid lasers are tested unpackaged on a temperature-controlled stage. We obtain single-mode, continuous-wave laser operation with threshold currents as low as 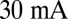 and single-side output powers as high as
and single-side output powers as high as 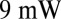 at room temperature
at room temperature 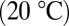 (Fig. 3B). Lasing occurs over temperatures spanning the range of 10–75 °C (Fig. 3A). Single-mode oscillation is observed over a wavelength span of
(Fig. 3B). Lasing occurs over temperatures spanning the range of 10–75 °C (Fig. 3A). Single-mode oscillation is observed over a wavelength span of  (from 1,530 nm to 1,575 nm), in lasers with different grating periods (a from
(from 1,530 nm to 1,575 nm), in lasers with different grating periods (a from  to
to  ). Fig. 3C shows a representative optical spectrum of a high-Q hybrid laser. Side-mode suppression ratios better than
). Fig. 3C shows a representative optical spectrum of a high-Q hybrid laser. Side-mode suppression ratios better than 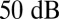 are obtained at each operating wavelength (Fig. 3D). The experimental optical spectrum agrees with simulated spectra for both the passive (Fig. 2B) and active (Fig. 2F) resonators. The lasing mode appears, as predicted from simulation, near the low-frequency band edge (offset ∼60 GHz), whereas the strongest side mode is just outside the low-frequency band edge.
are obtained at each operating wavelength (Fig. 3D). The experimental optical spectrum agrees with simulated spectra for both the passive (Fig. 2B) and active (Fig. 2F) resonators. The lasing mode appears, as predicted from simulation, near the low-frequency band edge (offset ∼60 GHz), whereas the strongest side mode is just outside the low-frequency band edge.
Fig. 3.

High-Q hybrid laser characterization results. (A) Light vs. pump current (L–I) curves as a function of the operating temperature, taken from a representative laser. (B) L–I and current vs. forward voltage (I–V) curves for a high-Q hybrid laser measured at room temperature  , taken from the laser with the highest one-sided output power. (C) Optical spectrum analyzer (OSA)-limited optical spectrum of a high-Q hybrid laser at a pump current of
, taken from the laser with the highest one-sided output power. (C) Optical spectrum analyzer (OSA)-limited optical spectrum of a high-Q hybrid laser at a pump current of 
 at
at 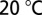 , demonstrating side-mode suppression of
, demonstrating side-mode suppression of  . The gray-shaded area denotes the bandgap. (D) OSA-limited optical spectra of high-Q hybrid lasers of varying grating periods taken at
. The gray-shaded area denotes the bandgap. (D) OSA-limited optical spectra of high-Q hybrid lasers of varying grating periods taken at 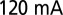
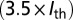 and
and 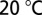 , demonstrating continuous-wave, single-mode lasing from 1,530 to 1,575 nm (C-band), with side-mode suppression ratios over
, demonstrating continuous-wave, single-mode lasing from 1,530 to 1,575 nm (C-band), with side-mode suppression ratios over  . (Inset) Relative position of the four spectra with respect to the spontaneous emission spectrum below threshold.
. (Inset) Relative position of the four spectra with respect to the spontaneous emission spectrum below threshold.
To characterize the temporal coherence of the high-Q hybrid laser, we measure the spectral density of the frequency fluctuations (20), as described in Materials and Methods. This avoids the ambiguity of the traditional self-heterodyne measurement method in discriminating between low-frequency (e.g.,  ) and high-frequency noise contributions to the spectral linewidth (21). By displaying this noise as a function of frequency, we can separate the individual noise mechanisms. We especially are interested in the high-frequency components of the noise spectrum, because this portion of the spectrum affects high–data-rate optical communications (22).
) and high-frequency noise contributions to the spectral linewidth (21). By displaying this noise as a function of frequency, we can separate the individual noise mechanisms. We especially are interested in the high-frequency components of the noise spectrum, because this portion of the spectrum affects high–data-rate optical communications (22).
Fig. 4 shows a typical frequency noise spectrum of a high-Q hybrid laser. Two distinct regions in the plot can be discerned. The first, up to approximately 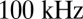 , displays a
, displays a  -type dependence, whereas the second segment, with a gentler slope, extends up to
-type dependence, whereas the second segment, with a gentler slope, extends up to  . The trend of Fig. 4 represents all the high-Q hybrid lasers tested. The observed frequency noise spectrum is dominated largely by noise of technical origin (e.g., laser-driving electronics). Because our data do not display a level white noise floor, we can place an upper bound only on the spontaneous emission-induced phase noise. This upper bound may be expressed in terms of a spectral linewidth (i.e., modified Schawlow–Townes linewidth) by using the value of the spectral density at the high-frequency end and multiplying it by
. The trend of Fig. 4 represents all the high-Q hybrid lasers tested. The observed frequency noise spectrum is dominated largely by noise of technical origin (e.g., laser-driving electronics). Because our data do not display a level white noise floor, we can place an upper bound only on the spontaneous emission-induced phase noise. This upper bound may be expressed in terms of a spectral linewidth (i.e., modified Schawlow–Townes linewidth) by using the value of the spectral density at the high-frequency end and multiplying it by 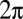 for the two-sided spectra measured in this work (23, 24). The narrowest linewidth attained is
for the two-sided spectra measured in this work (23, 24). The narrowest linewidth attained is 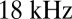 , measured at a pump current of
, measured at a pump current of 
 .
.
Fig. 4.
Frequency noise spectrum of the lowest-noise high-Q hybrid laser. The measurement is taken at a pump current of 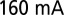
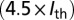 at
at 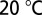 . Spikes at
. Spikes at 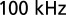 and
and 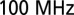 correspond to current source electronic noise and FM radio noise, respectively. A spectral linewidth of
correspond to current source electronic noise and FM radio noise, respectively. A spectral linewidth of  can be calculated for this laser by multiplying the power spectral density (PSD) value near
can be calculated for this laser by multiplying the power spectral density (PSD) value near 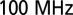 by
by  . Inset includes the full frequency noise spectrum, showing the feedback-suppressed low-frequency end of the spectrum as well as the onset of the MZI roll-off
. Inset includes the full frequency noise spectrum, showing the feedback-suppressed low-frequency end of the spectrum as well as the onset of the MZI roll-off  .
.
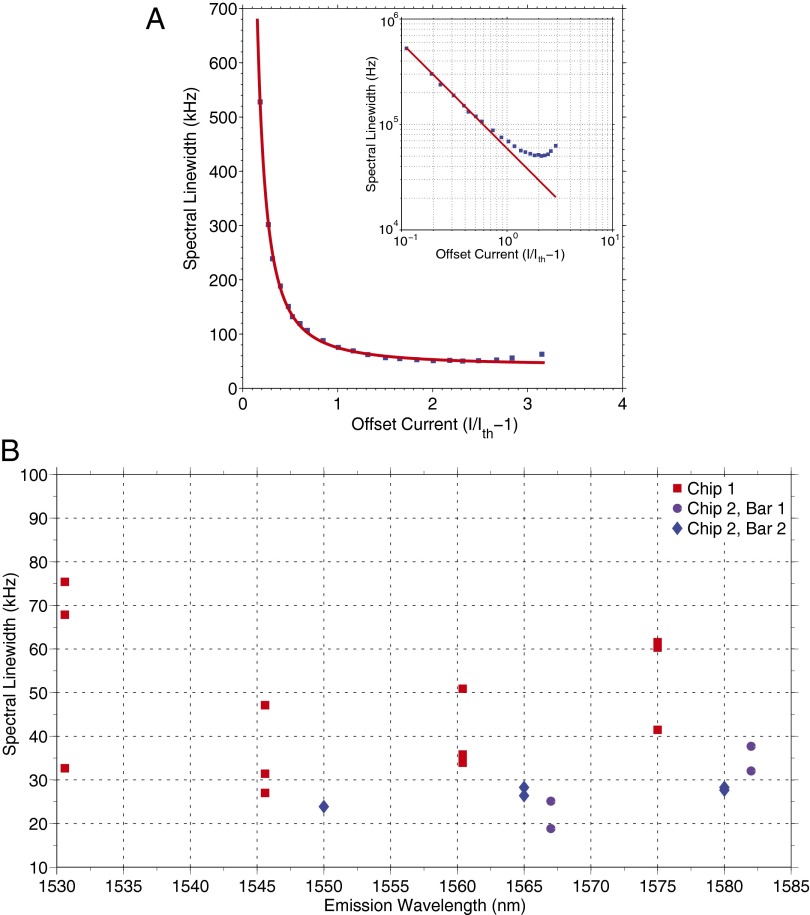
Fig. 5A presents the extracted spectral linewidth of a representative high-Q hybrid laser as a function of the normalized pump current offset from threshold. The linewidth decreases with increasing pump current, reflecting the increase in the total number of photons, 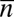 , stored in the laser resonator. Immediately above threshold
, stored in the laser resonator. Immediately above threshold  , the high-Q hybrid laser exhibits sub-megahertz–scale linewidths. These linewidths near threshold are much narrower than those of comparable narrow-linewidth SCLs at the same pump power (25) (see also Supporting Information), demonstrating it is the enhanced cavity Q and not strong pumping that is behind the superior coherence characteristics of the high-Q hybrid lasers. With further increase of the current, the linewidth decreases by more than an order of magnitude. Deviation from the expected linewidth dependence on pump current is observed in the form of a linewidth floor. This deviation is the result of increased side-mode competition (26) observed in the optical spectra of the lasers and probably caused by spatial hole burning. Narrow-linewidth performance is demonstrated across the entire C-band (Fig. 5B), obtained from lasers with varying grating periods and spanning different chips and laser bars.
, the high-Q hybrid laser exhibits sub-megahertz–scale linewidths. These linewidths near threshold are much narrower than those of comparable narrow-linewidth SCLs at the same pump power (25) (see also Supporting Information), demonstrating it is the enhanced cavity Q and not strong pumping that is behind the superior coherence characteristics of the high-Q hybrid lasers. With further increase of the current, the linewidth decreases by more than an order of magnitude. Deviation from the expected linewidth dependence on pump current is observed in the form of a linewidth floor. This deviation is the result of increased side-mode competition (26) observed in the optical spectra of the lasers and probably caused by spatial hole burning. Narrow-linewidth performance is demonstrated across the entire C-band (Fig. 5B), obtained from lasers with varying grating periods and spanning different chips and laser bars.
Fig. 5.
Linewidth characterization of high-Q hybrid lasers. (A) Spectral linewidth of a single high-Q hybrid laser as a function of the offset pump current from threshold  20 °C, taken from a representative laser. (Inset) The same dependence in log–log scale. (B) Distribution of the spectral linewidth of high-Q hybrid laser tested spanning three laser bars fabricated on two separate chips, as a function of their emission wavelength.
20 °C, taken from a representative laser. (Inset) The same dependence in log–log scale. (B) Distribution of the spectral linewidth of high-Q hybrid laser tested spanning three laser bars fabricated on two separate chips, as a function of their emission wavelength.
The ultimate linewidth of an SCL made using this paradigm is limited by two factors: the state of the art in passive resonators and the fraction of optical energy stored in III-V. Previously reported linewidths for hybrid Si/III-V DFB lasers are on the order of a few MHz [ (10)]. The high Q of the lasers reported here enables linewidths ∼200 times narrower than those previously reported, although Γ is comparable in both designs. Further linewidth reduction beyond the
(10)]. The high Q of the lasers reported here enables linewidths ∼200 times narrower than those previously reported, although Γ is comparable in both designs. Further linewidth reduction beyond the  reported here would be possible if, according to Eq. 2, the total cavity Q was increased, by increasing
reported here would be possible if, according to Eq. 2, the total cavity Q was increased, by increasing 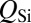 and/or decreasing Γ. With the
and/or decreasing Γ. With the  achieved in this work, further decreasing Γ would give an additional factor of 10 in linewidth reduction, without affecting threshold.
achieved in this work, further decreasing Γ would give an additional factor of 10 in linewidth reduction, without affecting threshold.
We have proposed a new paradigm for the design of high-coherence SCLs, demonstrated here with a spectral linewidth of 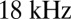 . Our approach circumvents historical limitations of laser design and raises the bar on the ultimate coherence of SCLs. The new figure of merit for coherence introduced in this work is the quality factor of the integral passive resonator, which is subject to the methods and techniques used. However, the paradigm itself is more generic than the specific tools used. These merely reflect the present state of the art in technology, and it is entirely likely that as technology, materials, and design methods advance, other methods to design high-Q passive resonators will emerge to push the coherence limits further.
. Our approach circumvents historical limitations of laser design and raises the bar on the ultimate coherence of SCLs. The new figure of merit for coherence introduced in this work is the quality factor of the integral passive resonator, which is subject to the methods and techniques used. However, the paradigm itself is more generic than the specific tools used. These merely reflect the present state of the art in technology, and it is entirely likely that as technology, materials, and design methods advance, other methods to design high-Q passive resonators will emerge to push the coherence limits further.
Materials and Methods
We pattern the passive resonator with e-beam lithography (Vistec EBPG 5000+, Zeon ZEP 520A resist) and transfer the pattern to silicon with a pseudo-Bosch process (Oxford 380). To turn the passive resonator into a high-Q hybrid laser, we smooth the waveguide sidewalls to improve  by growing 15 nm of dry thermal oxide (oxidation times calculated using the Massoud model). We strip the oxide with hydrofluoric acid (Transene Buffer HF-Improved), and regrow 20 nm of dry oxide. The silicon chip is prepared for direct wafer bonding through acetone and isopropyl alcohol (IPA) cleans followed by an organic stripping in Nano-Strip (Cyantek) for 1 min. An unpatterned III-V chip with an epistructure given in Supporting Information is prepared through acetone and IPA cleans followed by NH4OH:H2O 1:15 for 10 min. Both chip surfaces are activated for bonding with five “treatments” (five passes at 25 mm/s) in oxygen plasma at 200 W (Suss NP12). The chips are bonded directly by bringing them into contact and applying light pressure with tweezers. We are uncertain whether bonding is spontaneous or induced by the pressure. The bonded chips are annealed at 150 °C for 1 h, then at 285 °C for 5 h. After bonding, the InP handle is removed in HCl:H2O 1:3. We use ion implantation (H+, 170 keV, 5e14 cm−2) and an AZ5214E mask to define a current path above the silicon waveguide. We form the p-contact to p+-InGaAs above the current path by depositing Ti/Pt/Au (20 nm/50 nm/150 nm) and lifting off image-reversed AZ5210 resist. The III-V mesa is created by wet etching down to the n-contact layer (piranha H2SO4:H2O2:H2O 1:1:10 7 s, HCl:H2O 1:2 17 s, piranha 45 s). We form the n-contact to n+-InP by depositing Ge/Au/Ni/Au (30 nm/50 nm/12 nm/225 nm). The die is thinned to
by growing 15 nm of dry thermal oxide (oxidation times calculated using the Massoud model). We strip the oxide with hydrofluoric acid (Transene Buffer HF-Improved), and regrow 20 nm of dry oxide. The silicon chip is prepared for direct wafer bonding through acetone and isopropyl alcohol (IPA) cleans followed by an organic stripping in Nano-Strip (Cyantek) for 1 min. An unpatterned III-V chip with an epistructure given in Supporting Information is prepared through acetone and IPA cleans followed by NH4OH:H2O 1:15 for 10 min. Both chip surfaces are activated for bonding with five “treatments” (five passes at 25 mm/s) in oxygen plasma at 200 W (Suss NP12). The chips are bonded directly by bringing them into contact and applying light pressure with tweezers. We are uncertain whether bonding is spontaneous or induced by the pressure. The bonded chips are annealed at 150 °C for 1 h, then at 285 °C for 5 h. After bonding, the InP handle is removed in HCl:H2O 1:3. We use ion implantation (H+, 170 keV, 5e14 cm−2) and an AZ5214E mask to define a current path above the silicon waveguide. We form the p-contact to p+-InGaAs above the current path by depositing Ti/Pt/Au (20 nm/50 nm/150 nm) and lifting off image-reversed AZ5210 resist. The III-V mesa is created by wet etching down to the n-contact layer (piranha H2SO4:H2O2:H2O 1:1:10 7 s, HCl:H2O 1:2 17 s, piranha 45 s). We form the n-contact to n+-InP by depositing Ge/Au/Ni/Au (30 nm/50 nm/12 nm/225 nm). The die is thinned to  and cleaved into bars. Individual bars are annealed at
and cleaved into bars. Individual bars are annealed at 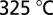 for 30 s. We antireflection coat the bars on both facets with 250 nm Al2O3.
for 30 s. We antireflection coat the bars on both facets with 250 nm Al2O3.
Passive Si resonators are characterized by measuring their frequency response in transmission mode. To speed data acquisition and improve resolution, necessary to measure narrow resonances, we use a tunable laser (Santec TSL-510, 1,510–1,630 nm), configured as a fast, optoelectronically controlled frequency-sweeping source (27) to interrogate the resonators. For calibration of the frequency sweep, part of the laser source is transmitted through a Mach–Zehnder interferometer (MZI), the output of which is used to convert the resonator’s temporal response to the frequency domain. Loaded quality factors are calculated by Lorentzian fitting of the transmission resonances.
We measure frequency noise by using an MZI as a frequency discriminator, with a differential delay shorter than the expected laser coherence time. The corresponding MZI free-spectral range (FSR) is 847 MHz. The interferometer converts laser phase fluctuations to intensity fluctuations when biased at quadrature and measured with a high-speed photodetector, the spectrum of which is obtained on an rf spectrum analyzer. The choice of interferometer delay is a tradeoff between frequency scan range and frequency gain. For this method to yield accurate results, the interferometer must remain at quadrature for the duration of a high-resolution measurement of the frequency spectrum. The hybrid lasers under test, not being packaged, are particularly sensitive to environmental temperature fluctuations, causing the laser center frequency to drift out of quadrature. We lock the interferometer in quadrature with negative electronic feedback to the laser’s pump current. The feedback loop bandwidth is kept below 100 Hz, enough to suppress low-frequency temperature-induced fluctuations while leaving the higher-frequency noise spectrum unaffected.
Supplementary Material
Acknowledgments
We are grateful to Prof. John Bowers and his group at the University of California, Santa Barbara for technical assistance. The authors acknowledge the Army Research Office, the National Science Foundation, and the Defense Advanced Research Projects Agency for financial support, as well as the Kavli Nanoscience Institute at the California Institute of Technology for providing technical and fabrication infrastructure.
Footnotes
Conflict of interest statement: The California Institute of Technology has filed a provisional patent application based on the work disclosed in the manuscript. C.T.S, S.T.S., and A.Y. are named as coinventors.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1400184111/-/DCSupplemental.
References
- 1.Ogita S, Kotaki Y, Matsuda M, Kuwahara Y, Ishikawa H. Long-cavity, multiple-phase-shift, distributed feedback laser for linewidth narrowing. Electron Lett. 1989;25:629–630. [Google Scholar]
- 2.Soda H, et al. Stability in single longitudinal mode-operation in GaInAsP-InP phase-adjusted DFB lasers. IEEE J Quantum Electron. 1987;23:804–814. [Google Scholar]
- 3.Ogita S, Kotaki Y, Ishikawa H, Imai H. Optimum design for multiple-phase-shift distributed feedback laser. Electron Lett. 1988;24:731–732. [Google Scholar]
- 4.Okai M, Tsuchiya T, Uomi K, Chinone N, Harada T. Corrugation-pitch-modulated MQW-DFB laser with narrow spectral linewidth (170 kHz) IEEE Photon Technol Lett. 1990;2:529–530. [Google Scholar]
- 5.Liou KY, Dutta NK, Burrus CA. Linewidth-narrowed distributed feedback injection lasers with long cavity length and detuned Bragg wavelength. Appl Phys Lett. 1987;50:489–491. [Google Scholar]
- 6.Ogita S, Yano M, Ishikawa H, Imai H. Linewidth reduction in DFB laser by detuning effect. Electron Lett. 1987;23:393–394. [Google Scholar]
- 7.Henry CH. Theory of the linewidth of semiconductor lasers. IEEE J Quantum Electron. 1982;18:259–264. [Google Scholar]
- 8.Fang AW, et al. Electrically pumped hybrid AlGaInAs-silicon evanescent laser. Opt Express. 2006;14(20):9203–9210. doi: 10.1364/oe.14.009203. [DOI] [PubMed] [Google Scholar]
- 9.Roelkens G, Van Thourhout D, Baets R, Nötzel R, Smit M. Laser emission and photodetection in an InP/InGaAsP layer integrated on and coupled to a Silicon-on-Insulator waveguide circuit. Opt Express. 2006;14(18):8154–8159. doi: 10.1364/oe.14.008154. [DOI] [PubMed] [Google Scholar]
- 10.Fang AW, Lively E, Kuo YH, Liang D, Bowers JE. A distributed feedback silicon evanescent laser. Opt Express. 2008;16(7):4413–4419. doi: 10.1364/oe.16.004413. [DOI] [PubMed] [Google Scholar]
- 11.Sun XK, et al. Electrically pumped hybrid evanescent Si/InGaAsP lasers. Opt Lett. 2009;34(9):1345–1347. doi: 10.1364/ol.34.001345. [DOI] [PubMed] [Google Scholar]
- 12.Yariv A, Sun X. Supermode Si/III-V hybrid lasers, optical amplifiers and modulators: A proposal and analysis. Opt Express. 2007;15(15):9147–9151. doi: 10.1364/oe.15.009147. [DOI] [PubMed] [Google Scholar]
- 13.Asano T, Song BS, Noda S. Analysis of the experimental Q factors (∼ 1 million) of photonic crystal nanocavities. Opt Express. 2006;14(5):1996–2002. doi: 10.1364/oe.14.001996. [DOI] [PubMed] [Google Scholar]
- 14.Akahane Y, Asano T, Song BS, Noda S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature. 2003;425(6961):944–947. doi: 10.1038/nature02063. [DOI] [PubMed] [Google Scholar]
- 15.Song BS, Noda S, Asano T, Akahane Y. Ultra-high-Q photonic double-heterostructure nanocavity. Nat Mater. 2005;4:207–210. [Google Scholar]
- 16.Kuramochi E, et al. Ultrahigh-Q one-dimensional photonic crystal nanocavities with modulated mode-gap barriers on SiO2 claddings and on air claddings. Opt Express. 2010;18(15):15859–15869. doi: 10.1364/OE.18.015859. [DOI] [PubMed] [Google Scholar]
- 17.Notomi M. Manipulating light with strongly modulated photonic crystals. Rep Prog Phys. 2010;73:096501. [Google Scholar]
- 18.Wu MC, Lo YH, Wang S. Linewidth broadening due to longitudinal spatial hole burning in a long distributed feedback laser. Appl Phys Lett. 1988;52:1119–1121. [Google Scholar]
- 19.Schatz R. Longitudinal spatial instability in symmetrical semiconductor lasers due to spatial hole burning. IEEE J Quantum Electron. 1992;28:1443–1449. [Google Scholar]
- 20.Sorin WV, Chang KW, Conrad GA, Hernday PR. Frequency-domain analysis of an optical FM discriminator. J Lightwave Technol. 1992;10:787–793. [Google Scholar]
- 21.Mercer LB. 1/f frequency noise effects on self-heterodyne linewidth measurements. J Lightwave Technol. 1991;9:485–493. [Google Scholar]
- 22.Kikuchi K. Impact of 1/f-type FM noise on coherent optical communications. Electron Lett. 1987;23:885–887. [Google Scholar]
- 23.Petermann K. Laser Diode Modulation and Noise. Dordrecht, The Netherlands: Kluwer; 1991. [Google Scholar]
- 24.Kikuchi K. Effect of 1/f-type FM noise on semiconductor laser linewidth residual in high-power limit. IEEE J Quantum Electron. 1989;25:684–688. [Google Scholar]
- 25.Hou L, Haji M, Akbar J, Marsh JH. Narrow linewidth laterally coupled 1.55 μm AlGaInAs/InP distributed feedback lasers integrated with a curved tapered semiconductor optical amplifier. Opt Lett. 2012;37(21):4525–4527. doi: 10.1364/OL.37.004525. [DOI] [PubMed] [Google Scholar]
- 26.Kruger U, Petermann K. The semiconductor laser linewidth due to the presence of side modes. IEEE J Quantum Electron. 1988;24:2355–2358. [Google Scholar]
- 27.Satyan N, Vasilyev A, Rakuljic G, Leyva V, Yariv A. Precise control of broadband frequency chirps using optoelectronic feedback. Opt Express. 2009;17(18):15991–15999. doi: 10.1364/OE.17.015991. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.