Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2014 Feb 10;111(8):2920–2925. doi: 10.1073/pnas.1310939111

Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses

Stan Schein a,b,c,1, James Maurice Gayed c
PMCID: PMC3939887  PMID: 24516137

Significance

The Greeks described two classes of convex equilateral polyhedron with polyhedral symmetry, the Platonic (including the tetrahedron, octahedron, and icosahedron) and the Archimedean (including the truncated icosahedron with its soccer-ball shape). Johannes Kepler discovered a third class, the rhombic polyhedra. Some carbon fullerenes, inorganic cages, icosahedral viruses, protein complexes, and geodesic structures resemble these polyhedra. Here we add a fourth class, “Goldberg polyhedra.” Their small (corner) faces are regular 3gons, 4gons, or 5gons, whereas their planar 6gonal faces are equilateral but not equiangular. Unlike faceted viruses and related carbon fullerenes, the icosahedral Goldberg polyhedra are nearly spherical. The reasoning and techniques presented here will enable discovery of still more classes of convex equilateral polyhedron with polyhedral symmetry.

Keywords: geometry, self-assembly, buckminsterfullerene, discrete curvature, planarity

Abstract

The three known classes of convex polyhedron with equal edge lengths and polyhedral symmetry––tetrahedral, octahedral, and icosahedral––are the 5 Platonic polyhedra, the 13 Archimedean polyhedra––including the truncated icosahedron or soccer ball––and the 2 rhombic polyhedra reported by Johannes Kepler in 1611. (Some carbon fullerenes, inorganic cages, icosahedral viruses, geodesic structures, and protein complexes resemble these fundamental shapes.) Here we add a fourth class, “Goldberg polyhedra,” which are also convex and equilateral. We begin by decorating each of the triangular facets of a tetrahedron, an octahedron, or an icosahedron with the T vertices and connecting edges of a “Goldberg triangle.” We obtain the unique set of internal angles in each planar face of each polyhedron by solving a system of n equations and n variables, where the equations set the dihedral angle discrepancy about different types of edge to zero, and the variables are a subset of the internal angles in 6gons. Like the faces in Kepler’s rhombic polyhedra, the 6gon faces in Goldberg polyhedra are equilateral and planar but not equiangular. We show that there is just a single tetrahedral Goldberg polyhedron, a single octahedral one, and a systematic, countable infinity of icosahedral ones, one for each Goldberg triangle. Unlike carbon fullerenes and faceted viruses, the icosahedral Goldberg polyhedra are nearly spherical. The reasoning and techniques presented here will enable discovery of still more classes of convex equilateral polyhedra with polyhedral symmetry.

Description and classification of geometric forms have occupied mathematicians since ancient times (1–4). The Greeks discovered the 5 Platonic polyhedra (including the icosahedron) and the 13 Archimedean polyhedra (3) [including the truncated icosahedron that resembles the soccer ball and Buckminsterfullerene (5)], all with regular faces. Kepler added two rhombic polyhedra (6, 7), one resembling ferritin cages (8, 9). These three classes of polyhedron, “equilateral” in that all their edges are of equal length, are all of the known convex equilateral polyhedra with polyhedral symmetry––icosahedral, octahedral, and tetrahedral. None of the face-regular Johnson solids have such symmetry (10).

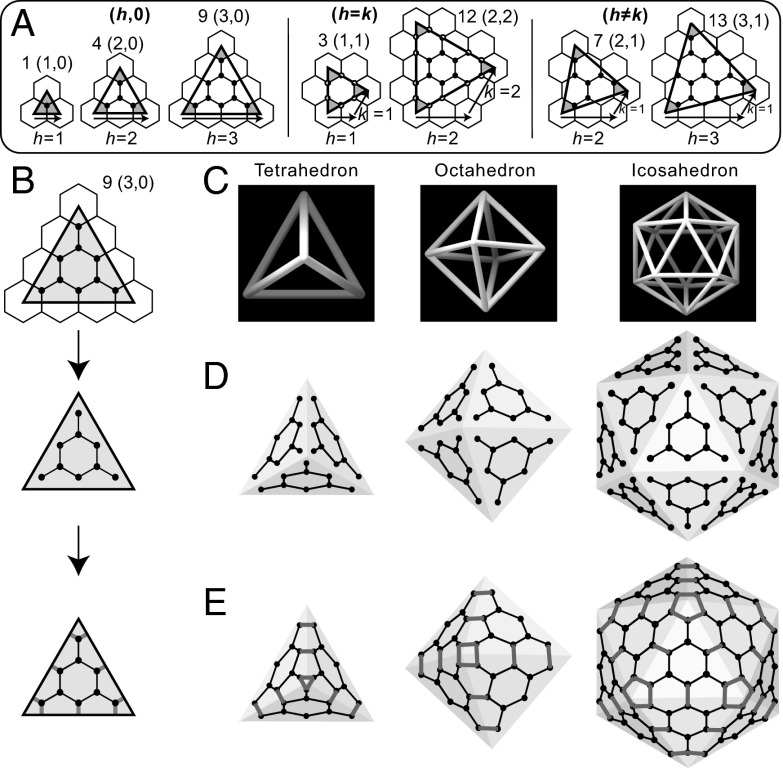
In 1937, Michael Goldberg (11) [and independently Donald Caspar and Aaron Klug in 1962 (12)] invented a method for constructing cages with tetrahedral, octahedral, and icosahedral symmetry: Over a tiling of hexagons, draw equilateral triangles of different sizes and orientations (Fig. 1A). With the bottom edge spanning h whole tiles rightward and k whole tiles at 60°, each Goldberg triangle encloses only certain numbers T = h2 + hk + k2 of vertices (11–13). Fig. 1A shows examples of the three groups of Goldberg triangles: the h, 0 group with T = 1, 4, and 9 vertices, the h = k group with T = 3 and 12, and the h ≠ k group with T = 7 and 13 (14). Now, use such a Goldberg triangle (e.g., T = 9 in Fig. 1B) to decorate each of the 4, 8, or 20 triangular facets of a tetrahedron, an octahedron, or an icosahedron (Fig. 1C), placing T vertices on each facet (Fig. 1D), and add additional edges that connect vertices across the boundaries of the facets (Fig. 1E) (11). The resulting tetrahedral, octahedral, or icosahedral cage (SI Text, Sec. 1) has 4T, 8T, or 20T trivalent vertices, 6gonal faces, and 4 triangles, 6 squares, or 12 pentagons as corner faces. However, at this point, edge lengths are unequal, and with nonplanar and coplanar faces, these cages are neither polyhedral nor convex (1).

Fig. 1.

Fig. 1.

Open in a new tab

Construction of cages with polyhedral symmetry from Goldberg triangles. (A) Drawn over a tiling of hexagons, a Goldberg triangle has T = h2 + hk + k2 trivalent vertices. Those in the h, 0 and h = k groups have mirror planes and are achiral. Those in the h ≠ k group do not and are chiral. (B) The T = 9 (h = 3, k = 0) Goldberg triangle encloses a patch of vertices and edges that can be connected to patches in neighboring triangles. (C) The tetrahedron, the octahedron, and the icosahedron have, respectively, 4, 8, and 20 equilateral triangular facets. (D) Placement of a patch from the T = 9 Goldberg triangle on each of those 4, 8, and 20 facets. (E) Addition of edges across boundaries of the facets.

For T = 1 and 3, we can transform the cages in Fig. 1E to ones with equal edge lengths (equilateral) and equal angles in 6gons (equiangular) (SI Text, Sec. 2.1). For T = 1 vertex per Goldberg triangle, this method produces three Platonic solids––the tetrahedron, the cube, and the dodecahedron. For T = 3, this method produces three Archimedean solids––the truncated tetrahedron, the truncated octahedron, and the truncated icosahedron. These cages are geometrically polyhedral because their faces are planar (1) and convex because they bulge outward at every vertex.

Could similarly symmetric convex equilateral polyhedra be created from Goldberg triangles with T > 3? We show that no such polyhedra are possible if the transformation requires both equilaterality and equiangularity. Even if the transformation merely encourages equal internal angles (SI Text, Sec. 2.1), the resulting “merely equilateral”––equilateral but not quite equiangular––tetrahedral, octahedral, and icosahedral cages (e.g., Fig. 2 A–E, Left and Fig. S1) have nonplanar 6gons, either “boat-” or “chair”-shaped (Fig. 2F), and are thus not polyhedral (1). Here, we show that the difference––convex polyhedra with planar 6gons for T = 1 and T = 3 but nonpolyhedral cages with nonplanar 6gons for T > 3––is due to the presence of edges with dihedral angle discrepancy (DAD) (15–18). We then show we can null all of the DADs and thus create a fourth class of equilateral convex polyhedron with polyhedral symmetry that we call “Goldberg polyhedra.”

Fig. 2.

Fig. 2.

Open in a new tab

Merely equilateral cages and Goldberg polyhedra. (A–D) For T = 4 (A), T = 7 (B), T = 9 (C), and T = 12 (D); merely equilateral cages have nonplanar faces (Left columns). By contrast, Goldberg polyhedra have planar faces (Middle columns). Planar faces have internal angles that sum (Σ) to 720° (Right columns). Coloring of 6gons and labeling of angles (Right) are consistent with corresponding Goldberg triangles in Fig. S2. (E) Additional examples showing that merely equilateral cages (Left) appear faceted, whereas Goldberg polyhedra (Right) appear nearly spherical (Table S3). (F) Side views of nonplanar 6gons of two types, boat and chair.

Results

DAD.

In Fig. 3A the dihedral angle A about the blue edge is the angle between the two flanking planes (green and pink), each plane defined by three points. For the trivalent vertex, the cosine of A is determined by end angle α and side angles β and γ (Eq. 1):

graphic file with name pnas.1310939111eq1.jpg

In this equation, side angles β and γ are interchangeable.

Fig. 3.

Fig. 3.

Open in a new tab

DAD in cages with T > 3. (A) Dihedral angle A about the blue edge is determined by end angle α and side angles β and γ (Eq. 1). (B) For the faces flanking the blue edge to be planar, the dihedral angles at the left and right ends of the blue edge must be equal. (C) The icosahedral T = 3 cage, the truncated icosahedron, with 60 vertices. Pentagons are shaded in the diagrams. Both ends of the blue edge are 566-type vertices with dihedral angles of 138.2°. (D) For T = 4, edges radiating like spokes from 5gons connect 566- to 666-type vertices (red dots). With regular 5gons and assuming regular 6gons, thus internal angles of 108° and 120°, dihedral angle A at the 566 end of the blue edge is 138.2°, but dihedral angle D at the 666 end is 180°. The difference, 180° – 138.2°, is a DAD of 41.8°, producing nonplanar (skew) 6gons flanking the blue edge. The nonplanarity of the right skew 6gon is angle E, that of the left is angle I, with E – I = DAD (19).

The left and right parts of Fig. 3B show a blue edge flanked by two 4gons. For the 4gons to be planar, the dihedral angles about the blue edge at its left and right ends must be the same. For example, in the truncated icosahedron (Fig. 3C), the blue edge runs from a 566 vertex (with α = 108°, β = γ = 120°) to another 566 vertex, so the dihedral angles are the same 138.2° at both ends.

By contrast, in the icosahedral T = 4 cage (Fig. 3D), each of the edges radiating like a spoke from a (shaded) 5gon connects a 566 vertex to a 666 vertex marked by a red disk. If the 6gons were equiangular, with internal angles of 120°, dihedral angle A about the 566 end (with α = 108°, β = γ = 120°) would be 138.2°, whereas dihedral angle D about the 666 end (with α = β = γ = 120°) would be 180°. The difference, a DAD of 41.8°, would make the 6gons flanking that blue spoke edge nonplanar (15, 16). With nonplanar faces flanking all of its spoke edges, this T = 4 cage would not be a polyhedron. Note, however, that internal angles in nonplanar 6gons sum to less than 720° and thus cannot all be 120°.

All Goldberg triangles with T ≥ 4 have spoke edges radiating from their (shaded) corner faces to 666 vertices (Fig. 1A). Even with internal angles of ∼120° in nearly equiangular 6gons, as in merely equilateral cages (Fig. 2 A–E, Left and Fig. S2) (SI Text, Secs. 2.1 and 2.2), all spoke edges have DADs. Thus, all merely equilateral cages with T ≥ 4 are nonpolyhedral.

Nulling DADs.

We introduced DAD to explain why the protein clathrin self-assembles into particular fullerene-shaped cages (19, 20). The mechanism we discovered, the head-to-tail exclusion rule (15–18), also explains the isolated-pentagon rule (21) observed for carbon fullerenes (22, 23). Here we use DAD for a fresh purpose.

We ask if by abandoning equiangularity (but maintaining equilaterality) in 6gons we can find a set of internal angles in the 6gons that would null the DADs about spoke (and other) edges and produce planar faces flanking those edges. [Symmetry already requires corner faces––3gons, 4gons, or 5gons––to be regular and thus equiangular (11).] Specifically, the DAD about the (blue) spoke edge in Fig. 3D would be zero if dihedral angles D and A were equal, thus Eq. 2:

graphic file with name pnas.1310939111eq2.jpg

For example, if internal angles α, β, and γ were, respectively, 60°, 135°, and 135° at one end of an edge and 90°, 90°, and 90° at the other, both A and D would be 90°, and the DAD would be zero.

Our first challenge then is to discover for cages with T ≥ 4 if it is possible to find a set of internal angles in 6gons that nulls all of the DADs in a cage and thus makes all of the faces planar. Our second challenge is to determine those internal angles––or conversely to show why such a set of internal angles does not exist.

Labeling 6gons and Internal Angles.

We begin by giving each symmetry-equivalent 6gon its own color in the Goldberg triangles that we investigated, achiral ones with T ≤ 49 and chiral ones with T ≤ 37 (Fig. 4A and Fig. S2).

Fig. 4.

Fig. 4.

Open in a new tab

Labeling 6gons, internal angles, and DADs in Goldberg triangles. (A) Goldberg triangles with T = 4, 7, 9, and 12. Different 6gon types are colored and numbered in accord with symmetry. Internal angles in 6gons are labeled in accord with symmetry and the taxonomy of planar equilateral 6gons, the latter shown in B. Different types of vertex, identified by different triplets of internal angles, are marked by circles of different colors. One example of each type of DAD edge is thickened. (B) Seven types of planar equilateral 6gon. The type with six different internal angles 123456, has three independent variables, as marked in the center of that 6gon. The remaining six types, constrained by symmetry, have fewer independent variables. (C) (Left) The planar equilateral 1212 4gon, a rhombus, has two different angles but one independent variable. (Center and Right): internal angles sum to 360°, but endpoints fail to match in both x- and y directions (Center) and in just the x direction (Right). (D) A planar equilateral 5gon with five different internal angles 12345 has two independent variables.

Planar equilateral 6gons can have seven different patterns of internal angles (Fig. 4B). Based on this taxonomy and symmetry, we label internal angles in 6gons of Goldberg triangles (Fig. 4A and Fig. S2) (SI Text, Secs. 3.1 and 3.2). Because of rotational symmetry and mirror planes, labeling of angles in Goldberg triangles (Fig. 4A and Fig. S2) is the same if the 6gons are merely equilateral (and nonplanar) or equilateral and planar. Angles in merely equilateral cages (Fig. S2 and Table S1) confirm the labeling (SI Text, Sec. 3.3). For each group of Goldberg triangles (h, 0; h = k; and h ≠ k), the number of unique internal 6gon angles increases with T (Table 1 and Table S2).

Table 1.

Equal numbers of DAD equations and independent variables

Group Indices T(h, k) Vertices 20T 6gon angles Vertex types DAD eqs 6gon ID# 6gon type Ind var Tot var
h, 0
1 (1,0) 20 0 1 0 #0 0
4 (2,0) 80 2 2 1 #1 122122 1 1
9 (3,0) 180 4 3 2 #1 122122 1 2
#2 121212 1
16 (4,0) 320 8 5 4 #1 122122 1 4
#2 122122 1
#3 123432 2
49 (7,0) 980 24 12 12 #1 122122 1 12
#2 122122 1
#3 122122 1
#4 123432 2
#5 123456 3
#6 123432 2
#7 123432 2
h = k
3 (1,1) 60 1 1 0 #1 111111 0 0
12 (2,2) 240 4 3 2 #1 122122 1 2
#2 122122 1
#3 111111 0
48 (4,4) 960 21 10 10 #1 122122 1 10
#2 123432 2
#3 122122 1
#4 123456 3
#5 122122 1
#6 122122 1
#7 122122 1
#8 111111 0
h ≠ k
7 (2,1) 140 6 3 3 #1 123456 3 3
13 (3,1) 260 12 5 6 #1 123456 3 6
#2 123456 3
37 (4,3) 740 36 13 18 #1 123456 3 18
#2 123456 3
#3 123456 3
#4 123456 3
#5 123456 3
#6 123456 3
Open in a new tab

Equal numbers of DAD equations and independent variables.

Numbers of Variables and Equations.

The number of independent variables in a planar equilateral n-gon with all different internal angles is n−3 (Fig. 4 B–D) (SI Text, Sec. 3.4). (Three internal angles fully specify a planar equilateral 6gon with the 123456 pattern.) A planar equilateral n-gon constrained by symmetry has fewer, from 2 to 0 for a 6gon (Fig. 4B). For each Goldberg triangle (Fig. 4A and Fig. S2), we identify each 6gon’s type and number of independent variables (Table 1 and Table S2). For achiral cages with 4 ≤ T ≤ 49 and for chiral with 7 ≤ T ≤ 37, the number of independent variables ranges from 1 to 18.

By definition, any edge with differently labeled internal angles at its ends––marked by differently colored circles in Fig. 4A and Fig. S2––is a DAD edge. We mark one example of each type in each Goldberg triangle as a thick black edge (Fig. 4A and Fig. S2). Each unique type provides its own “zero-DAD” equation like Eq. 2. Conversely, an edge with the same vertex types at its ends is generally not a DAD edge. However, two exceptions arise in chiral h ≠ k cages due to different arrangements of the same internal angles at the two ends of an edge (see Eq. 1) (SI Text, Sec. 3.5).

In a cage with all planar faces, all DADs are zero. Therefore, for a given cage, we compare the number of different types of DAD edge––hence different zero-DAD equations––with the number of independent variables. To our astonishment, for all of the cages we examined, even chiral ones, these numbers are equal (Table 1 and Table S2). Spurred by this finding, we have proven that the numbers are equal for all Goldberg cages. The proof focuses on the asymmetric unit, approximately demarcated by the thick black edges in each Goldberg triangle (Fig. S2). It then follows a divide-and-conquer strategy, splitting the cages into six groups: h = k with odd T and even T, h, 0 with odd T and even T, and h ≠ k with odd T and even T.

Thus, for each equilateral cage there may exist a unique “polyhedral solution,” a set of internal angles that nulls all of the DADs, makes the faces planar, and makes the vertices convex.

Solving the System of Equations for T = 4.

The Goldberg triangle for T = 4 (Fig. 4A) has one independent variable and one type of DAD edge. For the icosahedral cage, to compute the dihedral angle at the 5gon end of the DAD edge, we take advantage of the labeling of angles in Fig. 4A and replace α by 108° and β and γ in Eq. 1 by (360 − b)/2. To compute the dihedral angle at the 6gon end, we replace all of α, β, and γ in Eq. 1 by b. Then, we solve the zero-DAD Eq. 2 analytically, yielding 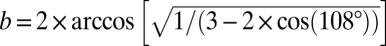Inline graphic or 116.565°, so a = 121.717°. The 6gons in this icosahedral Goldberg polyhedron are planar (Fig. 2A, Bottom Middle), confirmed by internal angles that sum to 720° (Σ in Fig. 2A, Bottom Right and Fig. S2).

Angle deficit is the difference between the sum of internal angles at a flat vertex (360°) and the sum at a vertex with curvature (1, 3). In the icosahedral T = 3 polyhedron (the truncated icosahedron, like C60), the 12 pentagons account for all 720° of the angle deficit required by Descartes’ rule, and each of the sixty 566 (108°, 120°, 120°) vertices around the pentagons has 12° of angle deficit. By contrast, in the icosahedral T = 4 Goldberg polyhedron, the 720° are distributed among all vertices, 8.565° for each of the sixty 566 vertices (108°, 121.717°, 121.717°) and 10.305° for each of the twenty 666 vertices (116.565°, 116.565°, 116.565°) (Fig. 2A, Bottom Right and Fig. S2).

The octahedral and tetrahedral polyhedral solutions for T = 4 may be computed as above, except that internal angles in corner faces (α in Eq. 1) are, respectively, 90° and 60° instead of 108°. For the octahedral T = 4 polyhedron, 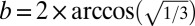Inline graphic or 109.471°, so a = 125.264° (Fig. 2A, Middle Right and Fig. S2). For the tetrahedral T = 4 polyhedron, 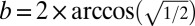Inline graphic or 90°, so a = 135° (Fig. 2A, Top Right and Fig. S2). Thus, for T = 4, for each of these three types of polyhedral symmetry there is one Goldberg polyhedron.

Mathematically Solving the Systems of Equations for T > 4 for Icosahedral Polyhedra.

For T > 4, we solve each system of n simultaneous zero-DAD equations like Eq. 2 with n variables for cages with T = 7, 9, 12, and 16 and n from 2 to 4 (Table 1 and Table S2; Fig. 4A and Fig. S2).

For example, the T = 9 cage has two zero-DAD equations and two variables (Fig. 4A). Given perimeter angle a (around the 5gon), we may obtain b (= 360° − 2a). Given spoke-end angle c, we may obtain d (= 240° − c). We thus choose angles a and c as the two independent variables. The two zero-DAD equations are both in the form of Eq. 2: DAD#1 is for the spoke edge from the orange vertex (108°-a-a) to the blue (c-b-b), and DAD#2 is for the “postspoke” edge from the blue vertex (b-c-b) to the red (a-a-d).

For each zero-DAD equation, the loci of solutions define a curve in the a–c plane (Fig. 5A). We calculate the DAD#1 curve analytically (Eq. S1; SI Text, Sec. 4.1) and the DAD#2 curve numerically (SI Text, Sec. 4.2). The curves intersect at the circled point (a, c) in Fig. 5A. The internal angles a, b, c, and d must also satisfy three inequalities: that internal angles add to <360° at each of the three vertex types––the orange (108°-a-a), blue (c-b-b), and red (a-a-d). These bounding inequalities (a < 126°, c > 2a − 120° and c < 4a − 360°) in the graph restrict (a, c) values for physically realizable, convex polyhedra to the shaded interior of the triangular region. We show the polyhedral solution, the values of internal angles in 6gons for T = 9, to different numbers of decimal places in Fig. 2C and Fig. S2 and under “polyhedra (Spartan)” and “polyhedra (solved)” in Table S1.

Fig. 5.

Fig. 5.

Open in a new tab

Polyhedral solutions. (A) For the icosahedral Goldberg polyhedron with T = 9 (Figs. 2C, Right and 4A), the circled intersection of the two curves gives perimeter angle a and spoke-end angle c. The DAD#1 (spoke) curve follows Eq. S1, the loci of solutions for the zero-DAD equation for the spoke edge. The DAD#2 curve shows numerical solutions for the zero-DAD equation for the postspoke edge. The shaded area is bounded by three inequalities, requiring sums of internal angles of <360° at each of the three vertex types. (B) For T = 12 (Figs. 2C, Right and 4A), the DAD#1 curve is the same as in A, but the DAD#2 curve is different. (C–E): As functions of T number, (C) perimeter angle a, (D) spoke-end angle c, and (E) dihedral angle (DH) about the spoke edge for all T ≥ 4 (filled diamonds) and about the postspoke edge for achiral polyhedra (filled squares). (F) As for T = 9 (A) and T = 12 (B) but for octahedral cages with planar faces. The circled intersection point, a = 135° and c = 180°, is on the corner of the boundary of the shaded region. (G) Correspondingly, octahedral cages with planar 6gons for T = 7, 9, and 12 have coplanar faces, collinear edges, and flat vertices. (H) For the equilateral tetrahedral T = 9 cage, the curve for the loci of solutions (Eq. S1) for the zero-DAD equation for the DAD#1 spoke edge lies outside the shaded region; also, the two zero-DAD curves do not intersect.

For T = 12 (Fig. 4A), and all achiral icosahedral cages for T > 4, the spoke edge (from the 108°-a-a vertex to the c-b-b vertex) and the labeling of 6gon #1 are the same as for T = 9, so the DAD#1 curves (Eq. S1) in Fig. 5 A and B are the same. Also, for achiral icosahedral polyhedra, the same bounding inequalities apply, giving the same shaded triangle. However, for T = 12, the zero-DAD equation for DAD#2 (from b-c-b to a-a-d in Fig. 4A) and its corresponding curve, obtained numerically, are different from those for T = 9, producing a different polyhedral solution (Fig. 5B).

For chiral icosahedral cages (e.g., with T = 7), we can reduce by one the number of both independent variables and DAD equations, from three to two for T = 7, by setting equal all of the internal angles around the perimeter of the corner faces (5gons), that is, by setting b = a (Fig. 4A) (SI Text, Sec. 4.3). Thus, for chiral cages the curve for the spoke DAD, originating in the orange vertex, now 108°-a-a instead of 108°-a-b, is also given by analytical Eq. S1. With two variables and equations, we use numerical methods (SI Text, Sec. 4.2) to obtain the icosahedral polyhedral solution for T = 7.

Solving the System of Equations for Icosahedral Polyhedra with Chemistry Software.

Alternatively, we can compute the structure of Goldberg polyhedra with Spartan chemistry software (24). Given equal numbers of equations and variables (Table 1 and Table S2), the polyhedral solution should be unique for each Goldberg triangle. Therefore, chemistry software that enforces planarity as well as equilaterality (SI Text, Sec. 5) should give the same angles as the mathematical solutions above. Indeed, for all of the polyhedra for which we obtained solutions mathematically, that is, for T = 4, 7, 9, 12, and 16, the internal angles agree (Table S1).

Having confirmed the solutions computed by chemistry software, we use Spartan to produce the icosahedral polyhedra for achiral cages with T ≤ 49 and chiral cages with T ≤ 37 (Fig. S2;Table 1 and Table S1). To validate these unique polyhedral solutions, we confirm for each that all DADs are zero (Eq. 2), internal angles in 6gons sum to 720°, internal angles at vertices sum to less than 360°, polyhedral symmetry still applies, and the cage is convex. Because of the possibility of “twist” (15), a DAD of zero about an edge does not by itself guarantee planarity of the two faces flanking that edge (Fig. S3). However, our mathematical solutions require a sum of 720° for each 6gon, enforcing planarity, and the chemistry software directly enforces planarity (SI Text, Sec. 5). Twist is thus precluded. Even for a cage as complex as T = 37, with 6 types of 6gon, 36 internal angles, 18 independent variables, and 18 zero-DAD equations (Table 1 and Table S2), this method works.

These data show that as T rises to infinity, perimeter angle (a for achiral icosahedral Goldberg polyhedra and a = b for chiral ones in Fig. 4A and Fig. S2) rises to approach 126° (Fig. 5C). Thus, angle deficit at each of the sixty 566 vertices (360°-2a-108°) would be <12°, leaving over angle deficit for 666 vertices. In addition, spoke-end angle (e.g., c for the achiral polyhedra in Fig. 4A and Fig. S2) rises to approach 144° (Fig. 5D). [Indeed, to nudge Spartan toward the global minimum, we can use estimates from these two graphs to temporarily constrain these angles (SI Text, Sec. 6).] As expected, as T increases, dihedral angles about the spoke edge and the postspoke edge rise to approach 180° (Fig. 5E).

For our merely equilateral cages, our settings in Spartan (SI Text, Sec. 2) encourage equiangularity, thus internal angles near 120° in 6gons (Figs. S1 and S2; Table S1). For carbon fullerenes, sp2 bonding also encourages bond angles near 120° in 6gons. Because regular 6gons tile a plane, the nearly equiangular (although nonplanar) 6gons in the interior of each triangular facet tend to flatten the facet. Thus, merely equilateral icosahedral cages exhibit a faceted or angular appearance (Fig. 2 A–E, Left and Figs. S1 and S2) like icosahedral carbon fullerenes (25) and some viruses (26), particularly when viewed along a two- or threefold axis (Fig. S4).

By contrast, the icosahedral Goldberg polyhedra are nearly spherical (Fig. 2 A–D, Middle, Fig. 2E, Right and Figs. S2 and S4; Table S3) like some other viruses (26). Indeed, some bacterial (27–32) and mammalian (33) double-stranded DNA viruses mature from a spherical to a faceted form that can withstand high pressure upon filling with DNA (34–36). The faceted form may be stronger because equiangularity may promote quasi-equivalent binding among subunits (37).

No Octahedral or Tetrahedral Goldberg Polyhedra for T > 4.

For the octahedral T = 9 polyhedron, Fig. 5F shows a unique solution, the circled point where the two DAD curves intersect, where perimeter angle a = 135° (thus b = 90°), and spoke-end angle c = 180° (thus d = 60°). This point lies on a corner of the shaded triangle, where internal angles sum to 360° at both (flat) orange and (flat) blue vertices (Fig. 4A). The chemistry software produces the corresponding T = 9 cage in Fig. 5G: With flat vertices and coplanar faces, the cage is not convex; with collinear edges, 6gons #2 are no longer 6gons. Thus, a convex equilateral octahedral Goldberg polyhedron does not exist for T = 9.

Fig. 5F tells the same story for T = 12, and indeed for all octahedral cages with T > 4. The curve labeled “DAD#1 (spoke)” is the same as that for T = 9 (Eq. S1 with σ = 90°), and although the curve labeled “DAD#2 for T = 12” is different from that for T = 9, the circled point of intersection is the same. The corresponding T = 12 cage (Fig. 5G) has flat vertices, coplanar faces, and collinear edges. So does the T = 7 cage (Fig. 5G) for many of the same reasons. Thus, convex equilateral octahedral Goldberg polyhedra do not exist for T > 4.

A similar graph (Fig. 5H) demonstrates that no tetrahedral Goldberg polyhedra exist for T > 4. In this case, the curve (Eq. S1 with σ = 60°) that represents the loci of solutions to the zero-DAD equation for the spoke edge (DAD#1) is the same for all T and resides entirely outside the shaded region; in addition, the DAD#2 curve does not intersect the DAD#1 curve.

Discussion

The fourth class of convex equilateral polyhedra with polyhedral symmetry consists of a single tetrahedral polyhedron (T = 4), a single octahedral one (T = 4), and a countable infinity (38) of icosahedral ones (T ≥ 4), one for each pair h, k of positive integers. To obtain these polyhedra, with all planar faces, it was necessary to use the invention of DAD as a measure of nonplanarity (15, 16) and to recognize that nonplanar 6gons of a Goldberg cage might be made planar by bringing all of the DADs in the cage to zero.

An “equilateral polyhedral solution” for a given Goldberg cage would thus consist of the set of internal angles that brings its DADs to zero. To obtain such a solution for a given cage, we identified all of its types of DAD and corresponding zero-DAD equations. We also counted its independent variables, a subset of the internal angles that fully determines all of its internal angles. We discovered that the numbers of equations and independent variables were equal, raising the possibility of finding unique polyhedral solutions. Depending on the number of equations and variables, we were able to obtain unique polyhedral solutions analytically, numerically, or with chemistry software––and to reject any nonconvex structures.

The reasoning developed here, specifically counting equations and variables to determine if an equilateral polyhedral solution is possible, and the techniques, particularly use of chemistry software as a geometry engine, can be applied to other types of cage (39, 40). For example, we can draw an equilateral triangle over a 3636 tiling (Fig. S5A)––instead of a 666 tiling as in Figs. 1A and 4A and Fig. S2, and apply that triangle to the facets of an icosahedron to create an equilateral icosahedral cage (with 3gons, 6gons, and twelve 5gons at the corners). This cage can then be transformed into a convex equilateral icosahedral polyhedron (Fig. S5B). As another example, we can transform an equilateral tetrahedral fullerene cage (Fig. S5C) into a convex equilateral tetrahedral polyhedron (Fig. S5D). In these ways, it should be possible to obtain additional classes of highly symmetric convex polyhedra. These polyhedra could be useful in applications requiring structures that approximate spheres (41).

Materials and Methods

We use Carbon Generator (CaGe) software (42) to produce protein data bank (pdb) files that can be read by Spartan chemistry software (SI Text, Secs. 1.1 and 1.2) to make cages with ≤250 vertices from custom atoms (SI Text, Sec. 2.1), equilateral with nearly equiangular 6gons (merely equilateral) (SI Text, Sec. 2.1), or with planar 6gons (SI Text, Sec. 5). We produce pdb files for larger cages by specifying triangular patches and then running the sym command in Chimera (SI Text, Sec. 1.2). We obtain polyhedral solutions analytically, numerically (SI Text, Secs. 4.1–4.3), or by use of Spartan (SI Text, Secs. 5 and 6).

Supplementary Material

Supporting Information
supp_111_8_2920__index.html (7.8KB, html)

Acknowledgments

We thank Phil Klunzinger of Wavefunction, Inc. for help with modifications of the parameter file (params.MMFF94) of Spartan to produce molecules composed of a custom atom with custom properties. We thank Jihee Woo for insightful discussions at the inception of this project. We thank Benjamin Irvine for asking if DADs of zero were sufficient to guarantee planarity of faces and for help with the proof that numbers of DAD equations and independent variables are equal. We also thank Klunzinger, Irvine, Franklin Krasne, Mae Greenwald, and Andrew Schein for helpful comments on the paper. Molecular graphics were performed with the University of California, San Francisco (UCSF) Chimera package (21), developed by the Resource for Biocomputing, Visualization, and Informatics at the UCSF, with support from the National Institutes of Health (National Center for Research Resources Grant 2P41RR001081, National Institute of General Medical Sciences Grant 9P41gM103311).

Footnotes

Conflict of interest statement: The University of California, Los Angeles may file a patent application for this work.

This article is a PNAS Direct Submission. P.F. is a guest editor invited by the Editorial Board.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1310939111/-/DCSupplemental.

References

  • 1.Coxeter HSM. Introduction to Geometry. 2nd Ed. New York: Wiley; 1969. [Google Scholar]
  • 2.Grünbaum B, Shephard GC. Tilings and Patterns. New York: Freeman; 1987. [Google Scholar]
  • 3.Cromwell PR. Polyhedra. Cambridge, UK: Cambridge Univ Press; 1997. [Google Scholar]
  • 4.Richeson DS. Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton: Princeton Univ Press; 2008. [Google Scholar]
  • 5.Kroto HW, Heath JR, O'Brien SC, Curl RF, Smalley RE. C-60 - Buckminsterfullerene. Nature. 1985;318(6042):162–163. [Google Scholar]
  • 6.Kepler J. Strena, seu De Nive Sexangula (The Six-Cornered Snowflake) Oxford: Clarendon; 1611. [Google Scholar]
  • 7. Kepler J (1619) Harmonices Mundi. Libri V; English translation of Book 2: JV Field, Kepler's Star Polyhedra, Vistas in Astronomy 23 (1979), 109–141.
  • 8.Ford GC, et al. Ferritin: Design and formation of an iron-storage molecule. Philos Trans R Soc London, Ser B. Biol Sci. 1984;304(1121):551–565. doi: 10.1098/rstb.1984.0046. [DOI] [PubMed] [Google Scholar]
  • 9.Smith JMA, Stansfield RFD, Ford GC, White JL, Harrison PM. A molecular-model for the quaternary structure of ferritin. J Chem Educ. 1988;65(12):1083–1084. [Google Scholar]
  • 10.Johnson NW. Convex polyhedra with regular faces. Can J Math. 1966;18(1):169–200. [Google Scholar]
  • 11.Goldberg M. A class of multi-symmetric polyhedra. Tohoku Math J. 1937;43:104–108. [Google Scholar]
  • 12.Caspar DL, Klug A. Physical principles in the construction of regular viruses. Cold Spring Harb Symp Quant Biol. 1962;27:1–24. doi: 10.1101/sqb.1962.027.001.005. [DOI] [PubMed] [Google Scholar]
  • 13.Coxeter HSM. Virus macromolecules and geodesic domes. In: Butcher JC, editor. A Spectrum of Mathematics; Essays Presented to H. G. Forder. Oxford: Auckland Univ Press/Oxford Univ Press; 1971. pp. 98–107. [Google Scholar]
  • 14.Fowler PW, Manolopoulos DE. An Atlas of Fullerenes. Oxford: Clarendon; 1995. [Google Scholar]
  • 15.Schein S, Sands-Kidner M. A geometric principle may guide self-assembly of fullerene cages from clathrin triskelia and from carbon atoms. Biophys J. 2008;94(3):958–976. doi: 10.1529/biophysj.107.110817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Schein S, Sands-Kidner M, Friedrich T. The physical basis for the head-to-tail rule that excludes most fullerene cages from self-assembly. Biophys J. 2008;94(3):938–957. doi: 10.1529/biophysj.107.110833. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Schein S, Friedrich T. A geometric constraint, the head-to-tail exclusion rule, may be the basis for the isolated-pentagon rule in fullerenes with more than 60 vertices. Proc Natl Acad Sci USA. 2008;105(49):19142–19147. doi: 10.1073/pnas.0807603105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Schein S. Architecture of clathrin fullerene cages reflects a geometric constraint—the head-to-tail exclusion rule—and a preference for asymmetry. J Mol Biol. 2009;387(2):363–375. doi: 10.1016/j.jmb.2009.01.044. [DOI] [PubMed] [Google Scholar]
  • 19.Crowther RA, Finch JT, Pearse BM. On the structure of coated vesicles. J Mol Biol. 1976;103(4):785–798. doi: 10.1016/0022-2836(76)90209-6. [DOI] [PubMed] [Google Scholar]
  • 20.Cheng Y, Boll W, Kirchhausen T, Harrison SC, Walz T. Cryo-electron tomography of clathrin-coated vesicles: Structural implications for coat assembly. J Mol Biol. 2007;365(3):892–899. doi: 10.1016/j.jmb.2006.10.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Pettersen EF, et al. UCSF Chimera—a visualization system for exploratory research and analysis. J Comput Chem. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
  • 22.Kroto HW. The stability of the fullerenes C-24, C-28, C-32, C-36, C-50, C-60 and C-70. Nature. 1987;329(6139):529–531. [Google Scholar]
  • 23.Schmalz TG, Seitz WA, Klein DJ, Hite GE. Elemental carbon cages. J Am Chem Soc. 1988;110(4):1113–1127. [Google Scholar]
  • 24. Hehre W, Ohlinger S (2006–2009) Spartan ’08 for Windows, MacIntosh and Linux: Tutorial and User’s Guide. (Wavefunction, Inc., Irvine, CA)
  • 25.Dresselhaus MS, Dresselhaus G, Avouris P. Carbon Nanotubes: Synthesis, Structure, Properties, and Applications. New York: Springer; 2001. [Google Scholar]
  • 26.Baker TS, Olson NH, Fuller SD. Adding the third dimension to virus life cycles: Three-dimensional reconstruction of icosahedral viruses from cryo-electron micrographs. Microbiol Mol Biol Rev. 1999;63(4):862–922. doi: 10.1128/mmbr.63.4.862-922.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Jiang W, et al. Coat protein fold and maturation transition of bacteriophage P22 seen at subnanometer resolutions. Nat Struct Biol. 2003;10(2):131–135. doi: 10.1038/nsb891. [DOI] [PubMed] [Google Scholar]
  • 28.Fokine A, et al. Structural and functional similarities between the capsid proteins of bacteriophages T4 and HK97 point to a common ancestry. Proc Natl Acad Sci USA. 2005;102(20):7163–7168. doi: 10.1073/pnas.0502164102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Agirrezabala X, et al. Quasi-atomic model of bacteriophage T7 procapsid shell: Insights into the structure and evolution of a basic fold. Structure. 2007;15(4):461–472. doi: 10.1016/j.str.2007.03.004. [DOI] [PubMed] [Google Scholar]
  • 30.Morais MC, et al. Conservation of the capsid structure in tailed dsDNA bacteriophages: The pseudoatomic structure of phi29. Mol Cell. 2005;18(2):149–159. doi: 10.1016/j.molcel.2005.03.013. [DOI] [PubMed] [Google Scholar]
  • 31.Gertsman I, et al. An unexpected twist in viral capsid maturation. Nature. 2009;458(7238):646–650. doi: 10.1038/nature07686. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Chen DH, et al. Structural basis for scaffolding-mediated assembly and maturation of a dsDNA virus. Proc Natl Acad Sci USA. 2011;108(4):1355–1360. doi: 10.1073/pnas.1015739108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Heymann JB, et al. Dynamics of herpes simplex virus capsid maturation visualized by time-lapse cryo-electron microscopy. Nat Struct Biol. 2003;10(5):334–341. doi: 10.1038/nsb922. [DOI] [PubMed] [Google Scholar]
  • 34.Smith DE, et al. The bacteriophage straight phi29 portal motor can package DNA against a large internal force. Nature. 2001;413(6857):748–752. doi: 10.1038/35099581. [DOI] [PubMed] [Google Scholar]
  • 35.Evilevitch A, Lavelle L, Knobler CM, Raspaud E, Gelbart WM. Osmotic pressure inhibition of DNA ejection from phage. Proc Natl Acad Sci USA. 2003;100(16):9292–9295. doi: 10.1073/pnas.1233721100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Gelbart WM, Knobler CM. Virology. Pressurized viruses. Science. 2009;323(5922):1682–1683. doi: 10.1126/science.1170645. [DOI] [PubMed] [Google Scholar]
  • 37.Stagg SM, et al. Structural basis for cargo regulation of COPII coat assembly. Cell. 2008;134(3):474–484. doi: 10.1016/j.cell.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Lang S. Real and Functional Analysis. 3rd Ed. New York: Springer; 1993. [Google Scholar]
  • 39.Pawley GS. Plane groups on polyhedra. Acta Crystallogr. 1962;15:49–53. [Google Scholar]
  • 40.Fowler PW, Cremona JE, Steer JI. Systematics of bonding in non-icosahedral carbon clusters. Theor Chim Acta. 1988;73:1–26. [Google Scholar]
  • 41. Vanhoenacker M (January 8, 2013) Digital globes offer a dynamic vision. NY Times, Science Section, p D1.
  • 42.Brinkmann G, Friedrichs OD, Lisken S, Peeters A, Van Cleemput N. CaGe - a virtual environment for studying some special classes of plane graphs - an update. Match-Commun Math Comput Chem. 2010;63(3):533–552. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_111_8_2920__index.html (7.8KB, html)
1310939111_pnas.201310939SI.pdf (114.6KB, pdf)
1310939111_sfig01.pdf (2.9MB, pdf)
1310939111_sfig02.pdf (15.8MB, pdf)
1310939111_sfig03.pdf (1.7MB, pdf)
1310939111_sfig04.pdf (4.2MB, pdf)
1310939111_sfig05.pdf (1.8MB, pdf)
1310939111_st01.doc (212.5KB, doc)
1310939111_st02.doc (92KB, doc)
1310939111_st03.doc (161.5KB, doc)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES