Structural insights into the effects of 2′-5′ linkages on the RNA duplex

Significance

The nonenzymatic replication of RNA is thought to have been a critical step in the emergence of simple cellular life from prebiotic chemistry. However, the chemical copying of RNA templates generates product strands that contain 2′-5′ backbone linkages and normal 3′-5′ linkages. Our recent finding that RNAs with such mixed backbones can still fold into functional structures raised the question of how RNA accommodates the presence of 2′-5′ linkages. Here we use X-ray crystallography and molecular dynamics simulations to reveal how 3′-5′–linked RNA duplexes accommodate interspersed 2′-5′ linkages. The diminished thermal and chemical stability of such RNA duplexes reflects local structural changes, but compensatory changes result in a global RNA duplex structure with relatively minor alterations.

Abstract

The mixture of 2′-5′ and 3′-5′ linkages generated during the nonenzymatic replication of RNA has long been regarded as a central problem for the origin of the RNA world. However, we recently observed that both a ribozyme and an RNA aptamer retain considerable functionality in the presence of prebiotically plausible levels of linkage heterogeneity. To better understand the RNA structure and function in the presence of backbone linkage heterogeneity, we obtained high-resolution X-ray crystal structures of a native 10-mer RNA duplex (1.32 Å) and two variants: one containing one 2′-5′ linkage per strand (1.55 Å) and one containing three such linkages per strand (1.20 Å). We found that RNA duplexes adjust their local structures to accommodate the perturbation caused by 2′-5′ linkages, with the flanking nucleotides buffering the disruptive effects of the isomeric linkage and resulting in a minimally altered global structure. Although most 2′-linked sugars were in the expected 2′-endo conformation, some were partially or fully in the 3′-endo conformation, suggesting that the energy difference between these conformations was relatively small. Our structural and molecular dynamic studies also provide insight into the diminished thermal and chemical stability of the duplex state associated with the presence of 2′-5′ linkages. Our results contribute to the view that a low level of 2′-5′ substitution would not have been fatal in an early RNA world and may in contrast have been helpful for both the emergence of nonenzymatic RNA replication and the early evolution of functional RNAs.

The capacity of RNA to act as both a carrier of genetic information and as a catalyst has led many to investigate its potential role as the first biopolymer (1–4). An early stage involving nonenzymatic replication simplifies RNA-first scenarios, but known nonenzymatic copying reactions generate a mixture of 3′-5′ and 2′-5′ backbone linkages because of the similar nucleophilicity and orientation of the 2′ and 3′ hydroxyl groups on ribose (Fig. 1). Although regioselectivity for the 3′-5′ linkage can be improved by using different metal ions or activated monomers, it reaches, at most, ∼90% (5–11). This lack of regiospecificity has been regarded as a central problem for the emergence of the RNA world, because the resulting backbone heterogeneity was expected to disrupt the folding, molecular recognition, and catalytic properties of functional RNAs. However, we recently observed that functional nucleic acid molecules can still evolve in the presence of nonheritable mixed DNA/RNA backbone heterogeneity (12), and known functional RNAs retain catalytic and ligand binding behavior in the presence of 2′-5′/3′-5′ backbone linkage heterogeneity (13).

Fig. 1.

Template-directed chemical incorporation of an activated monomer at the 3′ end of an RNA primer. (LG, leaving group: in contemporary biochemistry, LG = pyrophosphate, in model prebiotic reactions, LG = 2-methylimidazole). Extant enzyme polymerases produce homogeneous 3′-5′–linked RNA (left product), whereas known model prebiotic reactions produce both 3′-5′ and 2′-5′ (right product) linked RNA.

The well-known duplex-destabilizing property of 2′-5′ linkages can enable thermal strand separation of long RNA duplexes in the presence of the high Mg²⁺ concentrations required for known prebiotic copying reactions (13–16). However, the mechanism responsible for this destabilization has not yet been satisfactorily elucidated, although a very preliminary modeling study has suggested that the reduced base overlap between adjacent intrastrand bases caused by the 2′-5′ linkage might be one of the reasons for the decreased T_m (17). In addition, the diminished chemical stability of this linkage in the duplex state has been suggested as a potential proofreading mechanism for linkage heterogeneity in prebiotic RNA synthesis (5). These observations, coupled with the fact that strands containing these linkages can still template RNA primer extension (18), suggest that, far from being a problem, 2′-5′ backbone linkages may have been an essential feature of early (pre)-RNA.

Given the potential importance of mixed RNA backbone isomers in early evolution, we sought to elucidate the structural origins of the properties of mixed-backbone RNA duplexes. Although NMR structures of a homogeneously 2′-5′-linked DNA and RNA duplex as well as X-ray crystal structures of 2′-5′-linked dinucleotides have been reported (19–26), no crystallographic data are available on mixed-backbone RNA. Here we report high-resolution crystal structures of three RNA 10mer duplexes of the same self-complementary sequence, the first being native RNA, the second containing two, and the third containing six 2′-5′ linkages. These data, along with accompanying molecular dynamics simulations, provide clear structural insights into the origins of the above phenomena, as well as explaining how RNA duplexes adjust their overall and local structures to accommodate mixed regioisomers. Additionally, both duplexes containing 2′-5′ linkages crystallized more readily than the native RNA duplex, most likely due to additional interhelical interactions mediated by the surface exposed 3′-hydroxyl of the 2′-linked sugars, suggesting that the incorporation of 2′-5′ linkages into RNA structures may facilitate duplex packing and RNA crystallographic analysis.

Results

Structure Determination of Native and 2′-5′-Linked RNA Duplexes.

In this study, we examined the self-complementary RNA sequence 5′-CCGGCGCCGG-3′. We prepared fully 3′-5′–linked, as well as singly and triply 2′-5′ linkage substituted forms of this sequence as follows, with the 2′-5′ linkages denoted by asterisks: 5′-CCGGC*GCCGG-3′ and 5′-CCG*GC*GC*CGG-3′. These strands were crystallized in 10% (vol/vol) 2-methyl-2,4-pentanediol (MPD), 40 mM sodium cacodylate, pH 6.0, 12 mM spermine tetrahydrochloride, and 80 mM strontium (II) chloride at room temperature at a strand concentration of 0.25 mM. Each of the three RNA isomers crystallized under these conditions, but each did so in a different space group. Notably, the RNAs containing 2′-5′ linkages consistently formed much higher-quality crystals than fully 3′-5′–linked RNA. Both RNAs containing 2′-5′ linkages crystallized within 1 week, with most crystals diffracting to a resolution ≤2 Å. In contrast, all crystals obtained from the fully 3′-5′–linked RNA under these conditions diffracted only to ∼4–5 Å. Ultimately, a crystal of the fully 3′-5′–linked RNA that diffracted to high resolution was obtained after 4 weeks at 4 °C at a strand concentration of 0.08 mM. The data collection and refinement statistics of the three structures are listed in Table S1. Although the crystallization of the same native RNA has been reported (27), no structure has been deposited in the Protein Data Bank (PDB).

We initially attempted to solve the structure of the native RNA duplex by molecular replacement (MR) using an idealized RNA duplex model, generated with the molecular graphics toolkit Coot (28). To our surprise, this effort was not successful, nor were subsequent efforts based on energy-minimized versions of the model or structures that were further relaxed through molecular dynamics (MD) simulations. Ultimately, we applied ab initio methods, as implemented in ACORN (29), to build a model of the native RNA duplex derived solely from our high-resolution diffraction data (Materials and Methods). The overall rmsd between the final structure and the initial models ranges from 1.1 to 1.3 Å.

The two RNA structures containing 2′-5′ linkages were solved by MR, using the native structure as a starting search model. The single 2′-5′ RNA structure was solved by MR using a truncated native structure (missing the base pairs at each end) as the search model, after which the terminal residues were built into the density map before refinement. Similarly, the triple 2′-5′ RNA structure was solved by the same strategy starting from the single 2′-5′ RNA model.

Helix-Helix Interactions.

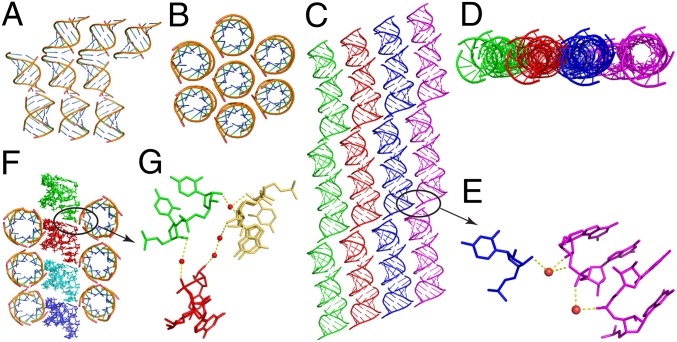
In the native structure, the 10-mer duplexes were generated by a symmetry operation, because the asymmetric unit contains only one strand of the duplex. The duplexes stack together end-to-end forming long helices. At the helical junctions, the two 5′-terminal bases are stacked on each other, as are the two 3′-terminal bases. Each long helix is surrounded by six columns of stacked double helices (Fig. 2 A and B). A similar type of duplex stacking mode is also observed in the singly 2′-5′-linked RNA structure. However, the repeating unit in this structure is a 30-bp pseudoduplex, formed by three stacked duplexes in the asymmetric unit. These units form endless duplexes with a slight kink every third duplex (Fig. 2C, stacking duplexes are identically colored). These stacked duplexes have more interactions with each other than the native RNA [cf. top view of singly modified RNA (Fig. 2D) vs. top view of native RNA (Fig. 2B)]. Further analysis of these interhelical interactions reveals that in these structures, the 3′-OH of the 2′-5′-linked C5 residue in the kinked duplex (black circle in Fig. 2C) interacts with the sugar and phosphate of the neighboring duplex via hydrogen bonds to bridging water molecules (Fig. 2E). In the RNA structure with three 2′-5′ backbone linkages, the duplexes also pack together end-to-end, but in this case, the 5′ and 3′ terminal bases are stacked on each other. In addition, the duplexes in this structure align in two perpendicular axes (Fig. 2F), in contrast to the native and the singly 2′-5′-linked RNA structures, in which all helical axes are parallel to one another. Here, as well, interduplex interactions occur at the 2′-5′ linkage via highly ordered water molecules (Fig. 2G).

Fig. 2.

Structures of duplexes containing zero, one, and three 2′-5′ linkages per strand, as discussed in the text. (A) Side view and (B) top view of native duplex stacking. (C) Side view and (D) top view of duplex stacking in strand containing one 2′-5′ linkage. Stacked duplexes are shown in the same color. (E) Atom-level view of interduplex interactions between the 3′-OH of the 2′-5′ linkage and neighboring ending bases G10, mediated by two highly ordered water molecules. (F) Overview of stacking in RNA duplex containing three 2′-5′ linkages per strand; two perpendicular axes exist. (G) Atom-level view of interduplex interactions between the 3′-OH of the 2′-5′ linkage at residue C7 and 2′-5′ linkages at residue C5 and G3 in other duplexes, mediated by four highly ordered water molecules. Water molecules are shown as red spheres and hydrogen bonds are indicated with yellow dashed lines.

Structural Features of RNA Duplexes Containing 2′-5′ Linkages.

Both mixed-backbone RNA strands form an A-type duplex with a very similar overall structure to the fully 3′-5′–linked RNA duplex (Fig. 3A). The rmsd between the native RNA and the duplex with one 2′-5′ linkage in each strand is 1.22 Å, whereas that between native and the duplex with three 2′-5′ linkages in each strand is 1.70 Å; the rmsd between the two modified RNAs is 0.89 Å. The major global difference between the native and mixed backbone structures is that the RNA backbone is compressed or kinked in strands containing the modified linkage (Fig. 3 B and C, by CURVES) (30). In the strand containing a single 2′-5′ linkage, the distance between P1 and P9 is 2.5 Å shorter than that in the native structure (Fig. 3B). The addition of two further 2′-5′ linkages diminishes the P1–P9 distance only by a further 1.1 Å (Fig. 3C). There are two conserved strontium atoms in the major grooves of each duplex and they have interactions with local residues through the same hydration pattern in all three structures.

Fig. 3.

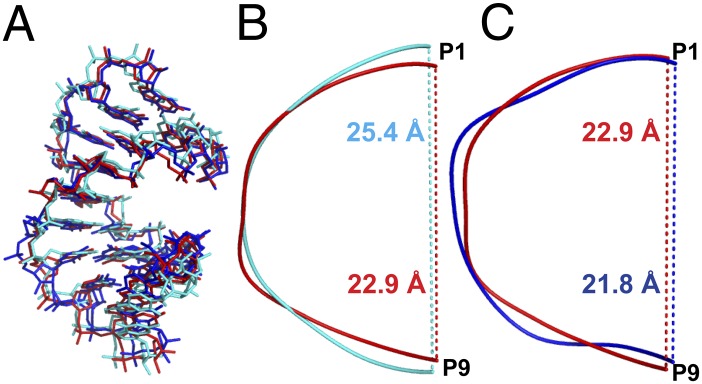
Structural comparison of native duplex (cyan), a duplex containing a single 2′-5′ linkage per strand (red), and a duplex containing three 2′-5′ linkages per strand (blue). (A) Overall duplex comparison of all of the three structures. (B) Backbone distance between P1 and P9 in native duplex (25.4 Å in cyan) and duplex containing single 2′-5′ linkage per strand (22.9 Å in red). (C) Backbone distance between P1 and P9 in duplex containing single 2′-5′ linkage per strand (22.9 Å in red) and duplex containing three 2′-5′ linkages per strand (21.8 Å in blue).

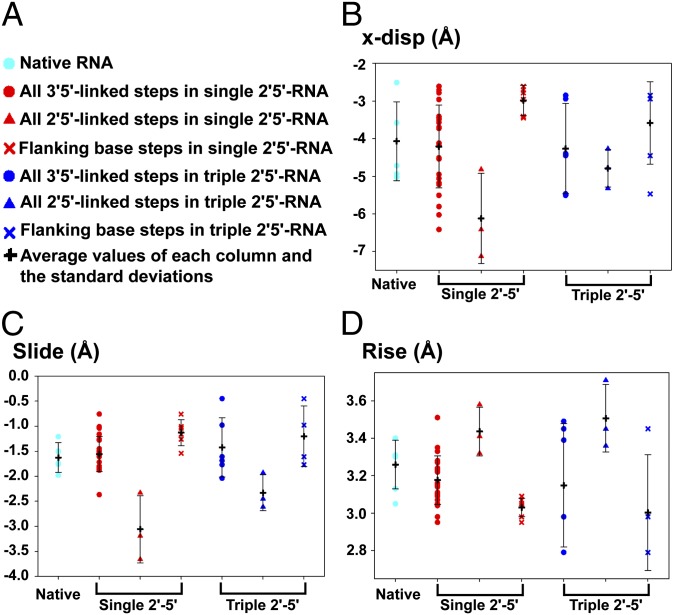
To compare the three RNA structures at a more detailed and local level, we calculated the base pair helical and step parameters for all three structures using the 3DNA software tools (31) (Fig. 4 and Table S2). The parameters for the duplex containing one 2′-5′ linkage per strand shown in Fig. 4 are values from all six strands of the three duplexes in one asymmetric unit; similarly, the parameters for the duplex containing three 2′-5′ linkages per strand are the values from both strands of the single duplex in the asymmetric unit. Consistent with the previous NMR structures of homogeneously 2′-5′-linked DNA and RNA duplexes (20, 22), the parameters that are most clearly perturbed at the sites of 2′-5′ linkages are the x displacement and slide, both of which strongly affect the extent of intrastrand base stacking. The x displacement is 1.2 Å greater than the average at step 5 of the singly 2′-5′-linked strand and 0.7 Å above average at step 3 and 1.7 Å above average at step 7 of the triply 2′-5′-linked strand. However, the effect of the increased x displacement is mostly local, due to compensation by the flanking base pairs, which exhibit lower than average x displacements (Fig. 4B). A similar effect of increased slide and rise is seen at the sites of 2′-5′ linkages, and again the effect is kept local by compensating decreased slide and rise at flanking positions (Fig. 4 C and D). Importantly, this structural perturbation also destabilizes the 2′-5′-linked duplex by shifting the rise (calculated using the local reference axis) (31, 32) from the optimal 3.3 Å (33) to suboptimal distances (around 3.0 Å for the two flanking base pair steps and 3.5 Å for the 2′-5′-linked base pair steps). Consequently, the stacking interactions of all three base pair steps are highly perturbed compared with the native duplex. Other structural parameters remain within the normal range of variation at sites of 2′-5′ linkages. All three structures show very similar average values for all parameters, indicating that partial substitution with 2′-5′ linkages does not grossly change the global RNA duplex structure.

Fig. 4.

Base pair step parameter plots of the three structures. (A) General legends for B–D. Cyan dots represent the native RNA base pairs, red dots represent all of the native 3′-5′ linkages in the single 2′-5′-linked RNA, red triangles represent the 2′-5′-linked base steps in all of the three asymmetric duplexes observed in the asymmetric unit of the single 2′-5′ RNA structure, and red X’s represent the two flanking base pairs connected with the 2′-5′-linked base pairs. Blue colored symbols represent the corresponding parameters for triple 2′-5′-linked RNA. For each panel, black crosses represent the mean values with error bars representing SDs. (B) x displacement, (C) slide, and (D) rise for the positions described in A (the 2′-endo form of G3 was used to calculate all helical parameters).

NMR studies of the fully 2′-5′-linked RNA duplexes have shown that the ribose sugar is in the 2′-endo conformation (vs. 3′-endo in standard RNA) and that the 3′-hydroxyl group has the potential to form a hydrogen bond with the nonbridging pro-S_P phosphate oxygen (22). Consistent with these previous observations, our structure of the RNA duplex containing a single 2′-5′ linkage in each strand (Fig. 5A) shows a 2′-endo sugar pucker in each of the six RNA strands in one asymmetric unit. Interestingly, the six 2′-5′-linked base steps are otherwise quite variable, with P-P distances ranging from 6.4 to 7.5 Å (mean, 6.7 Å), and a distance between O3′-O(S_P) ranging from 2.8 to 4.1 Å (mean, 3.4 Å). This variability is even more striking in the structure containing three 2′-5′ linkages per strand. As shown in Fig. 5 B and C, two conformations of the 2′-5′-linked G3-G4 step and its complementary C7-C8 step have been captured in this structure. G3 exhibits both 2′-endo and 3′-endo sugar pucker conformations, whereas C7 only shows the 3′-endo conformation. In addition, the distance between the two phosphate atoms in the 2′-5′-linked GC step (6.7 Å) is greater than that of the native RNA duplex (5.8 Å), as well as the distance calculated from the NMR structure (5.9 Å).

Fig. 5.

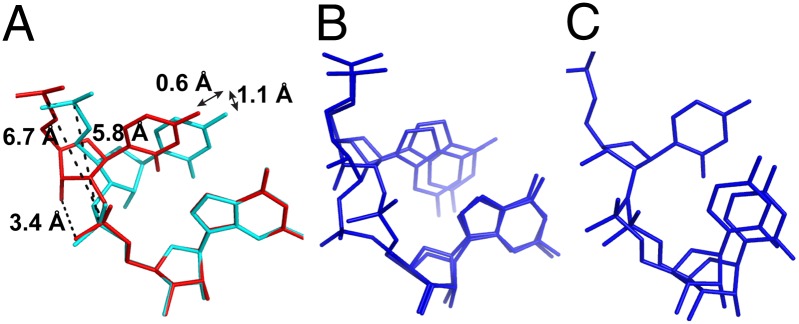
(A) Comparison of native (cyan) and 2′-5′-linked (red) C5-G6 steps. The 2′-5′ C5 exhibits a slide of 0.6 Å and a shift of 1.1 Å, compared with the native C5. The distances between the two phosphorous atoms are 6.7 Å for the 2′-5′-linked step and 5.8 Å for the 3′-5′–linked step. The 3′-OH forms weak hydrogen bonding contacts with the 3′-O-S_P, with a distance of 3.4 Å. (B) Mixed conformations of the G3-G4 step with both 2′-endo and 3′-endo sugar puckers of the 2′-linked G3 in the structure containing three 2′-5′ linkages per strand and (C) the mixed conformations of the C7-C8 step in the complementary strand, where C7 is only in the 3′-endo sugar pucker; C8 exhibits two conformations, corresponding to pairing with the two conformations of G3 in the other strand (as shown in B). Both B and C are shown in blue to be consistent with the color code in Figs. 3 and 4.

To further characterize the equilibrium properties of 2′-5′ linkages in RNA duplexes in solution, a total of 200 ns of unbiased MD simulations were performed to generate a conformational ensemble for each duplex (Table S3). The calculated ensemble average and SD of duplex structural parameters are consistent with the X-ray crystal structures (Tables S4 and S5), indicating that the empirical force field is adequate to describe the unique 2′-5′ linkages in our system. Simulations also confirmed that a 2′-5′ linkage shifts the upstream ribose to 2′-endo conformation, with its pseudorotation angle fluctuating around 162 degrees (Fig. S1A). This conformation is stabilized by a hydrogen bond between the 3′-OH and pro-S_P-oxygen of the phosphate during the simulation (Fig. S2). The pseudorotation angle of the adjacent G6 (Fig. S1B), as well as the base-paired G6 on the other strand (Fig. S1C) fluctuates around 18°, corresponding to the 3′-endo conformation. As expected, the pseudorotation angles of all of the 3′-5′–linked nucleotides are consistent with a 3′-endo sugar conformation (Table S5), whereas the sugar pucker of the terminal G10 dynamically switches between 3′-endo and 2′-endo (Fig. S1D).

Among the six base pair step parameters, 2′-5′ linkages only significantly affect slide, rise and twist in our MD simulations (Table S4). The structural perturbation on slide and rise is confined within the three nearest base pair steps by the same compensatory mechanism as we described. The 2′-5′ linkage also increases twist uniformly by 8–9° in all cases that we have studied (Table S4), suggesting that this is an inherent property of the 2′-5′ linkage. This effect, however, is not counterbalanced by adjacent base pair steps (Table S4). In fact, in the triple 2′-5′-linked duplex, the compound effect of three increased twists may play an unexpected role in lowering the T_m (vide infra).

In the MD simulations, in addition to the three base pair step parameters, 2′-5′ linkages also affect base pair buckle. In the native RNA duplex, base pairs are largely planar with average buckle amplitude varying between −5° and 5° (Table S5). In the single 2′-5′-linked duplex, however, average buckle amplitudes of base pairs 5 and 6 shift to 15° and −16°, respectively (Table S5). Consequently, the ΔBuckle between base pair 5 and 6 (defined as Buckle[i + 1] – Buckle[i]) decreases from −12° to −31°, consistent with the fact that increasing rise is often coupled with a more negative ΔBuckle (34). A similar effect is observed in the triple 2′-5′-linked system. The larger buckle amplitude may also reduce the T_m by weakening the base pair interactions (35).

Discussion

Previous modeling and NMR structural studies suggested that a large slide and x displacement of base pairs (>−1.7 and −2.5 Å) are required to form 2′-5′-linked duplexes and that this “lack of topological flexibility” is a main factor in the rejection of the 2′-5′ linkage by nature during the course of evolution (20). We confirm here that in RNA duplexes containing 11–33% 2′-5′ linkages, the 2′-5′-linked base pairs show larger slide and x displacement than the average values for 3′-5′–linked base pairs. However, the flanking 3′-5′–linked base pairs exhibit smaller than average slide and x displacement. As a result, isolated 2′-5′ linkages minimally perturb the overall structure. A major contribution to the structural flexibility of these strands is the variable sugar pucker of the 2′-5′-linked nucleotides. Although the 2′-endo sugar pucker is the predominantly observed conformation, some 2′-5′-linked residues can adopt both 2′-endo and 3′-endo conformations. Similar structural flexibility has also been observed in other natural and artificial DNA and RNA duplex systems capable of accommodating various perturbations (19, 36–41).

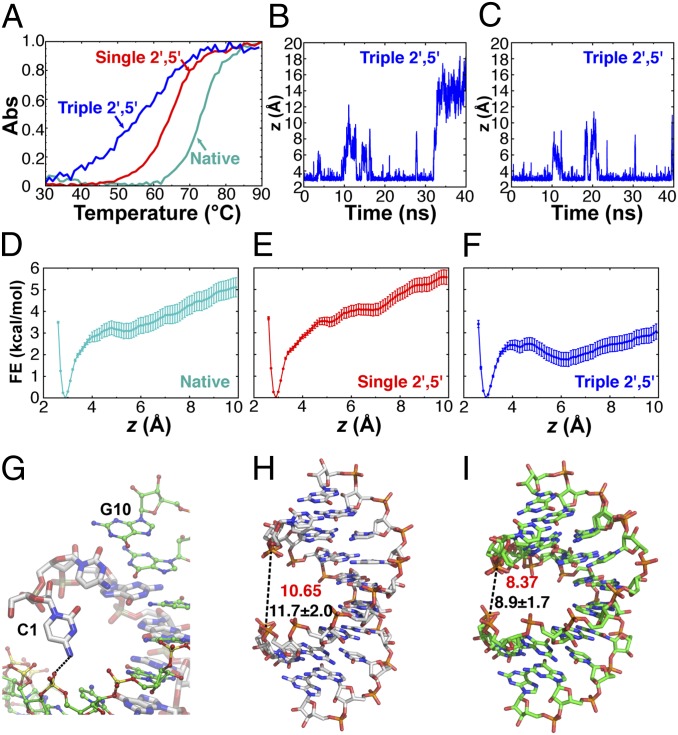
Although the average base step parameters are very similar in all three structures, the 2′-5′ linkages do induce subtle structural changes (e.g., the local stacking decrease in Fig. 5A and the global conformational change in Fig. 3 B and C). The accumulation of these perturbations as more 2′-5′ linkages are introduced decreases the overall stability of RNA duplex. It has been previously shown that the greater the fraction of 2′-5′ linkages in the duplex, the more the T_m is decreased, although the T_m drop is sequence dependent (14–16). We also observed a progressively destabilizing effect of additional 2′-5′ linkages in thermal denaturation studies. As shown in Fig. 6A, one 2′-5′ linkage in each strand causes the T_m to drop by 8.6 °C (72.1 °C for native and 63.5 °C for single 2′-5′), or by 4.3 °C per linkage. When six 2′-5′ linkages are present in the duplex, the T_m drops further, by 6.5 °C (to 57 °C) or by an average of 2.5 °C per linkage.

Fig. 6.

2′-5′ linkages facilitate terminal base pair unwinding. (A) Normalized T_ms of native 10mer: 5′-CCGGCGCCGG-3′ (cyan, T_m = 72.1 °C); single 2′-5′ 10-mer: 5′-CCGGC*GCCGG-3′ (red, T_m = 63.5 °C, ΔT_m = 8.6 °C); and triple 2′-5′ 10-mer: 5′-CCG*GC*GC*CGG-3′ (blue, T_m = 57 °C, ΔT_m = 15.1 °C) in 20 mM sodium phosphate (pH 7.0), 50 mM NaCl, and 10 mM MgCl₂. *2′-5′ linkages. (B and C) Time evolution of the collective variable z, the average heavy-atom distance of the three hydrogen bonds between each of the two terminal G-C base pairs in the triple 2′-5′-linked system during a 40-ns MD simulation. (D–F) Free energy profiles of terminal base pair unwinding in the native RNA structure and that containing one or three 2′-5′ linkages per strand respectively, calculated using z as the collective variable and reconstructed using the weighted histogram analysis method with Bayesian bootstrapping. The mean of 1,000 bootstrapped free energy profiles is shown; error bars are SDs. (G) A representative snapshot of the open state from the umbrella sampling illustrating the hydrogen bond between the exocyclic amino group of C1 in chain A and the backbone phosphate P4 of chain B in the RNA duplex with three 2′-5′ linkages. (H and I) Width of the major groove measured as the phosphate-to-phosphate distance (from P1 of chain A to P3 of chain B) for the native duplex and the triple 2′-5′ 10-mer duplex respectively; red, width in the crystal structure; black, average width calculated from MD simulations; ±SD.

The melting curve of the triple 2′-5′-linked RNA spans a significantly wider range (∼40 °C) compared with native or single 2′-5′-linked RNA (∼25 °C), suggesting that a larger fraction of the duplex is already partially unfolded at temperatures well below the T_m. Interestingly, MD simulations revealed that at room temperature, the terminal base pair in the triple 2′-5′-linked system is prone to unwind, which may contribute to a lower T_m, as well as a reduced melting cooperativity (Fig. 6 B and C). To further quantify this effect, we calculated the free energy change of the terminal base pair opening using the average heavy atom distance of the three hydrogen bonds between the terminal G-C pair as the collective variable. Recent improvement of the CHARMM force field (42) has largely remedied the issue of GC pair opening. Indeed, in all three cases, we observed a single free energy minimum around 3 Å that corresponds to a stable GC pair (Fig. 6 D–F). Compared with the native or single 2′-5′-linked duplex, the open state (6–10 Å) is ∼3 kcal/mol more stable in the triple 2′-5′-linked duplex. Visual inspection of the trajectories further revealed that the open state in the triple 2′-5′-linked system was stabilized by a hydrogen bond between the exocyclic amino group of C1 with the phosphate backbone (Fig. 6G). Such a hydrogen bond is more likely to form in the triple 2′-5′-linked system due to a narrower major groove (Fig. 6 H and I), which is caused by the additional twist (Tables S2 and S4) that 2′-5′ linkages introduce to the system.

Although the destabilizing effect of 2′-5′ linkages has been firmly established, a structural explanation has remained elusive. Based on our X-ray crystal structures and MD simulation results, we hypothesize that this can be at least partly explained by suboptimal rise distances that destabilize base stacking and by an increase in the buckle amplitude that weakens the base pair hydrogen bonding. Both effects will reduce the enthalpy of duplex formation and therefore lower the T_m. Although the 2′-5′ linkages can reduce the overlap area between adjacent intrastrand bases, they increase the adjacent interstrand base overlap accordingly. As a result, the overall base overlap area in the 2′-5′-linked duplexes is close to that in the native duplex and therefore is not a critical factor in determining the reduced T_m in this duplex (Fig. S3 and Table S6). Furthermore, free energy calculations showed that in the triple 2′-5′-linked system, the terminal base pair is more prone to unwind due to the cumulative effect of the additional twist caused by 2′-5′ linkages. We hypothesize that this effect may further reduce T_m as well as the melting cooperativity.

As we previously suggested, the diminished duplex stability of RNA containing 2′-5′ linkages may have been an adaptive feature that contributed to the emergence of RNA as the first biopolymer. To replicate, the strands of RNA (or RNA-like) duplexes must separate. Fully 3′-5′–linked RNA duplexes of ∼30 nt or longer do not fully dissociate in the presence of the high Mg²⁺ concentrations (∼10⁻²–10⁻¹ M) required to support RNA-based catalysis, even at 95 °C (13). The destabilizing effect of 2′-5′ linkages greatly facilitates thermal strand separation while still allowing for information transfer. On the other hand, 2′-5′ linkages have long been known to degrade more easily in the duplex form than 3′-5′ linkages (5). Our crystallographic data provide direct high-resolution structural confirmation of the origin of this phenomenon. The O3′-P-O5′ angle is 109.5° in the 2′-5′ linked CG step of singly 2′-5′-linked RNA (Fig. S4A), positioning O3′ closer to an in-line conformation vs. the native structure, which exhibits an O2′-P-O5′ angle of 58.5° (Fig. S4B). When applying the fitness score (Fig. S4C) developed by Breaker et al. (43), which combines both angle and distance, all 2′-5′ linkages are hot spots for in-line degradation (Fig. S4 D and E). Although the degradation associated with 2′-5′ linkages is likely to have been deleterious, the Sutherland laboratory recently reported a chemical ligation process facilitated by chemoselective O2′ acetylation, suggesting that degradation at the site of 2′-5′ linkages might be repaired to generate a normal 3′-5′ linkage (44).

We previously reported that limited (10–25%) substitution with 2′-5′ linkages allows for the retention of considerable catalytic activity and molecular recognition in folded RNA structures (13). The effects of specific 2′-5′ linkages on function are clearly context dependent. The RNA structures that we described here show that limited 2′-5′ substitution has only minor effects on overall duplex structure and that therefore 2′-5′ substitutions in the base paired stems of functional RNAs such as ribozymes would generally be expected to have minimal effects on activity. On the other hand, it is known that 2′-5′ substitution at some specific locations within non–base-paired regions of folded RNAs can severely compromise activity (13). A better understanding of the origin of these phenomena will require high resolution structures of aptamers and ribozymes containing 2′-5′ substitutions in a variety of locations; we are currently performing crystallographic studies directed toward these goals.

Materials and Methods

RNA Oligonucleotides Preparation.

RNA oligonucleotides were synthesized either by Oligos Etc. or in-house by standard solid phase synthesis techniques. The 2′-5′ linkages were synthesized using 3′-TBDMS (tert-butyldimethylsilyl)-phosphoramidites purchased from ChemGenes Corporation. Oligonucleotides were deprotected and then purified by both PAGE (15% wt/vol) and ion-exchange HPLC using a PA-100 column from Dionex at a flow rate of 1 mL/min. Buffer A was pure water, and buffer B contained 2 M ammonium acetate (pH 7.1). The RNA oligonucleotides were eluted with a linear gradient from 0% to 35% (vol/vol) buffer B in buffer A over 20 min. The collected fractions were lyophilized, desalted, and reconcentrated to 2 mM.

Crystallization.

RNA samples (1 mM duplex) were heated to 80 °C for 3 min, cooled slowly to room temperature, and placed at 4 °C overnight before crystallization. Nucleic Acid Mini Screen Kits, Natrix (Hampton Research), and Nuc-Pro-HTS (Jena Bioscience) were used to screen crystallization conditions at different temperatures using the hanging drop method.

Data Collection.

Perfluoropolyether was used as the cryoprotectant for crystal mounting. Data collection was taken under a liquid nitrogen stream at −174 °C. All diffraction data were collected at beam lines ALS 8.2.2 and 8.2.1 at Lawrence Berkeley National Laboratory. A number of crystals were scanned to find the one with highest resolution. A wavelength of 1.0 Å was chosen for data collection. The crystals were exposed for 1 s per image with a 1° oscillation angle. All data were processed using HKL2000 and DENZO/SCALEPACK (45).

Structure Determination and Refinement.

The native RNA structure was determined by ab initio methods using the program ACORN (29). The data were artificially extended to a resolution of 1.0 Å. Anisotropy correction was performed with the program PHASER (46). ACORN was run with 50,000 trials, starting with a randomly positioned single atom. The initial phases provided by the first trial with the fractional coordinates (0.18594, 0.26726, 0.04029) were refined by dynamic density modification (DDM0), resulting in a correlation coefficient of 17.5% after 57 cycles (47). The final E-map and F-map were interpretable, and both were used to help build the initial model in COOT (28). The two 2′-5′–modified RNAs structures were solved by molecular replacement with PHASER using a truncated native structure, generated by removing the 5′ and 3′ terminal bases of each strand as the search model. All of the three structures were refined using Refmac (48). The usual refinement protocol included 10 cycles of simulated annealing, positional refinement, restrained B-factor refinement, and bulk solvent correction. The stereo-chemical topology and geometrical restraint parameters of DNA/RNA were applied (49). The topologies and parameters for the 2′-5′ linkage were constructed using JLigand (50). After several cycles of refinement, a number of highly ordered waters were added. Cross-validation (51) with a 10% test set was monitored during the refinement. The σA-weighted maps (52) of the (2m|F_o| − D|F_c|) and the difference (m|F_o| − D|F_c|) density maps were computed and used throughout the model building.

Simulation Systems.

The native decamer RNA duplex and the single and triple 2′-5′-linked isomers were modeled on the basis of our 1.32-, 1.55- and 1.20-Å resolution X-ray crystal structures, respectively. For the system with three 2′-5′ linkages, two different simulation systems were set up according to the two distinctive sets of electron densities observed in the crystal structures (Table S3). The heavy Sr²⁺ ions were replaced by Mg²⁺. All four systems were then solvated in ∼48 × 64 × 48-ų water boxes and neutralized with K⁺. The final systems contained ∼1.2 × 10⁴ atoms including RNA, water, and ions.

MD Simulations.

A total of 200 ns of all-atom unbiased MD simulations were performed using the program NAMD 2.9 (53) with the CHARMM36 parameter set (42, 54). All simulations were performed using periodic boundary conditions in the isobaric-isothermal (NPT) ensemble. Langevin dynamics was used to keep the temperature at 298 K with a damping constant of 5 ps⁻¹, and a Langevin piston (55) was applied to maintain the pressure at 1 atm. The bonded, nonbonded, and electrostatic interactions were calculated at time steps of 1, 2, and 4 fs, respectively. The switching (cutoff) distance for nonbonded interaction was set at 10 (12) Å. To compute long-range electrostatic interactions, the Particle Mesh Ewald method (56) with a grid density of at least 1 Å⁻³ was used. The minimization and thermalization of all four complexes were performed as previously described (57). All systems were equilibrated for 10 ns followed by 40-ns production runs. For each duplex, a conformational ensemble composed of 20,000 snapshots was generated by taking one snapshot for every 2 ps from the 40-ns production run. For each snapshot, the structural parameters—including six base pair parameters, six local base pair step parameters, and pseudorotation angles for each nucleotide—were calculated using 3DNA (31). The two terminal base pairs are omitted for the 3DNA analysis, because they unwind frequently in the triple 2′-5′-linked duplex. The ensemble average and SDs are essentially the same compared with a smaller data set that is sampled for every 10 ps, suggesting the 2-ps sampling is sufficient to cover the entire trajectory.

Free Energy Calculations.

To test the hypothesis that the 2′-5′ linkages can facilitate the unwinding of the terminal base pair, we chose z, the average heavy atom distance of the three hydrogen bonds in the terminal G-C pair, as a collective variable. Its free energy profile, W(z), was calculated by umbrella sampling for both native and triple 2′,5′-linked duplexes. The potential energy of the system was biased with a harmonic potential, k(z − z_i)²/2, centered on successive values of z_i, from 2.5 to 10 Å with a 0.5-Å interval. The harmonic force constant, k, was chosen to be 10.0 kcal/mol/Ų. For each window, 2-ns umbrella sampling simulations were performed using five replicas (400 ps each) that start with different initial coordinates and velocities (Table S3), and the last 300 ps of trajectory was used for free energy calculations. The weighted-histogram analysis method (58) with Bayesian bootstrapping (59) was applied to reconstruct the unbiased free energy profile. A total of 1,000 Bayesian bootstrapping calculations were performed to generate the histograms obtained from umbrella sampling. The average and SD were calculated based on these 1,000 bootstrapped free energy profiles.