Remodeling of Integrated Contractile Tissues and Its Dependence on Strain-Rate Amplitude

Abstract

Here we investigate the origin of relaxation times governing the mechanical response of an integrated contractile tissue to imposed cyclic changes of length. When strain-rate amplitude is held constant as frequency is varied, fast events are accounted for by actomyosin cross-bridge cycling, but slow events reveal relaxation processes associated with ongoing cytoskeletal length adaptation. Although both relaxation regimes are innately nonlinear, these regimes are unified and their positions along the frequency axis are set by the imposed strain-rate amplitude.

The repeated interaction of myosin heads with actin filaments accounts for the active mechanical force that is generated within the airway smooth muscle cell [1–6]. But the airway smooth muscle cell is also characterized by its remarkable capacity to undergo extensive and relatively rapid cytoskeletal remodeling and length adaptation [7–10]; by means of this adaptation process, the airway smooth muscle cell is able to generate the same high force at almost any muscle length [8], whereas striated muscle cells cannot. Therefore, the airway smooth muscle cell is seen as being a highly malleable material, and in that regard it shares many features with inert soft glassy matter including materials such as foams, clays, pastes, colloids, and emulsions, all of which show relaxation dynamics that are not tied to any internal scale of time [11–20]. As such, the analogy between inert and living soft matter conflicts with the traditional physical picture of cell mechanical properties, which rests upon the central ideas that internal frictional stresses are invariably viscous stresses, and that associated molecular relaxation processes exhibit well-defined time scales and are driven by fluctuations of thermal origin [21–25]. In this Letter, we show that length adaptation on the one hand, and actomyosin bridge dynamics on the other, can be unified when viewed as a function of the strain-rate amplitude alone. This unification stems from the fact that both processes seem to rely upon molecular trapping events associated with weak molecular bonds, and the disruption of those weak bonds by imposed cyclic stretch in a manner that is mainly dependent upon strain-rate amplitude.

We picture the cytoskeleton as a system in which the rate of molecular rearrangements is governed by long-lived microconfigurations wherein stress-bearing molecules become trapped [11–18,20]. These microconfigurations might be glassy or fragile [17], by which we mean that rearrangements might be forced nonetheless, provided that molecular agitation of nonthermal origin should become large enough, such as by imposed mechanical strains occurring during every beat of the heart or inflation of the lung. Say that τ₀ is the time characterizing slow spontaneous microstructural rearrangements of the system at rest, and that τ is the time characterizing forced rearrangements of fragile components at a given strain rate γ̇ (where γ is the strain). For small strain rates, the relaxation time must remain close to its natural (slow) time scale, whereas for larger strain rates another time scale enters into the problem, namely, the strain rate itself [26]. Recognizing that 1/τ is a rate, Wyss et al. [26] proposed that the rate of structural rearrangements at a given strain rate is determined by the sum of the rate of unforced slow rearrangements and the rate of forced (fragile) rearrangements,

$$1/\tau ({\stackrel{.}{\gamma }}_0)\approx 1/{\tau }_0+K{\stackrel{.}{\gamma }}_0^{\nu },$$ (1)

where K is a prefactor and the exponent ν is close to unity. If so, then the rate of structural rearrangements is predicted to be not a function of the strain frequency, f, or of the strain amplitude, γ₀, individually, but only of their product, γ̇₀ = 2πfγ₀, the strain-rate amplitude.

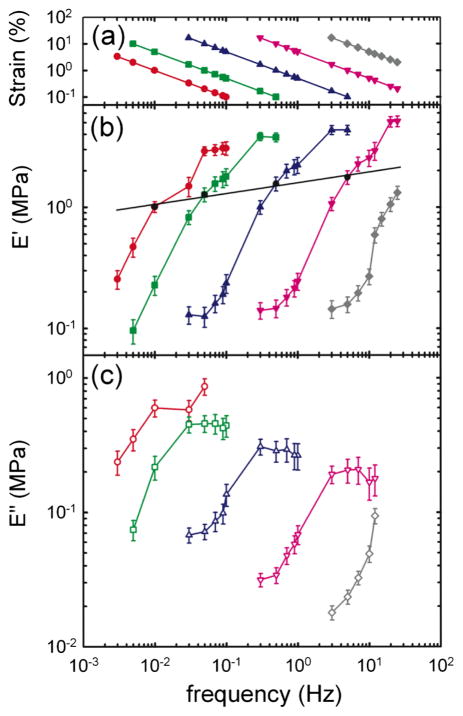
To determine the role of strain-rate amplitude, we used, as a model system, an activated airway smooth muscle (ASM)—a tissue whose mechanical response is dominated by the smooth muscle cell itself (methods are described in greater detail in the supplementary material [27]). Briefly, a freshly isolated sheep trachea muscle strip was placed between a length transducer and a force transducer. The muscle strip was then fully activated to obtain a maximal muscle contraction. After equilibrating, the muscle was subjected to sinusoidal length variations at frequency f about its reference length L_ref, and the resulting total force was measured. From each force-length curve, we calculated the effective storage modulus, or stiffness E′, and the loss modulus E″, which remain well defined and valid even in strongly nonlinear systems (Supplement 1 in [27]). For any fixed γ̇₀ [Fig. 1(a)], the strain amplitude γ₀ must decrease as f increases, and the storage modulus E′ showed a sigmoidal dependence upon frequency [Fig. 1(b)], as did E″ [Fig. 1(c)]. Remarkably, as γ̇₀ was increased over a range spanning almost four decades, sigmoidal response curves demonstrated little change of shape but shifted dramatically to higher frequencies. At any fixed frequency, however, stiffness systematically fell, a well-known phenomenon called fluidization [15,16,20].

FIG. 1.

(color online). (a) As the frequency f is increased, the strain amplitude γ₀ is decreased in order to maintain the strain-rate amplitude, γ̇₀ = 2πfγ₀, constant at 0.06 s⁻¹ (red circle), 0.314 s⁻¹ (green square), 3.14 s⁻¹ (blue triangle), 31.4 s⁻¹ (pink inverse triangle), and 314 s⁻¹ (gray diamond). (b) Elastic modulus E′ (solid symbols) and (c) loss modulus E″ (open symbols) vs frequency measured at different γ̇₀ (mean ± standard error over six muscle strips). For each γ̇₀, the shape of the response curve is mostly conserved, whereas the position of that curve along the frequency axis varies by orders of magnitude and is set by γ̇₀. A constant strain of 1% yields a weak power law [(b), solid line].

Importantly, when data points at fixed strain amplitude are connected (1% on Fig. 1(b), solid line), a weak power law dependence is recovered, implying dynamics that exhibit no characteristic scale of time (Supplement 3 in [27]). Such a response, called scale free, is observed for strains up to 10% (data not shown). This simple scale-free response is well known, appears to be universal at the cellular level, but remains unexplained [11,12,14,15]. We show below that this scale-free response decomposes into two distinct underlying processes that are both innately nonlinear: a fluidization response that depends only upon the imposed strain amplitude, and a time-scale response that depends only upon the imposed strain-rate amplitude.

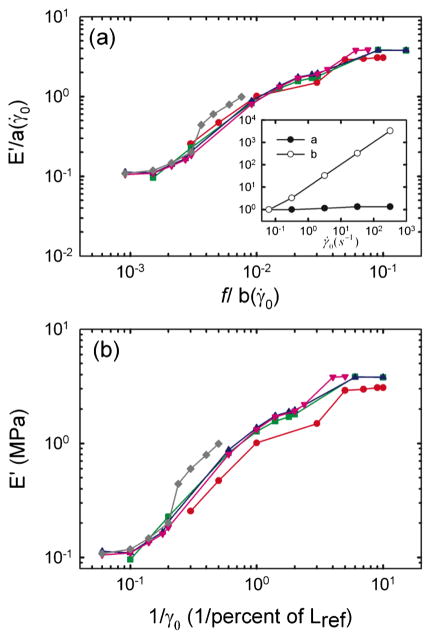
When we shifted stiffness data along the stiffness and frequency axes—a technique previously used in polymer melts [28]—all data merged into a single unifying relationship [Fig. 2(a)]. The scaling parameter along the stiffness axis, a(γ̇₀), varies by less than a factor of 2 for all γ̇₀. The scaling parameter along the frequency axis, b(γ̇₀), was directly proportional to γ̇₀ [Fig. 2(a), inset], indicative of the innately nonlinear nature of ASM stiffness (Supplement 1 in [27]) [26]. A similar collapse could be obtained for the loss modulus E″, using the same scaling parameter b(γ̇₀) and a different scaling parameter a(γ̇₀), also close to unity (data not shown). Remarkably, when we plotted stiffness versus the inverse of the applied strain amplitude, all stiffness data collapsed onto one single master curve [Fig. 2(b)], a collapse predicted by Eq. (1) (Supplement 2 in [27]).

FIG. 2.

(color online). (a) Following Wyss et al. [26] all curves are shifted onto the curve of lowest γ̇₀, dividing E′ by a scaling factor a(γ̇₀) and frequencies by a scaling factor b(γ̇₀). Inset: The scaling factor a(γ̇₀) is close to unity, whereas the scaling factor b(γ̇₀) scales with γ̇₀. (b) Elastic modulus E′ plotted vs the inverse of strain. For each γ̇₀, the shape of the curve is set by the strain alone. The symbols are the same as Fig. 1.

Taken altogether, these data show that the mechanical response of the airway smooth muscle is innately nonlinear, and that the shape of the response is invariant and set by the strain amplitude alone [Fig. 2(b)]. Surprisingly, although its shape is invariant, its position along the frequency axis is set not by an internal viscosity, elasticity, or any spontaneous molecular rate process, but instead by the imposed strain-rate amplitude (Fig. 1).

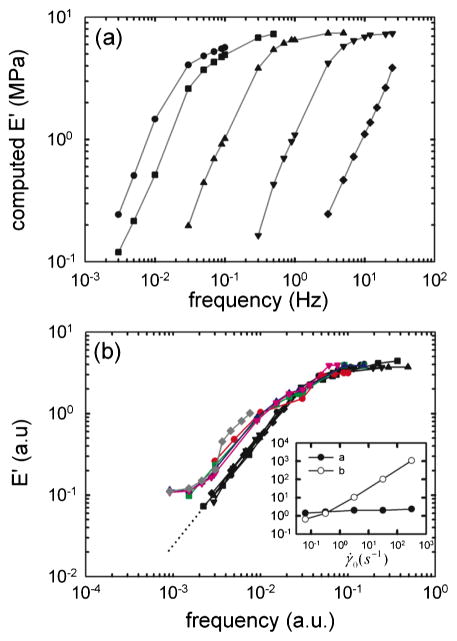
What is the contribution of actomyosin cross-bridge kinetics to this behavior? To address this question, we performed numerical computations using the latch regulation scheme of Hai and Murphy [2,3] integrated with Huxley’s sliding filament theory of muscle contraction [1], a model previously developed in our laboratory [4]. Following a comparable loading protocol, computed E′ responses were similar to measurements on ASM strips [Fig. 3(a)], and could also be collapsed onto a single master curve [Fig. 3(b)]. As in the tissue measurements, the scaling parameter a(γ̇₀) was close to unity and the scaling parameter b(γ̇₀) scaled with γ̇₀ [Fig. 3(b), inset]. When we matched data with computations in the regime where the frequency was the highest (and the strain amplitude was the lowest), a good agreement was obtained [Fig. 3(b)], describing a regime approximating isometric muscle contraction in the latch state, which is a regime dominated by the attached unphosphorylated cross bridges [5]. In that regime ASM dynamics could be attributed to forced actomyosin cross-bridge dynamics operating within a fixed structural lattice. As the frequency decreases (and strain amplitude increases), actomyosin cross bridges are perturbed, and the stiffness drops dramatically [6]. But at the lowest frequencies (and highest strain amplitudes), the slopes differed dramatically and values of the stiffness differed by an order of magnitude. These discrepancies thus expose a new domain of slow dynamics that cannot be accounted for by actomyosin interactions. Rather, we suggest that these slow dynamics are attributable to cytoskeletal remodeling (microstructural rearrangement) that is ongoing during slow deformations. The cytoskeleton is at every instant trying to adapt to the current muscle length—a process called length adaptation [8–10]—but length is continually changing and remodeling dynamics never quite catch up.

FIG. 3.

(color online). (a) Computed elastic modulus E′ using an actomyosin bridge dynamics model [4]. The symbols are the same as Fig. 1. (b) Using scaling factors a(γ̇₀) and b(γ̇₀) (inset), all computed stiffness curves (black) could be collapsed onto one master curve (black dotted line is extrapolations). When data obtained from the ASM strip [colored curves, from Fig. 2(a)] are superposed to numerical computations, a departure from actomyosin dynamics is observed at the lowest frequencies, and a new domain of slow dynamics is exposed. a.u.: arbitrary units.

Supplement 3 in [27] shows, at the level of the ASM strip, a series of rheological behaviors that are strikingly similar to those found in inert fragile or glassy materials. How can we reconcile cross-bridge kinetics with glassy dynamics? Even though Huxley’s theory of sliding filaments allows no remodeling, it shares with Sollich’s theory of soft glassy rheology certain central features [29]. For example, the partial differential equations governing conservation of binding probabilities in these two theories are remarkably similar in form [4,19,29]. As such, a trapped particle in soft glassy rheology could easily be interpreted as an actomyosin bridge, the energy depth of a well as a binding energy between actin and myosin, and the attempt frequency for a hop as an attachment-detachment rate of the actomyosin bridge.

Several theories have been recently developed to explain glassy dynamics within the cytoskeleton [30–32]. Each of these theories has at its center nonequilibrium molecular dynamics, although of very different kinds, and each provides important mechanistic insights, although none of them capture fragility [17] or slow structural rearrangements that comprise remodeling [13–17,20]. At the cellular level, the passive force of an isolated fibroblast cell deformed between two microplates has been shown to depend on the applied strain rate, as presented here [33]. Recently the dynamic modulus of human airway smooth muscle cells has been reported to depart from power law rheology at low frequencies [34], but the data presented here suggest that this reported departure could be attributable to an experiment protocol in which the strain rate was not controlled.

While the physical mechanism that underlies dynamics and associated slow remodeling of the cell remains poorly understood, we show here that, during cyclic forcing, these processes are organized by the strain-rate amplitude. Interestingly, these results unify scale-free dynamics [11,12,14,15], fluidization [15,16,20], cross-bridge kinetics [1–6], and length adaptation [7–10]. When strain-rate amplitude is held fixed, underlying relaxation processes at long time scales (Fig. 1) are exposed comparable to those that have been demonstrated only recently in inert fragile matter such as colloidal glasses [26]. While this unification is not explained by any traditional physical picture of cell rheology or polymer dynamics, it deepens substantially the analogy between living and inert soft matter.