Radiative transport produced by oblique illumination of turbid media with collimated beams

Abstract

We examine the general problem of light transport initiated by oblique illumination of a turbid medium with a collimated beam. This situation has direct relevance to the analysis of cloudy atmospheres, terrestrial surfaces, soft condensed matter, and biological tissues. We introduce a novel solution approach to the equation of radiative transfer that governs this problem, and develop a comprehensive spherical harmonics expansion method utilizing Fourier decomposition (SHEF_N). The SHEF_N approach enables the solution of problems lacking azimuthal symmetry and provides both the spatial and directional dependence of the radiance. We also introduce the method of sequential-order smoothing (SOS) that enables the calculation of accurate solutions from the results of two sequential low-order approximations. We apply the SHEF_N approach to determine the spatial and angular dependence of both internal and boundary radiances from strongly- and weakly-scattering turbid media. These solutions are validated using more costly Monte Carlo simulations and reveal important insights regarding the evolution of the radiant field generated by oblique collimated beams spanning ballistic and diffusely-scattering regimes.

I. INTRODUCTION

The general problem of collimated beam propagation and scattering in a turbid medium is important to fields as diverse as materials characterization [1, 2], biomedical optics [3–5], computer graphics [6], and geophysical remote sensing [7–9]. Applications in these areas utilize measurements of the spatial and/or angular radiance distributions in conjunction with radiative transport models to determine compositional and morphological properties [1–9]. Light transport in turbid media is modeled by the theory of radiative transfer [10, 11]. Development of general solutions to the equation of radiative transfer (ERT) is challenging due, in part, to the large number of independent variables. Monte Carlo (MC) simulations of photon transfer are often the most robust to solve the ERT, however the computational cost associated with obtaining a solution with sufficient accuracy and resolution can be computationally prohibitive. Although effective methods exist for solving the ERT in the limiting cases of single- and diffusive-scattering [11], the development of ERT solutions that are valid over spatial scales spanning a single-scattering mean-free path to several transport mean-free paths remains an important challenge [5, 7, 12–16].

Here, we present a comprehensive analysis of the radiative transport generated by oblique illumination of a turbid medium with a collimated beam using a generalized spherical harmonic expansion method. This problem is important for determining the composition and structure of turbid media on meso- and macro-scopic spatial scales [7, 17–21]. While many researchers have examined spherical harmonics expansion methods (P_N method [22]) and their variants to address the problem of collimated illumination, the implementations have been largely limited to cases of normal illumination possessing cylindrical symmetry [23–27], or isotropic illumination within an infinite medium [28–30]. Moreover, most of these studies consider only scalar metrics of the radiative field without providing any detailed directional information [23–25, 28, 29]. Other studies have provided detailed directional information but limit their consideration to azimuthally symmetric problems [26, 27, 30]. As a result, these previous methods either cannot accommodate or do not examine radiative transfer problems which employ sources that break cylindrical symmetry. This is an inherently more difficult problem since both polar and azimuthal variation in the spherical harmonic expansion must be considered.

We develop the N^th-order Spherical Harmonic Expansion with Fourier decomposition (SHEF_N) method to address these more general transport problems. The mathematical analysis uses the Fourier decomposition to obtain a system of differential equations for the expansion coefficients. We develop a detailed analysis of an associated generalized eigenvalue problem that provides two key parity relations that reduce the problem to a single quadrant of the transverse Fourier plane. Furthermore, we ascertain key mathematical properties of the generalized eigenvalue problem to enable a robust and unified solution framework for arbitrary expansion orders and illumination angles.

To demonstrate the utility of this framework, we consider both the remitted and internal light fields generated by oblique illumination of turbid media. Our results provide an unprecedented view of the evolution of the light field, produced by oblique collimated illumination, spanning the ballistic to diffusive scattering regimes. In this way SHEF_N provides a novel and comprehensive framework to predict the spatial and angular profiles of the radiance in both weakly- and strongly-scattering media over mesoscopic and macroscopic spatial scales. We validate these solutions through comparison with Monte Carlo simulations over a broad range of optical coefficients. In addition, we compare results for the spatially-resolved reflectance due to normal illumination with the standard diffusion approximation, which shows excellent agreement in the limit of high-scattering and large source-detector separations. Finally, we introduce a sequential-order smoothing (SOS) method that provides radiant field predictions with increased accuracy through a weighted combination of neigh-boring even-odd order SHEF_N solutions. This enables the use of two relatively low-order solutions to provide accuracy that would ordinarily be obtained only through a much higher order, and more computationally costly, solution.

II. THE EQUATION OF RADIATIVE TRANSFER

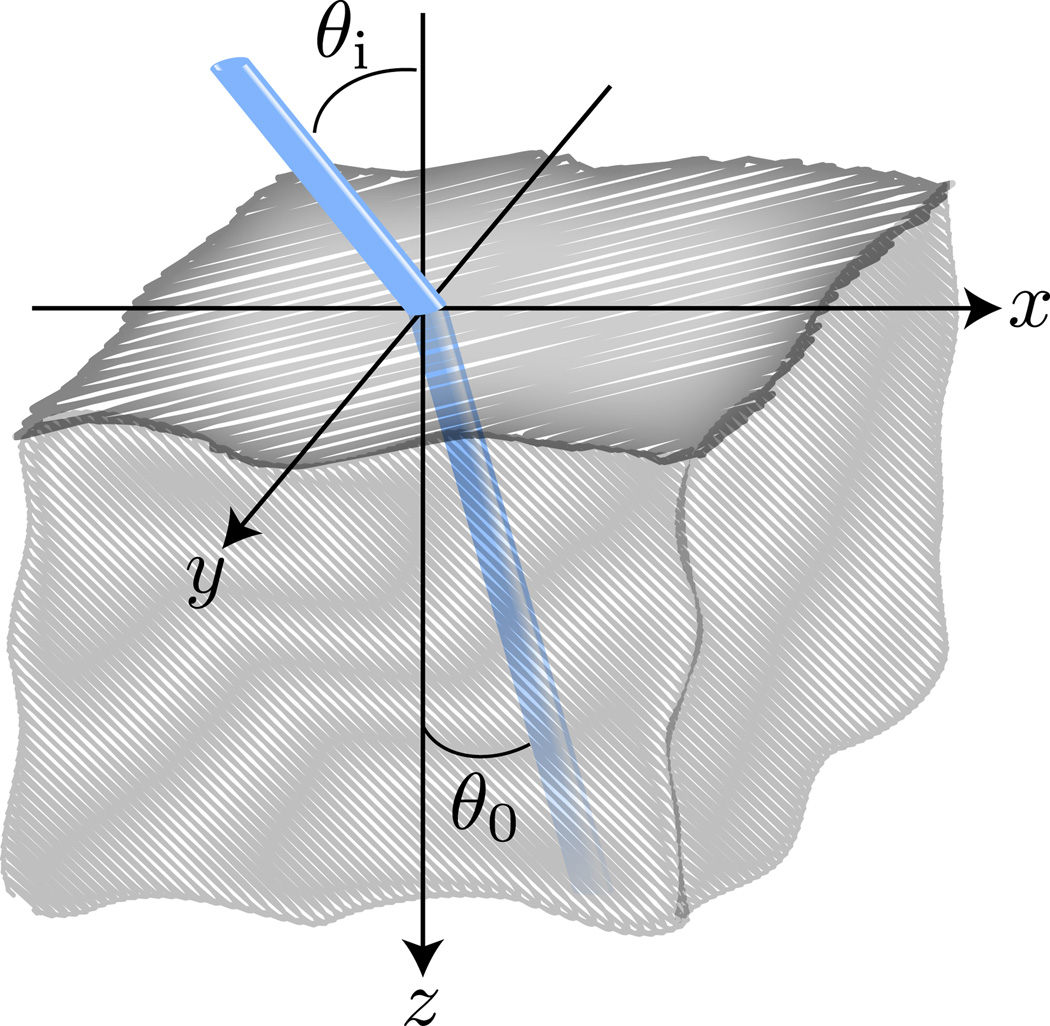
Consider the semi-infinite domain, z > 0, with boundary plane z = 0 composed of a uniform absorbing and scattering medium, with relative refractive index n as shown in Fig. 1. A continuous collimated beam is incident obliquely on z = 0 with angle of incidence θ_i. We choose a coordinate system such that the plane of incidence is the x-z-plane. The angle θ₀ in which the beam propagates into the turbid medium is governed by Snell’s law, sin θ_i = n sin θ₀.

Figure 1.

(Color online) Coordinate system for the problem showing a collimated beam obliquely incident on the turbid medium. The coordinate system is chosen so that the plane of incidence is the x-z-plane. The angle of incidence is θ_i. The beam refracts due to a refractive index mismatch at the boundary yielding a beam propagating in direction θ₀.

The radiance, L(r, Ω), represents the radiant flux per unit solid angle at position r = (x, y, z) propagating in direction Ω = (Ω_x, Ω_y, Ω_z) = (η cos ϕ, η sin ϕ, μ) where $\eta =\sqrt{1-{\mu }^2}$, μ = cos θ is the cosine of the polar angle, θ, and ϕ is the azimuthal angle. For this problem, L is governed by the following ERT

$$\mathbf{\Omega }·\nabla L+{\mu }_{t}L={\mu }_s{\int }_{4\pi }p(\mathbf{\Omega }\prime ·\mathbf{\Omega })L(\mathit{r},\mathbf{\Omega }\prime )\mathrm{d}\mathbf{\Omega }\prime ,\text{in}z>0,$$ (1)

subject to

$$L=\frac{2{\mu }_{\mathrm{i}}}{\pi {\rho }^2}\text{exp}[-\frac{2}{{\rho }^2}({\mu }_{\mathrm{i}}^2{x}^2+y^2)]\delta (\mathbf{\Omega }-{\mathbf{\Omega }}_0)+ℛL,\text{on}z=0\text{and}\mathbf{\Omega }·\mathbf{ẑ}>0.$$ (2)

Here, μ_t = μ_a+μ_s where μ_a and μ_s are the absorbing and scattering coefficients, respectively. The scattering phase function, p, gives the fraction of power scattering in direction Ω due to light incident in direction Ω′. Here, we have assumed that scattering is spherically symmetric so that p depends only on Ω′ · Ω. Boundary condition Eq. (2) gives the light incident on z = 0 corresponding to a Gaussian beam with radius ρ and the term ℛL accounts for any internal reflections due to the refractive index mismatch. Here, μ_i = cos θ_i and ${\mathbf{\Omega }}_0=(\sqrt{1-{\mu }_0^2},0,{\mu }_0)$.

Following Chandrasekhar [10], we represent the radiance as the sum of collimated and scattered radiances: L = L_c + L_s. Using the δ-Eddington rescaling [31], we find that a fraction of the collimated radiance, f_δ, is scattered directly forward along Ω₀ and remains in L_c. This results in a reduced attenuation coefficient μ̃_t = μ_a + μ̃_s = μ_a + μ_s (1 − f_δ) relative to the total interaction coefficient μ_t = μ_s + μ_a. Consequently, L_c is given by

$$L_c(\mathit{r},\mathbf{\Omega })=\frac{2{\mu }_{\mathrm{i}}}{\pi {\rho }^2}\text{exp}\{-\frac{2}{{\rho }^2}[{\mu }_{\mathrm{i}}^2{(x-\text{tan}{\theta }_{0}z)}^2+y^2]-\frac{{\mathrm{\mu ̃}}_t}{{\mu }_0}z\}\delta (\mathbf{\Omega }-{\mathbf{\Omega }}_0).$$ (3)

Then, the scattered radiance L_s is governed by

$$\mathbf{\Omega }·\nabla L_s+{\mu }_t{L}_s={\mu }_s{\int }_{4\pi }p(\mathbf{\Omega }\prime ·\mathbf{\Omega })L_s(\mathit{r},\mathbf{\Omega }\prime )\mathrm{d}\mathbf{\Omega }\prime +Q(\mathit{r},\mathbf{\Omega })\text{in}z>0,$$ (4)

where the source Q is defined as

$$Q(\mathit{r},\mathbf{\Omega })=\frac{2{\mu }_{\mathrm{i}}}{\pi {\rho }^2{\mu }_0}{\mathrm{\mu ̃}}_s\mathrm{p̃}({\mathbf{\Omega }}_0·\mathbf{\Omega })\text{exp}\{-\frac{2}{{\rho }^2}[{\mu }_{\mathrm{i}}^2{(x-\text{tan}{\theta }_{0}z)}^2+y^2]-\frac{{\mathrm{\mu ̃}}_t}{{\mu }_0}z\}.$$ (5)

Eq. (4) is subject to

$$L_s(\mathit{r},\mu >0,\varphi )=r_F(-\mu )L_s(\mathit{r},\mu <0,\varphi ),\text{on}z=0,$$ (6)

where r_F (μ) is the Fresnel reflection equation for natural light due to a refractive index mismatch at z = 0 [11].

III. SPHERICAL HARMONICS EXPANSION UTILIZING FOURIER DECOMPOSITION

We begin with the spherical harmonics

$$Y_{\ell ,m}(\mu ,\varphi )=\sqrt{\frac{(2\ell +1)}{4\pi }\frac{(\ell -|m|)!}{(\ell +|m|)!}}{P}_{\ell ,m}(\mu )\text{exp}(im\varphi ),$$ (7)

where P_ℓ,m(μ) is the associated Legendre polynomial of order ℓ = 0, 1, 2, … and degree m = −ℓ, …, ℓ, and $i=\sqrt{-1}$. The orthogonality relation is

$${\int }_{4\pi }{Y}_{\ell ,m}(\mu ,\varphi )Y_{\ell \prime ,m\prime }^{*}(\mu ,\varphi )\mathrm{d}\mathbf{\Omega }={\delta }_{\ell ,\ell \prime }{\delta }_{m,m\prime },$$ (8)

where δ_ℓ,ℓ′ is the Kronecker delta and Y* denotes the complex conjugate. Projecting the scattered radiance and phase function onto the spherical harmonics gives

$$L_s(\mathit{r},\mathbf{\Omega })=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\sqrt{\frac{2\ell +1}{4\pi }}{\psi }_{\ell ,m}(\mathit{r})Y_{\ell ,m}(\mathbf{\Omega })$$ (9)

and

$$p(\mathbf{\Omega }\prime ·\mathbf{\Omega })=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{g}_{\ell }{Y}_{\ell ,m}^{*}(\mathbf{\Omega }\prime )Y_{\ell ,m}(\mathbf{\Omega }),$$ (10)

respectively, where $\sqrt{(2\ell +1)/(4\pi )}$ is inserted for convenience. ψ_ℓ,m(r) and g_ℓ are the harmonic moments of the scattered radiance and the scattering phase function, respectively. Inserting Eqs. (9) and (10) into Eq. (4) and multiplying the resulting equation by the conjugate of the expansion, $\sqrt{4\pi /(2\ell \prime +1)}{Y}_{\ell \prime ,m\prime }^{*}(\mathbf{\Omega })$, followed by integration over all directions Ω gives

$$\frac{\partial }{\partial z}(a_{\ell ,m}{\psi }_{\ell +1,m}+b_{\ell ,m}{\psi }_{\ell -1,m})-\frac{1}{2}(\frac{\partial }{\partial x}-i\frac{\partial }{\partial y})(c_{\ell ,m}{\psi }_{\ell -1,m-1}-d_{\ell ,m}{\psi }_{\ell +1,m-1})+\frac{1}{2}(\frac{\partial }{\partial x}+i\frac{\partial }{\partial y})(e_{\ell ,m}{\psi }_{\ell -1,m+1}-f_{\ell ,m}{\psi }_{\ell +1,m+1})+(2\ell +1){\mu }_{t,\ell }{\psi }_{\ell ,m}=(2\ell +1)\frac{2{\mu }_{\mathrm{i}}}{\pi {\rho }^2{\mu }_0}{\mathrm{\mu ̃}}_s{q}_{\ell ,m}\text{exp}\{-\frac{2}{{\rho }^2}[{\mu }_{\mathrm{i}}^2{(x-\text{tan}{\theta }_{0}z)}^2+y^2]-\frac{{\mathrm{\mu ̃}}_t}{{\mu }_0}z\}.$$ (11)

This projection results in a countable infinity of coupled partial differential equations [22] for the harmonic moments, ψ_ℓ,m(r). The moments of the extinction coefficient are μ_t,ℓ ≡ μ_t − μ_sg_ℓ ≡ μ_a + μ_s(1 − g_ℓ) and the coefficients a through f are

$$\begin{array}{cc}{a}_{\ell ,m}=\sqrt{(\ell +1-m)(\ell +1+m)}\hfill & b_{\ell ,m}=\sqrt{(\ell -m)(\ell +m)}\hfill \\ c_{\ell ,m}=\sqrt{(\ell +m)(\ell -1+m)}\hfill & d_{\ell ,m}=\sqrt{(\ell +2-m)(\ell +1-m)}\hfill \\ e_{\ell ,m}=\sqrt{(\ell -m)(\ell -1-m)}\hfill & f_{\ell ,m}=\sqrt{(\ell +2+m)(\ell +1+m)}.\hfill \end{array}$$ (12)

Application of the phase function expansion [Eq. (10)] to the modified phase function of the interior source, p̃(Ω₀ · Ω), gives the source moments

$$q_{\ell ,m}({\mathbf{\Omega }}_0)=\sqrt{\frac{4\pi }{2\ell +1}}{\mathrm{g̃}}_{\ell }{Y}_{\ell ,m}^{*}({\mathbf{\Omega }}_0),$$ (13)

where g̃_ℓ is the ℓ^th moment of p̃.

To obtain computationally feasible solutions of the ERT, we truncate the spherical harmonic expansion at order N. The resulting band-limited harmonic spectrum gives rise to (N + 1)² coupled partial differential equations, which assumes ψ_ℓ>N,m = 0. We then Fourier transform Eq. (11) with respect to the transverse spatial variables (x, y)

$$\frac{\mathrm{d}}{\mathrm{d}z}(a_{\ell ,m}{\mathrm{\psi ̂}}_{\ell +1,m}+b_{\ell ,m}{\mathrm{\psi ̂}}_{\ell -1,m})-\frac{1}{2}(k_y+i{k}_x)(c_{\ell ,m}{\mathrm{\psi ̂}}_{\ell -1,m-1}-d_{\ell ,m}{\mathrm{\psi ̂}}_{\ell +1,m-1})-\frac{1}{2}(k_y-i{k}_x)(e_{\ell ,m}{\mathrm{\psi ̂}}_{\ell -1,m+1}-f_{\ell ,m}{\mathrm{\psi ̂}}_{\ell +1,m+1})+(2\ell +1){\mu }_{t,\ell }{\mathrm{\psi ̂}}_{\ell ,m}=(2\ell +1)\frac{{\mathrm{\mu ̃}}_s}{{\mu }_0}{q}_{\ell ,m}\text{exp}[-\frac{{\rho }^2}{8}(\frac{k_x^2}{{\mu }_{\mathrm{i}}^2}+k_y^2)-{\mu }_{d}z],$$ (14)

where μ_d ≡ μ̃_t/μ₀ + i tan θ₀k_x. The transverse Fourier moments (TFMs) are defined as

$${\mathrm{\psi ̂}}_{\ell ,m}(z|\mathit{k})\equiv \underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}{\psi }_{\ell ,m}(\mathit{r})\text{exp}[-i(k_{x}x+k_{y}y)]\mathrm{d}x\mathrm{d}y,$$ (15)

where k = (k_x, k_y) is the transverse wave-vector.

Next, we cast the system of equations [Eq. (14)] in vector form

$$\mathbf{A}\frac{\mathrm{d}}{\mathrm{d}z}\mathrm{\psi ̂}+\mathbf{B}\mathrm{\psi ̂}=\mathrm{𝒬̂}\text{exp}(-{\mu }_{d}z),$$ (16)

where the TFMs are the entries of the vector ψ̂, and the entries of the matrices A and B are constant with respect to z. The vector 𝒬̂ contains the harmonic moments of the transverse Fourier source, and the entries of these arrays map the (ℓ, m) pairs as [(0, 0), (−1, 1), (1, 0), (1, 1), …]. However, truncation of Eq. (14) at order N produces two algebraic equations for the outlying moments

$${\mathrm{\psi ̂}}_{N,\pm N}=\frac{1}{{\mu }_{t,N}}\{\frac{1}{2}(k_y\pm i{k}_x)\frac{\sqrt{2N(2N-1)}}{2N+1}{\mathrm{\psi ̂}}_{N-1,\pm (N-1)}+\frac{{\mathrm{\mu ̃}}_s}{{\mu }_0}{q}_{N,\pm N}\text{exp}[-\frac{{\rho }^2}{8}(\frac{k_x^2}{{\mu }_{\mathrm{i}}^2}+k_y^2)-{\mu }_{d}z\left]\right\}.$$ (17)

Substitution of these moments is required to formulate Eq. (16). This substitution modifies the (ℓ, m) = [N − 1,±(N − 1)] elements of both the diagonal of B

$$diag{(\mathbf{B})}_{\ell ,m}=(2\ell +1){\mu }_{t,\ell }+\{\begin{array}{cc}\frac{N(2N-1)k^2}{2(2N+1){\mu }_{t,N}},\hfill & \text{if}\ell ,m=N-1,\pm (N-1)\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (18)

and the source vector 𝒬̂

$${\mathrm{𝒬̂}}_{\ell ,m}=\frac{{\mathrm{\mu ̃}}_s}{{\mu }_0}\text{exp}[-\frac{{\rho }^2}{8}(\frac{k_x^2}{{\mu }_{\mathrm{i}}^2}+k_y^2\left)\right][(2\ell +1)q_{\ell ,m}-\{\begin{array}{cc}\frac{(k_y\mp i{k}_x)\sqrt{2N(2N-1)}{q}_{N,\pm N}}{2{\mu }_{t,N}},\hfill & \text{if}\ell ,m=N-1,\pm (N-1)\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}].$$ (19)

Following this substitution [(N + 1)² − 2] equations remain in Eq. (16).

Next, we seek the solution of Eq. (16) as the sum of homogeneous and particular solutions

$$\mathrm{\psi ̂}(z|\mathit{k})={\mathrm{\psi ̂}}^{(h)}(z|\mathit{k})+{\mathrm{\psi ̂}}^{(p)}(z|\mathit{k}).$$ (20)

The particular solution is given by ψ̂^(p) = (−μ_dA + B)⁻¹ 𝒬̂ exp(−μ_dz), and we seek the homogeneous solution in the form ψ̂^(h) = G exp(z/λ). Upon substitution of the homogeneous solution into Eq. (16), we obtain the generalized eigenvalue problem AG = −λBG. Analysis of the matrices of Eq. (16) provides valuable information regarding the generalized eigenvalue problem. First, while matrix A is real, symmetric, and possesses entries that are constant with respect to z, it is rank deficient. Matrix B is Hermitian and its entries depend on the optical coefficients and the transverse wave vector k, but not z. Thus, the generalized eigenvectors, G, form a basis. The rank deficiency of A, results in (N − 1) eigenvalues that are zero. To obtain a unique solution to a boundary value problem, we reject the eigenvectors corresponding to these zero eigenvalues. The remaining eigenvalues occur in positive/negative pairs that are either distinct or 1-fold degenerate. For even expansion orders, there are N distinct and N² degenerate eigenvalues. For odd expansion orders, there are (N + 1) distinct and (N² − 1) degenerate eigenvalues. In total, there are N(N + 1) non-zero eigenvalues for even or odd expansion orders, a quantity which is always even. The solution we seek for the semi-infinite turbid medium must additionally satisfy the condition ψ → 0 as z → ∞. Therefore, the eigenvectors corresponding to the positive eigenvalues must also be rejected. Using these mathematical properties, we represent the TFM solutions as

$$\mathrm{\psi ̂}(z|\mathit{k})=\sum _{j=1}^{N(N+1)/2}{C}_j{\mathbf{G}}_j\text{exp}(z/{\lambda }_j)+{(-{\mu }_d\mathbf{A}+\mathbf{B})}^{-1}\mathrm{𝒬̂}\text{exp}(-{\mu }_{d}z).$$ (21)

To determine the coefficients C_j in Eq. (21), we prescribe boundary conditions that conserve hemispherical moments of Eq. (6), due to the absence of a half-range orthogonality relationship for the spherical harmonics. These hemispherical conditions are extensions of the Marshak condition [32] and given by

$${\int }_{\mu >0}{L}_s(x,y,z=0,\mu ,\varphi )Y_{\mathrm{\Lambda },M}^{*}(\mu ,\varphi )\mathrm{d}\mu \mathrm{d}\varphi ={\int }_{\mu <0}{L}_s(x,y,z=0,\mu ,\varphi )r_F(-\mu )Y_{\mathrm{\Lambda },M}^{*}(-\mu ,\varphi )\mathrm{d}\mu \mathrm{d}\varphi .$$ (22)

Conceptually, this boundary condition requires the portion of the outwardly-directed (μ < 0) scattered radiation that is internally reflected at the boundary to equal the inwardly-directed (μ > 0) scattered radiation. This boundary condition accounts for propagation in polar and azimuthal angles and arbitrary refractive index mismatch. Following insertion of Eq. (9) for the scattered radiance and integration, the resulting linear equations couple harmonic modes of constant m at the boundary. Furthermore, the order and degree of the boundary expressions require (Λ − M) to be odd.

We use the Henyey-Greenstein scattering phase function [33] which is characterized by the scattering anisotropy g ≡ 〈cos ϑ〉 as

$$p(\text{cos}\vartheta )=\frac{1}{4\pi }\frac{1-g^2}{{(1-2g\text{cos}\vartheta +g^2)}^{3/2}},$$ (23)

where cos ϑ ≡ Ω′ · Ω. The harmonic moments of the Henyey-Greenstein scattering phase function are g_ℓ = g^ℓ. The δ-Eddington rescaling of the collimated radiance produces a modified scattering phase function, p̃(Ω₀ · Ω), for the transfer of radiation from collimated to scattered fields. Through a mapping of the moments of the rescaled phase function with the Henyey-Greenstein moments, f_δ = g^N+1 and g̃_ℓ = (g^ℓ − f_δ)/(1 − f_δ) [31].

To obtain a complete ERT solution, one must, in principle, compute the TFMs over the entire transverse Fourier plane. However, we exploit two key parity relations to reduce computation of the TFMs to a single quadrant of the transverse Fourier plane. Consider a collimated beam in direction Ω₀ which lies in the x-z plane. In this case, the TFMs satisfy the following conjugate symmetry with respect to k_x

$${\mathrm{\psi ̂}}_{\ell ,m}(k_x)={\mathrm{\psi ̂}}_{\ell ,m}^{*}(-k_x),\text{for}{k}_x\ne 0,$$ (24)

and the following symmetry with respect to k_y

$${\mathrm{\psi ̂}}_{\ell ,m}(k_y)={(-1)}^m{\mathrm{\psi ̂}}_{\ell ,-m}(-k_y),\text{for}{k}_y\ne 0.$$ (25)

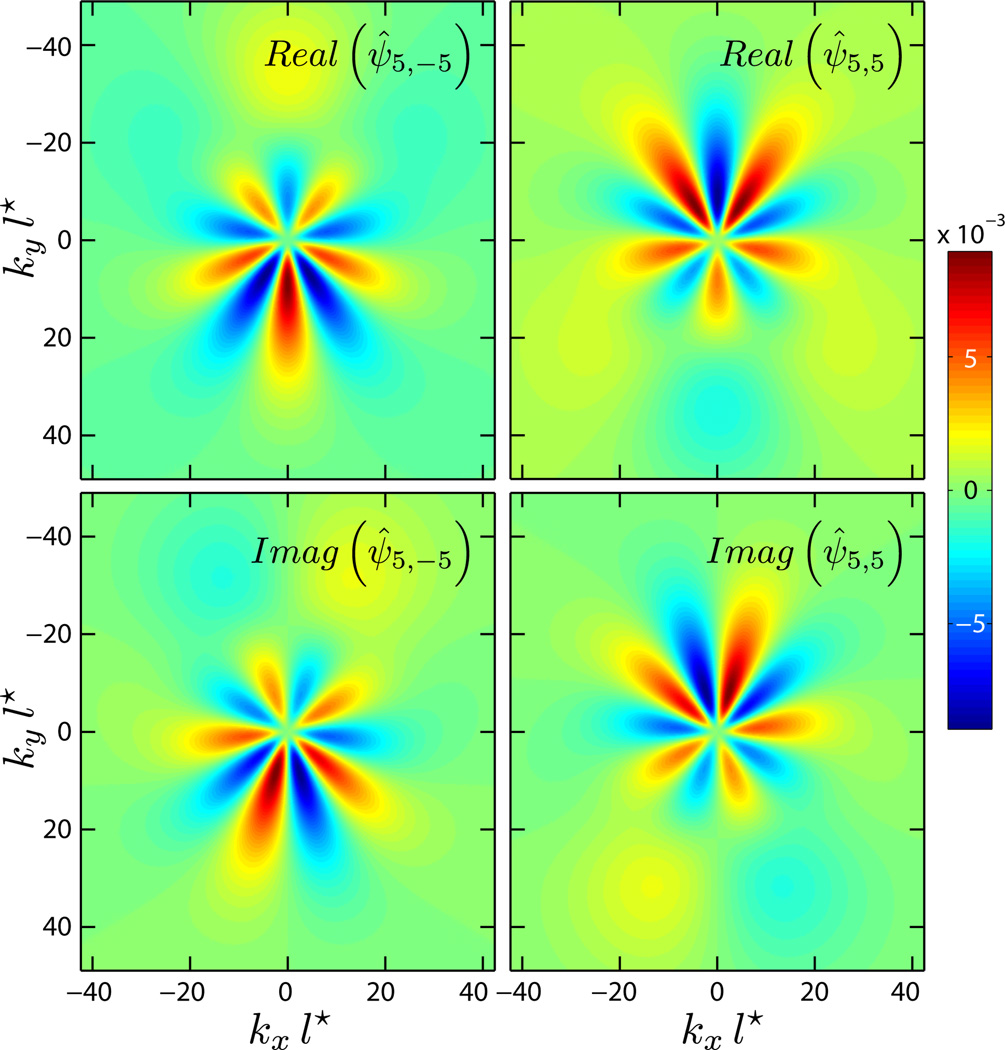
Figure 2 shows color contour plots of the real and imaginary components of ψ̂_5,±5, computed using SHEF₉. These plots show clearly that these TFMs satisfy the parity relations of Eqs. (24) and (25) and enables one to reduce the computation of the TFMs to a single quadrant, e.g., for k_x, k_y ≥ 0 only.

Figure 2.

(Color online) Contour plots displaying the real and imaginary components of the ψ̂_5,±5 TFMs at the surface (z = 0), displaying the intra- and inter-moment parity relations on the transverse wave-vector k. These plots are provided by SHEF₉ for θ_i = 45° and ${\mu }_s^{\prime }/{\mu }_a=100$.

IV. PROCEDURE TO COMPUTE SPATIALLY-RESOLVED RADIANT FIELDS

The procedure to evaluate the radiant field using the SHEF_N framework is segmented into three processes: (i) initialization, (ii) evaluation of frequency dependent solution in a single quadrant, and (iii) use of the single quadrant solution to obtain spatially-resolved radiance profiles.

Following the specification of an expansion order N, the Gaussian beam radius ρ with angle of incidence θ_i, and a set of optical properties {μ_a, μ_s, g, n}, the integrals of the boundary condition in Eq. (22) are computed for the given refractive index, n. Use of the azimuthal portion of the spherical harmonics orthogonality condition [Eq. (8)] gives 0 if m ≠ M. Then, Gaussian quadrature is employed to numerically integrate Eq. (22) with respect to μ for m = M, for odd instances of (Λ − M). Next, we compute the moments of the phase function g_ℓ, the extinction coefficients μ_t,ℓ, and the modified phase function g̃_ℓ, and evaluate the source moments q_ℓ,m(Ω₀) [Eq. (13)]. The final step of the initialization procedure populates matrix A and the frequency-independent portions of both matrix B and the source vector 𝒬̂ required in Eq. (16).

The procedure continues by evaluating the frequency-dependent TFM solutions for k_x, k_y ≥ 0. We choose the width and sampling of the frequency grid based on the Gaussian beam radius ρ and the cosine of the angle of incidence μ_i, so that the source term in Eq. (11) is adequately resolved. For the results below, we have set ${\mathit{k}}_{\text{max}}=4{\mu }_i\sqrt{5}/\rho {\mathit{k̂}}_x+4\sqrt{5}/\rho {\mathit{k̂}}_y$ and Δk = π/30k̂_x + π/(30μ_i)k̂_y. Then, for each frequency μ_d, B, and 𝒬 are evaluated, and we compute the particular solution coefficient (−μ_dA + B)⁻¹ 𝒬̂. Using A and B the generalized eigenvectors G and eigenvalues λ are computed using the QZ algorithm [34], and the eigenmodes for λ < 0 are retained. Next, the boundary conditions are employed to compute the unknowns C_j. The depth resolved TFMs are evaluated through Eq. (21), using Eq. (17) to evaluate the outlying moments ψ̂_N,±N.

Using the parity relations in Eqs. (24) and (25), the TFMs are determined over the entire transverse Fourier plane. Then, the spatially-resolved harmonic moments of the scattered radiance are computed via the inverse discrete Fourier transform

$${\psi }_{\ell ,m}(\mathit{r})=\frac{1}{4{\pi }^2}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{\psi ̂}}_{\ell ,m}(z|\mathit{k})\text{exp}[i(x{k}_x+y{k}_y)]\mathrm{d}\mathit{k}.$$ (26)

V. RESULTS

We examine spatial and angular radiant distributions provided by the SHEF_N framework for the case of a narrow collimated Gaussian beam of radius ρ incident at the origin on the surface of a turbid half-space. We consider various angles of incidence, θ_i, for a beam aligned in the x-z plane with ϕ_i = 0°. We present results for both N = 8 and 9 and consider two different sets of optical properties: ${\mu }_s^{\prime }/{\mu }_a=100$ and ${\mu }_s^{\prime }/{\mu }_a=1$, where the transport scattering coefficient, ${\mu }_s^{\prime }={\mu }_s(1-g)$, gives rise to the transport mean free path $l^{\star }=1/({\mu }_a+{\mu }_s^{\prime })$. We perform our analysis for a scattering anisotropy g = 0.8 and a relative refractive index n = 1.4 characteristic of a tissue/air interface [19, 24, 25]. Note that both the radiance and the spatial dimensions are non-dimensionalized relative to the transport mean free path ℓ*, such that the results for a given ${\mu }_s^{\prime }/{\mu }_a$ are scalable for different combinations of ${\mu }_s^{\prime }$ and μ_a that result in the ${\mu }_s^{\prime }/{\mu }_a$ ratio considered.

We compute the spatially-resolved reflectance and the angularly-resolved remitted radiance and compare these SHEF_N results with those provided by Monte Carlo simulations and/or the standard diffusion approximation. We simulated 10⁸ and 10⁹ photons for ${\mu }_s^{\prime }/{\mu }_a=100$ and ${\mu }_s^{\prime }/{\mu }_a=1$, respectively, where an increased number of photons is simulated for the latter case due to decreased scattering and increased absorption. Within the SHEF_N framework the reflectance equals the current of the scattered radiance crossing the boundary and is given by R(x, y) = −ψ_1,0(x, y, z = 0).

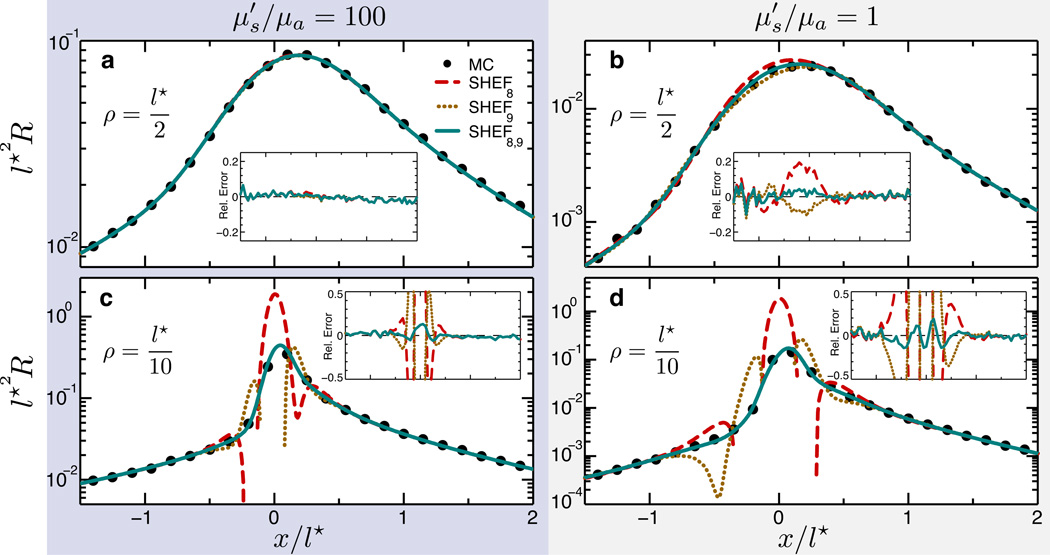
Figure 3 displays the spatially-resolved reflectance evaluated along the beam axis for an illumination angle θ_i = 45° for two beam radii ρ = [l*/2, l*/10]. For beam radius ρ = l*/2, the SHEF_N predictions show excellent correspondence with the MC results for ${\mu }_s^{\prime }/{\mu }_a=100$ (Fig. 3a). However for ${\mu }_s^{\prime }/{\mu }_a=1$ (Fig. 3b) the SHEF_N predictions close to the beam origin are inaccurate, especially at negative x-values. When the beam radius is reduced further to ρ = l*/10, reflectance predictions near the beam origin oscillate regardless of the optical properties (Fig. 3c,d). Truncation of the harmonic expansion at order N gives rise to these oscillations because they provide insufficient detail of the radiant field in regions where the transport is dominated by a sparse number of interactions with the medium. As a result, the deleterious effects of truncation are exacerbated when considering both narrow collimated sources and transport in weakly-scattering media, both of which result in radiant fields with high angular/spatial harmonic content. As a result, the spatial extent of the oscillations increases for weakly-scattering media as seen for ${\mu }_s^{\prime }/{\mu }_a=1$ (Fig. 3d).

Figure 3.

(Color online) Reflectance as a function of x at y = 0 for illumination with incident angle θ_i = 45° and beam radii ρ = l*/2 (a, b) and ρ = l*/10 (c, d). Comparison is provided for SHEF₈, SHEF₉ with Monte Carlo (MC) for strongly-scattering (${\mu }_s^{\prime }/{\mu }_a=100$) (a, c) and weakly-scattering (${\mu }_s^{\prime }/{\mu }_a=1$) (b, d) media. Also shown is the SOS extension SHEF_8,9 for all cases. The insets show the relative errors of SHEF_N with respect to Monte Carlo.

Since collimated illumination using beam radii smaller than the transport mean free path (ρ < l*) is a situation of high practical importance, these oscillations are not acceptable. To ameliorate these errors we take advantage of the observation that oscillations produced by sequential even-odd solution orders are completely out of phase. Thus, we introduce sequential-order smoothing (SOS) as the linear combination

$$L_{e,o}(\mathit{r},\mathbf{\Omega })=(1-\zeta )L_e(\mathit{r},\mathbf{\Omega })+\zeta L_o(\mathit{r},\mathbf{\Omega }),$$ (27)

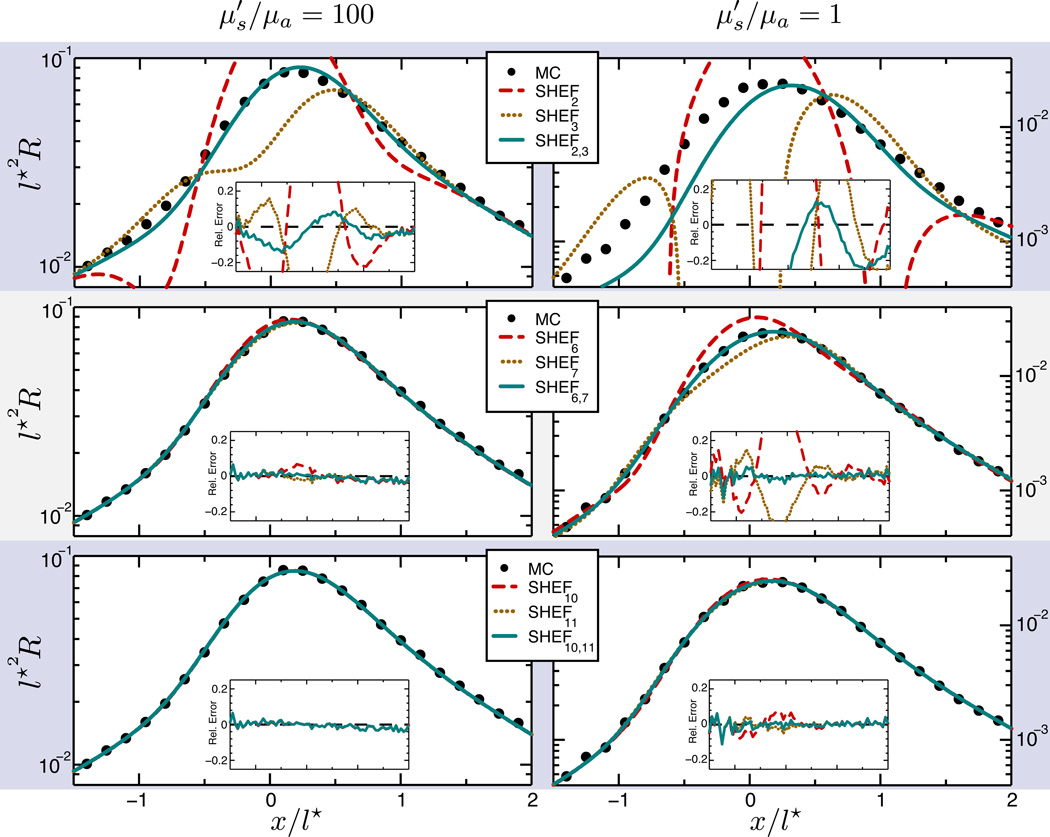
where the subscripts e and o represent the successive even and odd SHEF_N orders and ζ = (N_o+1)/(2N_o), where N_o is the odd expansion order. ζ weights the fraction of non-zero eigenvalues of the odd expansion order to the sum of non-zero eigenvalues of the successive even-odd expansions. We have found that SOS effectively removes these oscillations. Refined SHEF_8,9 reflectance predictions using SOS are also shown in Fig. 3, and clearly provide much better agreement with the MC results as shown in the inset plots for the relative error. Further SHEF_N results are provided for expansion order pairs [(2, 3); (6, 7); (10, 11)] in Fig. 4 with ρ = l*/2. These results show the improved accuracy of SHEF_N with increasing expansion order N. The additional improvement provided by SOS is most significant for low expansion orders and/or weakly-scattering media. Because SOS effectively removes the oscillations produced by SHEF_N, we are able to choose N solely on the desired level of accuracy. For what follows we will focus exclusively on presenting results for the narrow beam radius ρ = l*/10 using SHEF_8,9.

Figure 4.

(Color online) Reflectance as a function of x at y = 0 for illumination with incident angle θ_i = 45° and beam radius ρ = l*/2. SHEF_N results are provided for expansion order pairs [(2, 3); (6, 7); (10, 11)] and comparison is provided with Monte Carlo (MC) for strongly-scattering (${\mu }_s^{\prime }/{\mu }_a=100$) (left) and weakly-scattering (${\mu }_s^{\prime }/{\mu }_a=1$) (right) media. Also shown are the SOS solutions for each even-odd expansion order pair, and the insets show the relative errors of SHEF_N with respect to Monte Carlo.

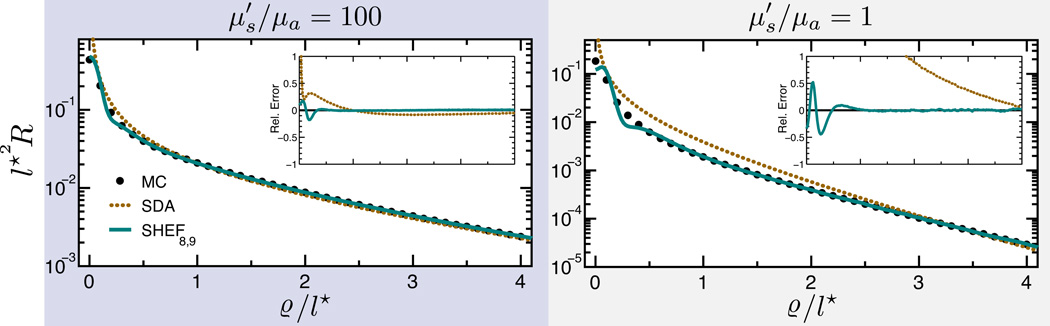
To appreciate the improved accuracy that the SHEF_N framework provides we consider the classic problem of spatially-resolved reflectance produced by normal beam illumination (θ_i = 0°). Figure 5 provides SHEF_8,9 predictions for this problem along with Monte Carlo simulation results and predictions by the standard diffusion approximation (SDA) using an extended source description [35, 36] in both strongly-scattering (${\mu }_s^{\prime }/{\mu }_a=100$) and weakly-scattering (${\mu }_s^{\prime }/{\mu }_a=1$) media. This approach accounts for the collimated illumination with an exponential distribution of image source dipoles rather than a point image source dipole.

Figure 5.

(Color online) Radially-resolved reflectance as a function of $\varrho =\sqrt{x^2+y^2}$ for illumination with a normally incident beam with radius ρ = l*/10. Comparison is provided for SHEF_8,9, standard diffusion approximation (SDA), and Monte Carlo (MC) for strongly-scattering (${\mu }_s^{\prime }/{\mu }_a=100$) (left) and weakly-scattering (${\mu }_s^{\prime }/{\mu }_a=1$) (right) media. The insets show the relative errors with respect to Monte Carlo.

These results demonstrate the significant benefits offered by the SHEF_N framework to predict these radially-resolved reflectance profiles. Specifically, for ${\mu }_s^{\prime }/{\mu }_a=100$, SHEF_8,9 provides greatly improved predictions at small radial locations (ϱ ≤ l*) as compared to the SDA. Moreover, the SHEF_8,9 solutions converge more rapidly to the MC results whereas the SDA predictions approach the MC results only for ϱ ≳ 4l*. For ${\mu }_s^{\prime }/{\mu }_a=1$ the SHEF_8,9 predictions are far superior to the SDA results at all radial locations. This is not surprising as is well-known that the SDA fails in situations where the reduced scattering is comparable to absorption [5, 22, 37]. By contrast, the SHEF_8,9 predictions in weakly-scattering media provide excellent accuracy for ϱ ≳ l*/2.

The use of the higher-order approximations provided by the SHEF_N framework, along with SOS, produce enhanced predictions of the radiance, the fundamental quantity of the ERT. Naturally when considering remitted optical signals, the radiance at the surface is the fundamental quantity for evaluation of the radiative flux captured by a detector with arbitrary orientation, dimension, and angle of acceptance. This remitted, or external, radiance, L_ex, at z = 0 (μ < 0) is computed from the scattered radiance, L_s,

$$L_{ex}(x,y,{\mu }_{ex},\varphi )=[1-r_F(-\mu )]L_s(x,y,\mu ,\varphi ),\text{on}z=0,$$ (28)

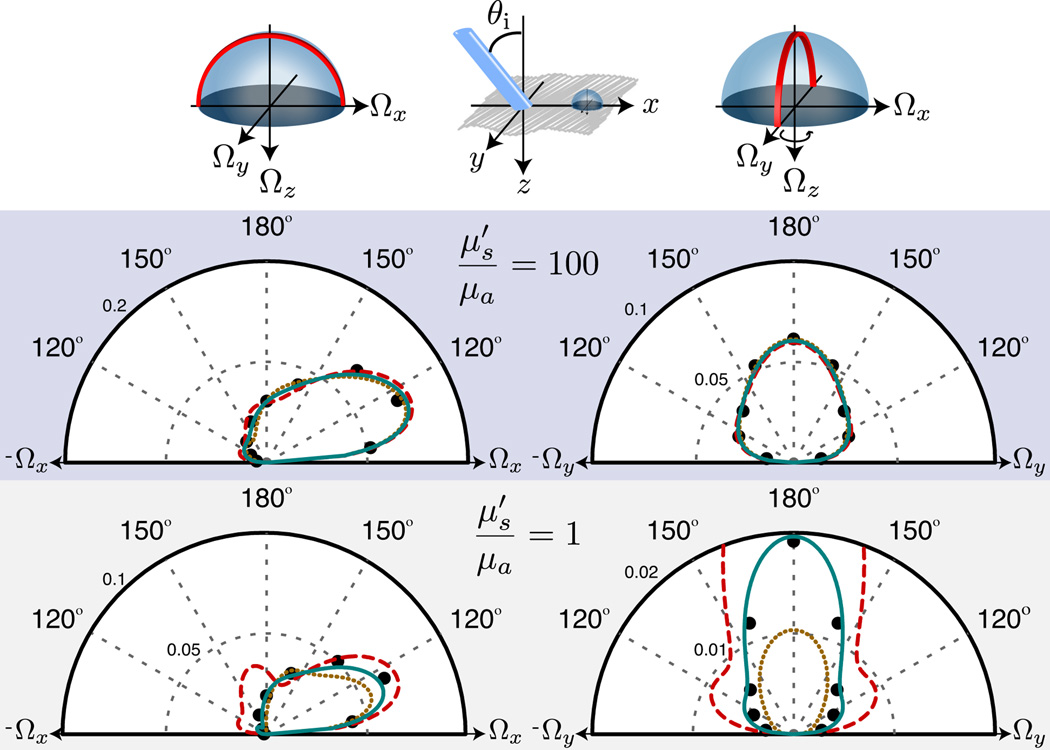
where the cosine of the polar angles μ and μ_ex are related through Snell’s law. Figure 6 displays angular distributions of the remitted radiance for Ω_x-Ω_z and Ω_y-Ω_z cross-sections provided by SHEF₈, SHEF₉, SHEF_8,9 and MC simulations at x = l*/2 on the beam axis for θ_i = 45°. It is important to note that the evaluation of the radiance using MC simulations is computationally costly, and yet provides the angular radiance profile only at discrete locations. While the truncation required to obtain SHEF₈, SHEF₉ predictions results in inaccurate and/or oscillatory predictions, application of SOS [Eq. (27)] provides an accurate, smooth, and continuous prediction for the angular radiance distribution. The results obtained at ${\mu }_s^{\prime }/{\mu }_a=100$ show that while the SHEF_8,9 prediction provides only a modest improvement in accuracy, it eliminates the significant oscillatory behavior displayed by both SHEF₈ and SHEF₉ predictions. By contrast, in the case of ${\mu }_s^{\prime }/{\mu }_a=1$, the heightened harmonic content of the radiance leads to inaccurate and highly oscillatory SHEF₈ and SHEF₉ predictions. However, the use of SOS dramatically improves both the accuracy and smoothness of the radiance profiles and yields predictions in excellent agreement with the MC results. Thus, application of SOS proves to be extremely valuable in providing accurate radiance profiles at these low orders.

Figure 6.

(Color online) Polar plots displaying angular distributions of the remitted radiance L_ex(θex) for Ω_x-Ω_z (i.e. ϕ = [0°, 180°]) (left) and Ω_y-Ω_z (i.e. ϕ = [90°, 270°]) (right) cross-sections at (x, y, z) = (l*/2, 0, 0) for an incident beam with radius ρ = l*/10 and angle θ_i = 45°. Results are provided for SHEF₈ (dashed red line), SHEF₉ (dotted gold line), SHEF_8,9 (solid teal line), and Monte Carlo (•) for strongly-scattering (${\mu }_s^{\prime }/{\mu }_a=100$) (top) and weakly-scattering (${\mu }_s^{\prime }/{\mu }_a=1$) (bottom) media.

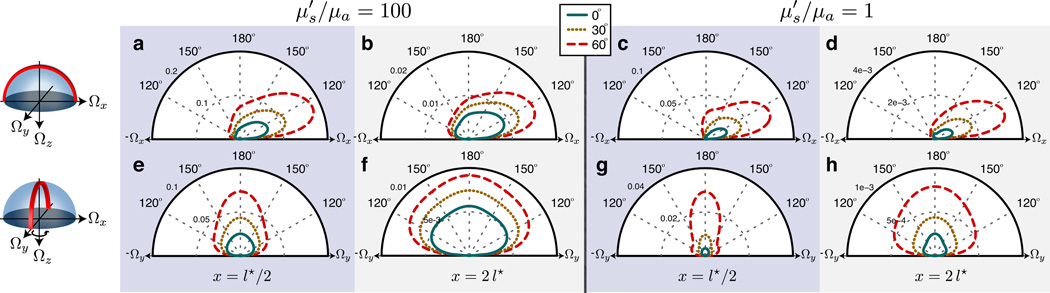
Figure 7 provides additional angular distributions of the remitted radiance for SHEF_8,9 at locations x = [l*/2, 2l*] on the beam axis, for incident beam angles of θ_i = [0°, 30°, 60°]. For locations proximal to the beam origin, variations in θ_i provide distinct angular spectra. However at locations more distal from the beam origin in strongly-scattering media (e.g., x = 2 l*, Fig. 7b,f), variations in θ_i have less impact on the angular spectrum. This displays the transition from a highly anisotropic radiant field close to the beam origin to a more diffusive field at more remote locations. By contrast, for weakly-scattering media at this same distal location, the effect of the illumination angle is preserved, and provides angular distributions which retain a high degree of anisotropy (Fig. 7d,h). Figures 3–7 exhibit the ability of SHEF_N combined with SOS to obtain accurate predictions, at relatively low approximation orders, for the complete radiance distributions at the surface of strongly- and weakly-scattering turbid media on spatial scales significantly smaller than the transport mean free path.

Figure 7.

(Color online) Polar plots displaying angular distributions of the remitted radiance L_ex(θ_ex) for Ω_x-Ω_z (i.e. ϕ = [0°, 180°]) (a–d) and Ω_y-Ω_z (i.e. ϕ = [90°, 270°]) (e–h) cross-sections provided by SHEF_8,9. Results are shown at proximal (x = l*/2) (a, c, e, g) and distal (x = 2 l*) (b, d, f, h) locations along the x-axis from an incident beam with radius ρ = l*/10 and illumination angles θ_i = [0°, 30°, 60°] for strongly-scattering (${\mu }_s^{\prime }/{\mu }_a=100$) (a, b, e, f) and weakly-scattering (${\mu }_s^{\prime }/{\mu }_a=1$) (c, d, g, h) media.

We have focused on radiance predictions at the surface because, apart from their importance for materials characterization, imaging, and remote sensing, the presence of the refractive index mismatch and optical property discontinuity makes them most difficult to predict. To visualize internal radiant fields, we examine both the scalar radiance, i.e. the fluence rate φ(r) = ∫_4π L(r, Ω) dΩ, and the full angular distribution of the radiance at discrete spatial locations. Recalling the radiant field inside the medium using SHEF_N is given by the superposition of scattered and collimated components, L(r, Ω) = L_s(r, Ω) + L_c(r, Ω), the fluence rate is

$$\phi (\mathit{r})={\psi }_{0,0}(\mathit{r})+\frac{2{\mu }_{\mathrm{i}}}{\pi {\rho }^2}\text{exp}\{-\frac{2}{{\rho }^2}[{\mu }_{\mathrm{i}}^2{(x-\text{tan}{\theta }_{0}z)}^2+y^2]-\frac{{\mathrm{\mu ̃}}_t}{{\mu }_0}z\},$$ (29)

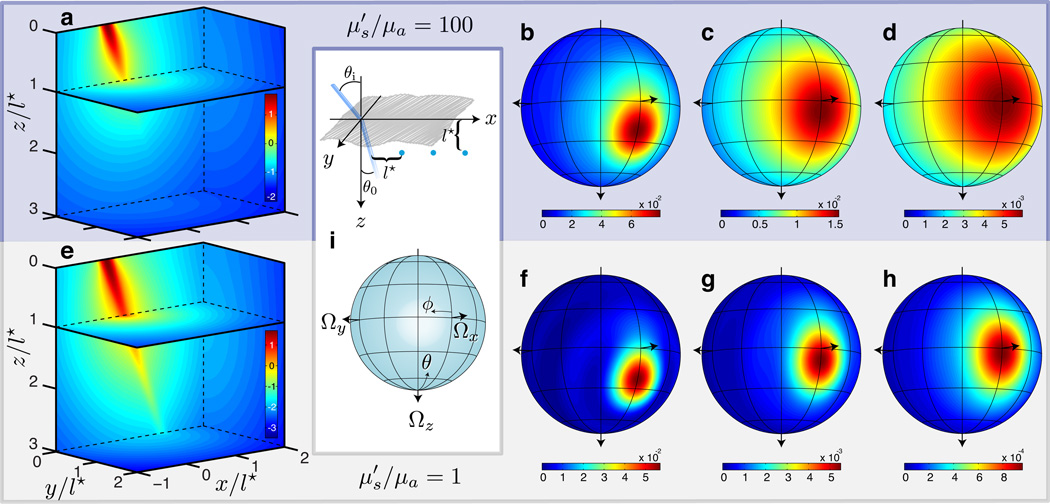
where, by definition, ψ_0,0(r) ≡ ∫_4π L_s(r, Ω) dΩ. Internal distributions are shown in Fig. 8 for the optical coefficients ${\mu }_s^{\prime }/{\mu }_a=100$ and ${\mu }_s^{\prime }/{\mu }_a=1$ for incident illumination angle θ_i = 30°. 3D spatial distributions of the scalar radiant field are displayed by various slices of the turbid volume (Fig. 8a,e). The spatial dispersion of the radiant field in weakly- versus strongly-scattering media is highlighted by the increased persistence of the collimated beam. Angular distributions of the radiant fields are shown at spatial locations on the beam axis at a depth of z = l* and transverse x-locations [l*, 2l*, 3l*] from the propagating collimated beam origin (viz. Fig. 8i). For strongly-scattering media (Fig. 8b–d), the radiant field at transverse locations more distal from the collimated beam display a stronger angular dispersion and demonstrates a transition towards a diffusive radiant field. Conversely, for weakly-scattering media (Fig. 8f–h), the angular spectrum of the radiant field remains much more localized at equivalent transverse locations. However, independent of the optical properties, the dominant propagation direction is comparable at equivalent locations, while the dispersion about this direction is reflective of the underlying sample turbidity. Moreover, it is important to note that all these radiance distributions lack azimuthal symmetry and thus cannot be predicted using P_N-based methods.

Figure 8.

(Color online) Internal radiant field distributions provided by SHEF_8,9 for an incident beam with radius ρ = l*/10 and illumination angle θ_i = 30° on strongly-scattering (${\mu }_s^{\prime }/{\mu }_a=100$) (a–d) and weakly-scattering (${\mu }_s^{\prime }/{\mu }_a=1$) (e–h) media. The 3D volumetric radiance distribution is displayed by the Log₁₀ fluence rate φ(r) (a, e) shown by an x-z slice at y = 0, x-y slices at z = [l*, 3l*], and a y-z slice at x = 2 l*. Angular radiant field distributions are shown at a depth of z = l* with y = 0 for x locations [l*, 2 l*, 3 l*] from the propagating collimated beam origin (b–d, f –h). The schematic (i) displays the corresponding spatial locations and the angular/directional coordinate system.

VI. CONCLUSIONS

The SHEF_N method provides an accurate and comprehensive framework for the prediction of both the internal and external radiances, L(r, Ω), produced by the illumination of turbid media with narrow oblique collimated beams. The use of the complete spherical harmonic expansion enables the consideration of problems that lack azimuthal symmetry. This provides capabilities far beyond the P_N approximation and are especially valuable for a broad number of applications in remote sensing, materials characterization, photorealistic rendering, and biomedical applications where the use of oblique illumination is common [6, 7, 17–21]. Moreover, the development of sequential-order smoothing (SOS) to combine SHEF_N predictions from successive even-odd expansion orders provides predictions with significantly enhanced accuracy. The use of SOS is shown to be particularly advantageous for beam radii smaller than l*, weakly-scattering media, and locations proximal to the beam. The improvements in accuracy and reduction in oscillatory behavior provided by SOS demonstrates this innovative approach to leverage two sequential low-order approximations to obtain solution quality that would otherwise only be accessible through the use of a much higher approximation order. Importantly, the use of SOS with any even/odd pair of sequential orders N and (N + 1) provides a higher quality solution than that provided by order (N + 2) but with lower computational cost.

We have demonstrated how the SHEF_N framework and SOS can be applied to obtain radiative transfer predictions that are accurate in both strongly- and weakly-scattering turbid media on mesoscopic spatial scales. As such, our results demonstrate that the SHEF_N framework provides a unified approach to predict and visualize the evolution of the radiant field from ballistic to diffusive regimes. Recent experimental and computational work has shown the importance of angular radiance distributions with regards to ascertaining optical properties on mesoscopic and macroscopic spatial scales [38, 39]. While a variety of approaches to obtain ERT solutions exist, including Monte Carlo (MC) simulations and the discrete ordinate method (DOM) [40, 41], the associated computational expense with these methods is large, especially when evaluating angular radiance distributions which lack azimuthal symmetry.

The comprehensive and systematic means by which SHEF_N provides complete internal and external radiance predictions makes it a powerful tool to explore issues concerning both a priori measurement design (forward problem) and a posteriori signal interpretation (inverse problem) in areas such as remote sensing and biomedical imaging. Additionally, methods that operate in the spatial Fourier domain, such as spatial frequency domain imaging [3], can directly employ the TFM solutions provided by the SHEF_N framework [Eq. (21)]. Extension to time-dependent problems can be achieved through a temporal-frequency-dependent total interaction coefficient without alteration of the overall solution approach. Layered media can be addressed by coupling region-wise solutions using additional boundary conditions at the media interface(s). Furthermore, because the SHEF_N framework provides complete representation of the spatial and angular characteristics of the radiance, one can leverage the general reciprocity property of the ERT. This enables an adjoint transfer mechanism to efficiently and accurately address both forward and inverse problems, such as optical tomography [5].