Modelling the Yeast Interactome

Abstract

The topology behind biological interaction networks has been studied for over a decade. Yet, there is no definite agreement on the theoretical models which best describe protein-protein interaction (PPI) networks. Such models are critical to quantifying the significance of any empirical observation regarding those networks. Here, we perform a comprehensive analysis of yeast PPI networks in order to gain insights into their topology and its dependency on interaction-screening technology. We find that: (1) interaction-detection technology has little effect on the topology of PPI networks; (2) topology of these interaction networks differs in organisms with different cellular complexity (human and yeast); (3) clear topological difference is present between PPI networks, their functional sub-modules, and their inter-functional “linkers”; (4) high confidence PPI networks have more “geometrical” topology compared to predicted, incomplete, or noisy PPI networks; and (5) inter-functional “linker” proteins serve as mediators in signal transduction, transport, regulation and organisational cellular processes.

As biological data accumulates at an ever increasing rate, the depth of our understanding of biological data has to keep up. Protein-protein interaction (PPI) networks are currently among the most available and studied molecular interaction data sets. A usual and intuitive way of representing these data is via graphs (or networks) where nodes are proteins, and edges — detected through interaction-detection wet-lab screening experiments¹,²,³,⁴,⁵,⁶,⁷,⁸,⁹ — are placed between them.

It is interesting that over a decade after the sequencing of human and yeast genomes has been completed, it is still unclear what the final size of those, and many other, interactomes will be. Recently, Stumpf et al. (2008)¹⁰ estimated interactome sizes of human and three eukaryotic organisms: they estimated the human interactome to have ≈ 650, 000 edges, C. elegans ≈ 200, 000 edges, D. melanogaster ≈ 75, 000 edges, and S. cerevisiae ≈ 25, 000–30, 000 edges. Their results indicated that the size of PPI networks of various organisms correlate well with the organism's apparent complexity, rather than the mere size of its genome.

The topology (i.e., structure) of a biological network is thought to be a by-product of stochastic chance and evolutionary necessity¹¹,¹²,¹³,¹⁴,¹⁵. On the other hand, there is a wide body of scientific evidence that contradicts the “chance and necessity” principle and corroborates the modular organisation of functions in biological networks¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵. To adequately model and analyse a network, we need to somehow understand this apparent “randomness coupled with evolution”. Yet, the issue of what networks in biology “look like” is still largely debated.

A network, therefore, typically represents a whole biological system; and modularity of a system refers to its ability to be broken down into smaller yet still cohesive sub-parts, often called “modules”²⁶,²⁷. There is a wide body of evidence which suggests that biological systems are comprised of distinct interacting modules¹⁸,¹⁹,²⁰,²¹,²⁵,²⁶,²⁷,²⁸. Identifying these distinct modules within biological systems is one of the essential steps in understanding cellular organization on a higher-level²⁵,²⁶,²⁹,³⁰. A module is often represented by a sub-network with more interactions between its elements than with elements of other modules. Still, inter-modular cross-talk is very prominent in PPI networks¹⁹,²³.

Techniques such as yeast-2-hybrid (Y2H), affinity purification (AP), mass spectrometric (MS) protein complex identification and many others are producing large amounts of experimental PPI data¹,²,³,⁴,⁵,⁶,⁷,⁸,⁹. These PPI data are publically available and stored in various databases such as the Biological General Repository for Interaction Datasets (BioGRID)³¹, IntAct³², Molecular INTeraction database (MINT)³³, Human Protein Reference Database (HPRD)³⁴, Biomolecular Interaction Network Database (BIND)³⁵ and the Database of Interacting Proteins (DIP)³⁶. Databases such as Search Tool for the Retrieval of Interacting Genes/Proteins (STRING)³⁷, Interologous Interaction Database (I2D)³⁸, and iRefIndex³⁹ combine large portions of the above-mentioned sources into single datasets. Since available PPI data sets still have high false-discovery rates²⁴,⁴⁰, we analyse data sets obtained from the following 16 PPI detection technologies³¹: affinity capture-luminescence (hereafter denoted by “acl” for brevity), affinity capture-MS (“acms”), affinity capture-RNA (“acrna”), affinity capture-western (“acw”), biochemical activity (“ba”), co-crystal structure (“cocs”), co-fractionation (“cof”), co-localisation (“col”), co-purification (“cop”), far western (“fw”), FRET (“fret”), PCA (“pca”), protein-peptide (“ppep”), protein-RNA (“prna”), reconstituted complex (“rc”) and yeast two-hybrid (“y2h”). However, some of these 16 biotechnologies generate very sparse PPI data (explained below), hence in the main text of our manuscript, we focus on the results of only those biotechnologies that produce PPI networks which are sufficiently dense to be modelled (Figure 1). Also, note that while “acrna”, “col” and “prna” are not PPIs in their strictest form, they are akin to PPIs and BioGRID classifies them into the physical protein interaction category alongside the rest of the PPI data (http://wiki.thebiogrid.org/doku.php/experimental_systems).

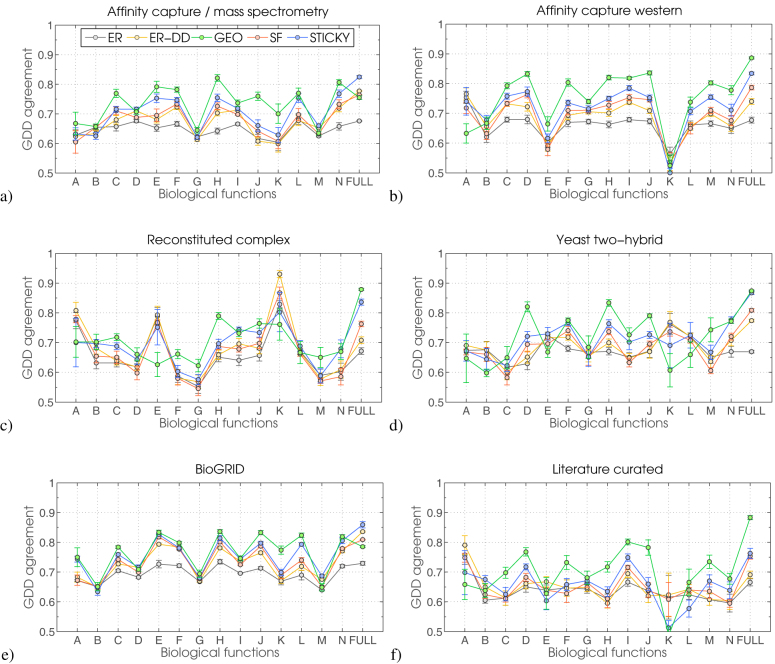
Figure 1. The fit of random graph models to yeast PPI networks.

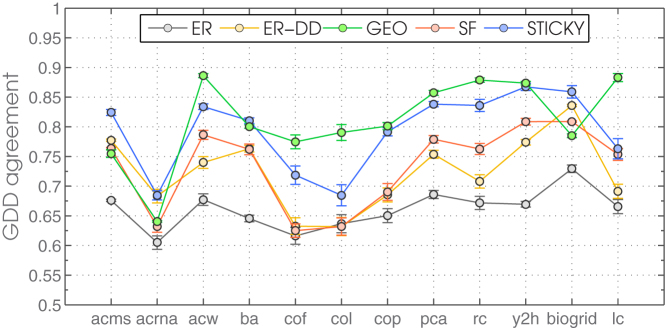
The fit of five random graph models (ER, ER-DD, GEO, SF and STICKY) to yeast PPI networks. The first 10 PPI networks listed on the x axis are extracted from BioGRID according to their evidence codes and labelled as described in the introductory section above. Label “biogrid” denotes a network comprised of all PPIs from BioGRID. Label “lc” denotes a network comprised of a literature curated set of PPIs from Reguly et al. (2006)⁵⁵.

In this paper, we study in depth the modelling of yeast S. cerevisiae PPI networks, as these are currently the most complete and accurate interaction networks. For evaluating the fit of model networks to PPI data, we use a range of six global and local network properties (detailed in Methods). Since they all give consistent results, for space constraints we present only the results of Graphlet Degree Distribution Agreement (GDDA) similarity measure (detailed in Methods; see Supplementary Text for other similarity measures). Also note that GDDA encompasses other network similarity measures (see Methods).

Although there were attempts to quantify the dependence of a network's structure on a given set of features such as age, or abundance of proteins in a cell¹⁴, none of them explored the dependency of network models on interaction-detection biotechnology. Also, to our knowledge, no other study addresses biotechnology-dependant modelling of functional sub-modules in PPI networks. Two recent papers dealt with characterising degree distributions of yeast transcriptional regulatory networks, and attempted to identify and explain microscopic features of human regulatory networks, such as motif patterns and highly connected network elements⁴¹,⁴². Other similar studies undertook dynamical modelling of regulatory networks using state-transition graphs while specifically focusing on regulatory control of T-helper cell activation and differentiation⁴³; or tested for simple edge overlaps between only two data sets: yeast two-hybrid and literature curated data sets⁴⁴.

There were a couple of attempts to model full PPI networks of yeast, fruit fly, worm and human⁴⁵,⁴⁶,⁴⁷; however the aim of those studies was not to quantify the topological features of PPI networks produced by different interaction-detection technologies, but rather to determine the best fitting theoretical model for various model organisms. Conversely, a study by Fernandes et al. (2010)⁴⁸ aims to quantify methodological biases in experimental data using a newly proposed measure for PPI network comparison. They find that only sufficiently large PPI data can be used for inter- and intra- species comparisons using the mentioned novel measure based on normalised correlations between node degrees, which is largely similar to one of the five random network models that we use, namely, the STICKY random model. In addition, they use a model akin to the degree distribution preservation model (ER-DD) used in our study as the only random model against which they compare, and some of the data sets they use are currently outdated by ten years or more. Moreover, the PPI data analysed in most of the above mentioned studies is now largely outdated and thus our work offers analysis on up-to-date yeast PPI data, comprising of roughly 75,000 interactions between almost 6,000 proteins. Also, unlike any of the previous studies, we dissect and model PPI data in several ways: 1) we examine networks created from all available protein-protein interaction data; 2) we examine sub-networks (modules) based on cellular functions; 3) we examine sub-networks based on interaction screening biotechnology; 4) we examine sub-networks based on the combination of cellular functions and interaction screening biotechnology; 5) we examine functional diversity between intra- and inter- function protein interactions; and finally, 6) we contrast the observed yeast results with those obtained for the human PPI data.

Ultimately, our work aims to shed new light in search for general principles that give rise to the structure and organisation of interaction networks²¹,⁴⁹.

Results

We analyse current yeast protein-protein interaction (PPI) networks using random graph models with the same number of nodes and edges as the data. We apply five most commonly used network models for modelling PPI networks (see Methods for details on these random models): Erdös-Rényi random graphs (ER)⁵⁰, Erdös-Rényi random graphs with the same degree distribution as the data (ER-DD)⁵¹, Geometric random graphs (constructed using 3-dimensional Euclidean space, denoted by GEO)⁵², Scale Free Barabási-Albert type networks (SF)⁵³ and stickiness-index based networks (STICKY)⁵⁴. To rule out any potential bias of random graph models towards a particular interaction-screening technology, we present the modelling results obtained for different yeast data sets (see Methods for details on the yeast data): 16 sub-networks of BioGRID based on different PPI detection biotechnologies; one network comprised of all PPIs available in BioGRID³¹; and one which represents a set of literature curated interactions⁵⁵.

As mentioned above, we use a range of six network properties to measure the fit between models and data, and they all yield consistent results. We find the yeast PPI networks to be best fit by GEO and STICKY random graph models (Figure 1): STICKY provides the best fit for the full PPI network from BioGRID and the “acms” network, it is tied with GEO to provide the best fit for “ba” and “y2h” networks, while GEO provides the best fit for all other data including the literature curated PPI network⁵⁵. Since “acms” and “y2h” have high coverage (81% and 60% of all proteins in BioGRID, respectively), and the literature curated data are likely of high confidence, it may be argued that STICKY fits higher coverage while GEO fits higher confidence data the best. However, if this is the case, it is not clear why “acw” and “rc” — which are also of high coverage (including 49% and 36% of all proteins in BioGRID, respectively) — are best fit by a GEO model.

GEO random graph model has previously been shown to model yeast PPI networks well⁴⁶,⁵⁶. STICKY random graph model is based on the normalised degree of a node and captures the fact that a pair of proteins is more likely to interact if both proteins have high stickiness indices than if this was not the case and it has also been shown to model PPI networks well⁵⁴. In Figure 1 and in all subsequent figures containing results of random graph modelling, the plots contain points and error bars, which correspond to the obtained averages of model-to-data fit, and standard deviations, respectively.

Note that this study is extensive in that it is based on the analysis of close to 20 million networks — including original PPI data, model networks and robustness and rewiring experiments. Testing what effect different inference models (e.g., spoke versus matrix models), or different types of experiments (e.g., high- versus low- throughput) have on PPI network topology is beyond the scope of this paper and could be done as a future follow-up study.

Next, we ask whether any topological difference exists between the PPI network as a whole and its sub-networks containing only one biological function, or whether any topological difference exists between sub-networks containing different biological functions. To this end, we extract and model functional sub-networks of yeast PPI data. Interestingly, we find that: (1) functional sub-modules tend to be organised geometrically regardless of their biological function, while (2) “communication links” between them tend to be STICKY (see below for details). Note that when modelling the yeast data, we noticed that some of the resulting functional sub-networks are very small and sparse so that they fall under a “region of instability” recently described in Hayes et al. (2013)⁵⁷. In brief, what that region suggests is that when a network is small and sparse (i.e., has a small number of nodes and edges), the structure of model networks of that size and density is unstable, so a model cannot be fit to such data. The following sections describe the structure of the yeast's functional sub-modules and their “linkers”.

Linked functional sub-modules of PPI networks

We extract functional sub-modules from yeast PPI data based on a functional annotation recently used in Costanzo et al. (2010)⁵⁸. This gives us 14 categories of biological function from which we can create functional sub-networks (see Methods for details on functional categories and their corresponding sub-networks). When extracted from full yeast PPI networks (“acms”, “acw”, “rc”, “y2h”, literature curated and BioGRID), most functional sub-networks are best modelled either by GEO or STICKY random graph models (Figure 2). However, many functional sub-networks that are neither GEO nor STICKY are, in fact, insufficiently large to be modelled accurately (i.e., fall into the “region of instability” described above, resulting in large error bars over all five random models).

Figure 2. The fit of random graph models to yeast PPI functional sub-networks.

We present results for four different biotechnologies — (a) “acms”, (b) “acw”, (c) “rc” and (d) “y2h” — as these data sets produce functional sub-networks dense enough to be modelled with confidence (explained above). Together, these four cover over 90% of all interactions in BioGRID (e). The literature curated set of PPIs⁵⁵ (f) also contains sufficient PPI data for all 14 functional subnetworks to be induced on it. On the x-axis, label FULL denotes the complete yeast PPI network (named in the panel's title) and labels A, B, C, …, N denote sub-networks of FULL broken down according to biological functions.

In all networks except for BioGRID, functional sub-networks “A” and “B” (i.e., “cell cycle progression/meiosis” and “nuclear-cytoplasmic transport”; see Supplementary Table ST2 for a full list of used biological function categories) have around 50 nodes and interactions, and should be disregarded when viewing the results since such tiny (sparse) networks cannot be modelled with confidence as previously described (we include it for completeness). The same holds true for modules “E”, “G”, “K” and “L” of the “y2h” and “literature curated” networks; modules “E” and “K” of the “rc” network; and module “K” of the “acw” network. Still, a consistent topological structure for functional sub-modules emerges (Figure 2): GEO networks provide the best fit for all functional sub-modules in PPI networks (irrespective of biotechnology) while STICKY is a competitor to GEO only for BioGRID data (Figure 2 e).

This suggests that yeast proteins which belong to functional modules within a PPI network are organised geometrically, while the PPI network that includes all available PPI data has both STICKY and GEO structure (Figures 1 and 2); we confirm the robustness of this modelling approach by randomly swapping node IDs, thus conserving all topological properties of the networks (see Figure SF3 in Supplementary Information). In contrast, we find that proteins linking functional sub-modules contribute to STICKY topology of the PPI network. These “linker” proteins may or may not be functionally annotated; if they are, then they are not physically interacting with proteins belonging to their functional sub-module, but with proteins belonging to other functional sub-modules (illustrated in Supplementary Figure SF1; see Discussion for more details on this). This GEO-STICKY topological duality in PPI data is easily seen by comparing degree distributions of intra- and inter-functional proteins (Figure 3). The degree distribution of all proteins within the network follows a power-law (blue circles in Figure 3) which indicates the presence of hubs. If we then break all proteins into two sets — intra- and inter- functional proteins, i.e., those that interact with proteins of the same function (green triangles in Figure 3) and those that do not (red squares in Figure 3), respectively — we see that intra-functional proteins have Poisson degree distribution just as GEO networks have (confirming that functional modules are GEO), while the degree distribution of inter-functional “linker” proteins follows a power-law as does the degree distribution of the entire PPI network. This means that the majority of cross-functional “linkers” are of lower degrees, i.e., make a link between single proteins in different functional modules, but that there exists a small number of “linkers” that provide high connectivity between functional modules (illustrated in Supplementary Figure SF1).

Figure 3. Degree distributions of intra- and inter- functional proteins.

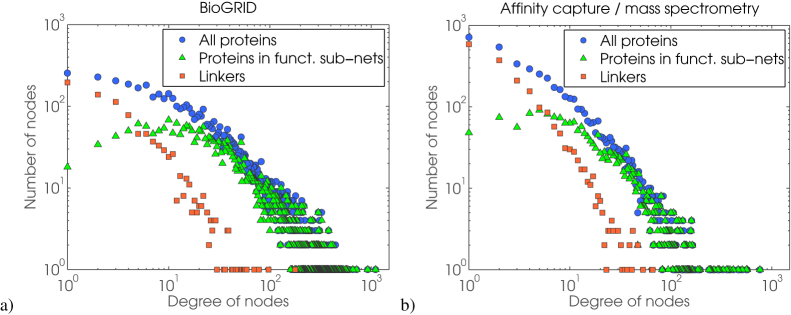
A log-log scale shows three degree distributions: – all proteins in a network, – proteins in functional sub-networks (intra-functional), and – “linker” proteins (inter-functional). Left panel shows degree distributions for the full BioGRID network. Right panel shows degree distributions for interaction data from affinity-capture coupled with mass spectrometry. We show only two data sets here, but we've verified that all PPI screening biotechnologies (listed in the introductory section) yield the same degree distribution patterns.

In addition, we find that “linkers” are almost exclusively disordered proteins — also known as intrinsically unstructured, or naturally unfolded proteins — whose lack of a fixed tertiary structure is said to be key to their diverse binding abilities (binding to enzymes, signalling receptors, regulators, etc.). We do this by comparing them against databases of known disordered proteins: MobiDB⁵⁹, IDEAL⁶⁰, and DisProt⁶¹. Also, we find “linkers” to be significantly (p-value ≤ 0.05; all p-values were adjusted using Benjamini-Hochberg multiple-hypothesis testing procedure) involved in:

• signal transduction (e.g., membrane trafficking, cell surface receptors).

• regulatory processes (e.g., biosynthesis, metabolism, transcriptional control).

• transport (e.g., trans-membrane, vesicle-mediated).

• organisation of membrane, chromatin, chromosomes, cytoskeleton, actin, macromolecular complex subunits, vesicles, mitochondrion, spindle, peroxisome and nuclear pores.

• modification of chromatin, histones and small proteins.

Interestingly, the disordered nature and, consequently, biochemical properties of “linkers” are ideal for exactly these types of biological functions — i.e., for mediating molecular interactions, for quickly initialising the signalling process, and for orchestrating regulatory and organisational events.

PPI network topology is independent of interaction-detection biotechnology

We showed above that the topology of functional sub-modules of PPI networks is geometric and that communication between them is done by disordered signalling, regulatory, or organisational proteins of relatively low connectivity. We test if this GEO-STICKY duality depends on the biotechnology used for detecting PPIs. Surprisingly, we observe the same GEO-STICKY duality across all screening biotechnologies.

In particular, we modelled 18 yeast PPI networks detected by different biotechnologies (Figure 1): 16 protein-protein interaction detecting methods listed above, 1 that combined all interaction-detecting methods, and 1 literature curated network of higher confidence. Surprisingly, different biotechnologies consistently produce PPI networks that are best fit by GEO or STICKY network models. In particular, out of those, six PPI networks are small and sparse so they fall into the region of instability (“acl”, “acrna”, “fw”, “fret”, “ppep” and “prna”) and could not be modelled with confidence. The remaining twelve PPI networks are either GEO or STICKY or in-between. In other words, the topology of the interactome seems not to be biotechnology-dependant.

Discussion

Whether the above-described results hold true across species is a subject of future research. Since the human PPI network is the second most studied, we check if similar holds for it as well. Indeed, we find that human interactome largely agrees with the above findings for yeast. However, the human PPI network seems to be “more sticky” than the yeast PPI network. As a source of human PPI data, we used Interlogous Interaction Database (I2D, http://ophid.utoronto.ca/). The dataset version is 2.0 and was obtained in October 2012. We included in the analysis the three variants of the I2D database:

• The network containing the complete set of all experimental and predicted interactions from I2D; it has 171,580 interactions between 14,745 proteins; we denote it by I2D-FULL.

• The network containing only the high-confidence experimental interactions, where we consider high confidence to be all interactions verified by at least two sources from which I2D got the data (so, this excludes orthology-based predicted interactions that exist in I2D-FULL, as well as low confidence interactions which come from a single source). This network, denoted by I2D-HC, contains 41,143 interactions between 9,647 proteins. Note that each publication is considered a unique “interaction supporting source”, but in some cases it might be possible that two publications with different PubMed (http://www.ncbi.nlm.nih.gov/pubmed) identifiers and with a number of years between them refer to a similar or updated version of the same initial data set — in this case it could be argued that the detected interaction is supported by only one rather than two sources and thus introduces a slight mismatch between the expected and actual HC data set; however since tracking such database changes cannot be automated, the community standardly defines high-confidence interactions as we do here.

• The third network (denoted by I2D-PRED) contains only predicted interactions; it has 59,898 interactions between 6,704 proteins.

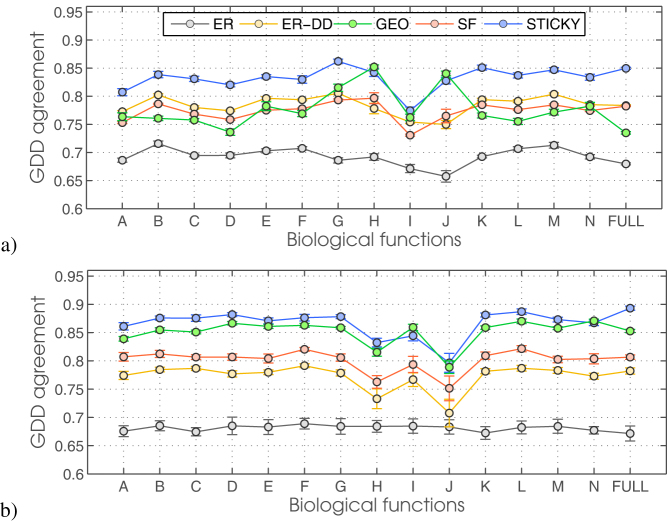
Specifically, the full network of human PPIs that includes predicted interaction (I2D-FULL) is best modelled by STICKY model followed by ER-DD and SF. Interestingly, the fit of STICKY to the network containing predicted interactions only (I2D-PRED) is as good as to the entire human PPI network (I2D-FULL) that contains predicted interactions, while if we exclude predicted and low confidence interactions from the network (I2D-HC), the fit of GEO improves (Supplementary Figure SF2). Hence, the topology of the full human PPI network seems to be dominated by predicted and low confidence interactions. Furthermore, analogous to the breakdown-by-function that we performed for yeast data, we model the functional sub-networks in I2D-FULL and I2D-HC human PPI networks. In total, this gives us 30 networks to analyse: 2 full PPI networks (I2D-FULL and I2D-HC) and 14 functional sub-networks for each of those two full PPI networks (see Methods for details on 14 functional categories for annotating human proteins). Unlike for yeast, we find that the full human PPI network (I2D-FULL) has mostly STICKY functional sub-modules: 11 out of 14 functional sub-networks are STICKY, while the remaining 3 are split between GEO and STICKY (see Figure 4). Interestingly, for the high confidence part of the human PPI network, the topology of the functional sub-networks is, just like in yeast, “more geometric”: 5 out of 14 were split between GEO and STICKY, while the remaining 9 had a marginal difference between GEO and STICKY. Hence, while the experimentally derived human PPI network has the topology of functional sub-modules very resemblant of that in yeast PPI network, these results may indicate that low confidence and interlogously predicted human PPIs may need to be re-examined.

Figure 4. The fit of random network models to functional sub-networks of two human PPI networks.

Top panel: full I2D network (I2D-FULL). Bottom panel: high confidence part of the I2D network (I2D-HC). The plot for I2D-PRED is almost identical to that of I2D-FULL, hence we do not include it.

Additionally, we found the “linkers” in the human PPI network to be enriched (p-value ≤ 0.05; all p-values were adjusted using Benjamini-Hochberg multiple-hypothesis testing procedure) in proteins from the Rab protein family, in particular, those involved in regulation of Rab GTPase activity and regulation of Rab protein signal transduction. Interestingly, the Rab protein family is an “umbrella term” for all the GO terms that we found in yeast's “linkers”. It is a member of Ras protein superfamily which consists of G-proteins functioning as an “on/off” switch for cellular processes. Ras is activated by G-protein coupled receptors (GPCRs) and regulates cell behaviour by signal transduction and is also involved in cytoskeletal dynamics and morphology, as well as membrane trafficking. We speculate that the reason for which we find “linkers” to be currently isolated from intra-functional proteins could be down to the hydrophobic nature of GPCR proteins, which reduces the ability of high-throughput screening to detect protein interactors of GPCRs.

Proteins that link multiple network disease-modules are considered to be effective drug-targets since, beside being independently regulated from the proteins belonging to a single module they are mostly non-hub nodes, and targeting non-hub nodes is crucial in mitigating unwanted side-effects of drug therapy⁶². Even more generally, nodes which link network modules of any kind provide cross-talk between signalling pathways which is an especially attractive property of putative drug targets. Hence, we show that topological properties of functional sub-networks in yeast and human interactomes are quite similar and linked with proteins whose function is preserved between yeast and human, and whose further exploration as effective drug-targets with controllable side-effects could potentially yield novel insight for pharmaceutical drug development.

Methods

Yeast protein-protein interaction data

For modelling the PPI network of baker's yeast (S. cerevisiae), we use data from BioGRID³¹ downloaded in October 2012 (version 3.1.93). Also, we use a set of literature curated PPIs from Reguly et al. (2006)⁵⁵ which we consider to be a “high confidence” set of PPIs.

Based on experimental evidence codes assigned to each interaction in BioGRID, we extract 16 networks of physical interactions (Supplementary Table SF1). In addition, we include a network based on the full set of BioGRID PPIs, which has 5,981 nodes and 74,542 edges. Together with the “high confidence” PPI network mentioned above, this gives us 18 yeast PPI networks (16 based on different biotechnology, 1 full from BioGRID and 1 high confidence from literature curation).

Yeast networks based on functional categories were constructed as follows. For each of the 18 above-described networks, we extracted functional sub-networks in order to see whether there is any variation in the topology of different functional sub-units within a cell and whether that variation could be attributed to experimental technology that produced them. Functional annotation of yeast proteins that we use represents an updated version of the annotation used by Costanzo et al. in their 2010 paper “Genetic landscape of a Cell”⁵⁸. The annotation covers 75% of proteins in BioGRID and separates them into 14 categories based on biological function (Supplementary Table SF2). We construct a subnetwork on a given function X by taking nodes annotated with that particular function and all edges between them (i.e., we construct an induced sub-graph on nodes involved in function X). This results in 270 distinct yeast networks: 18 above-described PPI networks plus each of those 18 PPI networks broken down into 14 functional categories (18 + 18 × 14 = 270).

Functional annotation of human proteins

If we want to model the functional sub-modules of the human interactome and compare their structure with those of yeast, we first need to find an appropriate protein-function annotation which is comparable to that given by Costanzo et al. (2010)⁵⁸ for the yeast interactome. Gene Ontology (GO, http://www.geneontology.org/) offers a directed acyclic graph (DAG) of biological functions along with a functional annotation for the human interactome. However, it contains hundreds of functional categories, which are based on a many-to-many annotation scheme: many proteins have multiple functional annotations, some proteins hundreds, or even thousands of annotations. The somewhat condensed version of GO functional annotation, GO Slim, was still too broad for our purposes, having around 100 functional groups and still being a many-to-many annotation scheme. Hence, we used GO Slim categories from Mouse Genome Informatics (MGI, http://www.informatics.jax.org/gotools/data/input/map2MGIslim.txt) which are specifically built to be consistent with the human GO annotation (GOA), and are much more concise than human GO Slim: there are 14 functional categories similar to those we use for yeast. We consider this annotation to be sufficiently compact for the purposes of modelling the human interactome and comparing the results to those obtained when modelling the yeast interactome (see Supplementary Table SF3 for a list of functional categories).

Random model fitting

To get insight into the structure (topology) of the PPI sub-networks, we compare them with different random network models. We construct random model networks with the same number of nodes and edges as the data. For modelling the PPI networks described above, we take into consideration five most commonly used network models:

• Erdös-Rényi random model (ER) represents uniformly distributed random interactions. An ER network is constructed by generating a fixed number of nodes and then randomly adding edges between uniformly chosen pairs of nodes, until the desired number of edges is reached⁵⁰.

• Generalized random model (ER-DD) represents an extension of the ER model in that the degree distribution of the nodes in the generated network matches the degree distribution of the nodes in the input network. An ER-DD network is constructed as follows. Each node is first assigned a “connection capacity”, after which edges are uniformly placed between randomly chosen pairs of nodes and their available “connection capacities” are reduced⁵¹.

• Geometric model (GEO) captures the spatial proximity relationships between nodes uniformly distributed inside a n-dimensional space⁵². We construct GEO network in 3-dimensional space by placing an edge between two nodes if the Euclidean distance between them is within a distance threshold, .

• Barabási-Albert Scale-free (SF-BA) model represents networks with power law degree distributions (i.e., scale-free topology). A SF-BA network is constructed from a small initial seed network and nodes are added iteratively: new nodes are attached to existing ones based on attachment probabilities, which, in turn, correspond to the degrees of existing nodes⁵³.

• The Stickiness-index based model (STICKY) is based on the assumption that the higher the degrees of two nodes, the more likely they are to interact⁵⁴. A STICKY network is constructed by randomly assigning stickiness-index values to all nodes. These values are proportional to degrees of nodes in the input network. Then, pairs of nodes are connected with the probability corresponding to the product of their stickiness-indices.

For each of these five random network models corresponding to each of the 300 data sub-networks (270 yeast networks described above and 30 human networks described in the main text), we generate 30 model networks. This produces 45,000 random model networks: 300 (yeast and human PPI networks) × 5 (random models) × 30 (network instances for each random model) = 45, 000 networks of the size of yeast and human PPI networks. To see which model fits the data, we measure the similarity between all our networks (human and yeast) and each of the 150 model networks (30 × 5 = 150 of them per data network) by computing the GDD-agreement between them (see below for details on GDD). We compute the average and standard deviation of the GDD agreement between the data networks and all of the 30 generated instances of one network model, and we do this for each of the five random network models.

Testing the robustness of the modelling approach

We test the robustness of the approach for random networks applied to functional sub-modules by swapping a percentage of IDs of nodes (10%, 20%, …, 100%) and computing the GDD agreement with all five random models. We create 50 sub-network instances for each of the 10 “rewiring steps” (e.g., 50 sub-network instances with 10% of nodes IDs are swapped in the original network, 50 sub-network instances with 20% of node IDs swapped in the original network, etc.); and for each rewired instance we compute 30 model instances of each of the five random network models. As this produces an extremely large number of networks — 18 networks (16 biotechnology networks, 1 full BioGRID network and 1 literature curated) × 14 (functional submodules) × 10 (rewiring steps from 10% to 100% in 10% increments) × 50 (instances of a rewiring) × 5 (random network models) × 30 (model instances) = 18, 900, 000 networks — and is computationally unfeasible to compute in a reasonable amount of time (we would need to generate almost 20 million random network models, compute graphlet and orbit counts for each of them, and then finally compute the GDDA score), thus we focused on three largest and most representative networks instead of all 18: affinity capture/mass spec, yeast two hybrid, and the full BioGRID network. The results are consistent across the three data sets: as the node IDs get increasingly permuted, the geometricity of the functional sub-modules drops (GEO model), while the topological randomness increases (ER and ER-DD); this is more apparent on sub-modules that have sufficient nodes and edges to be outside of the “region of instability” and be modelled with confidence (see caption under Figure SF3 for details).

Measuring network similarity

For modelling the PPI networks, we use a range of global (degree distribution, clustering coefficient, shortest paths, diameter, radius) and local (Graphlet Degree Distribution Agreement, GDDA) network properties to determine the fit between real and model data. Below, we give a brief explanation of each network property used.

• Degree of a node in a network is the number of connection is has to other nodes in the network.

• Degree distribution of a network is a probability distribution of degrees of all nodes in a given network. If P(k) is the percentage of nodes in the network that have degree k, then the degree distribution is the distribution of P(k) for all values of k.

• Clustering coefficient, C_i, of a node i is the proportion of the number of edges between its neighbours, E_i, and the maximum number of edges that could exist between the neighbors: 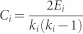, where k_i is the number of neighbours of i, i.e., the degree of node i. The average clustering coefficient is defined as the average of the clustering coefficients of all the nodes in the network: 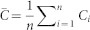, where n is the number of nodes in a network⁶³.

• Shortest path between two nodes, u and v, is the minimum number of edges that have to be traversed to get from u to v. The length of a shortest path between u and v is the distance from u to v.

• Eccentricity of a node v, 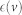, is the largest distance between v and any other node in the network.

• Diameter is the maximum eccentricity over all nodes in a network: .

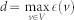• Radius is the minimum eccentricity over all nodes in a network: .

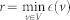• Graphlet degree distribution agreement (GDDA) is a measure which shows how similar the structure of two networks is. It is based on counting the occurrences of all small induced subgraphs with k nodes, graphlets, where k ∈ {2, 3, 4, 5}. By definition there are 73 grpahlet degree distributions (GDDs) for each data-to-model comparison. The distributions are scaled and normalized so that the dependencies between graphlets are taken into account and then the arithmetic average of such scaled and normalized distributions aggregates them into a single number in [0, 1]. Informally, GDDA is a generalisation of the degree distribution, so that instead of comparing only the degree distributions of two networks, it also compares how similar the two networks are in terms of distributions of sub-networks such as triangles and squares⁴⁶,⁵⁶. We chose GDDA over motifs⁶⁴ and spectral methods⁶⁵ because it has been shown to be a very robust, yet sensitive measure that encapsulates a large range of other commonly used measures, such as the degree distribution (1^st GDD), clustering coefficient (3^rd GDD), etc. See Supplementary Information for more details.

Author Contributions

V.J., R.S. and N.P. designed the experiments. V.J. performed the experiments. V.J., R.S. an N.P. wrote the main manuscript text. V.J. prepared the figures. All authors reviewed the manuscript. The authors have no competing financial interests.

Supplementary Material

Supplementary Information

Supplementary Information