Abstract
Previous efforts to model the diiron(IV) intermediate Q of soluble methane monooxygenase have led to the synthesis of a diiron(IV) TPA complex, 2, with an O-FeIV-O-FeIV-OH core that has two ferromagnetically coupled Sloc = 1 sites. Addition of base to 2 at −85 °C elicits its conjugate base 6 with a novel O=FeIV–O–FeIV=O core. In frozen solution 6 exists in two forms, 6a and 6b, that we have characterized extensively using Mössbauer and parallel mode EPR spectroscopy. The conversion between 2 and 6 is quantitative, but the relative proportions of 6a and 6b are solvent dependent. 6a has two equivalent high-spin (Sloc = 2) sites, which are antiferromagnetically coupled; its quadrupole splitting (0.52 mm/s) and isomer shift (0.14 mm/s) match those of intermediate Q. DFT calculations suggest that 6a assumes an anti conformation with a dihedral O=Fe-Fe=O angle of 180°. Mössbauer and EPR analyses show that 6b is a diiron(IV) complex with ferromagnetically coupled Sloc = 1 and Sloc = 2 sites to give total spin St = 3. Analysis of the zero-field splittings and magnetic hyperfine tensors suggests that the dihedral O=Fe-Fe=O angle of 6b is ~90°. DFT calculations indicate that this angle is enforced by hydrogen bonding to both terminal oxo groups from a shared water molecule. The water molecule pre-organizes 6b, facilitating protonation of one oxo group to regenerate 2, a protonation step difficult to achieve for mononuclear FeIV=O complexes. Complex 6 represents an intriguing addition to the handful of diiron(IV) complexes that have been characterized
Keywords: Mössbauer, EPR, DFT, nonheme, diiron(IV)
1. Introduction
Intermediate Q is a powerful oxidant that is formed in the catalytic cycle of soluble methane monooxygenase (sMMO). It has been shown to cleave the strongest aliphatic C-H bond (104 kcal mol−1) in a hydrocarbon to effect the hydroxylation of methane. sMMO-Q has an antiferromagnetically coupled diiron(IV) center (established by Mössbauer spectroscopy1,2) with an Fe2(μ-O)2 diamond core (deduced from EXAFS3). The individual iron(IV) centers of Q are proposed to be high-spin, based on the fact that they have an oxygen-rich ligand set that would be expected to exert a relatively weak ligand field1,2 and the observation that related high-valent intermediates such as X of class Ia ribonucleotide reductases (RNR)4 and J of taurine/α-ketoglutarate dioxygenase (TauD)5 have S = 2 iron(IV) centers. Like sMMO, the latter two enzymes have iron active sites with two carboxylate ligands per iron. In addition, cryo-reduction of Q results in the formation of a one-electron reduced FeIVFeIII species with an electronic structure very similar to that of intermediate X. The assignment of a high-spin iron(IV) state is also supported by several density functional theory (DFT) calculations.6–8
In the past decade, a large number of oxoiron(IV) model complexes have been synthesized and characterized to gain insight into whether the reactivity (hydrogen atom abstraction and/or oxo transfer) of the oxoiron(IV) unit depends on the iron spin state. Most of these complexes have been found to have S = 1 ground states,9,10 and only a few have been established to have S = 2 spin states.11–15 However, as the characterized high-spin oxoiron(IV) complexes require different supporting ligand environments to achieve the high-spin state, it is difficult to sort out the effects of the spin-state change on the reactivity differences from those that arise from other factors, such as the ligand basicity and architecture.
In a separate effort we have also characterized a family of high-valent diiron complexes that are derived from the same diiron(III) precursor and supported by the same tetradentate tripodal ligand L (Scheme 1). These complexes have [FeIVO] units, the spin states of which are modulated by the nature of second iron center.16–22 For 2, 3, and 4, the [FeIVO] unit has an Sloc = 1 state, but one-electron reduction of 2 to generate 5-OH results in the conversion of the FeIV=O unit from Sloc = 1 to Sloc = 2, accompanied by a 1000-fold increase in its ability to cleave C–H bonds.17
Scheme 1.
High-valent diiron complexes based on ligand L
Until recently, the high-spin diiron(IV) center had eluded modeling by synthetic chemists. This situation changed when Kodera et al.23 presented Mössbauer evidence for the formation of such a diiron(IV) unit in the reaction of H2O2 with the (μ-oxo)diiron(III) complex of 6-hpa (Scheme 1), where 6-hpa is a dinucleating version of L but without the ring substituents. This reaction gave rise to a relatively stable diiron adduct from which a solid was precipitated at −40 °C. Variable temperature Mössbauer studies of the as-isolated solid showed a temperature-dependent interconversion between two forms, K-7a and K-7b (these are, respectively, species 4a and 4b of Kodera et al.). K-7b, which represents ≈ 85% of Fe at 298 K, is a diiron(IV) center with two equivalent sites having an isomer shift and quadrupole splitting similar to that of intermediate Q. In section 4.3.3 we will present a critical discussion on the observations of Kodera et al.; for clarity we add the prefix K when referring to the two complexes of Kodera. The nature of K-7a and K-7b will be discussed in the light of the results of the present study.
In this paper, we report that treatment of 2 with strong base at −80 °C results in the formation of its conjugate base, 6, in 3:1 PrCN-CH3CN or CH2Cl2-MeCN solution. Upon freezing, 6 exhibits two spectral forms: 6a with cluster spin St = 0, resembling the high-valent species K-7b, and 6b with an St = 3 state that arises from a ferromagnetically coupled diiron(IV) system with local Sloc1 = 1 and Sloc2 = 2 sites. Our detailed spectroscopic studies of 6 in frozen solution, coupled with DFT calculations, place the high-spin iron(IV) assignment for 6a (as well as K-7b by extension) on a firm footing.
2. Materials and Methods
Butyronitrile (PrCN, 99%+) purchased from Aldrich was purified and dried according to reported procedures.24 Tetrabutylammonium fluoride hydrate (Bu4NF·xH2O) purchased from Aldrich (98%) was dried under vacuum at 40 °C.25 Anhydrous dichloromethane (CH2Cl2, >99.8%) and acetonitrile (MeCN, >99.8%) purchased from Aldrich were used without further treatment. Bu4NOH·30H2O, triethylamine and 1,2,4,5-tetramethylimidazole (Me4Im) were purchased from Aldrich and used without further treatment. Solution of 70 wt% H2O2 in H2O was obtained from the FMC Corporation. Bu4NOCD3 was prepared with a reported procedure.21 [FeIVO(L)(NCMe)]2+ was prepared by reaction of [FeII(L)(NCMe)2](OTf)2 with one equivalent of tBuSO2C6H4IO.26
Complex 1 was synthesized according to a reported procedure.20 Solutions of complex 2 in 3:1 CH2Cl2-MeCN or PrCN-MeCN mixed solvents were prepared and handled according to reported procedures.17 Briefly, a solution of 1 in MeCN was treated with ~0.85 equivalent of H2O2 at −40 °C and then diluted by three equal volumes of CH2Cl2 or PrCN chilled to −80 °C. Mössbauer analysis showed that for solutions prepared in this manner about 55–60% of iron belongs to 2, while 30–40% corresponds to S = 0 diiron(III) species.19 The use of mixed solvents allowed for the storage and performing subsequent reactions at temperatures as low as −85 °C, a condition needed for the trapping of very reactive intermediates.
UV-vis spectra were recorded on a Hewlett-Packard 8453A diode array spectrometer equipped with a cryostat from Unisoku Scientific Instruments, Osaka, Japan. This combination allows spectroscopic studies and sample preparation at temperatures down to −85 °C. In a typical UV-vis experiment, the solution of 2 was first transferred via a plastic syringe to a custom-made quartz cuvette precooled in the cryostat and then desired amount of base (typically less than 100 µL of a stock solution in 3:1 CH2Cl2-MeCN) was added via a micro syringe. A magnetic stir bar was used to facilitate mixing. The conversion of 2 to 6 was monitored on a UV-vis spectrometer.
The EPR samples of 6 were prepared in both 3:1 CH2Cl2-MeCN and 3:1 PrCN-MeCN (sample a). The Mössbauer samples were in 3:1 PrCN-MeCN and contained 95% 57Fe isotope, unless otherwise stated. These samples were typically prepared by mixing 2 and Bu4NF in a cuvette cooled to −80 or −85 °C by a Unisoku cryostat. The solution was then transferred via a glass pipette (chilled by liquid nitrogen) to an EPR tube or Mössbauer cup, followed by freezing in liquid nitrogen. For the Mössbauer sample b (see below), the solution was prepared in 3:1 CH2Cl2-MeCN and about 0.1 mL of solution was introduced into a Mössbauer cup containing five layers of filter paper, followed by freezing in liquid nitrogen. This technique was successfully employed in a previous study to obtain Mössbauer spectra of a sample in CH2Cl2.27 For the Mössbauer sample c (see below), the solution was prepared in a Mössbauer cup attached to an extension tube and cooled to −85 °C in the Unisoku cryostat. A magnetic stir bar was placed in the cup to facilitate mixing and removed by a magnet right before freezing the solution. Removal of the extension tube from the cup was performed in liquid nitrogen. This technique eliminates a transfer step prior to freezing and thus helps preventing the decay of 6. The sample prepared with this method contained the highest percentage of 6 (see below).
Continuous wave, X-band EPR spectra were recorded on a Bruker Elexys E-500 spectrometer equipped with an Oxford ESR 910 liquid Helium cryostat and an Oxford temperature controller. Mössbauer spectra were recorded using Janis Research Super-Varitemp dewars that allowed studies in applied magnetic fields up to 8.0 T, applied parallel to the observed γ-rays. Isomer shifts are quoted relative to Fe metal at 298 K. Mössbauer spectral simulations were performed using the WMOSS software package (SEE Co, Edina, MN, USA), and EPR spectra were simulated with SpinCount, a program developed by Dr. M. P. Hendrich at Carnegie Mellon University.
Density Functional Theory (DFT) calculations were performed using the quantum chemical software package Gaussian 09, revisions A02 and C01, see ref S1 of SI. Unless otherwise noted, all calculations were performed using the B3LYP/6–311G functional/basis set combination. Single point SCF calculations and geometry optimizations were completed using standard convergence criteria. For each particular state, TD DFT calculations gave only positive excitation energies, confirming the ground state character of the respective electronic configuration. All geometry optimizations were followed by analytical frequency calculations which allowed us to both confirm the presence of a true minimum for each stationary structure and determine the zero-point corrections to the predicted SCF energies. To computationally model the observed spectroscopic behavior of 6 two structural models were considered. The difference between these two models consists in the presence of a water molecule that interacts through robust supramolecular hydrogen bonds with the [(TPA)O=FeIV-O-FeIV=O(TPA)]2+ cation. For each structural model, we have investigated the predicted properties and relative energies of a series of eight distinct electronic configurations that differed from one another in the values of the local iron spins (high-spin, S = 2 vs. low-spin, S = 1) as well as by the nature of the spin coupling (antiferromagnetic vs. ferromagnetic). For the water-free structure of 6, a geometric model was constructed from scratch in an approximate anti conformation and was submitted to geometry optimization using the 4(2,2) configuration. Throughout this study we used a simplified structural model of the tris (pyridilmethyl) amine (TPA) ligand lacking the 3, 5-methyl and 4-methoxy substituents of the pyridil rings. For the 0(2,2), 0(1,1), 1(1,2), 1(2,1) broken-symmetry (BS) and 2(1,1), 3(1,2), 3(2,1) ferromagnetic (F) states we have used the fragment option of the guess keyword and the 4(2,2) optimized structure to generate the initial electronic guesses used for the subsequent SCF single point calculations and geometry optimizations. A similar procedure was followed to investigate the water-containing model of 6 starting from an initial geometry in which the terminal oxo groups are in syn conformation to accommodate the water bridge. The influence of the Hartree-Fock exchange contribution to the B3LYP functional on the relative SCF energies of the various electron configurations was assessed by performing a series of calculations in which this contribution was reduced to 0.75, 0.5 and 0.25 times the default value. The energy dependence on a given structural parameter, e.g. the [O=Fe-Fe=O] dihedral angle, was evaluated by performing relaxed scans in which one internal coordinate was kept fixed while optimizing all the others. The electric field gradient (EFG) parameters, ΔEQ and η, as well as the spin-dipolar hyperfine field tensor, ASD, were calculated using the Gaussian 09 properties, prop, keyword and the efg and epr options, respectively. The predicted isomer shifts were determined from the values of charge densities at the 57Fe nuclei using the calibration of Vrajmasu et al.28
3. Results
3.1 Formation of a New Diiron(IV) Species in Solution
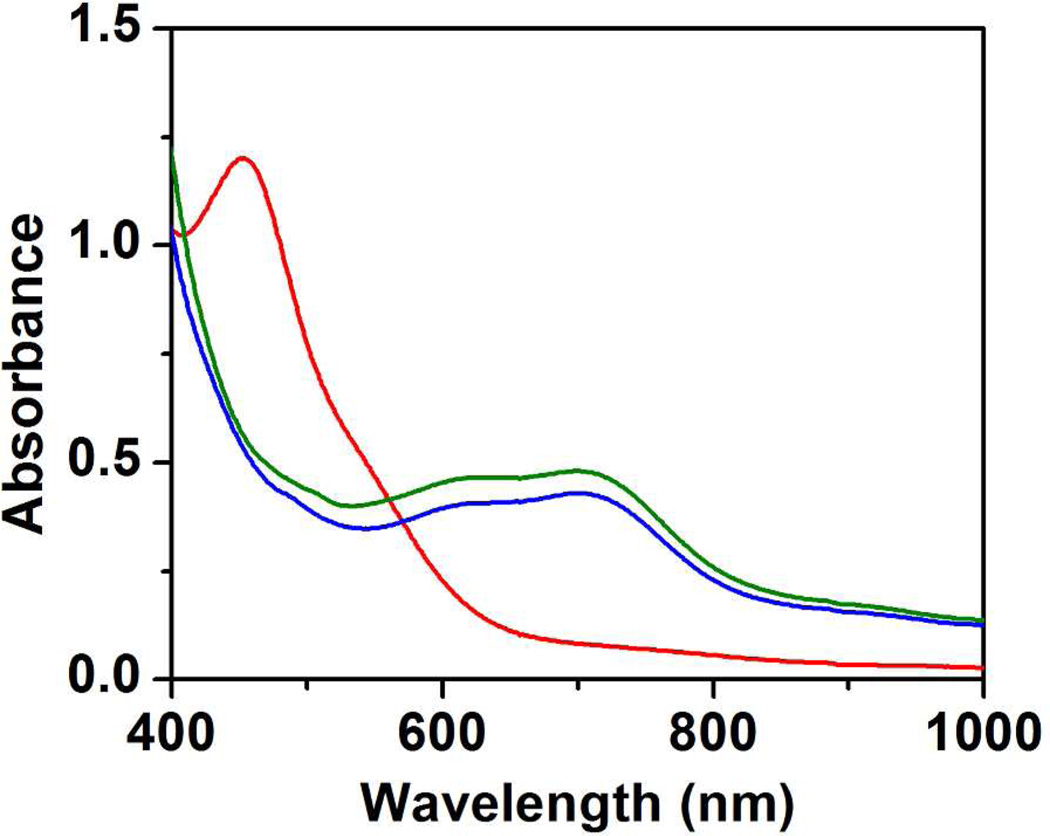
Complex 2 has a green color that corresponds to a broad absorption band in the 700-nm region (Figure 1, green line). Addition of Bu4NF (a powerful base in aprotic solvents)29 to 2 at −80 °C causes an instantaneous color change from green to orange, resulting from the loss of its long-wavelength absorption band and the formation of a new species (6) with an absorption peak at 450 nm (ε ~ 6000 M−1 cm−1 assuming 100% conversion, Figure 1, red line). Upon addition of the weak acid 2,6-lutidium perchlorate, the 450-nm absorption feature disappears and 2 is regenerated in 90% yield based on its characteristic absorption at 705 nm (ε = 2200 M−1 cm−1; Figure 1, blue line), suggesting that the conversion of 2 to 6 is nearly quantitative and reversible.
Figure 1.
UV-vis spectra of 0.2 mM 2 (green line), 6 (generated by adding 1.0 mM Bu4NF to 2, red line), and 2 (regenerated from adding 1.0 mM 2,6-lutidinium perchlorate to 6, blue line). Spectra were recorded in 3:1 CH2Cl2-MeCN at −80 °C.
Complex 6 can also be generated by adding other bases such as Bu4NOH, Bu4NOCD3, Et3N, and 1,2,4,5-tetramethylimidazole (Me4Im) (Figure S1). The amount of base needed to achieve conversion from 2 is determined by its basicity, requiring smaller amounts for stronger bases (e. g. 2.5 equiv. for Bu4NF, Bu4NOCD3 or Bu4NOH) and larger amounts for weaker bases (e. g. 10 equiv. for Et3N or 12.5 equiv. for Me4Im). These observations are consistent with the notion that the inter-conversion between 2 and 6 simply involves an acid-base equilibrium. The fact that the same spectral changes are observed with the addition of sterically hindered Me4Im also excludes the possibility that the added base acts as a ligand to the iron in the complex to form 6. We thus conclude that 6 is the conjugate base of 2. The only possible proton in 2 that is likely to be involved in an acid-base equilibrium is the FeIVO–H proton, so its loss upon treatment with base should generate a complex with a O=FeIV–O–FeIV=O core structure as proposed in Scheme 1.
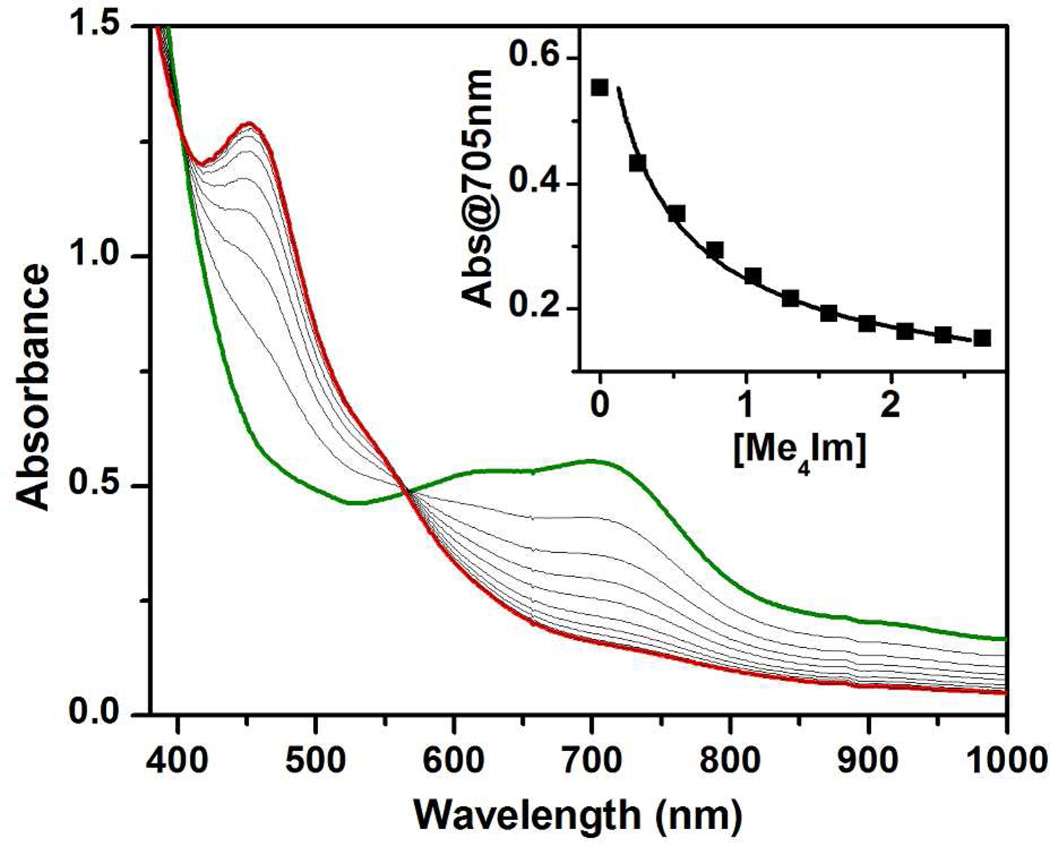
The titration of 2 with Me4Im reveals two isosbestic points at 403 and 566 nm (Figure 2), suggesting that the 2-to-6 conversion is a simple A-to-B process without noticeable involvement of an intermediate. By fitting the titration data (Figure 2, inset), the pKa of 2 can be estimated to be about 0.3 unit higher than that of the conjugate acid of Me4Im (pKa = 9.2 in water30). The high pKa of 2 suggests that 6 is a strong base and explains why it is readily protonated by 2,6-lutidinium ion to regenerate 2. In contrast, [FeIVO(L)(NCMe)]2+, the mononuclear oxoiron(IV) complex of L, retains its characteristic near-IR band at 720 nm with an unchanged extinction coefficient even after addition of 4 equiv. HClO4 (Figure S2), showing that protonation of the mononuclear FeIV=O unit does not occur to any significant extent. This observation suggests that the mononuclear oxoiron(IV) unit of FeIVO(TPA)(NCMe)] has a basicity even lower than that of ClO4− or CH3CN, the other potential bases present in solution. Similarly, mononuclear FeIV=O complexes supported by other N4 or N5 ligands have been shown to be stable in the presence of 50 mM HClO4 31 or up to 5 M CF3COOH,32 providing further evidence that such complexes are difficult to protonate. The significantly higher basicity of 6 may derive from the stabilization of the hydroxide proton in 2 by H-bonding to the nearby oxoiron(IV) motif (Scheme 1). The presence of this H-bonding interaction is supported by the EXAFS analysis of 2, which shows an Fe-Fe distance of 3.3 Å, 0.3 Å shorter than the 3.6 Å expected for a linear Fe–O–Fe unit due to bending of the Fe-O-Fe unit.18,19,22 Thus far the only other examples of characterized FeIV–OH species supported by similar ligand environments are [FeIV(BPMCN)(OH)(OOtBu)]2+ (BPMCN = N,N’-bis(2-pyridylmethyl)-N,N’-dimethyl-trans-1,2-diaminocyclohexane)33 and Compounds II of chloroperoxidase (CPO) and cytochrome P450.34–36 In these latter cases, the presence of another strongly basic ligand in the coordination sphere presumably increases the basicity of the FeIV=O group, leading to its protonation. However 6 is the only FeIV–OH species found thus far demonstrated to exhibit a reversible acid-base equilibrium.
Figure 2.
UV-vis spectroscopic changes upon titration of 0.2 mM 2 (green line) with Me4Im to generate 6 in 3:1 CH2Cl2-MeCN at −85 °C (red line). Inset: plot showing the absorbance at 705 nm vs concentration of added Me4Im. The pKa of 2 is estimated to be 0.3 units higher than that of the conjugate acid of Me4Im.
3.2. Mössbauer and EPR Studies
3.2.1 Introductory Remarks
Complex 6 is quite unstable in solution, thereby presenting a challenge to characterize its electronic structure. Thus, for our spectroscopic investigation, we carried out the conversion of 2 to 6 at −85 °C to retard its decay during sample preparation. We have studied a variety of samples containing 6 with Mössbauer and EPR spectroscopy, varying solvents, mixing procedures, transfer procedures of cold samples into Mössbauer cups and EPR tubes, using dry and wet solvents as well as varying freezing rates. For all samples we have observed two new diiron(IV) species, 6a and 6b, in the frozen state. (In the following we refer to the solution samples as 6, leaving open the question of whether 6 is some mixture of 6a and 6b.) Depending on the solvent, and to some extent on other conditions not yet understood, the proportions of the two species varied; however, their spectroscopic properties were always the same. We do not yet understand the factors that control the relative amounts of 6a vs. 6b in frozen solution, but the proportions are solvent-dependent. The present manuscript will focus on the electronic structure of the two species, deferring the questions of distributions to future studies. To guide the reader through the following sections: 6a is an antiferromagnetically coupled St = 0 diiron(IV) species with local high-spin Sloc1 = Sloc2 = 2 sites, while 6b is a ferromagnetically coupled St = 3 diiron(IV) complex with local Sloc1 = 1 and Sloc2 = 2 sites.
The starting diiron(III) complex 1 for the present study reacts with one equiv. H2O2 to yield diiron(IV) complex 2. This reaction typically yields Mössbauer samples for which 55–60% of the iron belongs to 2, while 30–40% corresponds to S = 0 diiron(III) species.37 In this manuscript and in the Supporting Information (SI) section we present spectra from preparations in different solvents (samples a, b, c, see Table 1) containing substantially different proportions of 6a and 6b. These particular preparations are well suited to introduce the new diiron(IV) species to the reader. All of our samples contain diiron(III) species, as well as St = 1/2 species 5-OH and 5-F (an analog of 5-OH where the OH− ligand has been replaced by F−), which have previously been well characterized over a wide range of applied magnetic fields.19 Also, the samples contain sometimes a small amount (typically ~ 3–10%) of mononuclear S = 5/2 FeIII. Complex 5-OH is a decay product of 6 resulting from H-abstraction, presumably from the PrCN and/or CH3CN solvent molecules. The diferric species in the sample are likely decay products that are difficult to distinguish from 1. The following sections are structured to guide the reader through the characterization of species 6a and 6b. We will show Mössbauer spectra recorded for samples prepared using 3:1 PrCN : MeCN as well as 3:1 CH2Cl2 : MeCN solvent mixtures. Given the nature of the project, the Mössbauer analysis is rather involved and we had to employ a few tricks to characterize the species of interest. We have tried to present the arguments in a way so that a reader with some background in Mössbauer spectroscopy can comfortably follow the main arguments. Table 1 lists the composition of the three samples as it emerged from Mössbauer and EPR analyses.
Table 1.
Approximate compositiona (% Fe) of the samples a, b, and c. Samples a and c are prepared in 3:1 PrCN:MeCN solvent mixtures while sample b was prepared in 3:1 CH2Cl2MeCN.
| Sample | 6a | 6b | 5-OH + 5-F | FeIII-O-FeIII | S = 5/2 FeIII | Totala |
|---|---|---|---|---|---|---|
| a | 12 | <3 | 12 + 8 | 48 | 5 | ~90 |
| b | 12 | 36 | 5–10 | 30 | 5–10 | ~90–100 |
| c | 32 | 22 | 10 | 30 | <3 | ~95–100 |
Spectral components 6a and 6b can be quantified quite well, but those of paramagnetic species like 5-OH/F and high-spin FeIII are more difficult to quantify and are possibly underestimated. Traces of mixed-valent complex 4 would be difficult to recognize in the Mössbauer spectra.
3.2.2 Mössbauer spectra of 6a
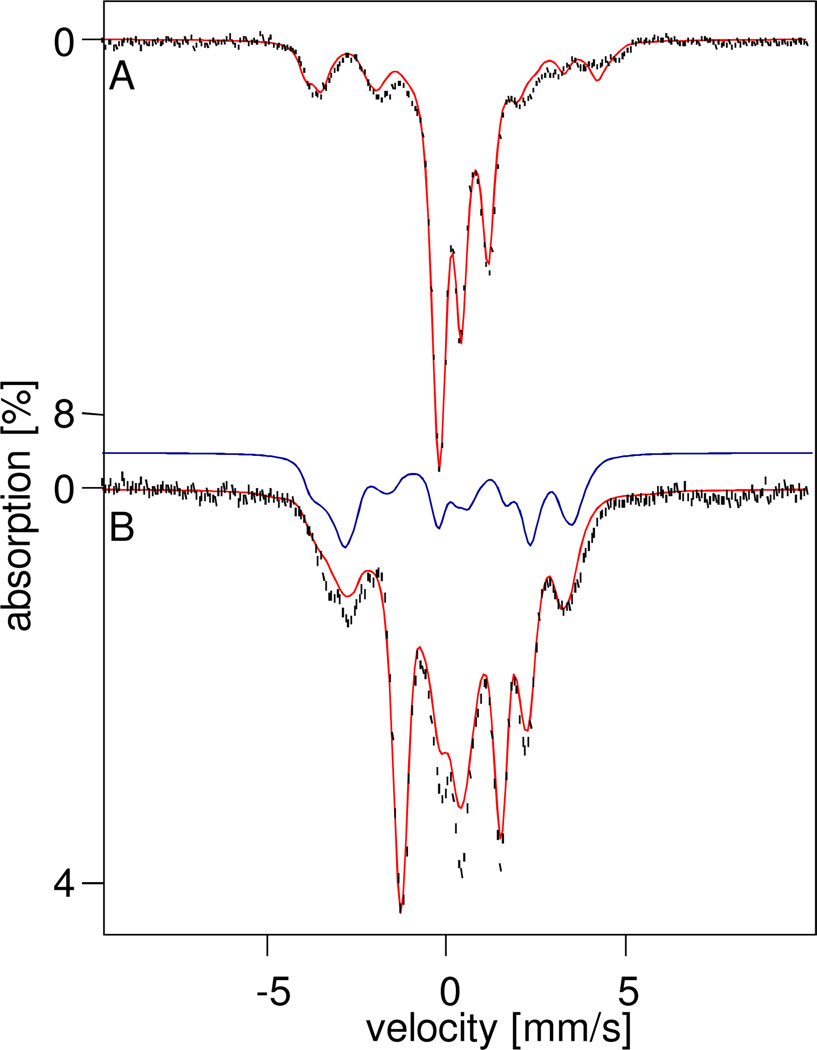
Figure 3 introduces the diiron(IV) species 6a, which can be most easily discerned in sample a. The spectra shown were obtained in a 3:1 PrCN : MeCN solvent mixture from a sample prepared for an EPR study. After collecting the EPR spectra, the EPR tube was crushed under liquid nitrogen and the frozen crumbs, after removing the quartz pieces, were placed into a Mössbauer cup. We used this procedure to assure that we studied the same sample with both techniques (6b, introduced below, is EPR-active). Analysis of the Mössbauer and EPR spectra (Figures S3–S6) revealed decay products (perhaps 35% of Fe), namely the S = 1/2 species 5-OH (≈ 12% of Fe) and 5-F (≈ 8% of Fe, see Figure S4) and 48% diferric species (roughly 15% more than generally found). In most samples studied, 20–30% of the Fe in 3:1 PrCN : MeCN samples (e.g. ~36% in CH2Cl2 : CH3CN sample b of Figure 5) is associated with species 6b, but sample a contains only ~3% of 6b, thereby allowing us to obtain a Mössbauer description of 6a with minimal interference from 6b.
Figure 3.
4.2 K Mössbauer spectra of 6 prepared in 3:1 PrCN : MeCN (crushed EPR sample, sample a) recorded in zero field (bottom). Top spectrum was obtained by applying a Fourier transform procedure (transform, source linewidth removal, followed by a backtransform) to the spectrum at the bottom. Species 6a is indicated by the red bracket in the top panel and the red solid line in the bottom panel. Approximate composition of the sample is given in Table 4.
Figure 5.
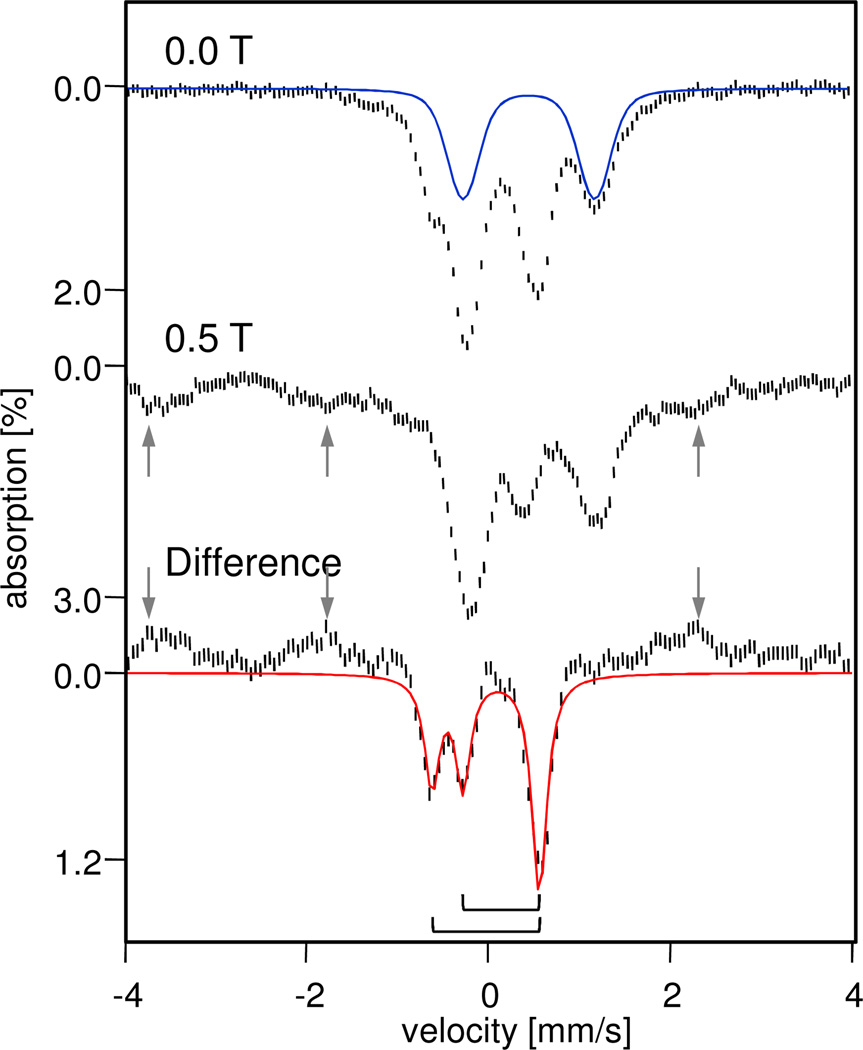
4.2 K Mössbauer spectra of 6 in 3:1 CH2Cl2:CH3CN, sample b. Top: Spectrum recorded in the absence of an applied magnetic field. The blue trace outlines the diferric contaminant, 1. Middle: Spectrum of the same sample recorded in a 0.5 T field applied parallel to the incident γ rays. Bottom: Difference spectrum "(Top) minus (Middle)". The spectrum illustrates that two doublets, indicated by brackets, are observed when no magnetic field is applied and are transformed into a spectrum exhibiting paramagnetic hyperfine structure upon the application of a 0.5 T magnetic field; some absorption lines of the paramagnetic component are marked by arrows. The red line represents a simulation to the two quadrupole doublets of 6b. See Table 1 for composition of the sample.
A Mössbauer spectrum is a convolution of the spectrum of the absorber with that of the 57Co source. A spectrum can be deconvoluted by taking its Fourier transform, removing the known line shape of the source (a Lorentzian of ~0.15 mm/s full width), followed by a backtransform.38 This procedure can sharpen the lines of the quadrupole doublets considerably, while it also effectively removes the contributions of broad paramagnetic components, like those of the S = 1/2 complexes 5-OH and 5-F and S = 5/2 FeIII species. In the raw data the paramagnetic components present in sample a (Figure 3 bottom) contribute the broad features extending from −4 mm/s to +5mm/s. The Fourier transform procedure applied to the 4.2 K zero field spectrum of sample a reveals two nested doublets that account for ca. 63% of the Fe in the sample (the sum of 6a, 6b, and 1). The two outermost features (48% of Fe) actually are best represented by two overlapping doublets (black brackets) with ΔEQ = 1.65 mm/s, δ = 0.45 mm/s and ΔEQ = 1.20 mm/s, δ = 0.45 mm/s. Since the conversion between 2 and 6 is reversible, it is highly unlikely for the diiron(IV) center of 2 to break down into mononuclear units upon addition of base, essentially excluding the possibility that 6a is a monomeric TPA complex. Moreover, 6 decays into dinuclear 4 and diferric species. Below, we will give arguments which lead to the conclusion that 6a is a diiron(IV) species containing two equivalent high-spin sites. Interestingly, the Mössbauer parameters of 6a are very similar to those reported for methane monooxygenase intermediate Q, namely ΔEQ = 0.53 mm/s and δ = 0.17 mm/s,1 which is thought to have an antiferromagnetic diiron(IV) center with local Sloc1 = Sloc2 = 2 sites.
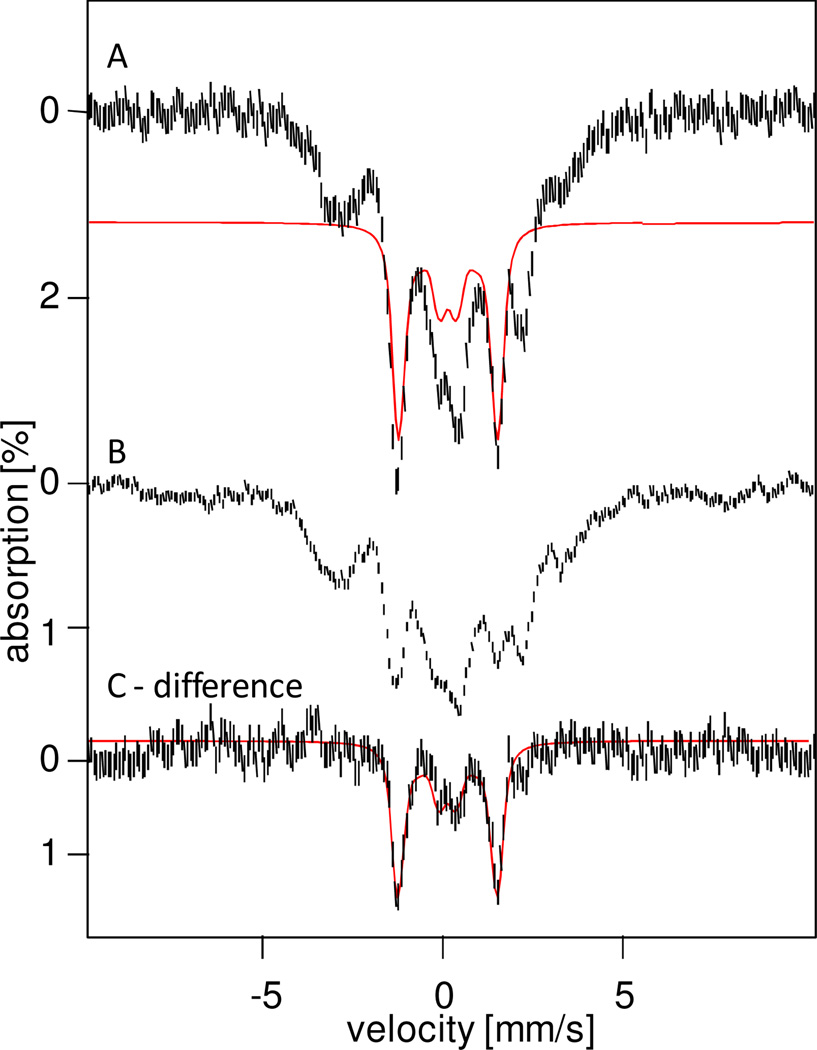
The diamagnetic nature of 6a is best demonstrated by recording its Mössbauer spectra in strong applied magnetic fields. Figures 4A and B show 8.0 T spectra of samples c and b, respectively. Inspection of Table 1 shows that both samples contain similar amounts of 1 (≈ 30%) and 5-OH (5–10%), but differ in the amounts of 6a, which represents 12% of the iron in sample b and 32% in sample c. Thus, the spectrum of 6a in a strong applied field can be observed in the difference spectrum "Sample c - Sample b" (Figure 4C), where the contributions of 1 and 5-OH will essentially cancel. Further, as shown below, for an 8.0 T applied field the contribution of 6b is spread over a wide range of Doppler velocities and is thus barely discernible in the difference spectrum. The spectral simulation for 6a, shown in red, assumes that only the applied field contributes to the magnetic splitting of 6a, demonstrating that this species is diamagnetic (cluster spin St = 0).
Figure 4.
4.2K, 8T Mössbauer spectra of samples c (A) and b (B). (C) Difference spectrum obtained by subtracting spectrum (B) from (A). The red lines in (A) and (C) represent spectral simulations assuming that 6a has an St = 0 ground state. See Table 1 for sample compositions and solvents.
3.2.3. Zero Field Mössbauer spectra of 6b
In this section we demonstrate that the deprotonation of 2 produces, in frozen solution, not only the St = 0 species 6a but also a paramagnetic diiron(IV) species (6b) with an St = 3 ground state. By taking the difference of the zero field (Figure 5, top) and 0.5 T (middle) spectra of sample b at 4.2 K, we obtain the difference spectrum shown in Figure 5 bottom, in order to reveal species with integer spin based on the following rationale. An applied field as weak as 0.5 T leaves the quadrupole doublets of S = 0 species (1 and 6a) essentially unaffected (broadening the lines by a mere 0.04 mm/s), resulting in the cancelation of these species in the difference spectrum. A similar cancellation, essentially complete, occurs for the half-integral-spin species 5-OH and 5-F, which exhibit broad, magnetically split features in both the 0 T and 0.5 T spectra. The difference spectrum then would originate only from paramagnetic species with integer spin (S > 0). The latter species generally exhibit quadrupole doublets in zero field that are transformed into magnetically split spectra by strong internal magnetic fields that can already be induced by applying magnetic fields as weak as 0.5 T (the detailed conditions that allow this transformation here are discussed below). Thus, we expect the difference spectrum of paramagnetic integer spin species to consist of quadrupole doublets superimposed on widely split magnetic features. Precisely a spectrum of this sort is shown in Figure 5 (bottom) from which we deduce the presence of a new paramagnetic species with integer spin (6b). In particular, the difference spectrum of Figure 5 shows a superposition of two doublets (brackets) with equal intensities that reveal 6b to be a diiron(IV) complex with two inequivalent sites.
The doublets of 6b have isomer shifts of δ(1) = −0.02(2) mm/s and δ(2) = 0.14(2) mm/s and quadrupole splittings of ΔEQ(1) = 1.17(3) mm/s and ΔEQ(2) = 0.82(4) mm/s (Table 2). Within the uncertainties the δ value of site 1 matches the δ values of the Sloc1,2 = 1 sites in the diiron(IV) complexes 2 and 3 (see Table 3), while δ(2) is close to the shift of the high-spin FeIV=O site in 5-OH, suggesting that 6b is a diiron(IV) complex with site spins Sloc1 = 1 and Sloc2 = 2. As shown below by EPR the two spins are ferromagnetically coupled to yield a system state with St = 3.
Table 2.
| Site | δ [mm/s] |
D [cm−1] |
E/D | ΔEQ [mm/s] |
η |
|
|
|
|||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 (Sloc1 = 1) | −0.02(2) | 2.3(3)a | 0.27(4)a | −1.17(3) | −2.0 | −2(2) | −7.2(2) | −8b | |||
| 2 (Sloc2 = 2) | 0.14(2) | 0.82(4) | −1.0(4) | −11(1) | −8.8(1) | > −20 |
determined from EPR. D is Dt and (E/D) = (E/D)t
value is between -6 and -15 T
Table 3.
Fine structure and hyperfine structure parameters of 6a and 6b (bold) and relevant related complexes. For 2, 5-OH and 5-F, only parameters for the FeIV=O sites are listed.
| Label/ Complex |
Stot | Sloc | δ [mm/s] |
local ZFS tensors | EFG tensor | 57Fe Hyperfine Tensor | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| D [cm−1] |
E/D | ΔEQ [mm/s] |
η | ax/gnβn [T] |
ay/gnβn [T] |
az/gnβn [T] |
||||
| 2a | 2 | 1 | −0.03 | - | +0.92 | 0 | −23.0 | −22.7 | −5.0 | |
| 6b (rotated frame)b | 3 | 1 | −0.02 | 1.17 | 0.33 | −21.6 | −24 | −6 | ||
| 6b | 3 | 1 | −0.02(2) | −1.17(3) | −2.0 | −6 | −21.6 | −24 | ||
| 2 | 0.14(2) | −0.82(4) | 0.0 | −16.5 | −13.2 | > −30 | ||||
| 5-OHc | 1/2 | 2 | 0.09 | −0.40 | 10 | −20.0 | −12.0 | −22.5 | ||
| 5-Fc | 1/2 | 2 | 0.10 | +0.60 | −0.7 | −18.6 | −13.4 | −26.3 | ||
| 6a | 0 | 2 | 0.14(1) | +0.52(2) | 0.5–1.0 | n/a | ||||
| K-7ad | nd | 2 | 0.13 | 0.44e | n.d. | |||||
| sMMOH-Qf | 0 | 2 | 0.17 | 0.53 | 1.0 | |||||
| 3g | 0 | 1 | −0.04(1) | 2.09(2) | 0.0 | |||||
| [FeIVO(TPA)(NCMe)]2+h | 1 | 0.01 | 28 | 0.00 | 0.92 | 0.9 | −23.5 | −23.5 | −5 | |
| [FeIVO(TMC)(NCMe)]2+i | 1 | 0.17 | 27 | 0.00 | 1.24 | 0.5 | −20.4 | −20.4 | −3 | |
| [FeIVO(PyTACN)(OH2)]2+j | 1 | 0.05 | 27 | 0.00 | 0.73 | 1 | −23.7 | −20.5 | −4.5 | |
| [FeIVO(N4Py)]2+k | 1 | −0.04 | 22.0 | 0.00 | 0.93 | 0–0.5 | −22.0 | −22.0 | −5.0 | |
| TauD-Jl | 2 | 0.30 | 10.5 | 0.01 | −0.90 | 0.0 | −18.4 | −17.6 | −31.0 | |
| [FeIVO(OH2)5]2+m | 2 | 0.38 | 9.7 | 0.00 | −0.33 | 0.0 | −20.3 | −20.3 | n/d | |
Data from ref. 37
The values in red list the parameters of 6b shown in a frame that is rotated by two 90° rotations relative to the (x, y, z) frame (black numbers, next row) used to analyze the EPR and Mössbauer spectra.
ref. 19
ref. 23; values at 25 K.
sign not determined
ref. 1
ref. 16
ref. 43
refit of Mössbauer data of ref 44 using g-values and zero-field splittings from ref. 39 and reported in ref. 45
ref. 46
ref. 49
ref. 11
For B > 0.2 T species 6b displays a fully developed magnetic hyperfine pattern that severely overlaps with that of 5-OH and 5-F (in 5-F the OH− of 5-OH is replaced by F−; see ref. 19). By a judicious choice of experimental conditions and using the fact that the Mössbauer spectra of the integer-spin complexes in small applied fields differ significantly from those of the half-integral spin complexes, such as 5-OH, we have been able to remove the spectral contributions of the decay product 5 almost entirely and prepare a fairly pure 0.5 T spectrum of 6b. As the ground state of 6b gives a fully developed hyperfine structure in applied fields near 0.2 T, it is expected that an EPR signal can be observed in parallel mode. To develop further the arguments for the Mössbauer analysis of 6b we first turn our attention to EPR.
3.2.4 Parallel mode X-band EPR shows that 6b has St = 3
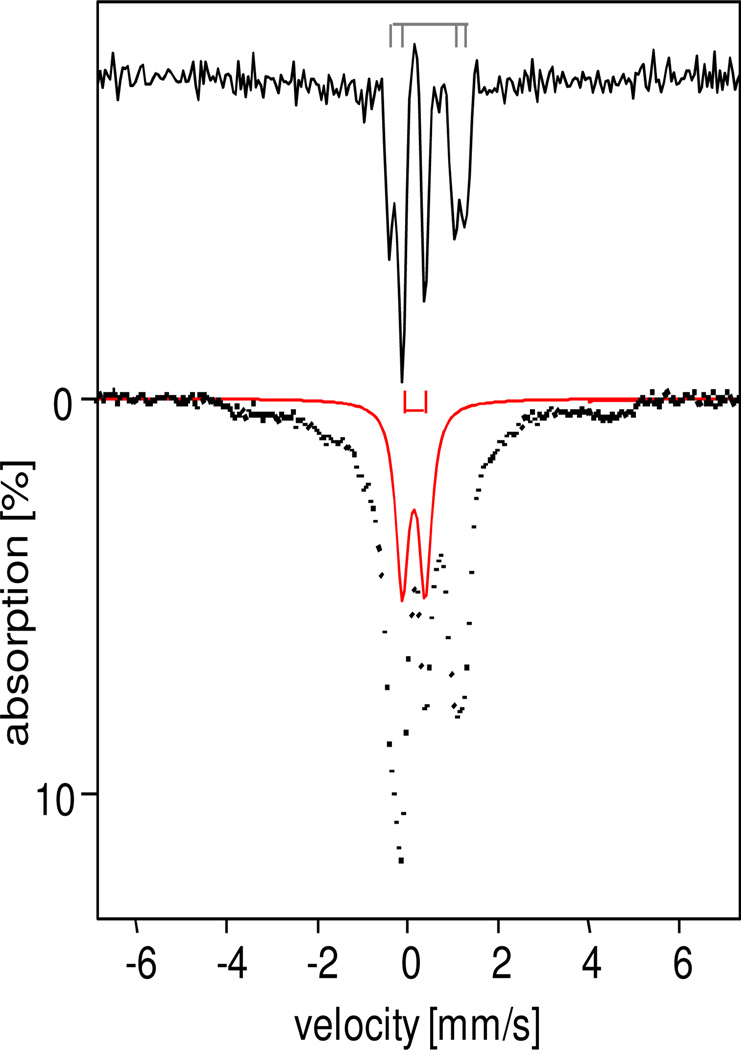
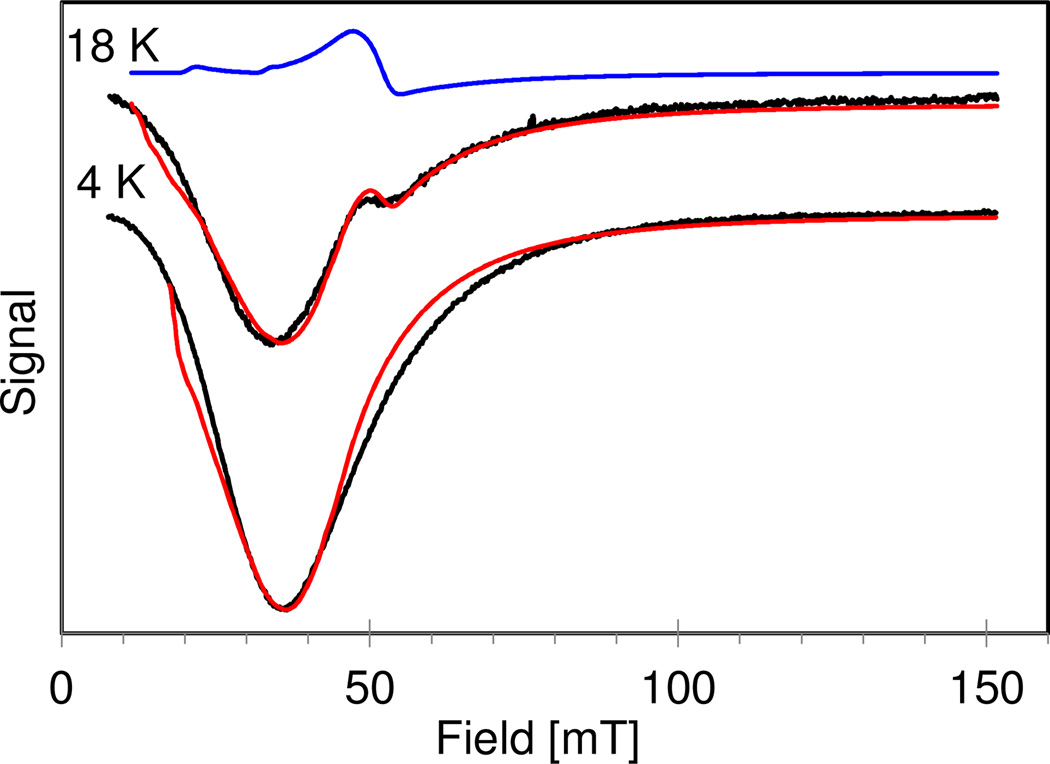
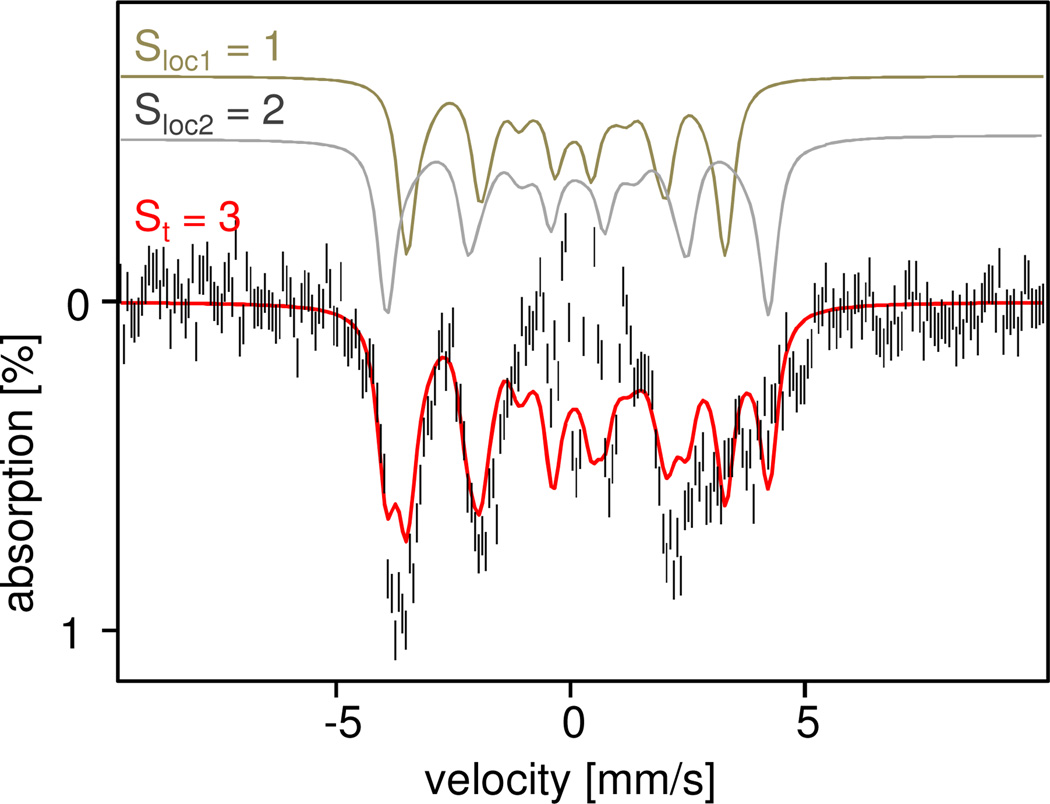
We have studied the X-band EPR spectra of 6b in 3:1 CH2Cl2 : MeCN as well as in 3:1 PrCN : MeCN solvent mixtures. Except for small line width variations the spectra of both mixtures were the same. However, the amount of 6b was consistently higher in 3:1 CH2Cl2 : MeCN, and for this reason we present spectra obtained in this solvent mixture. Figure 6 shows parallel mode X-band spectra recorded at 4 K and 18 K. Above 25 K the spectra were severely broadened by relaxation. The spins Sloc1 = 1 and Sloc2 = 2, deduced from the isomer shifts of the previous section, imply a system spin St = 3 in the case of ferromagnetic exchange coupling and St = 1 in the case of antiferromagnetic coupling. The EPR spectra reveal the presence of the two resonances that fit well to an St = 3 spin system Hamiltonian.
| (1) |
Figure 6.
X-band EPR spectra (black traces) recorded in parallel mode (B1 parallel B) at 4 K (bottom) and at 18 K (middle). Experimental conditions at 4K/18K: microwave power: 0.2 mW/20 mW; frequency: 9.267 GHz; modulation amplitude: 1 mT. Simulations (red traces) were obtained with SpinCount using the St = 3 spin Hamiltonian of eq 1 for D = 2.28 cm−1, E/D = 0.288; σ(E/D) = 0.023; gx,y,z = 2.00; packet width = 0.8 mT. Drawn separately in blue above the 18 K spectrum is a simulation for the excited geff ≈ 12 doublet.
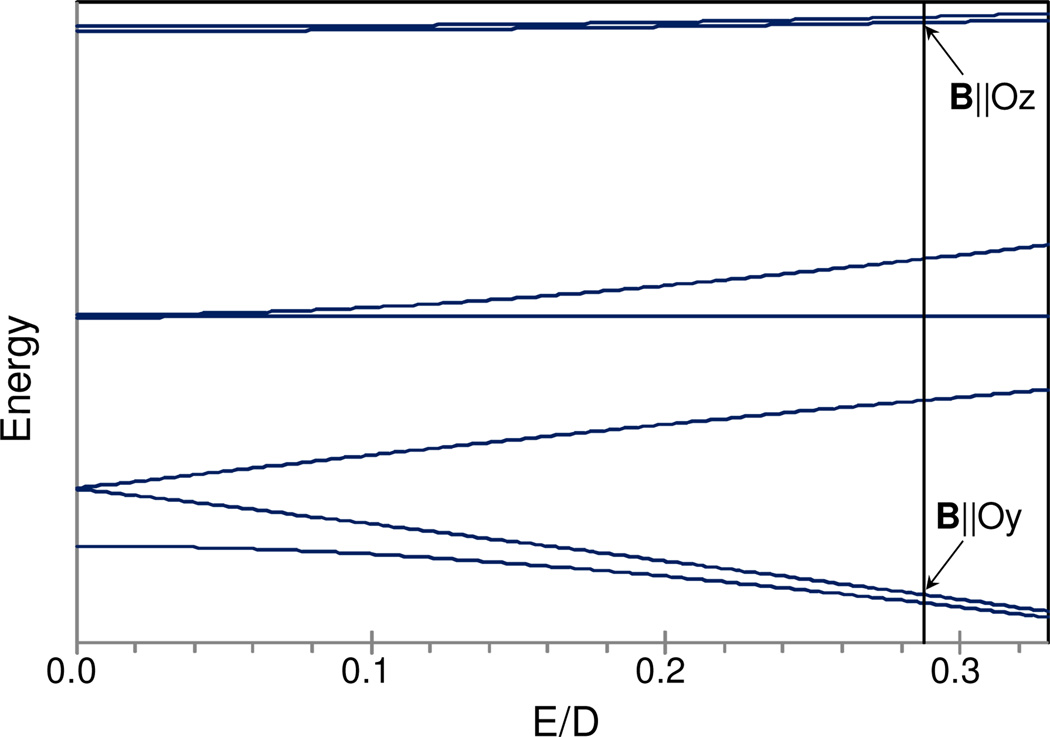
In the spin Hamiltonian of eq 1, the first term describes the zero field splittings (D, E) and the second term represents the electronic Zeeman interaction. The nature of the resonances with troughs near 35 mT and 55 mT (g ≈ 12) can be identified with the help of the graph in Figure 7 in which the energies of the seven sublevels of the St = 3 manifold are plotted versus the ratio E/D. The diagram has been plotted for D = +2.3 cm−1 and gx = gy = gz = 2.0 and indicates that the two resonances observed at 9.25 GHz microwave frequency originate from a system with E/D = 0.29. The major resonance, with a trough near 35 mT, reflects a transition between the ground state (the level with MS = 0 label for E/D = 0) and the MS = −1 level when the static field is along the molecular y direction (arrow, B‖Oy, Figure 7). The second transition arises from an excited magnetic substate resonance near geff ≈ 12 (arrow, B‖Oz) between the two levels with MS = ±3 parentage. Resonances between levels with MS = ±St parentage most frequently have effective g-values geff,z ≈ 2Stgz. Assuming gz to be near g = 2.0 for Sloc1 = 1 and Sloc2 = 2 FeIV=O sites 19,39, the feature near g = 12 indicates an St = 3 multiplet for 6b. The red lines in Figure 6 are spectral simulations for an St = 3 spin system using the parameters listed in the caption.1
Figure 7.
Energy levels of an St = 3 system plotted for D = +2.3 cm−1 and B = 0 versus the ratio E/D. The vertical line is drawn for E/D = 0.288. Arrows mark parallel mode transitions for the lower and upper quasi-doublets. The direction of the static field for which parallel mode transitions are observed is indicated.
We wish to comment briefly on the shape of the resonances. For βB << D the resonance condition of a nearly degenerate integer spin doublet can be written as , where Δ is the energy splitting of the (quasi) doublet in the absence of an applied magnetic field; i = x, y, z. geff,i is an effective g-value that depends on the value of St, E/D, and the intrinsic gi (eq 1) value. The shapes of the resonances are reasonably well reproduced by assuming that E/D has a Gaussian distribution around its mean E/D = 0.288, with standard deviation σE/D = 0.023. The calculated spectra yield for the lowest (ground) transition Δg = 0.324 cm−1 which is slightly larger than the microwave quantum in the parallel mode experiment, hν = 0.309 cm−1. For the quoted σE/D value the quantity Δg has a distribution with σΔ ≈ 0.05 cm−1 such that essentially only molecules with a Δg smaller than the mean (i. e. those having a larger E/D, see Figure 7) contribute to the absorption. The splitting of the excited state doublet is Δe = 0.151 cm−1 and its resonance is sharper than the one associated with the ground doublet. The blue line in Figure 6 shows a simulation for the excited (geff ≈ 12) state feature. From the temperature variation of the two signals we estimate D = 2.3 ± 0.3 cm−1.
3.2.5. Mössbauer spectra of 6b: paramagnetic hyperfine structure
In this section we turn our attention to the Mössbauer spectra of 6b recorded in applied magnetic fields. Identifying the spectral contributions of 6b was a formidable challenge, and we had to use some unusual methods. Figure 8 shows 4.2 K spectra recorded for sample c in fields of 500 mT and 8.0 T applied parallel to the incident γ beam. To extract the spectrum of 6b, we have used a procedure similar to the one described in more detail in section 3.2.3. The procedure exploits the fact that in weak applied fields the spectra of systems with half-integral spin (Kramers systems) differ fundamentally from those of non-Kramers systems (integer spin) such as 6b. The St = 1/2 complexes 5-OH and 5-F are Kramers systems that exhibit already fully developed magnetic hyperfine splittings in weak magnetic fields. In practice this condition is fulfilled for B ≥ 10 mT. Increasing B to 500 mT causes little change in such spectra, and taking a difference spectrum “500 mT minus 10 mT” will cancel the contribution of the contaminating 5-OH/5-F almost completely. In contrast, the magnetic hyperfine field, Bint, of 6b follows a gradually developing magnetization curve (Figure S7) predictable from the D and E/D values obtained from the analysis of the EPR data. For B = 10 mT, 6b exhibits two slightly broadened quadrupole doublets, while a fully developed magnetic pattern, corresponding to a Bint ≈ 24 T, is observed at B = 500 mT. By taking the difference spectrum ("500 mT minus 10 mT", Figure S8) the contributions of all species but 6b, i.e. 1, 6a and 5-OH/5-F, practically cancel. Moreover, after a few rounds of spectral simulations, we had obtained sufficient information to be able to remove the contribution of the 10 mT spectrum of 6b from the difference spectrum. This then yielded the 500 mT spectrum shown in Figure 9. In the following we describe the analysis of the field-dependent Mössbauer spectra of 6b.
Figure 8.
4.2 K Mössbauer spectra (Sample c) of 6 in 3:1 PrCN : CH3CN recorded for B = 0.5 T (A) and 8.0 T (B); B is applied parallel to the observed γ radiation. The red solid lines are the sum of the spectral simulations for 6a (32% of Fe), 6b (22%), 1-OH (10%), and 1 (30%). The sample contains a small fraction of high-spin FeIII (perhaps 5%), discernible in (B) between 6 and 8 mm/s Doppler velocity. A simulation for 6b is shown above the 8.0 T spectrum; the corresponding 0.5 T simulations are shown in Figure 9.
Figure 9.
4.2K, 0.5T Mössbauer spectrum of 6b (sample b) prepared as described in the text. The red line is a spectral simulation based on eqs 1 and 3. The simulated spectra for the Sloc1 = 1 and Sloc2 = 2 sites are shown above the data. The central, ±1 mm/s, region of the experimental spectrum is not well defined.
The EPR and Mössbauer data, taken together, show that 6b is a ferromagnetically coupled complex comprising Sloc1 = 1 and Sloc2 = 2 FeIV sites. We will assume that the system can be treated in the strong coupling limit for which the magnitude of J, the exchange coupling between the two sites in Ĥexch = JŜloc1·Ŝloc2 is large compared to Dloc1 and Dloc2, the zero field splitting (ZFS) parameters of sites 1 and 2. In the strong coupling limit, the ZFS tensor of the St = 3 multiplet is given by
| (2) |
where and are the spin projection factors (for details see ref 40). Comparison of calculated energy levels, g-values, and spin expectation values obtained in the coupled, |St = 3, M>, and the uncoupled, |Sloc1 = 1, m1>|Sloc2= 2, m2>, representation indicates that for the measured value Dt(St = 3) = Dt ≈ 2.3 cm−1 the coupled representation, i.e. eq 1, can be used to describe the St = 3 manifold, provided |J| > 30 cm−1.
To describe the Mössbauer spectra of 6b we amend the St = 3 Hamiltonian of eq 1 by terms describing the 57Fe hyperfine interactions, to obtain
| (3) |
with
| (4a) |
and
| (4b) |
From left to right, the terms of eq 4a describe respectively the magnetic hyperfine, electric quadrupole, and nuclear Zeeman interactions. The quadrupole interaction reflects the magnitude and symmetry of the electric field gradient (EFG) tensor; η = (Vxx − Vyy)/Vzz is the asymmetry parameter. The A-tensors of the St = 3 multiplet in the coupled representation can be expressed in terms of the corresponding local (uncoupled, local) parameters (eq 5)
| (5) |
The dominant contribution to the magnetic splitting of the Mössbauer spectra of sites i = 1, 2 is due to the magnetic hyperfine field B⃗int(i) = −〈Ŝt〉·A(i)/gnβn, where 〈Ŝt〉 is the expectation value of the total spin, Ŝt = Ŝloc1 + Ŝloc2. For the Dt and Et/Dt values of 6b, eq 1 yields for the lowest spin level spin expectation values that are nearly uniaxial for B < 0.2 T, namely |〈Ŝt y〉| >> |〈Ŝt x〉| ≈ |〈Ŝt z〉| see Figure S7. Given that Dt = +2.3 cm−1, for B < 3 T the 4.2 K spectra of 6b are only sensitive to Bint y(i) = −〈Ŝt y〉Ay(i)/gnβn, and as 〈Ŝt y〉 saturates for B ≈ 0.2 T to a value of ≈ −3 we can determine the components of the A-tensors along y.
The uniaxial properties of the ground quasi-doublet for B < 2 T simplify the analysis because the spectra for each site are only sensitive to Ay, the component of the EFG along y, and Δg = 0.324 cm−1 (known from EPR). However, it is well known that the uniaxial case suffers from an ambiguity problem. 41,42 Thus, the same spectra are obtained with different EFG tensors as long as the component of the EFG along Bint retains the same value. Assuming that the principal axes of all tensors in eqs 1 and 2 are collinear eliminates the ambiguity problem. Without this assumption, the data analysis would be hopelessly complex and become totally over-parametrized.
As indicated in Figure 9, the spectra of 6b consist of a superposition of two 6-line patterns, one for each iron site. The two low energy lines (on the left) of the two spectra nearly overlap, giving rise to two absorption bands near −4 mm/s Doppler velocity. In contrast, the high-energy lines do not overlap, creating within the noise nearly continuous absorption between +3 mm/s and +5 mm/s. Our spectral simulations, shown separately for the Sloc1 = 1 site and the Sloc2 = 2 site, describe the data reasonably well. The parameters used for simulating the spectra on the basis of eqs 1 and 3 are collected in Table 2. In order to facilitate comparison with other complexes, such as 2, 5-OH, and 5-F, we have listed in Table 3 the a-tensors of 6b in the uncoupled representation, using eq 5 (The local a values were verified by performing the simulations in the uncoupled representation). Figure 8A shows a simulation including the spectral components of all species; the fractions of Fe contributing to each component are listed in Table 1. Figure S9 shows the simulations for 6a, 6b, 5-OH + 5-F, and 1 separately, and these four species contribute a total of six spectra.
The 500 mT spectrum does not depend on the x and z components of the magnetic hyperfine tensors. A plot of 〈Ŝt x,y,z〉 vs. B (Figure S7) shows that the 8.0 T spectra are quite sensitive to Bint,x and Bint,y, while Bint,z is still rather small owing to the smaller values for 〈Ŝt z〉 = −1.5. In our simulations Ax and Az were adjusted to obtain a reasonable representation of the 8.0 T spectra of 6b. Although the decomposition of the spectra is not necessarily unique, we believe that the parameters for 6b quoted in Table 2 convey the essential features of the solution (see Figure S13 and Tables S6–S7).
3.2.6 Analysis of spin Hamiltonian parameters of 6b suggests (roughly) perpendicular Fe=O units
Diiron(IV) complex 2 and iron(III)iron(IV) complex 5-OH both have their terminal oxo and hydroxo groups in a syn relationship to each other, allowing a hydrogen bonding interaction between these groups to be formed and constraining the Fe–O–Fe angle to about 130°. Replacement of the hydroxo group by fluoride eliminates this interaction, and 5-F assumes a conformation for which the FeIV=O and the FeIII–F groups are oriented in an anti arrangement with an Fe–O–Fe angle of about 180°.19 Given that the conversion of 2 to 6 entails the deprotonation of the terminal OH group, it is expected that the hydrogen bonding interaction is lost and that 6 adopts an O=FeIV–O–FeIV=O structure with the terminal oxo groups in an anti conformation.
As both 6a and 6b derive, upon freezing, from the solution species 6, it seems reasonable to us to assume that both 6a and 6b have an O=FeIV–O–FeIV=O core structure as well, with perhaps a modification for 6b suggested in section 4.1. The interesting but puzzling question arises how 6a can have Sloc1 = Sloc2 = 2 while 6b has one Sloc1 = 1 site and one Sloc2 = 2 site. In our previous DFT analysis of the electronic structure of the HO–FeIII–O–FeIV=O core of 5-OH we learned that the energies of the configurations with SFe=O = 1 and SFe=O = 2 units are close enough in energy for the increased superexchange between the FeIV and FeIII sites to render the FeIV=O site high-spin.19 DFT calculations, discussed in the following section, strongly suggest that the oxo groups in 6a are anti. 6b, however, adopts a different conformation that results in a change in its electronic structure, as can be inferred from the following considerations.
The electronic structure of the Sloc1 = SFe=O = 1 site of 6b is expected to resemble those of the S = 1 FeIV=O site in 2 and its mononuclear variant, [LFeIV(O)(NCMe)]3+. Indeed, the hyperfine parameters of the FeIV=O site of 2 (listed in row 1 of Table 3) closely resemble those of the Sloc1 = 1 site of 6b (in row 1 of Table 3 the z axis corresponds to the direction of the Fe=O bond).37 If we rotate the coordinates of the SFe=O =1 site of 6b (row 3) by 90° around y followed by a 90° rotation around the new z axis, we obtain a set of hyperfine parameters (row 2, red) that strikingly resembles that of the FeIV=O sites of 2 and [LFeIV(O)(NCMe)]3+ (Table 3). Given the similarity of the hyperfine parameters, it is reasonable to assume that the SFe=O = 1 site of 6b has ZFS parameters similar to those of the FeIV=O sites in 2 and [LFeIV(O)(NCMe)]3+, viz. Dloc1(Sloc1=1) ≈ 27 cm−1 and Eloc1/Dloc1 ≈ 0 (As can be seen from Table 1 the value quoted for Dloc1 is typical for a variety of S = 1 FeIV=O complexes studied). In contrast, the zero-field splitting of high-spin FeIV=O complexes (Table 3) with octahedral type symmetries (5-or 6-coordinate) are positive with D ≈ 10 cm−1 and E/D ≈ 0; just as for the S = 1 complexes the major component of the ZFS tensor of the S = 2 species is along the Fe-oxo bond.
With the estimates Dloc1 (Sloc1 = 1) ≈ 27 cm−1 and Eloc1/Dloc1 ≈ 0 for the SFe=O = 1 site of 6b and Dloc2 (Sloc2 = 2) ≈ 10 cm−1 and Eloc2/Dloc2 ≈ 0 for the SFe=O = 2 site of 6b at hand we can infer the relative orientation of the Fe-O axes in 6b with the help of eq 2. The D-tensors in eq 2 are traceless, with principal components Dxx, Dyy, and Dzz. Commonly the coordinate system (x, y, z) is chosen such that |Dzz|≥|Dyy|≥|Dxx|. In this "proper" frame, and 0 ≤ E/D ≤ 1/3. From the preceding discussion and inspection of eq 2 it follows that the Fe=O bonds of 6b cannot be parallel or antiparallel, because such configurations would yield, using eq 2, an axial (Et/Dt ≈ 0) ZFS tensor with Dt ≈ 6 cm−1. In keeping with our assumption that all tensors of 6b are collinear (90° rotations permitted), the local frame (x1, y1, z1) of axial tensor Dloc1 can be oriented in three ways relative to D, the ZFS tensor that defines (x, y, z) in eq 1. Two orientations (z1‖z and z1‖y) yield negative values for Dloc2, namely −3.45 cm−1 and −10.2 cm−1, i.e. values not compatible with the positive values of known high-spin FeIV=O sites (Table 3). However, the third possible orientation of Dloc2 yields satisfactory values, Dloc2(Sloc2 = 2) = +8.25 cm−1 and Eloc2/Dloc2 ≈ 0 (= −0.05) in (x, y, z). This choice corresponds to a Dloc1(Sloc1 = 1) tensor that is rotated relative to Dt(St=3) such that its symmetry axis (which is along z1) is parallel to the x-axis of Dt. The A-tensor of Sloc1 = 1 FeIV=O site is, roughly, expected to be axial around the Fe-O bond, with two large components, A⊥ ≈ −21 T, and one small one, A‖ ≈ −5; see Table 3. If the above tensor orientations inferred from the zero-field splittings are correct, we must have the smallest component of A(1) along x, a suggestion borne out by the simulation parameters of Table 2. This analysis, admittedly quite rough, gives us some guidance for searching through sets of conformers that can be explored by DFT calculations. In fact, the DFT studies of section 4.1 suggest an explanation for our observations.
4. DFT Analysis and Discussion
4.1 DFT calculations
In previous reports37,19 we described the generation of two distinct diiron(IV) TPA* complexes from the reaction of 1 with H2O2, namely 2 with two ferromagnetically coupled Sloc1,2 = 1 sites and 3 with two antiferromagnetically coupled Sloc1,2 = 1 sites (see Scheme 1). Here we have presented, for the same TPA* ligand, data for two additional diiron(IV) complexes, namely 6a with two antiferromagnetically coupled Sloc1,2 = 2 sites and 6b consisting of a ferromagnetically coupled pair with an Sloc1 = 1 and Sloc2 = 2 site. Thus, the TPA* ligand can support individual iron(IV) centers in a diiron complex in two different spin states and with different coupling interactions. The spectral analyses of the preceding section have yielded two interesting novel species that raise some challenging questions: (i) Is the solution species, designated here as 6, homogeneous or does it consist of a mixture of two species? Presently, we cannot answer this question. (ii) What are the geometric structures and electronic configurations of 6a and 6b and how are they related? (iii) Why are the two Fe=O bonds in 6b roughly perpendicular? (iv) Why is one of the oxo groups in 6 readily protonated, in contrast to those of other species containing FeIV=O moieties, which are quite electrophilic and resist protonation? In the following we discuss our findings and offer considerations that provide some answers to these questions.
Species 6 is obtained by the deprotonation of the hydroxo group in the O=FeIV–O–FeIV–OH core of 2, suggesting a [O=Fe–O–Fe=O]2+ core for 6. The previously proposed structures of 2 and 5-OH have geometries for which the two non-bridging oxygen atoms are connected through a strong (1.4 to 1.8 Å) hydrogen bond forcing the O=FeamIV–O–FepyIV/III–OH structural motif to adopt a syn-like conformation. (The subscripts am and py refer to Fe atoms that have the terminal oxygen atom either trans to the TPA tertiary amine or to the nitrogen of a pyridine; this distinction is present also in the X-ray structures of 1).50,51 A key structural parameter is the OFeamFepyO dihedral angle, which is determined by the interplay of several competing interactions. On the one hand, steric interactions between the two bulky TPA ligands together with electrostatic repulsion between the two non-bridging oxo groups tend to maximize the OFeamFepyO dihedral angle and lead to an anti conformation. On the other hand, hydrogen bonding linking the two terminal oxygen atoms of the [FeO] moieties leads to a syn arrangement, as observed for 2 and 5-OH. Removal of the proton in the 2-to-6 conversion eliminates the hydrogen bond and yields a situation where steric and electrostatic repulsions are the dominant factors that control the conformation. Indeed, optimized geometries of [(TPA)O=FeIVam–O–FepyIV=O(TPA)]2+, obtained with the B3LYP/6–311G functional/basis set combination, adopt an anti conformation (regardless of the electronic configuration) corresponding to an OFeamFepyO dihedral angle of ~180° and a nearly linear Feam–O–Fepy bond angle for 6a (see Figure S10 and Tables S3–S5). A similar conformation was found for the fluoride derivative 5-F, where the hydroxo ligand of 5-OH is replaced with fluoride.19,22
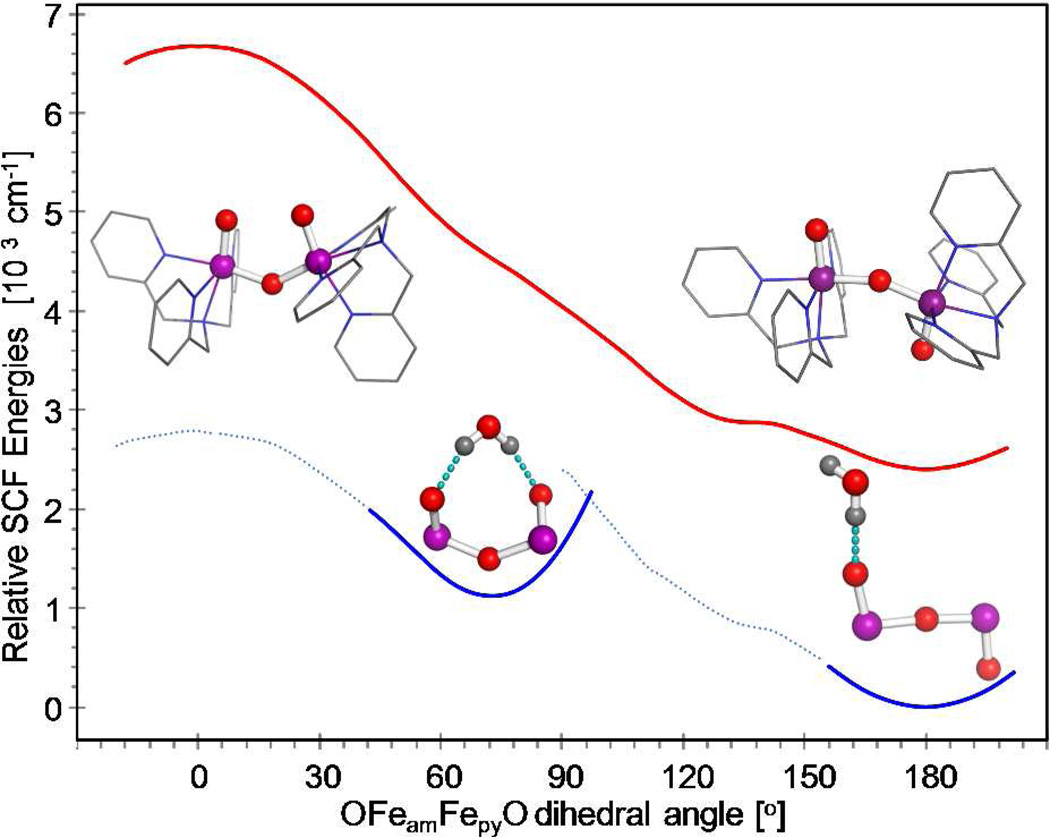
Analysis of the experimental zero-field splitting tensor of the S = 3 species 6b in section 3.2.7 has indicated that this complex adopts a conformation with two roughly orthogonal Fe=O bonds (OFeamFepyO ≈ 90°), in stark contrast with the predicted value of 180°. To resolve this apparent contradiction we explored by DFT the conformational dependence of the lowest electronic states in a series of relaxed scans of the dihedral angle. In these calculations we fixed the dihedral angle but allowed all other coordinates to be optimized. Inspection of Figure 10 (red curve) and Figure S15 reveals that the anti conformation has minimum energy. For a given electronic configuration, the anti to syn conversion requires ~12 kcal/mol, implying that a conformation with perpendicular Fe=O groups would be unstable (at least in the gas phase). The energy required for the anti to syn conversion corresponds roughly to the ~15.4 kcal/mol needed to move two point charges with 0.5 e charge from 5.26 Å to 2.66 Å, the interatomic distances predicted for the anti and syn conformers, respectively (0.5 e is approximately the value of the predicted Mulliken charges for the two terminal oxygen atoms; see Table S2). Therefore, the relaxed scans of the OFeamFepyO angle (Figures S15–S17) suggest that an additional constraint must operate to stabilize a structure with perpendicular terminal oxo groups. If a proton can enforce a syn conformation, as in 2 and 5, it is reasonable to consider the effect of a water molecule on the conformation of 6. Our preparations typically contained circa 6 equivalents of water: four equivalents present in 1,20 one equivalent from the one equivalent of 70% H2O2 solution added to produce 2 from 1, and one equivalent generated from reaction of 1 with H2O2 (see the reaction scheme in ref 20), not counting water that may have condensed into the sample during the cryogenic preparation and transfer into Mössbauer cups. A water molecule could interact with 6 by forming hydrogen bonds with either one or with both terminal oxo groups. Geometry optimization of [(TPA)O=FeIV–O–FeIV=O(TPA)]2+ in the anti conformation and in the presence of one additional water molecule predicts that the water will be strongly hydrogen-bonded to one of the terminal oxygen atoms. This is indicated in Figure 10 by the difference, at 180°, between the red and blue curves. A relaxed scan of the dihedral angle of 6 in the presence of a water molecule showed that at ~75° the two oxo groups are properly aligned for the water molecule to form hydrogen-bonds with both terminal oxygen atoms, resulting in the appearance of a second minimum (Figure S11).2
Figure 10.
Relative SCF energies as a function of the OFeamFepyO dihedral angle predicted for the Stot(Sam,Spy) = 0(2,2) configuration in the presence of a water molecule 10 Å away (red), and of a water molecule in close proximity to the O=FeIV–O–FeIV=O core (blue). The relaxed scans were obtained using the B3LYP/6–311G functional/basis-set. For the blue curve, the solid line indicates points along the scan where the hydrogen bonds with terminal oxo groups are the dominant interaction while the light dotted lines represent points for which the interaction of the water with the TPA ligands becomes sizable.
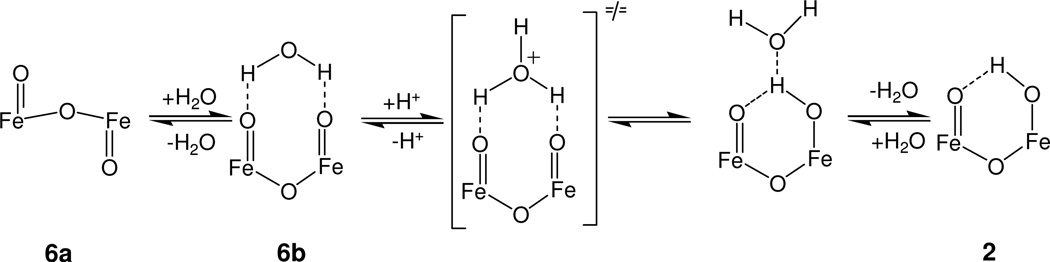
In addition to providing a justification for the stabilization of a structural conformation that espouses two nearly orthogonal Fe=O bonds, the interaction of [(TPA)O=FeIV–O–FeIV=O(TPA)]2+ with water may also offer a rationalization for the reversible protonation of 6 in liquid solution. Previously described oxoiron(IV) complexes exhibit electrophilic FeO sites that were not susceptible to protonation. This observation is consistent with the dearth of hydroxoiron(IV) species, except for P450 and CPO Compounds II34–36 and the turquoise-colored intermediate Tq described by Jensen et al.33 However, in contrast to what is observed for mononuclear complexes, protonation of 6 readily yields 2, which has a hydroxo group that is strongly stabilized by hydrogen bonding with the terminal oxo group of the second iron(IV) site. Thus, when 6 adopts a syn-like conformation the presence of a second terminal oxo group has a synergistic effect on protonation, adding to the driving force for the formation of 2. The additional water molecule considered above has two distinct effects: first, by interacting with both oxo groups, it preorganizes the O=Feam–O–Fepy=O core of 6 into a conformation that favors formation of 2; second, it functions as a proton acceptor site by mediating proton binding and release through a hydronium-containing transition state, see Scheme 2. Inspection of space filling models of the optimized structures predicted for the two minima of 6 in the presence of a water (Figure S12) shows that for the minimum at 180° the water molecule is shielded from outside by a neighboring TPA ligand. For the 75° minimum, the water molecule is engaged in hydrogen bonding with the two oxo groups, enforcing an orientation of the water that exposes its oxygen atom to the outside, in a space delimited by the bulky TPA ligands of the two sites (see Figure S12)
Scheme 2.
Proposed reaction mechanism for the water-mediated reversible protonation of complex 6.
4.2 Exchange couplings in 6a and 6b
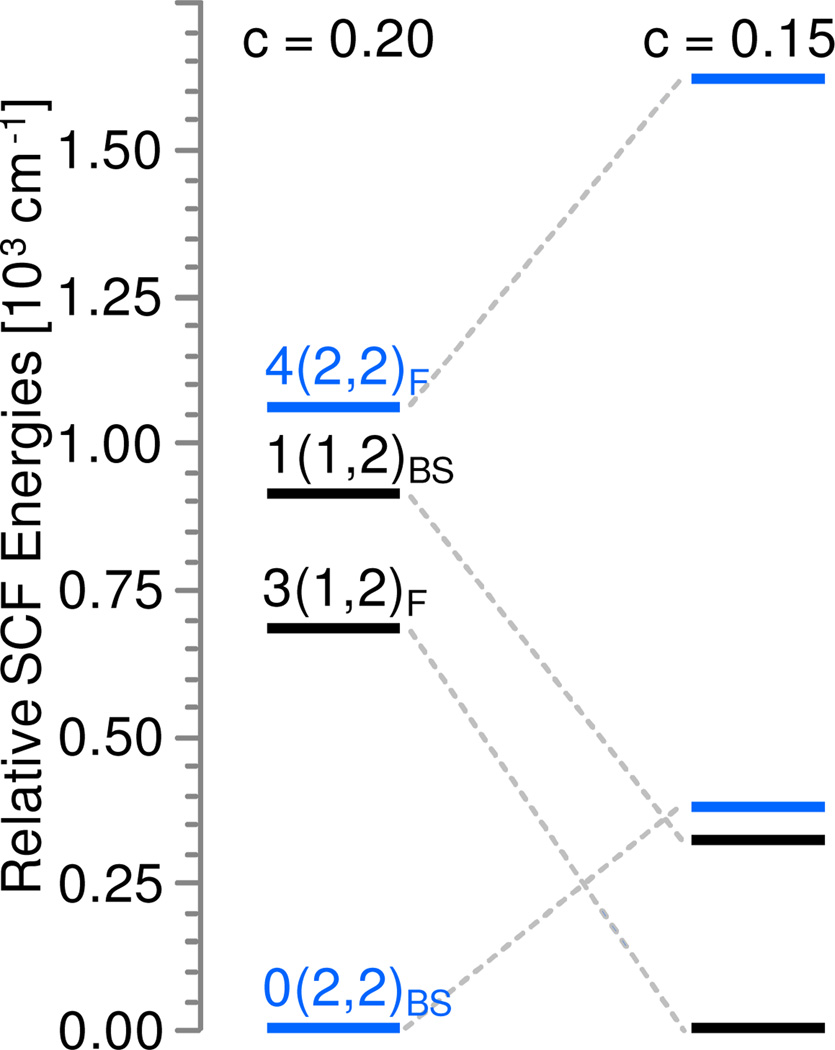
We wish to comment briefly on the exchange couplings leading to the coupled S = 0 and S = 3 states. Using the notation Stot(Sam,Spy)F,BS to indicate ferromagnetic (F) and broken symmetry (BS) states, the left column of Figure 11 shows for the anti conformer of 6 the two lowest spin ladders, Stot(2,2) and Stot(1,2); for clarity only the levels with maximum and minimum total spin are shown for each ladder. It can be seen that the 4(2,2)F and 0(2,2)BS levels (blue) bracket the 3(1,2)F and 1(1,2)BS levels.
Figure 11.
Change of the relative SCF energies predicted for the four lowest configurations of the anti conformer of 6 for two different values of c, the amount of Hartree-Fock exchange considered in the exchange functional, Exc = c ExcHF + (1-c)xcSlater + 0.72 Excnon-local. B3LYP is obtained for c = 0.2.
The energies of the (2,2) and (1,2) spin ladders span ranges of 1,060 cm−1 and 230 cm−1, which correspond to exchange coupling constants of J(2,2) = 132 cm−1 and J(1,2) = −38 cm−1, using the ℋ = J Sam•Spy convention. Note that the two spin ladders reflect antiferromagnetic and ferromagnetic coupling, respectively. The narrow energy range shows that local Sam = 1 and Sam = 2 configurations of the FeamIV=O site are close in energy such that external perturbations, such as nature of the solvent or aggregation upon freezing, may determine which of these local spin configurations is lowest. Moreover, the relaxed scans shown in Figure S15 indicate that J(2,2) and J(1,2) are strongly dependent on the OFeamFepyO dihedral angle. For example, for the second minimum at OFeamFepyO ~75° the calculated J values are 53 cm−1 and 3 cm−1, respectively. Because the local spin states are close in energy, we should anticipate that the predicted ground state may depend on the theoretical treatment of exchange interaction. To investigate one aspect of this problem we have varied the proportion of Hartree-Fock (HF) exchange in the B3LYP functional. Indeed, reduction of the HF exchange contribution to B3LYP, yielding B3LYPc (see refs 52–54) by a quarter of its original value (from 20% in B3LYP to 15%), yielded a 3(1,2) ground state for 180° and nearly degenerate 1(1,2) and 0(2,2) levels for the ~75° minimum, see Figures 11 and S14. Although we have not found a particular value for the amount of the HF exchange included in B3LYPc for which 0(2,2) is the predicted ground state configuration for one of the two minima and 3(1,2) for the other, the relevance of this result is that a minor adjustment to the functional yields either a 0(2,2) or a 3(1,2) configuration as the predicted ground state. The conclusion of our spectroscopic analysis, namely that for the S = 3 species (6b) the two FeIV=O bonds of 6 adopt an approximately perpendicular orientation, suggests that 6b corresponds to a 3(1,2) configuration pertaining to a syn conformation stabilized by the interaction of 6 with a water molecule such that the OFeamFepyO dihedral angle is ~ 75° (see Figure S11).
We have shown in ref 19 that 5-OH attains a 1/2(2, 5/2) ground state configuration that is stabilized by strong antiferromagnetic exchange interactions between the Sam = 2 of the iron(IV) and the Spy =5/2 of the high-spin ferric site. Consequently, for 5-OH we encountered a situation where superexchange interactions, promoted by a large Fe-O-Fe angle as well as by the increased number of exchange pathways available for local high spins, induced a spin state change at the oxoiron(IV) site. Inspection of the relative SCF energy diagrams shown in Figures 11, S14 and S15 suggests that for 6a a similar mechanism is operative. Thus, the 0(2,2) configuration, which comprises two high-spin iron(IV) sites, is stabilized with respect to other configurations by sizable antiferromagnetic interactions. As this mechanism is particularly effective for structures with large Fe-O-Fe angles, we assign 6a to a species that adopts a 0(2,2) configuration pertaining to an anti conformation as predicted for the minimum at OFeamFepyO = 180°.3
4.3 Relationship to Other Diiron(IV) Centers
While our investigation was progressing, Kodera and co-workers23 reported some remarkable observations regarding related high-valent diiron complexes. Their studies employed an octadentate dinucleating 6-HPA ligand consisting of two TPA units connected by an ethylene bridge via attachment to the 6-position of a pyridine on each TPA. From the reaction of [FeIII2(μ-O)(6-HPA)(OH2)2]4+ with 1.2 equiv. H2O2 and 2 equiv. Et3N in acetonitrile solution at −40 °C, a metastable species was formed; we will refer to this species as K-7. By addition of Et2O a solid could be precipitated. It will become apparent below that we must distinguish between the solution species K-7 and the solid species K-7a and K-7b. Mössbauer studies of the isolated solid at 295 K showed a quadrupole doublet, representing species K-7b, with ΔEQ = 0.44 mm/s and δ = 0.13 mm/s that represented 85% of the Fe; a minority species, K-7a, had ΔEQ = 1.64 mm/s and a δ = 0.35 mm/s. Upon lowering the temperature of the Mössbauer experiment, species K-7b decreased in intensity and was mostly replaced by K-7a, such that the latter became the dominant component (61% of Fe) at 25 K. The interconversion between the two species was reversible and controlled by changing the temperature, which Kodera et al. proposed to be an equilibrium between isomers with an FeIII2(μ-O)(μ-1,2-O2) core and an FeIV2(μ-O)(O)2 core (see Scheme 2 of Kodera et al.23). This system may thus represent the first example of reversible O–O bond cleavage in a diiron complex.
It should be noted that 6 and K-7 differ in two important respects. First, while K-7 is stable at −40 °C in CH3CN solution and at 25 °C in the solid state, 6 has a limited lifetime even at −80 °C, despite the fact that the diiron(IV) center in 6 is supported by a more electron donating ligand than 6-HPA. Secondly, K-7 exhibits visible absorption maxima at 500 nm (εM = 1100), 610 nm (εM = 820), and 783 nm (εM = 200), while 6 has a much more intense feature at 450 nm (εM ~ 6000) (Figure 1).
Nature of K-7b
Complexes K-7b and 6a exhibit a set of nearly identical ΔEQ and δ values (Table 3), suggesting that the two complexes share structural and electronic features. As shown in Section 3.2.3 complex 6a has St = 0 and must contain high-spin FeIV=O sites, based on our accumulated data for the complexes of Scheme 1. Given the similarities between 6a and K-7b, it is most probable that K-7b is an antiferromagnetically coupled high-spin diiron(IV) complex, as presumed by Kodera et al. (no magnetic data reported for K-7b in ref. 23).
Nature of K-7a
Kodera et al. formulate solid species K-7a as a diferric peroxo complex, [FeIII2(μ-O)(μ-1,2-O2)(6-HPA)]2+. The authors have tacitly assumed that the same distribution of species found in the solid exists for the species characterized in CH3CN solution by UV-vis and resonance Raman spectroscopy.23 In our view however, the K-7 solution species is a diferric peroxo complex, distinct from the K-7a and K-7b found in the solid state. In support of our interpretation we offer the following considerations.
The isomer shift of K-7a in the solid state (δ = 0.35 mm/s at 25 K) is quite unusual and significantly smaller than those of well characterized complexes with FeIII2(μ-O)(μ-1,2-O2) cores, which have δ = 0.50–0.55 mm/s.55 In fact, the δ value of 0.35 mm/s for K-7a is essentially the average of the isomer shift values for the well characterized FeIII2(μ-O)(μ-1,2-O2) complexes and those of (μ-oxo)diiron(IV) complexes 6a and K-7b, suggesting that solid state complex K-7a is not a bona fide peroxo complex but is instead a very interesting derivative that has undergone partial O–O bond homolysis to lose some of its peroxo character and in turn acquires a partial FeIII–O• or FeIV=O character, which would result in a decrease in its isomer shift relative to that a high-spin ferric center. Perhaps the ethylene tether joining the two TPA halves provides sufficient constraints to allow the reversible chemistry observed by Kodera in the solid state.
Nature of K-7
In MeCN solution, species K-7 exhibits a visible spectrum that strongly resembles those of complexes with FeIII2(μ-O)(μ-1,2-O2) cores, which arise from oxo- and peroxo-to-iron(III) charge transfer transitions.56 This assignment is supported by the resonance Raman spectrum of K-7 obtained in CH3CN solution at −40 °C showing bands at 529 cm−1 (Δ18O = −23 cm−1; λexc 407 nm) and at 820 cm−1 (Δ18O = −43 cm−1; λexc 607 nm). As we have shown for other complexes with FeIII2(μ-O)(μ-1,2-O2) cores,56 we assign these features respectively to the νsym(Fe–O–Fe) and the ν(O–O) of [FeIII2(μ-O)(μ-1,2-O2)(6-HPA)]2+. We thus disagree with Kodera’s interpretation that the 529- and 820-cm−1 features observed in solution arise from K-7b, the isomer with FeIV2(μ-O)(O)2 core, and arise respectively from the νsym(Fe–O–Fe) and ν(Fe=O) modes of K-7b. However the Raman properties of the 820 cm−1 feature are inconsistent with this assignment for two reasons. Firstly, Hooke’s Law predicts that a ν(Fe=O) mode at 820 cm−1 should have an 18O isotope shift of 35 cm−1, which is 8 cm−1 smaller than observed; in fact, the observed 43-cm−1 downshift approaches that predicted for a diatomic O–O oscillator (46 cm−1). Secondly, the 820 cm−1 feature was observed with 607-nm excitation, indicating that it is in resonance with the 620-nm band that is very likely to be a peroxo-to-iron(III) LMCT band. In contrast, the ν(Fe=O) modes of nonheme iron(IV)-oxo complexes studied thus far have only been observed with near-UV excitation due to the high energy of the oxo-to-iron(IV) LMCT transition.57 Thus, in our interpretation, [FeIII2(μ-O)(μ-1,2-O2)(6-HPA)]2+ is the species present in CH3CN solution at −40 °C; it is thermally stable at this temperature like a number of other complexes that have FeIII2(μ-O)(μ-1,2-O2) cores.55,56,58 The analogous intermediate presumably also forms in the reaction of 1 with H2O2 to generate 2. However we have been unsuccessful in our attempts to observe such a peroxo intermediate, perhaps because it decays too quickly to be observed. Clearly, the introduction of the ethylene tether between TPA units is an important design feature of the novel chemistry discovered by Kodera.
Relation of 6 to sMMOH intermediate Q
Complexes 6a and K-7b are the only synthetic diiron(IV) complexes characterized to date to have individual high-spin iron(IV) sites. Interestingly, they exhibit ΔEQ and δ values that are nearly identical to those of intermediate Q of sMMOH, which has been deduced to have a high-spin diiron(IV) center.1 This close match of the ΔEQ and δ values could be fortuitous, because the iron sites of sMMOH intermediate Q are more oxygen-rich than those of 6a and K-7b (FeNO4/5 versus FeN4O2). The reliability of the spin state assignment for these centers is limited by the strong antiferromagnetic coupling present in these complexes, which prevents the Mössbauer technique from probing excited spin states of the diiron(IV) center. Thus, the only parameters obtainable are ΔEQ and δ that describe the observed quadrupole doublet. ΔEQ is generally not diagnostic of the spin state of an iron center, so the spin state assignment is based solely on the isomer shift value, which depends not only on oxidation and spin state but also on the nature of the ligands and the coordination geometry. The spin state assignment is rendered even more difficult by the limited number of high-spin iron(IV) complexes available for comparison. The iron(IV) centers of sMMOH intermediate Q were assigned a high-spin state based on the argument that its oxygen-rich coordination environment could not support a low-spin iron(IV) center, a notion that has not been contradicted by the many DFT calculations on Q.6–8 On the other hand, the spin state assignments for the iron(IV) centers of 6a, and by inference of K-7b, are greatly strengthened by the availability of complexes related to 6a shown in Scheme 1, which have either low-spin or high-spin FeIV=O centers (Table 3). Particularly useful are the FeIIIFeIV complexes 5-OH and 5-F, which have St = 1/2 resulting from antiferromagnetic coupling of a high-spin FeIII (S = 5/2) site to the FeIV=O site: an St = 1/2 can only result if the SFe=O = 2. The measured isomer shifts for the FeIV=O sites of 5-OH and 5-F are 0.09 mm/s and 0.10 mm/s, respectively,19 values distinctly larger than those of the S = 1 complexes 218 and [FeIVO(TPA)(NCMe)]2+,43 which have δ values near 0.0 mm/s (see Table 3).
The close agreement between the Mössbauer parameters Q and 6a does not imply that 6a is necessarily a good electronic model for Q, as the iron sites in the two complexes have very different coordination environments, O-donor-rich for Q and N-donor-rich. Moreover Q and 6a differ in diiron core structure, with Q having an Fe2(μ-O)2 diamond core as deduced from EXAFS analysis3 and 6a having an open O=Fe–O–Fe=O core. From DFT calculations, 6 has six spin multiplets within an energy range of ca 1,000 cm−1, in sharp contrast to intermediate Q, which has no low-lying excited spin states. The latter property is likely to be a consequence of the significant stabilization of the S = 2 state over the S = 1 state because of the weaker-field O-donor-rich environment. On the other hand, the TPA ligand appears to provide an environment wherein S = 1 and S = 2 states are close in energy. Clearly, it would be important to generate diiron(IV) complexes supported by an O-donor-rich coordination sphere.
Supplementary Material
Acknowledgments
This work has been supported by NIH Grants GM38767 (to LQ) and EB-001475 (to EM) and NSF grant CHE1012485 (to EM). Furthermore, this work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575 under grant TG-CHE070073 (to ELB).
Footnotes
Given that both a ground and an excited state resonance are observed from the same multiplet, there is no parameter set for which our data can fit to an St = 1 system, eliminating the possibility that 6b is antiferromagnetically coupled.
A dihedral angle of 75° is not in conflict with our analysis of the S = 3 ZFS tensor, which was based on the rough, but necessary, assumption that all tensors of 6b have collinear principal axes.
The DFT calculations favor the 3(1,2) conformation by ca. 1000 cm−1 over 3(2,1), i. e. the Sloc = 2 FeIV=O site for which the oxo group is trans to a pyridine, see Table S1.
Supporting Information
Additional Mössbauer spectra and simulations, as well as a summary of DFT results and references. This material is available free of charge at http://pubs.acs.org.
References
- 1.Lee S-K, Fox BG, Froland WA, Lipscomb JD, Münck E. J. Am. Chem. Soc. 1993;115:6450. [Google Scholar]
- 2.Liu KE, Valentine AM, Wang D, Huynh BH, Edmondson DE, Salifoglou A, Lippard SJ. J. Am. Chem. Soc. 1995;117:10174. [Google Scholar]
- 3.Shu L, Nesheim JC, Kauffmann K, Münck E, Lipscomb JD, Que L., Jr Science. 1997;275:515. doi: 10.1126/science.275.5299.515. [DOI] [PubMed] [Google Scholar]
- 4.Sturgeon BE, Burdi D, Chen S, Huynh BH, Edmondson DE, Stubbe J, Hoffman BM. J. Am. Chem. Soc. 1996;118:7551. [Google Scholar]
- 5.Price JC, Barr EW, Tirupati B, Bollinger JM, Jr, Krebs C. Biochemistry. 2003;42:7497. doi: 10.1021/bi030011f. [DOI] [PubMed] [Google Scholar]
- 6.Siegbahn PEM. Inorg. Chem. 1999;38:2880. doi: 10.1021/ic981332w. [DOI] [PubMed] [Google Scholar]
- 7.Gherman BF, Dunietz BD, Whittington DA, Lippard SJ, Friesner RA. J. Am. Chem. Soc. 2001;123:3836. doi: 10.1021/ja0055108. [DOI] [PubMed] [Google Scholar]
- 8.Han WG, Noodleman L. Inorg. Chim. Acta. 2008;361:973. doi: 10.1016/j.ica.2007.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Que L., Jr Acc. Chem. Res. 2007;40:493. doi: 10.1021/ar700024g. [DOI] [PubMed] [Google Scholar]
- 10.McDonald AR, Que L., Jr Coord. Chem. Rev. 2013;257:414. [Google Scholar]
- 11.Pestovsky O, Stoian S, Bominaar EL, Shan X, Münck E, Que L, Jr, Bakac A. Angew. Chem. Int. Ed. 2005;44:6871. doi: 10.1002/anie.200502686. [DOI] [PubMed] [Google Scholar]
- 12.England J, Guo Y, Farquhar ER, Young VG, Jr, Münck E, Que L., Jr J. Am. Chem. Soc. 2010;132:8635. doi: 10.1021/ja100366c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lacy DC, Gupta R, Stone KL, Greaves J, Ziller JW, Hendrich MP, Borovik AS. J. Am. Chem. Soc. 2010:12188. doi: 10.1021/ja1047818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.England J, Guo Y, Van Heuvelen KM, Cranswick MA, Rohde GT, Bominaar EL, Münck E, Que L., Jr J. Am. Chem. Soc. 2011;133:11880. doi: 10.1021/ja2040909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bigi JP, Harman WH, Lassalle-Kaiser B, Robles DM, Stich TA, Yano J, Britt RD, Chang CJ. J. Am. Chem. Soc. 2012;134:1536. doi: 10.1021/ja207048h. [DOI] [PubMed] [Google Scholar]
- 16.Xue G, Wang D, De Hont R, Fiedler AT, Shan X, Münck E, Que L., Jr Proc. Natl. Acad. Sci. U. S. A. 2007;104:20713. doi: 10.1073/pnas.0708516105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xue G, De Hont R, Münck E, Que L., Jr Nat. Chem. 2010;2:400. doi: 10.1038/nchem.586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Xue G, Fiedler AT, Martinho M, Münck E, Que L., Jr Proc. Natl. Acad. Sci. U.S.A. 2008;105:20615. [Google Scholar]
- 19.De Hont RF, Xue G, Hendrich MP, Que L, Jr, Bominaar EL, Münck E. Inorg. Chem. 2010;49:8310. doi: 10.1021/ic100870v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Do LH, Xue G, Que L, Jr, Lippard SJ. Inorg. Chem. 2012;51:2393. doi: 10.1021/ic202379b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xue G, Pokutsa A, Que L., Jr J. Am. Chem. Soc. 2011;133:16657. doi: 10.1021/ja207131g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Xue G, Geng C, Ye S, Fiedler AT, Neese F, Que L., Jr Inorg. Chem. 2013;52:3976. doi: 10.1021/ic3027896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kodera M, Kawahara Y, Hitomi Y, Nomura T, Ogura T, Kobayashi Y. J. Am. Chem. Soc. 2012;134:13236. doi: 10.1021/ja306089q. [DOI] [PubMed] [Google Scholar]
- 24.Armarego WLF, Perrin DD. Purification of Laboratory Chemicals. Butterworth-Heinemann; Oxford: p. 1997. [Google Scholar]
- 25.Cox DP, Terpinski J, Lawrynowicz WJ. Org. Chem. 1984;49:3216. [Google Scholar]
- 26.England J, Martinho M, Farquhar ER, Frisch JR, Bominaar EL, Münck E, Que L., Jr Angew. Chem. Int. Ed. 2009;48:3622. doi: 10.1002/anie.200900863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Frisch JR, Vu VV, Martinho M, Münck E, Que L., Jr Inorg. Chem. 2009;48:8325. doi: 10.1021/ic900961k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vrajmasu V, Münck E, Bominaar EL. Inorg. Chem. 2003;42:5974. doi: 10.1021/ic0301371. [DOI] [PubMed] [Google Scholar]
- 29.Sun H, DiMagno SG. J. Am. Chem. Soc. 2005;127:2050. doi: 10.1021/ja0440497. [DOI] [PubMed] [Google Scholar]
- 30.Lenarcik B, Ojczenasz P. J. Heterocyclic Chem. 2002;39:287. [Google Scholar]
- 31.Fukuzumi S, Morimoto Y, Kotani H, Naumov P, Lee YM, Nam W. Nat. Chem. 2010;2:756. doi: 10.1038/nchem.731. [DOI] [PubMed] [Google Scholar]
- 32.Wang D, Zhang M, Bühlmann P, Que L., Jr J. Am. Chem. Soc. 2010;132:7638. doi: 10.1021/ja909923w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jensen MP, Costas M, Ho RYN, Kaizer J, Payeras AMi, Münck E, Que L, Jr, Rohde JU, Stubna A. J. Am. Chem. Soc. 2005;127:10512. doi: 10.1021/ja0438765. [DOI] [PubMed] [Google Scholar]
- 34.Green MT, Dawson JH, Gray HB. Science. 2004;304:1653. doi: 10.1126/science.1096897. [DOI] [PubMed] [Google Scholar]
- 35.Behan RK, Hoffart LM, Stone KL, Krebs C, Green MT. J. Am. Chem. Soc. 2006;128:11471. doi: 10.1021/ja062428p. [DOI] [PubMed] [Google Scholar]
- 36.Stone KL, Behan RK, Green MT. Proc. Natl. Acad. Sci. U. S. A. 2006;103:12307. doi: 10.1073/pnas.0603159103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Martinho M, Xue G, Fiedler AT, Que L, Jr, Bominaar EL, Münck E. J. Am. Chem. Soc. 2009;131:5823. doi: 10.1021/ja8098917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dunham WR, Harding L, Sands RH. Eur. J. Biochem. 1993;214:1. doi: 10.1111/j.1432-1033.1993.tb17889.x. [DOI] [PubMed] [Google Scholar]
- 39.Krzystek J, England J, Ray K, Ozarowski A, Smirnov D, Que L, Jr, Telser J. Inorg. Chem. 2008;47:3483. doi: 10.1021/ic800411c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bencini A, Gatteschi D. Electron Paramagnetic Resonance of Exchange Coupled Systems. Springer Verlag; Berlin: p. 1990. [Google Scholar]
- 41.Zimmermann R, Münck E, Brill WJ, Shah VK, Henzl MT, Rawlings J, Orme-Johmson WH. Biochim. Biophys. Acta. 1978;537:185. doi: 10.1016/0005-2795(78)90504-4. [DOI] [PubMed] [Google Scholar]
- 42.Dabrowski L, Piekoszewski J, Suwalski J. Nucl. Inst. Methods. 1971;91:93. [Google Scholar]
- 43.Lim MH, Rohde JU, Stubna A, Bukowski MR, Costas M, Ho RYN, Münck E, Nam W, Que L., Jr Proc. Natl. Acad. Sci. U. S. A. 2003;100:3665. doi: 10.1073/pnas.0636830100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rohde JU, In JH, Lim MH, Brennessel WW, Bukowski MR, Stubna A, Münck E, Nam W, Que L., Jr Science. 2003;299:1037. doi: 10.1126/science.299.5609.1037. [DOI] [PubMed] [Google Scholar]
- 45.Van Heuvelen KM, Fiedler AT, Shan X, De Hont RH, Meier KK, Bominaar EL, Münck E, Que L., Jr Proc. Natl. Acad. Sci. U. S. A. 2012;109:11933. doi: 10.1073/pnas.1206457109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Company A, Prat I, Frisch JR, Mas-Ballesté R, Güell M, Juhász G, Ribas X, Münck E, Luis JM, Que L, Jr, Costas M. Chem. Eur. J. 2011;17:1622. doi: 10.1002/chem.201002297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kaizer J, Klinker EJ, Oh NY, Rohde JU, Song WJ, Stubna A, Kim J, Nam W, Münck E, Que L., Jr J. Am. Chem. Soc. 2004;126:472. doi: 10.1021/ja037288n. [DOI] [PubMed] [Google Scholar]
- 48.Klinker EJ, Jackson TA, Jensen MP, Stubna A, Juhász G, Bominaar EL, Münck E, Que L., Jr Angew. Chem. Int. Ed. 2006;45:7394. doi: 10.1002/anie.200602799. [DOI] [PubMed] [Google Scholar]
- 49.Sinnecker S, Svensen N, Barr EW, Ye S, Bollinger JM, Jr, Neese F, Krebs C. J. Am. Chem. Soc. 2007;129:6168. doi: 10.1021/ja067899q. [DOI] [PubMed] [Google Scholar]
- 50.Hazell A, Jensen KB, McKenzie CJ, Toftlund H. Inorg. Chem. 1993;33:3127. [Google Scholar]
- 51.Wilkinson EC, Dong Y, Que L., Jr J. Am. Chem. Soc. 1994;116:8394. [Google Scholar]
- 52.Reiher M, Salomon O, Hess BA. Theor. Chem. Acc. 2001;107:48. [Google Scholar]
- 53.Salomon O, Reiher M, Hess BA. J. Chem. Phys. 2002;117:4729. [Google Scholar]
- 54.Huang SP, Shiota Y, Yoshizawa K. Dalton Trans. 2013;42:1011. doi: 10.1039/c2dt31304a. [DOI] [PubMed] [Google Scholar]
- 55.Cranswick MA, Meier KK, Shan X, Stubna A, Kaizer J, Mehn MP, Münck E, Que L., Jr Inorg. Chem. 2012;51:10417. doi: 10.1021/ic301642w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Fiedler AT, Shan X, Mehn MP, Kaizer J, Torelli S, Frisch JR, Kodera M, Que L., Jr J. Phys. Chem. A. 2008;112:13037. doi: 10.1021/jp8038225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jackson TA, Rohde JU, Seo MS, Sastri CV, DeHont R, Stubna A, Ohta T, Kitagawa T, Münck E, Nam W, Que L., Jr J. Am. Chem. Soc. 2008;130:12394. doi: 10.1021/ja8022576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kryatov SV, Taktak S, Korendovych IV, Rybak-Akimova EV, Kaizer J, Torelli S, Shan X, Mandal S, MacMurdo V, Mairata i Payeras A, Que L., Jr Inorg. Chem. 2005;44:85. doi: 10.1021/ic0485312. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.