Abstract
Transcriptional delay can significantly impact the dynamics of gene networks. Here we examine how such delay affects bistable systems. We investigate several stochastic models of bistable gene networks and find that increasing delay dramatically increases the mean residence times near stable states. To explain this, we introduce a non-Markovian, analytically tractable reduced model. The model shows that stabilization is the consequence of an increased number of failed transitions between stable states. Each of the bistable systems that we simulate behaves in this manner.
Transcriptional delay [41] in gene networks is the dynamical consequence of the sequential nature of protein production [1–4]. For transcriptional signaling this delay is further compounded by the time it takes for transcription factors to find their target promoters [5, 6]. Previous theoretical work has shown that such delay can significantly affect the dynamics of gene networks and play an important role in a variety of naturally-occurring genetic network architectures. For example, delay produces oscillations in models of networks containing transcriptional negative feedback loops [3, 7–11]. In addition, delayed negative feedback is theorized to govern the dynamics of circadian oscillators [2, 12], a hypothesis experimentally verified in mammalian cells [13]. Experiments also suggest that transcriptional delay can produce robust, tunable oscillations in synthetic gene circuits [14, 15].
In this Letter we study the impact of delay on bistable gene networks. Bistability is a central characteristic of biological switches: It is essential in the determination of cell fate in multicellular organisms [16], the regulation of cell-cycle oscillations during mitosis [17], and the maintenance of epigenetic traits in microbes [18]. Due to the stochastic nature of gene expression, bistable gene networks can randomly switch between stable states [19]. This phenomenon has been studied in many contexts, including the lysis/lysogeny switch of bacteriophage λ [20, 21], bacterial persistence [22], and synthetically constructed positive feedback loops [23, 24].
While delay and bistability have been extensively studied, the impact of transcriptional delay on bistable gene networks is not clear. In general, the interaction between delay and stochasticity is complex. Modeling suggests delay affects the stochastic properties of gene expression [25–28], and that stochastic delay can accelerate signaling in genetic pathways [4]. The effect of delay on the mean first passage times for Langevin-approximations to bistable gene networks has been studied, but no general principles have been proposed. Indeed, many results appear to contradict each other [29–33]. There are many possible reasons for these discrepancies. For instance, Langevin approximations can fail at small system sizes typically found inside cells, and ad hoc choices of Langevin models can lead to different predictions for the same underlying system.
Here, we investigate a variety of bistable gene networks using a modified version of the Gillespie algorithm that allows us to incorporate transcriptional delay [34]. Although the details and dimensionality of the networks differ, in each the mean residence times near the stable states increase dramatically with even modest increases in transcriptional delay time (See Fig. 1). In some cases, stability increases despite the fact that the stationary distributions show no appreciable change. To explain this phenomenon, we construct a non-Markovian, analytically tractable model. The model predicts that the enhanced stability is due to an increase in the number of failed transitions between stable states. Exact stochastic simulations of each bistable system verify this prediction.
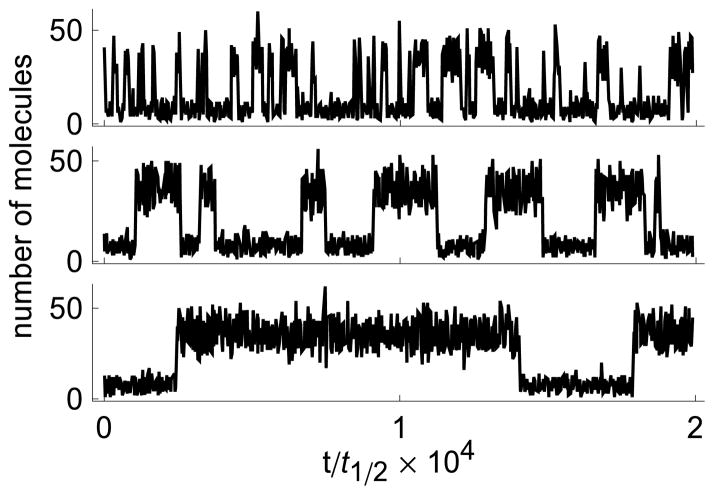
FIG. 1. Sample trajectories for a single gene positive feedback loop.
From top to bottom, the three timeseries correspond to transcriptional delays τ = 0, t1/2, and 2t1/2, where t1/2 is the half-life of the protein.
Models and simulations
To explore the impact of transcriptional delay on bistable gene networks, we simulated three common systems: 1) A single-gene positive feedback loop; 2) the co-repressive toggle switch [23]; and 3) the lysis/lysogeny switch of phage λ [21]. Details about the models, parameters, and simulations can be found in the Supplementary Information (SI).
Consider the single-gene positive feedback loop shown in Fig. 2-A. The corresponding deterministic dynamics are given by the delay differential equation
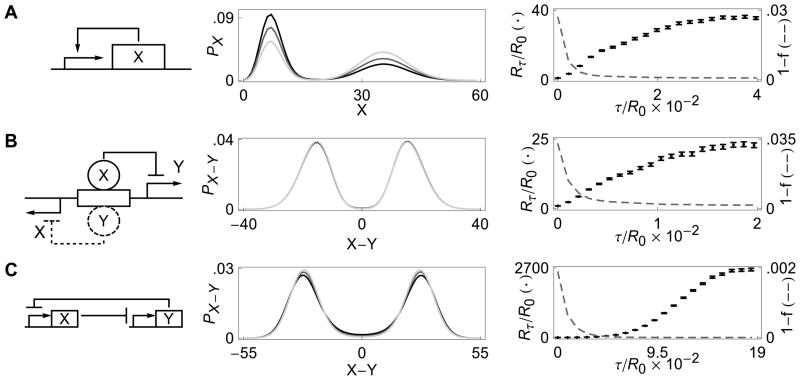
FIG. 2. The impact of transcriptional delay on three different genetic networks.
Left panels show the three different gene networks, center panels show the stationary distributions at three different values of transcriptional delay, τ, and right panels illustrate the increase in residence times (dots) and the decrease in the probability of a successful transition (dashed lines) with increasing τ. Rτ denotes the mean residence time in the metastable states at delay τ. The lighter stationary distributions correspond to larger delays; (A) Positive feedback model with stationary distributions at τ = 0, 1, 2, and R0 = 227; (B) λ–phage model with stationary distributions at τ = 0, 5, 10, and R0 = 4829; (C) Co-repressive toggle switch with stationary distributions at τ = 0, 0.45, 0.9, and R0 = 489.
| (1) |
where x is the number of proteins per unit volume, α the basal transcription rate due to leakiness of the promoter, β the increase in transcription rate due to protein binding to the promoter, b the Hill coefficient, c the concentration of x needed for half-maximal induction, γ the degradation rate coefficient of the protein, and τ is the transcriptional delay time.
This positive feedback loop is bistable for a range of parameters. As shown in the SI, the stability of the two fixed points generally decreases with an increase in delay in Eq. (1).
In the corresponding stochastic model, births and deaths occur at rates indicated in the equation. We chose parameters for which the system switches stochastically between the two stable states, and examined a biophysically relevant range of delays. These were on the order of the protein half-life, but small compared to the transition timescales.
While an increase in delay destabilized the fixed points in the deterministic model, in the stochastic counterpart it resulted in a sharp increase in the average residence time near the stable states (See Fig. 1 and 2-A, panel 3). Qualitatively similar behavior was observed in other models of bistable gene networks we examined (See Fig. 2). Although these systems are quite different, increasing transcriptional delay has qualitatively the same effect in all cases.
Simulations showed that with an increase in transcriptional delay: a) the mean residence time near the stable states increases (right panels of Fig. 2); b) the probability of a successful transition decreases; and c) the increase in stability may not be accompanied by a consistent change in the stationary distribution (center panels of Fig. 2). These observations appear to be independent of the model system and therefore may have an underlying, unified explanation. However, since the stationary distributions do not necessarily change in the manner predicted by Kramers’ theory [35], a new explanation of the phenomenon is necessary.
Reduced model
In order to obtain a unified description of the observed increase in stability with an increase in transcriptional delay, we introduce a generalized 3-state reduced model (RM). Two of the states in the model correspond to neighborhoods of the two stable fixed points. We call these states H (high) and L (low). The third state is an intermediate state, I, corresponding to a neighborhood of the separatrix. All transitions between H and L must pass through I. Therefore, the RM represents a coarse projection of a general bistable model where large fluctuations push the system from the stable states into a neighborhood of the separatrix.
Due to transcriptional delay, the transition rates between the states depend on the history of the system. This is particularly important when the system is in state I. In the absence of delay the system has no memory; the likelihood of a transition to either stable state from a neighborhood of the separatrix is determined only by the present state of the system. However, in the presence of delay, this likelihood will depend on the past.
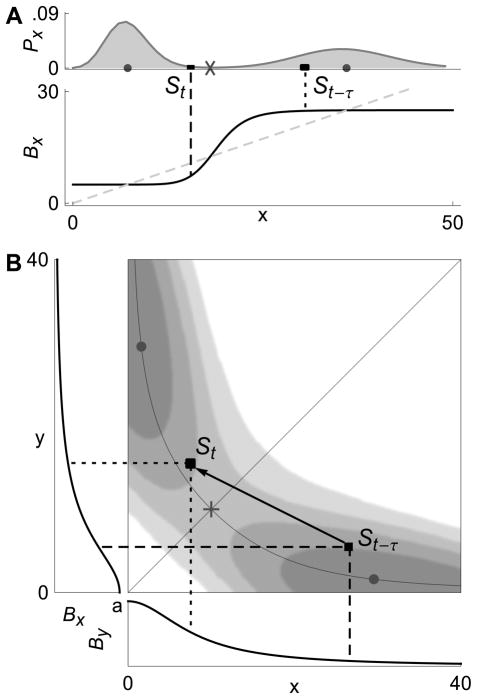
As a particular example, consider the positive feedback loop (Fig. 2A). At the upper stable state, which corresponds to state H in the RM, protein production is high. Consider a large fluctuation from this state that takes the system away from the upper fixed point, to state St shown in Fig. 3A. In the presence of transcriptional delay, birth rates are determined by the state St−τ = x(t − τ). The larger τ, the more likely it is that x(t − τ) is in state H, near the fixed point whose neighborhood has just been abandoned. But the birth rates in state H are high and favor motion back toward H (See Fig. 3A). Therefore, the trajectory is pulled back towards the stable state it came from. Thus, memory in the system acts as a “rubber band” and causes resistance to transitions.
FIG. 3. Phase space dynamics.
The state of the system at time t − τ and time t is shown in the case of (A) a positive feedback loop, and (B) a genetic toggle switch. Mature proteins enter the population at time t at rates determined by the state at time t − τ. In (A), at time t, the birth rate Bx of x is larger in the past, and production is higher than if the birth rate was determined by the present state of the system, St. This facilitates a return to the previously visited stable state. A similar explanation holds for (B) (see text). Stationary densities are shown in both cases.
The situation is similar for the genetic toggle switch, a network of two mutually repressing genes expressing proteins x and y. At the stable states of this system (dots in Fig. 3B), the birth rate of one protein is high, and that of the other is low. Consider a fluctuation away from state H, where x is high and y low, to state St = (x(t), y(t)). Birth rates are again determined by the state St−τ = (x(t − τ), y(t − τ)). As shown in Fig. 3B, in state St−τ both the birth rates of x and y at t − τ favor motion back to H. Hence in systems of interacting genes, the “rubber band” effect may be even stronger.
To capture the effects of memory in the RM, the transition rates between states are assumed to depend on the state of the system in the past. We define , for i, j, k ∊; {H, I, L}, as the rate of transition from state j to state k, given that τ units in the past the system was in state i. Not all transitions are possible, as transitions out of states H and L must go into state I.
We make several assumptions on these transition rates. First, the delay τ is small compared to the mean residence time in each of the stable states. Therefore, if the system is in state H or L at time t, it is unlikely that it was in state I at time t − τ.
Second, we assume that the six transition rates, , out of state I are at least an order of magnitude larger than transition rates out of states L and H. This corresponds to the assumption that the system will exit the vicinity of the separatrix much more quickly than the vicinity of a stable fixed point.
Finally, we assume that for time τ after entering state I, the system is more likely to return to its previous state. In other words, we assume
| (2) |
where
is the probability of transitioning from state I to state j ∈ {H, L} given the system was in state i a time τ in the past. This assumption captures the “rubber band” effect illustrated in Fig. 3, i.e. delayed protein production favors a return to the stable state that was visited last.
Metastability as a function of delay
We now analyze the stability of states H and L as a function of the delay, τ. Let RH denote the residence time for state H. We compute the expected value E[RH ]; the computations for L are analogous. Once the system enters state H, it will make a number of failed transitions of the form H → I → H before eventually making a successful transition H → I → L. Let fH denote the probability of a failed transition, that is, the probability that a transition H → I → H occurs conditioned on the system having been in state H for at least time τ. We have
| (3) |
where we define ZH (τ) by
Note that fH is a convex linear combination of and . When τ = 0 (Markovian case), . As τ increases away from zero, fH moves toward .
Let FH denote the random time needed to complete a failed transition and let SH denote the time needed for a successful transition. Assuming that the delay is small compared to the characteristic residence times in the stable states, we obtain the key estimate for E[RH ]. Writing R = RH, f = fH, F = FH, S = SH, and , we have
| (4) |
The primary contribution in Eq. (4) comes from the term f(1 − f)−1 representing the mean number of failed transitions of the form H → I → H before a successful transition H → I → L. The terms E[F ] and E[S] are not very sensitive to τ. On the other hand, because of the inequalities (2), f(1 − f) −1 grows rapidly as τ increases from τ = 0. If the states H and L are sufficiently stable, the expected time spent in each state before a large fluctuation is approximately λ−1.
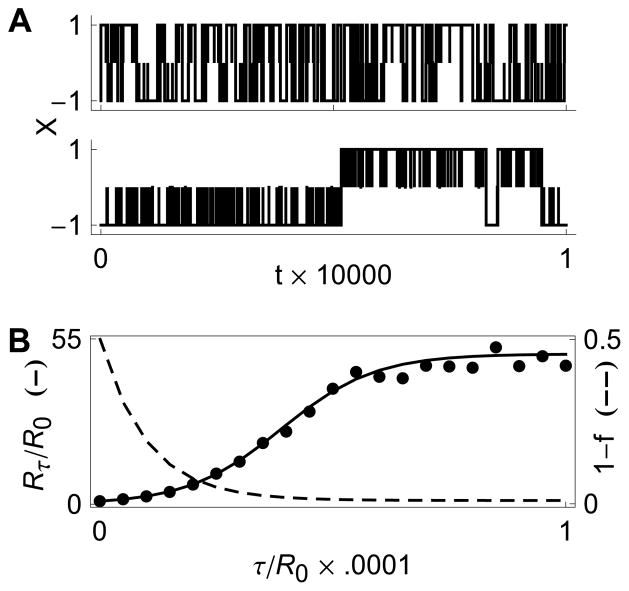
Fig. 4B illustrates that the RM qualitatively behaves like the models shown in Fig. 2.
FIG. 4. The reduced model.
(A) Sample trajectories for the 3-state RM. Top and bottom trajectories correspond to τ = 0 and τ = 0.03, respectively. (B) The estimated increase in mean residence time as a function of delay given by Eq. (4) (Left axis, solid line) compared to values obtained by simulating the RM (bold circles). The dashed line represents the probability of a successful transition as a function of delay (Right axis).
Concluding remarks
The existence of multiple stable states is a common feature of genetic networks, such as those that determine cell fate in multicellular organisms [16]. Since noise is ubiquitous in gene networks, mechanisms that stabilize dynamics are essential. We have shown that transcriptional delay can stabilize bistable gene networks. The tendency to return to the state from which the system just escaped increases with delay.
The RM proposed in this Letter depends on neither the explicit underlying model, the specific distribution of delay times, nor on the exact mechanism that produces the delay. Therefore, we conclude: (a) That distributed delay will stabilize bistable systems, provided the delay distribution is not close to the residence times of the system; as shown in SI Fig. S2, this is indeed the case; (b) A decrease in stability can be observed by delaying degradation and keeping production instantaneous (see SI Fig. S3). The explanation given in Fig. 3 carries over to this case: Delayed death pushes the system away from the stable state that was just visited; and (c) The particular details of the mechanism that produce the delay are not important (these mechanisms are yet to be characterized completely experimentally). Hence, the effect should be observable even in more detailed models that explicitly model sequential protein production.
In some previous studies of bistable systems in the presence of delay, it was assumed that the delay time was on the order of the residence time [36, 37]. In this case, it was sufficient to consider reductions with only two states, e.g. H and L. However, transcriptional delays in gene networks are typically much smaller than residence times. As we have shown here, in such systems it is therefore appropriate to introduce an additional intermediate state, e.g. I, in a reduced model.
Transcriptional delay introduces a number of other dynamical changes to stochastic bistable systems. For instance, typical transition paths between the stable states change with delay (see SI Fig. S4). Such changes depend on the specifics of the individual models, and cannot be understood using the reduction described above. Precise results for large deviations in delayed Langevin equations have been obtained [30, 38]. However, the correct Langevin approximations of the models we consider here need to include delay in the diffusion term [39, 40]). Extensions of previous large deviation approaches may provide more detailed information about transitions between states in particular models of genetic switches.
Supplementary Material
Acknowledgments
We thank Lee DeVille for insightful discussions. This work was funded by the NIH, through the joint NSF/NIGMS Mathematical Biology Program grant R01GM104974, Robert A. Welch Foundation grant C-1729, and a John S. Dunn Foundation Collaborative Research Award Program administered by the Gulf Coast Consortia.
References
- 1.McAdams HH, Shapiro L. Science. 1995;269:650. doi: 10.1126/science.7624793. [DOI] [PubMed] [Google Scholar]
- 2.Smolen P, Baxter DA, Byrne JH. Biophys J. 2002;83:2349. doi: 10.1016/S0006-3495(02)75249-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mather W, Bennett MR, Hasty J, Tsimring LS. Phys Rev Lett. 2009;102:068105. doi: 10.1103/PhysRevLett.102.068105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Josić K, Ott W, Lopez JM, Shiau LJ, Bennett MR. PLoS Comp Biol. 2011;7:e1002264. doi: 10.1371/journal.pcbi.1002264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Berg OG, Winter RB, von Hippel PH. Biochem. 1981;20:6929. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
- 6.Li GW, Berg OG, Elf J. Nat Phys. 2009;5:294. [Google Scholar]
- 7.Amir A, Meshner S, Beatus T, Stavans J. Molec Microbiol. 2010;76:428. doi: 10.1111/j.1365-2958.2010.07111.x. [DOI] [PubMed] [Google Scholar]
- 8.Goodwin BC. Adv Enzyme Regul. 1965;3:425. doi: 10.1016/0065-2571(65)90067-1. [DOI] [PubMed] [Google Scholar]
- 9.Lewis J. Curr Biol. 2003;13:1398. doi: 10.1016/s0960-9822(03)00534-7. [DOI] [PubMed] [Google Scholar]
- 10.Monk NA. Curr Biol. 2003;13:1409. doi: 10.1016/s0960-9822(03)00494-9. [DOI] [PubMed] [Google Scholar]
- 11.Smolen P, Baxter DA, Byrne JH. Am J Physiol. 1999;277:C777. doi: 10.1152/ajpcell.1999.277.4.C777. [DOI] [PubMed] [Google Scholar]
- 12.Sriram K, Gopinathan MS. J Theor Biol. 2004;231:23. doi: 10.1016/j.jtbi.2004.04.006. [DOI] [PubMed] [Google Scholar]
- 13.Ukai-Tadenuma M, Yamada RG, Xu H, Ripperger JA, Liu AC, Ueda HR. Cell. 2011;144:268. doi: 10.1016/j.cell.2010.12.019. [DOI] [PubMed] [Google Scholar]
- 14.Stricker J, Cookson S, Bennett MR, Mather WH, Tsimring LS, Hasty J. Nature. 2008;456:516. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tigges M, Marquez-Lago TT, Stelling J, Fussenegger M. Nature. 2009;457:309. doi: 10.1038/nature07616. [DOI] [PubMed] [Google Scholar]
- 16.Hong T, Xing J, Li L, Tyson JJ. BMC Syst Biol. 2012;6:66. doi: 10.1186/1752-0509-6-66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.He E, Kapuy O, Oliveira RA, Uhlmann F, Tyson JJ, Novák B. Proc Natl Acad Sci USA. 2011;108:10016. doi: 10.1073/pnas.1102106108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ozbudak EM, Thattai M, Lim HN, Shraiman BI, van Oudenaarden A. Nature. 2004;427:737. doi: 10.1038/nature02298. [DOI] [PubMed] [Google Scholar]
- 19.Kepler TB, Elston TC. Biophys J. 2001;81:3116. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Aurell E, Sneppen K. Phys Rev Lett. 2002;88:048101. doi: 10.1103/PhysRevLett.88.048101. [DOI] [PubMed] [Google Scholar]
- 21.Warren PB, ten Wolde PR. J Phys Chem B. 2005;109:6812. doi: 10.1021/jp045523y. [DOI] [PubMed] [Google Scholar]
- 22.Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. Science. 2004;305:1622. doi: 10.1126/science.1099390. [DOI] [PubMed] [Google Scholar]
- 23.Gardner TS, Cantor CR, Collins JJ. Nature. 2000;403:339. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 24.Nevozhay D, Adams RM, Van Itallie E, Bennett MR, Balázsi G. PLoS Comp Biol. 2012;8:e1002480. doi: 10.1371/journal.pcbi.1002480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bratsun D, Volfson D, Tsimring LS, Hasty J. Proc Natl Acad Sci USA. 2005;102:14593. doi: 10.1073/pnas.0503858102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Grönlund A, Lötstedt P, Elf J. Proc Natl Acad Sci USA. 2010;107:8171. doi: 10.1073/pnas.0913317107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Maithreye R, Sarkar RR, Parnaik V, Sinha S. PLoS One. 2008;3:e2972. doi: 10.1371/journal.pone.0002972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Scott M. Phys Rev E. 2009;80:031129. doi: 10.1103/PhysRevE.80.031129. [DOI] [PubMed] [Google Scholar]
- 29.Wang C, Yi M, Yang K. Systems Biology (ISB). 2011 IEEE International Conference on; 2011. pp. 101–110. [Google Scholar]
- 30.Schwartz IB, Carr TW, Billings L, Dykman M. 2012 arXiv:1207.7278v1. [Google Scholar]
- 31.Jia ZL. Chin Phys Lett. 2008;25:1209. [Google Scholar]
- 32.Lei J, He G, Liu H, Nie Q. Nonlinearity. 2009;22:2845. doi: 10.1088/0951-7715/22/12/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang C-J. Int J Mod Phys B. 2013;27:1350085. [Google Scholar]
- 34.Schlicht R, Winkler G. J Math Biol. 2008;57:613. doi: 10.1007/s00285-008-0178-y. [DOI] [PubMed] [Google Scholar]
- 35.Hänggi P, Talkner P, Borkovec M. Rev Mod Phys. 1990;62:251. [Google Scholar]
- 36.Tsimring L, Pikovsky A. Phys Rev Lett. 2001;87:250602. doi: 10.1103/PhysRevLett.87.250602. [DOI] [PubMed] [Google Scholar]
- 37.Masoller C. Phys Rev Lett. 2003;90:020601. doi: 10.1103/PhysRevLett.90.020601. [DOI] [PubMed] [Google Scholar]
- 38.Fischer M, Imkeller P. Stoch Dyn. 2005;5:247. [Google Scholar]
- 39.Brett T, Galla T. 2013 http://arxiv.org/abs/1302.7166.
- 40.Tian T, Burrage K, Burrage PM, Carletti M. J Comput Appl Math. 2007;205:696. [Google Scholar]
- 41.Here, we define “transcriptional delay” as the time from initiation of protein production to the first binding of a target promoter. This time includes not only transcription, but also, e.g. translation, folding, and diffusion.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.