Accelerating Dynamic Magnetic Resonance Imaging (MRI) for Lung Tumor Tracking Based on Low-Rank Decomposition in the Spatial–Temporal Domain: A Feasibility Study Based on Simulation and Preliminary Prospective Undersampled MRI

Abstract

Purpose

To evaluate a low-rank decomposition method to reconstruct down-sampled k-space data for the purpose of tumor tracking.

Methods and Materials

Seven retrospective lung cancer patients were included in the simulation study. The fully-sampled k-space data were first generated from existing 2-dimensional dynamic MR images and then down-sampled by 5 × −20 × before reconstruction using a Cartesian undersampling mask. Two methods, a low-rank decomposition method using combined dynamic MR images (k-t SLR based on sparsity and low-rank penalties) and a total variation (TV) method using individual dynamic MR frames, were used to reconstruct images. The tumor trajectories were derived on the basis of autosegmentation of the resultant images. To further test its feasibility, k-t SLR was used to reconstruct prospective data of a healthy subject. An undersampled balanced steady-state free precession sequence with the same undersampling mask was used to acquire the imaging data.

Results

In the simulation study, higher imaging fidelity and low noise levels were achieved with the k-t SLR compared with TV. At 10 × undersampling, the k-t SLR method resulted in an average normalized mean square error <0.05, as opposed to 0.23 by using the TV reconstruction on individual frames. Less than 6% showed tracking errors >1 mm with 10 × down-sampling using k-t SLR, as opposed to 17% using TV. In the prospective study, k-t SLR substantially reduced reconstruction artifacts and retained anatomic details.

Conclusions

Magnetic resonance reconstruction using k-t SLR on highly undersampled dynamic MR imaging data results in high image quality useful for tumor tracking. The k-t SLR was superior to TV by better exploiting the intrinsic anatomic coherence of the same patient. The feasibility of k-t SLR was demonstrated by prospective imaging acquisition and reconstruction.

Introduction

Respiratory motion has posed significant challenges in lung cancer radiation therapy. Effective management of the motion to reduce normal tissue dose and maintain tumor coverage requires the precise knowledge of internal anatomies before and during the treatment. Despite the drawbacks of low lung signal intensity and strong magnetic susceptibility effects, magnetic resonance imaging (MRI) has found increasing applications in imaging moving lung tumors (1–5) because of its unique capacity to acquire 2-dimensional (2D) dynamic images in an arbitrarily orientation for an extended time period. In particular, for patients presented with lung cancer, dynamic 2D lung MRI is a safe and robust method to characterize internal organ motion. It has been shown that dynamic MRI of sagittal and coronal slices was better suited than 4-dimensional (4D) computed tomography (CT) for characterization of the lung tumor motion over a long time period (>200 seconds) that produces sufficient data for robust motion statistical analysis (4, 6, 7). The emergence of MRI-guided radiation therapy has further afforded the opportunity to visualize and adapt to moving anatomy during treatment, enhancing the role of MRI in intrafractional tumor motion management (8–10). In the previous studies a high-speed MRI sequence (eg, a steady-state free precession imaging sequence [11]) was used to achieve an acquisition speed of 4–8 2D frames per second, varying for imaging quality, resolution, and field of view (FOV). Although the technique is useful to quantify respiration-induced tumor motion, the low dimensionality limits derivation of 3-dimensional (3D) tumor motion trajectories, deformation vector fields, which have significant implications in the accuracy of radiation therapy that depends on cumulative dose calculation, derivation of the lung ventilation map, and lung function-based treatment planning (12). Acquiring multiple or orthogonal slices can provide partial 3D motion information, but the latency between slices cannot be ignored for the current frame rates. Although a similar approach used in 4D CT to re-bin 2D imaging slices could be utilized to generate “4D MRI” images (13), the process suffered from the same motion artifacts that have adversely affected 4D CT. Because the bottleneck of MR speed is the number of data points that can be sampled in a given time, undersampling of the k-space is a practical approach to shorten imaging time and increase temporal resolution. Recently, various compressed sensing techniques (14–16) have been used to accelerate imaging acquisition, exploiting the intrinsic sparsity of the MR images. A comparatively new approach that showed similar efficacy was to reconstruct the MR images from subsampled k-space data, exploiting the rank deficiency of images (17). In the matrix completion problem, it was shown that a low-rank matrix could be recovered from incomplete sampling of its entries by computing the matrix of minimum nuclear norm that fits the data (18). More recently several investigators (19–21) showed that a combination of transform domain sparsity with rank deficiency led to reconstruction results superior to a single method.

Although extensive research has been performed on the topic of compressed sensing MRI, its applications for lung imaging and lung tumor tracking have not been reported. In the study the combination of transform domain sparsity with rank deficiency is used to reconstruct spatial–temporal lung dynamic MRI data, and its ability to track lung tumor motion is quantified.

Methods and Materials

Data acquisition and simulation

The performance and the feasibility of accelerated dynamic lung MRI were evaluated on both retrospective and prospective undersampled 2D lung MRI datasets. For the retrospective study, the MRI was performed using a Cartesian balanced steady-state free precession (SSFP) sequence (5–10 images per second, sagittal and coronal orientations) on a 1.5 T Siemens Avanto MRI scanner (Siemens Medical Solutions, Erlangen, Germany) with a 6-channel body receive coil array and a spine coil on 7 lung cancer patients (all had visible tumors). Data were acquired with the following scan parameters: time to repetition/time to echo (TR/TE): 3/1.04 ms; FOV: 300 × 360 mm²; flip angle: 52°; slice thickness: 7 mm; matrix dimension: 160 × 192, GRAPPA 2 (24 reference lines) and partial Fourier of 6/8. Fully sampled k-space data were retrospectively generated from the reconstructed images to provide a simulation framework similar to the prospectively undersampled acquisition. These patients were imaged for 300 seconds, resulting in 1500–3000 2D images for each patient.

In addition to the retrospective simulation study, a preliminary prospective study was performed on a healthy volunteer. The real-time MRI was performed using a prospectively undersampled Cartesian balanced SSFP sequence (sagittal orientation) on a same-model MRI scanner with the following scan parameters: TR/TE: 4.29/2.05 ms; FOV: 272 × 322 mm²; flip angle: 60°; slice thickness: 7 mm; matrix dimension: 310 × 368. The random undersampling was set to 8 ×, so that the updated frame rate was 1 frame per 163 ms. A k-space lines pairing technique was used in the prospective sequence to mitigate artifacts caused by field in-homogeneity, motion, and eddy currents due to SSFP balanced gradients within the TR (22).

K-space sampling scheme

A Cartesian random undersampling scheme with fully sampled low frequencies as shown in Figure 1 was used in both the retrospective and prospective studies, except that in the simulation study the data corresponding to the 2D dynamic lung MRI were randomly undersampled in the k-space, with different undersampling factors corresponding to retention of 20% to 5% of the original full sampled data with the randomly generated undersampling scheme described. In this article an undersampling ratio of 20% is equivalent to undersampling fold of 5 ×.

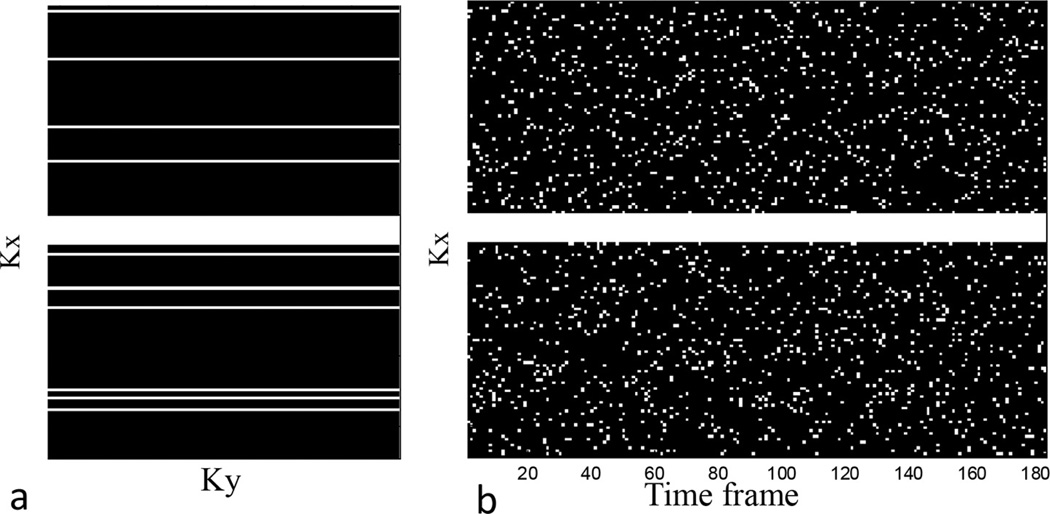
Fig. 1.

The k-t sampling scheme used in the retrospective and prospective studies. (a) Sampling mask for a single frame. (b) Sampling mask for 180 frames. The center 10 pixels are consistently sampled.

For each nonuniform undersampling (NUS) simulation, a different mask was generated, and unacquired k-space locations were filled with zeros before inverse Fourier transformation.

Low-rank and L1-norm regularization on sequential dynamic MRI images

Because of the quasi-periodic nature of the thoracic anatomies, the combined sequential dynamic MRI images were assumed rank deficient. Generalizing the sparse vector x to a low-rank matrix X, we have the following optimization problem:

$$\text{arg}\underset{X}{\text{min}}\mathit{\text{rank}}(X)s.t.{\Vert F_{p}X-d\Vert }_2^2<\epsilon$$ [1]

where F_p is the partial Fourier measurement operator, d is the sampled data collected from the scanner, and ε is a fidelity factor. The l₂-norm constraint modulates the objective function so that the reconstruction remains consistent with the measured data within the tolerance σ. In this study, the rank penalty can be applied using a nuclear norm (19–21), which was replaced with the Schatten p-norm that is mathematically tractable (23). Schatten p-norm is defined as $\phi (X)={({\sum }_{i=1}^{\text{min}\{m,n\}}{\sigma }_i^p)}^{1/p}$, 0 < p < 1, where σ are the singular values of matrix X. Using Lagrange’s multipliers, the above constrained optimization problem can be formulated as

$$\text{arg}\underset{X}{\text{min}}{\Vert F_{p}X-d\Vert }^2+{\lambda }_1\varphi (X)$$ [2]

For P = 1, the spectral penalty term simplifies to the nuclear norm. In this study, P = .1 was used because of its superior performance on the particular subject cohort. The P = .1 norm is highly nonconvex and could lead to local minima, but despite the potential pitfall, the same nonconvex norms have been shown highly effective in MRI reconstruction from very sparse sampling (19–21), such as the ones used in this study.

To further improve the reconstruction results, image transform domain sparsity has been exploited and combined with the low-rank property. The sparse gradients of dynamic images were exploited using the total variation (TV) constraint in the combined spatial and temporal domain (21). The optimization problem was formulated as

$$\text{arg}\underset{X}{\text{min}}{\Vert F_{p}X-d\Vert }^2+{\lambda }_1\varphi (X)+{\lambda }_{2}TV(X)$$ [3]

Definition of the TV norm will be given in the next section. λ1, λ2 are regularization parameters. We used Equation 3, named as k-t SLR (21), for our lung dynamic MRI data reconstruction.

To exploit the correlations between the temporal profiles of the voxels, the spatial–temporal signals were rearranged in a matrix X. The unconstrained optimization problem (Eq. 3) was first reformulated as a constrained minimization problem using variable splitting, and then a 3-step alternating minimization scheme (24) was used to solve it. The detailed process to solve Equation 3 can be found in reference 21.

Reconstruction using TV on individual dynamic MRI frames

For comparison, the undersampled MR images were also reconstructed individually using compressed sensing without considering their temporal coherence.

The reconstructed image x is a solution to the constrained optimization problem (25):

$$\text{arg}\underset{x}{\text{min}}{\Vert \Psi x\Vert }_{1}s.t.{\Vert F_{p}x-d\Vert }_2^2<\epsilon$$ [4]

where Ψ is the sparsity transform (in which the reconstructed data, x, is sparse), and ‖r‖_n is the l_n norm defined by ${\Vert r\Vert }_n={(\sum _i{|r_i|}^n)}^{1/n}$, for n>0.

We used TV as the regularizer to exploit image sparsity and preserve edges. Consequently, the constrained problem in Equation 5 can be written as:

$$\underset{x}{\text{arg min}}\mathrm{\alpha }TV(x)+\mathrm{\beta }{\Vert x\Vert }_1+\frac{1}{2}{\Vert F_{p}x-d\Vert }_2^2$$ [5]

where α and β are 2 positive parameters that weigh the sparsity against the data consistency, and x is the final dataset. TV is described as:

$$TV(u)=\sum _{ij}{({({\nabla }_1{u}_{ij})}^2+{({\nabla }_2{u}_{ij})}^2)}^{1/2}$$ [6]

where ∇₁ and ∇₂ denote the gradient operators on the first and second coordinates, respectively. Utilization of both L1 and TV norms may seem redundant, but doing so has been shown to help reconstruct smooth images at little extra computational cost (26). Because of the repetitive nature of breathing patterns spanning such duration, and to avoid busy figure presentation without losing generality, only the first 120 images were used in the present study; but the singular values of the first 120 images and the complete image set of a patient were compared.

The regularization parameters were optimized in a separate pilot study by retrospectively undersampling 2 datasets from the collection of 7 lung MRI and minimizing the normalized mean square errors (NMSEs) between the compressed sensing reconstructed and original images. Before reconstruction, retrospective images were normalized using their maximum image intensity, which allows using consistent regularization parameters.

The number of iterations chosen for the reconstruction algorithm is a balance between reconstruction time and image quality. The optimal number of iterations was defined as when the reconstruction could not improve the results further on the basis of NMSE measures and visual assessment. As a result, 50 inner-iterations and 10 outer-iterations were performed on all study subjects.

Evaluation of reconstructions

To evaluate the performance of the low-rank and sparsity-based reconstruction methods in the simulation study, images recovered from undersampled data were compared qualitatively as well as quantitatively with the original images. The difference between the reconstructed and original images was calculated, and visual analysis was performed to identify residual artifacts and loss of information. Quantitative analysis was done in terms of overall NMSE. For each trial, NMSE reconstruction error was computed as:

$$NMSE=\frac{{\Vert u-ū\Vert }_2^2}{{\Vert ū\Vert }_2^2}$$ [7]

where ‖․‖₂ denotes the L2 norm, and u and ū denote the reconstructed and original images, respectively.

To determine the usefulness of the reconstructed images for image guided radiation therapy, the tumor motion trajectories of the 7 patients calculated from the reconstructed and the original images were compared. To quantify tumor motion trajectories, the reconstructed images were first up-sampled by 5-fold in the imaging domain using cubic interpolation, in realization that registration accuracies greater than the imaging resolution are often attainable (27). The tumor was autosegmented, matching a tumor template contoured from the first frame and subsequent frames using maximum cross-correlation:

$$\mathit{\text{max}}C(\Delta x,\Delta y)=\int \int T(x_0,y_0)\mathrm{x̅}(x_0-\Delta x,y_0-\Delta y)$$ [8]

where T is the template matrix, and x̅ is the complex conjugation of the reconstructed image. The tumor segmentation accuracy on fully sampled images was previously visually validated on the same patient cohort (4, 7). Tumor motion trajectories were established on the basis of the contour center.

The correlation coefficients, the number of points with error >1 mm, and the average absolute errors between the original trajectories and the undersampled trajectories were calculated. The 1-mm error threshold was selected on the basis of the consideration that for radiation therapy relying on dynamic tumor tracking, the total error is a composite of dynamic multileaf collimator tracking and tumor motion tracking errors. Because 1-mm dynamic multileaf collimator tracking accuracy has been shown to be achievable (28), the same accuracy threshold was selected for tumor tracking.

We compared the reconstruction results of k-t SLR with the TV reconstruction for undersampling data.

Because of the lack of ground truth and single subject number, prospectively acquired images were only visually inspected.

Results

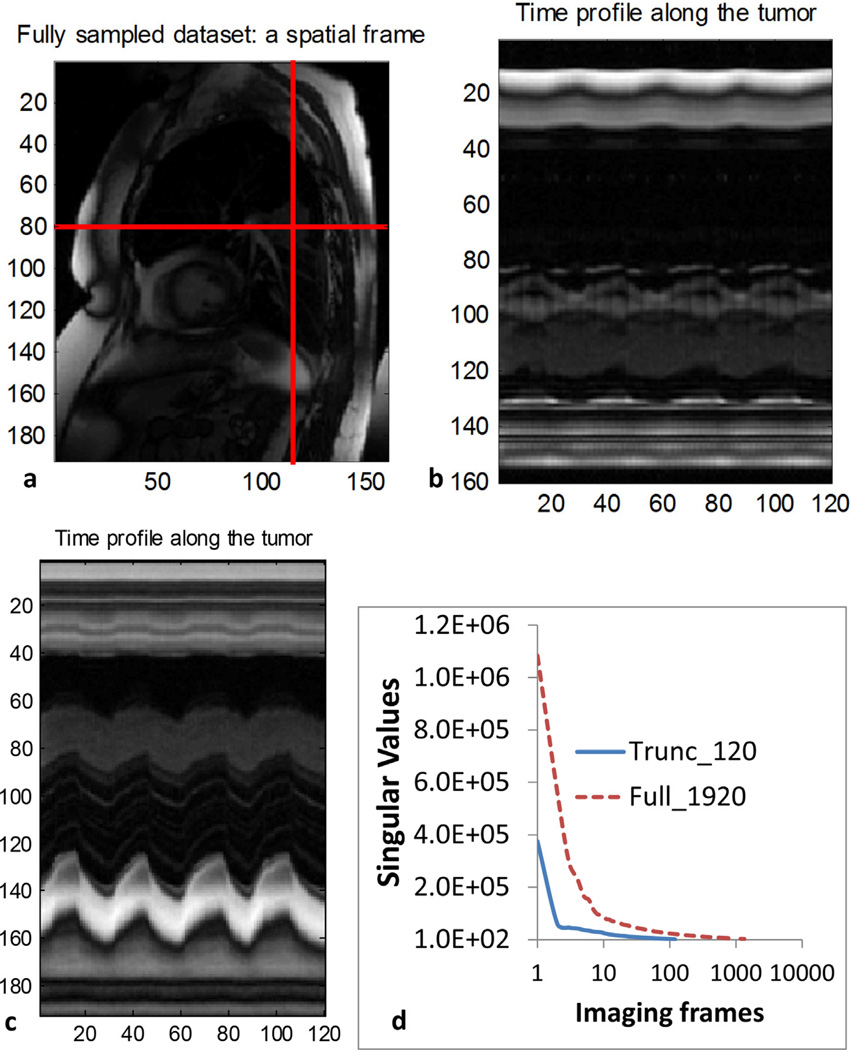
The signal sparsity in the spatial–temporal domain can be appreciated in Figure 2. The sequential 2D dynamic images of a patient, such as the one shown in Figure 2a, were combined into a 3D matrix. A vertical and a horizontal line of the first 120 2D images were rearranged to be new spatial–temporal 2D images that show strong repetitive patterns, supporting the low-rank assumption. Figure 2d shows the singular values of the first 120 images and full 1920 images of a patient. It is clear that in both cases, the singular values decreased rapidly and showed minimal residuals after 10.

Fig. 2.

(a) A frame of the dynamic magnetic resonance images for retrospective simulation study. Two perpendicular lines in the sequential dynamic images were stacked to create (b) and (c). (d) The singular values of 120 and 1920 frames, respectively.

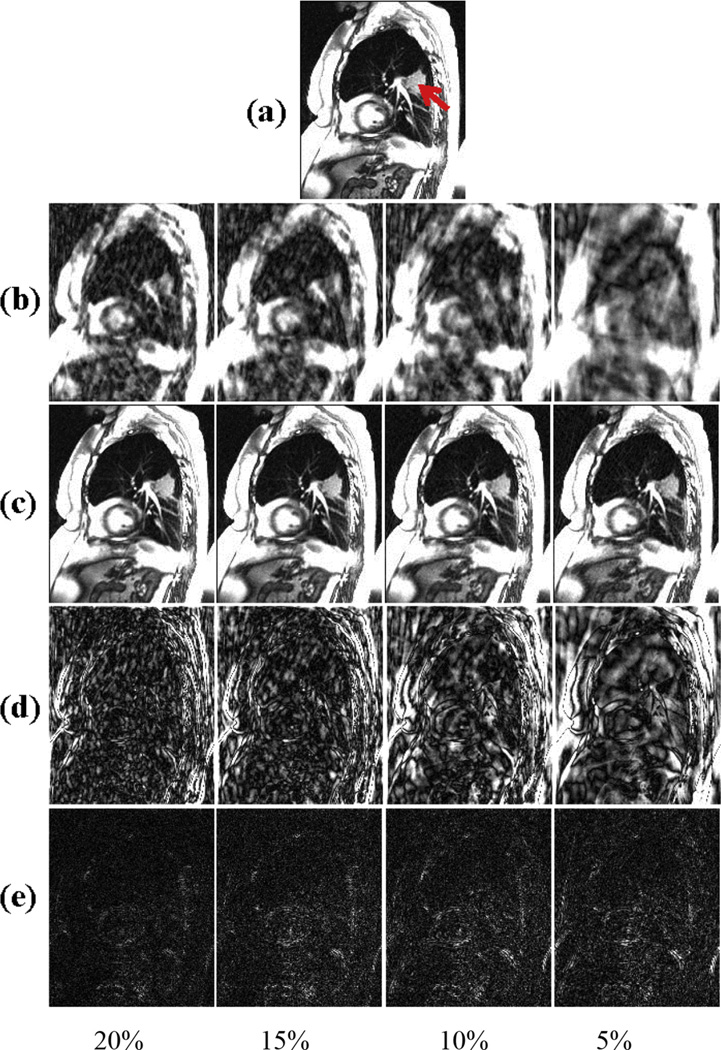
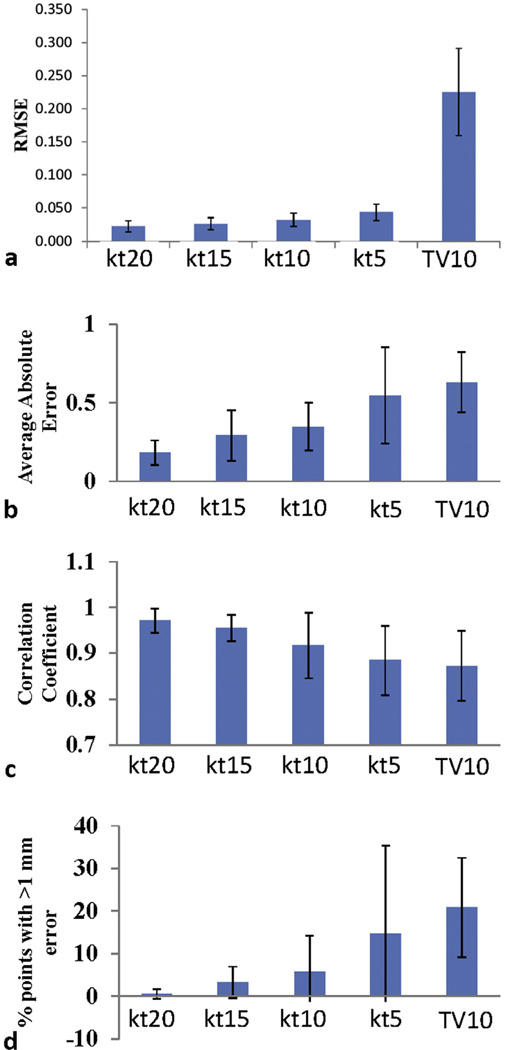
The resultant 2D dynamic lung MR images in the retrospective simulation study from the 4 sampling ratios data with various down-sampling ratios (5 × −20 ×) are shown in Figure 3. As expected, direct reconstruction from undersampled k-space data results in noisy images that degraded imaging details, such as blood vessels, and became unusable for tumor tracking at undersampling >10 ×. The k-t SLR reconstructed images showed good retention of the detail and very little increase in imaging artifacts, even at the highest undersampling fold of 20 ×. The performance of k-t SLR on combined spatial–temporal imaging data and TV on individual dynamic MR frames is compared in Figure 4. At the undersampling fold of 10 ×, although TV was able to reduce imaging noise compared with NUS images, the imaging texture is less realistic compared with k-t SLR, with loss of imaging details such as the blood vessels. The observation was confirmed by NMSE measurement of the images. The NMSE of the k-t SLR reconstruction of the undersampled datasets increased moderately with increasing undersampling fold but remained lower than 0.05 (Fig. 5a), as opposed to 0.225 of TV reconstructed images with the 10 × undersampling rate.

Fig. 3.

(a) Sagittal view from a time point extracted from the fully sampled 2D lung dynamic magnetic resonance imaging data of a cancer subject. The location of the lung tumor is indicated by the arrow. (b) Direct reconstructed images using zero-filling at sampling ratios of 20%, 15%, 10%, and 5% for the sampling scheme 1. (c) Corresponding recovered images using k-t SLR; (d) difference between the zero-filling (c) and the original data; (e) difference between the original (a) and k-t SLR reconstructed data (b).

Fig. 4.

Comparison of k-t SLR results with total variation for lung magnetic resonance imaging data at sampling ratio of 10%. (a) Coronal view from a time point extracted from the fully sampled 2-dimensional lung dynamic magnetic resonance imaging data of a cancer subject; (b) undersampling images at sampling ratios of 10%; (c) corresponding recovered images with k-t SLR; (d) corresponding recovered images with total variation.

Fig. 5.

(a) Mean normalized mean square errors value of the reconstructed images. “kt” and “tv” denote recovery methods of k-t SLR and total variaion reconstruction of individual frames, respectively. The numbers following kt and cs denote undersampling ratios (%). (b) Correlation between the tumor motion for the fully sampled data and reconstructed data. (c) Average absolute tracking errors. (d) The percentage of tracking points with >1 mm error. All values were computed on the basis of the total tumor $\text{displacement}=\sqrt{\Delta x^2+\Delta y^2}$.

Figure 5b–d shows the tumor tracking results for all 7 patients. The estimated total tumor displacements from the fully sampled and reconstructed data were found to be well correlated (Fig. 5b): the average correlation coefficient for 7 patients and all undersampling ratios was found to be ≥0.85. At the 10 × sampling rate, the correlation coefficient of k-t SLR is slightly better than TV (0.92 vs 0.87). Both the average tracking error (Fig. 5c) and the number of tracking points with >1 mm error (Fig. 5d) increased with decreasing undersampling ratio, but the k-t SLR method consistently outperformed the TV method. For undersampling ratio >10 ×, TV was not able to produce useful images for tumor tracking.

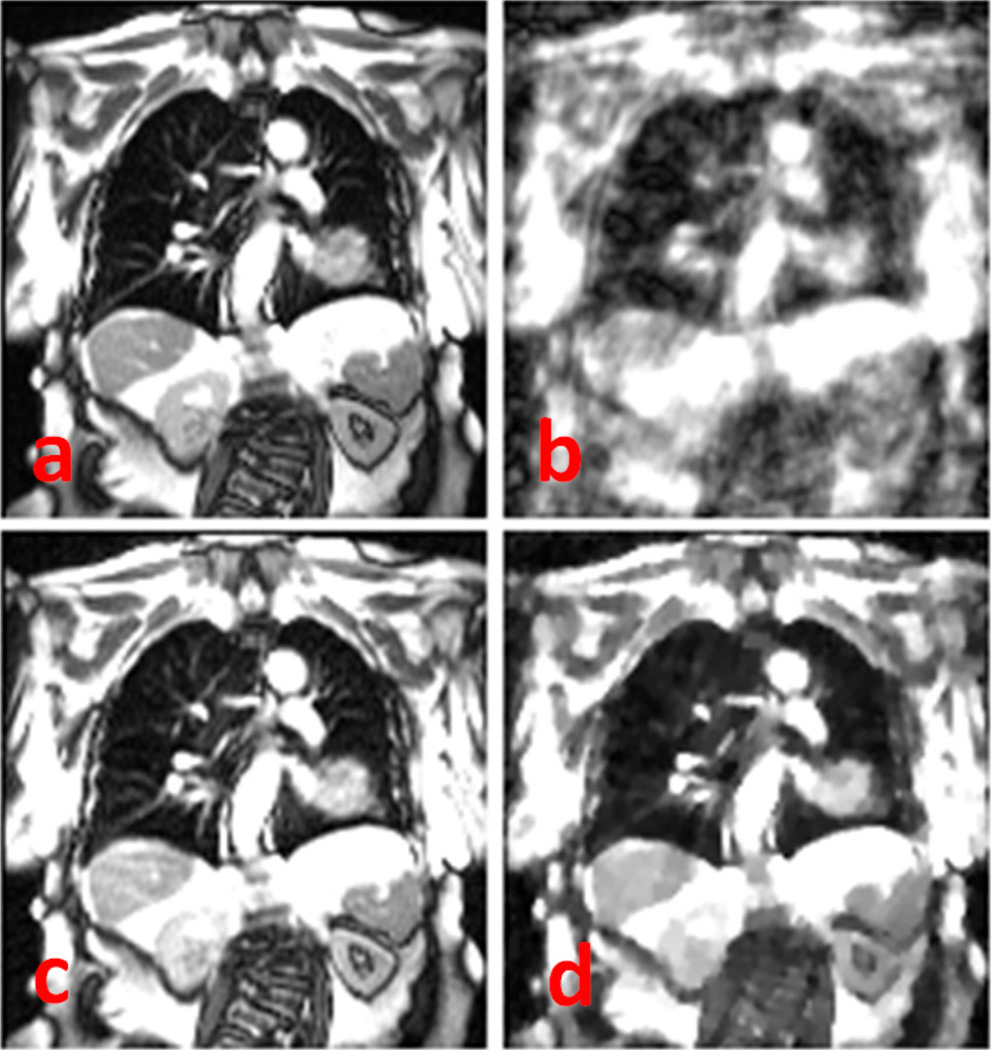
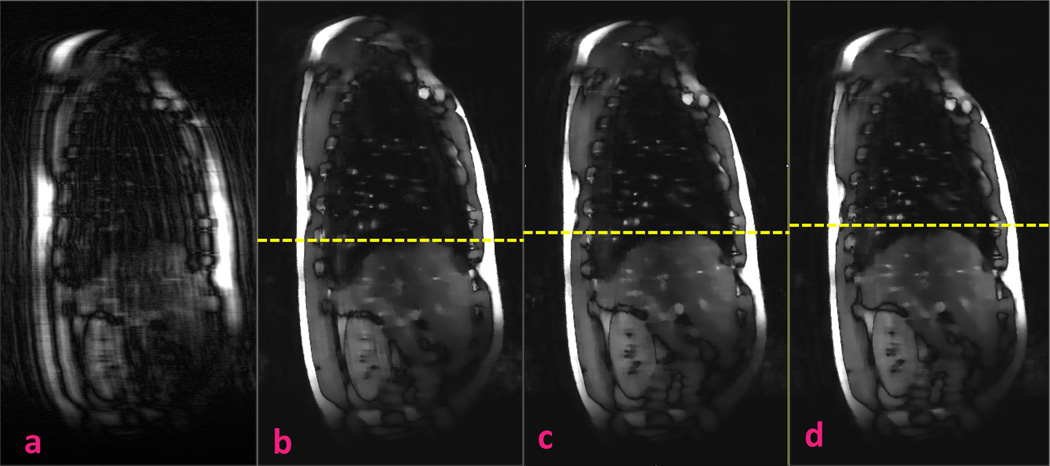
Figure 6 shows the results of the prospectively acquired 8 × undersampled dynamic MRI using NUS and k-t SLR. The NUS image quality is unusable, but the k-t SLR image has substantially reduced the incoherence artifacts and retained imaging details such as the blood vessels.

Fig. 6.

Prospectively acquired 8 × undersampled dynamic magnetic resonance imaging using (a) nonuniform undersampling and (b–d) k-t SLR. The k-t SLR results include 3 frames at end of inhalation, middle, and end of exhalation, respectively. Yellow dotted lines denote the diaphragm apex positions.

On average it took 14 seconds to reconstruct a 2D image using the MATLAB (MathWorks, Natick, MA) k-t SLR program on a personal computer with a quad-core central processing unit clocked at 2.4 GHz and 16 GB memory, with most time consumed by the conjugate gradient solver and single value decomposition.

Discussion

Imaging reconstruction from undersampled k-space data in MR has been extensively researched in areas such as cardiac and brain imaging, but the applications on lung images have been rarely reported. A recent application of low-rank decomposition to take the advantage of lung anatomy spatial–temporal coherence has been demonstrated for 4D cone beam CT reconstruction of digital phantoms (29, 30). To the authors’ best knowledge, this is the first study in the radiation therapy context, where the lung tumor tracking is of particular interest and long duration of dynamic MR images is performed.

Imaging artifacts from reconstructing down-sampled k-space data can be effectively suppressed by TV. However, lung MR images are not sparse, and TV on individual frames resulted in appreciable imaging quality degradation even with modestly down-sampled data.

Because of the intrinsic anatomic coherence of the same patient, in theory, very little new additional information is needed to update each imaging frame for a prolonged imaging acquisition. We showed that the k-t SLR reconstruction exploiting the advantage clearly retained more imaging details and textures than the TV method on individual frames. The difference is expected to contribute to the ability of tracking smaller features and the accuracy of deformable registration.

The reconstruction method for accelerated undersampled MRI is compatible with dynamic 3D imaging. Additional acceleration is possible with the second encoding direction. Emerging MR-guided radiation therapy systems provide the hardware capacity for continuous intrafractional motion monitoring, but the potential is not fully realized without dynamic 3D imaging acquisition. We have used the lung tumor MR as a model system, but similar applications are expected in other regions such as the upper abdomen, where the organs move significantly with respiratory motion.

Simulation studies are valuable to compare reconstruction techniques, but the undersampling strategy has to be implemented in the pulse sequence acquisition to realize the benefits. Different from simulation study, undersampled data acquisition is subject to physical limitation in the sampling trajectories. Furthermore, SSFP sequences are inherently sensitive to signal phase errors caused by field inhomogeneity, motion, and eddy currents due to its balanced gradients within the TR. However, our prospective study indicates that these challenges are surmountable using methods such as k-space lines pairing.

Current computation time using the MATLAB program does not allow real-time implementation; however, we expect substantial computational improvement with implementation of reconstruction algorithms such as Split-Bregman and parallel computing on graphic processing units GPUs (31).

Conclusions

A k-t SLR method to reconstruct retrospectively heavily down-sampled quasi-periodic lung dynamic MR data is demonstrated here. The method results in superior imaging quality compared with compressed sensing reconstruction of individual dynamic MR imaging frames, allowing accurate tumor tracking. The same method was also successfully implemented in prospective undersampled MRI reconstruction. This study demonstrates the potential of increasing dynamic MR acquisition volumes for complete organ motion monitoring.

Summary.

To study the feasibility of accelerating dynamic MRI acquisition, we evaluate the performance of a low-rank decomposition method (k-t SLR) for reconstructing heavily down-sampled k-space data. The k-t SLR method is shown to recover images with little degradation and is generally superior to compressed sensing reconstruction of individual imaging frames. Our preliminary prospective MRI acquisition and reconstruction support this observation.