Calibration of Wide-Field Deconvolution Microscopy for Quantitative Fluorescence Imaging

Abstract

Deconvolution enhances contrast in fluorescence microscopy images, especially in low-contrast, high-background wide-field microscope images, improving characterization of features within the sample. Deconvolution can also be combined with other imaging modalities, such as confocal microscopy, and most software programs seek to improve resolution as well as contrast. Quantitative image analyses require instrument calibration and with deconvolution, necessitate that this process itself preserves the relative quantitative relationships between fluorescence intensities. To ensure that the quantitative nature of the data remains unaltered, deconvolution algorithms need to be tested thoroughly. This study investigated whether the deconvolution algorithms in AutoQuant X3 preserve relative quantitative intensity data. InSpeck Green calibration microspheres were prepared for imaging, z-stacks were collected using a wide-field microscope, and the images were deconvolved using the iterative deconvolution algorithms with default settings. Afterwards, the mean intensities and volumes of microspheres in the original and the deconvolved images were measured. Deconvolved data sets showed higher average microsphere intensities and smaller volumes than the original wide-field data sets. In original and deconvolved data sets, intensity means showed linear relationships with the relative microsphere intensities given by the manufacturer. Importantly, upon normalization, the trend lines were found to have similar slopes. In original and deconvolved images, the volumes of the microspheres were quite uniform for all relative microsphere intensities. We were able to show that AutoQuant X3 deconvolution software data are quantitative. In general, the protocol presented can be used to calibrate any fluorescence microscope or image processing and analysis procedure.

INTRODUCTION

At the primary step of observing and imaging, microscopes are completely visually oriented. Image processing, however, with the various software programs available, allows for the quantification of various aspects of the specimen. In particular, fluorescence microscopy has been used to quantify the localization, dynamics, and interactions of cellular molecules.^1–3 Also, many techniques enable quantification of fluorescence intensity: fluorescence recovery after photobleaching, fluorescence loss in photo-bleaching, fluorescence resonance energy transfer, and fluorescence lifetime imaging.^1,2,4 Such quantification of data allows for the measurement and scaling of the intensity values so that changes indistinguishable by the eye may be measured.

Several considerations need to be addressed when performing quantitative analysis. First, illumination stability of the light source can be one of the main sources of variability.^1,2,5 In wide-field microscopes, the output of the mercury lamps can fluctuate up to 10% on time-scales of milliseconds to seconds and becomes more prominent as the lamp ages.^1,2 Another source of noise is the photon shot noise or the uncertainty in the charge-coupled device (CCD) camera detection of a photon.^1,2 The relative contribution of shot noise decreases with increasing photon counts; hence, to minimize photon shot noise, as many photons as possible need to be collected without damaging the sample.^1,2

With wide-field microscopes, pixels in a large field of view are imaged simultaneously. The collection of a large amount of light, including out-of-focus light, results in high sensitivity. However, the wide-field images also have reduced contrast as a result of significant background from the out-of-focus light. On the other hand, confocal laser-scanning microscopes (CLSMs) illuminate the sample point-by-point and remove out-of-focus light by passing only the in-focus-emitted fluorescence through a pinhole; hence, confocal microscopes improve the image contrast.^1,2 In turn, the exclusion of much of the out-of-focus light leads to lower sensitivity of CLSMs when compared with wide-field microscopes.

Furthermore, CCD cameras used with wide-field microscopes have better quantum efficiency—the percent of photons that reaches the detector that are converted into photo electrons or signal within the images—than the photomultiplier tubes used with CLSMs.⁶ Consequently, in situations with little out-of-focus light [e.g., thin specimens (<30 μm) or thick specimens with the fluorescence signal confined to a narrow volume], wide-field imaging produces “statistically better-defined images” for the same amount of illumination.^1,2,6 Deconvolution can then be used to improve the contrast in these images to levels comparable with CLSMs.

When light travels through the microscope, it is diffracted by the optical elements. As a result of diffraction, the light is spread, and subresolution objects appear bigger than they actually are. The resultant, three-dimensional (3D) distribution of each point of fluorescence within the specimen is referred to as the point-spread function (PSF).^1,2,7 In other words, when the subresolution object is imaged it is convolved by the optics and looks like a PSF that is much larger than the original object in the image.^1,2

Deconvolution is the process of estimating the morphology of the actual object that gave rise to the blurred image. There are three major types of deconvolution approaches: deblurring, restorative, and restorative blind deconvolution.

Deblurring or Nearest Neighbor-Based Deconvolution

The deblurring method removes the out-of-focus light in an image with the assumption that most of the out-of-focus light results from its two “neighbors”: the image axial section above and the section below. The method works especially well with low numerical aperture lenses or relatively large section spacings.^1,2 As a result of the assumptions and simple estimates of the out-of-focus light, however, there are inherent errors with the method, and it should not be used for quantitative analysis.^1,2 However, as it can be calculated rapidly, deblurring methods can be used to produce high-contrast images for quickly evaluating sample morphology.^1,2

Restorative Deconvolution

Restorative deconvolution methods use the theoretical or measured PSF to try to estimate the actual object that produced the image before it was convolved with the PSF.^1,2 The PSF can be calculated (theoretical PSF) based on the optical properties of the microscope (e.g., objective lens, numerical aperture, sampling frequency, color of light) or measured using subresolution fluorescent microspheres [∼100 nm diameter for high numerical aperture (NA) objectives]. After an estimation of the object is made, this estimation is convolved with the PSF to generate a new image, which is compared with the original collected image, and the difference between the two images is determined using algorithm-dependent techniques. If the difference between the images is larger than a predetermined factor, then the process is repeated until the estimated image is not significantly different than the collected image. The term iterative is used for this repetition. An advantage of restorative deconvolution is that the out-of-focus light is not removed, such as light rejected by the pinhole in confocal imaging, but is rather reassigned to its original location, yielding images with a much higher signal-to-noise (S/N) ratio than the initial wide-field images. Huygens (Scientific Volume Imaging, The Netherlands) and AutoQuant X3 (Media Cybernetics, Rockville, MD, USA) are examples of commercial software packages that offer restorative deconvolution algorithms. Deconvolution Lab is a plug-in that is available for ImageJ or FIJI, but it requires the user to measure the PSF of their microscope. Deconvolution Lab is more geared to advanced deconvolution users but offers a lot of flexibility, with seven different deconvolution algorithms from which to choose.^8,9 In general, it is best to use a carefully measured PSF for deconvolution, as it will provide the algorithm with the exact characteristics of the microscope. However, if the PSF is not measured properly, it will introduce errors in the analysis, and the theoretical PSF would be a better starting point for the algorithm. For detailed instructions, on how to prepare subresolution microsphere samples and manufacture specific protocols on how to measure CLSM PSFs, see Cole et al.⁷ These protocols can be adapted easily for measuring wide-field microscope PSFs.

Blind Deconvolution

Blind deconvolution is an extension to restorative deconvolution. However, in this case, both the object and the PSF are treated as unknown. The initial PSF estimate is the theoretical function, but then, the PSF is modified as part of the deconvolution algorithm, which derives the PSF from the actual image data. Afterwards, the morphology of the object is estimated and convolved with the derived PSF. In the subsequent iterations, not only is the object estimation altered but also, the PSF estimate.^10,11 AutoQuant X3 (Media Cybernetics) is a commercial software package that has an optional algorithm for blind deconvolution.

Aberrations

It should be noted that aberrations as a result of instrument performance, objective lens quality, and sample preparation have a significant impact on any fluorescence imaging experiment, including deconvolution analysis. If the microscope stage drifts, the z-focus drifts, or the DIC optics are in place, the PSF of the microscope or of the image stacks will not be accurate.⁷ If objective lenses are not performing well and show aberrations, such as coma or astigmatisms, the lenses need to be repaired or replaced. If samples are not prepared properly with the correct coverslip thickness or if the sample mounting media are not well-matched with the immersion media, then spherical aberrations can be a problem. Spherical aberrations cause asymmetric distortions in the PSF, and these aberrations change and typically become more problematic when imaging deeper into thick specimens.^12–15 They can be minimized by matching the indices of refraction of the sample mounting medium and the lens immersion medium as well as possible. Spherical aberrations are most prominent when imaging into aqueous samples with oil immersion lenses. Many deconvolution algorithms have correction features and/or image preprocessing steps that can minimize spherical aberrations. The ideal way to correct for spherical aberrations is to measure the actual PSF of the microscope using subresolution fluorescent microspheres.⁷ In this study, we looked specifically at microspheres that were in close proximity to the coverslip and used 0.170 mm-thick coverslips so spherical aberrations were not an issue (see Supplemental Fig. 1).

There is a great deal of previous work that has looked at quantitative deconvolution.^1,2,16 However, in this study, we present a simple and straightforward protocol for testing whether wide-field microscopes are quantitative and whether deconvolution algorithms maintain that quantitative intensity relationship in 3D image stacks of fluorescent calibration microspheres. Many researchers use image deconvolution as a way to improve measurements of the 3D morphology of samples and also to improve image S/N. However, deconvolution is often not a central part of their research. Therefore, we wanted to test the simplest scenario using the default parameters of the commercial AutoQuant X3 deconvolution software package and inputting the theoretical PSF in the algorithm. This is a scenario many people use in the McGill Advanced BioImaging Facility (ABIF). It should be noted that much time could be spent measuring instrument PSFs and optimizing deconvolution algorithm settings for more ideal performance, but that was not the aim of this study. For further general and advanced information on deconvolution, there are many informative beginner and advanced articles.^{1,2,11,14,16–18}

MATERIALS AND METHODS

Reagents

• InSpeck Green (505/515), 2.5 μm calibration microspheres with relative intensities of 0.2%, 0.8%, 2.3%, 10.6%, 30.0%, and 100%, Cat. No. I-7219 (Life Technologies, Carlsbad, CA, USA); note: each set of calibration microspheres comes with a lot-specific set of flow cytometry data, giving the precise intensity relationship between the microspheres.

• No. 1.5 coverslips, 18 mm × 18 mm, certified to be 0.170 ± 0.005 mm, Cat. No. 474030-9010-000 (Carl Zeiss Canada, Toronto, ON)

• Microscope slides, Fisherbrand, Cat. No. 12-552-3 (Fisher Scientific, Ottawa, ON, Canada)

• ProLong Gold mounting medium, Cat. No. P36934 (Life Technologies)

Equipment

• Power of the mercury lamp was measured using a FieldMaxII-TOP Laser Power/Energy Meter, Cat. No. 1098580 (Coherent, Santa Clara, CA, USA).

• Images were collected using an Axiovert 200M fully automated inverted microscope, the AxioVision software, 100×/1.40-NA Plan-Apochromat lens, 13 FITC 450–490 filter cube, and AxioCam monochrome camera (1388×1040 pixels; 0.0645 μm). All microscope components were from Carl Zeiss (Jena, Germany).

Preparation of the Fluorescent Calibration Microsphere Slides (As Adapted from Cole et al.⁷)

1. InSpeck Green calibration microspheres, from 0% to 100% relative intensity, were vortexed briefly.

2. The microspheres were sonicated in a water bath for 20 min to break up any aggregates.

3. The lab bench tabletop was wiped clean with ethanol. Gloves were worn for succeeding steps to avoid fingerprint smudges on the slides and coverslips.

4. Microscope slides were washed with 70% ethanol and wiped dry with Kimwipes.

5. No. 1.5 coverslips were washed with 70% ethanol and held with forceps in a Bunsen burner flame, two times. Take care, as the glass cracks if flamed for too long. This creates a hydrophilic surface on the glass, allowing for better spreading of the microsphere droplet. Carrying out the step once often left blots of dirt on the coverslips; repetition ensured clean, shiny coverslip surfaces. A separate coverslip was prepared for each relative intensity of calibration microspheres that was used.

6. Right before pipetting the microspheres onto the coverslips, the microsphere vials were vortexed briefly.

7. A sample of 10 μl calibration microsphere solution of each intensity was pipetted onto each coverslip. The coverslips were then covered with a metal pan or aluminum foil to protect them from light and dust.

8. Solutions were dried on the coverslips for 1–2 h.

9. A small drop of ProLong Gold was applied onto each microscope slide. ProLong Gold has a refractive index of 1.46, which nearly matches the indices of refraction of the glass and immersion oil (1.515).⁷ The similar indices of refraction increase microscope resolution by decreasing the loss of highly diffracted light from refraction at the interfaces of different media.⁷

10. Using forceps, the coverslips were placed with the microspheres facing down onto the ProLong Gold. Coverslips were held at a 45° angle and then released slowly to minimize the formation of air bubbles. Then, the coverslip was pressed lightly with a cotton-tip applicator to force any air bubbles to the edges of the coverslip and out of the sample.

11. Each slide was then flipped over and propped up at each end with an empty microscope slide placed lengthwise so that the microspheres stayed on the coverslip.

12. The samples were kept in the dark at room temperature overnight for the ProLong Gold to cure.

Microsphere Imaging

1. The mercury arc lamp and the wide-field microscope were turned on.

2. The power of the mercury lamp (100 W) was adjusted to 50% and warmed up for at least 30 min for stabilization of the output intensity. It is best not to use the lamp below 50% intensity, as fluctuations in power output can occur. Note that not all mercury lamps have this kind of power adjustment.

3. While the lamp was heating up, the 100× oil immersion 1.4-NA objective lens was cleaned. Any excess oil on the lens was removed by folding a piece of lens paper three times lengthwise into a long rectangle and sweeping it across the lens three times, using a fresh area of the paper with each sweep.⁷ The process was repeated two more times: once with lens cleaner and once with distilled water on the paper.

4. The filter cube was set to FITC 450–490 nm.

5. Before proceeding to imaging, the FieldMaxII-TOP Laser Power/Energy Meter (Coherent) was used to measure the lamp power directly. The detector was placed on the 10× objective lens and immobilized using Blu-Tack. A wavelength (λ) of 470 nm was set, the light in the room was turned off, and the power meter was zeroed by pressing on “Zero”. Subsequently, the fluorescent lamp shutter was opened, and the measurement of the power was obtained by pressing on “Auto”. Power measurements at 0.5% and 5% lamp intensity were obtained by placing neutral density (ND) filters of 1% or 10% directly in the light path, respectively. After the measurements were recorded, the power meter detector was removed from the objective lens.

6. The 100×/1.40-NA Plan-Apochromat oil immersion lens was put in place, and a small drop of immersion oil standardized for room temperature was applied.

7. A calibration microsphere slide was placed, coverslip facing down, on the objective lens and viewed through the eyepieces. After focusing in a region of sparse microsphere concentration (to allow for single microsphere intensity measurements), the microspheres were viewed in the software with the live imaging function.

8. We ensured that the imaging settings were not resulting in detector saturation. Many software packages have an image display look-up table that shows pixels reading zero as one color and saturated pixels as another color, with all other pixels showing up as grayscale. In the Zeiss software, the overexposure button in the live view was used to verify that the microsphere intensity signal was not saturated in the images. The overexposure feature shows pixels reading zero as blue, saturated pixels red, and all other pixels with grayscale intensities. It is imperative for quantitative fluorescence data of the corresponding intensities that the intensities do not exceed the linear range of the detection system.^1,2,11 To attenuate saturation, ND filters could be put in place, or the power of the mercury lamp could be adjusted directly if the lamp has the capability. For the protection of the sample and the fluorophores, it is always best to reduce the intensity of the incident light whenever possible. Saturation can also be avoided by using shorter camera exposure times.

9. A z-stack, with a pixel size in x, y, and z axes of 0.0645 × 0.0645 × 0.3 μm, respectively, was collected. The sampling should adhere to Nyquist sampling or higher for deconvolution. Cole et al.⁷ show a table of suggested lateral and axial resolutions for various lenses and also provide equations to make the calculations on one's own. It was verified that: (1) significant sampling was obtained for deconvolution, and (2) the entire microsphere was imaged within the z-stack.

10. At least three z-stacks were acquired of different microspheres in different fields of view.

11. Once the z-stack was collected, it was saved as (1) the original software file format (.zvi) and (2) the 16-bit .tif file format with 0% compression.

12. Steps 7–11 were repeated for the microsphere slides of various relative intensities.

13. All images were taken at a single imaging session to avoid changes in lamp intensity.

Image Processing

Images were deconvolved using the restorative iterative deconvolution algorithm with default settings, without or with the addition of blind deconvolution in AutoQuant X3 (Media Cybernetics). Based on our experience in a life sciences core facility, the majority of users of commercial deconvolution software does not spend a significant amount of time studying and optimizing deconvolution software settings. Therefore, all programs were used with the default settings, unless noted otherwise. Afterwards, Imaris version 7.5.2 or version 7.6.2 (Bitplane, South Windsor, CT, USA) was used to measure the mean intensity and volume of the microspheres in the original and the deconvolved images. In Imaris, the surface function was used to create an isosurface of each of the microspheres. Settings of “Surface area detail level” of 0.5 μm and “background subtraction with diameter of largest sphere which fits into the object” of 0.3 μm were used. The surfaces were generated using the intensity thresholding automatically determined by the software. The Imaris automatic thresholding is based on k-means clustering and dividing the image intensity histogram into two populations using the algorithm developed by Ridler and Calvard.¹⁹ This method of thresholding is very robust and offers an objective way to identify the microsphere boundaries without any user bias. If necessary, the microsphere selections were filtered using a minimum voxel threshold to remove small volume object artifacts. The voxel thresholding enabled the same number of microspheres to be measured for the corresponding image stacks in the wide-field and the deconvolved images so that the same microspheres were accounting for the statistics of each image set.

RESULTS

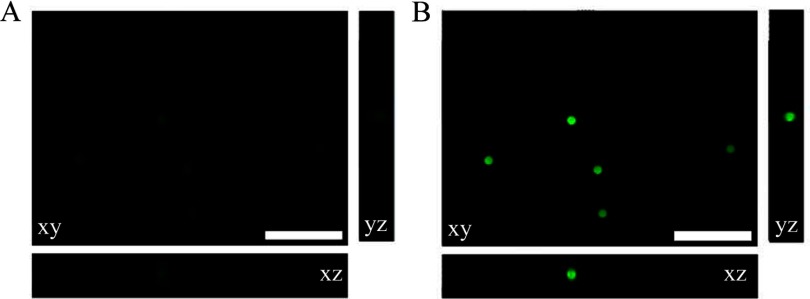
To determine whether the AutoQuant X3 iterative deconvolution algorithm, with or without blind deconvolution, retains the relative quantitative fluorescence intensity information, three sets (Set 1, 2, and 3) of microscope slides were prepared separately with calibration microspheres of six different relative intensities of 0.2%, 0.8%, 2.3%, 10.6%, 30.0%, and 100%, given by the manufacturer. At least three wide-field microscope z-stack images were taken of each microsphere slide in different regions of the sample. For Set 1, all microspheres were imaged using 0.5% power and 120 ms exposure time. For Set 2, all microspheres were imaged using 0.5% power and 80 ms exposure time. For Set 3, the mercury bulb power was low, and the microspheres of lower intensities (0.2% and 0.8%) were not visible at 0.5% mercury lamp power. Consequently, 0.2%, 0.8%, and 2.3% microspheres were imaged with 5% power, and 10.6%, 30.0%, and 100% microspheres were imaged with 0.5% power. The exposure time of 80 ms was used for all microsphere slides in Set 3. The exposure times and measured lamp powers were used to scale the microsphere intensities so they could be compared between data sets. All z-stacks were deconvolved using the iterative deconvolution algorithm, with or without blind deconvolution, using the default settings in AutoQuant X3 (Fig. 1). One sample of 0% microsphere intensity (i.e. unlabelled microspheres) was prepared and no fluorescence signal was observed. As expected, following blind deconvolution, there was improved image contrast and decreased out-of-focus blur (compare Fig. 1A with B). This is especially prominent in the xz-axis and yz-axis views with the disappearance of the emanating cones of out-of-focus light (compare Fig. 1C with D). Note that there is some asymmetry in the profile of these microspheres (see yz and zy profiles in Fig. 1C). This could be a result of (1) a slight defect in the objective lens, leading to a coma artifact (Supplemental Fig. 1); (2) indices of refraction differences between the immersion oil and the ProLong Gold; or (3) lensing effects that can be seen with these large microspheres. Blind deconvolution reassigns the out-of-focus light to its original location; therefore, the intensities of the microspheres increase significantly, as evident when the same intensity display scale is applied on the original wide-field and blind deconvolution images (Fig. 2) Note that the microspheres are barely visible (Fig. 2A) on the same intensity scale as the high-intensity blind deconvolution images (Fig. 2B).

Figure 1.

Original and deconvolved wide-field microscope images of calibration microspheres. (A) An xy, xz, and yz view of 30% InSpeck Green fluorescent calibration microspheres imaged on a Zeiss Axiovert 200M microscope with a 100×/1.4-NA oil immersion lens and AxioCam high-resolution camera with mercury lamp power of 0.5% and exposure time of 120 ms. (B) Images as in A deconvolved with the blind deconvolution algorithm and the default settings in AutoQuant X3. (C and D) Zoomed-in images of one of the microspheres in A and B, respectively. Image display settings were adjusted independently so images appear to be of similar intensity, although deconvolved images have much higher intensities. Scale bars are 10 μm (A and B) and 3 μm (C and D).

Figure 2.

Original and deconvolved wide-field microscope images of calibration microspheres viewed with the same intensity display settings. Images were collected as in Fig. 1 but with original image display settings (A) adjusted with the same display settings as the blind deconvolved images (B) to emphasize that deconvolved images have a much higher S/N. Scale bars are 50 μm.

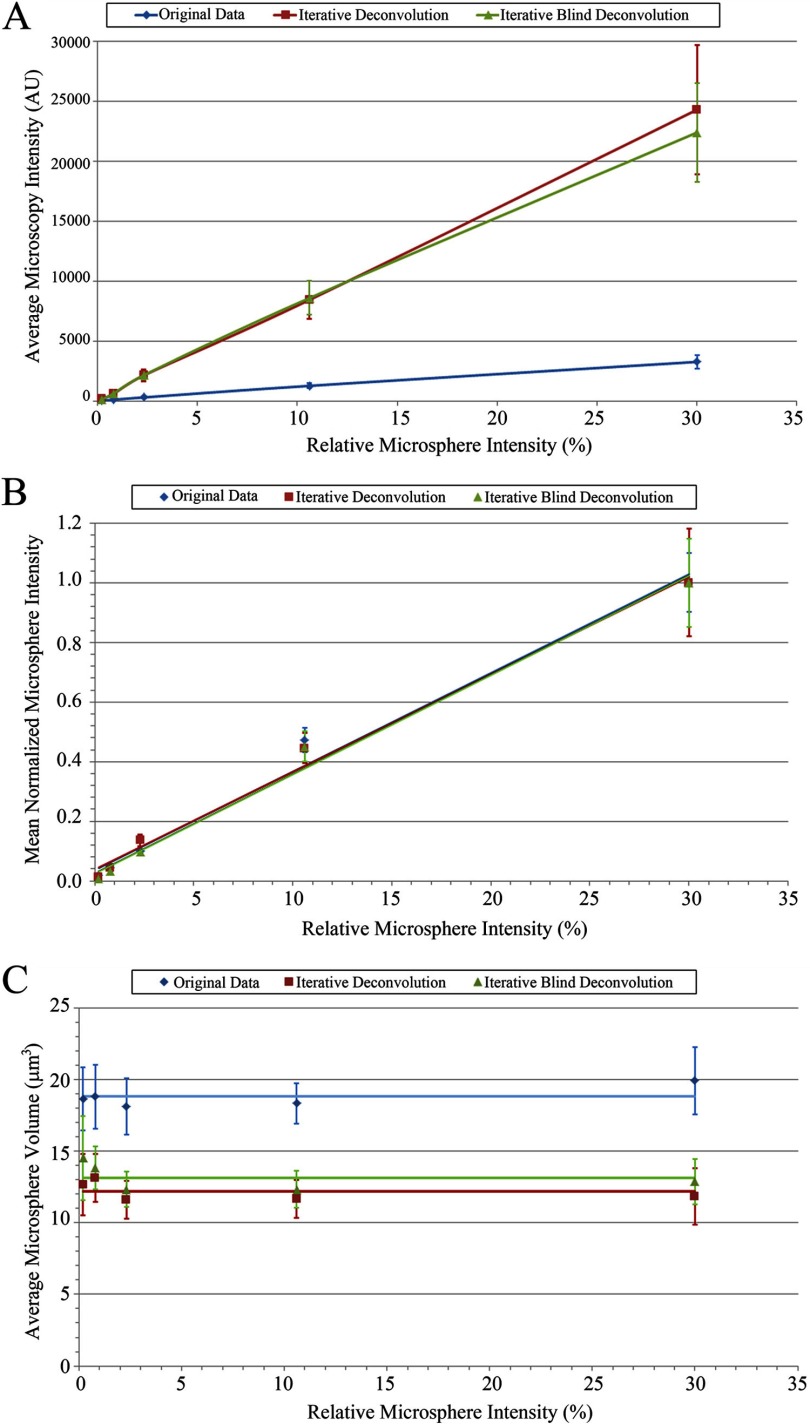
Subsequently, Imaris 3D image analysis software was used to measure the mean intensity and volume of the microspheres in the original and the deconvolved images. The quantitative data for multiple image stacks at relative microsphere intensities were then averaged for the original wide-field data, the iterative deconvolved data, and the iterative blind deconvolved data.

As the deconvolution algorithms reassign the out-of-focus light to its origin, higher S/N ratios are seen. Thus, the following expected observations were made:

1. The deconvolved microspheres have fivefold higher average intensities than the wide-field microspheres for all microsphere intensities (Table 1 and Fig. 3A).

2. The deconvolved microspheres have ∼70% lower volumes than the wide-field microspheres for all microsphere intensities as a result of increased contrast and the fact that the deconvolution algorithm minimizes the distortion of microsphere within the image and the spreading of light caused by diffraction (Table 1 and Fig. 3C).

TABLE 1.

Average intensity mean and volume, of microspheres plus or minus the SD from three experiments

Bead intensity (%)	Number of image stacks	Number of beads	Intensity mean original data	Volume (μm3) original data	Intensity mean iterative deconvolution	Volume (μm3) iterative deconvolution	Intensity mean iterative blind deconvolution	Volume (μm3) iterative blind deconvolution
0.2	14	83	56 ± 4	19 ± 2	180 ± 30	13 ± 2	160 ± 30	15 ± 3
0.8	14	88	126 ± 14	19 ± 2	620 ± 95	13 ± 2	650 ± 100	14 ± 2
2.3	15	121	310 ± 42	18 ± 2	2150 ± 490	12 ± 1	2160 ± 350	12 ± 1
10.6	13	67	1280 ± 190	18 ± 1	8450 ± 1560	12 ± 1	8600 ± 1400	12 ± 1
30.0	15	131	3280 ± 550	20 ± 2	24,300 ± 5400	12 ± 2	22,400 ± 4100	13 ± 2
Average				19 ± 2		12 ± 2		13 ± 2

Intensity and volume data are presented for original wide-field data, iterative deconvolution data, and iterative blind deconvolution data.

Figure 3.

Wide-field calibration, increased intensity, and preservation of the quantitative mean intensity relationship upon deconvolution and reduction in microsphere volume. Graphs of the average microsphere intensity (A), average normalized microsphere intensity (B), and average microsphere volume (C), as determined using Imaris 3D image analysis software for the original wide-field data (blue diamonds), iterative deconvolution data (red squares), and iterative blind deconvolution data (green triangles), plotted against the relative microsphere intensities given by the microsphere manufacturer. (A and B) Lines are linear regression best fits. (C) Horizontal lines correspond to the average volume of all of the microspheres from all three slide sets for each condition. Error bars are sd of the mean values for three experiments.

Quantitative Intensity Information

The data from the images taken at 5% mercury lamp power were adjusted to the 0.5% power by multiplying the measured power ratio of the mercury bulb power at 0.5% (0.0535 mW) and 5% power (0.6460 mW), which is 0.0828, to each intensity measurement derived from Imaris. Then, the relative average intensity of the calibration microspheres in the wide-field and the deconvolved images were graphed against the actual microsphere intensities from the manufacturer. Subsequently, a linear line of regression was fit to the scatter plots to see if the relationship between the defined relative microsphere intensity and the measured mean intensity showed the expected linear relationship (Fig. 3A).

Intensity means of microspheres from original and deconvolved images showed linear correlation, with the relative microsphere intensities from the manufacturer's specifications (Table 1 and Fig. 3B). The intensity data from the 100% intensity microspheres were consistently lower than expected, by ∼20%, compared with the other microspheres in the original images. This is likely a result of some dye self-quenching with the high concentration of dye in the 100% intensity microspheres. Hence, further analyses were carried out with just the five calibration microspheres of lower intensities: 0.2%, 0.8%, 2.3%, 10.6%, and 30.0%.

The mean intensity of each calibration microsphere was normalized by first dividing by the maximum intensity for all of the microspheres in a given sample (i.e. 30.0% microspheres) for a specific experimental run and then averaging all of the microsphere intensities. When the normalized intensity means were graphed against the actual microsphere intensities, all three experimental data sets (Sets 1, 2, and 3) yielded trend lines with slopes of ∼0.03 and coefficient of determination (R²) values of >0.98—before and after deconvolution. As the slopes of the graphs reflect the quantitative relationship between various fluorescence intensities, the similar magnitudes in-slope for the original images and the deconvolved images clearly indicate that deconvolution using the AutoQuant X3 blind deconvolution algorithm preserves the relative quantitative intensity data (Fig. 3B).

Data from all three experiments were combined for original data, iterative deconvolution data, and iterative blind deconvolution data. All data sets resulted in linear trend lines with similar slopes (0.0331, 0.0327, and 0.0333, respectively) and high R² values (0.9869, 0.9911, and 0.9905, respectively; Fig. 3B). There was no significant difference between the iterative deconvolution and the iterative blind deconvolution. This is not surprising, as the PSF for these images is very close to the theoretical (Supplemental Fig. 1), and images were collected of microspheres near the coverslip in a thin sample. Blind deconvolution is particularly useful when imaging deep into samples when it is difficult to have an accurately measured PSF and when spherical aberrations can be significant.

Volume

The volumes of the calibration microspheres in the original wide-field images and the deconvolved images were determined using the Imaris software. As expected, for all three experiments, the average volumes are consistent across the microspheres of different fluorescence intensities for the original wide-field and deconvolved images (Table 1 and Fig. 3C). Deconvolution did decrease the average volume from 19 ± 2 to 13 ± 2 μm³, as a result of increased contrast and the reassignment of out-of-focus light toward the center of the microspheres, which restores microsphere shape. The deconvolved microsphere image volume of 13 μm³ is approaching the expected volume of 8 μm³, based on the sphere diameter of 2.5 μm. The microspheres do not appear spherical as a result of diffraction along the z-axis. In fact, they are distorted and oblong along the z-axis. Therefore, the microsphere volume measurements are expected to be larger than the actual microsphere size. Deconvolution does improve the z-axis resolution but does not completely correct the microsphere distortion, so volume measurements are still much larger than expected. There was no significant difference in the measured microsphere volumes between the iterative deconvolution and iterative blind deconvolution data (Table 1 and Fig 3C).

We attempted to repeat our analysis using Huygens Essential deconvolution software. When using the default settings in the software and a theoretical PSF, we found microspheres to be very symmetric and less oblong along the z-axis than the original or the AutoQuant X3 deconvolution data (average volume of 10±2). However, the intensity data did not maintain a linear relationship. We are convinced that this is a file-formatting/scaling-factor issue causing a distortion of the intensity information, but we were unable to correct this using the Huygens Essential software. Thus, the Huygens software can likely give quantitative intensity data but not using the default settings and file formats available with Huygens Essential. Huygens Professional would likely yield quantitative data but requires more advanced deconvolution training, and users need to spend considerable time setting up and optimizing the deconvolution algorithm settings and learn how to adjust the scaling factor during file-format conversions.

DISCUSSION

In this study, our aims were to calibrate our wide-field microscope and determine whether the AutoQuant X3 restorative deconvolution algorithms retained quantitative intensity information. Data collected using calibration microspheres supported that our wide-field microscope is quantitative, and they did indeed show a linear response to the different intensity microspheres (Fig. 3A and B). Following deconvolution, this linear response is not only maintained but also shows similar magnitudes in-slope upon normalization (Fig. 3A and B). As the slope of the plots reflect a change in the quantitative relationship between various fluorescence intensities, the similar magnitudes in-slope clearly indicate that deconvolution preserves the relative relationship between fluorescence intensities. The robustness of the calibration yielded the wide-field and deconvolution graphs of the intensity means against the actual microsphere intensities, with slopes of ∼0.03 and R² values of >0.985, before and after deconvolution (Fig. 3B).

As a result of deconvolution algorithms reassigning the out-of-focus light to their origin, higher S/N images are seen following deconvolution, and the microspheres have higher intensity means and much rounder shapes (Figs. 1 and 2). As a result, the deconvolved microspheres have lower volumes than the wide-field image microspheres (Table 1 and Fig. 3C). Deconvolution decreased the measured volume to 70% of the original image volumes, which is much closer to the expected volume of 8 μm³, based on the actual microsphere size.

It should be noted that in our hands, the 100% intensity microspheres had lower average intensity means and sums than expected, and they were eliminated from further analysis. This may be caused by the phenomenon of concentration quenching that causes highly concentrated fluorophores to have lower intensities than expected as a result of the intermolecular quenching between nearby fluorophores.²⁰

It is imperative for any quantitative imaging experiments to test and validate that the equipment is generating quantitative data. It is also important to validate that any image processing or analysis steps applied to the data maintain quantitative intensity information. Overall, we have presented a protocol for calibration microsphere sample preparation, imaging, and analysis. This protocol should be useful to others for calibrating instruments for quantitative imaging and ensuring instrument quality control. In addition, we have demonstrated that the iterative deconvolution and iterative blind deconvolution algorithms in AutoQuant X3 maintain the linear relationship in calibrated microsphere intensities and more importantly, their relative intensity changes. We are now confident that the use of AutoQuant X3 is appropriate and accurate for quantitative fluorescence imaging.

DISCLOSURE

The authors declare no conflict of interest.