Uncertainty in MR tracer kinetic parameters and water exchange rates estimated from T₁-weighted dynamic contrast enhanced MRI

Abstract

Purpose

The aim of this study was to assess the uncertainty in estimation of MR tracer kinetic parameters and water exchange rates in T₁-weighted dynamic contrast enhanced (DCE)-MRI.

Methods

Simulated DCE-MRI data were used to assess four kinetic models; general kinetic model with a vascular compartment (GKM2), GKM2 combined with the 3S2X model (SSM2), adiabatic approximation of the tissue homogeneity model (ATH), and ATH combined 3S2X model (ATHX).

Results

In GKM2 and SSM2, increase in transfer constant (K^trans) led to underestimation of vascular volume fraction (v_b), and increase in v_b led to overestimation of K^trans. Such coupling between K^trans and v_b was not observed in ATH and ATHX. The precision of estimated intracellular water lifetime (τ_i) was substantially improved in both SSM2 and ATHX when K^trans > 0.3 min⁻¹. K^trans and v_b from ATHX model had significantly smaller errors than those from ATH model (p<0.05).

Conclusion

The results of this study demonstrated the feasibility of measuring τ_i from DCE-MRI data albeit low precision. While the inclusion of the water exchange model improved the accuracy of K^trans, v_b, and the interstitial volume fraction estimation (v_e), it lowered the precision of other kinetic model parameters within the conditions investigated in this study.

INTRODUCTION

T₁-weighted dynamic contrast enhanced (DCE) MRI data have been used to estimate physiologically relevant MR tracer kinetic parameters, such as transfer constant (K^trans), vascular volume fraction (v_b), and extravascular extracellular volume fraction (v_e) (1–3). It has been demonstrated that such kinetic parameters can be used for diagnosis of cancer (4,5) as well as for prediction (6,7) and monitoring (8) of treatment response. However, accurate estimation of the kinetic parameters from DCE-MRI data still remains a challenging problem, particularly when additional model parameters, such as inter-compartmental water exchange rates (9–11), are included.

DCE-MRI data are usually acquired with a short TR where a repetitively pulsed system rapidly approaches a steady state described by Ernest and Anderson (12). For a system of multiple compartments with chemical exchange, Spencer and Fishbein (13) presented an analytical solution for the steady state magnetization of each compartment and demonstrated that the apparent T₁ values of multiple compartments deviate from the original T₁ values (with no exchange) as TR increases. When TR approaches zero, the apparent T₁ values approach the original T₁ values. On the other hand, the smaller the flip angle (α) is, the larger the deviation of apparent T₁ from the original T₁ is. These observations that Spencer and Fishbein (13) reported are closely related to T₁-weighted DCE-MRI scans which are usually performed with a short TR (~5 ms) and a small α (~10°) for fast 3D imaging, leading to a question whether the water exchange effect should be included for accurate and robust estimation of the kinetic parameters.

Water exchange effect has also been observed in DCE-MRI studies using inversion recovery prepared 2D gradient echo sequences (14). Landis et al (15) measured the T₁ of rat skeletal muscle infused with an MRI contrast agent (CA), gadolinium diethylenetriamine pentaacetic acid (Gd-DTPA), which typically stays in the interstitial space and does not enter the intracellular space. They found that the relationship between the measured T₁ and CA concentration was not linear and was better described by a non-linear model that included water exchange between tissue compartments. Several other studies in tumor imaging reported that the influence of water exchange needed to be included based on goodness of fitting of the model to the DCE-MRI data (16–18). However, it has not been shown whether such better model fitting can lead to more accurate and precise estimation of the kinetic model parameters.

Hence, the present study was conducted to assess the uncertainty in kinetic model parameters estimated using two representative MRI CA kinetic models; extended general kinetic model (GKM2) (19) and extended shutter speed model (SSM2) (20). In addition, we also conducted a similar study to investigate the effect of water exchange in adiabatic approximation to the tissue homogeneity model (ATH) (21) which assumes the capillary bed as a plug-flow system and the interstitial space as one compartment, and the ATH model combined with the 3S2X water exchange model (ATHX). Since there is no means to independently and accurately measure the same kinetic parameters measured by DCE-MRI, we used realistic simulation data in this study.

METHODS

Data simulation

Realistic DCE-MRI data were generated in two steps; calculation of the CA concentrations in tissue compartments with a bolus injection and conversion to corresponding MRI signal curves. The CA concentration curve of a single voxel was simulated using a single blood tissue exchange unit provided in the multiple path, multiple tracer, indicator dilution 4 region (MMID4) model (National Simulation Resources, University of Washington) which models capillaries as axially distributed blood-tissue exchange units (22). It was assumed that the voxel of interest for simulation did not contain any large vessel such that optional large vessels in the MMID4 model were not included in the simulation. The blood-tissue exchange unit has four regions: intravascular, endothelial, interstitial, and parenchymal intracellular spaces. Volume fraction of the endothelium was assumed to be negligible in the current study. The capillary length was set to 0.1 cm; the number of segments was 31; the axial diffusion coefficients for plasma and interstitial fluid region were 1e-5 cm²/s. Volume fractions of the intravascular, interstitial, and intracellular spaces were noted as v_b, v_e and v_i, respectively. It was assumed that the three compartments were connected in a linear form such that there was no direct exchange of CA molecules between the intravascular and intracellular compartments. It was also assumed that the permeability of cellular membrane to CA was zero.

The equilibrium ¹H₂O magnetizations of the intravascular, interstitial and intracellular compartments (M_b0, M_e0 and M_i0) were assumed to be proportional to the volume fractions of the three compartments. In this linear form of three tissue compartments, we also assumed that there was no direct exchange of the water molecules between the intravascular and intracellular compartments. The magnetizations of three compartments (M_b, M_e and M_i) were described using the three-site-two-exchange (3S2X) model proposed by Spencer and Fishbein (13):

$${dM}_b/dt=R_{1b}(M_{b0}-M_b)-k_{be}{M}_b+k_{eb}{M}_e$$ (1)

$${dM}_e/dt=R_{1e}(M_{e0}-M_e)+k_{be}{M}_b-(k_{eb}+k_{ei})M_e+k_{ie}{M}_i$$ (2)

$${dM}_i/dt=R_{1i}(M_{i0}-M_i)+k_{ei}{M}_e-k_{ie}{M}_i$$ (3)

where R_1b, R_1e and R_1i are the longitudinal relaxation rates in three compartments, k_AB denotes the rate constant from compartment A to compartment B. The four rate constants used in Eqs. (1), (2) and (3) can also be expressed in terms of water lifetimes (τ_b, τ_e and τ_i) and volume fractions of the three compartments by keeping mass balance: k_be = τ_b⁻¹; k_eb = τ_e⁻¹−(v_i/v_e)τ_i⁻¹; k_ei = τ_e⁻¹−(v_b/v_e)τ_b⁻¹; k_ie = τ_i⁻¹. We assumed that the water fraction in each compartment was 1 for simplicity in this study.

MRI signal was calculated for the case of using a spoiled gradient recalled echo sequence. The transverse relaxation rate was assumed not affected within the CA concentrations considered in this study. The longitudinal relaxation rates of the three compartments prior to contrast injection (R_1b0, R_1e0 and R_1i0) were assumed to be 0.67 s⁻¹. The CA relaxivity was held constant as 3.8 mM⁻¹s⁻¹ in all three compartments. The relationship between relaxation rate R₁(t) and CA concentration C(t) is assumed linear within each compartment; R_1j(t)=r_1jC_j(t)+R_1j0 where j=b, e and i. Then, the observed magnetization of the 3S2X system in Eqs. (1), (2) and (3) for the given TR and α was calculated using the Ernst-Anderson relationship (13,20). Matrix exponential was calculated using a function provided in Matlab (MathWorks, Natick, MA), expm, which was implemented based on a scaling and squaring algorithm with a Pade approximation method (23). Sum of the magnetizations in all three compartments was used as the corresponding MRI signal.

Arterial input function (AIF) for data simulation with the MMID4 was obtained from a DCE-MRI data set measured in one of the external iliac arteries of a patient from our previous study (24) (dots in Figure 1(a)). A bi-exponential clearance function convoluted with a box-shaped function (25) was fitted to the measurement data, in order to generate a noise-free, realistic AIF model that can provide data at any given temporal resolution. The AIF model, C_b(t) as shown with the solid line in Figure 1(a), was defined as

Figure 1.

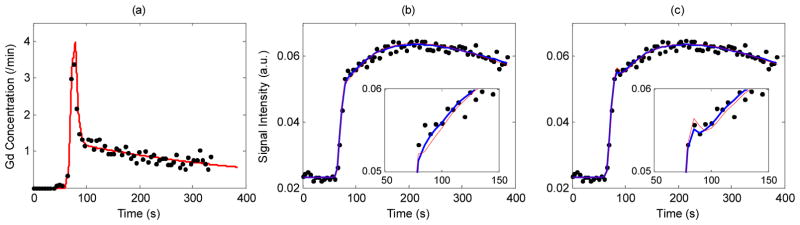
(a) Measured AIF from prostate DCE-MRI data (black dots) and the box-exponential clearance function fit (red solid line) used for simulation. (b) Representative MRI data generated using the MMID4 and the 3S2X model (K^trans=0.25/min with PS=0.28/min and F_p=1.2/min, v_b=0.06, v_e=0.45, τ_b=0.05s, τ_i=0.2s and T_c=3s) with noise level SNR=20 (black dots) and the model fits using SSM2 (blue thick line) and GKM2 (red thin line). (c) Similar to (b) with ATHX (blue thick line) and ATH (red thin line).

$$C_b(t)=B(t)\ast f(t)$$ (4)

with B(t) = 1 for 8.6 s<t<9.6 s and B(t) = 0 elsewhere, and f(t) = Aexp(−Bt)+Cexp(−Dt) with A = 2.9125, B = 0.4070, C = 0.6447 and D = 0.0028. * is a convolution operator. This AIF model was used to generate all simulation data in this study.

The simulation of DCE-MRI data was initially conducted with a temporal resolution of 0.2 s. Subsequently, the time intensity curve generated from the simulation was re-sampled to a lower resolution of 5 s that is more easily achievable in an MRI experiment. The under-sampling process was repeated to generate 100 data sets with randomly chosen starting point between 0 and 5 s. These data were combined with Rician noise by assuming the simulated MRI signal was the real part of complex MRI data and adding independent Gaussian noise to imaginary and real data. In this simulation study, signal to noise ratio (SNR) was defined as the ratio of the baseline signal to the standard deviation of the Gaussian noise applied to the imaginary and real part of the complex data. Figure 1(b) shows an example of the MRI data generated for SNR=20 with typical SSM2 and GKM2 model fits. Similarly, Figure 1(c) shows the same MRI data generated for SNR=20 with typical ATH and ATHX model fits. Data with SNR=20 were used throughout the study unless specified otherwise.

MR tracer kinetic models

The simulation data with the known tissue parameters described above were used to assess the uncertainty in measurement of parameters of two groups of tissue kinetic models; one based on the general kinetic model (GKM) (1) and another based on the adiabatic approximation to the tissue homogeneity (ATH) model (21). The first group included extended general kinetic model (GKM2) (19) and extended shutter speed model (SSM2) (20). Both GKM2 and SSM2 models are based on Kety model extended to include a vascular compartment, shown in Eq. (5):

$$C_{\mathit{tis}}(t)=v_b{C}_b(t)+K^{\mathit{trans}}{\int }_0^t{C}_b(u)exp\left(-\frac{K^{\mathit{trans}}}{v_e}(t-u)\right)du$$ (5)

where C_tis(t) is the CA concentration of the whole tissue in a voxel. In GKM2, the longitudinal relaxation rate of tissue, R₁(t), was calculated using a linear relationship; R₁(t) = R₁₀ + r₁C_tis(t) where r₁ was 3.8 mM⁻¹s⁻¹ and R₁₀ was 0.67 s⁻¹. With given TR and α, the steady-state magnetization was calculated using the Ernst-Anderson relationship for spoiled gradient recalled echo pulse sequence (13,20). Thus, there were 3 free parameters (K^trans, v_e and v_b) to estimate in GKM2.

SSM2 takes into account the effect of water exchange between compartments when estimating the longitudinal relaxation rates for given CA concentrations. The two terms in the right hand side of Eq. (5) represent the CA concentrations in the intravascular and interstitial compartments, respectively. The CA concentration in the intracellular space was assumed zero. Then, the steady-state magnetization was calculated using the 3S2X model described in the above Data Simulation section. SSM2 had 5 free parameters (K^trans, v_e, v_b, τ_b and τ_i). SSM2 parameter estimation was performed with and without fixing τ_b as a free parameter for parameter estimation.

The second group of kinetic models included ATH and ATHX models. In the tissue homogeneity (TH) model, the CA concentration in the intravascular space is defined as a function of both time and distance along the length of the capillary (26). An approximate closed-form solution in time domain, known as the ATH model, was derived based on the adiabatic approximation that CA concentration in the extravascular space changes slowly compared to that of the intravascular space (21). The ATH model has recently been used in DCE-MRI data analysis (27–29). It is defined as follows:

$$C_{\mathit{tis}}(t)=F_p{\int }_0^{T_c}{C}_b(t-u)du+K^{\mathit{trans}}{\int }_0^{t-T_c}{C}_b(u)exp\left(-\frac{K^{\mathit{trans}}}{V_e}(t-u)\right)du$$ (6)

where F_p is plasma flow and T_c=v_b/F_p is mean transit time. K^trans is a function of both F_p and permeability surface area product (PS), given as K^trans = [1−exp(−PS/F_p)]F_p. Thus, there were 4 free parameters (PS, F_p, v_e and T_c) for the ATH model. In the ATHX model, the two terms on the right hand side of Eq. (6) were assumed to represent the CA concentration in the intravascular and interstitial compartments. Thus, the ATHX model had 6 free parameters (PS, F_p, v_e, T_c, τ_b and τ_i). Similar to SSM2, ATHX parameter estimation was performed with and without fixing τ_b as a constant, in order to assess whether it would be necessary to keep τ_b as a free parameter for estimation.

The model parameters were estimated by minimizing the sum of squares of the difference between the simulation data and the model fit. Parameter estimation was conducted using the Simplex (30) method provided in Matlab (MathWorks, Natick, MA). The result of parameter estimation can be sensitive to initial values (27,31), particularly when the data is noisy. For each noisy time-intensity curve (out of 100 noisy time-intensity curves per each parameter set), we used 50 randomly selected initial guess values and selected the result with the lowest cost function value as the final result. This study was conducted using a Sun Microsystems cluster computer system from New York University high performance computing service which allowed us to use 64 computing threads at a time. Estimation of the kinetic parameters using the numerical integration time step of 1 s took about 0.1 min for GKM2 and ATH models and about 2 min for SSM2 and ATHX.

Effect of MRI scan parameters

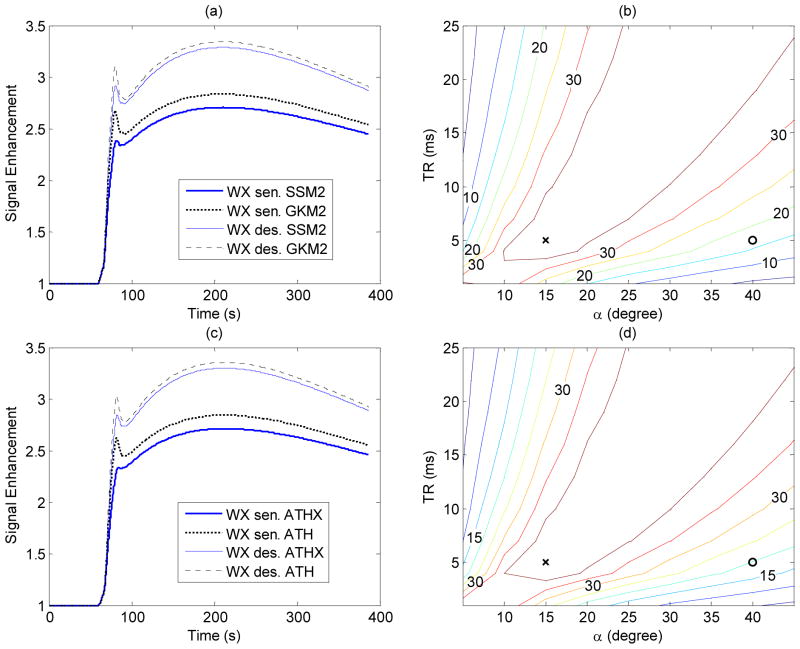
As reported by Spencer and Fishbein (13) earlier, MRI scan parameters, such as TR and α, determine how much water exchange affects the apparent T₁ of the target tissue with respect to the original T₁ values of individual compartments. The kinetic models with and without the water exchange terms were used to demonstrate the difference between two models (GKM2.vs. SSM2 and ATH.vs. ATHX) as a function of TR and α. The kinetic parameters were assumed to be K^trans = 0.25 min⁻¹, v_e = 0.45 and v_b = 0.06 as reported for a breast cancer (27). In SSM2 and ATHX, τ_i and τ_b were assumed to be 200 ms and 50 ms, respectively. The sum of absolute differences between these two curves (SDC) was used as a global measure of the effect of water exchange in various imaging condition with different TR (0 – 25 ms) and α (0 – 50°). Although not all combinations of TR and α are practically useful, the SDC contour in these ranges was generated to assess the general trend of the water exchange effect. This analysis was performed to provide an overview of how the result in this study (conducted for TR = 5 ms and α = 15°) would change in different MRI scan protocols.

Simulation of different tissue conditions

The baseline tissue parameters for simulation were v_b = 0.06, v_e =0.15, v_i = 0.79, PS = 0.345 ml/(g•min), F_p = 1.2 ml/(g•min), τ_b = 0.05 s, and τ_i = 0.2 s. Since there has not been a study, to our best knowledge, that measured all the parameters considered in our study, it was not possible to choose the baseline values from one reference. Instead, the baseline values were selected based on several previous studies (18,20,27). With the given F_p and PS, the baseline transfer constant K^trans was 0.30 min⁻¹. Data simulation was conducted by changing one parameter at a time as shown in Table 1. Tissue parameters could be related to each other in some degree. But, for the simplicity in the simulation study, we varied one parameter at a time, except the volume fractions. When changing either v_e or v_b, v_i was varied inversely proportional to the change such that the sum of the volume fractions remained 1.

Table 1.

Kinetic model parameters used for the simulation studies.

	Baseline	Ktrans change	ve change	vb change	τi change
Ktrans (min−1)	0.30	0.05, 0.15, 0.30, 0.45, 0.60	0.30	0.30	0.30
ve	0.15	0.15	0.10, 0.20, 0.30, 0.40, 0.50	0.15	0.15
vb	0.06	0.06	0.06	0.02, 0.05, 0.08, 0.11, 0.14	0.06
τi (s)	0.2	0.2	0.2	0.2	0.10, 0.30, 0.50, 0.70, 0.90

Statistical analysis

Accuracy of the estimated parameters was measured by the difference between the median of estimated value and the true value used for data simulation. Precision was assessed in terms of coefficient of variation (CV = standard deviation/mean). In addition, kinetic models were compared in terms of Bayesian Information Criterion (BIC), defined in Eq. (7)

$$\mathit{BIC}=ln\left(\frac{\mathit{RSS}}{N}\right)+k\frac{ln(N)}{N}$$ (7)

where RSS is the residual of sum of squares, N is the number of data points, and k is the number of free parameters (27). Wilcoxon signed-rank test was used to test the difference in accuracy or precision between kinetic models with and without the water exchange terms. A p-value of less than 0.05 was considered significant.

RESULTS

The influence of water exchange on DCE-MRI signal depending on MRI scan parameters, TR and α, is depicted in Figure 2, in terms of difference between the time intensity curves expected from kinetic models with and without the water exchange model. Figure 2(a) shows representative examples of GKM2 and SSM2 time-intensity curves for K^trans = 0.25 min⁻¹, v_e = 0.45, and v_b = 0.06 that were reported for a breast cancer (27), when the data acquisition protocol was water-exchange sensitized (TR = 5 ms and α = 15°) and water-exchange desensitized (TR = 5 ms and α = 40°). The SDC for the given TR and α was defined as the sum of absolute differences between these two data sets. Figure 2(b) shows a contour plot of SDC as a function of TR and α. It can be observed that, when α is small (< 10°), the SDC decreases as TR increases. For short TRs (< 5 ms), SDC decreases as α increases. The basic pattern of the SDC did not change noticeably by using different kinetic model parameters. The uncertainty analysis in the present study was conducted for α = 15° and TR = 5 ms, marked by a cross in Figure 2(b). Similar observation was made for ATH and ATHX models as shown in Figure 2(c) and (d).

Figure 2.

The effect of water exchange on DCE-MRI time intensity curve depending on the scan condition. (a) Representative MRI signal curves generated using GKM2 and SSM2 models (K^trans=0.25/min with PS=0.28/min and F_p=1.2/min, v_b=0.06, v_e=0.45, τ_b=0.05s, τ_i=0.2s and T_c=3s) in two scan conditions; water-exchange (WX) sensitized (TR=5ms, flip angle=15°) and water-exchange desensitized (TR=5ms, flip angle=40°). (b) Contour plot of sum of absolute difference between GKM2 and SSM2 curves (SDC) for different flip angle α and TR values. The cross (x) and circle (o) marks correspond to water-exchange-sensitized acquisition (TR=5ms, flip angle=15°) and water-exchange-desensitized acquisition (TR=5ms, flip angle=40°) respectively. (c) and (d) are same as (a) and (b) but with the ATHX and ATH models.

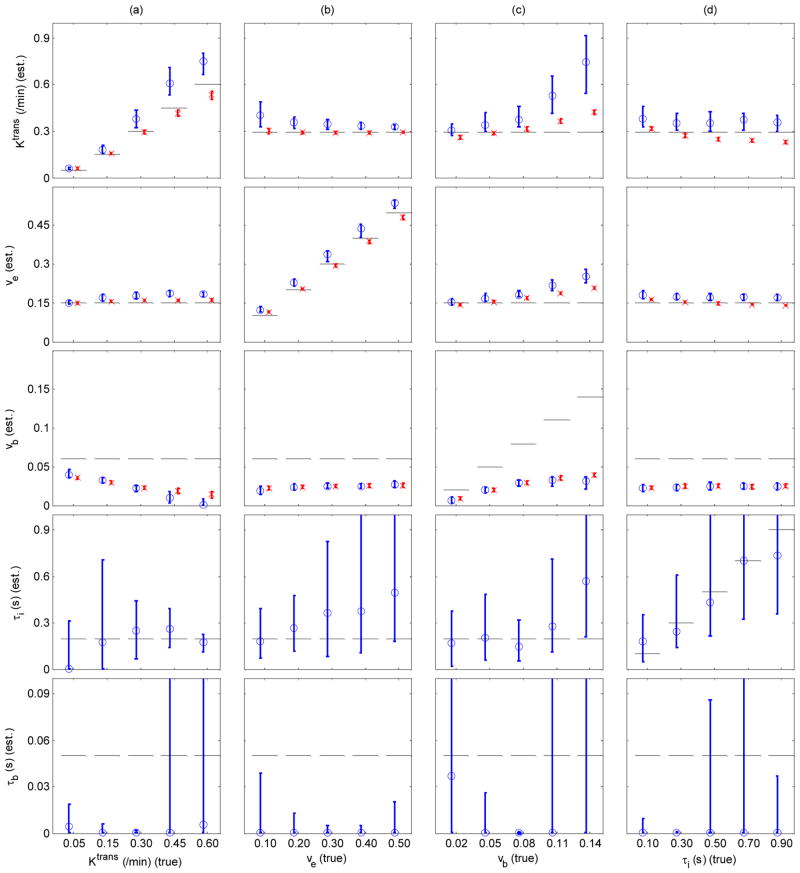
Figure 3 shows that SSM2 and GKM2 model parameters estimated by fitting the models to the simulated data with SNR=20. Each column of plots in Figure 3 represents a set of cases where one parameter was varied while holding the other parameters same. SSM2 K^trans estimates were higher (4 – 152%) than the true values, particularly for large true K^trans or v_b. SSM2 v_e estimates were also higher (1 – 69%) than the true values except for small K^trans and v_b. In all cases, GKM2 K^trans and v_e had smaller errors (1 – 44% for K^trans and 2 – 38% for v_e) than the SSM2 estimates with smaller inter-quartile range (IQR). The IQR of K^trans increased with increase in K^trans, while that of τ_i decreased. There was no particular extremum observed in terms of IQR. v_b was largely underestimated in both models; the error became bigger as K^trans or v_b increased. Increase of v_b resulted in increase of the estimated K^trans in both models. The estimated τ_i in SSM2 has poor precision (CV = 52 – 170%). When τ_i increased, SSM2 K^trans did not change noticeably whereas GKM2 K^trans decreased by 27% (Figure 3(d)). However, the accuracy of SSM2 and GKM2 parameter estimation was substantially improved when a vascular dispersion function (32,33) was used together with a higher temporal resolution of 0.2 s/frame. (Supplemental Figure 1). Figure 3 also shows that τ_b estimates were close to 0 (≪ 50 ms). Another separate study of SSM2 estimation with τ_b fixed to 1 ms also produced similar results (Supplemental Figure 2).

Figure 3.

Accuracy and precision of SSM2 (circles and solid blue lines) and GKM2 (crosses and dashed red lines) parameter estimation. Each column represents a case where all model parameters were held constant except one parameter; K^trans (a), v_e (b), v_b (c) and τ_i (d). In each column, the parameter varied during generation of reference data is shown on the x-axis. Plotted are the median and inter-quartile ranges of estimated parameters from 100 noisy data sets for each case. Horizontal dashed lines represent the true values used for the reference data.

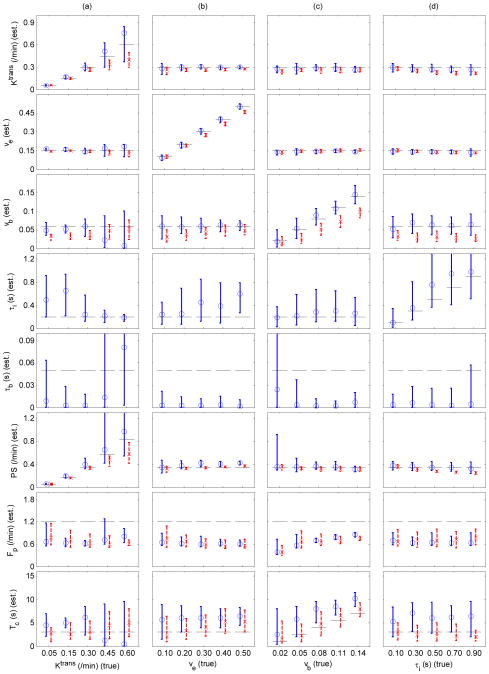
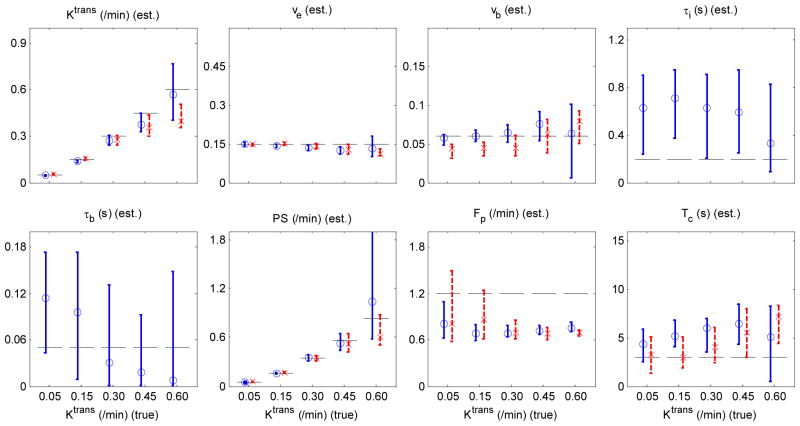
The results of ATH and ATHX parameter estimation are summarized in Figure 4. For K^trans ≤ 0.3 min⁻¹, both ATH and ATHX had reasonably accurate estimates of K^trans and v_e. But for K^trans > 0.3 min⁻¹, ATH K^trans was smaller than the true value (34%) and ATHX K^trans was bigger than the true value (26 %). The accuracy of v_b estimation was substantially improved compared to those of GKM2 and SSM2 and did not show any systematic change due to K^trans as in GKM2 and SSM2. The accuracy and precision of τ_i estimation were markedly improved when K^trans > 0.3 min⁻¹, compared with when K^trans ≤ 0.3 min⁻¹. It can also be noted that, unlike in GKM2 and SSM2, increase of v_b did not induce any noticeable effect on the estimated K^trans in both ATH and ATHX models. Increase in τ_i led to underestimation of ATH K^trans by up to 26%, but much less in ATHX K^trans (11%). Similar to what was observed in SSM2, τ_b estimates were close to 0 (≪ 50 ms) and ATHX parameter estimation with τ_b fixed to 1 ms also produced similar results (Supplemental Figure 3).

Figure 4.

Accuracy and precision of ATHX (circles and solid blue lines) and ATH (crosses and dashed red lines) parameter estimation. Each column represents a case where all parameters were held constant except one parameter; K^trans (a), v_e (b), v_b (c) and τ_i (d). In each column, the parameter varied for generation of reference data is shown on the x-axis. Plotted are the median and inter-quartile ranges of the estimated parameters from 100 noisy data for each case. Horizontal dashed lines represent the true values used for the reference data.

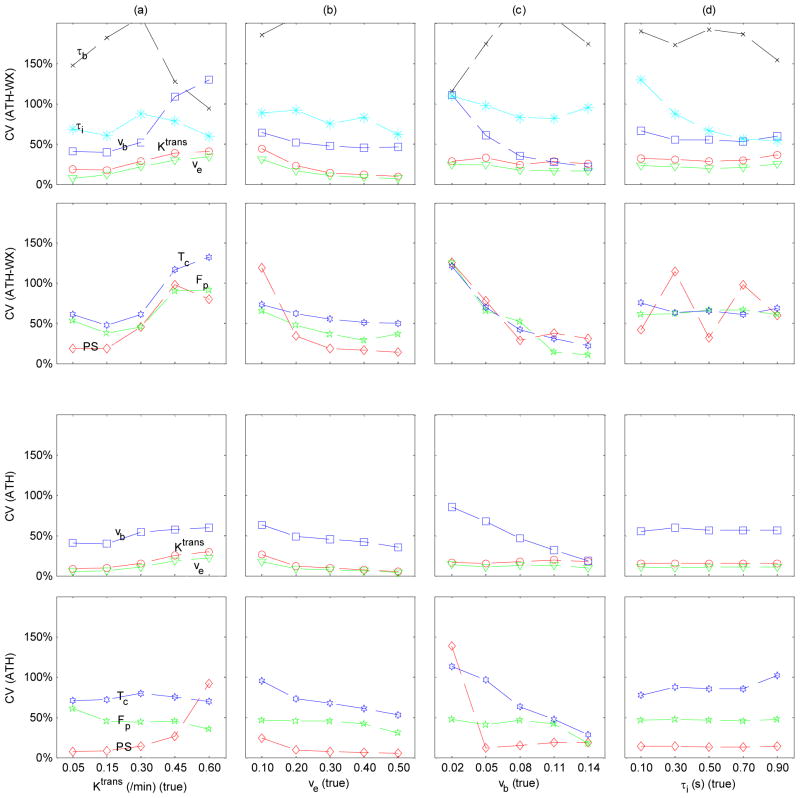
Precisions of the estimated parameters for ATHX and ATH model were assessed in terms of the CV as shown in Figure 5 for SNR = 20. For ATHX model in the top two rows, v_e (triangles) had smallest CVs in all cases presented. The CV of v_e increased substantially (339 %) as K^trans increased from 0.05 to 0.6 min⁻¹. K^trans (circles) had up to 142 % higher CV than v_e and showed similar pattern of increased CV for large K^trans values. The CV of v_b (squares) also increased substantially (219 %) by increase in K^trans or decreased substantially (81 %) by decrease in v_b. The bottom two rows of Figure 5 show the CV of ATH model parameters. Table 2 presents a summary of the uncertainty of kinetic parameters estimated by the two models. Kinetic parameters (K^trans and v_b) estimated by ATHX had significantly smaller errors than those of ATH (p < 0.05). ATH K^trans, v_e, PS and F_p had significantly smaller CVs than those of ATHX (p < 0.05).

Figure 5.

Coefficient of variation (CV) of estimated ATHX (top 2 rows) and ATH (bottom 2 rows) model parameters (red circles for K^trans, green triangles for v_e, blue squares for v_b, black crosses for τ_b, cyan asterisks for τ_ι, red diamonds for PS, green pentagrams for F_p and blue hexagram for T_c) depending on the change in one parameter as noted in the x-axis. Each column represents a case of changing only one parameter; K^trans (a), v_e (b), v_b (c) and τ_i (d).

Table 2.

Comparison between ATH and ATHX in terms of accuracy and precision (SNR=20). Accuracy was defined as the percent difference from the true value and precision as coefficient of variance. Accuracy and precision of each parameter were measured from the data sets shown in Figure 4 and Figure 5 where the selected parameter was at the nominal value (K^trans = 0.30 min⁻¹, v_e = 0.15, v_b = 0.06, and τ_i = 0.2 s).

	ATH		ATHX
	Error (%)	CV (%)	Error (%)	CV(%)
Ktrans (min−1)	−13.14 ± 10.37	15.27 ± 6.22	−0.11 ± 9.64*	27.08 ± 9.35*
ve	−5.15 ± 5.38	10.79 ± 4.50	−1.73 ± 8.29	19.26 ± 7.55*
vb	−37.29 ± 13.25	50.68 ± 14.37	−7.04 ± 25.02*	58.26 ± 27.65
τi (s)	—	—	54.22 ± 67.95	80.63 ± 19.00
τb (s)	—	—	−81.94 ± 35.37	179.38 ± 36.19
PS	−5.63 ± 11.85	23.43 ± 32.80	9.50 ± 8.98*	55.50 ± 37.95*
Fp	−44.81 ± 7.66	43.17 ± 8.30	−45.55 ± 8.03	55.79 ± 26.76*
Tc	14.29 ± 34.14	74.85 ± 19.55	79.97 ± 58.48*	66.45 ± 28.09*

^*represents a significant difference (p < 0.05) between ATH and ATHX.

Performances of kinetic models were also compared in terms of BIC (data not shown). Out of 20 different tissue parameter sets included in this study (5 different values/parameter × 4 parameters as shown in Table 1), the median BICs of SSM2 in 17 cases were significantly smaller than those of GKM2. In contrast, the median BICs of ATHX were significantly larger (p < 0.05) than those of ATH in 14 cases, as there was no improvement in goodness of fitting by using the water exchange in those cases.

Figure 6 shows a comparison between ATHX and ATH in a water-exchange-desensitized acquisition scheme (TR = 5ms, α = 40°), as opposed to the water-exchange-sensitized scheme (TR = 5 ms, α = 15°) used for the above results. The ATH parameters from the water-exchange-desensitized scan in Figure 6 were not noticeably different from those from the water-exchange-sensitized scan in Figure 4. In contrast, the ATHX parameters showed more noticeable difference, particularly for τ_i, as its IQR becomes substantially large even with high K^trans (> 0.3 min⁻¹). However, inclusion of the water exchange terms, as in the ATHX model, did not lower the accuracy of other kinetic parameters even in the water-exchange-desensitized scan condition.

Figure 6.

Comparison between ATHX (blue circles and solid lines) and ATH (red crosses and dashed lines) when a water-exchange-desensitized protocol (TR = 5ms, flip angle = 40°) was used. Horizontal dashed lines represent the true values used for the reference data.

DISCUSSION

Tracer kinetic models for DCE-MRI data provide a non-invasive means to probe tissue microenvironment. It remains, however, challenging to assess the accuracy and precision of the estimated model parameters as there is no gold standard method to independently validate the measured kinetic parameters. When more complex models, such as SSM2 and ATHX, are employed for data analysis, goodness of fitting alone may not be sufficient to ensure that the estimated parameters accurately reflect the corresponding biophysical properties of the tissue. Hence, in this study, we used simulation data generated from well established tissue models, MMID4 (22) and 3S2X (13), and assessed the uncertainty of kinetic model parameters including intravascular and intracellular water lifetimes (τ_b and τ_i). We found that the K^trans, v_e and v_b values estimated using ATHX had higher accuracy than those from other kinetic models. The accuracy of τ_i was relatively high for high K^trans, but the precision of τ_i estimation varied substantially depending on K^trans. Although our findings are based on simulation data, they can be helpful in interpreting the result from a kinetic model analysis of actual data.

One of the main findings in the present study is a good agreement of K^trans and v_e between ATH and ATHX for small K^trans (≤0.3 min⁻¹), as well as in between GKM2 and SSM2. This observation is consistent with what Buckley et al reported earlier from their DCE-MRI study of the skeletal muscle (34). Buckley et al found that there was no significant difference between K^trans values estimated using no exchange (NX) assumption and fast exchange limit (FXL) assumption, implying that the influence of intracellular-interstitial water exchange is negligible (34). The K^trans values reported in that study were typically smaller than 0.1 min⁻¹ in which we made a similar observation that the influence of water exchange was small, if not negligible. Note that there are some differences between our models and the ones Buckley et al used, as we included a vascular compartment in the kinetic models and also used a full 3S2X model instead of using only a part of the solution. Nevertheless, the small effect of water exchange with low K^trans was consistently observed.

For large K^trans (> 0.3 min⁻¹), however, we found that the ATH K^trans was substantially underestimated, while ATHX K^trans was estimated with a better accuracy (error < 26 % for the whole range of K^trans values tested). This observation is consistent with previous reports comparing GKM and SSM (both without vascular components) which demonstrated that GKM could not follow the early fast rising portion of the enhancement curve (16–18). Thus, our results substantiate the previous findings that the effect of water exchange between tissue compartments should be considered when K^trans is relatively high as in the leaky vessels of a tumor.

The median of τ_i estimation from multiple noisy data (SNR=20) approached the true value used for simulation data in most of the cases, however, the precision was poor in general. The accuracy of τ_i decreased substantially with smaller K^trans values. This observation is also consistent with the report by Buckley et al where they found poor precision of τ_i in skeletal muscles with low K^trans (34). The poor precision of τ_i could also be related to a considerably large overlap of τ_i values of malignant and benign breast lesions (5,35), as well as in between complete responders and partial responders to chemoradiation therapy in head and neck cancer patients (7). τ_i has been a parameter of interest because it could potentially represent cell membrane viability. But there has been no study to substantiate its potential as a useful biomarker in a DCE-MRI study. When a higher CA dose injection (higher magnitude of AIF CA concentration) was used for simulation data, we found that the precision of τ_i was noticeably improved (data not shown). Another possibility of improving the precision is to reduce the number of fitting parameters. Since τ_b is difficult to estimate as shown in this study, it could rather be fixed to a small value. As shown in Supplemental Figures 2 and 3, we also assessed ATHX and SSM2 analyses with τ_b fixed to 1 ms. We found the overall trend of both accuracy and precision did not change noticeably by using a fixed τ_b. Further study is warranted to investigate a means to improve the precision of τ_i measurement.

While our study was conducted with the SSM2 model based on the 3S2X water exchange model, an approximation of the SSM2 model, commonly known as the fast exchange regime (FXR) edited model, has been used more often in previous studies (16–18). The FXR model is an approximation of the full model for the case where the long relaxation term in the biexponential solution of the two-site exchange model is the dominant term when the CA concentration is approximately less than 5 mM (15) The contribution of the short relaxation term, ignored in the FXR model, can vary along the contrast enhancement curve and also depending on the different kinetic parameters included in this study. The FXR model also assumes that the vascular contribution is negligible. These two assumptions were not used in the SSM2 model used in our study. It may not be straightforward to apply the results of this study to the FXR model. But it can be expected that the FXR model would give somewhat similar result if the two assumptions for the FXR model are met.

The poor SNR commonly seen with fast imaging methods could be another limiting factor in utilizing the benefit of more comprehensive models, such as the ATHX model. We investigated the uncertainty of ATH and ATHX model parameters using the simulated data with noise level at SNR=5 for limited cases (data not shown). The increased noise reduced the accuracy and precision of parameter estimation substantially for both models as expected. Although the accuracy of ATHX was still better than that of ATH at SNR=5, the difference would become negligible when the noise level increases furthermore.

Given the temporal resolution and SNR used in the current study, we believe our results of the ATH model are compatible with the observations in other studies using the ATH model. Buckley (27) performed a simulation study with the MMID4 model (similar to our current study) and showed that using GKM leads to systematic overestimation of K^trans and underestimation of v_b, and the ATH model provides more accurate estimation. Nash et al (29) assessed different kinetic models for lung cancer DCE-MRI data and found that the ATH model was the best model based on Akaike’s information criterion. In both ATH and ATHX models, F_p was underestimated and T_c had a poor precision. This is consistent with the observation by Kershaw and Cheng (36) in which they investigated the accuracy of ATH parameters depending on temporal resolution. Kershaw and Cheng reported that a low temporal resolution, such as 4.5 s/frame or 6.5 s/frame, lead to underestimation of F_p and a poor precision of T_c, which is consistent with what we observed in this study. Kershaw and Cheng also showed that the accuracy of F_p and the precision of T_c improved substantially with a high temporal resolution of 1.5 s. In the current study, we found that the ATHX model parameters had better accuracy than the ATH model parameters. Although the ATHX parameters had lower precision than the ATH parameters, please note that the CV values reported in our study (Table 2 for both ATH and ATHX) are similar to the CV values reported in the study by Kershaw and Buckley (28) on the precision of ATH parameter estimation. Hence, we believe our simulation study results are within the expected range of outcomes from using the ATH or ATHX models.

The present study was conducted to investigate the uncertainty of tracer kinetic parameters in a realistic situation with noise. However, we could not include all important factors that could affect pharmacokinetic data analysis of DCE-MRI data, such as temporal resolution, baseline T₁ measurement, B₁ field inhomogeneity, and motion artifacts. Further simulation studies on these factors can provide useful insights that investigators using similar DCE-MRI and kinetic model analysis should be aware of. This study was focused on investigating the uncertainty of contrast kinetic model parameters in a wide range of values, in order to assess whether the model parameters are adequate and robust to represent changes in tissue microenvironment, although it might have not include all the parameter combinations possible in reality. Considering different kinetic models have their own limitations in either accuracy or precision, we reckon that a simpler model with a higher precision could be preferred to a more comprehensive model with a compromised precision, depending on the need specific to applications. The current study was performed with 100 noisy data sets in each case. Precision of the estimated parameter can depend on the number of data sets used. However we expect that the relative levels of precision between parameters would remain similar to our results.

The uncertainty of estimated kinetic model parameters can also be affected by cross-correlations, if any, between the estimated parameters. Although our current study was not specifically designed to assess the parameter correlations, the results can be used to take a cursory look at some possible parameter correlations within the limited conditions investigated in our study. For instance, the first column of Figure 3 shows that, in both GKM2 and SSM2, the estimated v_b monotonically decreased as both true and estimated K^trans values increased. Note that such negative association of the two parameters was not observed when other parameters were varied as shown in other columns of Figure 3. Another example can be found with v_b change. When true v_b increased as in the third column of Figure 3, both K^trans and v_e estimates increased, showing a positive correlation. Again note that these two parameters did not show such correlation when other parameters were varied as shown in other columns of Figure 3. These two examples demonstrate that correlation between kinetic model parameter estimates may exist in certain cases. However, it is not a simple, fixed behavior of model parameters, but rather a complex phenomena with different behaviors depending on the parameter values. It may also depend on experimental conditions, such as temporal resolution and SNR. Furthermore, a presence of parameter correlation does not necessarily indicate over-parameterization. These correlations among three parameters, K^trans, v_e, and v_b, were not observed in ATH and ATHX models, which have one more parameter than GKM2 and SSM2, respectively, as shown in Figure 4. On the other hand, simultaneous estimation of PS and F_p in ATH or ATHX model was found challenging; the precisions of PS and F_p were low when the true values of one or both parameters were high, and the distribution of the estimates show different patterns of trends when the precision was low. Investigation of relationship between estimated parameters was beyond the scope of this study. However, it is an important issue that deserves more thorough investigation in future studies.

In conclusion, the present study demonstrated that ATHX model parameters could be used to probe complex tissue microenvironment. It was also shown that SSM2 model with a vascular dispersion function can provide the parameter accuracy similar to that of ATHX which has the same number of model parameters. The results from the present simulation study are consistent with previous observations with actual data analyses and provide helpful information for data interpretation. It has been demonstrated that τ_i can be estimated from DCE-MRI data albeit poor precision and the trend of τ_i change can also be detected. Inclusion of τ_i parameter in the ATHX model resulted in more accurate estimation of K^trans, v_e and v_b, but with lower precisions. Further investigation is warranted to improve the accuracy and precision of τ_i measurement, while keeping the accuracy and precision of other parameters same or better, in order to use this parameter for practical application.