Nonrigid Autofocus Motion Correction for Coronary MR Angiography with a 3D Cones Trajectory

Abstract

Purpose:

To implement a nonrigid autofocus motion correction technique to improve respiratory motion correction of free-breathing whole-heart coronary magnetic resonance angiography (CMRA) acquisitions using an image-navigated 3D cones sequence.

Methods:

2D image navigators acquired every heartbeat are used to measure superior-inferior, anterior-posterior, and right-left translation of the heart during a free-breathing CMRA scan using a 3D cones readout trajectory. Various tidal respiratory motion patterns are modeled by independently scaling the three measured displacement trajectories. These scaled motion trajectories are used for 3D translational compensation of the acquired data, and a bank of motion-compensated images is reconstructed. From this bank, a gradient entropy focusing metric is used to generate a nonrigid motion-corrected image on a pixel-by-pixel basis. The performance of the autofocus motion correction technique is compared with rigid-body translational correction and no correction in phantom, volunteer, and patient studies.

Results:

Nonrigid autofocus motion correction yields improved image quality compared to rigid-body-corrected images and uncorrected images. Quantitative vessel sharpness measurements indicate superiority of the proposed technique in 14 out of 15 coronary segments from three patient and two volunteer studies.

Conclusion:

The proposed technique corrects nonrigid motion artifacts in free-breathing 3D cones acquisitions, improving image quality compared to rigid-body motion correction.

Introduction

Respiratory motion of the heart is one of the most significant challenges to coronary magnetic resonance angiography (CMRA) due to the need for high-spatial-resolution acquisitions that require long scan times spanning many cardiac and respiratory cycles. Despite the existence of a vast body of literature addressing respiratory motion in cardiac magnetic resonance imaging (MRI), many challenges remain (1). Breath-held CMRA requires patient cooperation and limits imaging time, making it difficult to achieve adequate signal-to-noise ratio (SNR), spatial resolution, and whole-heart coverage (2-4). Respiratory gating techniques that use diaphragmatic navigators and correlation factors (typically 0.6) to limit data acquisition to an end-expiratory acceptance window and to correct for superior-inferior motion of the heart suffer from low imaging efficiencies that prolong acquisition times (5, 6). Self-navigation techniques derive the position of the heart directly from the imaging data. Translational motion correction has been performed using beat-to-beat acquisition of 1D (7-10), 2D (11-16), and 3D (17, 18) images or projections of the heart, yielding improvements in both respiratory motion correction and scan efficiency compared to diaphragmatic navigators. However, translational motion compensation can be insufficient for correcting the complex nonrigid respiratory motion of the heart, especially when large gating acceptance windows are used (19-21). Correction of 3D affine motion has been realized for CMRA using binning techniques (22-24) and subject-adapted models from calibration data (25). Nonrigid model-based motion correction techniques (26,27) have recently been applied to CMRA using an interleaved 2D image acquisition to calibrate the nonrigid motion model (28).

Model-based motion correction approaches typically require the acquisition of calibration data, which can add complexity and prolong the scan protocol. A class of autofocus techniques requires no additional calibration data and uses a focusing-metric-based optimization to suppress motion artifacts (29-31). Autofocus techniques simplify the scan protocol by eliminating navigator acquisitions and model calibration. Instead, this complexity is shifted to image reconstruction, which involves the solution of a high-dimensional optimization problem. These autofocus techniques have been limited to rigid-body motion correction, and adaptation of these methods to account for nonrigid motion would add a significant computational burden without additional knowledge of the underlying motion. Recently, hybrid approaches have been developed that utilize motion information measured from navigator acquisitions to simplify the autofocus reconstruction (32,33). In the CMRA approach developed by Moghari, et al., 1D motion measurements from diaphragmatic navigators are used to bin the acquired data, and autofocus reconstruction is applied iteratively to data from each bin to yield a final image with rigid-body 3D translational motion correction. In the approach developed by Cheng, et al., 3D motion measurements from butterfly navigators are used to limit the search space for nonrigid autofocus motion correction. The motion model used in this approach approximates nonrigid motion using localized linear translations. The implementation is a relatively simple and straightforward technique that is analogous to autofocus off-resonance correction techniques, which reconstruct a bank of frequency-compensated images and then use a focusing metric to assemble the final image (34-36).

In this work, we adapt a recently developed nonrigid autofocus motion correction technique (33) to compensate for respiratory motion in free-breathing CMRA. We apply the technique for retrospective motion correction of CMRA data acquired with a 3D cones acquisition (14,37). In our approach, beat-to-beat acquisition of 2D image navigators (iNAVs) is used to measure the translational motion of the heart during the scan (11-14, 16). This proposed motion compensation technique, combined with the favorable motion properties of the 3D cones trajectory, overcomes several disadvantages of other CMRA approaches. First, nonrigid respiratory motion of the heart is corrected via a flexible algorithm that can compensate for a wide range of nonrigid motion using a set of motion basis functions. These motion basis functions are used to reconstruct a bank of rigid-body motion-compensated 3D images, and a focusing metric is applied on a pixel-by-pixel basis to select the best-focused pixel from the bank of reconstructed images. Second, respiratory-induced motion of the heart is directly measured using iNAVs of the heart. This 2D iNAV approach eliminates the need for correlation factors to relate navigator motion measurements (e.g., from 1D diaphragmatic navigators) to cardiac motion. Furthermore, the 3D cones readout provides an inherent robustness to motion artifacts due to the repetitive sampling of the center of k-space. Motion primarily yields diffuse, blurring artifacts, making it possible to perform retrospective nonrigid autofocus motion correction of all acquired data (100% scan efficiency).

We demonstrate this autofocus 3D cones imaging technique for free-breathing CMRA. We assess the performance of the proposed algorithm using phantom, volunteer, and patient studies. Image quality and vessel depiction are compared with no motion correction, rigid-body motion correction, and nonrigid autofocus motion correction. Using quantitative vessel sharpness measurements, nonrigid autofocus motion correction is shown to be superior to rigid-body correction for 14 out of 15 coronary segments from three patient and two volunteer studies.

Methods

Image Acquisition

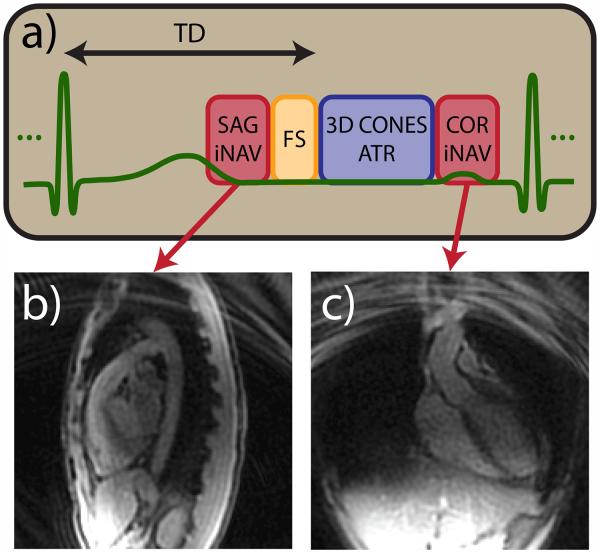
Free-breathing, whole-heart, 3D CMRA data are acquired using a multiphase 3D cones sequence with leading and trailing iNAVs (14). The acquisition is cardiac triggered, and the full set of cones interleaves is segmented and acquired over multiple heartbeats. To reduce image degradation caused by cardiac motion, the segment duration (temporal resolution of each cardiac phase) is typically limited to 65–100 ms and acquired during the quiescent period in mid-diastole. To enable the measurement and subsequent correction of superior-inferior (SI), anterior-posterior (AP), and right-left (RL) translation of the heart due to respiratory motion, sagittal and coronal 2D iNAVs are acquired before and after cones data acquisition every heartbeat, respectively. A fat-saturation module and alternating repetition time balanced steady-state free precession (ATR-SSFP) readout are used to suppress the signal from fat. The acquisition scheme is illustrated in Fig. 1. A detailed description of the 3D cones coronary acquisition can be found in (14).

Figure 1.

Cardiac-triggered 3D cones acquisition scheme. (a) 3D cones data acquisition is preceded by a spiral sagittal iNAV acquisition and fat suppression module. 3D cones interleaves are acquired using an ATR-SSFP readout for additional fat suppression. Multiple imaging phases are acquired during the 3D cones data acquisition period. A spiral coronal iNAV acquisition immediately follows the cones data acquisition. Representative sagittal (b) and coronal (c) iNAVs acquired during one heartbeat of a volunteer study are shown.

Autofocus Motion Compensation and Image Reconstruction

We use an adaptation of the nonrigid autofocus motion correction technique developed by Cheng, et al. (33). This technique reconstructs a final image using many different locally affine corrections. Translational motion of the heart in the SI, AP, and RL directions is measured from iNAVs, and the amplitudes of these measurements are scaled to generate a set of motion basis functions. A bank of motion-compensated images is reconstructed, and a focusing metric is used to assemble the final image.

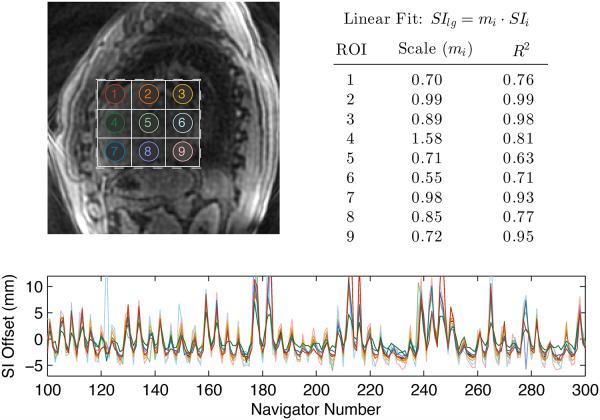
The use of scaled SI, AP, and RL motion trajectories is motivated by the observation that the motion in different regions of the heart is highly correlated, having the same underlying cyclic respiratory pattern but different amplitudes of motion. This observation is illustrated in Fig. 2, which shows SI motion estimates derived from sagittal iNAVs using 9 different regions-of-interest (ROIs). Linear regression was performed to compare motion estimates from each small ROI with those derived from a large ROI covering the heart. The table in Fig. 2 summarizes the results of each linear fit. All R² values are above 0.6, indicating a strong linear correlation between measurements derived from small and large ROIs. Scale factors range between 0.55 and 1.58, which suggests that different ROIs experience different amplitudes of SI motion.

Figure 2.

Comparison of SI motion estimates derived from different regions of the heart. SI motion estimates derived from nine small ROIs (labeled in top-left image) were compared to the SI estimate derived from a large ROI covering the heart (dashed rectangle). The SI estimates were normalized by subtracting the mean, yielding the trajectories shown in the bottom plot. The resulting trajectories have a similar cyclic pattern due to respiratory motion, but the amplitudes of the motion differ for each ROI. Motion estimates from each small ROI were fit to those derived from the large ROI using a linear model. The resulting scale factors (m_i) and R² values (top right) indicate a strong linear correlation between measurements derived from the small and large ROIs.

The use of many small ROIs for motion estimation has several disadvantages. First, a mutual information optimization technique (described in more detail below) is used to derive translational motion from iNAVs. These evaluations are computationally expensive, and repeating these optimizations for each ROI can greatly increase the image reconstruction time. Second, the motion estimates become noisier and less robust when smaller ROIs are used, particularly when these ROIs lack significant image features. Because of these drawbacks, we derive bulk SI, AP, and RL motion trajectories from a single ROI covering the whole heart. These measured trajectories are then scaled following the procedure outlined below.

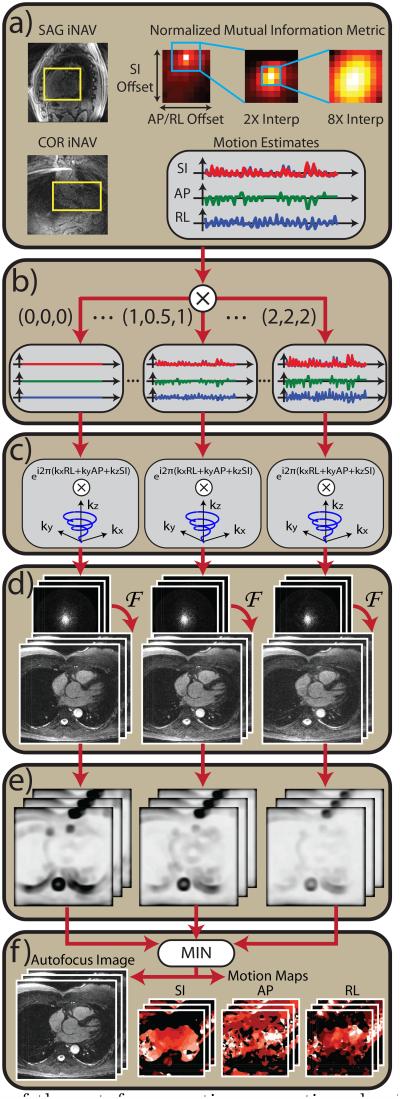
A block diagram of the proposed nonrigid autofocus algorithm is shown in Fig. 3. The following steps summarize the overall procedure.

1. Motion estimation from sagittal and coronal iNAVs (Fig. 3a). A multiresolution mutual information registration technique is used to estimate the SI, AP, and RL translation of the heart from each acquired iNAV frame (38). The motion estimation closely follows the least-squares technique used by Wu, et al. (14), except that we instead use a normalized mutual information metric (39), which we found to be more robust than least squares, especially in regions containing few image features. A reference iNAV frame is chosen at end expiration, and the normalized mutual information,

   $$NMI({\text{iNAV}}_{ref},{\text{iNAV}}_{tgt})=\frac{H\left({\text{iNAV}}_{ref}\right)+H\left({\text{iNAV}}_{tgt}\right)}{H({\text{iNAV}}_{ref},{\text{iNAV}}_{tgt})},$$ [1]

   between the reference frame (iNAV_ref) and each target frame (iNAV_tgt) is computed. The joint entropy,

   $$H(X,Y)=-\sum _{x,y}p(x,y)\text{log}p(x,y),$$ [2]

   and marginal entropy,

   $$H\left(X\right)=-\sum _{x}p\left(x\right)\text{log}p\left(x\right),$$ [3]

   are computed using the joint and marginal histograms (p(x, y) and p(x), respectively) of the reference and target iNAV frames. Each target iNAV is translated to find the SI and AP/RL (sagittal / coronal iNAVs) displacements that maximize the normalized mutual information. A three-step multi-resolution optimization technique is used with 1×, 2× and 8× zero-padded interpolation of the iNAVs to efficiently obtain high-fidelity SI, AP, and RL displacement estimates (40). A rectangular ROI surrounding the heart is manually specified, and the normalized mutual information is evaluated for pixels positioned within this ROI after translation. Using this procedure, time series of SI and AP displacements and SI and RL displacements are derived from the sagittal and coronal iNAVs, respectively.

2. Construction of motion basis set (Fig. 3b). A motion basis set is constructed by scaling the SI, AP, and RL displacement measurements. First, the measurements are normalized by subtracting the mean SI, AP, or RL displacement. This normalization simply changes the reference respiratory position, and it minimizes bulk shifting of the image induced by scaling. The normalized trajectories are scaled using several different scale factors. In this work, evenly spaced scale factors between 0× and 2× are used. We use 9 SI scale factors (0×, 0.25×, … , 2×), 9 AP scale factors (0×, 0.25×, … , 2×), and 5 RL scale factors (0×, 0.5×, … , 2×). In some subjects, the amplitude of the RL motion is larger than the AP motion, and we instead use 9 RL and 5 AP scale factors. The motion basis set is composed of the product space of scaled SI, AP, and RL trajectories (9 × 9 × 5 = 405 unique sets in this work).

3. Motion compensation of k-space data (Fig. 3c). The k-space data are compensated for SI, AP, and RL translation by applying the appropriate linear phase modulation. SI motion estimates are obtained both before and after the data acquisition period from a leading sagittal iNAV and a trailing coronal iNAV, and linear interpolation is used to assign an SI offset to each interleave. A single AP and RL displacement is obtained per heartbeat, and all interleaves acquired during the heartbeat are corrected with the same AP and RL displacement.

4. Gridding reconstruction (Fig. 3d). 3D gridding followed by a 3D fast Fourier transform (FFT) is used to reconstruct each motion-compensated dataset, and root sum of squares is used to combine data from multiple coils.

5. Evaluation of focusing metric (Fig. 3e). Each motion-compensated image is evaluated using a localized gradient entropy focusing metric (33, 41). For each image, the gradient entropy is computed over an s × s × s window centered about each pixel, where s is the window size in cm. A Hann window is used to more heavily weight the metric near the center of the window. Implementation of the gradient entropy computation followed the method used in (33). The window size (s) affects the smoothness of the motion compensation applied to the final image. Advantages and disadvantages of large and small window sizes are discussed below.

6. Reconstruction of final motion-corrected image (Fig. 3f). The final motion-compensated image is assembled on a pixel-by-pixel basis by choosing the “best-focused” pixel from the bank of 3D motion-compensated reconstructions. Here, “best-focused” is defined as the dataset with the minimum gradient entropy value at each pixel. In this way, the final image is assembled in a piecewise manner, using the gradient entropy value to determine the optimal motion-compensated reconstruction for each pixel. By storing the optimal SI, AP, and RL scale factors for each pixel, the algorithm also yields 3D motion maps showing the amplitude of motion in these directions.

Figure 3.

Block diagram of the autofocus motion correction algorithm. (a) A normalized mutual information metric is used to estimate SI, AP, and RL displacements from sagittal and coronal iNAVs. (b) A set of motion basis waveforms is constructed by amplitude-scaling the measured SI, AP, and RL displacements. (c) For each set of motion basis waveforms, 3D translational correction is applied in k-space via phase modulation. (d) Motion-compensated images are reconstructed using 3D gridding followed by a 3D FFT. (e) A localized gradient entropy focusing metric is computed for each image. (f) Pixelwise minimization of the focusing metric yields the final image and SI, AP, and RL motion maps.

Metric Window Size

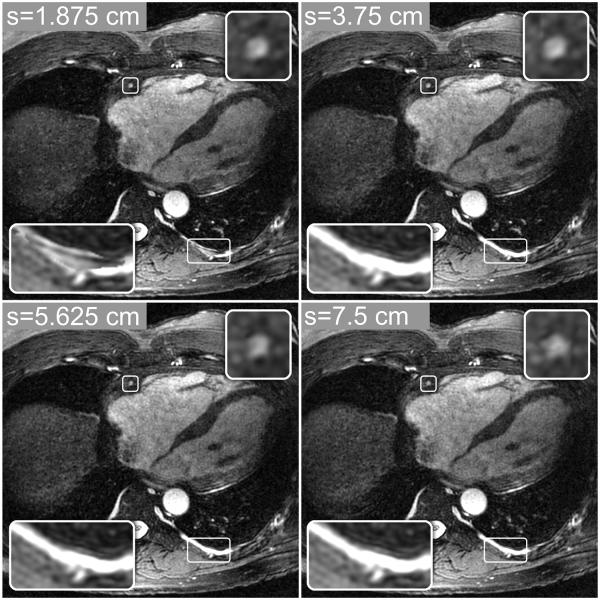
The window size (s) used for the localized gradient entropy metric allows a tradeoff between the degree of nonrigid motion modeling and the introduction of noise-like artifacts and discontinuities in the final image. Large values of s yield more spatial filtering, which promotes smooth and gradual motion changes but may not adequately correct nonrigid motion. Small values of s can better model more localized motion variations across the image but may amplify noise and yield visible discontinuities in the final image due to rapid spatial variations of the metric. This tradeoff is illustrated in Fig. 4, which shows autofocus reconstructions computed with four different window sizes: s = 1.875, 3.75, 5.625, and 7.5 cm (15, 30, 45, and 60 voxels). Although the differences in these four images are subtle, small discontinuities and noise-like artifacts can be seen in the image with s = 1.875 cm (bottom-left inset images), and increased blurring of some features can be seen in the reconstructions with s = 5.625 and 7.5 cm (top-right inset images). A window size of s = 3.75 cm (30 voxels) was used in all of the autofocus reconstructions in this work.

Figure 4.

Autofocus reconstructions computed with four integration window sizes. Smaller window sizes (e.g., s = 1.875 and 3.75 cm), can better model localized motion variations, yielding better nonrigid motion compensation. However, rapid motion variations permitted by small window sizes (e.g., s = 1.875 cm) can yield discontinuities in the final image (bottom-left inset images), where neighboring pixels are reconstructed with very different motion scales. Larger window sizes (e.g., s = 5.625 and 7.5 cm) lead to more spatial filtering of the metric, yielding smooth and gradual motion variations. These images have fewer artifacts and image discontinuities from rapid motion variations, but they also show increased blurring of some features (top-right inset images) due to poorer nonrigid motion modeling.

Experimental Setup

To test and evaluate the proposed motion correction algorithm, phantom, volunteer, and patient studies were carried out on a 1.5 T whole-body scanner with maximum gradient amplitude of 40 mT/m and maximum slew rate of 150 mT/m/ms (GE Healthcare, Waukesha, WI). An eight-channel cardiac array was used for all studies, and cardiac triggering was performed using a peripheral plethysmograph. The scan protocol consisted of a three-plane localizer, used to plan the iNAV slice locations and locate an axial slab covering the whole heart, followed by two-chamber and four-chamber 2D CINE scans, used to determine the trigger delay (TD) and duration of the mid-diastolic cardiac rest period. Our protocol was approved by the institutional review board, and written informed consent was obtained before scanning all subjects.

A fully sampled 3D cones ATR-SSFP acquisition was designed to image a 32 × 32 × 14 cm³ field of view (FOV) at a spatial resolution of 1.25 × 1.25 × 1.25 mm³. The segmented multi-phase acquisition consisted of 3–8 cardiac phases acquired using 12–18 cones readouts per segment yielding temporal resolutions of 65–98 ms per cardiac phase. The iNAVs were acquired using a 12-interleave 2D spiral gradient-echo sequence with an FOV of 28 × 28 cm², resolution of 3.1 × 3.1 mm², and slice thickness of 8 mm (75.6 ms/iNAV). Details of the ATR-SSFP acquisition, catalyzation scheme, and spiral iNAV acquisition are given in (14).

SI, AP, and RL displacements were derived from the iNAVs using manually specified ROIs covering the whole heart, and these measured displacements were used for retrospective rigid-body translational motion correction and nonrigid autofocus motion correction of all acquired 3D cones data (100% scan efficiency). A window size of s = 3.75 cm was used for all autofocus reconstructions. Thin-slab maximum intensity projection (MIP) reformats through the right coronary artery (RCA), left main (LM), left anterior descending (LAD), and left circumflex (LCx) arteries were generated to directly compare the motion correction techniques. All images were reconstructed using 2× zero-padding of k-space, yielding an interpolated resolution of 0.625 × 0.625 × 0.625 mm³.

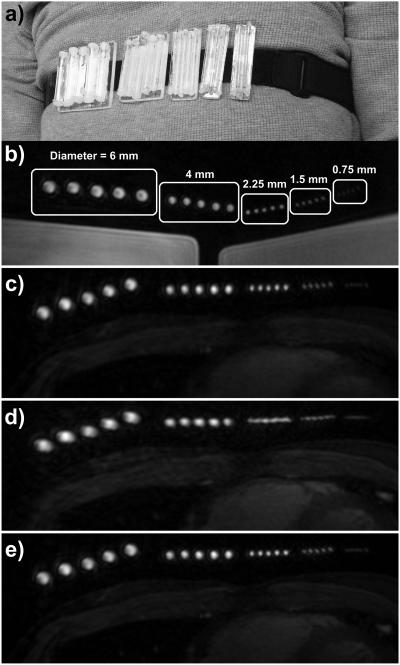
To assess the differences in image quality between the different motion correction schemes, a fiduciary resolution phantom was constructed and strapped around the chest of a volunteer during a free-breathing scan. The phantom consisted of five groups of equally spaced vials of nickel-chloride-doped water wither inner diameters of 0.75, 1.5, 2.25, 4, and 6 mm. Each group contained five vials of the same diameter, which were attached to a polycarbonate backing. Spacing between the vials was approximately equal to the inner diameter. Velcro was used to attach each group of vials to an elastic belt that could be strapped around the chest of a volunteer (Fig. 5a). The ability to resolve these vials gives an indication of the effectiveness of the different motion compensation techniques.

Figure 5.

Free-breathing study with resolution phantom. (a) Photograph showing the resolution phantom strapped around the chest of a volunteer. The phantom consisted of five groups of five equally spaced vials, with inner diameters of 6, 4, 2.25, 1.5, and 0.75 mm. (b) An axial slice through the phantom is shown using a static 3D cones acquisition with the phantom strapped around a large doped-water phantom. The inner diameters of each vial are labeled. (c–e) A free-breathing 3D cones acquisition was carried out with the phantom strapped around the chest of a volunteer. An axial slice through the phantom is shown from images reconstructed with (c) no motion correction, (d) rigid-body translational motion correction using SI, AP, and RL trajectories derived from iNAVs located on the volunteer’s heart, and (e) autofocus motion correction using the same iNAV measurements as (d).

Qualitative analysis of vessel sharpness was performed by two board-certified cardiologists. For the two volunteer and three patient studies, thin-slab MIP reformats of the proximal-to-mid RCA, LAD, and LCx were generated with OsiriX. Reconstructions with no motion correction, rigid-body correction, and autofocus correction were placed in random order and displayed in succession, and the two blinded readers independently assigned integer rank scores (14, 42) to each reformat (1–3: highest to lowest vessel sharpness, respectively).

Quantitative analysis of vessel sharpness was performed using the image edge profile acutance (IEPA) metric (14, 43, 44). The IEPA metric provides an objective method to rank order images reconstructed with different motion correction schemes. Higher IEPA values are associated with increased vessel sharpness. For the volunteer and patient studies, IEPA measurements were computed at 0.5-cm intervals along 8-cm segments of the RCA, LAD, and LCx and then averaged to yield a mean IEPA score for each coronary segment. The mean IEPA scores were compared for reconstructions with no motion correction, rigid-body correction, and autofocus correction. For the three reconstructions, IEPA measurements were evaluated at identical locations along each vessel using 2D cross-sectional ROIs generated with OsiriX and exported to MATLAB (MathWorks, Natick, MA). Each ROI was interpolated by a factor of 10 in both dimensions using cubic interpolation, and the RMS gradient (defined in (44)) was computed along each of 32 evenly spaced radial profiles passing through the center of each vessel. The IEPA measurement for each ROI was obtained by averaging the 32 RMS gradient measurements and normalizing by the difference between the maximum and minimum signal values across all 32 profiles, as described in (44).

Results

A free-breathing resolution phantom study was conducted on a healthy volunteer, and data from five free-breathing subject scans (two healthy volunteers and three patients) were reconstructed with no motion correction, rigid-body correction, and nonrigid autofocus correction for direct comparison and quantitative analysis. A total of 3–8 cardiac phases were acquired for each scan, adding robustness to cardiac motion and allowing retrospective selection of the best phase for visualizing the coronary arteries. Image analysis and comparison of the different motion correction techniques were carried out for a single diastolic phase in which the coronary arteries were well-depicted. Subject-specific parameters are listed in Table 1.

Table 1.

Subject-Specific Imaging Parameters

	Volunteer			Patient
	RPa	A	B	A	B	C
Cardiac phases	3	3	8	3	4	8
Views per segment	14	14	12	16	18	12
Temporal resolution (ms)	76	76	65	87	98	65
Mean heart rate (bpm)	70	72	51	62	47	46
Scan time (HBs)	702	702	819	615	547	819
Scan time (min:s)	10:03	9:47	16:02	9:51	11:37	17:53
Cardiac phase analyzed	2	3	4	2	3	4
Scales (SI × AP × RL)b	9×5×9	9×5×9	9×9×5	9×5×9	9×9×5	9×9×5

^aFree-breathing resolution phantom (RP) study.

^bNumber of motion scale factors used for autofocus reconstruction.

Resolution Phantom Study

A baseline, motion-free dataset was acquired with the resolution phantom around a large doped-water phantom. The 3D cones acquisition was cardiac triggered using a simulated 80 beat-per-minute electrocardiogram (ECG) waveform, and three phases were acquired using 14 readouts per phase to match the acquisition scheme used for the subsequent in-vivo study. Figure 5b shows a representative axial slice from the second phase. The resolution phantom was strapped around the chest of a healthy volunteer, and a free-breathing scan was conducted using the same sequence parameters. An axial slice from the second phase is shown in Figs. 5c–e (cropped and windowed to best depict the resolution phantom). Due to the inherent robustness of 3D cones to motion, the reconstruction with no motion correction (Fig. 5c) depicts the phantom well, with only minor blurring artifacts. SI, AP, and RL displacements were measured from sagittal and coronal iNAVs located on the heart and used for rigid-body motion correction (Fig. 5d). Because motion measurements were obtained from the heart and not the chest wall, rigid-body motion correction blurs the resolution phantom (attached to chest wall). Figure 5e shows the result of autofocus reconstruction using the same measured SI, AP, and RL displacements and 9 SI, 5 AP, and 9 RL scale factors (RL motion was larger than AP motion for this subject). The nonrigid autofocus motion correction algorithm yields a phantom reconstruction (Fig. 5e) that is very similar in quality to that of the static acquisition (Fig. 5b) while simultaneously focusing the chest wall and heart. Some blurring of the 0.75 mm vials can be seen in the autofocus reconstruction, but the ability to clearly resolve the 1.5 mm vials suggests that resolution has been restored to a level that is near that of the designed 1.25 mm isotropic resolution of the cones acquisition.

Volunteer Studies

Two free-breathing volunteer studies were carried out, and data were reconstructed with no motion correction, rigid-body motion correction, and nonrigid autofocus motion correction. For volunteer A, RL motion was larger than AP motion, and thus 9 SI, 5 AP, and 9 RL scale factors were used for autofocus reconstruction. For volunteer B, AP motion was larger than RL motion, and 9 SI, 9 AP, and 5 RL scale factors were used.

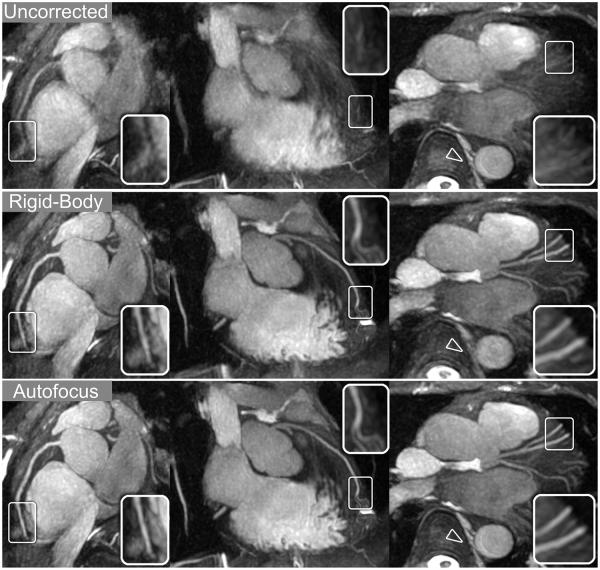
Reconstructions for volunteer A were reformatted into oblique thin-slab MIPs to show the RCA, LAD, and LCx (Fig. 6). Compared to no correction, rigid-body motion correction yields a significant improvement in the depiction of the coronary arteries. Further improvements from nonrigid autofocus correction are most apparent in distal regions of the coronary arteries (magnified in inset images). Non-cardiac features such as the spinal column and descending aorta (arrowheads) are also well-depicted after autofocus reconstruction.

Figure 6.

Reformatted thin-plane MIPs for volunteer A. Reconstructions using no motion compensation (top row), rigid-body translational motion compensation (middle row), and autofocus motion compensation (bottom row) were reformatted to show the RCA (left column), LAD (middle column), and LCx (right column). Rigid-body correction yields significant sharpening of the coronary arteries and cardiac features while blurring non-cardiac features such as the spinal column and descending aorta (arrowheads). Autofocus motion correction yields subtle improvements in the depiction of the coronary arteries (magnified in inset images) and is able to simultaneously sharpen non-cardiac features.

Patient Studies

Three free-breathing patient studies were carried out, and data were reconstructed with no motion correction, rigid-body motion correction, and nonrigid autofocus motion correction. Short-axis reformats for patient C are shown in Figs. 7a–c. Both cardiac features (e.g., papillary muscles, magnified in inset images) and non-cardiac features (e.g., anterior chest wall) are reconstructed with very little motion blurring using the nonrigid autofocus technique (Fig. 7c). These features cannot be simultaneously corrected using a “global” motion correction approach, as demonstrated in Figs. 7a–b.

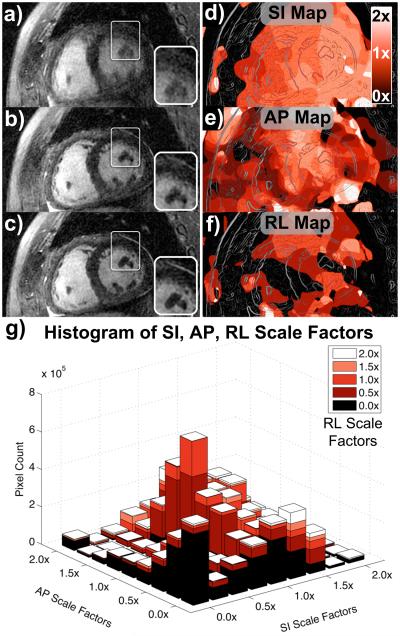
Figure 7.

Short-axis reformats for patient C. Oblique short-axis reformats were reconstructed with no motion correction (a), rigid-body translational motion correction (b), and autofocus motion correction (c). The depiction of both non-cardiac and cardiac features (e.g., papillary muscles, magnified in inset images) improves significantly with autofocus motion correction. SI motion maps (d), AP motion maps (e), and RL motion maps (f) were derived from the autofocus algorithm and reformatted into the same oblique plane as (a–c). Lighter shades of red correspond to motion scales near 2× (white), and darker shades of red correspond to motion scales near 0× (black). The chest wall has little SI and RL motion, but moderate AP motion. An outline of the image features is superimposed on the motion maps for reference. A histogram of the SI, AP, and RL scale factors selected by the algorithm is shown in (g).

Figures 7d–f show the SI, AP, and RL motion maps derived by the autofocus algorithm, respectively. The motion maps are reformatted into the same short-axis plane, and the outline of image features is superimposed for reference. Darker shades of red correspond to less motion (scale factors near 0×), and lighter shades of red correspond to more motion (scale factors near 2×). The motion maps show good agreement with the known motion of the heart and surrounding anatomy. For example, the anterior chest wall was reconstructed with no SI or RL motion compensation, but a moderate level of AP motion. Long-axis reformats (not shown) show that the SI motion scale increases when moving from the base to the apex of the heart, consistent with prior studies (19).

A histogram of the SI, AP, and RL scale factors selected by the algorithm is shown in Fig. 7g. To simplify display of the multi-dimensional histogram, only pixels within a cylindrical ROI containing the heart are displayed. Inclusion of the entire image in the histogram analysis results in very large bins near the 0× scale factors due to the large number of pixels in the dataset that have little or no motion. Likewise, low-SNR regions such as the lungs and background are often reconstructed with arbitrary scale factors, which would complicate the histogram. Note that the histogram mass is centered near the 1× scale factors, but a wide range of motion scale factors is selected by the algorithm.

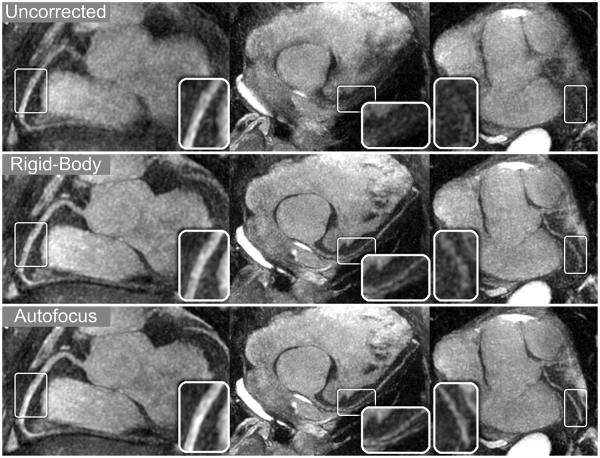
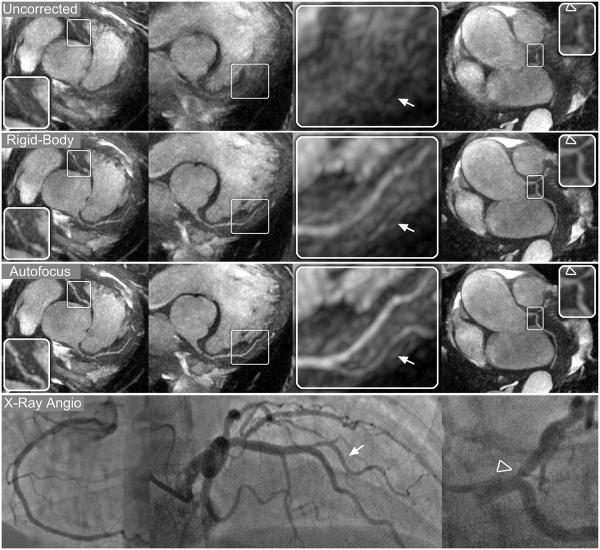
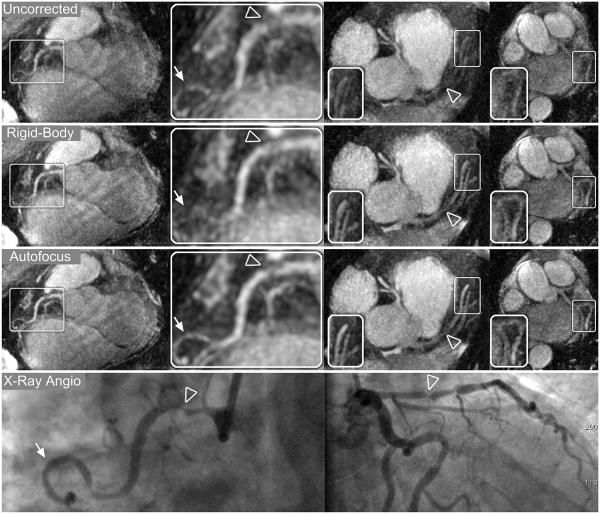
Thin-slab MIP reformats for patients A–C are shown in Figs. 8-10, respectively. Images were reconstructed with no motion correction (first row), rigid-body motion correction (second row), and nonrigid autofocus motion correction (third row). For patient A (Fig. 8), the depiction of the RCA, LAD, and LCx improves significantly with nonrigid autofocus motion correction. Magnified segments of each vessel (inset images) show a substantial reduction of motion blurring artifacts with autofocus reconstruction. For patient B (Fig. 9), rigid-body motion correction improves the depiction of the proximal coronary arteries, but the distal portions of these arteries still show residual motion blurring. Nonrigid autofocus motion correction yields significant improvements in the distal portions of the coronary arteries (inset images). Patient B also underwent cardiac catheterization, which identified stenoses in the RCA and LAD (arrowheads, bottom row). These stenoses are well-depicted in the autofocus-motion-corrected MR images. For patient C (Fig. 10), the coronary arteries are best depicted with nonrigid autofocus motion correction. Magnified segments of the coronary arteries (inset images) show the improvement in vessel sharpness resulting from nonrigid autofocus motion correction. Patient C also underwent cardiac catheterization, which identified a 50% narrowing in the proximal LAD (arrowhead, bottom row). This narrowing is well-visualized in the autofocus-motion-corrected MR image.

Figure 8.

Reformatted thin-plane MIPs for patient A. Reconstructions using no motion compensation (top row), rigid-body translational motion compensation (middle row), and autofocus motion compensation (bottom row) were reformatted to show the RCA (left column), LAD (middle column), and LCx (right column). Rigid-body correction yields significant sharpening of the coronary arteries, and further improvements in vessel depiction result from autofocus motion correction. The improved vessel depiction is particularly noticeable in the inset images, which show magnified segments of each vessel.

Figure 10.

Reformatted thin-plane MIPs for patient C. Reconstructions using no motion compensation (first row), rigid-body translational motion compensation (second row), and autofocus motion compensation (third row) were reformatted to show the RCA and LAD (left column), LAD system (center columns), and LCx (right column). Rigid-body correction yields significant sharpening of the coronary arteries, and further improvements in vessel depiction result from autofocus motion correction. The improved vessel depiction is particularly noticeable in the magnified sections of the LAD and first diagonal (arrows, right-center column), RCA, and LCx (inset images). A 50% narrowing in the proximal LAD was identified on x-ray angiograms (arrowhead, bottom row) and is well-depicted after autofocus motion correction.

Figure 9.

Reformatted thin-plane MIPs for patient B. Reconstructions using no motion compensation (first row), rigid-body translational motion compensation (second row), and autofocus motion compensation (third row) were reformatted to show the RCA (left columns), LAD and proximal RCA (right-center column), and LCx (right column). Nonrigid autofocus motion correction yields the best depiction of the coronary arteries. Significant improvements in vessel sharpness can be seen in distal segments of the RCA (arrows), LAD, and LCx (inset images). Stenoses in the RCA (arrowheads, magnified in left-center column) and LAD (arrowheads, right-center column) are well-depicted after autofocus motion correction and well-correlated with x-ray angiograms (bottom row).

Image Analysis

Qualitative and quantitative vessel sharpness measurements for each subject and coronary segment are listed in Tables 2 and 3. For each coronary segment, the best combined qualitative rank scores and best IEPA measurements among the three motion correction schemes are underlined. Among all 15 segments analyzed, autofocus-corrected images either received the best combined qualitative rank scores (12 of 15 segments) or were tied with rigid-body correction for the best combined rank scores (3 of 15 segments). In 14 of the 15 segments analyzed, autofocus-corrected images had the highest (best) IEPA sharpness measurement. For patient B, rigid-body correction yielded a higher IEPA sharpness score than nonrigid autofocus correction for the LAD. The proximal segment of this artery contained a large diseased portion that was not well-delineated in cross-sectional images due to relatively low signal intensity. The resulting IEPA scores, which measure intensity gradients through radial profiles of the vessel, could be less meaningful for this segment. For this segment, the nonrigid autofocus correction was ranked best by both readers, which also suggests that the poorer IEPA score is due to a limitation of the IEPA metric rather than inferior performance of the autofocus algorithm in the diseased vessel segment.

Table 2.

Qualitative Rank Scoring of Vessel Sharpness

Reconstruction	Uncorrected	Rigid-Body	Autofocus
Volunteer A
RCA rank score	(3, 3)	(2, 1)	(1, 2)
LAD rank score	(3, 3)	(2, 2)	(1, 1)
LCx rank score	(3, 3)	(2, 2)	(1, 1)
Volunteer B
RCA rank score	(3, 3)	(2, 1)	(1, 2)
LAD rank score	(3, 3)	(2, 2)	(1, 1)
LCx rank score	(2, 3)	(3, 2)	(1, 1)
Patient A
RCA rank score	(3, 3)	(2, 2)	(1, 1)
LAD rank score	(3, 3)	(2, 2)	(1, 1)
LCx rank score	(3, 3)	(2, 2)	(1, 1)
Patient B
RCA rank score	(2, 3)	(3, 2)	(1, 1)
LAD rank score	(3, 3)	(2, 2)	(1, 1)
LCx rank score	(3, 3)	(2, 2)	(1, 1)
Patient C
RCA rank score	(3, 3)	(2, 2)	(1, 1)
LAD rank score	(3, 3)	(2, 2)	(1, 1)
LCx rank score	(3, 3)	(1, 2)	(2, 1)

Rank scores are reported as (reader 1, reader 2).

The best combined score(s) in each case is underlined.

Table 3.

Quantitative Vessel Sharpness Measurements

Reconstruction	Uncorrected	Rigid-Body	Autofocus
Volunteer A
RCA sharpness	6.14	7.13	7.24
LAD sharpness	6.14	7.89	8.07
LCx sharpness	6.21	7.86	7.98
Volunteer B
RCA sharpness	6.79	7.39	7.65
LAD sharpness	6.84	7.85	7.94
LCx sharpness	6.93	7.37	7.69
Patient A
RCA sharpness	4.60	4.81	5.03
LAD sharpness	4.84	6.10	6.16
LCx sharpness	5.80	6.25	6.69
Patient B
RCA sharpness	6.14	6.33	6.63
LAD sharpness	4.91	5.53	5.39
LCx sharpness	4.61	4.73	5.16
Patient C
RCA sharpness	5.65	6.45	6.60
LAD sharpness	5.81	7.38	8.05
LCx sharpness	6.13	7.01	7.28

Sharpness values are in normalized units (Mean IEPA × 1000).

The highest (best) value in each case is underlined.

Discussion

We have demonstrated improved motion correction of free-breathing 3D cones CMRA images using the proposed nonrigid autofocus motion correction algorithm. The algorithm was able to simultaneously focus anatomical features within the entire imaging region, each of which moved with distinct motion paths. Both static and moving features such as the heart, aorta, chest wall, and spinal column were reconstructed with very little motion blurring. Such nonrigid motion correction is not possible with “global” motion correction techniques such as retrospective 3D translation or affine correction.

Unlike many model-based nonrigid motion correction techniques that require tailored acquisition of calibration data, the proposed technique only requires measurement of SI, AP, and RL translation, which could be obtained via navigator acquisitions, self-navigation, or potentially from external sensors or cameras. Thus, the technique can be retrospectively applied to a wide number of datasets in which this global motion displacement information has been acquired. Furthermore, the algorithm is flexible and can easily be applied to other acquisition types. A similar nonrigid autofocus technique has been previously applied to abdominal 3D Cartesian imaging (33), where motion results in coherent ghosting artifacts. However, the 3D cones trajectory is better suited for this autofocus technique due to its motion-blurring properties.

In addition to simultaneously sharpening both cardiac and non-cardiac image features, the nonrigid autofocus algorithm yielded improved motion correction and sharpening of the coronary arteries compared to rigid-body correction. Quantitative vessel sharpness measurements using the IEPA metric showed an improvement in vessel sharpness in 14 of 15 vessel segments. The IEPA metric, which has been used in previous studies to evaluate vessel sharpness (14,44), provided a means of cross-validating images reconstructed with the proposed nonrigid autofocus technique, which uses a gradient entropy focusing metric that has been successfully applied in a number of autofocus applications (30, 31, 33, 41).

Further assessment and validation of the nonrigid autofocus algorithm was conducted with the resolution phantom experiment. Although the free-breathing resolution phantom study assessed motion of the chest wall, not the heart directly, the experiment provided a relatively straightforward method to evaluate the proposed nonrigid autofocus technique. This experiment tested the ability of the algorithm to correct chest wall motion using scaled motion trajectories that were derived from measurements of the heart. The similarity of the autofocus-motion-corrected images and the static phantom images gives validity to the proposed nonrigid model and motion basis set (Fig. 5).

The choice of window size (s) used for the localized motion metric is guided by a tradeoff between the degree of nonrigid motion modeling (improves with smaller window sizes) and the introduction of image artifacts and discontinuities (improves with larger window sizes). In this work, a window size of s = 3.75 cm (30 voxels) yielded good nonrigid motion correction with few discontinuities and image artifacts. However, further optimization of this parameter may be required when carrying out this technique in larger patient populations or different applications. In applications where an adequate tradeoff between image artifacts and nonrigid motion modeling cannot be obtained, additional methods of enforcing smoothness in the motion maps, proposed by Cheng, et al. (33), can be employed.

Scaling of the measured SI, AP, and RL motion trajectories must be implemented with care to prevent mis-registration of the motion-corrected images. Adding a constant offset to any of the measured motion trajectories yields a bulk shift of the image after translational motion correction. This is analogous to changing the reference frame that is used for motion estimation, such that the motion-corrected image is reconstructed at a different respiratory position. Scaling the measured motion trajectories has two effects. First, it models larger or smaller tidal motion by scaling the peak-to-peak amplitude of the cyclic respiratory motion trajectory. Second, it induces a bulk shift of the image by increasing or decreasing the mean respiratory position. The first effect is desired, as it models different amounts of tidal motion that are present throughout the imaged volume. The second effect is not desired, as it causes image mis-registration that can result in image artifacts and discontinuities in the final autofocus image. By subtracting the mean displacement from the measured motion trajectories before scaling, the mean respiratory displacement is not affected by scaling. We have found that this normalization allows scaling of the trajectories to be used to model tidal changes in respiration without inducing a bulk shift of the image. While we have had success using this approach in volunteer and patient studies representing a variety of breathing patterns, it may be inadequate in cases where respiratory motion is highly erratic or contains many large outliers. In these cases, it may be necessary to employ other techniques (e.g., scaling about the median or about a moving average) to prevent mis-registration artifacts.

In this study, the autofocus technique was demonstrated in a small population of two volunteers and three patients. While the qualitative and quantitative vessel sharpness results are promising, the lack of statistical power due to the small number of subjects necessitates future validation studies using a larger patient population. Also, further testing is required to establish the validity of the motion basis set used here, which assumes correlated motion in different regions of the heart. While the single-subject analysis in Fig. 2 serves as an illustration of the correlation assumption, respiratory motion varies substantially among individuals, and future studies using a large patient population are necessary to validate this assumption. Additionally, such a study could lead to improvements in the motion model and motion basis set used by the autofocus algorithm, which could further improve the performance of the technique. A future validation study could also be used to investigate differences, if any, between peripheral gating (used in this study) and ECG gating, and the extent to which the autofocus algorithm could be used to correct for cardiac motion due to variations in gating times.

A disadvantage of the nonrigid autofocus technique is computation time, which scales with the number of motion basis sets (scale factors) used by the algorithm. For non-Cartesian imaging, the gridding and FFT implementations are the most computationally expensive operations of the autofocus algorithm. Because these operations must be repeated for every motion scale, they can significantly increase the total computation time when a large search space is used. We implemented multi-threaded gridding and FFT routines in C++ and were able to reduce the computation time to 40 seconds for each motion compensation, gridding, FFT, and focusing metric computation (steps b–e in Fig. 3) using a dual 2.6 GHz Xeon x5650 CPU with 72 GB RAM. Using a total of 9 × 9 × 5 = 405 scale factors requires 270 min to compute the autofocus reconstruction. This computation time can be reduced with optimized C++ or graphics processing unit implementations of the k-space motion compensation (Fig. 3c) and focus metric evaluation (Fig. 3e), which are currently implemented in MATLAB. The computation time could be further reduced using interpolation techniques similar to those used for off-resonance correction (45, 46), which could potentially allow the synthesis of different motion-corrected images using a smaller number of 3D reconstructions.

Additional reductions in computation time or improvements in motion correction may be possible through reduction or expansion of the search space. For example, a smaller number of scale factors near 0 × and 1 × could potentially be used to reduce the computation time with little degradation of image quality, as suggested by the histogram in Fig. 7g. Augmentation of the search space using motion estimates derived from several smaller ROIs (e.g., Fig. 2), coil-specific measurements, additional navigator acquisitions, or sensor measurements could be used to potentially yield further nonrigid motion correction. In addition, a variety of different motion models (including the scaling technique used here) could be used to derive new motion trajectories from measured trajectories. Optimizing this search space is not trivial and is left as an area for future research.

Conclusion

We have applied a nonrigid autofocus motion correction technique to retrospectively correct free-breathing 3D cones CMRA images. The proposed algorithm approximates nonrigid respiratory motion using a set of scaled 3D translation measurements derived from 2D iNAV acquisitions, and a final motion-corrected image is reconstructed using an image-based focusing metric. In phantom, volunteer, and patient studies, the nonrigid autofocus algorithm yielded an improvement in image quality and coronary vessel sharpness compared to rigid-body translational motion correction.