Abstract
Most structure prediction algorithms consist of initial sampling of the conformational space, followed by re-scoring and possibly refinement of a number of selected structures. Here we focus on protein docking, and show that while decoupling sampling and scoring facilitates method development, integration of the two steps can lead to substantial improvements in docking results. Since decoupling is usually achieved by generating a decoy set containing both non-native and near-native docked structures, which are then used for scoring function construction, we first review the roles and potential pitfalls of decoys in protein-protein docking, and show that some type of decoys are better than others for method development. We then describe three case studies showing that complete decoupling of scoring from sampling is not optimal for solving realistic docking problems. Although some of the examples are based on our own experience, the results of the CAPRI docking and scoring experiments also show that decoupling leads to worse results. Next we investigate how the selection of training and decoy sets affects the performance of the scoring functions obtained. Finally, we discuss pathways to better integration of the two steps, and show some algorithms that achieve a certain level of integration. Although we focus on protein-protein docking, our observations also apply to other conformational search problems, including protein structure prediction and the docking of small molecules to proteins.
Keywords: Molecular interaction, protein-protein docking, conformational search, structure refinement, CAPRI docking experiment, scoring function, molecular mechanics, Monte Carlo method, structure-based potential
Introduction
Most structure prediction algorithms consist of initial sampling of the conformational space, followed by re-scoring and possibly refinement of a number of selected structures. Here we focus on protein-protein docking,1-3 but we believe that our observations are more general, and also apply to other conformational search problems, including protein structure prediction and the docking of small molecules to proteins. The challenge for predictive protein docking is to obtain computationally a model of the bound complex based on the coordinates of the unbound component molecules.1-3 If no a priori information on the complex is available, the initial sampling must explore a large number of conformations using a relatively simple energy function to keep the method computationally feasible. The search yields a set of candidate structures, in which the two partners contact each other without major steric overlaps and possibly possess desirable properties such as some level of steric, electrostatic, and chemical complementarity. However, the simple scoring schemes generally provide limited accuracy, and the sampling needs to be followed by a scoring step, aimed at identifying near-native conformations among the structures from the initial search. At this point fewer structures are considered, and since the structures can be refined, one can use more accurate but computationally more expensive scoring functions, approximating the binding free energy.3
Although the sampling step itself requires a scoring function and thus sampling and scoring do not inherently differ, they are frequently considered separate and largely independent.4 Indeed, the two steps have very different aims, and their decoupling simplifies method development. The goal of sampling is generating a set of structures that include the possible highest number of near-native conformations, where the term “near-native” may refer to structures in which the ligand (usually the smaller protein) is as far as 5 Å or even 10 Å RMSD from the ligand in the X-ray structure of the complex. Due to the limitations on energy function and sampling schedule, the resulting decoy sets also include a large number of false positive structures that are not near-native, but in terms of the main physical and chemical characteristics (e.g., interaction energy, steric overlap, interface area, etc.) may not be very different from the near-native ones. Sampling has its own criteria of success, e.g., the number of near-native conformations among, say, the 1000 top scoring structures, or the numerical efficiency of the search, and such criteria are frequently used for comparing different sampling methods. Once generated, the decoys can be stored, and used for the development of scoring and refinement methods. Since a variety of scoring functions can be tested on the same set of decoys, this approach provides an excellent way of comparing different approaches. In fact, scoring is frequently the critical step in docking, and hence decoupling the two steps and focusing on scoring functions is clearly justifiable. Accordingly, the organizers of the Critical Assessment of Predicted Interactions (CAPRI),5 the first community-wide experiment devoted to protein docking, recently added a separate scoring “competition”.6
We agree that decoupling of sampling and scoring leads to well-defined computational problems that are simpler to study, and that decoys played a very positive role in the development of docking methodology. However, the goal of this review is to show that integration of the two steps can lead to substantial improvements in docking results. This also implies that sampling and scoring algorithms, developed largely independently from each other, are not likely to be optimal when combined into a docking procedure. We understand that in the asymptotic limit of having an ideal scoring function and dense sampling, decoupling would not lead to any problem. However, in practice we can sample only a very small fraction of potential conformations, and scoring functions can account only for selected properties of protein complexes, leading to strong interdependence of sampling and scoring. Since the two steps can be formally decoupled by the use of a decoy set, we first review the roles and optimal construction of decoys in protein-protein docking, and show that some type of decoys are better than others for method development. We then describe three case studies showing that the complete decoupling of scoring from sampling is not optimal when developing a docking algorithm. Although some of the examples are based on our own experience, the results of the CAPRI docking and scoring experiments also show that decoupling leads to worse results. Next we investigate the effect of decoy set selection on the scoring functions obtained. Finally, we discuss pathways to better integration of the two steps.
Decoys in Protein-Protein Docking
The use of docking decoys may have been inspired by the fact that decoys played important roles in the development of protein structure prediction methods.7 Early folding decoys were usually perturbation based, obtained by partial unfolding of native protein structures, either by high-temperature molecular dynamics or by introducing small random perturbations into nonregular fragments of the protein.7-10 The more recent decoys are generally simulation based, i.e., have been generated by direct structure prediction or folding simulations.11-15 These latter decoys are better models for the discrimination problems that occur in protein structure prediction, and hence are preferable to perturbation based decoys. Special simulation based decoys are also available for loop prediction.16
Similarly to structure prediction, decoys for protein docking can be obtained either by perturbation or by docking. Perturbation based decoys can be constructed either by slightly misplacing the component proteins in a co-crystallized complex, or by first superimposing the unbound (separately crystallized) proteins on their bound counterparts in the complex and then generating perturbations of the resulting structure. Since such perturbed conformations are unlikely to occur in the process of docking, both approaches yield somewhat unrealistic decoys. In contrast, docking based decoys are generated either by docking the unbound (separately crystallized) proteins, or by docking the two (bound) protein structures extracted from the complex. As we will discuss, the use of unbound protein structures is highly preferable, as decoys obtained by re-docking the bound component proteins are likely to lead to scoring functions that are far from optimal for use in realistic docking problems. All decoy sets should include a number of near-native conformations and possibly the native complex as well, although the inclusion of the latter is clearly not very useful for scoring function development, since the exact native structure is sampled with zero probability in the process of docking.
It appears that the earliest study using protein-protein docking decoys is due to Shoichet and Kuntz,17 who included structures from docking both bound and unbound protein structures in the same decoy sets, and since some near-native complexes obtained from bound structures had both lower RMSD and much lower energy, finding them was largely trivial. The Vakser group docked unbound protein structures using the GRAMM program,18 and we used the resulting sets to test scoring strategies.19 For each complex the decoy set also included near-native conformations obtained by superimposing the unbound proteins over good matches of the bound structure,19 and adding such “artificial” structures made their identification based on scoring function values too easy. Sternberg and associates docked unbound protein structures using the FTDock program,20 and for each complex selected structures that had relatively good scores and spanned an RMSD range from 5 to 60 Å.21 However, they also had to add four near-native conformations obtained by perturbations. Although this construction reduced the RMSD gap between near-native and non-native structures seen in the previous decoys,17,19 the number of structures below 10 Å RMSD was still very small.21,22 As docking methods have improved, more realistic decoy sets were generated. The DOCKGROUND set of docking decoys23 was built from unbound protein structures using the Gramm-X server.24 Each set contains 100 structures with low GRAMM energy resulting in high surface complementarity, and at least one near-native match per complex. Extensive sets of decoys, based on the protein docking benchmarks25-28 and generated by various versions of the ZDOCK29 and ZRANK30 programs are provided by the Weng lab (http://zlab.bu.edu/zdock/decoys.shtml). The RosettaDock decoys include sets based on perturbation as well as sets obtained by unbound docking, some of which do not include any near-native structures (http://graylab.jhu.edu/docking/decoys/).31
Although decoys are still being constructed by perturbation,32 the more recent sets obtained by direct docking usually include many near-native structures, and hence there is no need for adding perturbation based decoys. More generally, since the main goal of decoys is facilitating the development of scoring functions that can identify near-native structures among the ones generated in the sampling step, we believe that optimizing scoring functions for discriminating “artificial” structures that have been obtained by perturbations rather than by docking will not lead to the development of scoring functions that are optimal for solving realistic docking and discrimination problems. The aim of facilitating the development of docking methods also emphasizes that decoys obtained by docking bound (i.e., co-crystallized) structures have limited utility.33,34 Indeed, rigid body docking of the bound structures of two components in a complex is a purely geometric problem, and for this case the optimal scoring function is the simple shape complementarity, which should provide good discrimination if the conformational space is densely sampled.35 Thus, the use of decoy sets obtained by docking bound structures is unlikely to yield scoring functions that are optimal when docking unbound protein structures.35 Using flexible docking but starting from bound structures is essentially a perturbation based approach,32 and since the conformational space differs from one that would be sampled in a real problem of docking unbound protein structures, our previous criticism still applies.
Decoupling of Sampling and Scoring is Not Optimal
In this section we describe three case studies to show that better integration of the sampling and scoring schedules can substantially improve docking results. Thus, although we recognize that decoupling through the use of decoys facilitates the development of both sampling algorithms and scoring functions, the two steps should be properly aligned for optimizing the performance of combined docking methods.
Sampling and scoring in the CAPRI docking experiment
The latest results of the CAPRI protein docking and scoring experiments (for rounds 13-19) clearly show that decoupling sampling and scoring may lead to loss of accuracy.6 In these rounds the 65 participating research groups and 10 automated servers had 14 targets, each being an unpublished experimentally determined structure of a protein-protein complex. The predictor groups were given the atomic coordinates of the component proteins or of their homologues, and they had to model the complexes. The models were evaluated by independent assessors and grouped into highly accurate, medium accuracy, acceptable, and incorrect categories on the basis of the fraction of native contacts, the backbone root mean square deviation of the ligand (L_RMS) from the reference ligand structure after superimposing the receptor structures, and the backbone RMSD of the interface residues (I_RMS). The calculation of these measures and the exact definitions of categories are given in the paper describing the evaluation of the results;6 here we note only that for the highly accurate, medium accuracy, acceptable, and incorrect models the ligand RMSD is given by L_RMS < 1Å, 1Å < L_RMS < 5Å, 5Å < L_RMS < 10Å, and L_RMS > 10Å, respectively. Each participating group was entitled to submit ten predictions for each target. The assessors considered all ten models, and the results for each group include the number of predictions in each of the four categories.6
As innovation, in the more recent rounds of CAPRI the organizer added a scoring category to the prediction experiment in order to promote scoring function development.6 To obtain a meaningful decoy set for this scoring experiments, the predictor groups were invited to submit up to 100 of their best predictions. Immediately after all the predictions are submitted, the uploaded models are shuffled into a large decoy set and made available to all groups as part of the scoring experiment. The “scorer” groups are invited to re-rank all the uploaded models using their preferred scoring function and submit their own 10 best ranking ones.6 Thus, the focus from docking, which includes both sampling and scoring, is shifted solely to the scoring of structures generated by the entire group of predictors.
The use of the same quality criteria in both docking and scoring experiments makes the results comparable. Table I shows the results submitted by the 10 best predictors and the results by the 10 best scorers. Following the notation used by the evaluators,6 results are shown in the form x/y***/z**, where x denotes the number of at least acceptable models, y*** is the number of high accuracy submissions, and z** is number of medium accuracy ones. As shown in Table I, the average results are substantially better for the predictors than for the scorers. As a matter of fact, the best scorer is only as good as the 9th best predictor, which happens to be our automated docking server ClusPro. One potential weakness of this analysis is that the best predictors and the best scorers are not necessarily the same. Therefore in Table II we compare the results of the 8 groups who submitted models for exactly the same targets in both experiments, and were among the top performers in at least one category. Table I shows that, on the average, the predictors produce more accurate models than the scorers, whereas Table II show that this also applies individually to 6 of the 8 groups that worked on the same problems both as predictors and as scorers. Thus, if the best docking groups would just resubmit their predictions to the scoring competition they would perform better than any scoring group. In addition, groups who participated actively in both scoring and docking performed worse in the scoring experiment. Despite the fact that scorers had access to all of the sampled structures, their scoring functions were clearly not optimal for finding the near-native structures in the decoys sets generated by many different groups. Thus, each scoring function performs best considering only the structures generated by the same group, demonstrating the strong interdependence between sampling and scoring.
Table I. 10 Best Performing Predictor and Scorer Groups in Rounds 13-19 of CAPRI6.
| Predictor group | Predictor Summary | Scorer Group | Scorer Summary |
|---|---|---|---|
| Vajda | 6/4***/2** | Bonvin | 5/1***/3** |
| Zacharias | 6/4***/1** | Bates | 5/1***/2** |
| Zou | 6/3***/2** | Zou | 4/3***/1** |
| Eisenstein | 6/3***/1** | Weng | 4/2***/1** |
| Wolfson | 6/3***/1** | Wang | 4/1***/1** |
| Weng | 6/2***/2** | Fernandez-Recio | 3/1***/2** |
| Zhou | 6/2***/2** | Wolfson | 3/1*** |
| Bonvin | 6/1***/4** | Haliloglu | 2/1***/1** |
| CLUSPRO | 5/1***/3** | Camacho | 2/1***/1** |
| Fernandez-Recio | 5/2** | Takeda-Shitake | 2/1***/1** |
| Average | 5.2/3.1***/1.8** | Average | 3.4/1.3***/1.4** |
Table II. Results of Predictor and Scorer Group for the Same Targets in Rounds 13-19 of CAPRI6.
| Predictor group | Predictor Summary | Scorer Group | Scorer Summary |
|---|---|---|---|
| Bonvin | 6/1***/4** | Bonvin | 5/1***/3** |
| Zou | 6/3***/2** | Zou | 4/3***/1** |
| Weng | 6/2***/2** | Weng | 4/2***/1** |
| Wolfson | 6/3***/1** | Wolfson | 3/1*** |
| Fernandez-Recio | 5/2** | Fernandez-Recio | 3/1***/2** |
| Bates | 4/1***/1** | Bates | 5/1***/2** |
| Camacho | 4/1***/1** | Camacho | 2/1***/1** |
| Wang | 3/1***/1** | Wang | 4/1***/1** |
Selecting a scoring function requires information on sampling strategy
We discuss rigid body docking methods as an example to show that no effective scoring can be developed if one does not know how the decoys have been constructed. Rigid body methods, based either on the fast Fourier transform (FFT) correlation approach20,29,35,36 or geometric matching,37 are capable of globally sampling of the entire rotational/translational space. The FFT-based methods systematically sample billions of docked conformations on a grid using correlation-type scoring functions.3,38 Although the sampling is defined by the grid and hence it is independent of the scoring function, the results are not. For example, introducing the method in 1992, Katchalski-Katzir and co-workers used a stepwise approximation of the van der Waals energy term representing the measure of shape complementarity.35 While they obtained good results when docking bound protein structures, the method did not work at all for unbound proteins. It is easy to identify the reason why the method failed. The bound and unbound structures of proteins generally differ, and since the van der Waals term is very sensitive to small changes in the atomic coordinates, even conformations very close to the native can have very high energies, much higher than some structures in which the component proteins barely interact with each other. Although the systematic sampling evaluates energies for some 109 conformations, one retains and analyzes only a small number, usually between 1000 and 2000 structures that have low energies. Thus, the use of a scoring function that strongly penalizes steric clashes would most likely eliminate all near-native structures from this small set. We emphasize that an energy function, which is fine for docking bound structures (provided the grid size is small enough), leads to complete failure as soon as unbound protein structures are considered. In order to avoid this failure, the FFT based docking methods use “smooth” interaction potentials that account for the inaccuracies in the atomic positions and the effects of the grid based approximation. Although the potential may include molecular mechanics energy terms, the forces need to be “tolerant” to interatomic clashes. Accordingly, the groups using FFT based methods have developed smooth truncated van der Waals and electrostatics models.18,20,29,36
In all FFT-based docking methods that were successful in the CAPRI protein docking experiment,6 the initial sampling was followed by re-scoring and possibly refinement.3 Assuming that sampling and scoring can be fully decoupled, the resulting scoring functions would be independent of the ways the decoys were generated. However, this is clearly not the case. As discussed, FFT-based rigid methods such as ZDOCK29 and PIPER36 use “soft” potentials, and thus yield structures that may have some atomic overlaps. Thus, re-scoring either requires a “soft” potential or performing some type of refinement to remove clashes. Although after refinement by energy minimization one can use a scoring function that includes molecular mechanics energy terms, even this can be done only using the same geometric parameters (e.g., van der Waals radii) that were used in the energy minimization. For example, the ClusPro server39 generates structures that have already been minimized using the Charmm potential to remove steric clashes,40 and hence the scoring function can include a van der Waals term, but only using the same Charmm parameters. Thus, the decoy set clearly depends on the method used for sampling, and this affects the scoring function and the refinement strategy.
Sampling with a more accurate scoring function is better than sampling first and scoring later
Any docking method can be placed between two extreme strategies. One extreme is to sample first using a simple energy function (e.g., a term representing shape complementarity), retain many structures, and score them using a more accurate method (e.g., adding knowledge-based or statistical potentials to the scoring function)41-44 to find the near-native structures. The other extreme is to build the more accurate but computationally more expensive scoring function directly into the sampling step, and retain fewer structures. Although it is more difficult to implement, we strongly believe that the second strategy yields superior results. We learned this when testing our intermolecular potential called DARS (Decoys As the Reference State).45 We used the potential both for scoring docked structures and for the sampling step in our docking program PIPER.36 Both strategies have been tested on several classes of protein-protein complexes from the protein docking benchmark.45 Docking tests were performed using an energy function that included DARS, van der Waals, and electrostatic terms, and retained the 2000 lowest energy structures. In the scoring tests we first generated 20,000 structures using only the van der Waals term as the energy function, then scored and ranked the structures with DARS and electrostatics, again retaining the 2000 best scoring structures.45
We expected that the two tests would produce similar results in terms of the number of near-native conformations among the 2000 structures retained, possibly with minor differences. However, inclusion of the energy function directly into the sampling protocol performed consistently better, for all classes of protein-protein complexes, than the two-step procedure of separate sampling followed by scoring.45 In hindsight the origin of this difference is easy to understand. Although the FFT correlation method systematically samples all possible configurations on a grid, we retain only 20,000 structures with the lowest van der Waals energies. As already discussed, these structures have relatively good shape complementarity without major steric overlaps, but do not necessarily include near-native conformations that are expected to also have good electrostatic and chemical complementarity. Thus, the decoys set is far from optimal. In contrast, near-native structures are more likely retained when sampling uses the complete energy function, which includes electrostatics and DARS terms, in addition to the van der Waals energy. Our results45 convincingly show that this is the case, and hence the docking program PIPER36 as well as the new version of our protein docking server ClusPro46 include DARS in the energy function used for the sampling. We note that the Weng group also added a pairwise potential to the energy function used in the popular docking program ZDOCK, thereby substantially improving the docking results.47
Effects of Training and Decoy Sets on Scoring Functions
The main use of decoys is the development of scoring functions. In this section we show three examples of how the selection of training and decoy sets affects the performance of the scoring functions obtained.
Dependence of a scoring function on the training set
It is easy to show that a scoring function based on a training set heavily depends on the nature of complexes selected. We discuss our DARS (Decoys As the Reference State) potential as an example. DARS is based on the inverse Boltzmann approach, and defines pairwise interaction energies by εIJ = -RT ln(pIJ), where R is the gas constant, T is the temperature, and pIJ denotes the probability of two atoms of types I and J interacting.45 This probability is approximated by the ratio pIJ = νobs (I,J)/νref (I,J) where νobs (I,J) is the frequency of interacting atom pairs of types I and J in a training set, and νref (I,J) is the expected frequency of interacting atom pairs of types I and J, based on a decoy set.
To determine the frequencies νobs (I, J) we used a training set of protein-protein complexes including 621 interfaces from 466 protein entries. The resulting potential yielded very good results for enzyme-inhibitor complexes, but substantially lower quality predictions for antigen-antibody complexes.45 It was not difficult to find that the origin of this difference is the choice of the training set. Of the 621 interfaces in the set, 404 were from homodimers that have excellent pairing of shapes and hydrophobic patches on the two sides of the interface. Since the interface in enzyme-inhibitor complexes also have good geometric complementarity and are largely desolvated,48 the training set was highly relevant, and it also included a number of enzyme-inhibitor pairs. In contrast, the interfaces in antigen-antibody complexes are more planar and generally less hydrophobic, and thus it is not surprising that the potential trained on a set with many homodimers48 is not optimal for such interactions. As a matter of fact, to derive a better potential for antigen-antibody pairs we needed a training set consisting of this type of complexes, and we also had to change the potential itself to account for the inherent asymmetry of the interactions and for the limited number of available structures.49 We note that to obtain the expected frequencies νref (I, J) of interactions, we generated a “reference” set of docked conformations using only shape complementarity as the scoring function (i.e., without any account for the atom types). Since no atom types were considered, the choice of the complexes included in the reference set had much smaller effect on the DARS potential.45 As we will show, this is not the case for some other scoring functions based on decoys.
To account for the difference between enzyme-inhibitor and antigen-antibody complexes, we adjusted the weights of energy terms in the scoring function used in our docking program PIPER, in addition to different DARS potentials. The scoring function is given by E = Eattr + w1 Erep + w2 Eelec + w3 EDARS, where Eattr and Erep denote attractive and repulsive contributions to the van der Waals energy, Eelec is the electrostatic term modeled by a truncated Coulombic expression, and EDARS is the DARS potential.36 To determine appropriate values for the weighting parameters w1, w2, and w3, we selected small sets of enzyme-inhibitor and antigen-antibody complexes, for each complex generated 20,000 docked conformation using some initial values for the weights, and for each set used logistic regression to optimize the weighting coefficients. This was done several times iteratively to achieve convergence. The coefficient w1 of the repulsive contribution to the van der Waals energy turned out to be essentially independent of the type of the complex. However, the optimal weight w2 of the electrostatic component is three times larger for antigen–antibody than for enzyme–inhibitor complexes, in agreement with the fact that the latter complexes generally have a less polar interface.36 We note that the weighs of energy terms are similarly adjusted in other docking algorithms, e.g., in RosettaDock, to optimize results.31
Dependence of a scoring function on the decoy set: Example 1
We consider the iterative method of constructing a distance-dependent knowledge-based scoring function as introduced by Huang and Zou.50 The key idea of the iterative method is to improve an interatomic pair potential until it can distinguish true binding modes from non-native decoys in decoy set. Huang and Zou considered crystal structures of 851 dimeric complexes from the Protein Data Bank,51 and for each complex generated 1000 decoy structures using the docking program ZDOCK.29 They added the native binding mode as the 1001th structure to the decoy set. The iterative idea is very good, since the iteration continues until the desired selectivity is achieved. In addition, the method circumvents the need for a reference state that is required in the traditional construction of knowledge-based potentials such as DARS.45 However, the resulting potential seems to heavily depend on the selection of the decoy set. Huang and Zou generated the decoys by docking bound structures, and instead of seeking near-native conformations, the function was trained to find the native structure for each complex.50 Results indicate that these may not have been the best choices. The function was tested by scoring decoys generated by ZDOCK.29 For the bound test cases, the scoring function worked extremely well, and yielded a success rate of 98.9% if the top 10 ranked orientations were considered. However, for the realistic problem of docking unbound component proteins the success rate dropped to 40.7%, emphasizing the importance of using realistic decoys.50 It would be interesting to see how the results would improve if the decoys were obtained by docking unbound structures, and the goal was identifying near-native rather than native conformations.
Dependence of a scoring function on the decoy set: Example 2
Ravikant and Elber developed scoring functions based on discriminatory learning.52 Similarly to the iterative constructions just described,50 discriminatory learning starts with the construction of a large decoy set and explicitly incorporates detailed information from native and non-native binding modes. The basic idea is to select scoring function parameters that minimize the number of violations (i.e., when the score of a non-native decoy complex is better than the score of a near-native structure). Such parameters were found by solving an optimization problem with a very large set of inequality constraints. The authors selected a set of 640 complexes, and docked the unbound protein structures or their close homologues to generate decoys using Patchdock.53 A typical number of sampled orientations for each complex was 16,000, which were used to generate 160,000 inequalities (they considered up to 10 near-native structures to be discriminated from the incorrect structures).52 The entire decoy set resulted in over 50 million constraints. The optimization problem was solved by linear programming.
More recently, Ravikant and Elber developed an improved scoring function also based on discriminatory learning.54 They made two main improvements relative to the earlier method, both of interest to this review. First, although the authors used the same training set as before,52 for each complex they performed exhaustive sampling on a grid using the fast Fourier transform approach. The enhanced sampling revealed that the earlier results based on the more limited sampling may have been program dependent and not appropriate for other sampling techniques. When attempts were made to use the potential obtained using PatchDock for exhaustive sampling, it was found to generate significant number of false positives, emphasizing the dependence of the scoring function on the sampling schedule used for creating the decoy set.54 The second significant addition to the method is the iterative improvement of the scoring function. This aspect makes the method similar to the one by Huang and Zou,50 but Ravikant and Elber also included the docking step in the iteration, i.e., the method updates the list of decoy structures considered in the construction of the scoring function when the parameters of the latter change.54 The procedure starts by docking all pairs of proteins using a current estimate for the parameters. As new violations are discovered, new inequalities are added to the system, and the parameter values are updated. This process is continued until no new violations are discovered, and thus the algorithm iteratively achieves optimal alignment of sampling and scoring steps.
Examples of Integration: Scoring by Sampling
As shown in the previous section, the iterative scoring function construction by Ravikant and Elber integrates the sampling and scoring step, both driven by the same scoring function, optimized for the best discrimination of near-native and non-native structures.54 Here we discuss three more examples of docking methods in which sampling and scoring are integrated. The general approach used in these methods is using a scoring function to bias the sampling, and then ranking the conformations in the scoring stage based on the distributions of the generated structures rather than re-scoring them with a different scoring function. We show that the well-known Monte Carlo methods are in this category, but also show two approaches that, according to our experience, can substantially improve docking results.
Monte Carlo methods
Docking methods based on Monte Carlo minimization represent natural integration of sampling and scoring, as the very essence of the Metropolis Monte Carlo approach is to bias the sampling toward low energy regions of the energy surface. RosettaDock31 and ICM-DISCO55 both include a first stage of rigid body searches in the rotational/translational space using simplified models, but this stage serves only to select the regions of interests that will be exposed to more extensive search. ICM-DISCO retains a few hundred low-energy conformations, whereas RosettaDock selects the centers of low-energy clusters. In ICM-DISCO the retained solutions are further optimized with flexible interface ligand side chains using a biased probability Monte Carlo procedure55. In RosettaDock the Monte Carlo minimization in translational and rotational coordinates is integrated with repacking the interface side chains using a backbone-dependent rotamer library.31 At this stage the search is based on flexible protein models and detailed energy functions. Since the Monte Carlo trajectories in both ICM-DISCO and RosettaDock are expected to converge toward the low energy regions of the conformational space, and flexibility is introduced directly in sampling, there is no need for a separate scoring stage. In fact, using ICM-DISCO one usually selects the lowest energy structures as predictions of the native complex.55 In RosettaDock, the 200 best-scoring structures are clustered on the basis of pair-wise RMSD using a hierarchical clustering algorithm with a 2.5 Å clustering radius.31 The clusters with the most members are selected as the final predictions, ranked according to the cluster sizes. The cluster size, or the degeneracy of the docked position, may be related to the entropy of the bound complex (see below). According to the CAPRI results,6,56,57 both RosettaDock and ICM-DISCO generated highly accurate predictions for a number of targets, and the methods are among the bests if we know the approximate binding mode.3
Scoring based on cluster size
While the integration of sampling and scoring occurs naturally in Monte Carlo type docking methods, in methods based on the fast Fourier transform (FFT) correlation approach the two stages are always separate. Here we focus on the sampling stage, which systematically evaluates an energy expression, given as the sum of correlation functions, on a grid.36 As we discussed, the results of docking versus scoring tests showed that the use of the most accurate scoring function (within the limit of computational feasibility) directly in the sampling stage yields more near-native structures than using first a simpler function (e.g., shape complementarity), followed by re-scoring a number of retained structures using the more accurate function.45
As mentioned, the rigid body approximation in the sampling stage requires the use of “smooth” scoring functions that are not sensitive to small steric overlaps, which leads to a large number of false positive structures. Therefore, the question arises how to reduce the number of structures that will be subjected to computationally costly refinement. As implemented in our ClusPro server, we cluster the 1000 retained structures using pairwise root mean square deviation (RMSD) as the distance measure, and retain a number of the largest clusters.39,46 As shown in Figure 1, the biophysical meaning of clustering is isolating highly populated low-energy basins of the energy landscape.58 It is easy to show that large clusters are more likely to include native structures. The globally sampled conformational space can be considered as a canonical ensemble with the partition function Z = Σj exp(-Ej/RT), where Ej is the energy of the jth pose, and we sum over all poses. For the kth cluster the partition function is given by Zk = Σj exp(Ej/RT), where the sum is restricted to poses within the cluster. Based on these values, the probability of the kth cluster is given by Pk = Zk/Z. However, since the low energy structures are selected from a relatively narrow energy range (e.g., below E1 in Fig. 1), and the energy values are calculated with considerable error, it is reasonable to assume that these energies do not differ, i.e., Ej=E for all j. This simplification implies that Pk=exp(-E/RT)×Nk/Z and thus the probability Pk is proportional to Nk, where Nk is the number of samples in the kth cluster. It was shown39 that the 30 largest clusters contain at least one near-native structure for 93% of the complexes in the original protein docking benchmark set.25 Ranking the clusters in terms of size rather than an empirical energy, the selection of near-native structures relies on clustering rather than any scoring function, and the scoring function is used only for biasing the sampling. We note that our approach is similar to the one used in RosettaDock, where also the largest clusters formed by low energy structures are considered as predictions of the target complex structure.31 However, in ClusPro the sampling and clustering-based selection steps are so heavily integrated that we were unable to participate in the CAPRI scoring experiment.6
Figure 1.
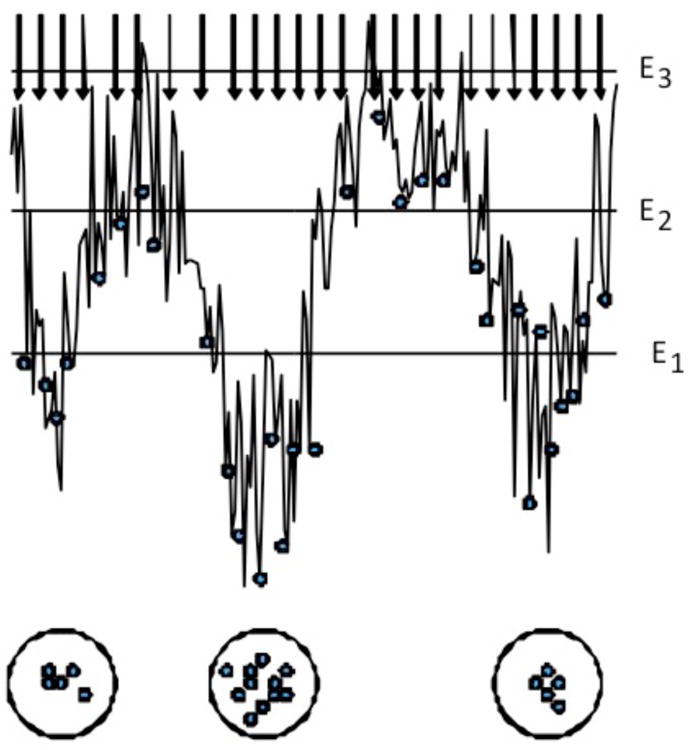
Identification of near-native structures by clustering. Large clusters of low energy conformations identify minima with broad region of attraction. E1, E2, and E3 denote energy levels that determine the conformations retained for further analysis.
Stability analysis: scoring by sampling
As described, rigid sampling and clustering in ClusPro yield up to 30 clusters. Ranking the clusters by size is only a rough approximation, based on the assumptions that all retained structures are energetically equivalent, and thus we need a more reliable approach to the identification of clusters that are likely to be close to the native state, or at least to remove clusters that are not. Focusing on a few representatives from each cluster, it is computationally feasible to perform refinement by energy minimization, and one can use any scoring function, including molecular mechanics and structure-based terms. Some of the rigid body methods use this approach, for example, ZDOCK29 is followed by the refinement program RDOCK,59 more recently replaced by ZRANK.30 Similarly, rigid sampling using PatchDock53 can be followed by FireDock.60
In the ClusPro server we refine the retained structures by energy minimization using the Charmm potential40 in order to remove steric overlaps, but the ranking of clusters is still based on their size, which assume that all low energy structures have essentially the same energy.39 Thus, the question arises how the near-native and non-native structures can be discriminated. We have found that the most reliable discrimination between near-native and non-native clusters was not achieved by simply by minimization and then using a scoring function but by re-sampling the regions of the conformational space occupied by large clusters. The method is based on the hypothesis that any near-native cluster is located in a broad energy funnel. We test this property by starting short Monte Carlo minimization (MCM) simulations from a number of structures in the cluster.61 Each simulation step includes both repacking of the interface side chains and rotational and translational moves.31 Convergence for a substantial fraction of MCM trajectories to a region within the cluster indicates a broad funnel, and the point of convergence provides an improved estimate of the native structure (see Fig. 2). 61 Conversely, diverging trajectories indicate that a substantive free energy funnel does not exist, and hence the cluster is not near-native 61. Thus, the scoring is replaced by fairly intensive sampling of the regions of interest. Since the decision whether or not a cluster is near-native is based on statistical analysis of many simulation trajectories, the effect of the inevitable noise in the results due to the ruggedness of the energy surface is reduced. As mentioned, the use of a Monte Carlo method means that sampling and scoring are properly aligned.
Figure 2.
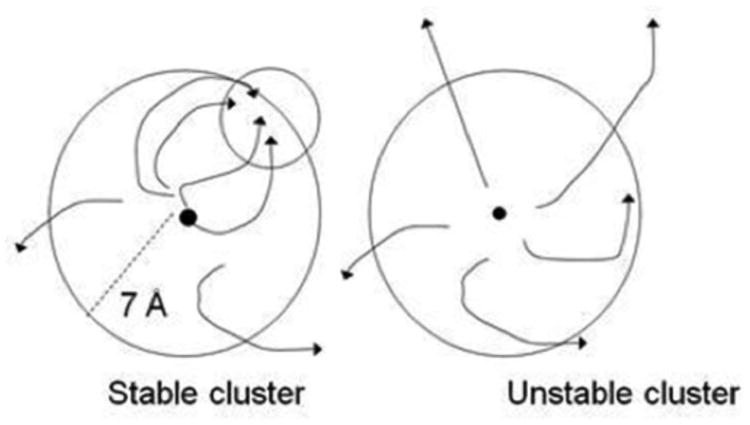
Stability analysis. Monte Carlo minimization trajectories in stable and unstable clusters.
Conclusions
We hope that the case studies described in this paper justify a number of conclusions as follows.
Decoupling of sampling and scoring may facilitate method development, but optimal alignment of the two steps can substantially improve the results of a combined docking algorithm.
Any scoring function based on a decoy set is substantially affected by the properties of the decoys such as the complex structures included, the method of generating docked conformations, and the native or near-native structures in the set. Based on the previous observation, this implies that the decoys should be generated by a sampling schedule that is as similar as possible to the one that will be used for the actual docking.
The above observations imply that decoy sets obtained by perturbing native complex structures or by docking bound (i.e., co-crystallized) structures result in scoring functions that are not optimal in a realistic problem of docking unbound (separately crystallized) protein structures. Furthermore, decoy sets should include near-native conformations generated from unbound proteins by the sampling algorithm itself, rather than native complex structures.
Given a scoring function that accounts for a various contributions to the binding energy (e.g., shape complementarity, electrostatics, desolvation), it is better to include all these factors in the potential used for the initial sampling (assuming that it is computationally feasible), rather than to sample with a simpler potential and then to score with the more complete function.
To align sampling and scoring, sampling should be biased toward regions of the conformational space that are considered to be optimal according to the scoring function. This condition is naturally met in Monte Carlo type algorithms.
We described further examples of aligning sampling with scoring. In ClusPro the scoring function governs the sampling in the initial rigid body docking, and we simply retain the highly populated clusters of low energy structures. The largest clusters are refined using stability analysis, which is based on Monte Carlo minimization, and thus also integrates sampling and scoring, albeit using a different scoring function. The second example is the iterative discriminatory learning method of scoring function construction by Ravikant and Elber. A number of decoys, selected on the basis of the current scoring function, are used to update the scoring function parameters, and this step is repeated until convergence.
While we are convinced that our observations are fairly general, we provided here only a few examples of docking algorithms with well-integrated sampling and scoring steps. There is no doubt that similar integration is present in many other algorithms. In addition, while considerations are restricted to protein-protein docking, most of the ideas promoted here are likely to apply to other areas of molecular modeling.
Acknowledgments
Grant sponsor: NIH; Grant numbers: GM093147, GM061867; Grant sponsor: National Science Foundation; Grant number: DBI1147082
References
- 1.Ritchie DW. Recent progress and future directions in protein-protein docking. Curr Protein Pept Sci. 2008;9:1–15. doi: 10.2174/138920308783565741. [DOI] [PubMed] [Google Scholar]
- 2.Andrusier N, Mashiach E, Nussinov R, Wolfson HJ. Principles of flexible protein-protein docking. Proteins. 2008;73:271–289. doi: 10.1002/prot.22170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Vajda S, Kozakov D. Convergence and combination of methods in protein-protein docking. Curr Opin Struct Biol. 2009;19:164–170. doi: 10.1016/j.sbi.2009.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Feng JA, Marshall GR. SKATE: a docking program that decouples systematic sampling from scoring. J Comput Chem. 2010;31:2540–2554. doi: 10.1002/jcc.21545. [DOI] [PubMed] [Google Scholar]
- 5.Janin J, Henrick K, Moult J, Eyck LT, Sternberg MJ, Vajda S, Vakser I, Wodak SJ. CAPRI: a Critical Assessment of PRedicted Interactions. Proteins. 2003;52:2–9. doi: 10.1002/prot.10381. [DOI] [PubMed] [Google Scholar]
- 6.Lensink MF, Wodak SJ. Docking and scoring protein interactions: CAPRI 2009. Proteins. 2010;78:3073–3084. doi: 10.1002/prot.22818. [DOI] [PubMed] [Google Scholar]
- 7.Park B, Levitt M. Energy functions that discriminate X-ray and near native folds from well-constructed decoys. J Mol Biol. 1996;258:367–392. doi: 10.1006/jmbi.1996.0256. [DOI] [PubMed] [Google Scholar]
- 8.Samudrala R, Levitt M. Decoys ‘R’ Us: a database of incorrect conformations to improve protein structure prediction. Protein Sci. 2000;9:1399–1401. doi: 10.1110/ps.9.7.1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Felts AK, Gallicchio E, Wallqvist A, Levy RM. Distinguishing native conformations of proteins from decoys with an effective free energy estimator based on the OPLS all-atom force field and the Surface Generalized Born solvent model. Proteins. 2002;48:404–422. doi: 10.1002/prot.10171. [DOI] [PubMed] [Google Scholar]
- 10.Seok C, Rosen JB, Chodera JD, Dill KA. MOPED: method for optimizing physical energy parameters using decoys. J Comput Chem. 2003;24:89–97. doi: 10.1002/jcc.10124. [DOI] [PubMed] [Google Scholar]
- 11.Yang JS, Chen WW, Skolnick J, Shakhnovich EI. All-atom ab initio folding of a diverse set of proteins. Structure. 2007;15:53–63. doi: 10.1016/j.str.2006.11.010. [DOI] [PubMed] [Google Scholar]
- 12.Rohl CA, Strauss CE, Misura KM, Baker D. Protein structure prediction using Rosetta. Methods Enzymol. 2004;383:66–93. doi: 10.1016/S0076-6879(04)83004-0. [DOI] [PubMed] [Google Scholar]
- 13.Tsai J, Bonneau R, Morozov AV, Kuhlman B, Rohl CA, Baker D. An improved protein decoy set for testing energy functions for protein structure prediction. Proteins. 2003;53:76–87. doi: 10.1002/prot.10454. [DOI] [PubMed] [Google Scholar]
- 14.John B, Sali A. Comparative protein structure modeling by iterative alignment, model building and model assessment. Nucleic Acids Res. 2003;31:3982–3992. doi: 10.1093/nar/gkg460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang J, Zhang Y. A novel side-chain orientation dependent potential derived from random-walk reference state for protein fold selection and structure prediction. PLoS One. 2010;5:e15386. doi: 10.1371/journal.pone.0015386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jacobson MP, Pincus DL, Rapp CS, Day TJ, Honig B, Shaw DE, Friesner RA. A hierarchical approach to all-atom protein loop prediction. Proteins. 2004;55:351–367. doi: 10.1002/prot.10613. [DOI] [PubMed] [Google Scholar]
- 17.Shoichet BK, Kuntz ID. Protein docking and complementarity. J Mol Biol. 1991;221:327–346. doi: 10.1016/0022-2836(91)80222-g. [DOI] [PubMed] [Google Scholar]
- 18.Vakser IA. Low-resolution docking: prediction of complexes for underdetermined structures. Biopolymers. 1996;39:455–464. doi: 10.1002/(SICI)1097-0282(199609)39:3%3C455::AID-BIP16%3E3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- 19.Camacho CJ, Gatchell DW, Kimura SR, Vajda S. Scoring docked conformations generated by rigid-body protein-protein docking. Proteins. 2000;40:525–537. doi: 10.1002/1097-0134(20000815)40:3<525::aid-prot190>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 20.Gabb HA, Jackson RM, Sternberg MJ. Modelling protein docking using shape complementarity, electrostatics and biochemical information. J Mol Biol. 1997;272:106–120. doi: 10.1006/jmbi.1997.1203. [DOI] [PubMed] [Google Scholar]
- 21.Sternberg MJ, Gabb HA, Jackson RM, Moont G. Protein-protein docking. Generation and filtering of complexes. Methods Mol Biol. 2000;143:399–415. doi: 10.1385/1-59259-368-2:399. [DOI] [PubMed] [Google Scholar]
- 22.Murphy J, Gatchell DW, Prasad JC, Vajda S. Combination of scoring functions improves discrimination in protein-protein docking. Proteins. 2003;53:840–854. doi: 10.1002/prot.10473. [DOI] [PubMed] [Google Scholar]
- 23.Liu S, Gao Y, Vakser IA. DOCKGROUND protein-protein docking decoy set. Bioinformatics. 2008;24:2634–2635. doi: 10.1093/bioinformatics/btn497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tovchigrechko A, Vakser IA. GRAMM-X public web server for protein-protein docking. Nucleic Acids Res. 2006;34:W310–314. doi: 10.1093/nar/gkl206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chen R, Mintseris J, Janin J, Weng Z. A protein-protein docking benchmark. Proteins. 2003;52:88–91. doi: 10.1002/prot.10390. [DOI] [PubMed] [Google Scholar]
- 26.Mintseris J, Wiehe K, Pierce B, Anderson R, Chen R, Janin J, Weng Z. Protein-Protein Docking Benchmark 2.0: an update. Proteins. 2005;60:214–216. doi: 10.1002/prot.20560. [DOI] [PubMed] [Google Scholar]
- 27.Hwang H, Pierce B, Mintseris J, Janin J, Weng Z. Protein-protein docking benchmark version 3.0. Proteins. 2008;73:705–709. doi: 10.1002/prot.22106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hwang H, Vreven T, Janin J, Weng Z. Protein-protein docking benchmark version 4.0. Proteins. 2010;78:3111–3114. doi: 10.1002/prot.22830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen R, Li L, Weng Z. ZDOCK: an initial-stage protein-docking algorithm. Proteins. 2003;52:80–87. doi: 10.1002/prot.10389. [DOI] [PubMed] [Google Scholar]
- 30.Pierce B, Weng Z. ZRANK: reranking protein docking predictions with an optimized energy function. Proteins. 2007;67:1078–1086. doi: 10.1002/prot.21373. [DOI] [PubMed] [Google Scholar]
- 31.Gray JJ, Moughon S, Wang C, Schueler-Furman O, Kuhlman B, Rohl CA, Baker D. Protein-protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J Mol Biol. 2003;331:281–299. doi: 10.1016/s0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- 32.Launay G, Simonson T. A large decoy set of protein-protein complexes produced by flexible docking. J Comput Chem. 2011;32:106–120. doi: 10.1002/jcc.21604. [DOI] [PubMed] [Google Scholar]
- 33.Mitra P, Pal D. dockYard--a repository to assist modeling of protein-protein docking. J Mol Model. 2011;17:599–606. doi: 10.1007/s00894-010-0758-9. [DOI] [PubMed] [Google Scholar]
- 34.Tobi D, Bahar I. Optimal design of protein docking potentials: efficiency and limitations. Proteins. 2006;62:970–981. doi: 10.1002/prot.20859. [DOI] [PubMed] [Google Scholar]
- 35.Katchalski-Katzir E, Shariv I, Eisenstein M, Friesem AA, Aflalo C, Vakser IA. Molecular surface recognition: determination of geometric fit between proteins and their ligands by correlation techniques. Proc Natl Acad Sci U S A. 1992;89:2195–2199. doi: 10.1073/pnas.89.6.2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kozakov D, Brenke R, Comeau SR, Vajda S. PIPER: an FFT-based protein docking program with pairwise potentials. Proteins. 2006;65:392–406. doi: 10.1002/prot.21117. [DOI] [PubMed] [Google Scholar]
- 37.Schneidman-Duhovny D, Inbar Y, Nussinov R, Wolfson HJ. Geometry-based flexible and symmetric protein docking. Proteins. 2005;60:224–231. doi: 10.1002/prot.20562. [DOI] [PubMed] [Google Scholar]
- 38.Smith GR, Sternberg MJ. Prediction of protein-protein interactions by docking methods. Curr Opin Struct Biol. 2002;12:28–35. doi: 10.1016/s0959-440x(02)00285-3. [DOI] [PubMed] [Google Scholar]
- 39.Comeau SR, Gatchell DW, Vajda S, Camacho CJ. ClusPro: an automated docking and discrimination method for the prediction of protein complexes. Bioinformatics. 2004;20:45–50. doi: 10.1093/bioinformatics/btg371. [DOI] [PubMed] [Google Scholar]
- 40.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. Charmm - a Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 41.Zhang C, Liu S, Zhou Y. Docking prediction using biological information, ZDOCK sampling technique, and clustering guided by the DFIRE statistical energy function. Proteins. 2005;60:314–318. doi: 10.1002/prot.20576. [DOI] [PubMed] [Google Scholar]
- 42.Liang S, Meroueh SO, Wang G, Qiu C, Zhou Y. Consensus scoring for enriching near-native structures from protein-protein docking decoys. Proteins. 2009;75:397–403. doi: 10.1002/prot.22252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Moont G, Gabb HA, Sternberg MJ. Use of pair potentials across protein interfaces in screening predicted docked complexes. Proteins. 1999;35:364–373. [PubMed] [Google Scholar]
- 44.Lu H, Lu L, Skolnick J. Development of unified statistical potentials describing protein-protein interactions. Biophys J. 2003;84:1895–1901. doi: 10.1016/S0006-3495(03)74997-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chuang GY, Kozakov D, Brenke R, Comeau SR, Vajda S. DARS (Decoys As the Reference State) potentials for protein-protein docking. Biophys J. 2008;95:4217–4227. doi: 10.1529/biophysj.108.135814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Comeau SR, Kozakov D, Brenke R, Shen Y, Beglov D, Vajda S. ClusPro: performance in CAPRI rounds 6-11 and the new server. Proteins. 2007;69:781–785. doi: 10.1002/prot.21795. [DOI] [PubMed] [Google Scholar]
- 47.Mintseris J, Pierce B, Wiehe K, Anderson R, Chen R, Weng Z. Integrating statistical pair potentials into protein complex prediction. Proteins. 2007;69:511–520. doi: 10.1002/prot.21502. [DOI] [PubMed] [Google Scholar]
- 48.Lo Conte L, Chothia C, Janin J. The atomic structure of protein-protein recognition sites. J Mol Biol. 1999;285:2177–2198. doi: 10.1006/jmbi.1998.2439. [DOI] [PubMed] [Google Scholar]
- 49.Brenke R, Hall DR, Chuang GY, Comeau SR, Beglov D, Vajda S, Kozakov D. Application of asymmetric statistical potentials to antibody-antigen docking. Bioinformatics. 2012;28:2608–2614. doi: 10.1093/bioinformatics/bts493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Huang SY, Zou X. An iterative knowledge-based scoring function for protein-protein recognition. Proteins. 2008;72:557–579. doi: 10.1002/prot.21949. [DOI] [PubMed] [Google Scholar]
- 51.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ravikant DV, Elber R. PIE-efficient filters and coarse grained potentials for unbound protein-protein docking. Proteins. 2010;78:400–419. doi: 10.1002/prot.22550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schneidman-Duhovny D, Inbar Y, Nussinov R, Wolfson HJ. PatchDock and SymmDock: servers for rigid and symmetric docking. Nucleic Acids Res. 2005;33:W363–367. doi: 10.1093/nar/gki481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ravikant DV, Elber R. Energy design for protein-protein interactions. J Chem Phys. 2011;135:065102. doi: 10.1063/1.3615722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Fernandez-Recio J, Totrov M, Abagyan R. ICM-DISCO docking by global energy optimization with fully flexible side-chains. Proteins. 2003;52:113–117. doi: 10.1002/prot.10383. [DOI] [PubMed] [Google Scholar]
- 56.Lensink MF, Mendez R, Wodak SJ. Docking and scoring protein complexes: CAPRI 3rd Edition. Proteins. 2007;69:704–718. doi: 10.1002/prot.21804. [DOI] [PubMed] [Google Scholar]
- 57.Mendez R, Leplae R, Lensink MF, Wodak SJ. Assessment of CAPRI predictions in rounds 3-5 shows progress in docking procedures. Proteins. 2005;60:150–169. doi: 10.1002/prot.20551. [DOI] [PubMed] [Google Scholar]
- 58.Kozakov D, Clodfelter KH, Vajda S, Camacho CJ. Optimal clustering for detecting near-native conformations in protein docking. Biophys J. 2005;89:867–875. doi: 10.1529/biophysj.104.058768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Li L, Chen R, Weng Z. RDOCK: refinement of rigid-body protein docking predictions. Proteins. 2003;53:693–707. doi: 10.1002/prot.10460. [DOI] [PubMed] [Google Scholar]
- 60.Andrusier N, Nussinov R, Wolfson HJ. FireDock: Fast interaction refinement in molecular docking. Proteins. 2007;69:139–159. doi: 10.1002/prot.21495. [DOI] [PubMed] [Google Scholar]
- 61.Kozakov D, Schueler-Furman O, Vajda S. Discrimination of near-native structures in protein-protein docking by testing the stability of local minima. Proteins. 2008;72:993–1004. doi: 10.1002/prot.21997. [DOI] [PMC free article] [PubMed] [Google Scholar]


